Abstract
In the case of the point defect in a crystal, the inverse Radon’s problem in X-ray diffraction microtomography has been solved. As is known, the crystal-lattice defect displacement field function f(r) = h·u(r) determines phases − (±h)-structure factors incorporated into the Takagi–Taupin equations and provides the 2D image patterns by diffracted and transmitted waves propagating through a crystal (h is the diffraction vector and u(r) is the displacement field crystal-lattice-defects vector). Beyond the semi-kinematical approach for obtaining the analytical problem solution, the difference-equations-scheme of the Takagi–Taupin equations that, in turn, yield numerically controlled-accuracy problem solutions has been first applied and tested. Addressing the inverse Radon’s problem solution, the χ2-target function optimization method using the Nelder–Mead algorithm has been employed and tested in an example of recovering the Coulomb-type point defect structure in a crystal Si(111). As has been shown in the cases of the 2D noise-free fractional and integrated image patterns, based on the Takagi–Taupin solutions in the semi-kinematical and difference-scheme approaches, both procedures provide the χ2-target function global minimum, even if the starting-values of the point-defect vector is chosen rather far away from the reference up to 40% in relative units. In the cases of the 2D Poisson-noise image patterns with noise levels up to 5%, the figures-of-merit values of the optimization procedures by the Nelder–Mead algorithm turn out to be high enough; the lucky trials number is 85%; and in contrast, for the statistically denoised 2D image patterns, they reach 0.1%.
1. Introduction
There is nothing supernova if one says the innovative method of computed X-ray diffraction microtomography promotes ongoing tomorrow’s perspectives for the studies of crystal-lattice-defects, pushing one step further by propelling innovations in the semiconductor materials investigation to a more smart level in fabricating new nanoscaled structures with advanced electronic and optical properties. It will occur due to the development and application of relevant high-resolution X-ray diffraction techniques, reciprocal-space mapping (RSM) [1,2,3,4,5], and computer-aided X-ray diffraction microtomography (XRDMT) [5,6,7,8,9,10]. Both gather the 2D image pattern (IP) information recorded within the reciprocal and direct spaces, and these are utilized to decode the 2D IP data in the materials diagnostics. In the concept of a direct method, by decoding the reference 2D IP data, one can recover the crystal-lattice defect structure (see [9,10]). The latter is solving the inverse Radon problem in the XRDMT using the measured and model-simulated 2D IP data to restore the point defect displacement field function in crystals, where the figure-of-merit (FOM) value of recovery depends on the noise level of the 2D Poisson noise IP data. As was shown in [10], the noise- filtering of the 2D IP data with 3–10% noisy levels yields a reduction in the noise level of the order of their values, at least decreasing the convergence FOMs in processing the χ2-target function optimization. One have demonstrated that the 2D IP data denoising effect is effective and can be achieved by statistically averaging several noise-contaminated 2D IP data sets [10].
Further, one uses the term “denoising the 2D IP data” as a sense of digitally noisy filtering without harming the reference signal in the 2D detector pixel. On the contrary, some noisy-filtering methods [11,12,13,14], e.g., the singular-value decomposition-based denoising method [11], the convolutional neural networks [12], bilateral filtering [13], and Hamming’s method [14], lead to uncontrolled digital accuracy of the reference 2D IP data in the post-processing stage.
The present study is a comprehensive exploration of recovering the nanoscale point defect structure in the case of a spherical inclusion incorporated in the middle of the plane-parallel plate of crystal Si(111). An incident X-ray radiation is the monochromatic linear-polarized plane wave with wavelength λ = 0.0709 nm, the X-ray extinction length Λ = 36.287 μm, the diffraction vector is the Bragg angle θB = 10.65°.
The displacement field function around the spherical inclusion located at point r = r0 is given by the Coulomb-type function.
where
Hereafter, the thin crystal Si(111) is the plane-parallel plate, and the sample thickness T is assumed to be Λ. Each of the integrated (entire) 2D IP data frames simulated with square lateral dimension contains 182 182 pixels. Accordingly, the linear size of each pixel is about 0.4 μm. In accordance with the characteristics of ESRF-Grenoble synchrotron facilities, the spatial resolution of the CCD hybrid detectors employed at the X-ray diffraction tomography beamlines is about 1 μm, the X-ray flux are about 103 per pixel, and the exposure time is 0.1 sec. per 2D IP data frame.
The investigation goal is the comprehensive recovery of the reference vector characterizing the displacement field function (1) being retrieved with controlled by FOM-value digital accuracy using the modeling of 2D Poisson-noise IP data frames in both approaches of the semi-kinematical [10] and the difference-scheme [15] for solving the Takagi–Taupin equations in the XRDMT optics.
The schematic of the XRDMT setup is drawn in Figure 1.
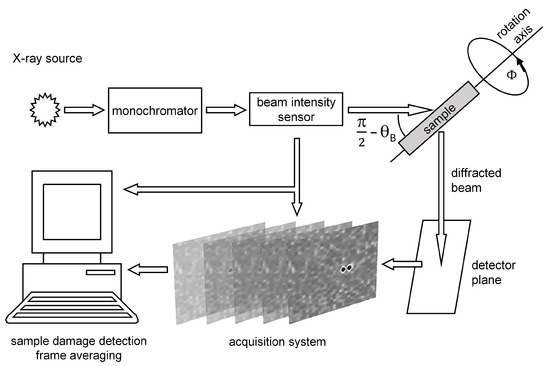
Figure 1.
Schematic of setup for acquiring the 2D IP data in the frame multimode regime The frameset is for the sample rotation angle Φ to be fixed.
It allows bringing the 2D IP data to the frame multimode regime when several 2D IP data frames can be recorded in the sample rotation angle value to be fixed. Such a setup is necessary for improving the single-pixel signal-to-noise ratio by acquiring the 2D IP data frames.
In general, the χ2-target function is defined as
Here, is the reference-type 2D noisy IP frame for the sample rotation angle . is the modeling 2D IP frame for ; the current fitting-vectors ={} of the displacement function , = (0, 0, z0) is the defect position in a sample, z0 = T/2, integer k is the current iteration number, k = 1, 2, 3, …, K, K is the cycle termination number. The function are determined by the vector } in the units of the extinction length Λ/π.
To control fitting the χ2-target function, , one introduces the fitting FOM parameter, defined as
Using the semi-kinematical diffraction optics approach [9] to model the functions , and , one has launched fitting the χ2-target according to the procedure (2), which aims to recover the Coulomb-type point-defect function . The sample Si(111) is the rectangular prism in the coordinates (X, Y, Z) nominated in the units of Λ/π, 0 ≤ Z ≤ π, −π ≤ X(T) ≤ π, −π≤ Y(T) ≤ π, T = . Total grid crystal sizes along the dimensionless coordinates (X, Y, Z) are 61 × 61 × 21. The case of the Poisson-noise with levels of 1% and 3% has been taken into consideration. For processing the χ2-target function for simulating the 2D Poisson-noise IP data frames, one has employed the Poisson random value generator [16].
2. The Recovery Issue in the XRDMT Results
2.1. Semi-Kinematical Diffraction Optics Approach
We begin a computer-aided recovery of the displacement field function (1) using the semi-kinematical diffraction optics approach (cf. [9]). As explained in [4,9], the theoretical approach is valid for describing the 2D frame area directly linked to the nearby vicinity area of the crystal-lattice defect. As was shown in [9], the semi-kinematic approach describes diffraction scattering of X-rays by a Coulomb-type point defect as a purely phase object in a thin crystal. This allows us to provide visualization of the defect in the 2D-IP region, which corresponds to the so-called direct defect contrast [4].
In proceeding with the χ2-target function , one applies a joint quasi-Newton–Levenberg–Marquardt–simulated annealing (NLMSA) algorithm (cf. in [9,17,18,19] for details). In this case, the lateral sizes of the calculated 2D IP frames are 61 × 61 grid pixels.
In the previous work [10], the calculations of the 2D IP frames, the Poisson-noise levels of 2% and 4%, and the sample rotation angle range Φ = {−20°, 20°}, have been performed and analyzed. Here, as an illustration, one presents and analyzes the simulated results for the 2D IP frames at the Poisson-noise levels of 1% and 3%.
In Figure 2, there are the 2D IP frames calculated using the semi-kinematical approach of the X-ray diffraction optics theory.
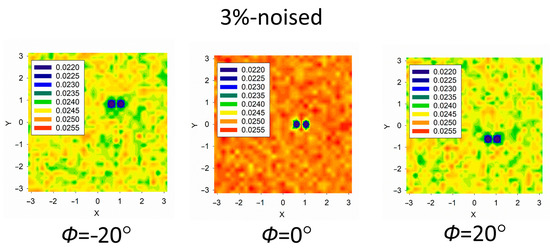
Figure 2.
The 2D Poisson-noise IP frames were calculated using the semi-kinematical approach. The noise level is 3%. The sample rotation angles Φ are −20° (left), 0° (middle), and 20° (right). The dimensionless coordinates (X, Y) are given in the units of Λ/π.
For recovering the displacement field function (1) in accordance with processing the χ2-target function (2), the 2D Poisson-noise IP frames with noise levels of 1% and 3% have been employed, which were calculated in the semi-kinematical approach of the diffraction optics.
The corresponding results for retrieving the reference vector (true) of the point defect displacement function (1) in dependence of the 2D Poisson-noise IP frame quantity are listed in Table 1.

Table 1.
Results of recovering the reference vector (true). The noise levels of the 2D Poisson-noise frames under consideration are given in the first column. The start vectors (start) have been chosen randomly within 40% around The sample rotation angle Φ area is lying from −20° to +20°. Depending on the number of sample rotation angles equidistantly lying in the interval {−20° to +20°}, the 2D Poisson-noise IP frame quantity is pointed out in the second column. The retrieved vectors are given in the third column.
Lucky trials are assumed to have FOM values less than 0.1.
Lucky trials, the last column, are assumed to have the FOM values less than 0.1.
Analyzing the datasets in Table 1, one can see a clear tendency when the 2D Poisson-noise IP frame quantity increases, from the number 3 to 31, the corresponding FOM -values decrease, i.e., it does mean the quality of lucky trials is improved. This allows us to conclude that the recovery strategy of further increasing of quantity of the 2D Poisson-noise IP frames would inevitably enhance the digital accuracy of recovering the reference (true).
2.2. The Diffraction Optics Rigorous Approach, the Takagi–Taupin Equations in the Finite Differences
In the differential form, the canonic Takagi–Taupin takes the form (cf. [20,21])
where (s0, sh) is the oblique-coordinate system, .
The boundary conditions for the wave field electric vector take the form
Here above, the deviation parameter α = (2k h + h2)/2k2 = –sin(2θB)ΔθB is a measure of the angular deviation ΔθB of an incident X-ray monochromatic plane-wave from the exact Bragg angle θB. Coefficient χ0 is the zero-Fourier- and χh, are the h-, –h-Fourier components of electric susceptibility χ(r) for a perfect crystal. In our case, the scalar function f(r) is the point defect displacement field function defined by Equation (1).
Recently in [15], a numerical solution of the boundary-valued Cauchy problem (4)–(5) with the point defect displacement field function (1) has been built up for the sample rotation angle Φ = 0° using the Takagi–Taupin equations in the finite differences. The important thing is that the numerical solutions of the boundary-valued Cauchy problem (4)–(5) with a controlled accuracy of 10−4 have been obtained and digitally controlled by the criterion for thin (non-absorbing) crystal Si(111)
where I0(s0,sh) and Ih(s0,sh) are the transmitted and diffracted intensities at the current point s0,sh.
In the case of using the semi-kinematic theory approach, the Levenberg-Marquardt algorithm was used to solve the problem in combination with the simulated annealing method (qNLMSA) [9]. Such a combination of the above methods allows the program to overcome local minima and increases the robustness of the optimization (advantages), but at the expense of increasing the total number of iterative steps (disadvantage).
A certain limitation for using the qNLMSA method is the number of pixels used in the 2D IP formation, since the size of the arrays (the first derivative Jacobian matrices and the second derivative Hessian matrices) can complicate and/or disrupt the qNLMSA program. In our case, when the image is constructed as 2D frames with sizes of 182 × 182 pixels, other methods that do not use finite-difference derivative matrices should be chosen. In our study, the highly robust Nelder–Mead (N-M) polyhedron method was applied [22].
As an example, the 2D noise-free IP frame calculated along with the numerical solution of the boundary-valued Cauchy problem (4)–(5) is shown in Figure 3, top left in the linear pixel size units; the linear pixel size is 0.4 μm; the total image size is 182 × 182. Appropriately, going back to our work, the 2D Poisson-noise IP frames with a noise level of 5% have been simulated, see Figure 3, top left, using the Poisson random value generator [14] many times, namely: n = {1, 102, 104}, see, e.g., the 2D Poisson-noise IP frame in Figure 3 bottom left for n = 1.
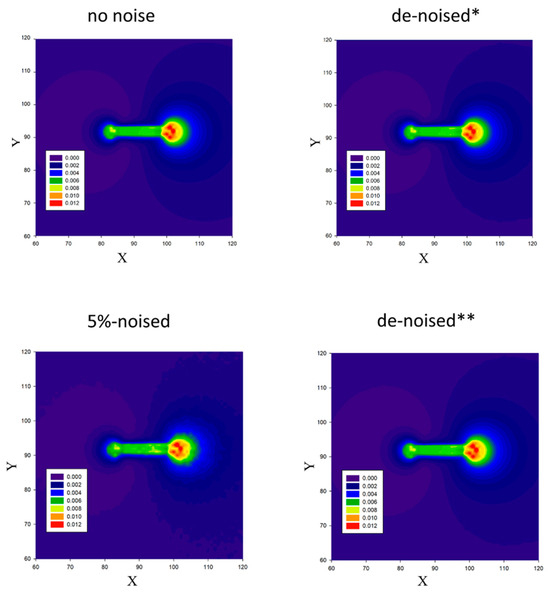
Figure 3.
The 2D no-noise IP frame (top left) and the 2D 5%-Poisson-noise IP frame (bottom left). The denoised * and denoised ** 2D IP frames are assigned for n = 102 top right and n = 104 bottom right, respectively. The sample rotation angle is Φ = 0°. The coordinates (X, Y) are given in linear pixel-size units. The pixel numbers (91,91) correspond to the beginning of the coordinate system (x, y). The linear pixel size is 0.4 μm.
Afterward, the obtained 2D Poisson-noise IP frames were denoised according to the statistical average method [9]. At the final stage, post-processing the χ2-target function K, aiming to recover the reference vector (true), we employed the Nelder–Mead (N-M) algorithm [22]. The values of the start vector (start) were randomly chosen within the 40% range around the reference vector (true). The flow equation for applying the (N-M) algorithm is derived in Appendix A, and some details of the computer (N-M) algorithm script are given in Appendix B.
The post-processing results for recovering the reference vector (true) of the point defect displacement field function (1) for the sample rotation angle Φ = 0° are listed in Table 2.

Table 2.
Results of the post-processing vector K. The values of the start vectors (start) were chosen randomly within the 40% range around the true vector . Lucky trials are assumed to be the FOM less than 0.02.
As is seen from the dataset in Table 2, there is a stable tendency to decrease the FOM with increasing the statistically average 2D IP frame number. Hence, one may claim the statistical average procedure [9] applied to the 2D Poisson-noise IP frames allows us to enhance the accuracy of recovering the point defect displacement field function by improving the signal-to-noise ratio in the computer-aided XRDMT.
3. Discussion
In the present exploration, based on the Poisson-noise statistical properties, there was an aim to exploit them and, if possible, to solve the inverse Radon problem of the XRDMT diagnostics in the case of the Coulomb-type point defect displacement field function . The latter is characterized by the three-parameter reference vector (true). For the first time, in the case of the 2D Poisson-noise IP frames-entire area imaging (see Figure 3), higher digital accuracy recovery of the point defect structure has been achieved by applying the statistical average method [9]. By using the (N-M) algorithm [22], recovering the Coulomb-type point defect structure has been performed.
It is worth emphasizing that, in contrast to using the semi-kinematic theory approach, in manipulating the 2D entire imaging of the Coulomb-type point defect in a crystal Si(111), one has used the robust Nelder–Mead (N-M) polyhedron method, which allows us to avoid the problems of using the qNLMSA algorithm in processing the χ2-target function optimization. The conducted research allows us to claim that, as large as possible, the number of 2D IP frames recorded with a noise counting level of up to 5% secures the digital-accuracy information and decreases the FOM with increasing the 2D IP frames to be statistically averaged (see Table 2).
Here, it is appropriate to emphasize that the key point in this study, which made it possible to improve the digital accuracy of solving the inverse Radon problem in the scope of the XRDMT technology, is the noise-filtering method of the direct statistical averaging of the 2D Poisson-noise entire area imaging frames proposed (see [9] for details).
As to collecting a large number of the 2D IP frames for employing (switching on) the statistical average procedure [9], it is worth keeping in mind that the 2D IP frame registration rate by the 2D CCD hybrid pixel detector has to be high enough. The latter can be altered within a wide range from one kHz to tens of MHz, controlled by the X-ray intensity value per detector pixel. Supposing the exposure X-ray time is about 0.1 sec per one 2D IP frame, one may design one hundred of the 2D IP frames, at least if each pixel catches 103 photons/sec in the functional pattern part of the 2D IP frames to be collected.
It is interesting that beyond recovering the crystal-lattice defects, the 2D IP frame-by-frame processing allows us to unveil the radiation crystal atomic structure damage by comparing the 2D IP frames one after another and then matching them at the detector registration panel by applying the DATCMP program [23].
4. Conclusions
In this paper, the goal of our study is to unveil a good XRDMT method for purposes of the digital characterization of the crystal-lattice defect structures. The key point of the XRDMT is the fact that it provides a robust, unambiguous procedure to solve a crystal-lattice defect structure with digital accuracy. The test above completes our previous studies in the field of recovering the nanoscale defect structure in crystals.
In contrast to the work [9], the main advance of the present study is the (N-M) algorithm [22] applied for processing the χ2- target function has allowed us to solve the inverse Radon problem of the XRDMT en Gros in the case of a set of the 2D Poisson-noise entire area imaging frames recorded.
It is essential for future sequent works that this study carried out in this paper shows the way and opens some opportunities to employing the XRDMT technique as an effective digital tool for exploring the crystal-lattice defect structures, such as various clusters, small dislocation loops, quantum wells, and quantum wires.
Author Contributions
Conceptualization, F.N.C.; data curation, V.V.V.; software, P.V.K.; formal analysis, F.N.C. and P.V.K.; investigation, P.V.K. and V.V.V.; software, V.V.V.; writing—original draft, F.N.C., P.V.K. and V.V.V.; writing—review and editing, F.N.C., P.V.K. and V.V.V.; visualization, P.V.K. and V.V.V.; supervision, F.N.C.; project administration, F.N.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation within the state assignment FSRC «Crystallography and Photonics» RAS (X-ray diffraction microtomography data analysis).
Data Availability Statement
Data are contained within this article.
Acknowledgments
The authors are deeply indebted to Asadchikov, V.E., and Zolotov, D.A., for fruitful discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
To retrieve the reference vector (true) via processing of the χ2-target function , (2) by the (N-M) algorithm [22], one employs the flow equation as follows:
Do
- –
- Assign the starting vector .
- –
- Evaluate the differential according to the (N-M) algorithm activated, 1 ≤ k ≤ K.
- –
- Evaluate the FOM value Ɽk (3) for each k.
The (N-M) algorithm is in action until the 10−10.
- –
- Terminate processing the χ2-target function which becomes less than 10−10 and or the FOM-value becomes less than 10−6 for k = K]
End Do.
Based on the flow equation, processing to recover the vector has been carried out for the 2D no-noised and de-noised IP frames collected. The (N-M) algorithm-program source code has been implemented in Fortran linked with C++ for the difference-scheme diffraction optics approach to solving the Takagi–Taupin equations for revealing the point defect displacement function as the dll (dynamic link library). The input data program made requires the 2D IP data frames for the sample rotation angles array ; the relative noise level values array to add the Poisson noise to the reference 2D IPs frames, and the starting .
In each pixel of the reference 2D IP frames, the Poisson noise has been added using the Devroye algorithm code [15]. In the final stage, this work program yields the vector to be fitted the best concerning the reference vector (true).
Appendix B
The Nelder–Mead algorithm [22] application is in the sequential movement and deformation of the simplex around the extremum of the χ2-target function
Let it be necessary to find the unconditional minimum of the χ2-target function of the n-variables.
The (N-M) algorithm parameters are the following:
- (i)
- the reflection parameter α > 0 was selected as 1.0.
- (ii)
- the compression factor β > 0 was selected as 0.5.
- (iii)
- the stretching factor γ > 0 was selected as 2.0.
The following steps in the search are carried out:
- Preparing step: select (n + 1)-points of vector i = (pi(1), pi(2), …, pi(n)), i = 1, 2, …, n + 1, to form a simplex of the n-dimensional space. At these vectors, the values of the -function are calculated: 1 = , 2 = , …, n + 1 = .
- Sort step: from the simple vertices, one chooses three vectors: h with the largest of the selected values of the function h, g with the next largest value g (i) and l with the smallest value of the function l.
- Find the gravity center of all the vectors, with the exception of h: c=.
- Reflection step: one reflects the vector h in relation to xc with the coefficient α and gets the vector r calculating the function r = (r). The new vector p-coordinates are calculated using the formula: r = (1 + α) c − α h.
- Next step: one looks at how much one has managed to reduce the -function looking r –value in the rows h, g, l.If r < l. If the direction is right, one can increase the step, and one can do the “stretching factor” step. The next vector will be e = (1 − γ) c + γ r and e = (e). If e < r, one expands the simplex to this vector: assign h the value of e and go to step 9.If r < e, then one moved too far: assign h the value of r and go to step 9.If l < r < g, then the choice of a vector is not bad (the new one is better than the previous two). One assigns h the value of r and goes to step 9.If g < r < h, then swap the values h and r. One also needs to swap the values r and h, and then one goes to step 6.If h < r, then, one goes to step 6.
- Compression step: one chooses the vector s = β h + (1 − β) c and calculates the value (s).
- If s < h, one assigns {h} as {s} and goes to step 9.
- If s > h, the initial {s}-point set was chosen to be the best. One does the “global simplex compression” for the vector with the smallest value l: i ← l + (i − l)/2, i ≠ l.
- Last step: a convergence verification. One estimates the variance of a set of vectors . The aim is to check the mutual vicinity of the simplex vertices that are assumed to be vector vicinity about the desired value. If the accuracy is not good enough, one continues further processing, beginning from step 2.
In our study, in the case of the crystal-lattice point defect (1), the vector in search is the space dimension n equal to 3.
References
- Bowen, D.K.; Tanner, B.K. High Resolution X-ray Diffractometry and Topography; Taylor & Francis: New York, NY, USA, 1998. [Google Scholar]
- Darowski, N.; Pietsch, U.; Zhuang, Y.; Zerlauth, S.; Bauer, G.; Lübbert, D.; Baumbach, T. In-plane strain and strain relaxation in laterally patterned periodic arrays of Si/SiGe quantum wires and dot arrays. Appl. Phys. Lett. 1998, 73, 806–808. [Google Scholar] [CrossRef]
- Pavlov, K.M.; Punegov, V.I. Statistical dynamical theory of X-ray diffraction in the Bragg case: Application to triple-crystal diffractometry. Acta Crystallogr. A 2000, 56, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Authier, A. Dynamical Theory of X-ray Diffraction; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Benediktovitch, A.; Feranchuk, I.; Ulyanenkov, A. Theoretical Concepts of X-ray Nanoscale Analysis; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Ludwig, W.; Cloetens, P.; Härtwig, J.; Baruchel, J.; Hamelin, B.; Bastie, P. Three-dimensional imaging of crystal defects by ‘topo-tomography. J. Appl. Crystallogr. 2001, 34, 602–607. [Google Scholar] [CrossRef]
- Danilewsky, A.N.; Wittge, J.; Croell, A.; Allen, D.; McNally, P.; Vagovič, P.; dos Santos Rolo, T.; Li, Z.; Baumbach, T.; Gorostegui-Colinas, E.; et al. Dislocation dynamics and slip band formation in silicon: In-situ study by X-ray diffraction imaging. J. Crystallogr. Growth 2011, 318, 1157–1163. [Google Scholar] [CrossRef]
- Hänschke, D.; Danilewsky, A.; Helfen, L.; Hamann, E.; Baumbach, T. Correlated three-dimensional imaging of dislocations: Insights into the onset of thermal slip in semiconductor wafers. Phys. Rev. Lett. 2017, 119, 215504. [Google Scholar] [CrossRef] [PubMed]
- Chukhovskii, F.N.; Konarev, P.V.; Volkov, V.V. Towards a solution of the inverse X-ray diffraction tomography challenge: Theory and iterative algorithm for recovering the 3D displacement field function of Coulomb-type point defects in a crystal. Acta Crystallogr. A 2020, 76, 16–25. [Google Scholar] [CrossRef] [PubMed]
- Chukhovskii, F.N.; Konarev, P.V.; Volkov, V.V. Denoising of the Poisson-noise statistics 2D image patterns in the computer X-ray diffraction tomography. Crystals 2023, 13, 561. [Google Scholar] [CrossRef]
- Yang, W.; Hong, J.-Y.; Kim, J.-Y.; Paik, S.; Lee, S.H.; Park, J.-S.; Lee, G.; Kim, B.M.; Jung, Y.-J. A novel singular value decomposition- based denoising method in 4-dimensional computed tomography of the brain in stroke patients with statistical evaluation. Sensors 2020, 20, 3063. [Google Scholar] [CrossRef] [PubMed]
- Hendriksen, A.A.; Bührer, M.; Leone, L.; Merlini, M.; Vigano, N.; Pelt, D.M.; Marone, F.; di Michiel, M.; Batenburg, K.J. Deep denoising for multi-dimensional synchrotron X-ray tomography without high-quality reference data. Sci. Rep. 2021, 11, 11895. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Schumacher, T. Improved denoising of structural vibration data employing bilateral filtering. Sensors 2020, 20, 1423. [Google Scholar] [CrossRef] [PubMed]
- Hamming, R.W. Numerical Methods for Scientists and Engineers; Mc Graw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Grigorev, V.A.; Konarev, P.V.; Chukhovskii, F.N.; Volkov, V.V. X-ray, Synchrotron and Neutron Techniques. J. Surf. Investig. 2023, in press. [Google Scholar]
- Devroye, L. The computer generation of Poisson random variables. Computing 1981, 26, 197–207. [Google Scholar] [CrossRef]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Takagi, S. Dynamical theory of diffraction applicable to crystals with any kind of small distortion. Acta Crystallogr. 1962, 15, 1311–1312. [Google Scholar] [CrossRef]
- Taupin, D. Théorie dynamique dela ladiffraction des rayons X par les cristaux déformés. Bull. Soc. Fr. Miner. 1964, 87, 469–511. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R.A. Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Franke, D.; Kikhney, A.G.; Svergun, D. Automated acquisition and analysis of small angle X-ray scattering data. Nucl. Instrum. Methods Phys. Res. A 2012, 689, 52–59. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).