Tailoring the Graphene Properties for Electronics by Dielectric Materials
Abstract
:1. Introduction
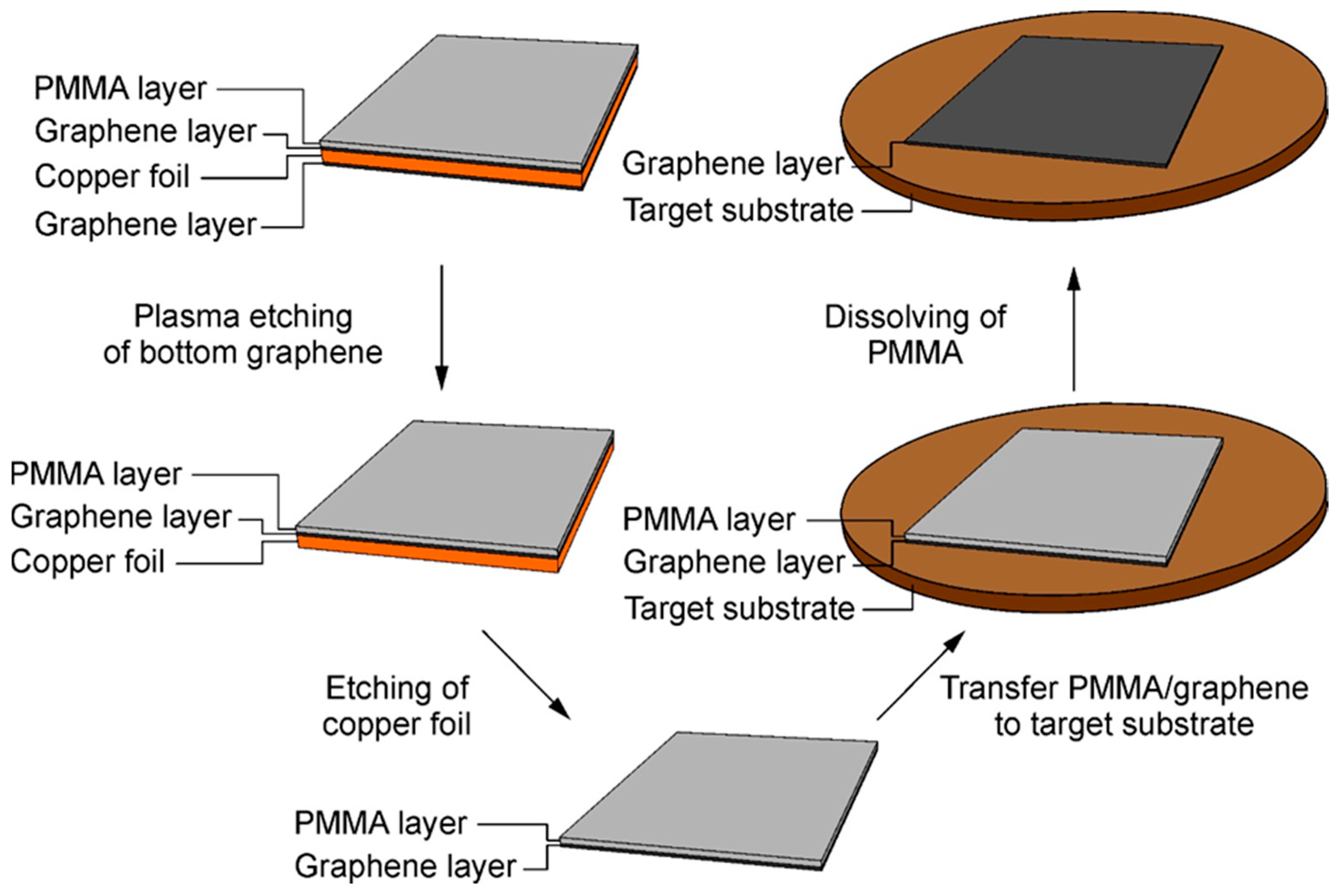
2. Materials and Methods
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef]
- Castriota, M.; Politano, G.G.; Vena, C.; De Santo, M.P.; Desiderio, G.; Davoli, M.; Cazzanelli, E.; Versace, C. Variable Angle Spectroscopic Ellipsometry investigation of CVD-grown monolayer graphene. Appl. Surf. Sci. 2019, 467–468, 213–220. [Google Scholar] [CrossRef]
- Xia, Y.; Gao, W.; Gao, C. A Review on Graphene-Based Electromagnetic Functional Materials: Electromagnetic Wave Shielding and Absorption. Adv. Funct. Mater. 2022, 32, 2204591. [Google Scholar] [CrossRef]
- Lin, C.-H.; Chen, Y.-S.; Lin, J.-T.; Wu, H.C.; Kuo, H.-T.; Lin, C.-F.; Chen, P.; Wu, P.C. Automatic Inverse Design of High-Performance Beam-Steering Metasurfaces via Genetic-type Tree Optimization. Nano Lett. 2021, 21, 4981–4989. [Google Scholar] [CrossRef]
- Liao, C.; Li, Y.; Tjong, S.C. Graphene Nanomaterials: Synthesis, Biocompatibility, and Cytotoxicity. Int. J. Mol. Sci. 2018, 19, 3564. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef]
- Narayan, J.; Bezborah, K. Author response for “Recent advances in the functionalization, substitutional doping and applications of graphene/graphene composite nanomaterials”. RSC Adv. 2024, 14, 13413–13444. [Google Scholar] [CrossRef]
- Döğüşcü, D.K.; Sarı, A.; Hekimoğlu, G. Effects of graphene doping on shape stabilization, thermal energy storage and thermal conductivity properties of PolyHIPE/PEG composites. J. Energy Storage 2024, 76, 109804. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Bolotin, K.; Sikes, K.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Özyilmaz, B.; Jarillo-Herrero, P.; Efetov, D.; Kim, P. Electronic transport in locally gated graphene nanoconstrictions. Appl. Phys. Lett. 2007, 91, 192107. [Google Scholar] [CrossRef]
- Lherbier, A.; Blase, X.; Niquet, Y.-M.; Triozon, F.; Roche, S. Charge transport in chemically doped 2D graphene. Phys. Rev. Lett. 2008, 101, 036808. [Google Scholar] [CrossRef]
- Berger, C.; Song, Z.M.; Li, T.B.; Li, X.B.; Ogbazghi, A.Y.; Feng, R.; Dai, Z.N.; Marchenkov, A.N.; Conrad, E.H.; First, P.N.; et al. Ultrathin epitaxial graphite: 2D electron gas properties and a route toward graphene-based nanoelectronics. J. Phys. Chem. B 2004, 108, 19912–19916. [Google Scholar] [CrossRef]
- Bandurin, D.A.; Svintsov, D.; Gayduchenko, I.; Xu, S.G.; Principi, A.; Moskotin, M.; Tretyakov, I.; Yagodkin, D.; Zhukov, S.; Taniguchi, T.; et al. Resonant terahertz detection using graphene plasmons. Nat. Commun. 2018, 9, 5392. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Y.; Tian, C.; Girit, C.; Zettl, A.; Crommie, M.; Shen, Y.R. Gate-Variable Optical Transitions in Graphene. Science 2008, 320, 206–209. [Google Scholar] [CrossRef]
- Shao, Y.; Wang, J.; Wu, H.; Liu, J.; Aksay, I.A.; Lin, Y. Graphene based electrochemical sensors and biosensors: A review. Electroanal. Int. J. Devoted Fundam. Pract. Asp. Electroanal. 2010, 22, 1027–1036. [Google Scholar] [CrossRef]
- Minot, E.D.; Yaish, Y.; Sazonova, V.; McEuen, P.L. Determination of electron orbital magnetic moments in carbon nanotubes. Nature 2004, 428, 536–539. [Google Scholar] [CrossRef]
- Shi, Y.; Dong, X.; Chen, P.; Wang, J.; Li, L.J. Effective doping of single-layer graphene from underlying SiO2 substrates. Phys. Rev. B 2009, 79, 115402. [Google Scholar] [CrossRef]
- Scarfe, S.; Cui, W.; Luican-Mayer, A.; Ménard, J.-M. Systematic THz study of the substrate effect in limiting the mobility of graphene. Sci. Rep. 2021, 11, 8729. [Google Scholar] [CrossRef]
- Van Velson, N.; Zobeiri, H.; Wang, X. Rigorous prediction of Raman intensity from multi-layer films. Opt. Express 2020, 28, 35272–35283. [Google Scholar] [CrossRef]
- Bruna, M.; Ott, A.K.; Ijäs, M.; Yoon, D.; Sassi, U.; Ferrari, A.C. Doping dependence of the raman spectrum of defected graphene. ACS Nano 2014, 8, 7432–7441. [Google Scholar] [CrossRef] [PubMed]
- Mackay, T.G.; Lakhtakia, A. The Transfer-Matrix Method in Electromagnetics and Optics; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Tomaino, J.L.; Jameson, A.D.; Kevek, J.W.; Paul, M.J.; Van Der Zande, A.M.; Barton, R.A.; Lee, Y.S. Terahertz imaging and spectroscopy of large-area single-layer graphene. Opt. Express 2011, 19, 141–146. [Google Scholar] [CrossRef] [PubMed]
- van Exter, M.; Grischkowsky, D. Carrier dynamics of electrons and holes in moderately doped silicon. Phys. Rev. B 1990, 41, 12140. [Google Scholar] [CrossRef] [PubMed]
- Gayduchenko, I.A.; Fedorov, G.E.; Moskotin, M.V.; Yagodkin, D.I.; Seliverstov, S.V.; Goltsman, G.N.; Kuntsevich, A.Y.; Rybin, M.G.; Obraztsova, E.D.; Leiman, V.G.; et al. Manifestation of plasmonic response in the detection of sub-terahertz radiation by graphene-based devices. Nanotechnology 2018, 29, 245204. [Google Scholar] [CrossRef] [PubMed]
- Das Sarma, S.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 2011, 83, 407–470. [Google Scholar] [CrossRef]
- Bukowska, H.; Meinerzhagen, F.; Akcöltekin, S.; Ochedowski, O.; Neubert, M.; Buck, V.; Schleberger, M. Raman spectra of graphene exfoliated on insulating crystalline substrates. New J. Phys. 2011, 13, 063018. [Google Scholar] [CrossRef]
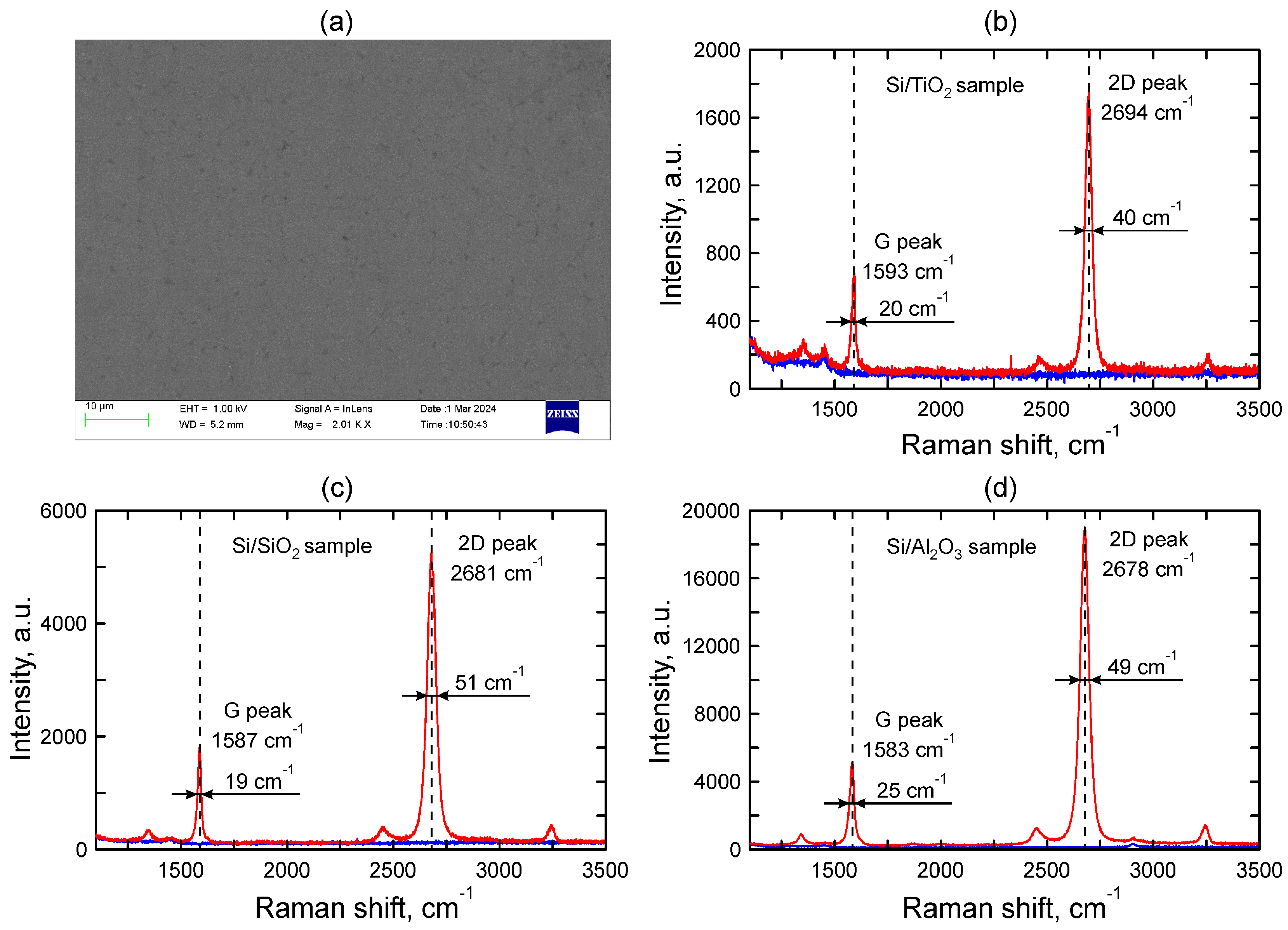
| Graphene on TiO2 | Graphene on SiO2 | Graphene on Al2O3 | |
|---|---|---|---|
| G-peak position (cm−1) | 1593 | 1587 | 1583 |
| FWHM of G-peak (cm−1) | 20 ± 2 | 20 ± 2 | 25 ± 2 |
| 2D-peak position (cm−1) | 2694 | 2681 | 2678 |
| FWHM of 2D-peak (cm−1) | 40 ± 3 | 50 ± 3 | 50 ± 3 |
| I2D/IG | 2.53 | 2.88 | 3.69 |
| ns, 1012/cm2 | 5 ± 1 | 2 ± 0.5 | ±1 |
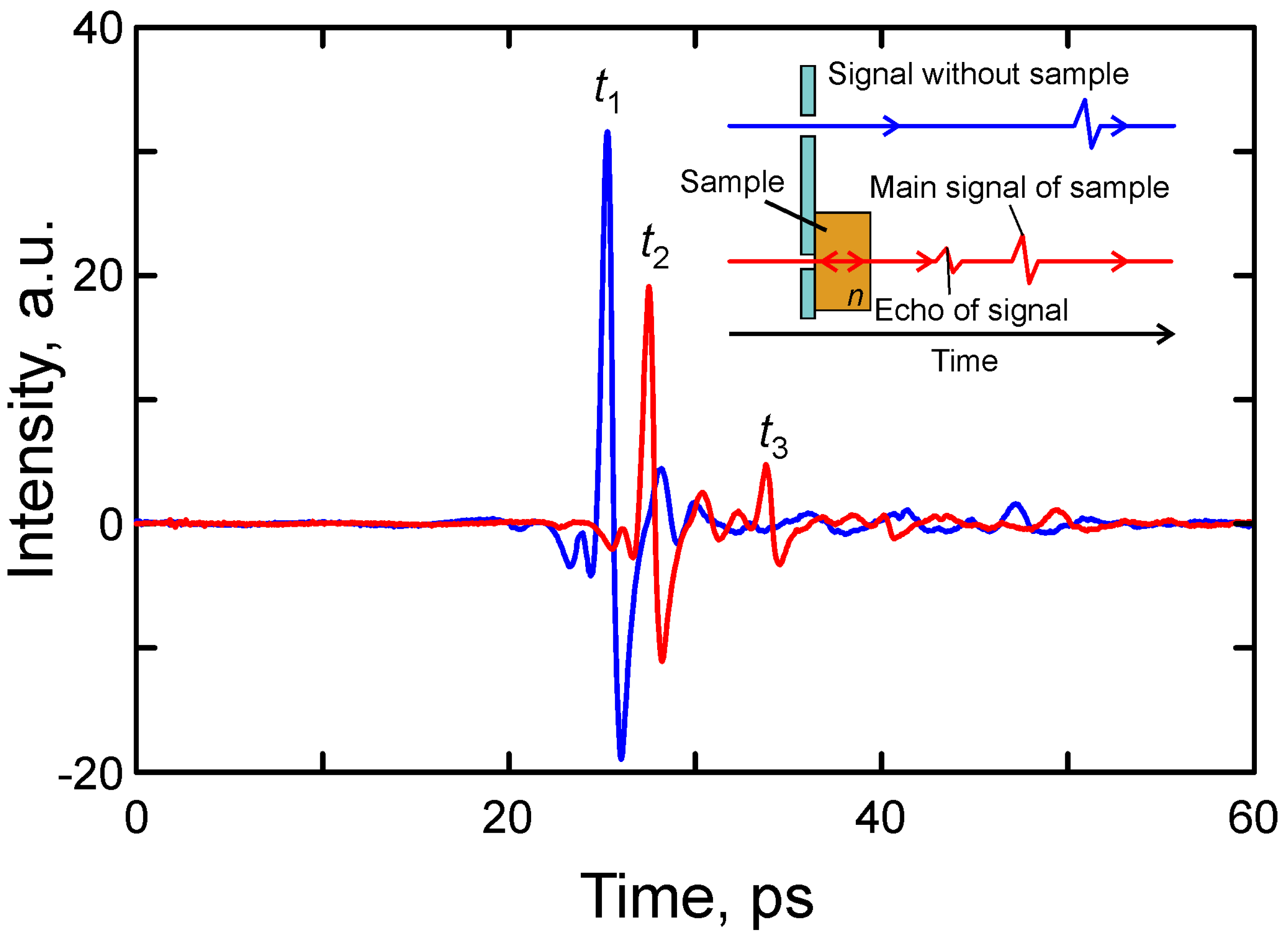
| Si/TiO2 | Si/SiO2 | Si/Al2O3 | |
|---|---|---|---|
| t1, ps | 25.28953 | 25.30211 | 25.25176 |
| t2, ps | 27.51762 | 27.49245 | 27.47986 |
| t3, ps | 33.78651 | 33.66062 | 33.74874 |
| n | 3.46 | 3.45 | 3.46 |
| dcalc, μm | 271.7 | 267.9 | 271.7 |
| dmeas, μm | 275 | 275 | 275 |
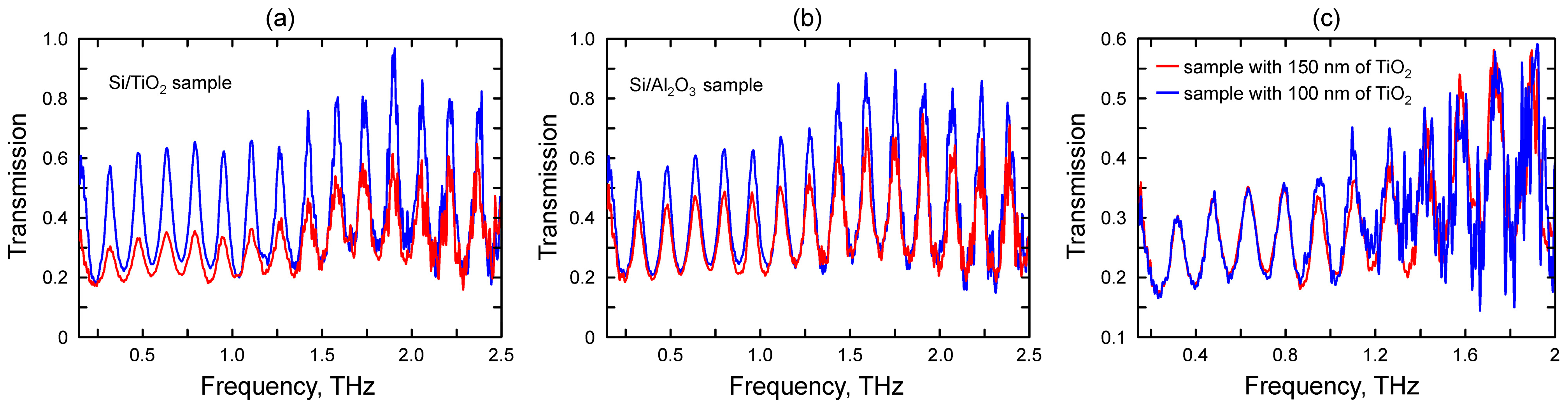
| Drude’s Parameter | Si/TiO2 | Si/SiO2 | Si/Al2O3 |
|---|---|---|---|
| n | 3.46 | 3.45 | 3.46 |
| d, μm | 271.7 | 267.9 | 271.7 |
| τsub, fs | 100 ± 20 | 100 ± 20 | 100 ± 20 |
| σ0, s/m | 11 ± 0.5 | 29 ± 1 | 11 ± 0.5 |
| τgraph, fs | 90 ± 5 | 90 ± 5 | 70 ± 5 |
| Rsheet, Ω/sq | 350 ± 50 | 550 ± 50 | 900 ± 50 |
| ns, 1012/cm2 | 4.5 ± 0.25 | 1.5 ± 0.08 | 0.7 ± 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otoo, I.A.; Saushin, A.; Owusu, S.; Karvinen, P.; Suvanto, S.; Svirko, Y.; Kuzhir, P.; Fedorov, G. Tailoring the Graphene Properties for Electronics by Dielectric Materials. Crystals 2024, 14, 595. https://doi.org/10.3390/cryst14070595
Otoo IA, Saushin A, Owusu S, Karvinen P, Suvanto S, Svirko Y, Kuzhir P, Fedorov G. Tailoring the Graphene Properties for Electronics by Dielectric Materials. Crystals. 2024; 14(7):595. https://doi.org/10.3390/cryst14070595
Chicago/Turabian StyleOtoo, Isaac Appiah, Aleksandr Saushin, Seth Owusu, Petri Karvinen, Sari Suvanto, Yuri Svirko, Polina Kuzhir, and Georgy Fedorov. 2024. "Tailoring the Graphene Properties for Electronics by Dielectric Materials" Crystals 14, no. 7: 595. https://doi.org/10.3390/cryst14070595
APA StyleOtoo, I. A., Saushin, A., Owusu, S., Karvinen, P., Suvanto, S., Svirko, Y., Kuzhir, P., & Fedorov, G. (2024). Tailoring the Graphene Properties for Electronics by Dielectric Materials. Crystals, 14(7), 595. https://doi.org/10.3390/cryst14070595








