Indentation Behavior Assessment of As-Built, Solution, and Artificial Aged Heat-Treated Selective Laser Melting Specimens of AlSi10Mg
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Utilization
2.2. Specimen Preparation Using SLM
2.3. The Heat Treatment Process
2.4. Hardness Indentation Testing and Data Gathering
- σtrue = true stress, and
- εtrue = true strain.
2.5. Finite Element Analysis Simulation
3. Results and Discussion
3.1. Rockwell Hardness Test Results
Effect of Developed Porosity on the Indentation Behavior
3.2. SEM Analysis of Indentation Images
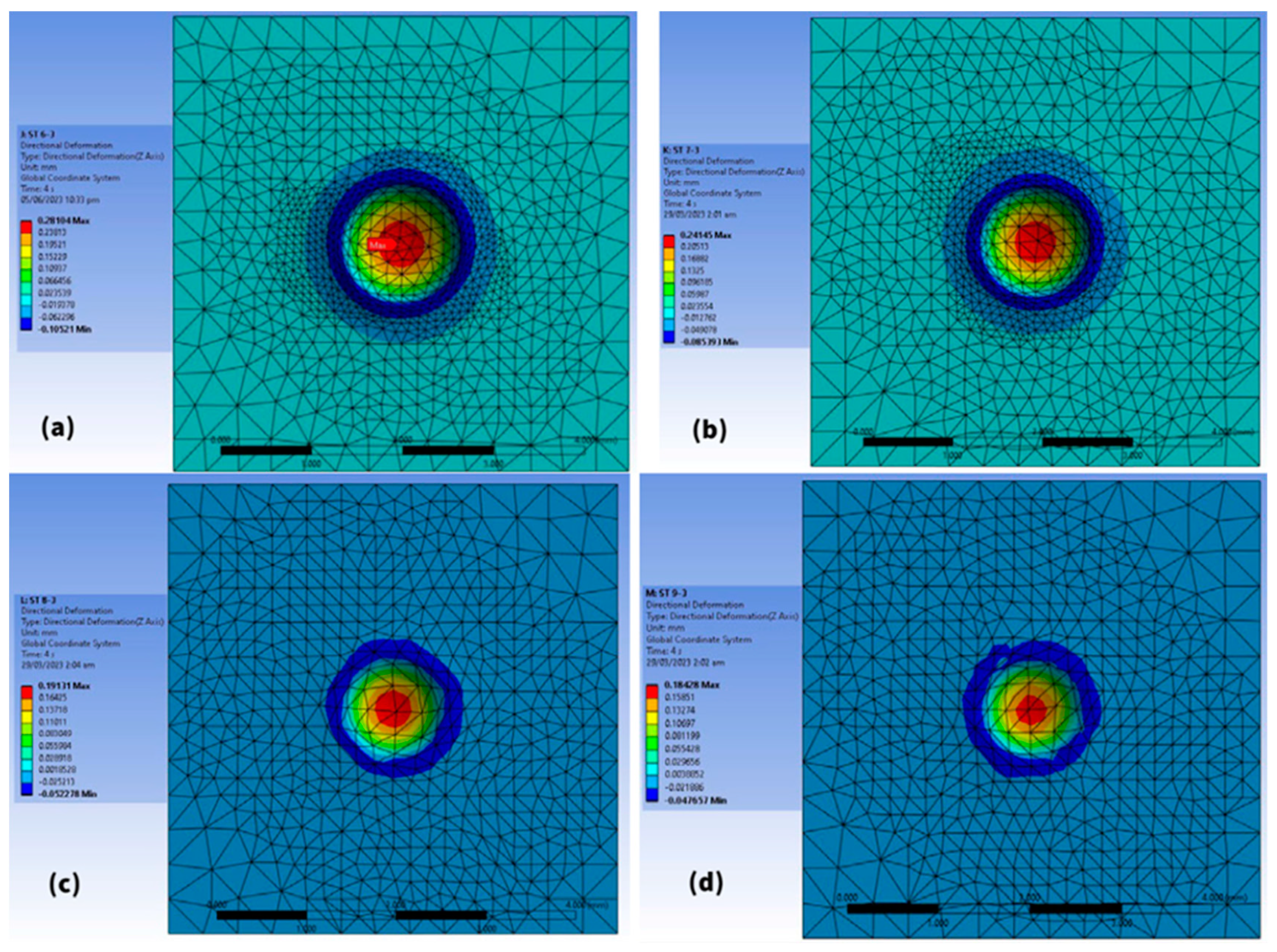
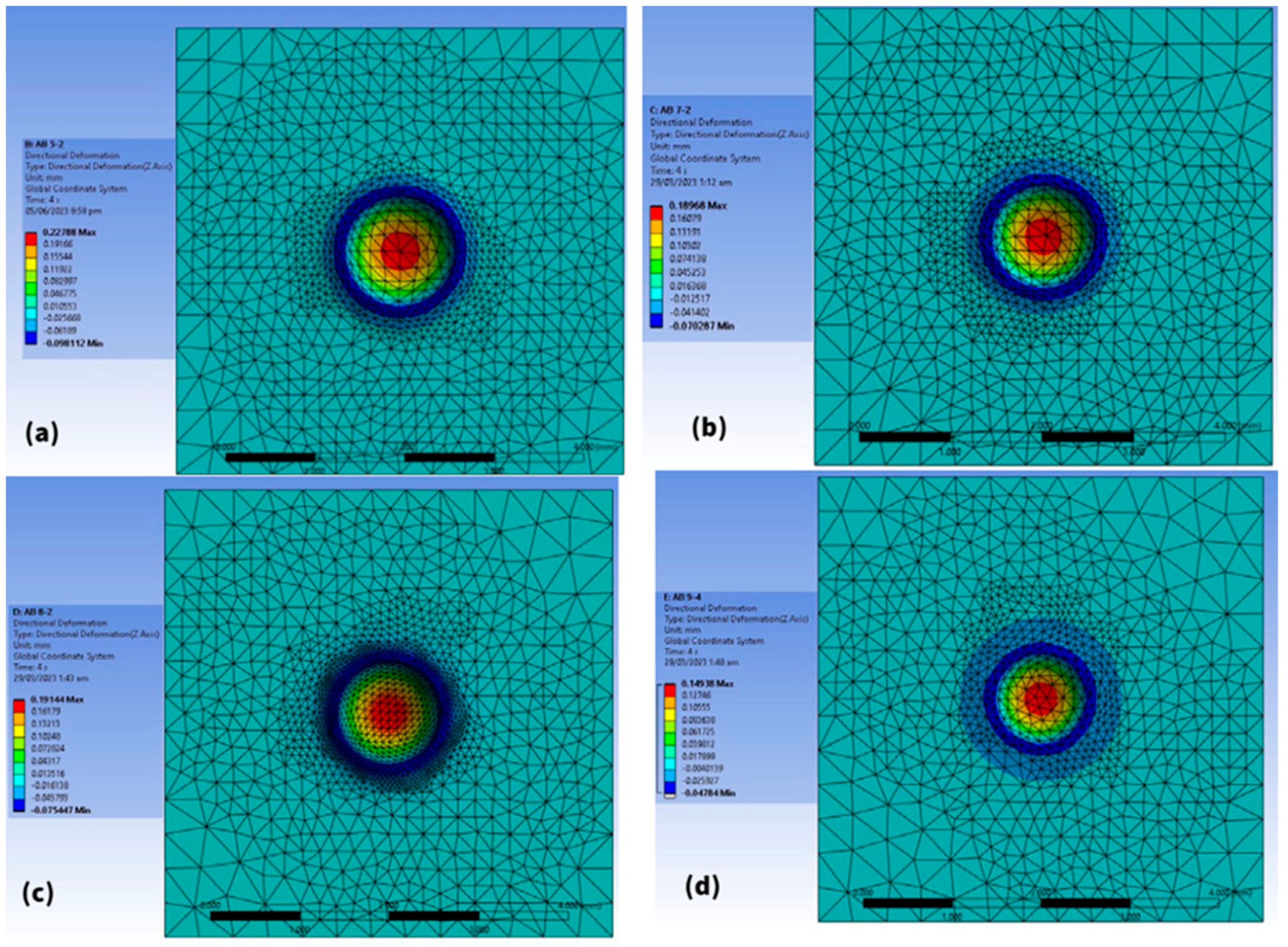
3.3. FEA Simulation Results
3.4. Comparison of Specimen’s Thickness, FEA Simulation, and Heat Treatment with Experimental Observations
3.4.1. Effect of Specimen Thickness and Experimental Observations
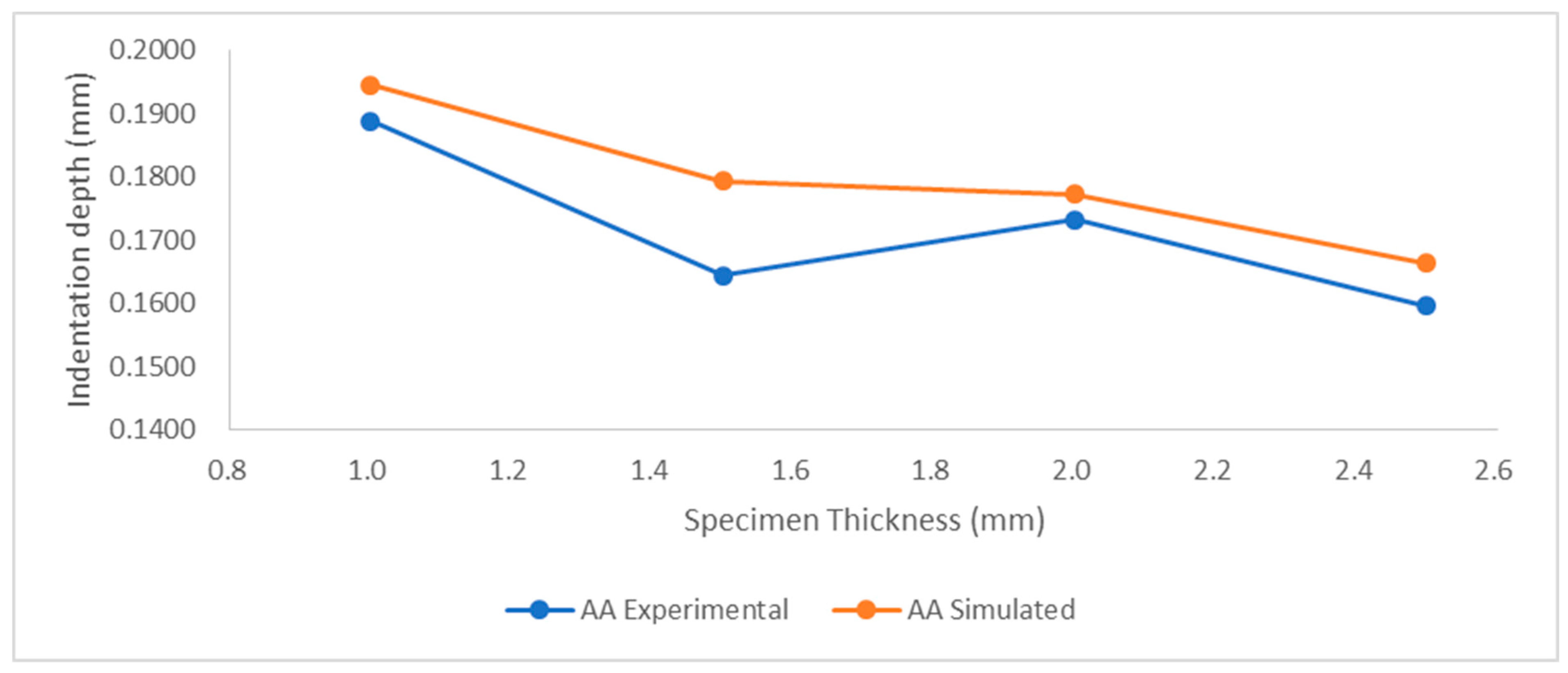
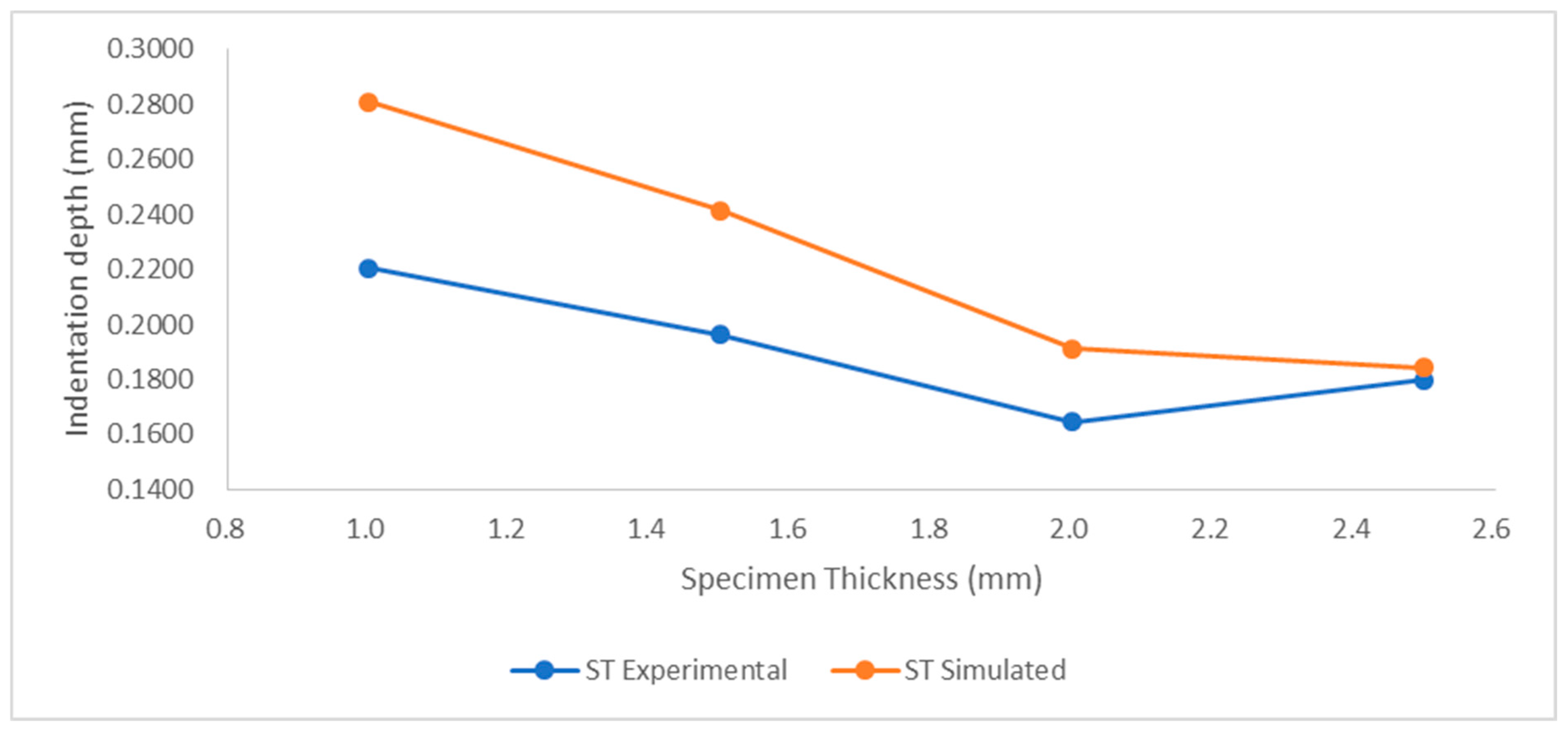
3.4.2. Simulation Results and Consolidation with Experimental Results
3.4.3. Effect of Different Heat Treatments
4. Conclusions
- [1].
- The specimens in the AB conditions showed the highest Rockwell hardness value of 75.50 HRFW with the smallest average indentation depth of 0.1547 mm at 2.5 mm specimen thickness with an overall consistent trend. The AA specimens clustered around similar Rockwell hardness values with the smallest indent at 2.5 mm and the largest indent on 1.0 mm-thick specimens, while the ST specimens showed slightly inconsistent trends in hardness values that are due to the increased ductility, and depicted the lowest indentation depth in a 2.0 mm- instead of a 2.5 mm-thick specimen.
- [2].
- For the available four specimen thicknesses, hardness values for the AB, ST, and AA post-treatment of SLM AlSi10Mg varied—generally, increasing hardness was observed for increasing thickness. Vice versa, the indentation depths showed a general decrease with increasing specimen thickness, resulting in higher Rockwell hardness value trends.
- [3].
- The declination in the indentation depths could be caused by an improvement in the porosity behavior against the increase in the wall thickness of SLM printing and heat-treatment execution. The occurrence of micro and macro porosity in the AB, ST, and AA conditions indicated a reduction from 1.5 mm to 2.5 mm-thick specimens. In addition, the SEM images revealed the formation of wrinkled patterns more prominently on the indentation surfaces of AA and AB specimens.
- [4].
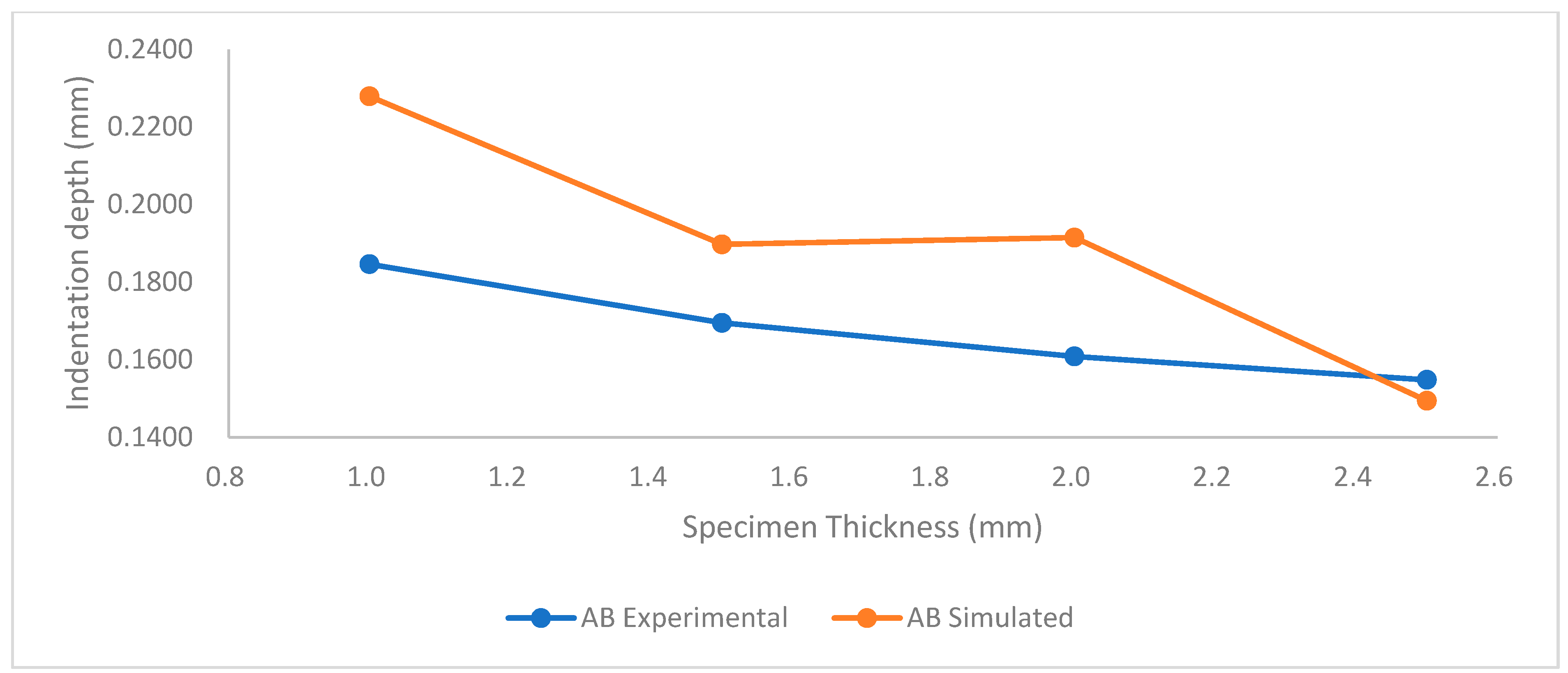
- The FEA simulation revealed the nearest accurate depth of indentation with a difference of 2.4% at 2.0 mm for AA, 2.5% at 2.5 mm for ST, and 3.5% for 2.5 mm-thick specimens for the AB condition. It is observed that the simulations for the thickest specimen showed the lowest difference in comparison to experimental values.
- [5].
- Simulation using FEA was found to be generally reliable based on the initial material data provided to the material library. Non-linear material behavior data are crucial to achieving more accurate simulation results, where AA specimens showed a highest accuracy of 95.43% with experimental results.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nys, N.; König, M.; Neugebauer, P.; Jones, M.J.; Gruber-Woelfler, H. Additive Manufacturing as a Rapid Prototyping and Fabrication Tool for Laboratory Crystallizers—A Proof-of-Concept Study. Org. Process. Res. Dev. 2023, 27, 1455–1462. [Google Scholar] [CrossRef]
- Soundararajan, B.; Sofia, D.; Barletta, D.; Poletto, M. Review on modeling techniques for powder bed fusion processes based on physical principles. Addit. Manuf. 2021, 47, 102336. [Google Scholar] [CrossRef]
- Ahmadi, M.; Tabary, S.B.; Rahmatabadi, D.; Ebrahimi, M.; Abrinia, K.; Hashemi, R. Review of selective laser melting of magnesium alloys: Advantages, microstructure and mechanical characterizations, defects, challenges, and applications. J. Mater. Res. Technol. 2022, 19, 1537–1562. [Google Scholar] [CrossRef]
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E.; Sing, S.L. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2, 041101. [Google Scholar] [CrossRef]
- Gokuldoss, P.K.; Kolla, S.; Eckert, J. Additive Manufacturing Processes: Selective Laser Melting, Electron Beam Melting and Binder Jetting—Selection Guidelines. Materials 2017, 10, 672. [Google Scholar] [CrossRef] [PubMed]
- Trevisan, F.; Calignano, F.; Lorusso, M.; Pakkanen, J.; Aversa, A.; Ambrosio, E.P.; Lombardi, M.; Fino, P.; Manfredi, D. On the Selective Laser Melting (SLM) of the AlSi10Mg Alloy: Process, Microstructure, and Mechanical Properties. Materials 2017, 10, 76. [Google Scholar] [CrossRef] [PubMed]
- Prashanth, K.G.; Scudino, S.; Eckert, J. Defining the tensile properties of Al-12Si parts produced by selective laser melting. Acta Mater. 2017, 126, 25–35. [Google Scholar] [CrossRef]
- Muthuswamy, P. Influence of powder characteristics on properties of parts manufactured by metal additive manufacturing. Lasers Manuf. Mater. Process. 2022, 9, 312–337. [Google Scholar] [CrossRef]
- Amir, B.; Samuha, S.; Sadot, O. Influence of Selective Laser Melting Machine Source on the Dynamic Properties of AlSi10Mg Alloy. Materials 2019, 12, 1143. [Google Scholar] [CrossRef]
- Romano, S.; Abel, A.; Gumpinger, J.; Brandão, A.; Beretta, S. Quality control of AlSi10Mg produced by SLM: Metallography versus CT scans for critical defect size assessment. Addit. Manuf. 2019, 28, 394–405. [Google Scholar] [CrossRef]
- Brandl, E.; Heckenberger, U.; Holzinger, V.; Buchbinder, D. Additive manufactured AlSi10Mg samples using Selective Laser Melting (SLM): Microstructure, high cycle fatigue, and fracture behavior. Mater. Des. 2012, 34, 159–169. [Google Scholar] [CrossRef]
- Muhammad, M.; Nezhadfar, P.D.; Thompson, S.; Saharan, A.; Phan, N.; Shamsaei, N. A comparative investigation on the micro-structure and mechanical properties of additively manufactured aluminum alloys. Int. J. Fatigue 2021, 146, 106165. [Google Scholar] [CrossRef]
- Zhang, Y.; Majeed, A.; Muzamil, M.; Lv, J.; Peng, T.; Patel, V. Investigation for macro mechanical behavior explicitly for thin-walled parts of AlSi10Mg alloy using selective laser melting technique. J. Manuf. Process. 2021, 66, 269–280. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Everitt, N.M.; Ashcroft, I.; Tuck, C. Reducing porosity in AlSi10Mg parts processed by selective laser melting. Addit. Manuf. 2014, 1, 77–86. [Google Scholar] [CrossRef]
- Majeed, A.; Ahmed, A.; Liu, B.; Ren, S.; Yang, J. Influence of wall thickness on the hardness of AlSi10Mg alloy parts manufactured by selective laser melting. Procedia CIRP 2019, 81, 459–463. [Google Scholar] [CrossRef]
- Maleki, E.; Bagherifard, S.; Bandini, M.; Guagliano, M. Surface post-treatments for metal additive manufacturing: Progress, challenges, and opportunities. Addit. Manuf. 2020, 37, 101619. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Wu, Y.; Gong, H.; Liu, L. Determination of the effect of cold working compression on residual stress reduction in quenched aluminum alloy 2219 block. SV-JME 2019, 65, 311–318. [Google Scholar] [CrossRef]
- Qin, Z.; Li, B.; Zhang, H.; Wilfried, T.Y.A.; Gao, T.; Xue, H. Effects of shot peening with different coverage on surface integrity and fatigue crack growth properties of 7B50-T7751 aluminum alloy. Eng. Fail. Anal. 2022, 133, 106010. [Google Scholar] [CrossRef]
- Laleh, M.; Sadeghi, E.; Revilla, R.I.; Chao, Q.; Haghdadi, N.; Hughes, A.E.; Xu, W.; De Graeve, I.; Qian, M.; Gibson, I.; et al. Heat treatment for metal additive manufacturing. Prog. Mater. Sci. 2023, 133, 101051. [Google Scholar] [CrossRef]
- Shakil, S.; Hadadzadeh, A.; Amirkhiz, B.S.; Pirgazi, H.; Mohammadi, M.; Haghshenas, M. Additive manufactured versus cast AlSi10Mg alloy: Microstructure and micromechanics. Results Mater. 2021, 10, 100178. [Google Scholar] [CrossRef]
- Prashanth, K.G.; Eckert, J. Formation of metastable cellular microstructures in selective laser melted alloys. J. Alloy. Compd. 2017, 707, 27–34. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Zhang, J.; Medvedev, A.; Sarker, A.; Ruan, D.; Lu, G.; Faruque, O.; Brandt, M. Effect of build orientation on the quasi-static and dynamic response of SLM AlSi10Mg. Mater. Sci. Eng. A 2020, 788, 139445. [Google Scholar] [CrossRef]
- Rubben, T.; Revilla, R.I.; De Graeve, I. Influence of heat treatments on the corrosion mechanism of additive manufactured AlSi10Mg. Corros. Sci. 2018, 147, 406–415. [Google Scholar] [CrossRef]
- Majeed, A.; Muzamil, M.; Khan, M.A.; Malik, E.H.; Huzaifa, M.; Lv, J.; Dar, N.U. Comprehensive Mechanical Behavior of Thin-Walled Additively-Manufactured Parts of AlSi10Mg by SLM in As-Built, Post-Solution, and Aging Treatment Conditions. JOM 2023, 75, 3067–3082. [Google Scholar] [CrossRef]
- Majeed, A.; Muzamil, M.; Lv, J.; Liu, B.; Ahmad, F. Heat treatment influences densification and porosity of AlSi10Mg alloy thin-walled parts manufactured by selective laser melting technique. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 267. [Google Scholar] [CrossRef]
- Majeed, A.; Zhang, Y.; Lv, J.; Peng, T.; Atta, Z.; Ahmed, A. Investigation of T4 and T6 heat treatment influences on relative density and porosity of AlSi10Mg alloy components manufactured by SLM. Comput. Ind. Eng. 2020, 139, 106194. [Google Scholar] [CrossRef]
- Majeed, A.; Ahmed, A.; Salam, A.; Sheikh, M.Z. Surface quality improvement by parameters analysis, optimization and heat treatment of AlSi10Mg parts manufactured by SLM additive manufacturing. Int. J. Light. Mater. Manuf. 2019, 2, 288–295. [Google Scholar] [CrossRef]
- Chen, H.; Cai, L.; Bao, C. A novel model for determining tensile properties and hardness of steels by spherical indentations. Strain 2020, 56, e12365. [Google Scholar] [CrossRef]
- Asiri, S.; Wagih, A.; Eltaher, M. Predictive model for spherical indentation on elastoplastic nanocomposites: Loading and unloading behavior. Ceram. Int. 2018, 45, 3088–3100. [Google Scholar] [CrossRef]
- American Society for Testing and Materials. Committee E-28 on Mechanical Testing. Standard Test Methods for Rockwell Hardness of Metallic Materials; ASTM: West Conshohocken, PA, USA, 2022. [Google Scholar]
- ASTM. Standard Test Methods for Tension Testing of Metallic Materials. Annual Book of ASTM Standards; ASTM: West Conshohocken, PA, USA, 2001; Volume 9. [Google Scholar]
- Akhtar, M.; Samiuddin, M.; Muzamil, M.; Siddiqui, M.A.; Khan, R.; Alsaleh, N.A.; Siddiqui, A.K.; Djuansjah, J.; Majeed, A. Mechanical Behavior of Selective Laser Melting (SLM) Parts with Varying Thicknesses in a Saline Environment under Different Exposure Times. Materials 2024, 17, 1959. [Google Scholar] [CrossRef]
- Wang, L.; Sun, J.; Yu, X.; Shi, Y.; Zhu, X.; Cheng, L.; Liang, H.; Yan, B.; Guo, L. Enhancement in mechanical properties of selectively laser-melted AlSi10Mg aluminum alloys by T6-like heat treatment. Mater. Sci. Eng. A 2018, 734, 299–310. [Google Scholar] [CrossRef]
- Majeed, A.; Zhang, Y.F.; Lv, J.X.; Peng, T.; Waqar, S.; Atta, Z. Study the effect of heat treatment on the relative density of SLM built parts of alsi10 mg alloy. In Proceedings of the 48th International Conference on Computers and Industrial Engineering, CIE 2018, Auckland, New Zealand, 2–5 December 2018. [Google Scholar]
- Strauß, L.; Lübbecke, S.; Löwisch, G. Optimizing the Solution Annealing of Additively Manufactured AlSi10Mg. HTM J. Heat Treat. Mater. 2023, 78, 300–316. [Google Scholar] [CrossRef]
- Li, Y.T.; Jiang, X.; Wang, X.T.; Leng, Y.X. Integration of hardness and toughness in (CuNiTiNbCr) Nx high entropy films through nitrogen-induced nanocomposite structure. Scr. Mater. 2024, 238, 115763. [Google Scholar] [CrossRef]
- Guo, Q.; Hou, H.; Pan, Y.; Pei, X.; Song, Z.; Liaw, P.K.; Zhao, Y. Hardening-softening of Al0.3CoCrFeNi high-entropy alloy under nanoindentation. Mater. Des. 2023, 231, 112050. [Google Scholar] [CrossRef]
- Clayton, J.; Lloyd, J.; Casem, D. Simulation and dimensional analysis of instrumented dynamic spherical indentation of ductile metals. Int. J. Mech. Sci. 2023, 251, 108333. [Google Scholar] [CrossRef]










| Laser Power (W) | Scan Speed (mm/s) | Hatch Space (μm) | Layer Thickness (μm) | Beam Focus Diameter (µm) | Scanning Strategy with Check-Board |
|---|---|---|---|---|---|
| 320 | 900 | 80 | 30 | 80 | 67° |
| Sr. No. | Specimen Number | Post-Treatment | Thickness (t) (mm) |
|---|---|---|---|
| 1 | AA-1 | AA | 1.0 |
| 2 | AA-2 | AA | 1.5 |
| 3 | AA-3 | AA | 2.0 |
| 4 | AA-4 | AA | 2.5 |
| 5 | ST-1 | ST | 1.0 |
| 6 | ST-2 | ST | 1.5 |
| 7 | ST-3 | ST | 2.0 |
| 8 | ST-4 | ST | 2.5 |
| 9 | AB-1 | AB | 1.0 |
| 10 | AB-2 | AB | 1.5 |
| 11 | AB-3 | AB | 2.0 |
| 12 | AB-4 | AB | 2.5 |
| Sr. No. | Specimen Number | Thickness (mm) | Rockwell Hardness (HRFW) 1 | Rockwell Hardness (HRFW) 2 | Average Hardness (HRFW) | Avg. Radius of Indent (mm) | Depth of Indent (mm) |
|---|---|---|---|---|---|---|---|
| 1 | AA-1 | 1.0 | 45.0 | 47.0 | 46.00 | 0.5140 | 0.1888 |
| 2 | AA-2 | 1.5 | 64.0 | 64.5 | 64.25 | 0.4839 | 0.1645 |
| 3 | AA-3 | 2.0 | 58.5 | 62.0 | 60.25 | 0.4950 | 0.1732 |
| 4 | AA-4 | 2.5 | 66.0 | 61.5 | 63.75 | 0.4774 | 0.1596 |
| 5 | ST-1 | 1.0 | 41.0 | 38.0 | 39.50 | 0.5490 | 0.2204 |
| 6 | ST-2 | 1.5 | 60.5 | 53.0 | 56.75 | 0.5226 | 0.1962 |
| 7 | ST-3 | 2.0 | 61.5 | 61.5 | 61.50 | 0.4839 | 0.1645 |
| 8 | ST-4 | 2.5 | 54.0 | 55.5 | 54.75 | 0.5032 | 0.1798 |
| 9 | AB-1 | 1.0 | 45.0 | 48.5 | 46.75 | 0.5090 | 0.1846 |
| 10 | AB-2 | 1.5 | 55.0 | 55.0 | 55.00 | 0.4903 | 0.1695 |
| 11 | AB-3 | 2.0 | 60.0 | 62.0 | 61.00 | 0.4790 | 0.1608 |
| 12 | AB-4 | 2.5 | 75.0 | 76.0 | 75.50 | 0.4710 | 0.1547 |
| Sr. No. | Specimen Number | Thickness (mm) | Depth of Indent Experimental (mm) | Depth of Indent ANSYS (mm) |
|---|---|---|---|---|
| 1 | AA-1 | 1.0 | 0.1888 | 0.1946 |
| 2 | AA-2 | 1.5 | 0.1645 | 0.1794 |
| 3 | AA-3 | 2.0 | 0.1732 | 0.1773 |
| 4 | AA-4 | 2.5 | 0.1596 | 0.1664 |
| 5 | ST-1 | 1.0 | 0.2204 | 0.2810 |
| 6 | ST-2 | 1.5 | 0.1962 | 0.2415 |
| 7 | ST-3 | 2.0 | 0.1645 | 0.1913 |
| 8 | ST-4 | 2.5 | 0.1798 | 0.1843 |
| 9 | AB-1 | 1.0 | 0.1846 | 0.2279 |
| 10 | AB-2 | 1.5 | 0.1695 | 0.1897 |
| 11 | AB-3 | 2.0 | 0.1608 | 0.1914 |
| 12 | AB-4 | 2.5 | 0.1547 | 0.1494 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamil, A.S.; Muzamil, M.; Akhtar, M.; Alsaleh, N.; Khan, R.; Samiuddin, M.; Siddiqui, A.K.; Yang, J.; Djuansjah, J. Indentation Behavior Assessment of As-Built, Solution, and Artificial Aged Heat-Treated Selective Laser Melting Specimens of AlSi10Mg. Crystals 2024, 14, 610. https://doi.org/10.3390/cryst14070610
Kamil AS, Muzamil M, Akhtar M, Alsaleh N, Khan R, Samiuddin M, Siddiqui AK, Yang J, Djuansjah J. Indentation Behavior Assessment of As-Built, Solution, and Artificial Aged Heat-Treated Selective Laser Melting Specimens of AlSi10Mg. Crystals. 2024; 14(7):610. https://doi.org/10.3390/cryst14070610
Chicago/Turabian StyleKamil, Abubakr Shahnawaz, Muhammad Muzamil, Maaz Akhtar, Naser Alsaleh, Rashid Khan, Muhammad Samiuddin, Ali Khursheed Siddiqui, Junzhou Yang, and Joy Djuansjah. 2024. "Indentation Behavior Assessment of As-Built, Solution, and Artificial Aged Heat-Treated Selective Laser Melting Specimens of AlSi10Mg" Crystals 14, no. 7: 610. https://doi.org/10.3390/cryst14070610
APA StyleKamil, A. S., Muzamil, M., Akhtar, M., Alsaleh, N., Khan, R., Samiuddin, M., Siddiqui, A. K., Yang, J., & Djuansjah, J. (2024). Indentation Behavior Assessment of As-Built, Solution, and Artificial Aged Heat-Treated Selective Laser Melting Specimens of AlSi10Mg. Crystals, 14(7), 610. https://doi.org/10.3390/cryst14070610







