Cluster Odd-Parity Multipoles by Staggered Orbital Ordering in Locally Noncentrosymmetric Crystals
Abstract
1. Introduction
2. Symmetry Analysis
3. Model
4. Results
5. Discussion
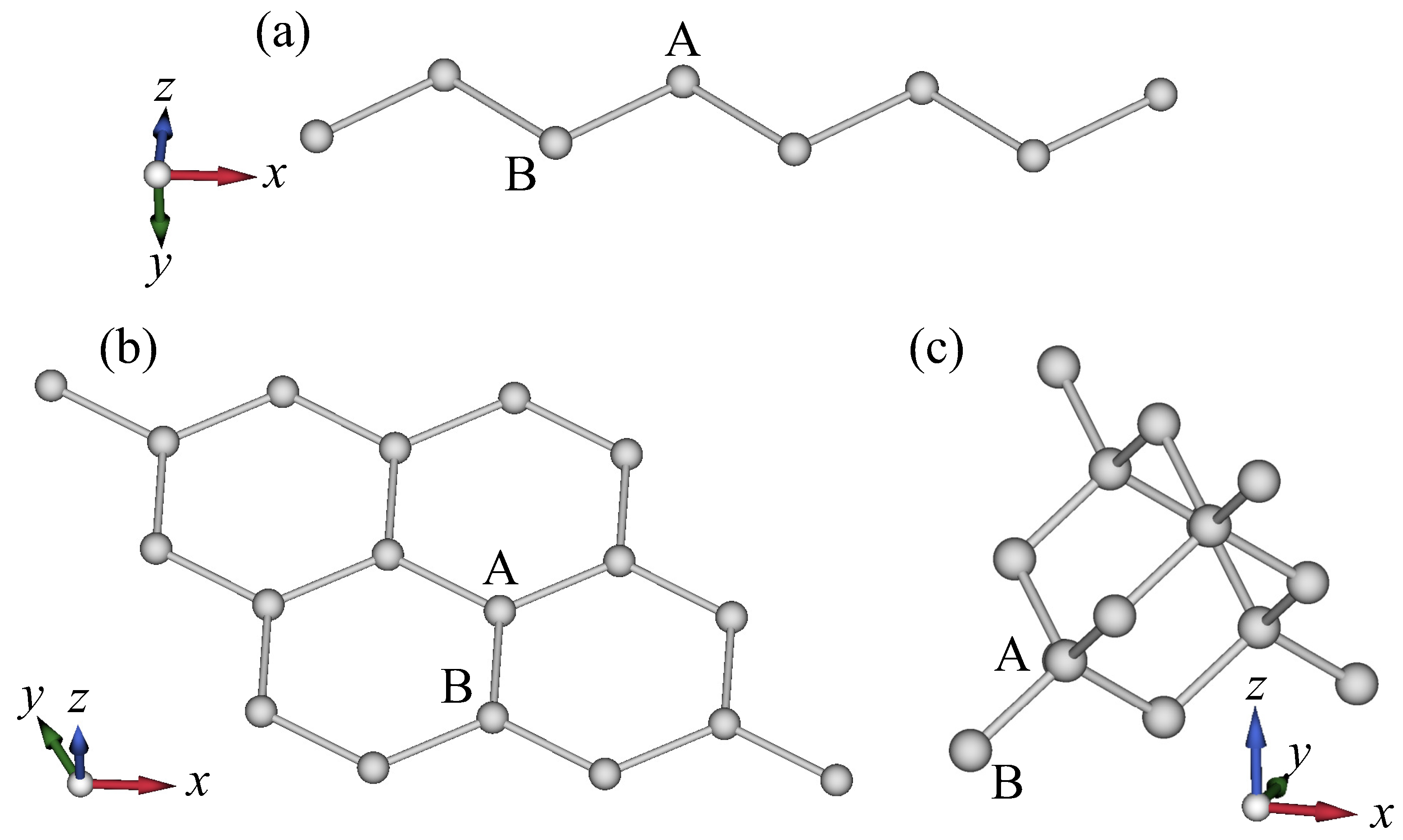
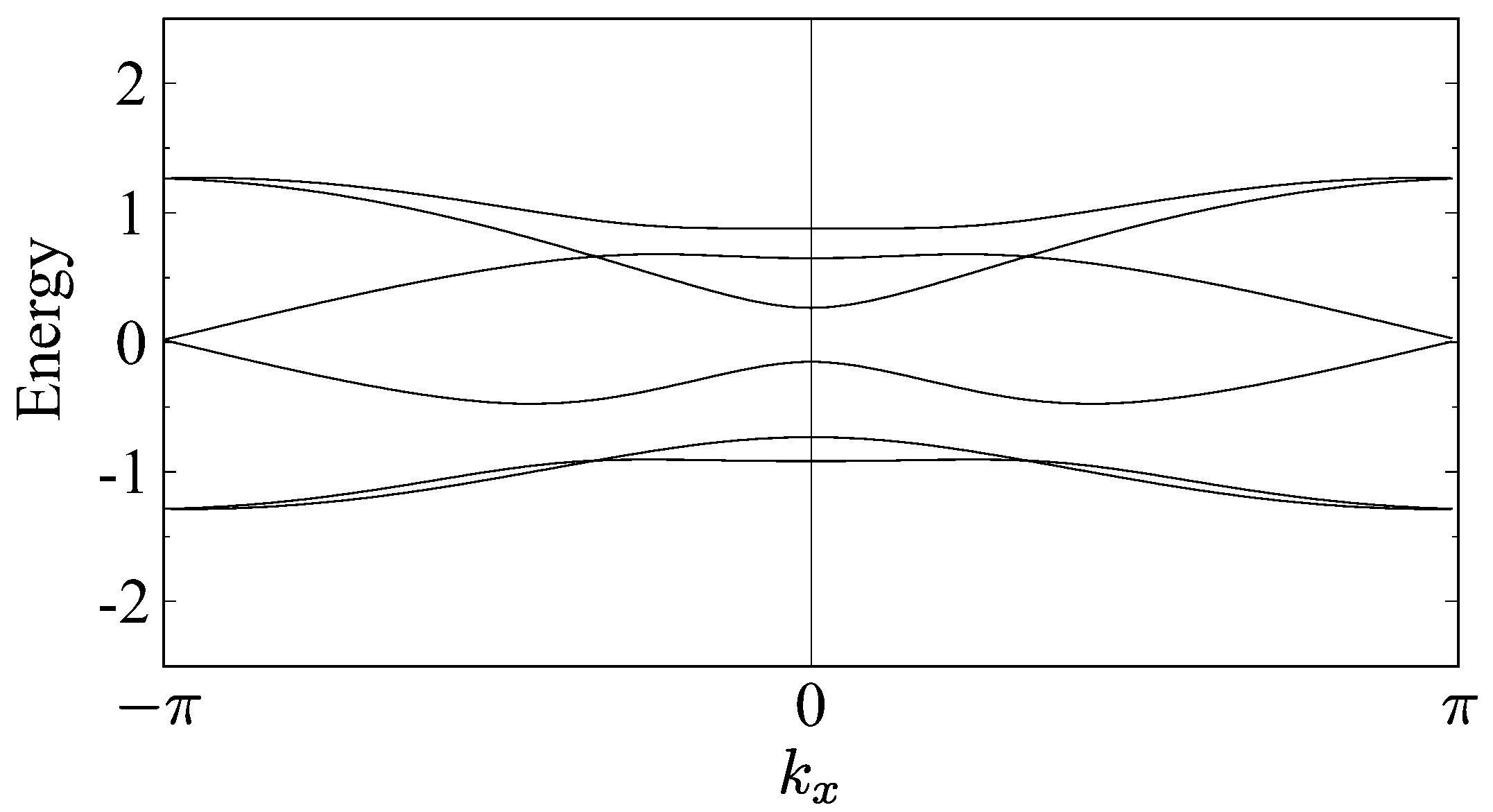
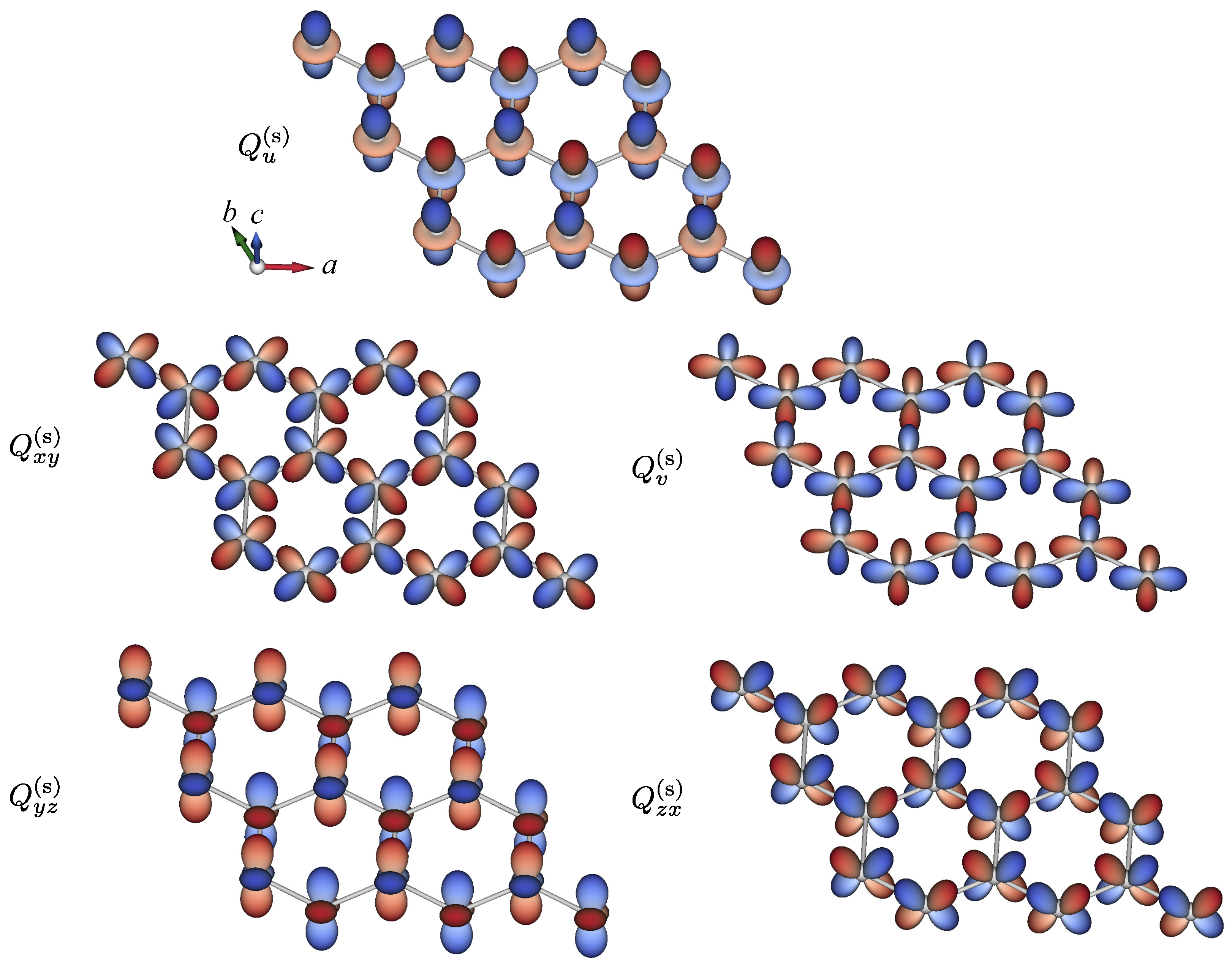
5.1. Honeycomb Structure
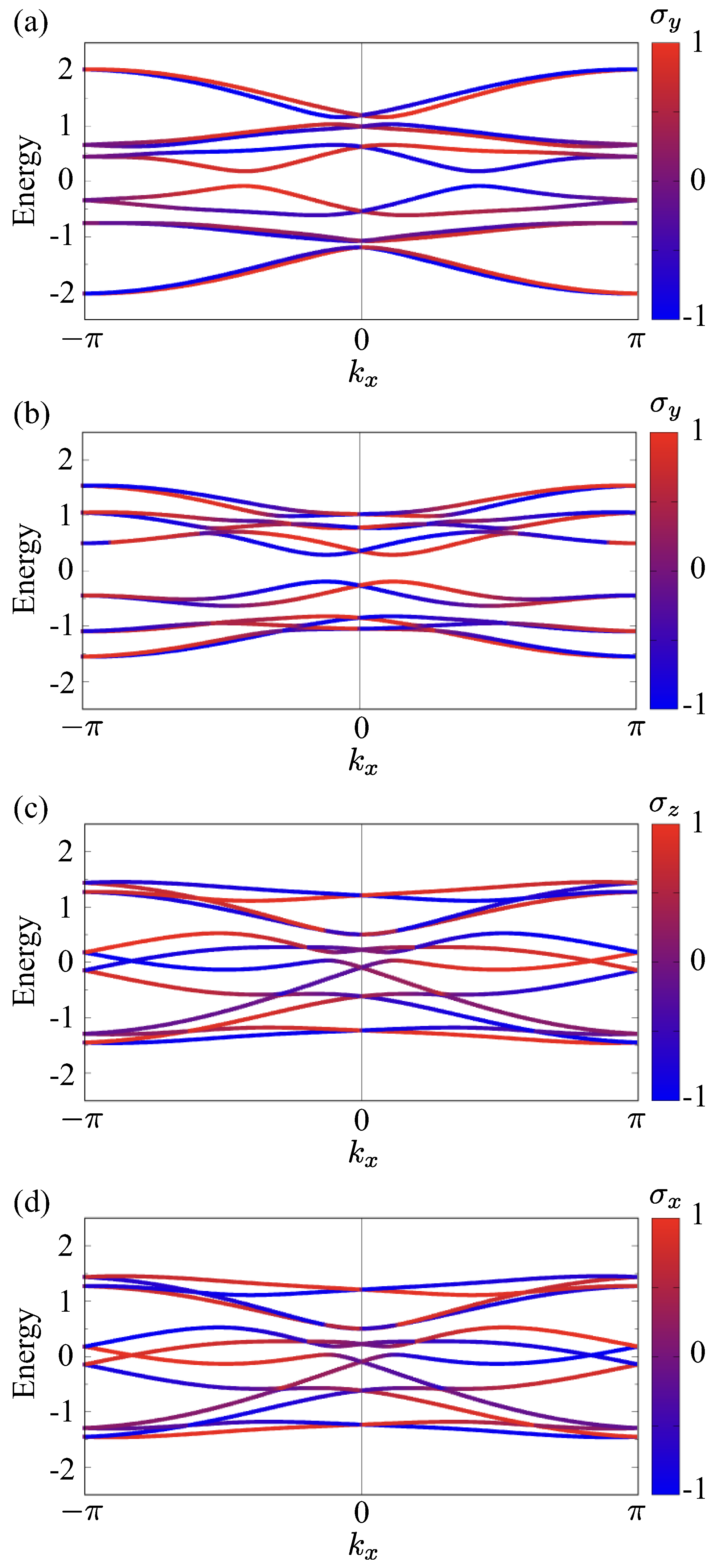
5.2. Diamond Structure
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aizu, K. Polarization, Pyroelectricity, and Ferroelectricity of Ionic Crystals. Rev. Mod. Phys. 1962, 34, 550–576. [Google Scholar] [CrossRef]
- Resta, R. Macroscopic polarization in crystalline dielectrics: The geometric phase approach. Rev. Mod. Phys. 1994, 66, 899–915. [Google Scholar] [CrossRef]
- Van Den Brink, J.; Khomskii, D.I. Multiferroicity due to charge ordering. J. Phys. Condens. Matter 2008, 20, 434217. [Google Scholar] [CrossRef]
- Ideue, T.; Hamamoto, K.; Koshikawa, S.; Ezawa, M.; Shimizu, S.; Kaneko, Y.; Tokura, Y.; Nagaosa, N.; Iwasa, Y. Bulk rectification effect in a polar semiconductor. Nat. Phys. 2017, 13, 578. [Google Scholar] [CrossRef]
- Tokura, Y.; Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 2018, 9, 3740. [Google Scholar] [CrossRef] [PubMed]
- Frigeri, P.A.; Agterberg, D.F.; Koga, A.; Sigrist, M. Superconductivity without Inversion Symmetry: MnSi versus CePt3Si. Phys. Rev. Lett. 2004, 92, 097001. [Google Scholar] [CrossRef] [PubMed]
- Bauer, E.; Sigrist, M. (Eds.) Non-Centrosymmetric Superconductors: Introduction and Overview (Lecture Notes in Physics), 2012th ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Dresselhaus, M.S.; Dresselhaus, G.; Jorio, A. Group Theory: Application to the Physics of Condensed Matter; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Frigeri, P.A.; Agterberg, D.F.; Sigrist, M. Spin susceptibility in superconductors without inversion symmetry. New J. Phys. 2004, 6, 115. [Google Scholar] [CrossRef]
- Palazzese, S.; Landaeta, J.; Subero, D.; Bauer, E.; Bonalde, I. Strong antisymmetric spin–orbit coupling and superconducting properties: The case of noncentrosymmetric LaPtSi. J. Phys. Condens. Matter 2018, 30, 255603. [Google Scholar] [CrossRef] [PubMed]
- Rashba, E.I. Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 1960, 2, 1109–1122. [Google Scholar]
- Ishizaka, K.; Bahramy, M.; Murakawa, H.; Sakano, M.; Shimojima, T.; Sonobe, T.; Koizumi, K.; Shin, S.; Miyahara, H.; Kimura, A.; et al. Giant Rashba-type spin splitting in bulk BiTeI. Nat. Mater. 2011, 10, 521–526. [Google Scholar] [CrossRef]
- Bahramy, M.S.; Arita, R.; Nagaosa, N. Origin of giant bulk Rashba splitting: Application to BiTeI. Phys. Rev. B 2011, 84, 041202(R). [Google Scholar] [CrossRef]
- Sunko, V.; Rosner, H.; Kushwaha, P.; Khim, S.; Mazzola, F.; Bawden, L.; Clark, O.; Riley, J.; Kasinathan, D.; Haverkort, M.; et al. Maximal Rashba-like spin splitting via kinetic-energy-coupled inversion-symmetry breaking. Nature 2017, 549, 492–496. [Google Scholar] [CrossRef] [PubMed]
- Takashima, R.; Fujimoto, S. Supercurrent-induced skyrmion dynamics and tunable Weyl points in chiral magnet with superconductivity. Phys. Rev. B 2016, 94, 235117. [Google Scholar] [CrossRef]
- Wang, B.Z.; Lu, Y.H.; Sun, W.; Chen, S.; Deng, Y.; Liu, X.J. Dirac-, Rashba-, and Weyl-type spin-orbit couplings: Toward experimental realization in ultracold atoms. Phys. Rev. A 2018, 97, 011605(R). [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Cheng, Y.C.; Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 2011, 84, 153402. [Google Scholar] [CrossRef]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699. [Google Scholar] [CrossRef]
- Ugeda, M.M.; Bradley, A.J.; Shi, S.F.; Felipe, H.; Zhang, Y.; Qiu, D.Y.; Ruan, W.; Mo, S.K.; Hussain, Z.; Shen, Z.X.; et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 2014, 13, 1091. [Google Scholar] [CrossRef] [PubMed]
- Kormányos, A.; Zólyomi, V.; Drummond, N.D.; Burkard, G. Spin-Orbit Coupling, Quantum Dots, and Qubits in Monolayer Transition Metal Dichalcogenides. Phys. Rev. X 2014, 4, 011034. [Google Scholar] [CrossRef]
- Fu, L. Parity-Breaking Phases of Spin-Orbit-Coupled Metals with Gyrotropic, Ferroelectric, and Multipolar Orders. Phys. Rev. Lett. 2015, 115, 026401. [Google Scholar] [CrossRef]
- Kozii, V.; Fu, L. Odd-Parity Superconductivity in the Vicinity of Inversion Symmetry Breaking in Spin-Orbit-Coupled Systems. Phys. Rev. Lett. 2015, 115, 207002. [Google Scholar] [CrossRef]
- Venderbos, J.W.F.; Kozii, V.; Fu, L. Odd-parity superconductors with two-component order parameters: Nematic and chiral, full gap, and Majorana node. Phys. Rev. B 2016, 94, 180504(R). [Google Scholar] [CrossRef]
- Hayami, S.; Yanagi, Y.; Kusunose, H.; Motome, Y. Electric Toroidal Quadrupoles in the Spin-Orbit-Coupled Metal Cd2Re2O7. Phys. Rev. Lett. 2019, 122, 147602. [Google Scholar] [CrossRef] [PubMed]
- Hirose, H.T.; Terashima, T.; Hirai, D.; Matsubayashi, Y.; Kikugawa, N.; Graf, D.; Sugii, K.; Sugiura, S.; Hiroi, Z.; Uji, S. Electronic states of metallic electric toroidal quadrupole order in Cd2Re2O7 determined by combining quantum oscillations and electronic structure calculations. Phys. Rev. B 2022, 105, 035116. [Google Scholar] [CrossRef]
- Hayami, S.; Yanagi, Y.; Kusunose, H. Spontaneous antisymmetric spin splitting in noncollinear antiferromagnets without spin-orbit coupling. Phys. Rev. B 2020, 101, 220403. [Google Scholar] [CrossRef]
- Murakami, S.; Nagaosa, N.; Zhang, S.C. Dissipationless quantum spin current at room temperature. Science 2003, 301, 1348–1351. [Google Scholar] [CrossRef] [PubMed]
- Murakami, S.; Nagaosa, N.; Zhang, S.C. Spin-Hall Insulator. Phys. Rev. Lett. 2004, 93, 156804. [Google Scholar] [CrossRef]
- Sinova, J.; Culcer, D.; Niu, Q.; Sinitsyn, N.A.; Jungwirth, T.; MacDonald, A.H. Universal Intrinsic Spin Hall Effect. Phys. Rev. Lett. 2004, 92, 126603. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, S. Emergent Nodal Excitations due to Coexistence of Superconductivity and Antiferromagnetism: Cases with and without Inversion Symmetry. J. Phys. Soc. Jpn. 2006, 75, 083704. [Google Scholar] [CrossRef]
- Fujimoto, S. Fermi liquid theory for heavy fermion superconductors without inversion symmetry: Magnetism and transport coefficients. J. Phys. Soc. Jpn. 2007, 76. [Google Scholar] [CrossRef]
- Edelstein, V.M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 1990, 73, 233–235. [Google Scholar] [CrossRef]
- Yip, S.K. Two-dimensional superconductivity with strong spin-orbit interaction. Phys. Rev. B 2002, 65, 144508. [Google Scholar] [CrossRef]
- Fujimoto, S. Magnetoelectric effects in heavy-fermion superconductors without inversion symmetry. Phys. Rev. B 2005, 72, 024515. [Google Scholar] [CrossRef]
- Yoda, T.; Yokoyama, T.; Murakami, S. Orbital Edelstein Effect as a Condensed-Matter Analog of Solenoids. Nano Lett. 2018, 18, 916–920. [Google Scholar] [CrossRef] [PubMed]
- Massarelli, G.; Wu, B.; Paramekanti, A. Orbital Edelstein effect from density-wave order. Phys. Rev. B 2019, 100, 075136. [Google Scholar] [CrossRef]
- Yip, S. Noncentrosymmetric superconductors. Annu. Rev. Condens. Matter Phys. 2014, 5, 15–33. [Google Scholar] [CrossRef]
- Sigrist, M.; Agterberg, D.F.; Fischer, M.H.; Goryo, J.; Loder, F.; Rhim, S.H.; Maruyama, D.; Yanase, Y.; Yoshida, T.; Youn, S.J. Superconductors with staggered non-centrosymmetricity. J. Phys. Soc. Jpn. 2014, 83, 061014. [Google Scholar] [CrossRef]
- Smidman, M.; Salamon, M.; Yuan, H.; Agterberg, D. Superconductivity and spin–orbit coupling in non-centrosymmetric materials: A review. Rep. Prog. Phys. 2017, 80, 036501. [Google Scholar] [CrossRef] [PubMed]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent spin-valley-orbital physics by spontaneous parity breaking. J. Phys. Condens. Matter 2016, 28, 395601. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Unified description of electronic orderings and cross correlations by complete multipole representation. J. Phys. Soc. Jpn. 2024, 93, 072001. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous Multipole Ordering by Local Parity Mixing. J. Phys. Soc. Jpn. 2015, 84, 064717. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Cysne, T.P.; Guimarães, F.S.M.; Canonico, L.M.; Rappoport, T.G.; Muniz, R.B. Orbital magnetoelectric effect in zigzag nanoribbons of p-band systems. Phys. Rev. B 2021, 104, 165403. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in PT-symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Suzuki, Y. Tunneling spin current in systems with spin degeneracy. Phys. Rev. B 2022, 105, 075201. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Y.; Xiao, D. Intrinsic Nonlinear Hall Effect in Antiferromagnetic Tetragonal CuMnAs. Phys. Rev. Lett. 2021, 127, 277201. [Google Scholar] [CrossRef] [PubMed]
- Kirikoshi, A.; Hayami, S. Microscopic mechanism for intrinsic nonlinear anomalous Hall conductivity in noncollinear antiferromagnetic metals. Phys. Rev. B 2023, 107, 155109. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Kusunose, H. Nonlinear spin Hall effect in PT-symmetric collinear magnets. Phys. Rev. B 2022, 106, 024405. [Google Scholar] [CrossRef]
- Kondo, H.; Akagi, Y. Nonlinear magnon spin Nernst effect in antiferromagnets and strain-tunable pure spin current. Phys. Rev. Res. 2022, 4, 013186. [Google Scholar] [CrossRef]
- Sumita, S.; Yanase, Y. Superconductivity in magnetic multipole states. Phys. Rev. B 2016, 93, 224507. [Google Scholar] [CrossRef]
- Tokura, Y.; Nagaosa, N. Orbital physics in transition-metal oxides. Science 2000, 288, 462–468. [Google Scholar] [CrossRef] [PubMed]
- Khomskii, D.; Mostovoy, M. Orbital ordering and frustrations. J. Phys. A 2003, 36, 9197. [Google Scholar] [CrossRef]
- Streltsov, S.V.; Khomskii, D.I. Orbital physics in transition metal compounds: New trends. Phys. Usp. 2017, 60, 1121. [Google Scholar] [CrossRef]
- Khomskii, D.I.; Streltsov, S.V. Orbital effects in solids: Basics, recent progress, and opportunities. Chem. Rev. 2021, 121, 2992–3030. [Google Scholar] [CrossRef] [PubMed]
- Pen, H.F.; van den Brink, J.; Khomskii, D.I.; Sawatzky, G.A. Orbital Ordering in a Two-Dimensional Triangular Lattice. Phys. Rev. Lett. 1997, 78, 1323–1326. [Google Scholar] [CrossRef]
- Kumar, S.; Kampf, A.P.; Majumdar, P. Domain Formation and Orbital Ordering Transition in a Doped Jahn-Teller Insulator. Phys. Rev. Lett. 2006, 97, 176403. [Google Scholar] [CrossRef]
- Lv, W.; Wu, J.; Phillips, P. Orbital ordering induces structural phase transition and the resistivity anomaly in iron pnictides. Phys. Rev. B 2009, 80, 224506. [Google Scholar] [CrossRef]
- Lee, C.C.; Yin, W.G.; Ku, W. Ferro-Orbital Order and Strong Magnetic Anisotropy in the Parent Compounds of Iron-Pnictide Superconductors. Phys. Rev. Lett. 2009, 103, 267001. [Google Scholar] [CrossRef]
- Kurihara, R.; Mitsumoto, K.; Akatsu, M.; Nemoto, Y.; Goto, T.; Kobayashi, Y.; Sato, M. Critical Slowing Down of Quadrupole and Hexadecapole Orderings in Iron Pnictide Superconductor. J. Phys. Soc. Jpn. 2017, 86, 064706. [Google Scholar] [CrossRef]
- Voleti, S.; Maharaj, D.D.; Gaulin, B.D.; Luke, G.; Paramekanti, A. Multipolar magnetism in d-orbital systems: Crystal field levels, octupolar order, and orbital loop currents. Phys. Rev. B 2020, 101, 155118. [Google Scholar] [CrossRef]
- Paramekanti, A.; Maharaj, D.D.; Gaulin, B.D. Octupolar order in d-orbital Mott insulators. Phys. Rev. B 2020, 101, 054439. [Google Scholar] [CrossRef]
- Hirai, D.; Sagayama, H.; Gao, S.; Ohsumi, H.; Chen, G.; Arima, T.h.; Hiroi, Z. Detection of multipolar orders in the spin-orbit-coupled 5d Mott insulator Ba2MgReO6. Phys. Rev. Res. 2020, 2, 022063. [Google Scholar] [CrossRef]
- Mansouri Tehrani, A.; Spaldin, N.A. Untangling the structural, magnetic dipole, and charge multipolar orders in Ba2MgReO6. Phys. Rev. Mater. 2021, 5, 104410. [Google Scholar] [CrossRef]
- Lovesey, S.W.; Khalyavin, D.D. Magnetic order and 5d1 multipoles in a rhenate double perovskite Ba2MgReO6. Phys. Rev. B 2021, 103, 235160. [Google Scholar] [CrossRef]
- Morin, P.; Schmitt, D.; De Lacheisserie, E.D.T. Magnetic and quadrupolar properties of PrPb3. J. Magn. Magn. Mater. 1982, 30, 257–264. [Google Scholar] [CrossRef]
- Takigawa, M.; Yasuoka, H.; Tanaka, T.; Ishizawa, Y. NMR Study on the Spin Structure of CeB6. J. Phys. Soc. Jpn. 1983, 52, 728–731. [Google Scholar] [CrossRef]
- Lüthi, B.; Blumenröder, S.; Hillebrands, B.; Zirngiebl, E.; Güntherodt, G.; Winzer, K. Elastic and magnetoelastic effects in CeB6. Z. Phys. 1984, 58, 31–38. [Google Scholar] [CrossRef]
- Effantin, J.; Rossat-Mignod, J.; Burlet, P.; Bartholin, H.; Kunii, S.; Kasuya, T. Magnetic phase diagram of CeB6. J. Magn. Magn. Mater. 1985, 47–48, 145–148. [Google Scholar] [CrossRef]
- Erkelens, W.A.C.; Regnault, L.P.; Burlet, P.; Rossat-Mignod, J.; Kunii, S.; Kasuya, T. Neutron scattering study of the antiferroquadrupolar ordering in CeB6 and Ce0.75La0.25B6. J. Magn. Magn. Mater. 1987, 63–64, 61–63. [Google Scholar] [CrossRef]
- Morin, P.; Rouchy, J.; Yonenobu, K.; Yamagishi, A.; Date, M. Interplay of antiferromagnetic and antiferroquadrupolar interactions in DyAg and other rare earth intermetallic compounds. J. Magn. Magn. Mater. 1989, 81, 247–258. [Google Scholar] [CrossRef]
- Nakamura, S.; Goto, T.; Kunii, S.; Iwashita, K.; Tamaki, A. Quadrupole-strain interaction in rare earth hexaborides. J. Phys. Soc. Jpn. 1994, 63, 623–636. [Google Scholar] [CrossRef]
- Sakai, O.; Shiina, R.; Shiba, H.; Thalmeier, P. A new interpretation of NMR in quadrupolar ordering phase of CeB6-Consistency with neutron scattering. J. Phys. Soc. Jpn. 1997, 66, 3005–3007. [Google Scholar] [CrossRef]
- Shiina, R.; Shiba, H.; Thalmeier, P. Magnetic-field effects on quadrupolar ordering in a Γ 8-quartet system CeB6. J. Phys. Soc. Jpn. 1997, 66, 1741–1755. [Google Scholar] [CrossRef]
- Nakao, H.; Magishi, K.i.; Wakabayashi, Y.; Murakami, Y.; Koyama, K.; Hirota, K.; Endoh, Y.; Kunii, S. Antiferro-quadrupole ordering of CeB6 studied by resonant X-ray scattering. J. Phys. Soc. Jpn. 2001, 70, 1857–1860. [Google Scholar] [CrossRef]
- Tanaka, Y.; Staub, U.; Katsumata, K.; Lovesey, S.; Lorenzo, J.; Narumi, Y.; Scagnoli, V.; Shimomura, S.; Tabata, Y.; Onuki, Y.; et al. Direct and quantitative determination of the orbital ordering in CeB6 by X-ray diffraction. Europhys. Lett. 2004, 68, 671. [Google Scholar] [CrossRef]
- Onimaru, T.; Sakakibara, T.; Aso, N.; Yoshizawa, H.; Suzuki, H.S.; Takeuchi, T. Observation of Modulated Quadrupolar Structures in PrPb3. Phys. Rev. Lett. 2005, 94, 197201. [Google Scholar] [CrossRef] [PubMed]
- Ishii, I.; Muneshige, H.; Suetomi, Y.; K. Fujita, T.; Onimaru, T.; T. Matsumoto, K.; Takabatake, T.; Araki, K.; Akatsu, M.; Nemoto, Y.; et al. Antiferro-Quadrupolar Ordering at the Lowest Temperature and Anisotropic Magnetic Field-Temperature Phase Diagram in the Cage Compound PrIr2Zn20. J. Phys. Soc. Jpn. 2011, 80, 093601. [Google Scholar] [CrossRef]
- Sakai, A.; Nakatsuji, S. Kondo Effects and Multipolar Order in the Cubic PrTr2Al20 (Tr = Ti, V). J. Phys. Soc. Jpn. 2011, 80, 063701. [Google Scholar] [CrossRef]
- Onimaru, T.; Matsumoto, K.T.; Inoue, Y.F.; Umeo, K.; Sakakibara, T.; Karaki, Y.; Kubota, M.; Takabatake, T. Antiferroquadrupolar Ordering in a Pr-Based Superconductor PrIr2Zn20. Phys. Rev. Lett. 2011, 106, 177001. [Google Scholar] [CrossRef]
- Sakai, A.; Kuga, K.; Nakatsuji, S. Superconductivity in the Ferroquadrupolar State in the Quadrupolar Kondo Lattice PrTi2Al20. J. Phys. Soc. Jpn. 2012, 81, 083702. [Google Scholar] [CrossRef]
- Onimaru, T.; Nagasawa, N.; Matsumoto, K.; Wakiya, K.; Umeo, K.; Kittaka, S.; Sakakibara, T.; Matsushita, Y.; Takabatake, T. Simultaneous superconducting and antiferroquadrupolar transitions in PrRh 2 Zn 20. Phys. Rev. B 2012, 86, 184426. [Google Scholar] [CrossRef]
- Matsumura, T.; Yonemura, T.; Kunimori, K.; Sera, M.; Iga, F.; Nagao, T.; Igarashi, J.i. Antiferroquadrupole order and magnetic field induced octupole in CeB6. Phys. Rev. B 2012, 85, 174417. [Google Scholar] [CrossRef]
- Tsujimoto, M.; Matsumoto, Y.; Tomita, T.; Sakai, A.; Nakatsuji, S. Heavy-Fermion Superconductivity in the Quadrupole Ordered State of PrV2Al20. Phys. Rev. Lett. 2014, 113, 267001. [Google Scholar] [CrossRef]
- Matsumoto, K.T.; Onimaru, T.; Wakiya, K.; Umeo, K.; Takabatake, T. Effect of La Substitution in PrIr2Zn20 on the Superconductivity and Antiferro-Quadrupole Order. J. Phys. Soc. Jpn. 2015, 84, 063703. [Google Scholar] [CrossRef]
- Kubo, T.; Kotegawa, H.; Tou, H.; Higashinaka, R.; Nakama, A.; Aoki, Y.; Sato, H. Absence of Magnetic Dipolar Phase Transition and Evolution of Low-Energy Excitations in PrNb2Al20 with Crystal Electric Field Γ3 Ground State: Evidence from 93Nb-NQR Studies. J. Phys. Soc. Jpn. 2015, 84, 074701. [Google Scholar] [CrossRef]
- Onimaru, T.; Kusunose, H. Exotic Quadrupolar Phenomena in Non-Kramers Doublet Systems—The Cases of PrT2Zn20 (T = Ir, Rh) and PrT2Al20 (T = V, Ti)—. J. Phys. Soc. Jpn. 2016, 85, 082002. [Google Scholar] [CrossRef]
- Cameron, A.S.; Friemel, G.; Inosov, D.S. Multipolar phases and magnetically hidden order: Review of the heavy-fermion compound Ce1−xLaxB6. Rep. Prog. Phys. 2016, 79, 066502. [Google Scholar] [CrossRef]
- Onimaru, T.; Izawa, K.; Matsumoto, K.T.; Yoshida, T.; Machida, Y.; Ikeura, T.; Wakiya, K.; Umeo, K.; Kittaka, S.; Araki, K.; et al. Quadrupole-driven non-Fermi-liquid and magnetic-field-induced heavy fermion states in a non-Kramers doublet system. Phys. Rev. B 2016, 94, 075134. [Google Scholar] [CrossRef]
- Portnichenko, P.Y.; Akbari, A.; Nikitin, S.E.; Cameron, A.S.; Dukhnenko, A.V.; Filipov, V.B.; Shitsevalova, N.Y.; Čermák, P.; Radelytskyi, I.; Schneidewind, A.; et al. Field-Angle-Resolved Magnetic Excitations as a Probe of Hidden-Order Symmetry in CeB6. Phys. Rev. X 2020, 10, 021010. [Google Scholar] [CrossRef]
- Tanida, H.; Muro, Y.; Matsumura, T. La Substitution and Pressure Studies on CeCoSi: A Possible Antiferroquadrupolar Ordering Induced by Pressure. J. Phys. Soc. Jpn. 2018, 87, 023705. [Google Scholar] [CrossRef]
- Tanida, H.; Mitsumoto, K.; Muro, Y.; Fukuhara, T.; Kawamura, Y.; Kondo, A.; Kindo, K.; Matsumoto, Y.; Namiki, T.; Kuwai, T.; et al. Successive Phase Transition at Ambient Pressure in CeCoSi: Single Crystal Studies. J. Phys. Soc. Jpn. 2019, 88, 054716. [Google Scholar] [CrossRef]
- Matsumura, T.; Kishida, S.; Tsukagoshi, M.; Kawamura, Y.; Nakao, H.; Tanida, H. Structural Transition in the Hidden Ordered Phase of CeCoSi. J Phys. Soc. Jpn. 2022, 91, 064704. [Google Scholar] [CrossRef]
- Manago, M.; Ishigaki, A.; Tou, H.; Harima, H.; Tanida, H.; Kotegawa, H. Ferroic quadrupolar ordering in CeCoSi revealed using 59Co NMR measurements. Phys. Rev. B 2023, 108, 085118. [Google Scholar] [CrossRef]
- Garaud, J.; Carlström, J.; Babaev, E.; Speight, M. Chiral CP2 skyrmions in three-band superconductors. Phys. Rev. B 2013, 87, 014507. [Google Scholar] [CrossRef]
- Akagi, Y.; Amari, Y.; Sawado, N.; Shnir, Y. Isolated skyrmions in the CP2 nonlinear sigma model with a Dzyaloshinskii-Moriya type interaction. Phys. Rev. D 2021, 103, 065008. [Google Scholar] [CrossRef]
- Amari, Y.; Akagi, Y.; Gudnason, S.B.; Nitta, M.; Shnir, Y. CP2 skyrmion crystals in an SU(3) magnet with a generalized Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2022, 106, L100406. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Dahlbom, D.; Barros, K.; Batista, C.D. CP2 skyrmions and skyrmion crystals in realistic quantum magnets. Nat. Commun. 2023, 14, 3626. [Google Scholar] [CrossRef]
- Hayami, S.; Tsutsui, S.; Hanate, H.; Nagasawa, N.; Yoda, Y.; Matsuhira, K. Cluster Toroidal Multipoles Formed by Electric-Quadrupole and Magnetic-Octupole Trimers: A Possible Scenario for Hidden Orders in Ca5Ir3O12. J. Phys. Soc. Jpn. 2023, 92, 033702. [Google Scholar] [CrossRef]
- Shibata, K.; Naka, M.; Jeschke, H.O.; Otsuki, J. Spin-orbital ordering in alkali superoxides. Phys. Rev. B 2024, 109, 235115. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Nomoto, T.; Arita, R.; Yanagi, Y.; Hayami, S.; Kusunose, H. Multipole expansion for magnetic structures: A generation scheme for a symmetry-adapted orthonormal basis set in the crystallographic point group. Phys. Rev. B 2019, 99, 174407. [Google Scholar] [CrossRef]
- Kusunose, H.; Oiwa, R.; Hayami, S. Symmetry-adapted modeling for molecules and crystals. Phys. Rev. B 2023, 107, 195118. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Microscopic Description of Electric and Magnetic Toroidal Multipoles in Hybrid Orbitals. J. Phys. Soc. Jpn. 2018, 87, 033709. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Yanagi, Y.; Kusunose, H. Classification of atomic-scale multipoles under crystallographic point groups and application to linear response tensors. Phys. Rev. B 2018, 98, 165110. [Google Scholar] [CrossRef]
- Li, X.; Cao, T.; Niu, Q.; Shi, J.; Feng, J. Coupling the valley degree of freedom to antiferromagnetic order. Proc. Natl. Acad. Sci. USA 2013, 110, 3738–3742. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Yanagi, Y.; Kusunose, H. Optical Selection Rules in Spin–Orbit Coupled Systems on Honeycomb Lattice. J. Phys. Soc. Jpn. 2017, 86, 083703. [Google Scholar] [CrossRef]
- Yanagi, Y.; Hayami, S.; Kusunose, H. Manipulating the magnetoelectric effect: Essence learned from Co4Nb2O9. Phys. Rev. B 2018, 97, 020404. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayami, S. Nonreciprocal magnons due to symmetric anisotropic exchange interaction in honeycomb antiferromagnets. Phys. Rev. B 2020, 101, 224419. [Google Scholar] [CrossRef]
- Oishi, R.; Umeo, K.; Shimura, Y.; Onimaru, T.; Strydom, A.M.; Takabatake, T. Antiferromagnetic order in the honeycomb Kondo lattice CePt6Al3 induced by Pd substitution. Phys. Rev. B 2021, 104, 104411. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides AOsO4(A = K, Rb, and Cs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
- Ishitobi, T.; Hattori, K. Magnetoelectric Effects and Charge-Imbalanced Solenoids: Antiferro Quadrupole Orders in a Diamond Structure. J. Phys. Soc. Jpn. 2019, 88, 063708. [Google Scholar] [CrossRef]
- Yamaura, J.i.; Hiroi, Z. Crystal structure and magnetic properties of the 5d transition metal oxides AOsO4(A = K, Rb, Cs). Phys. Rev. B 2019, 99, 155113. [Google Scholar] [CrossRef]
- Maharaj, D.D.; Sala, G.; Stone, M.B.; Kermarrec, E.; Ritter, C.; Fauth, F.; Marjerrison, C.A.; Greedan, J.E.; Paramekanti, A.; Gaulin, B.D. Octupolar versus Néel Order in Cubic 5d2 Double Perovskites. Phys. Rev. Lett. 2020, 124, 087206. [Google Scholar] [CrossRef]
- Winkler, R.; Zülicke, U. Theory of electric, magnetic, and toroidal polarizations in crystalline solids with applications to hexagonal lonsdaleite and cubic diamond. Phys. Rev. B 2023, 107, 155201. [Google Scholar] [CrossRef]

| OP | IR (Orbital) | IR (Cluster) | Odd-Parity Multipole | ASOC |
|---|---|---|---|---|
| , | ||||
| , | ||||
| , | ||||
| , | ||||
| , , |
| OP | IR (Orbital) | IR (Cluster) | Odd-Parity Multipole | ASOC |
|---|---|---|---|---|
| , | ||||
| , |
| OP | IR (Orbital) | IR (Cluster) | Odd-Parity Multipole | ASOC |
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Cluster Odd-Parity Multipoles by Staggered Orbital Ordering in Locally Noncentrosymmetric Crystals. Crystals 2024, 14, 632. https://doi.org/10.3390/cryst14070632
Hayami S. Cluster Odd-Parity Multipoles by Staggered Orbital Ordering in Locally Noncentrosymmetric Crystals. Crystals. 2024; 14(7):632. https://doi.org/10.3390/cryst14070632
Chicago/Turabian StyleHayami, Satoru. 2024. "Cluster Odd-Parity Multipoles by Staggered Orbital Ordering in Locally Noncentrosymmetric Crystals" Crystals 14, no. 7: 632. https://doi.org/10.3390/cryst14070632
APA StyleHayami, S. (2024). Cluster Odd-Parity Multipoles by Staggered Orbital Ordering in Locally Noncentrosymmetric Crystals. Crystals, 14(7), 632. https://doi.org/10.3390/cryst14070632






