Cluster Odd-Parity Multipoles by Staggered Orbital Ordering in Locally Noncentrosymmetric Crystals
Abstract
:1. Introduction
2. Symmetry Analysis
3. Model
4. Results
5. Discussion
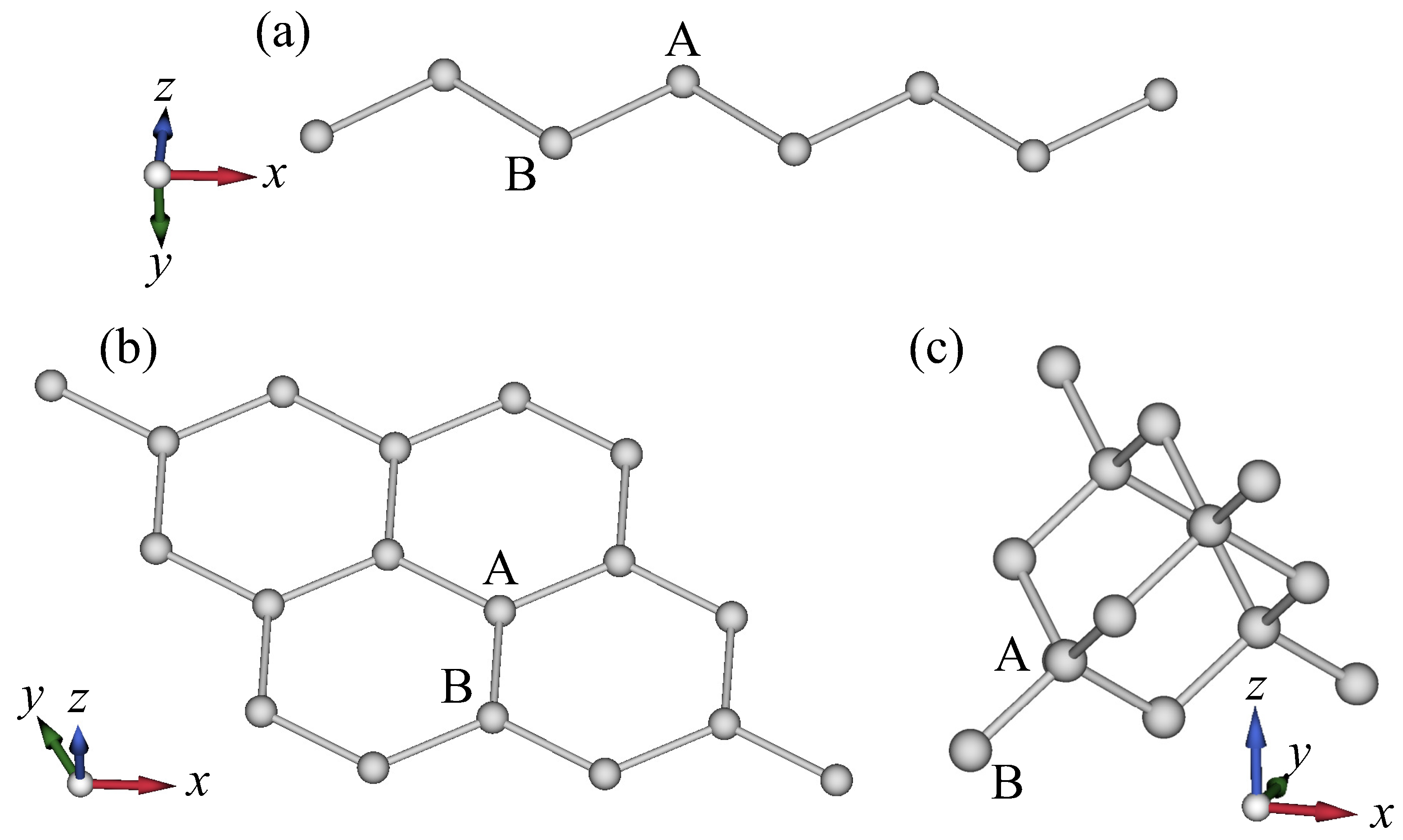
5.1. Honeycomb Structure
5.2. Diamond Structure
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aizu, K. Polarization, Pyroelectricity, and Ferroelectricity of Ionic Crystals. Rev. Mod. Phys. 1962, 34, 550–576. [Google Scholar] [CrossRef]
- Resta, R. Macroscopic polarization in crystalline dielectrics: The geometric phase approach. Rev. Mod. Phys. 1994, 66, 899–915. [Google Scholar] [CrossRef]
- Van Den Brink, J.; Khomskii, D.I. Multiferroicity due to charge ordering. J. Phys. Condens. Matter 2008, 20, 434217. [Google Scholar] [CrossRef]
- Ideue, T.; Hamamoto, K.; Koshikawa, S.; Ezawa, M.; Shimizu, S.; Kaneko, Y.; Tokura, Y.; Nagaosa, N.; Iwasa, Y. Bulk rectification effect in a polar semiconductor. Nat. Phys. 2017, 13, 578. [Google Scholar] [CrossRef]
- Tokura, Y.; Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 2018, 9, 3740. [Google Scholar] [CrossRef] [PubMed]
- Frigeri, P.A.; Agterberg, D.F.; Koga, A.; Sigrist, M. Superconductivity without Inversion Symmetry: MnSi versus CePt3Si. Phys. Rev. Lett. 2004, 92, 097001. [Google Scholar] [CrossRef] [PubMed]
- Bauer, E.; Sigrist, M. (Eds.) Non-Centrosymmetric Superconductors: Introduction and Overview (Lecture Notes in Physics), 2012th ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Dresselhaus, M.S.; Dresselhaus, G.; Jorio, A. Group Theory: Application to the Physics of Condensed Matter; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Frigeri, P.A.; Agterberg, D.F.; Sigrist, M. Spin susceptibility in superconductors without inversion symmetry. New J. Phys. 2004, 6, 115. [Google Scholar] [CrossRef]
- Palazzese, S.; Landaeta, J.; Subero, D.; Bauer, E.; Bonalde, I. Strong antisymmetric spin–orbit coupling and superconducting properties: The case of noncentrosymmetric LaPtSi. J. Phys. Condens. Matter 2018, 30, 255603. [Google Scholar] [CrossRef] [PubMed]
- Rashba, E.I. Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 1960, 2, 1109–1122. [Google Scholar]
- Ishizaka, K.; Bahramy, M.; Murakawa, H.; Sakano, M.; Shimojima, T.; Sonobe, T.; Koizumi, K.; Shin, S.; Miyahara, H.; Kimura, A.; et al. Giant Rashba-type spin splitting in bulk BiTeI. Nat. Mater. 2011, 10, 521–526. [Google Scholar] [CrossRef]
- Bahramy, M.S.; Arita, R.; Nagaosa, N. Origin of giant bulk Rashba splitting: Application to BiTeI. Phys. Rev. B 2011, 84, 041202(R). [Google Scholar] [CrossRef]
- Sunko, V.; Rosner, H.; Kushwaha, P.; Khim, S.; Mazzola, F.; Bawden, L.; Clark, O.; Riley, J.; Kasinathan, D.; Haverkort, M.; et al. Maximal Rashba-like spin splitting via kinetic-energy-coupled inversion-symmetry breaking. Nature 2017, 549, 492–496. [Google Scholar] [CrossRef] [PubMed]
- Takashima, R.; Fujimoto, S. Supercurrent-induced skyrmion dynamics and tunable Weyl points in chiral magnet with superconductivity. Phys. Rev. B 2016, 94, 235117. [Google Scholar] [CrossRef]
- Wang, B.Z.; Lu, Y.H.; Sun, W.; Chen, S.; Deng, Y.; Liu, X.J. Dirac-, Rashba-, and Weyl-type spin-orbit couplings: Toward experimental realization in ultracold atoms. Phys. Rev. A 2018, 97, 011605(R). [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Cheng, Y.C.; Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 2011, 84, 153402. [Google Scholar] [CrossRef]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699. [Google Scholar] [CrossRef]
- Ugeda, M.M.; Bradley, A.J.; Shi, S.F.; Felipe, H.; Zhang, Y.; Qiu, D.Y.; Ruan, W.; Mo, S.K.; Hussain, Z.; Shen, Z.X.; et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 2014, 13, 1091. [Google Scholar] [CrossRef] [PubMed]
- Kormányos, A.; Zólyomi, V.; Drummond, N.D.; Burkard, G. Spin-Orbit Coupling, Quantum Dots, and Qubits in Monolayer Transition Metal Dichalcogenides. Phys. Rev. X 2014, 4, 011034. [Google Scholar] [CrossRef]
- Fu, L. Parity-Breaking Phases of Spin-Orbit-Coupled Metals with Gyrotropic, Ferroelectric, and Multipolar Orders. Phys. Rev. Lett. 2015, 115, 026401. [Google Scholar] [CrossRef]
- Kozii, V.; Fu, L. Odd-Parity Superconductivity in the Vicinity of Inversion Symmetry Breaking in Spin-Orbit-Coupled Systems. Phys. Rev. Lett. 2015, 115, 207002. [Google Scholar] [CrossRef]
- Venderbos, J.W.F.; Kozii, V.; Fu, L. Odd-parity superconductors with two-component order parameters: Nematic and chiral, full gap, and Majorana node. Phys. Rev. B 2016, 94, 180504(R). [Google Scholar] [CrossRef]
- Hayami, S.; Yanagi, Y.; Kusunose, H.; Motome, Y. Electric Toroidal Quadrupoles in the Spin-Orbit-Coupled Metal Cd2Re2O7. Phys. Rev. Lett. 2019, 122, 147602. [Google Scholar] [CrossRef] [PubMed]
- Hirose, H.T.; Terashima, T.; Hirai, D.; Matsubayashi, Y.; Kikugawa, N.; Graf, D.; Sugii, K.; Sugiura, S.; Hiroi, Z.; Uji, S. Electronic states of metallic electric toroidal quadrupole order in Cd2Re2O7 determined by combining quantum oscillations and electronic structure calculations. Phys. Rev. B 2022, 105, 035116. [Google Scholar] [CrossRef]
- Hayami, S.; Yanagi, Y.; Kusunose, H. Spontaneous antisymmetric spin splitting in noncollinear antiferromagnets without spin-orbit coupling. Phys. Rev. B 2020, 101, 220403. [Google Scholar] [CrossRef]
- Murakami, S.; Nagaosa, N.; Zhang, S.C. Dissipationless quantum spin current at room temperature. Science 2003, 301, 1348–1351. [Google Scholar] [CrossRef] [PubMed]
- Murakami, S.; Nagaosa, N.; Zhang, S.C. Spin-Hall Insulator. Phys. Rev. Lett. 2004, 93, 156804. [Google Scholar] [CrossRef]
- Sinova, J.; Culcer, D.; Niu, Q.; Sinitsyn, N.A.; Jungwirth, T.; MacDonald, A.H. Universal Intrinsic Spin Hall Effect. Phys. Rev. Lett. 2004, 92, 126603. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, S. Emergent Nodal Excitations due to Coexistence of Superconductivity and Antiferromagnetism: Cases with and without Inversion Symmetry. J. Phys. Soc. Jpn. 2006, 75, 083704. [Google Scholar] [CrossRef]
- Fujimoto, S. Fermi liquid theory for heavy fermion superconductors without inversion symmetry: Magnetism and transport coefficients. J. Phys. Soc. Jpn. 2007, 76. [Google Scholar] [CrossRef]
- Edelstein, V.M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 1990, 73, 233–235. [Google Scholar] [CrossRef]
- Yip, S.K. Two-dimensional superconductivity with strong spin-orbit interaction. Phys. Rev. B 2002, 65, 144508. [Google Scholar] [CrossRef]
- Fujimoto, S. Magnetoelectric effects in heavy-fermion superconductors without inversion symmetry. Phys. Rev. B 2005, 72, 024515. [Google Scholar] [CrossRef]
- Yoda, T.; Yokoyama, T.; Murakami, S. Orbital Edelstein Effect as a Condensed-Matter Analog of Solenoids. Nano Lett. 2018, 18, 916–920. [Google Scholar] [CrossRef] [PubMed]
- Massarelli, G.; Wu, B.; Paramekanti, A. Orbital Edelstein effect from density-wave order. Phys. Rev. B 2019, 100, 075136. [Google Scholar] [CrossRef]
- Yip, S. Noncentrosymmetric superconductors. Annu. Rev. Condens. Matter Phys. 2014, 5, 15–33. [Google Scholar] [CrossRef]
- Sigrist, M.; Agterberg, D.F.; Fischer, M.H.; Goryo, J.; Loder, F.; Rhim, S.H.; Maruyama, D.; Yanase, Y.; Yoshida, T.; Youn, S.J. Superconductors with staggered non-centrosymmetricity. J. Phys. Soc. Jpn. 2014, 83, 061014. [Google Scholar] [CrossRef]
- Smidman, M.; Salamon, M.; Yuan, H.; Agterberg, D. Superconductivity and spin–orbit coupling in non-centrosymmetric materials: A review. Rep. Prog. Phys. 2017, 80, 036501. [Google Scholar] [CrossRef] [PubMed]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent spin-valley-orbital physics by spontaneous parity breaking. J. Phys. Condens. Matter 2016, 28, 395601. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Unified description of electronic orderings and cross correlations by complete multipole representation. J. Phys. Soc. Jpn. 2024, 93, 072001. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous Multipole Ordering by Local Parity Mixing. J. Phys. Soc. Jpn. 2015, 84, 064717. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Cysne, T.P.; Guimarães, F.S.M.; Canonico, L.M.; Rappoport, T.G.; Muniz, R.B. Orbital magnetoelectric effect in zigzag nanoribbons of p-band systems. Phys. Rev. B 2021, 104, 165403. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in PT-symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Suzuki, Y. Tunneling spin current in systems with spin degeneracy. Phys. Rev. B 2022, 105, 075201. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Y.; Xiao, D. Intrinsic Nonlinear Hall Effect in Antiferromagnetic Tetragonal CuMnAs. Phys. Rev. Lett. 2021, 127, 277201. [Google Scholar] [CrossRef] [PubMed]
- Kirikoshi, A.; Hayami, S. Microscopic mechanism for intrinsic nonlinear anomalous Hall conductivity in noncollinear antiferromagnetic metals. Phys. Rev. B 2023, 107, 155109. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Kusunose, H. Nonlinear spin Hall effect in PT-symmetric collinear magnets. Phys. Rev. B 2022, 106, 024405. [Google Scholar] [CrossRef]
- Kondo, H.; Akagi, Y. Nonlinear magnon spin Nernst effect in antiferromagnets and strain-tunable pure spin current. Phys. Rev. Res. 2022, 4, 013186. [Google Scholar] [CrossRef]
- Sumita, S.; Yanase, Y. Superconductivity in magnetic multipole states. Phys. Rev. B 2016, 93, 224507. [Google Scholar] [CrossRef]
- Tokura, Y.; Nagaosa, N. Orbital physics in transition-metal oxides. Science 2000, 288, 462–468. [Google Scholar] [CrossRef] [PubMed]
- Khomskii, D.; Mostovoy, M. Orbital ordering and frustrations. J. Phys. A 2003, 36, 9197. [Google Scholar] [CrossRef]
- Streltsov, S.V.; Khomskii, D.I. Orbital physics in transition metal compounds: New trends. Phys. Usp. 2017, 60, 1121. [Google Scholar] [CrossRef]
- Khomskii, D.I.; Streltsov, S.V. Orbital effects in solids: Basics, recent progress, and opportunities. Chem. Rev. 2021, 121, 2992–3030. [Google Scholar] [CrossRef] [PubMed]
- Pen, H.F.; van den Brink, J.; Khomskii, D.I.; Sawatzky, G.A. Orbital Ordering in a Two-Dimensional Triangular Lattice. Phys. Rev. Lett. 1997, 78, 1323–1326. [Google Scholar] [CrossRef]
- Kumar, S.; Kampf, A.P.; Majumdar, P. Domain Formation and Orbital Ordering Transition in a Doped Jahn-Teller Insulator. Phys. Rev. Lett. 2006, 97, 176403. [Google Scholar] [CrossRef]
- Lv, W.; Wu, J.; Phillips, P. Orbital ordering induces structural phase transition and the resistivity anomaly in iron pnictides. Phys. Rev. B 2009, 80, 224506. [Google Scholar] [CrossRef]
- Lee, C.C.; Yin, W.G.; Ku, W. Ferro-Orbital Order and Strong Magnetic Anisotropy in the Parent Compounds of Iron-Pnictide Superconductors. Phys. Rev. Lett. 2009, 103, 267001. [Google Scholar] [CrossRef]
- Kurihara, R.; Mitsumoto, K.; Akatsu, M.; Nemoto, Y.; Goto, T.; Kobayashi, Y.; Sato, M. Critical Slowing Down of Quadrupole and Hexadecapole Orderings in Iron Pnictide Superconductor. J. Phys. Soc. Jpn. 2017, 86, 064706. [Google Scholar] [CrossRef]
- Voleti, S.; Maharaj, D.D.; Gaulin, B.D.; Luke, G.; Paramekanti, A. Multipolar magnetism in d-orbital systems: Crystal field levels, octupolar order, and orbital loop currents. Phys. Rev. B 2020, 101, 155118. [Google Scholar] [CrossRef]
- Paramekanti, A.; Maharaj, D.D.; Gaulin, B.D. Octupolar order in d-orbital Mott insulators. Phys. Rev. B 2020, 101, 054439. [Google Scholar] [CrossRef]
- Hirai, D.; Sagayama, H.; Gao, S.; Ohsumi, H.; Chen, G.; Arima, T.h.; Hiroi, Z. Detection of multipolar orders in the spin-orbit-coupled 5d Mott insulator Ba2MgReO6. Phys. Rev. Res. 2020, 2, 022063. [Google Scholar] [CrossRef]
- Mansouri Tehrani, A.; Spaldin, N.A. Untangling the structural, magnetic dipole, and charge multipolar orders in Ba2MgReO6. Phys. Rev. Mater. 2021, 5, 104410. [Google Scholar] [CrossRef]
- Lovesey, S.W.; Khalyavin, D.D. Magnetic order and 5d1 multipoles in a rhenate double perovskite Ba2MgReO6. Phys. Rev. B 2021, 103, 235160. [Google Scholar] [CrossRef]
- Morin, P.; Schmitt, D.; De Lacheisserie, E.D.T. Magnetic and quadrupolar properties of PrPb3. J. Magn. Magn. Mater. 1982, 30, 257–264. [Google Scholar] [CrossRef]
- Takigawa, M.; Yasuoka, H.; Tanaka, T.; Ishizawa, Y. NMR Study on the Spin Structure of CeB6. J. Phys. Soc. Jpn. 1983, 52, 728–731. [Google Scholar] [CrossRef]
- Lüthi, B.; Blumenröder, S.; Hillebrands, B.; Zirngiebl, E.; Güntherodt, G.; Winzer, K. Elastic and magnetoelastic effects in CeB6. Z. Phys. 1984, 58, 31–38. [Google Scholar] [CrossRef]
- Effantin, J.; Rossat-Mignod, J.; Burlet, P.; Bartholin, H.; Kunii, S.; Kasuya, T. Magnetic phase diagram of CeB6. J. Magn. Magn. Mater. 1985, 47–48, 145–148. [Google Scholar] [CrossRef]
- Erkelens, W.A.C.; Regnault, L.P.; Burlet, P.; Rossat-Mignod, J.; Kunii, S.; Kasuya, T. Neutron scattering study of the antiferroquadrupolar ordering in CeB6 and Ce0.75La0.25B6. J. Magn. Magn. Mater. 1987, 63–64, 61–63. [Google Scholar] [CrossRef]
- Morin, P.; Rouchy, J.; Yonenobu, K.; Yamagishi, A.; Date, M. Interplay of antiferromagnetic and antiferroquadrupolar interactions in DyAg and other rare earth intermetallic compounds. J. Magn. Magn. Mater. 1989, 81, 247–258. [Google Scholar] [CrossRef]
- Nakamura, S.; Goto, T.; Kunii, S.; Iwashita, K.; Tamaki, A. Quadrupole-strain interaction in rare earth hexaborides. J. Phys. Soc. Jpn. 1994, 63, 623–636. [Google Scholar] [CrossRef]
- Sakai, O.; Shiina, R.; Shiba, H.; Thalmeier, P. A new interpretation of NMR in quadrupolar ordering phase of CeB6-Consistency with neutron scattering. J. Phys. Soc. Jpn. 1997, 66, 3005–3007. [Google Scholar] [CrossRef]
- Shiina, R.; Shiba, H.; Thalmeier, P. Magnetic-field effects on quadrupolar ordering in a Γ 8-quartet system CeB6. J. Phys. Soc. Jpn. 1997, 66, 1741–1755. [Google Scholar] [CrossRef]
- Nakao, H.; Magishi, K.i.; Wakabayashi, Y.; Murakami, Y.; Koyama, K.; Hirota, K.; Endoh, Y.; Kunii, S. Antiferro-quadrupole ordering of CeB6 studied by resonant X-ray scattering. J. Phys. Soc. Jpn. 2001, 70, 1857–1860. [Google Scholar] [CrossRef]
- Tanaka, Y.; Staub, U.; Katsumata, K.; Lovesey, S.; Lorenzo, J.; Narumi, Y.; Scagnoli, V.; Shimomura, S.; Tabata, Y.; Onuki, Y.; et al. Direct and quantitative determination of the orbital ordering in CeB6 by X-ray diffraction. Europhys. Lett. 2004, 68, 671. [Google Scholar] [CrossRef]
- Onimaru, T.; Sakakibara, T.; Aso, N.; Yoshizawa, H.; Suzuki, H.S.; Takeuchi, T. Observation of Modulated Quadrupolar Structures in PrPb3. Phys. Rev. Lett. 2005, 94, 197201. [Google Scholar] [CrossRef] [PubMed]
- Ishii, I.; Muneshige, H.; Suetomi, Y.; K. Fujita, T.; Onimaru, T.; T. Matsumoto, K.; Takabatake, T.; Araki, K.; Akatsu, M.; Nemoto, Y.; et al. Antiferro-Quadrupolar Ordering at the Lowest Temperature and Anisotropic Magnetic Field-Temperature Phase Diagram in the Cage Compound PrIr2Zn20. J. Phys. Soc. Jpn. 2011, 80, 093601. [Google Scholar] [CrossRef]
- Sakai, A.; Nakatsuji, S. Kondo Effects and Multipolar Order in the Cubic PrTr2Al20 (Tr = Ti, V). J. Phys. Soc. Jpn. 2011, 80, 063701. [Google Scholar] [CrossRef]
- Onimaru, T.; Matsumoto, K.T.; Inoue, Y.F.; Umeo, K.; Sakakibara, T.; Karaki, Y.; Kubota, M.; Takabatake, T. Antiferroquadrupolar Ordering in a Pr-Based Superconductor PrIr2Zn20. Phys. Rev. Lett. 2011, 106, 177001. [Google Scholar] [CrossRef]
- Sakai, A.; Kuga, K.; Nakatsuji, S. Superconductivity in the Ferroquadrupolar State in the Quadrupolar Kondo Lattice PrTi2Al20. J. Phys. Soc. Jpn. 2012, 81, 083702. [Google Scholar] [CrossRef]
- Onimaru, T.; Nagasawa, N.; Matsumoto, K.; Wakiya, K.; Umeo, K.; Kittaka, S.; Sakakibara, T.; Matsushita, Y.; Takabatake, T. Simultaneous superconducting and antiferroquadrupolar transitions in PrRh 2 Zn 20. Phys. Rev. B 2012, 86, 184426. [Google Scholar] [CrossRef]
- Matsumura, T.; Yonemura, T.; Kunimori, K.; Sera, M.; Iga, F.; Nagao, T.; Igarashi, J.i. Antiferroquadrupole order and magnetic field induced octupole in CeB6. Phys. Rev. B 2012, 85, 174417. [Google Scholar] [CrossRef]
- Tsujimoto, M.; Matsumoto, Y.; Tomita, T.; Sakai, A.; Nakatsuji, S. Heavy-Fermion Superconductivity in the Quadrupole Ordered State of PrV2Al20. Phys. Rev. Lett. 2014, 113, 267001. [Google Scholar] [CrossRef]
- Matsumoto, K.T.; Onimaru, T.; Wakiya, K.; Umeo, K.; Takabatake, T. Effect of La Substitution in PrIr2Zn20 on the Superconductivity and Antiferro-Quadrupole Order. J. Phys. Soc. Jpn. 2015, 84, 063703. [Google Scholar] [CrossRef]
- Kubo, T.; Kotegawa, H.; Tou, H.; Higashinaka, R.; Nakama, A.; Aoki, Y.; Sato, H. Absence of Magnetic Dipolar Phase Transition and Evolution of Low-Energy Excitations in PrNb2Al20 with Crystal Electric Field Γ3 Ground State: Evidence from 93Nb-NQR Studies. J. Phys. Soc. Jpn. 2015, 84, 074701. [Google Scholar] [CrossRef]
- Onimaru, T.; Kusunose, H. Exotic Quadrupolar Phenomena in Non-Kramers Doublet Systems—The Cases of PrT2Zn20 (T = Ir, Rh) and PrT2Al20 (T = V, Ti)—. J. Phys. Soc. Jpn. 2016, 85, 082002. [Google Scholar] [CrossRef]
- Cameron, A.S.; Friemel, G.; Inosov, D.S. Multipolar phases and magnetically hidden order: Review of the heavy-fermion compound Ce1−xLaxB6. Rep. Prog. Phys. 2016, 79, 066502. [Google Scholar] [CrossRef]
- Onimaru, T.; Izawa, K.; Matsumoto, K.T.; Yoshida, T.; Machida, Y.; Ikeura, T.; Wakiya, K.; Umeo, K.; Kittaka, S.; Araki, K.; et al. Quadrupole-driven non-Fermi-liquid and magnetic-field-induced heavy fermion states in a non-Kramers doublet system. Phys. Rev. B 2016, 94, 075134. [Google Scholar] [CrossRef]
- Portnichenko, P.Y.; Akbari, A.; Nikitin, S.E.; Cameron, A.S.; Dukhnenko, A.V.; Filipov, V.B.; Shitsevalova, N.Y.; Čermák, P.; Radelytskyi, I.; Schneidewind, A.; et al. Field-Angle-Resolved Magnetic Excitations as a Probe of Hidden-Order Symmetry in CeB6. Phys. Rev. X 2020, 10, 021010. [Google Scholar] [CrossRef]
- Tanida, H.; Muro, Y.; Matsumura, T. La Substitution and Pressure Studies on CeCoSi: A Possible Antiferroquadrupolar Ordering Induced by Pressure. J. Phys. Soc. Jpn. 2018, 87, 023705. [Google Scholar] [CrossRef]
- Tanida, H.; Mitsumoto, K.; Muro, Y.; Fukuhara, T.; Kawamura, Y.; Kondo, A.; Kindo, K.; Matsumoto, Y.; Namiki, T.; Kuwai, T.; et al. Successive Phase Transition at Ambient Pressure in CeCoSi: Single Crystal Studies. J. Phys. Soc. Jpn. 2019, 88, 054716. [Google Scholar] [CrossRef]
- Matsumura, T.; Kishida, S.; Tsukagoshi, M.; Kawamura, Y.; Nakao, H.; Tanida, H. Structural Transition in the Hidden Ordered Phase of CeCoSi. J Phys. Soc. Jpn. 2022, 91, 064704. [Google Scholar] [CrossRef]
- Manago, M.; Ishigaki, A.; Tou, H.; Harima, H.; Tanida, H.; Kotegawa, H. Ferroic quadrupolar ordering in CeCoSi revealed using 59Co NMR measurements. Phys. Rev. B 2023, 108, 085118. [Google Scholar] [CrossRef]
- Garaud, J.; Carlström, J.; Babaev, E.; Speight, M. Chiral CP2 skyrmions in three-band superconductors. Phys. Rev. B 2013, 87, 014507. [Google Scholar] [CrossRef]
- Akagi, Y.; Amari, Y.; Sawado, N.; Shnir, Y. Isolated skyrmions in the CP2 nonlinear sigma model with a Dzyaloshinskii-Moriya type interaction. Phys. Rev. D 2021, 103, 065008. [Google Scholar] [CrossRef]
- Amari, Y.; Akagi, Y.; Gudnason, S.B.; Nitta, M.; Shnir, Y. CP2 skyrmion crystals in an SU(3) magnet with a generalized Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2022, 106, L100406. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Dahlbom, D.; Barros, K.; Batista, C.D. CP2 skyrmions and skyrmion crystals in realistic quantum magnets. Nat. Commun. 2023, 14, 3626. [Google Scholar] [CrossRef]
- Hayami, S.; Tsutsui, S.; Hanate, H.; Nagasawa, N.; Yoda, Y.; Matsuhira, K. Cluster Toroidal Multipoles Formed by Electric-Quadrupole and Magnetic-Octupole Trimers: A Possible Scenario for Hidden Orders in Ca5Ir3O12. J. Phys. Soc. Jpn. 2023, 92, 033702. [Google Scholar] [CrossRef]
- Shibata, K.; Naka, M.; Jeschke, H.O.; Otsuki, J. Spin-orbital ordering in alkali superoxides. Phys. Rev. B 2024, 109, 235115. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Nomoto, T.; Arita, R.; Yanagi, Y.; Hayami, S.; Kusunose, H. Multipole expansion for magnetic structures: A generation scheme for a symmetry-adapted orthonormal basis set in the crystallographic point group. Phys. Rev. B 2019, 99, 174407. [Google Scholar] [CrossRef]
- Kusunose, H.; Oiwa, R.; Hayami, S. Symmetry-adapted modeling for molecules and crystals. Phys. Rev. B 2023, 107, 195118. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Microscopic Description of Electric and Magnetic Toroidal Multipoles in Hybrid Orbitals. J. Phys. Soc. Jpn. 2018, 87, 033709. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Yanagi, Y.; Kusunose, H. Classification of atomic-scale multipoles under crystallographic point groups and application to linear response tensors. Phys. Rev. B 2018, 98, 165110. [Google Scholar] [CrossRef]
- Li, X.; Cao, T.; Niu, Q.; Shi, J.; Feng, J. Coupling the valley degree of freedom to antiferromagnetic order. Proc. Natl. Acad. Sci. USA 2013, 110, 3738–3742. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Yanagi, Y.; Kusunose, H. Optical Selection Rules in Spin–Orbit Coupled Systems on Honeycomb Lattice. J. Phys. Soc. Jpn. 2017, 86, 083703. [Google Scholar] [CrossRef]
- Yanagi, Y.; Hayami, S.; Kusunose, H. Manipulating the magnetoelectric effect: Essence learned from Co4Nb2O9. Phys. Rev. B 2018, 97, 020404. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayami, S. Nonreciprocal magnons due to symmetric anisotropic exchange interaction in honeycomb antiferromagnets. Phys. Rev. B 2020, 101, 224419. [Google Scholar] [CrossRef]
- Oishi, R.; Umeo, K.; Shimura, Y.; Onimaru, T.; Strydom, A.M.; Takabatake, T. Antiferromagnetic order in the honeycomb Kondo lattice CePt6Al3 induced by Pd substitution. Phys. Rev. B 2021, 104, 104411. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides AOsO4(A = K, Rb, and Cs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
- Ishitobi, T.; Hattori, K. Magnetoelectric Effects and Charge-Imbalanced Solenoids: Antiferro Quadrupole Orders in a Diamond Structure. J. Phys. Soc. Jpn. 2019, 88, 063708. [Google Scholar] [CrossRef]
- Yamaura, J.i.; Hiroi, Z. Crystal structure and magnetic properties of the 5d transition metal oxides AOsO4(A = K, Rb, Cs). Phys. Rev. B 2019, 99, 155113. [Google Scholar] [CrossRef]
- Maharaj, D.D.; Sala, G.; Stone, M.B.; Kermarrec, E.; Ritter, C.; Fauth, F.; Marjerrison, C.A.; Greedan, J.E.; Paramekanti, A.; Gaulin, B.D. Octupolar versus Néel Order in Cubic 5d2 Double Perovskites. Phys. Rev. Lett. 2020, 124, 087206. [Google Scholar] [CrossRef]
- Winkler, R.; Zülicke, U. Theory of electric, magnetic, and toroidal polarizations in crystalline solids with applications to hexagonal lonsdaleite and cubic diamond. Phys. Rev. B 2023, 107, 155201. [Google Scholar] [CrossRef]

| OP | IR (Orbital) | IR (Cluster) | Odd-Parity Multipole | ASOC |
|---|---|---|---|---|
| , | ||||
| , | ||||
| , | ||||
| , | ||||
| , , |
| OP | IR (Orbital) | IR (Cluster) | Odd-Parity Multipole | ASOC |
|---|---|---|---|---|
| , | ||||
| , |
| OP | IR (Orbital) | IR (Cluster) | Odd-Parity Multipole | ASOC |
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Cluster Odd-Parity Multipoles by Staggered Orbital Ordering in Locally Noncentrosymmetric Crystals. Crystals 2024, 14, 632. https://doi.org/10.3390/cryst14070632
Hayami S. Cluster Odd-Parity Multipoles by Staggered Orbital Ordering in Locally Noncentrosymmetric Crystals. Crystals. 2024; 14(7):632. https://doi.org/10.3390/cryst14070632
Chicago/Turabian StyleHayami, Satoru. 2024. "Cluster Odd-Parity Multipoles by Staggered Orbital Ordering in Locally Noncentrosymmetric Crystals" Crystals 14, no. 7: 632. https://doi.org/10.3390/cryst14070632
APA StyleHayami, S. (2024). Cluster Odd-Parity Multipoles by Staggered Orbital Ordering in Locally Noncentrosymmetric Crystals. Crystals, 14(7), 632. https://doi.org/10.3390/cryst14070632






