Recent Developments in Transmission Electron Microscopy for Crystallographic Characterization of Strained Semiconductor Heterostructures
Abstract
1. Introduction
2. Characterization Methods in TEM
2.1. Electron Diffraction Techniques
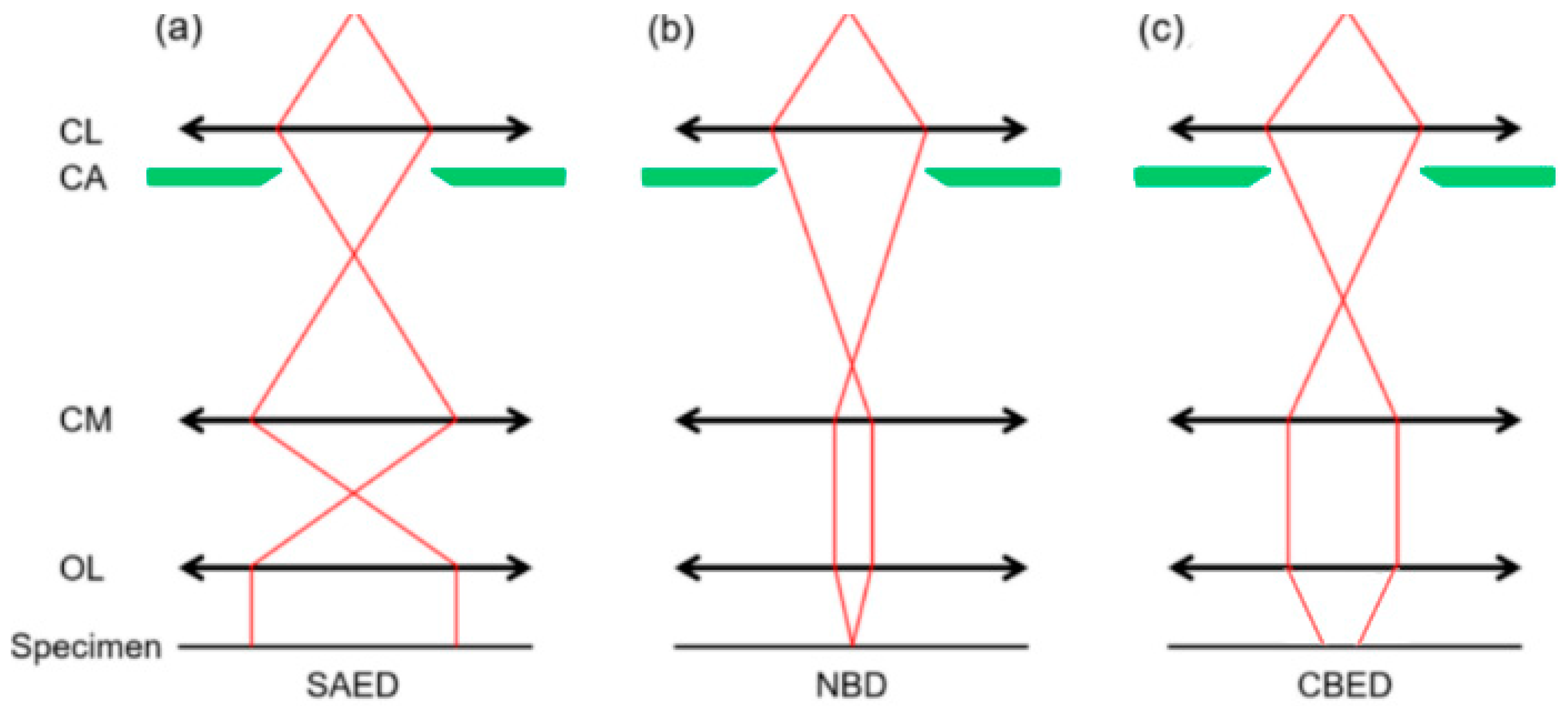
2.1.1. Selected Area Electron Diffraction
2.1.2. Convergent-Beam Electron Diffraction
2.1.3. Nanobeam Electron Diffraction
2.1.4. Precession Electron Diffraction
2.2. Weak Beam Dark Field and Two-Beam Condition Imaging
2.2.1. Imaging Under Two-Beam Condition (TBC)
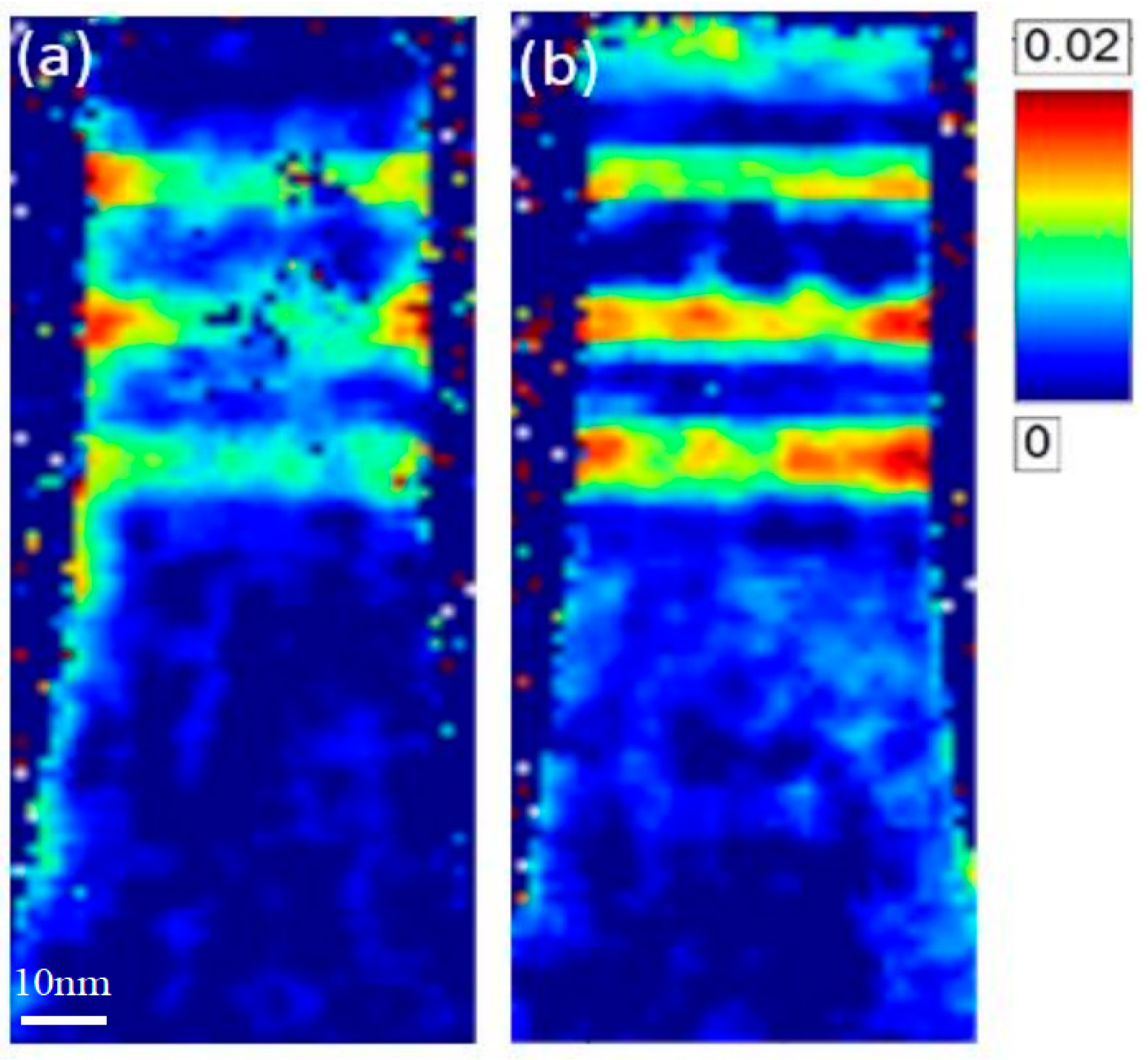
2.2.2. Weak Beam Dark Field Imaging
2.3. High-Resolution Scanning TEM (HRSTEM)
2.3.1. High-Angle Annular Dark-Field Imaging
2.3.2. Low-Angle Annular Dark-Field (LAADF) Imaging
2.3.3. Bright-Field (BF) Imaging
2.4. 4D-STEM, Ultrafast Pump-Probe TEM, and Differential Phase Contrast (DPC)
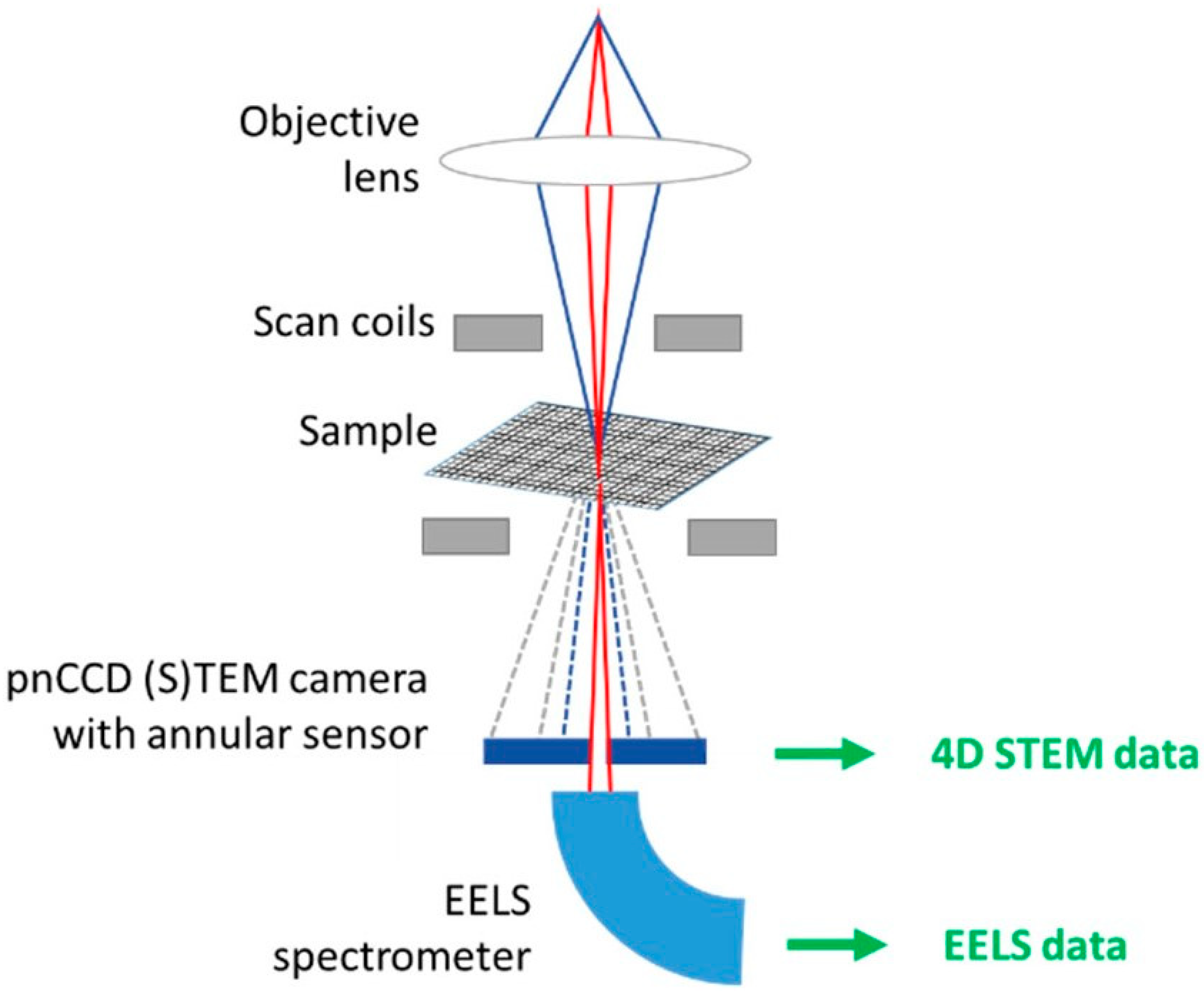
2.4.1. 4D-STEM
2.4.2. Ultrafast TEM
2.4.3. Differential Phase Contrast (DPC)
2.5. Ptychography, Tomography, and Electron Holography
2.5.1. Ptychography
2.5.2. Tomography
2.5.3. Electron Holography
2.6. TEM and Application
2.7. Summary
3. In Situ TEM
3.1. Sample Preparation and Mounting for In Situ TEM
3.2. In Situ Technology and Application
3.2.1. Thermal Dynamics of Strain and Dislocations
3.2.2. Stress-Induced Deformation and Phase Transformation
3.3. Challenges for In Situ TEM Applications
3.4. Summary of This Section
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Dayeh, S.A. Electron transport in indium arsenide nanowires. Semicond. Sci. Technol. 2010, 25, 024004. [Google Scholar] [CrossRef]
- Yoon, J.; Jo, S.; Chun, I.S.; Jung, I.; Kim, H.-S.; Meitl, M.; Menard, E.; Li, X.; Coleman, J.J.; Paik, U. GaAs photovoltaics and optoelectronics using releasable multilayer epitaxial assemblies. Nature 2010, 465, 329–333. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.L.; Fitzgerald, E.A.; Bulsara, M.T.; Currie, M.T.; Lochtefeld, A. Strained Si, SiGe, and Ge channels for high-mobility metal-oxide-semiconductor field-effect transistors. J. Appl. Phys. 2005, 97, 011101. [Google Scholar] [CrossRef]
- Shi, B.; Zhao, H.; Wang, L.; Song, B.; Suran Brunelli, S.T.; Klamkin, J. Continuous-wave electrically pumped 1550 nm lasers epitaxially grown on on-axis (001) silicon. Optica 2019, 6, 1507–1514. [Google Scholar] [CrossRef]
- Fujii, T.; Hiraki, T.; Aihara, T.; Nishi, H.; Takeda, K.; Sato, T.; Kakitsuka, T.; Tsuchizawa, T.; Matsuo, S. Development of an epitaxial growth technique using iii–v on a si platform for heterogeneous integration of membrane photonic devices on Si. Appl. Sci. 2021, 11, 1801. [Google Scholar] [CrossRef]
- Lee, S.-M.; Kwong, A.; Jung, D.; Faucher, J.; Biswas, R.; Shen, L.; Kang, D.; Lee, M.L.; Yoon, J. High performance ultrathin GaAs solar cells enabled with heterogeneously integrated dielectric periodic nanostructures. ACS Nano 2015, 9, 10356–10365. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.-J.; Holloway, P.H. Ohmic contacts to II–VI and III–V compound semiconductors. In Processing of Wide Band Gap Semiconductors; Elsevier: Amsterdam, The Netherlands, 2000; pp. 80–150. [Google Scholar]
- Sammak, A. Silicon-Based Integration of Groups III, IV, V Chemical Vapor Depositions in High-Quality Photodiodes. Ph.D. Thesis, University of Tehran, Tehran, Iran, 2012. [Google Scholar]
- Das, S.R. Advances in InSb and InAs Nanowire Based Nanoelectronic Field Effect Transistors. In Nanoelectronics; Elsevier: Amsterdam, The Netherlands, 2019; pp. 355–373. [Google Scholar]
- Biermanns, A.; Rieger, T.; Bussone, G.; Pietsch, U.; Grützmacher, D.; Ion Lepsa, M. Axial strain in GaAs/InAs core-shell nanowires. Appl. Phys. Lett. 2013, 102, 043109. [Google Scholar] [CrossRef]
- Walther, T.; Cullis, A.; Norris, D.; Hopkinson, M. Nature of the Stranski-Krastanow transition during epitaxy of InGaAs on GaAs. Phys. Rev. Lett. 2001, 86, 2381–2384. [Google Scholar] [CrossRef] [PubMed]
- Riedl, T.; Kunnathully, V.S.; Trapp, A.; Langer, T.; Reuter, D.; Lindner, J.K. Size-dependent strain relaxation in InAs quantum dots on top of GaAs (111)A nanopillars. Adv. Mater. Interfaces 2022, 9, 2102159. [Google Scholar] [CrossRef]
- Jallipalli, A.; Balakrishnan, G.; Huang, S.; Khoshakhlagh, A.; Dawson, L.; Huffaker, D. Atomistic modeling of strain distribution in self-assembled interfacial misfit dislocation (IMF) arrays in highly mismatched III–V semiconductor materials. J. Cryst. Growth 2007, 303, 449–455. [Google Scholar] [CrossRef]
- Hirashita, N.; Moriyama, Y.; Sugiyama, N.; Toyoda, E.; Takagi, S.-i. Misfit strain relaxation in strained-Si layers on silicon-germanium-on-insulator substrates. Appl. Phys. Lett. 2006, 89, 091916. [Google Scholar] [CrossRef]
- Shilkrot, L.E.; Srolovitz, D.J.; Tersoff, J. Morphology evolution during the growth of strained-layer superlattices. Phys. Rev. B 2000, 62, 8397–8409. [Google Scholar] [CrossRef]
- Vullum, P.E.; Nord, M.; Vatanparast, M.; Thomassen, S.F.; Boothroyd, C.; Holmestad, R.; Fimland, B.-O.; Reenaas, T.W. Quantitative strain analysis of InAs/GaAs quantum dot materials. Sci. Rep. 2017, 7, 45376. [Google Scholar] [CrossRef]
- Ohtani, H.; Kobayashi, K.; Ishida, K. Thermodynamic study of phase equilibria in strained III–V alloy semiconductors. J. Phase Equilibria 2001, 22, 276–286. [Google Scholar] [CrossRef]
- Chen, C.-C.; Zhu, C.; White, E.R.; Chiu, C.-Y.; Scott, M.; Regan, B.; Marks, L.D.; Huang, Y.; Miao, J. Three-dimensional imaging of dislocations in a nanoparticle at atomic resolution. Nature 2013, 496, 74–77. [Google Scholar] [CrossRef]
- Kaiser, U. TEM Characterization of Nanostructured Materials-Opportunities and Challenges. Microsc. Microanal. 2003, 9, 218. [Google Scholar] [CrossRef]
- Epp, J. X-ray diffraction (XRD) techniques for materials characterization. In Materials Characterization Using Nondestructive Evaluation (NDE) Methods; Elsevier: Amsterdam, The Netherlands, 2016; pp. 81–124. [Google Scholar]
- Trache, A.; Meininger, G.A. Atomic force microscopy (AFM). Curr. Protoc. Microbiol. 2008, 8, 2C.2.1–2C.2.17. [Google Scholar] [CrossRef] [PubMed]
- Rouvière, J.L.; Mouti, A.; Stadelmann, P. Measuring strain on HR-STEM images: Application to threading dislocations in Al0.8In0.2N. J. Phys. Conf. Ser. 2011, 326, 012022. [Google Scholar] [CrossRef]
- Nellist, P.; Pennycook, S. The principles and interpretation of annular dark-field Z-contrast imaging. In Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 2000; Volume 113, pp. 147–203. [Google Scholar]
- Knyazev, S.N.; Kudrya, A.V.; Komarovskiy, N.Y.; Parkhomenko, Y.N.; Molodtsova, E.V.; Yushchuk, V.V. Methods of dislocation structure characterization in AIII BV semiconductor single crystals. Mod. Electron. Mater. 2022, 8, 131–140. [Google Scholar] [CrossRef]
- Bender, H.; Bosch, E.G.; Richard, O.; Mendez, D.; Favia, P.; Lazić, I. 3D characterization of nanowire devices with STEM based modes. Semicond. Sci. Technol. 2019, 34, 114001. [Google Scholar] [CrossRef]
- Jo, J.; Tchoe, Y.; Yi, G.-C.; Kim, M. Real-time characterization using in situ RHEED transmission mode and TEM for investigation of the growth behaviour of nanomaterials. Sci. Rep. 2018, 8, 1694. [Google Scholar] [CrossRef]
- Fan, Z.; Zhang, L.; Baumann, D.; Mei, L.; Yao, Y.; Duan, X.; Shi, Y.; Huang, J.; Huang, Y.; Duan, X. In situ transmission electron microscopy for energy materials and devices. Adv. Mater. 2019, 31, 1900608. [Google Scholar] [CrossRef]
- Guo, H.; Tan, X.; Zhang, S. In situ TEM study on the microstructural evolution during electric fatigue in 0.7 Pb (Mg1/3Nb2/3) O3–0.3 PbTiO3 ceramic. J. Mater. Res. 2015, 30, 364–372. [Google Scholar] [CrossRef][Green Version]
- Kaoumi, D.; Gautier, T.; Adamson, J.; Kirk, M. Using In-Situ TEM to Characterize the Microstructure Evolution of Metallic Systems under External Solicitation. Microsc. Microanal. 2015, 21, 111–112. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, C.; Wu, X.; Chu, J. Review in situ transmission electron microscope with machine learning. J. Semicond. 2022, 43, 081001. [Google Scholar] [CrossRef]
- Shen, Y.; Sun, L. Setting up a nanolab inside a transmission electron microscope for two-dimensional materials research. J. Mater. Res. 2015, 30, 3153–3176. [Google Scholar] [CrossRef][Green Version]
- Xu, Z.; Tan, X.; Han, P.; Shang, J. In situ transmission electron microscopy study of electric-field-induced microcracking in single crystal Pb (Mg 1/3 Nb 2/3)O3–PbTiO 3. Appl. Phys. Lett. 2000, 76, 3732–3734. [Google Scholar] [CrossRef]
- Fan, Z.; Tan, X. Dual-stimuli in-situ TEM study on the nonergodic/ergodic crossover in the 0.75 (Bi1/2Na1/2) TiO3–0.25 SrTiO3 relaxor. Appl. Phys. Lett. 2019, 114, 212901. [Google Scholar] [CrossRef]
- Nielsen, M.H.; Aloni, S.; De Yoreo, J.J. In situ TEM imaging of CaCO(3) nucleation reveals coexistence of direct and indirect pathways. Science 2014, 345, 1158–1162. [Google Scholar] [CrossRef]
- Dong, J.; Bai, H.; Deng, Y.; Liu, S.; Wang, X.; Qiu, Y.; Shi, Y.; Walther, T. Transmission electron microscopy of epitaxial semiconductor materials and devices. J. Phys. D Appl. Phys. 2024, 58, 043001. [Google Scholar] [CrossRef]
- Weirich, T.E.; Zou, X.; Ramlau, R.; Simon, A.; Cascarano, G.L.; Giacovazzo, C.; Hovmöller, S. Structures of nanometre-size crystals determined from selected-area electron diffraction data. Acta Crystallogr. Sect. A 2000, 56, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, M.; Tsuda, K. Convergent-beam electron diffraction. J. Electron Microsc. 2011, 60, S245–S267. [Google Scholar] [CrossRef] [PubMed]
- Armigliato, A.; Frabboni, S.; Gazzadi, G.C. Electron diffraction with ten nanometer beam size for strain analysis of nanodevices. Appl. Phys. Lett. 2008, 93, 161906. [Google Scholar] [CrossRef]
- Rauch, E.F.; Portillo, J.; Nicolopoulos, S.; Bultreys, D.; Rouvimov, S.; Moeck, P. Automated nanocrystal orientation and phase mapping in the transmission electron microscope on the basis of precession electron diffraction. Z. Krist. 2010, 225, 103–109. [Google Scholar] [CrossRef]
- Eggeman, A.S.; Midgley, P.A. Precession electron diffraction. In Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 2012; Volume 170, pp. 1–63. [Google Scholar]
- Williams, D.B.; Carter, C.B.; Williams, D.B.; Carter, C.B. Weak-beam dark-field microscopy. In Transmission Electron Microscopy: A Textbook for Materials Science, 2nd ed.; Springer: New York, NY, USA, 2009; pp. 463–481. [Google Scholar]
- Klenov, D.O.; Stemmer, S. Contributions to the contrast in experimental high-angle annular dark-field images. Ultramicroscopy 2006, 106, 889–901. [Google Scholar] [CrossRef] [PubMed]
- Mitsuishi, K.; Hashimoto, A.; Takeguchi, M.; Shimojo, M.; Ishizuka, K. Imaging properties of bright-field and annular-dark-field scanning confocal electron microscopy. Ultramicroscopy 2010, 111, 20–26. [Google Scholar] [CrossRef]
- Davydova, N.; Finders, J.; McNamara, J.; van Setten, E.; van Lare, C.; Franke, J.-H.; Frommhold, A.; Capelli, R.; Kersteen, G.; Verch, A. Fundamental understanding and experimental verification of bright versus dark field imaging. In Proceedings of the Extreme Ultraviolet Lithography, Virtual Conference, 7 June 2020; pp. 40–57. [Google Scholar]
- Mireles, A.; Shi, C.; Park, J.; Shin, B.; Sung, S.H.; Ophus, C.; Hovden, R.; Kang, K.; Han, Y. Using 4D-STEM to Map 3D Morphologies of 2D Materials. Microsc. Microanal. 2023, 29, 262–263. [Google Scholar] [CrossRef]
- Lazić, I.; Bosch, E.G.; Lazar, S. Phase contrast STEM for thin samples: Integrated differential phase contrast. Ultramicroscopy 2016, 160, 265–280. [Google Scholar] [CrossRef] [PubMed]
- Buzug, T.M. Computed tomography. In Springer Handbook of Medical Technology; Springer: Berlin/Heidelberg, Germany, 2011; pp. 311–342. [Google Scholar]
- Dunin-Borkowski, R.E.; Kovács, A.; Kasama, T.; McCartney, M.R.; Smith, D.J. Electron Holography. In Springer Handbook of Microscopy; Hawkes, P.W., Spence, J.C.H., Eds.; Springer: Cham, Switzerland, 2019; pp. 767–818. [Google Scholar]
- Tivol, W.F. Selected area electron diffraction and its use in structure determination. Microsc. Today 2010, 18, 22–28. [Google Scholar] [CrossRef]
- Ayoola, H.O.; House, S.D.; Bonifacio, C.S.; Kisslinger, K.; Saidi, W.A.; Yang, J.C. Evaluating the accuracy of common γ-Al2O3 structure models by selected area electron diffraction from high-quality crystalline γ-Al2O3. Acta Mater. 2020, 182, 257–266. [Google Scholar] [CrossRef]
- Clément, L.; Pantel, R.; Kwakman, L.F.T.; Rouvière, J.L. Strain measurements by convergent-beam electron diffraction: The importance of stress relaxation in lamella preparations. Appl. Phys. Lett. 2004, 85, 651–653. [Google Scholar] [CrossRef]
- Williamson, M.; van Dooren, P.; Flanagan, J. Quantitative analysis of the accuracy and sensitivity of strain measurements from nanobeam electron diffraction. In Proceedings of the 2015 IEEE 22nd International Symposium on the Physical and Failure Analysis of Integrated Circuits, Hsinchu, Taiwan, 29 June–2 July 2015; pp. 197–200. [Google Scholar]
- Mugnaioli, E.; Gorelik, T.; Kolb, U. “Ab initio” structure solution from electron diffraction data obtained by a combination of automated diffraction tomography and precession technique. Ultramicroscopy 2009, 109, 758–765. [Google Scholar] [CrossRef] [PubMed]
- Champness, P.E. Electron Diffraction in the Transmission Electron Microscope; Garland Science: New York, NY, USA, 2020. [Google Scholar]
- Nakajima, H.; Kotani, A.; Harada, K.; Mori, S. Electron diffraction covering a wide angular range from Bragg diffraction to small-angle diffraction. Microscopy 2018, 67, 207–213. [Google Scholar] [CrossRef]
- Cowley, J.M.; Goodman, P.; Vainshtein, B.K.; Zvyagin, B.B.; Dorset, D.L. Electron diffraction and electron microscopy in structure determination. In International Tables for Crystallography Volume B: Reciprocal Space; Shmueli, U., Ed.; Springer: Dordrecht, The Netherlands, 2001; pp. 276–345. [Google Scholar]
- Pooch, A.; Seidling, M.; Kerker, N.; Röpke, R.; Rembold, A.; Chang, W.-T.; Hwang, I.-S.; Stibor, A. Coherent properties of a tunable low-energy electron-matter-wave source. Phys. Rev. A 2018, 97, 013611. [Google Scholar] [CrossRef]
- Kacher, J.; Landon, C.; Adams, B.L.; Fullwood, D. Bragg’s Law diffraction simulations for electron backscatter diffraction analysis. Ultramicroscopy 2009, 109, 1148–1156. [Google Scholar] [CrossRef] [PubMed]
- Playford, H.; Keen, D.; Tucker, M. Local structure of crystalline and amorphous materials using reverse Monte Carlo methods. Neutron News 2016, 27, 17–21. [Google Scholar] [CrossRef]
- Wen, J.; Wang, R.; Lu, G. Distortion of the zeroth-order Laue-zone pattern caused by dislocations in a silicon crystal. Acta Crystallogr. Sect. A 1989, 45, 422–427. [Google Scholar] [CrossRef]
- Kattan, N.; Hou, B.; Fermín, D.J.; Cherns, D. Crystal structure and defects visualization of Cu2ZnSnS4 nanoparticles employing transmission electron microscopy and electron diffraction. Appl. Mater. Today 2015, 1, 52–59. [Google Scholar] [CrossRef]
- Morniroli, J.-P.; Ji, G.; Jacob, D. A systematic method to identify the space group from PED and CBED patterns part I—Theory. Ultramicroscopy 2012, 121, 42–60. [Google Scholar] [CrossRef] [PubMed]
- Ponce, A.; Aguilar, J.A.; Tate, J.; Yacamán, M.J. Advances in the electron diffraction characterization of atomic clusters and nanoparticles. Nanoscale Adv. 2021, 3, 311–325. [Google Scholar] [CrossRef]
- Czigány, Z.; Kis, V.K. Acquisition and evaluation procedure to improve the accuracy of SAED. Microsc. Res. Tech. 2023, 86, 144–156. [Google Scholar] [CrossRef] [PubMed]
- Shukla, D.; Mohammad, A.; Ilhom, S.; Willis, B.G.; Okyay, A.K.; Biyikli, N. Real-time in situ process monitoring and characterization of GaN films grown on Si (100) by low-temperature hollow-cathode plasma-atomic layer deposition using trimethylgallium and N2/H2 plasma. J. Vac. Sci. Technol. A 2021, 39, 022406. [Google Scholar] [CrossRef]
- Takashiri, M.; Miyazaki, K.; Tsukamoto, H. Structural and thermoelectric properties of fine-grained Bi0.4Te3.0Sb1.6 thin films with preferred orientation deposited by flash evaporation method. Thin Solid Film. 2008, 516, 6336–6343. [Google Scholar] [CrossRef]
- Rosenkranz, S.; Krogstad, M.; Osborn, R. New Developments in the Use of Single Crystal Diffuse Scattering to Probe Nanoscale Correlations in Crystalline Materials. In Proceedings of the Acta Crystallographica A—Foundation and Advances, Portland, OR, USA, 29 July–3 August 2022; p. A216. [Google Scholar]
- Saha, A.; Pattison, A.; Mecklenburg, M.; Brewster, A.; Ercius, P.; Rodriguez, J.A. Beyond Microed: Ab Initio Crystal Structures Using 4D-STEM. Available online: https://escholarship.org/uc/item/2qs6x5s1 (accessed on 4 February 2025).
- Abbasi, P.; Fenning, D.P.; Pascal, T.A. Investigation of local distortion effects on X-ray absorption of ferroelectric perovskites from first principles simulations. Nanoscale 2023, 15, 5193–5200. [Google Scholar] [CrossRef] [PubMed]
- Toda, A.; Ikarashi, N.; Ono, H. Local lattice strain measurements in semiconductor devices by using convergent-beam electron diffraction. J. Cryst. Growth 2000, 210, 341–345. [Google Scholar] [CrossRef]
- Nucci, J.A.; Keller, R.R.; Krämer, S.; Volkert, C.A.; Gross, M.E. Localized Measurement of Strains in Damascene Copper Interconnects by Convergent-Beam Electron Diffraction. MRS Online Proc. Libr. (OPL) 2000, 612, D8.5.1. [Google Scholar] [CrossRef]
- Akaogi, T.; Tsuda, K.; Terauchi, M.; Tanaka, M. Lattice parameter determination of a strained area of an InAs layer on a GaAs substrate using CBED. Microscopy 2004, 53, 11–19. [Google Scholar] [CrossRef]
- Johnson, D.H. Signal-to-noise ratio. Scholarpedia 2006, 1, 2088. [Google Scholar] [CrossRef]
- Förster, A.; Brandstetter, S.; Schulze-Briese, C. Transforming X-ray detection with hybrid photon counting detectors. Philos. Trans. R. Soc. A 2019, 377, 20180241. [Google Scholar] [CrossRef] [PubMed]
- Schulze-Briese, C.; DeCarlo, S. A new electron-counting detector for electron diffraction. Acta Crystallogr. A—Found. Adv. 2017, 73, C1350. [Google Scholar] [CrossRef]
- Munshi, J.; Rakowski, A.M.; Savitzky, B.; Ophus, C.; Henderson, M.L.; Cholia, S.; Chan, M.K. 4D> Crystal: Deep Learning Crystallographic Information From Electron Diffraction Images. Microsc. Microanal. 2021, 27, 2774–2776. [Google Scholar] [CrossRef]
- Friedrich, T.; Yu, C.-P.; Verbeeck, J.; Van Aert, S. Phase object reconstruction for 4D-STEM using deep learning. Microsc. Microanal. 2023, 29, 395–407. [Google Scholar] [CrossRef]
- Saitoh, K.; Yonezawa, T.; Nambu, H.; Tanimura, S.; Uchida, M. Orbital angular momentum-resolved convergent-beam electron diffraction by the post-selected injection of electron beam. Microscopy 2022, 71, 374–379. [Google Scholar] [CrossRef]
- Zeltmann, S.E.; Müller, A.; Bustillo, K.C.; Savitzky, B.H.; Minor, A.M.; Ophus, C. Improved 4D-STEM strain mapping precision using patterned probes. Microsc. Microanal. 2019, 25, 1958–1959. [Google Scholar] [CrossRef]
- Morikawa, D.; Tsuda, K. Local crystal symmetry and structure at CaTiO3 twin boundaries. Appl. Phys. Lett. 2021, 118, 092901. [Google Scholar] [CrossRef]
- Tsuda, K.; Sagawa, R.; Hashiguchi, H.; Kondo, Y. Local structural study of ferroelectric domain boundaries using STEM-CBED with a fast pixelated STEM detector. Microsc. Microanal. 2019, 25, 1996–1997. [Google Scholar] [CrossRef]
- Ozdol, V.; Gammer, C.; Jin, X.; Ercius, P.; Ophus, C.; Ciston, J.; Minor, A. Strain mapping at nanometer resolution using advanced nano-beam electron diffraction. Appl. Phys. Lett. 2015, 106, 253107. [Google Scholar] [CrossRef]
- Yamanaka, J.; Oguni, T.; Sano, Y.; Ohshima, Y.; Onogawa, A.; Hara, K.O.; Arimoto, K. Evaluation of Lattice-Spacing of SiGe/Si by NBD using Two-condenser-lens TEM. Microsc. Microanal. 2022, 28, 2812–2813. [Google Scholar] [CrossRef]
- Pekin, T.C.; Gammer, C.; Ciston, J.; Minor, A.M.; Ophus, C. Optimizing disk registration algorithms for nanobeam electron diffraction strain mapping. Ultramicroscopy 2017, 176, 170–176. [Google Scholar] [CrossRef]
- Li, J.; Reboh, S.; Chao, R.; Loubet, N.; Guillorn, M.; Yamashita, T.; Gaudiello, J. Nanobeam diffraction and geometric phase analysis for strain measurements in Si/SiGe nanosheet structures. Microsc. Microanal. 2016, 22, 1528–1529. [Google Scholar] [CrossRef]
- Rouviere, J.-L.; Sarigiannidou, E. Theoretical discussions on the geometrical phase analysis. Ultramicroscopy 2005, 106, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Baumann, F.H. High precision two-dimensional strain mapping in semiconductor devices using nanobeam electron diffraction in the transmission electron microscope. Appl. Phys. Lett. 2014, 104, 262102. [Google Scholar] [CrossRef]
- Kryvyi, S.; Kret, S.; Domagala, J.Z.; Wojnar, P. Reconstruction of three-dimensional strain field in an asymmetrical curved core–shell hetero-nanowire. Nanotechnology 2023, 34, 445705. [Google Scholar] [CrossRef] [PubMed]
- Sakai, A. Operando analysis of local strain induced by inverse piezoelectric effect in AlGaN/GaN HEMT using synchrotron radiation nanobeam x-ray diffraction. In Proceedings of the Gallium Nitride Materials and Devices XVI, Virtual Conference, 6–11 March 2021; p. 1168629. [Google Scholar]
- Zhao, D.; Xie, K.Y. Dislocation imaging by precession electron diffraction. Microsc. Microanal. 2020, 26, 226–227. [Google Scholar] [CrossRef]
- Bashir, A.; Millar, R.W.; Gallacher, K.; Paul, D.J.; Darbal, A.D.; Stroud, R.; Ballabio, A.; Frigerio, J.; Isella, G.; MacLaren, I. Strain analysis of a Ge micro disk using precession electron diffraction. J. Appl. Phys. 2019, 126, 235701. [Google Scholar] [CrossRef]
- Midgley, P.A.; Eggeman, A.S. Precession electron diffraction–a topical review. IUCrJ 2015, 2, 126–136. [Google Scholar] [CrossRef]
- Sinkler, W.; Marks, L.D. Characteristics of precession electron diffraction intensities from dynamical simulations. Z. Krist. 2010, 225, 47–55. [Google Scholar] [CrossRef]
- Ciston, J.; Deng, B.; Marks, L.; Own, C.; Sinkler, W. A quantitative analysis of the cone-angle dependence in precession electron diffraction. Ultramicroscopy 2008, 108, 514–522. [Google Scholar] [CrossRef]
- Own, C.; Sinkler, W.; Marks, L. Rapid structure determination of a metal oxide from pseudo-kinematical electron diffraction data. Ultramicroscopy 2006, 106, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Dorset, D.L.; Gilmore, C.J.; Jorda, J.L.; Nicolopoulos, S. Direct electron crystallographic determination of zeolite zonal structures. Ultramicroscopy 2007, 107, 462–473. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Patel, A.; Barbosa, A.; Hansen, M.H.; Wang, A.L.; Dong, J.; Zhang, Y.; Umale, T.; Karaman, I.; Shamberger, P. A reference-area-free strain mapping method using precession electron diffraction data. Ultramicroscopy 2023, 247, 113700. [Google Scholar] [CrossRef]
- Li, J.; Mochizuki, S.; Stuckert, E.; Tierney, L.; Toole, K.; Conte, R.; Loubet, N. Precession electron diffraction (PED) strain characterization in stacked nanosheet FET structure. In Proceedings of the International Symposium for Testing and Failure Analysis, Pasadena, CA, USA, 30 October–3 November 2022; pp. 74–77. [Google Scholar]
- Jeong, J.; Cautaerts, N.; Dehm, G.; Liebscher, C.H. Automated crystal orientation mapping by precession electron diffraction-assisted four-dimensional scanning transmission electron microscopy using a scintillator-based CMOS detector. Microsc. Microanal. 2021, 27, 1102–1112. [Google Scholar] [CrossRef]
- Corrêa, L.M.; Ortega, E.; Ponce, A.; Cotta, M.A.; Ugarte, D. High precision orientation mapping from 4D-STEM precession electron diffraction data through quantitative analysis of diffracted intensities. Ultramicroscopy 2024, 259, 113927. [Google Scholar] [CrossRef] [PubMed]
- Vijayalakshmi, M.; Saroja, S.; Mythili, R. Convergent beam electron diffraction—A novel technique for materials characterisation at sub-microscopic levels. Sadhana 2003, 28, 763–782. [Google Scholar] [CrossRef]
- Bekarevich, R.; Mitsuishi, K.; Ohnishi, T.; Uesugi, F.; Takeguchi, M.; Inaguma, Y.; Ohno, T.; Takada, K. Two-dimensional Gaussian fitting for precise measurement of lattice constant deviation from a selected-area diffraction map. Microscopy 2018, 67, i142–i149. [Google Scholar] [CrossRef]
- Ghamarian, I.; Liu, Y.; Samimi, P.; Collins, P.C. Development and application of a novel precession electron diffraction technique to quantify and map deformation structures in highly deformed materials—As applied to ultrafine-grained titanium. Acta Mater. 2014, 79, 203–215. [Google Scholar] [CrossRef]
- Fultz, B.; Howe, J.M. Transmission Electron Microscopy and Diffractometry of Materials; Springer Science & Business Media: Cham, Switzerland, 2012. [Google Scholar]
- Balogh, L.; Ribárik, G.; Ungár, T. Stacking faults and twin boundaries in fcc crystals determined by x-ray diffraction profile analysis. J. Appl. Phys. 2006, 100, 023512. [Google Scholar] [CrossRef]
- Loh, Y.L. The Ewald sphere construction for radiation, scattering, and diffraction. Am. J. Phys. 2017, 85, 277–288. [Google Scholar] [CrossRef]
- Dub, P.; Litzman, O. The Ewald dynamical diffraction theory–ninety years later. Acta Crystallogr. Sect. A 2005, 61, 209–222. [Google Scholar] [CrossRef] [PubMed]
- Howie, A.; Whelan, M.J. Diffraction contrast of electron microscope images of crystal lattice defects—II. The development of a dynamical theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1961, 263, 217–237. [Google Scholar]
- Howie, A.; Whelan, M.J. Diffraction contrast of electron microscope images of crystal lattice defects—III. Results and experimental confirmation of the dynamical theory of dislocation image contrast. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1962, 267, 206–230. [Google Scholar]
- Dickey, F.M. Laser Beam Shaping: Theory and Techniques; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Dickey, F.M.; Weichman, L.S.; Shagam, R.N. Laser beam shaping techniques. In Proceedings of the High-Power Laser Ablation III, Santa Fe, NM, USA, 24–28 April 2000; pp. 338–348. [Google Scholar]
- Saitoh, K.; Nambu, H.; Tanaka, N.; Uchida, M. Propagation properties of electron vortex beams. Microsc. Microanal. 2015, 21, 671–672. [Google Scholar] [CrossRef]
- Thirunavukkarasu, G.; Mousley, M.; Babiker, M.; Yuan, J. Even-odd effect in higher-order holographic production of electron vortex beams with nontrivial radial structures. Phys. Rev. A 2019, 99, 013608. [Google Scholar] [CrossRef]
- Bonef, B.; Shah, R.D.; Mukherjee, K. Fast diffusion and segregation along threading dislocations in semiconductor heterostructures. Nano Lett. 2019, 19, 1428–1436. [Google Scholar] [CrossRef]
- Munshi, J.; Rakowski, A.; Savitzky, B.H.; Zeltmann, S.E.; Ciston, J.; Henderson, M.; Cholia, S.; Minor, A.M.; Chan, M.K.; Ophus, C. Disentangling multiple scattering with deep learning: Application to strain mapping from electron diffraction patterns. npj Comput. Mater. 2022, 8, 254. [Google Scholar] [CrossRef]
- Estakhri, N.M.; Norris, T.B. Coherent Two-photon Backscattering and Induced Angular Quantum Correlations in Multiple-Scattered Two-Photon States of the Light. arXiv 2024, arXiv:2401.13176. [Google Scholar]
- Lin, Y.R.; Li, Y.; Zinkle, S.J.; Arregui-Mena, J.D.; Burke, M.G. Application of Weak-Beam Dark-Field STEM for Dislocation Loop Analysis. Microsc. Microanal. 2024, 30, 681–691. [Google Scholar] [CrossRef] [PubMed]
- Mawson, T.; Nakamura, A.; Petersen, T.; Shibata, N.; Sasaki, H.; Paganin, D.; Morgan, M.; Findlay, S. Suppressing dynamical diffraction artefacts in differential phase contrast scanning transmission electron microscopy of long-range electromagnetic fields via precession. Ultramicroscopy 2020, 219, 113097. [Google Scholar] [CrossRef]
- Fultz, B.; Howe, J. Diffraction contrast in TEM images. In Transmission Electron Microscopy and Diffractometry of Materials; Springer: Berlin/Heidelberg, Germany, 2013; pp. 349–427. [Google Scholar]
- Qiu, Y.; Cristiano, F.; Huet, K.; Mazzamuto, F.; Fisicaro, G.; La Magna, A.; Quillec, M.; Cherkashin, N.; Wang, H.; Duguay, S. Extended defects formation in nanosecond laser-annealed ion implanted silicon. Nano Lett. 2014, 14, 1769–1775. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Sun, H.; AJia, I.A.; Roqan, I.S.; Zhang, D.; Dai, J.; Chen, C.; Feng, Z.C.; Li, X. Significant internal quantum efficiency enhancement of GaN/AlGaN multiple quantum wells emitting at~ 350 nm via step quantum well structure design. J. Phys. D Appl. Phys. 2017, 50, 245101. [Google Scholar] [CrossRef]
- Donatelli, J.J.; Spence, J.C. Inversion of many-beam Bragg intensities for phasing by iterated projections: Removal of multiple scattering artifacts from diffraction data. Phys. Rev. Lett. 2020, 125, 065502. [Google Scholar] [CrossRef] [PubMed]
- Spence, J.; Donatelli, J. Inversion of many-beam Bragg intensities for phasing by iterated projections: Removal of multiple scattering artifacts. Microsc. Microanal. 2020, 26, 2456–2457. [Google Scholar] [CrossRef]
- MacLaren, I.; Frutos-Myro, E.; McGrouther, D.; McFadzean, S.; Weiss, J.K.; Cosart, D.; Portillo, J.; Robins, A.; Nicolopoulos, S.; Nebot del Busto, E. A comparison of a direct electron detector and a high-speed video camera for a scanning precession electron diffraction phase and orientation mapping. Microsc. Microanal. 2020, 26, 1110–1116. [Google Scholar] [CrossRef] [PubMed]
- Pennycook, S.J.; Nellist, P.D. Scanning Transmission Electron Microscopy: Imaging and Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Miao, J. High Resolution Imaging of Dislocations Using Weak Beam Dark Field STEM. Microsc. Microanal. 2020, 26, 1220–1222. [Google Scholar] [CrossRef]
- Miao, J.; Singh, S.; Tessmer, J.; Shih, M.; Ghazisaeidi, M.; DeGraef, M.; Mills, M. Dislocation characterization using weak beam dark field stem imaging. Microsc. Microanal. 2018, 24, 2202–2203. [Google Scholar] [CrossRef]
- Iwata, H.; Saka, H. Resolving individual Shockley partials of a dissociated dislocation by STEM. Philos. Mag. Lett. 2017, 97, 74–81. [Google Scholar] [CrossRef]
- Dennler, N.; Foncubierta-Rodriguez, A.; Neupert, T.; Sousa, M. Learning-based defect recognition for quasi-periodic HRSTEM images. Micron 2021, 146, 103069. [Google Scholar] [CrossRef] [PubMed]
- Stroppa, D.G.; Zagonel, L.F.; Montoro, L.A.; Leite, E.R.; Ramirez, A.J. High-Resolution Scanning Transmission Electron Microscopy (HRSTEM) techniques: High-resolution imaging and spectroscopy side by side. ChemPhysChem 2012, 13, 437–443. [Google Scholar] [CrossRef]
- Miao, L.; Chmielewski, A.; Mukherjee, D.; Alem, N. Picometer-precision atomic position tracking through electron microscopy. J. Vis. Exp. 2021, 173, 1–15. [Google Scholar] [CrossRef]
- Martinez, G.; Rosenauer, A.; De Backer, A.; Verbeeck, J.; Van Aert, S. Quantitative composition determination at the atomic level using model-based high-angle annular dark field scanning transmission electron microscopy. Ultramicroscopy 2014, 137, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Robb, P.D.; Craven, A.J. Column ratio mapping: A processing technique for atomic resolution high-angle annular dark-field (HAADF) images. Ultramicroscopy 2008, 109, 61–69. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Santiago, P.; Rendón, L.; Germán, C.; Pal, U. HAADF Imaging: An effective technique for the study of nonhomogeneousnanostructures. J. Nanosci. Nanotechnol. 2005, 5, 1172–1176. [Google Scholar] [CrossRef] [PubMed]
- Walther, T. A new experimental procedure to quantify annular dark field images in scanning transmission electron microscopy. J. Microsc. 2006, 221, 137–144. [Google Scholar] [CrossRef] [PubMed]
- Abe, E. Atomic-scale characterization of nanostructured metallic materials by HAADF/Z-contrast STEM. Mater. Trans. 2003, 44, 2035–2041. [Google Scholar] [CrossRef][Green Version]
- Cao, F.; Zheng, J.; Jiang, Y.; Chen, B.; Wang, Y.; Hu, T. Experimental and DFT characterization of η′ nano-phase and its interfaces in AlZnMgCu alloys. Acta Mater. 2019, 164, 207–219. [Google Scholar] [CrossRef]
- Wang, W.; Cai, W. Dynamic observation and motion tracking of individual gold atoms with HAADF-STEM imaging. RSC Adv. 2021, 11, 11057–11061. [Google Scholar] [CrossRef] [PubMed]
- Erni, R.; Browning, N.D. Valence electron energy-loss spectroscopy in monochromated scanning transmission electron microscopy. Ultramicroscopy 2005, 104, 176–192. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Zhang, X.; Liu, P.; Deng, Y.; Hu, W.; Chen, L.; Zhu, J.; Chen, S.; Wang, Z.; Shi, Y.; et al. Clustering in gallium ion beam sputtered compound materials driven by bond strength and interstitial/vacancy reaction. Appl. Phys. Lett. 2023, 123, 102101. [Google Scholar] [CrossRef]
- Phillips, P.J.; De Graef, M.; Kovarik, L.; Agrawal, A.; Windl, W.; Mills, M. Atomic-resolution defect contrast in low angle annular dark-field STEM. Ultramicroscopy 2012, 116, 47–55. [Google Scholar] [CrossRef]
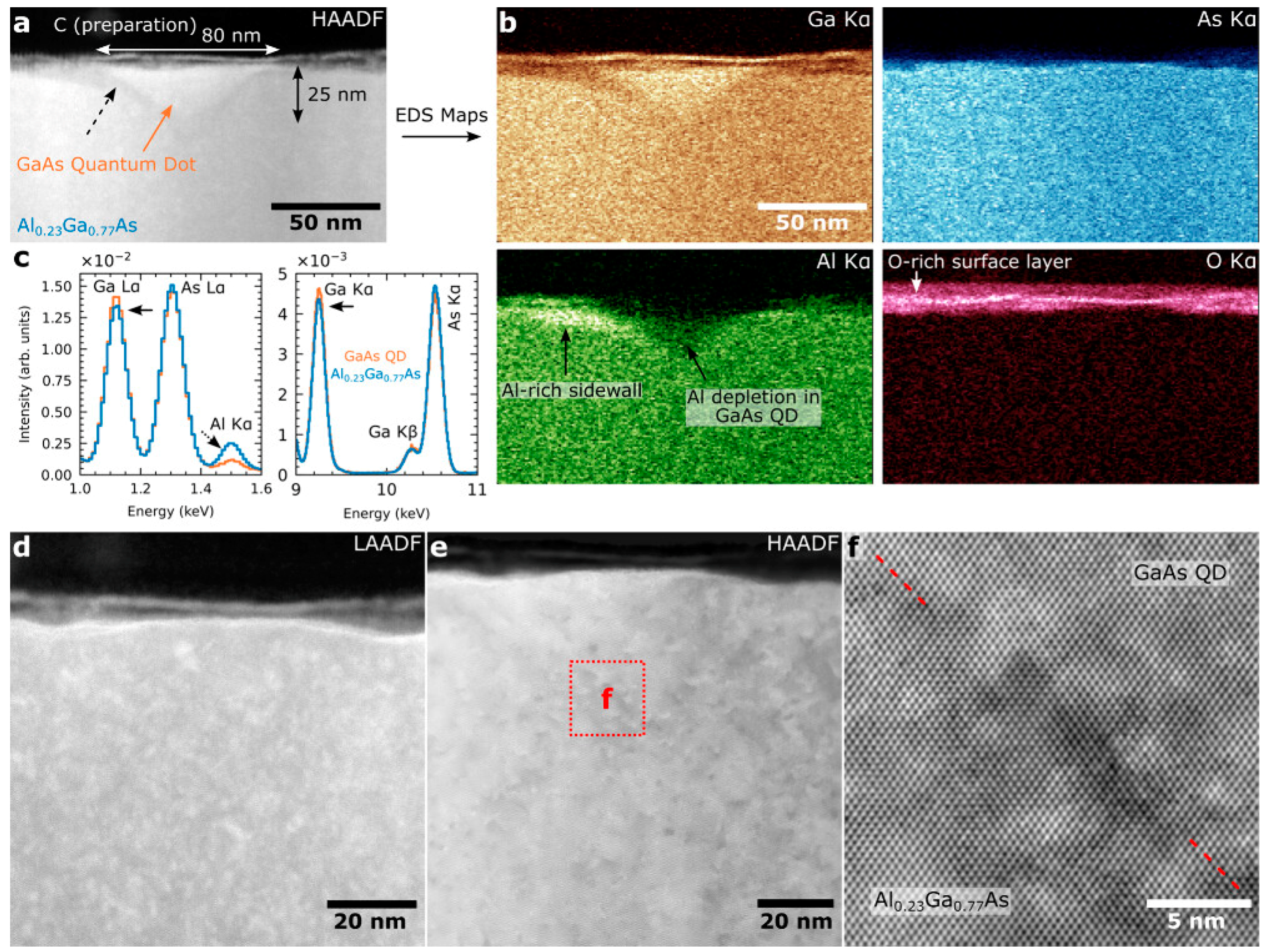
- Zhang, Y.; Grünewald, L.; Cao, X.; Abdelbarey, D.; Zheng, X.; Rugeramigabo, E.P.; Verbeeck, J.; Zopf, M.; Ding, F. Unveiling the 3D Morphology of Epitaxial GaAs/AlGaAs Quantum Dots. Nano Lett. 2024, 24, 10106–10113. [Google Scholar] [CrossRef] [PubMed]
- Prabhakaran, P.; Kim, W.J.; Lee, K.-S.; Prasad, P.N. Quantum dots (QDs) for photonic applications. Opt. Mater. Express 2012, 2, 578–593. [Google Scholar] [CrossRef]
- Hodoroaba, V.-D. Energy-dispersive X-ray spectroscopy (EDS). In Characterization of Nanoparticles; Elsevier: Amsterdam, The Netherlands, 2020; pp. 397–417. [Google Scholar]
- Nesher, O.; Elkind, S.; Adin, A.; Palty, U.; Pelleg, O.; Jacobsohn, E.; Markovitz, T.; Szafranek, I.; Calahora, Z.; Schlesinger, J.O. Performance of BF focal plane array 320x256 InSb detectors. In Proceedings of the Infrared Technology and Applications XXVIII, Seattle, WA, USA, 7–11 July 2002; pp. 699–707. [Google Scholar]
- Seki, T.; Ooe, K.; Nogami, M.; Ikuhara, Y.; Shibata, N. Towards High-Throughput Low Dose Observation by OBF STEM. Microsc. Microanal. 2024, 30, ozae044.925. [Google Scholar] [CrossRef]
- Ooe, K.; Seki, T.; Yoshida, K.; Kohno, Y.; Ikuhara, Y.; Shibata, N. Direct imaging of local atomic structures in zeolite using optimum bright-field scanning transmission electron microscopy. Sci. Adv. 2023, 9, eadf6865. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Syaranamual, G.J.; Lee, K.H.; Bao, S.; Wang, Y.; Lee, K.E.K.; Fitzgerald, E.A.; Pennycook, S.J.; Gradecak, S.; Michel, J. Effectiveness of InGaAs/GaAs superlattice dislocation filter layers epitaxially grown on 200 mm Si wafers with and without Ge buffers. Semicond. Sci. Technol. 2020, 35, 095036. [Google Scholar] [CrossRef]
- Kim, H.; Geum, D.-M.; Ko, Y.-H.; Han, W.-S. Effects of High-Temperature Growth of Dislocation Filter Layers in GaAs-on-Si. Nanoscale Res. Lett. 2022, 17, 126. [Google Scholar] [CrossRef] [PubMed]
- George, I.; Becagli, F.; Liu, H.; Wu, J.; Tang, M.; Beanland, R. Dislocation filters in GaAs on Si. Semicond. Sci. Technol. 2015, 30, 114004. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Zaumseil, P.; Arguirov, T.; Kittler, M.; Tillack, B. Low threading dislocation density Ge deposited on Si(100) using RPCVD. Solid-State Electron. 2011, 60, 2–6. [Google Scholar] [CrossRef]
- Tang, M.; Chen, S.; Wu, J.; Jiang, Q.; Kennedy, K.; Jurczak, P.; Liao, M.; Beanland, R.; Seeds, A.; Liu, H. Optimizations of defect filter layers for 1.3-μm InAs/GaAs quantum-dot lasers monolithically grown on Si substrates. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 50–56. [Google Scholar] [CrossRef]
- Arehart, A.; Moran, B.; Speck, J.; Mishra, U.; DenBaars, S.; Ringel, S. Effect of threading dislocation density on Ni∕n-GaN Schottky diode IV characteristics. J. Appl. Phys. 2006, 100, 023709. [Google Scholar] [CrossRef]
- Choi, D.; Ge, Y.; Harris, J.S.; Cagnon, J.; Stemmer, S. Low surface roughness and threading dislocation density Ge growth on Si (001). J. Cryst. Growth 2008, 310, 4273–4279. [Google Scholar] [CrossRef]
- Kaida, R.; Akiyama, T.; Nakamura, K.; Ito, T. Theoretical study for misfit dislocation formation at InAs/GaAs (001) interface. J. Cryst. Growth 2017, 468, 919–922. [Google Scholar] [CrossRef]
- Johnston-Peck, A.C.; Herzing, A.A. Four-Dimensional Scanning Transmission Electron Microscopy: Part I: Imaging, Strain Mapping, and Defect Detection. EDFA Tech. Artic. 2023, 25, 12–22. [Google Scholar] [CrossRef]
- Coupin, M.J.; Wen, Y.; Lee, S.; Saxena, A.; Ophus, C.; Allen, C.S.; Kirkland, A.I.; Aluru, N.R.; Lee, G.-D.; Warner, J.H. Mapping nanoscale electrostatic field fluctuations around graphene dislocation cores using four-dimensional Scanning Transmission Electron Microscopy (4D-STEM). Nano Lett. 2023, 23, 6807–6814. [Google Scholar] [CrossRef] [PubMed]
- Zeltmann, S.E.; Müller, A.; Bustillo, K.C.; Savitzky, B.; Hughes, L.; Minor, A.M.; Ophus, C. Patterned probes for high precision 4D-STEM Bragg measurements. Ultramicroscopy 2020, 209, 112890. [Google Scholar] [CrossRef]
- Han, Y.; Nguyen, K.; Cao, M.; Cueva, P.; Xie, S.; Tate, M.W.; Purohit, P.; Gruner, S.M.; Park, J.; Muller, D.A. Strain mapping of two-dimensional heterostructures with sub-picometer precision. Nano Lett. 2018, 18, 3746–3751. [Google Scholar] [CrossRef]
- Ophus, C. Four-dimensional scanning transmission electron microscopy (4D-STEM): From scanning nanodiffraction to ptychography and beyond. Microsc. Microanal. 2019, 25, 563–582. [Google Scholar] [CrossRef]
- Haas, B.; Mittelberger, A.; Meyer, C.; Plotkin-Swing, B.; Dellby, N.; Krivanek, O.; Lovejoy, T.; Koch, C. High-fidelity 4D-STEM enabled by live processing at 15,000 detector frames per second. Microsc. Microanal. 2021, 27, 994–997. [Google Scholar] [CrossRef]
- Haase, R.; Royer, L.A.; Steinbach, P.; Schmidt, D.; Dibrov, A.; Schmidt, U.; Weigert, M.; Maghelli, N.; Tomancak, P.; Jug, F. CLIJ: GPU-accelerated image processing for everyone. Nat. Methods 2020, 17, 5–6. [Google Scholar] [CrossRef] [PubMed]
- Robinson, A.W.; Wells, J.; Nicholls, D.; Moshtaghpour, A.; Kirkland, A.I.; Browning, N.D. Real-time Experimental 4-D STEM Using Compressive Sensing. Microsc. Microanal. 2024, 30, 1891–1893. [Google Scholar] [CrossRef]
- Shi, C.; Cao, M.; Muller, D.; Han, Y. Rapid and semi-automated analysis of 4D-STEM data via unsupervised learning. Microsc. Microanal. 2021, 27, 58–59. [Google Scholar] [CrossRef]
- Han, Y.; Shi, C.; Cao, M.; Jiang, Y. Assisting 4D-STEM Data Processing with Unsupervised Machine Learning. Microsc. Microanal. 2022, 28, 414–417. [Google Scholar] [CrossRef]
- Shi, C.; Cao, M.C.; Rehn, S.M.; Bae, S.-H.; Kim, J.; Jones, M.R.; Muller, D.A.; Han, Y. Uncovering material deformations via machine learning combined with four-dimensional scanning transmission electron microscopy. npj Comput. Mater. 2022, 8, 114. [Google Scholar] [CrossRef]
- Han, Y. Understanding Strain and Deformation in 2D Materials Via 4D-STEM and Cryo-EM. In Proceedings of the Electrochemical Society Meeting Abstracts 243, Hynes Convention Center and Sheraton, Boston, Boston, MA, USA, 28 May–2 June 2023; p. 1308. [Google Scholar]
- Harikrishnan, K.; Yoon, D.; Shao, Y.-T.; Mele, L.; Mitterbauer, C.; Muller, D. Dose-efficient strain mapping with high precision and throughput using cepstral transforms on 4D-STEM data. Microsc. Microanal. 2021, 27, 1994–1996. [Google Scholar] [CrossRef]
- Huth, M.; Eckert, B.; Aschauer, S.; Hedley, E.; Nellist, P.; Majewski, P.; Strüder, L.; Soltau, H. Combine 4D STEM and EELS Using a Fast Pixelated Direct Detector with Center Hole. Microsc. Microanal. 2023, 29, 401–402. [Google Scholar] [CrossRef]
- Sagawa, R.; Hashiguchi, H.; Nakamura, A.; Shibagaki, S.; Kazama, Y.; Muth, M.; Imari, Y.E.; Kroner, V.; Aschauer, S. Simultaneous Acquisition of 4D and EELS Data by Newly Developed Pixelated STEM Detector. Microsc. Microanal. 2024, 30. [Google Scholar] [CrossRef]
- Craig, I.M.; Van Winkle, M.; Ophus, C.; Bediako, D.K. Considerations for extracting moiré-level strain from dark field intensities in transmission electron microscopy. arXiv 2024, arXiv:2406.04515. [Google Scholar] [CrossRef]
- Motoki, K.; Engel, Z.; Matthews, C.M.; Ahmad, H.; McCrone, T.M.; Harada, K.; Doolittle, W.A. Observation of interfacial strain relaxation and electron beam damage thresholds in Al0.3In0.7N/GaN heterostructures by transmission electron microscopy. J. Vac. Sci. Technol. B 2022, 40, 052210. [Google Scholar] [CrossRef]
- Biefeld, R.M.; Koleske, D.D.; Cederberg, J.G. 3—The Science and Practice of Metal-Organic Vapor Phase Epitaxy (MOVPE). In Handbook of Crystal Growth (Second Edition); Kuech, T.F., Ed.; North-Holland: Boston, MA, USA, 2015; pp. 95–160. [Google Scholar]
- Xing, Z.; Yang, W.; Yuan, Z.; Li, X.; Wu, Y.; Long, J.; Jin, S.; Zhao, Y.; Liu, T.; Bian, L.; et al. Growth and Characterization of High In-content InGaN grown by MBE using Metal Modulated Epitaxy Technique (MME). J. Cryst. Growth 2019, 516, 57–62. [Google Scholar] [CrossRef]
- Arbouet, A.; Caruso, G.M.; Houdellier, F. Ultrafast transmission electron microscopy: Historical development, instrumentation, and applications. Adv. Imaging Electron Phys. 2018, 207, 1–72. [Google Scholar]
- Shimojima, T.; Nakamura, A.; Ishizaka, K. Development and applications of ultrafast transmission electron microscopy. Microscopy 2023, 72, 287–298. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, E.; Leonhardt, D.; Roehling, J. Ultrafast transmission electron microscopy: Techniques and applications. Microsc. Today 2021, 29, 46–54. [Google Scholar] [CrossRef]
- Ropers, C.; Solli, D.R.; Schulz, C.P.; Lienau, C.; Elsaesser, T. Localized multiphoton emission of femtosecond electron pulses from metal nanotips. Phys. Rev. Lett. 2007, 98, 043907. [Google Scholar] [CrossRef]
- Mattes, M.; Volkov, M.; Baum, P. Femtosecond electron beam probe of ultrafast electronics. Nat. Commun. 2024, 15, 1743. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.; Rubiano da Silva, N.; Liang, W.; Ropers, C.; Schäfer, S. Nanoscale diffractive probing of strain dynamics in ultrafast transmission electron microscopy. Struct. Dyn. 2018, 5, 014302. [Google Scholar] [CrossRef]
- Cremons, D.R.; Plemmons, D.A.; Flannigan, D.J. Femtosecond electron imaging of defect-modulated phonon dynamics. Nat. Commun. 2016, 7, 11230. [Google Scholar] [CrossRef] [PubMed]
- Lubk, A.; Zweck, J. Differential phase contrast: An integral perspective. Phys. Rev. A 2015, 91, 023805. [Google Scholar] [CrossRef]
- Shibata, N.; Findlay, S.D.; Kohno, Y.; Sawada, H.; Kondo, Y.; Ikuhara, Y. Differential phase-contrast microscopy at atomic resolution. Nat. Phys. 2012, 8, 611–615. [Google Scholar] [CrossRef]
- De Graaf, S.; Ahmadi, M.; Lazić, I.; Bosch, E.G.; Kooi, B.J. Imaging atomic motion of light elements in 2D materials with 30 kV electron microscopy. Nanoscale 2021, 13, 20683–20691. [Google Scholar] [CrossRef] [PubMed]
- Sheth, L.K.; Piotrowski, A.L.; Voss, N.R. Visualization and quality assessment of the contrast transfer function estimation. J. Struct. Biol. 2015, 192, 222–234. [Google Scholar] [CrossRef]
- Sorzano, C.; Jonic, S.; Núñez-Ramírez, R.; Boisset, N.; Carazo, J. Fast, robust, and accurate determination of transmission electron microscopy contrast transfer function. J. Struct. Biol. 2007, 160, 249–262. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Biskupek, J.; Kaiser, U.; Rose, H. Integrated differential phase contrast (IDPC)-STEM utilizing a multi-sector detector for imaging thick samples. Microsc. Microanal. 2022, 28, 611–621. [Google Scholar] [CrossRef] [PubMed]
- Thust, A. High-resolution transmission electron microscopy on an absolute contrast scale. Phys. Rev. Lett. 2009, 102, 220801. [Google Scholar] [CrossRef] [PubMed]
- Seifer, S.; Houben, L.; Elbaum, M. Flexible STEM with simultaneous phase and depth contrast. Microsc. Microanal. 2021, 27, 1476–1487. [Google Scholar] [CrossRef]
- Cao, S.; Chi, M.; More, K.L. Electromagnetic field reconstructions of 4D-STEM datasets using ptychography and differential phase contrast imaging. Microsc. Microanal. 2019, 25, 66–67. [Google Scholar] [CrossRef]
- Li, G.; Zhang, H.; Han, Y. 4D-STEM ptychography for electron-beam-sensitive materials. ACS Cent. Sci. 2022, 8, 1579–1588. [Google Scholar] [CrossRef] [PubMed]
- Müller, K.; Krause, F.F.; Béché, A.; Schowalter, M.; Galioit, V.; Löffler, S.; Verbeeck, J.; Zweck, J.; Schattschneider, P.; Rosenauer, A. Atomic electric fields revealed by a quantum mechanical approach to electron picodiffraction. Nat. Commun. 2014, 5, 5653. [Google Scholar] [CrossRef] [PubMed]
- Hüe, F.; Rodenburg, J.; Maiden, A.; Sweeney, F.; Midgley, P. Wave-front phase retrieval in transmission electron microscopy via ptychography. Phys. Rev. B 2010, 82, 121415. [Google Scholar] [CrossRef]
- Pennycook, T.J.; Martinez, G.T.; Nellist, P.D.; Meyer, J.C. High dose efficiency atomic resolution imaging via electron ptychography. Ultramicroscopy 2019, 196, 131–135. [Google Scholar] [CrossRef] [PubMed]
- Pennycook, T.J.; Martinez, G.T.; Nellist, P.D.; Meyer, J.C. High dose efficiency atomic resolution phase imaging with electron ptychography. Microsc. Microanal. 2018, 24, 196–197. [Google Scholar] [CrossRef]
- Valzania, L.; Dong, J.; Gigan, S. Accelerating ptychographic reconstructions using spectral initializations. Opt. Lett. 2021, 46, 1357–1360. [Google Scholar] [CrossRef]
- Yu, X.; Bicer, T.; Kettimuthu, R.; Foster, I. Topology-aware optimizations for multi-gpu ptychographic image reconstruction. In Proceedings of the ACM International Conference on Supercomputing, Virtual Conference, 14–17 June 2021; pp. 354–366. [Google Scholar]
- Babu, A.V.; Zhou, T.; Kandel, S.; Bicer, T.; Liu, Z.; Judge, W.; Ching, D.J.; Jiang, Y.; Veseli, S.; Henke, S. Deep learning at the edge enables real-time streaming ptychographic imaging. Nat. Commun. 2023, 14, 7059. [Google Scholar] [CrossRef] [PubMed]
- Hill, M.O.; Calvo-Almazan, I.; Allain, M.; Holt, M.V.; Ulvestad, A.; Treu, J.; Koblmuller, G.; Huang, C.; Huang, X.; Yan, H. Measuring three-dimensional strain and structural defects in a single InGaAs nanowire using coherent X-ray multiangle Bragg projection ptychography. Nano Lett. 2018, 18, 811–819. [Google Scholar] [CrossRef] [PubMed]
- Fewster, P.F. Reciprocal space mapping. Crit. Rev. Solid State Mater. Sci. 1997, 22, 69–110. [Google Scholar] [CrossRef]
- Stockmar, M.; Hubert, M.; Dierolf, M.; Enders, B.; Clare, R.; Allner, S.; Fehringer, A.; Zanette, I.; Villanova, J.; Laurencin, J. X-ray nanotomography using near-field ptychography. Opt. Express 2015, 23, 12720–12731. [Google Scholar] [CrossRef]
- Aslan, S.; Liu, Z.; Nikitin, V.; Bicer, T.; Leyffer, S.; Gursoy, D. Deep priors for ptycho-tomography. Microsc. Microanal. 2020, 26, 2466. [Google Scholar] [CrossRef]
- Alpers, A.; Gardner, R.J.; König, S.; Pennington, R.S.; Boothroyd, C.B.; Houben, L.; Dunin-Borkowski, R.E.; Batenburg, K.J. Geometric reconstruction methods for electron tomography. Ultramicroscopy 2013, 128, 42–54. [Google Scholar] [CrossRef] [PubMed]
- Dahmen, T.; Kohr, H.; Lupini, A.R.; Baudoin, J.-P.; Kübel, C.; Trampert, P.; Slusallek, P.; de Jonge, N. Combined tilt-and focal-series tomography for HAADF-STEM. Microsc. Today 2016, 24, 26–31. [Google Scholar] [CrossRef]
- Vanrompay, H.; Bladt, E.; Albrecht, W.; Béché, A.; Zakhozheva, M.; Sánchez-Iglesias, A.; Liz-Marzán, L.M.; Bals, S. 3D characterization of heat-induced morphological changes of Au nanostars by fast in situ electron tomography. Nanoscale 2018, 10, 22792–22801. [Google Scholar] [CrossRef] [PubMed]
- Ke, X.; Turner, S.; Quintana, M.; Hadad, C.; Montellano-López, A.; Carraro, M.; Sartorel, A.; Bonchio, M.; Prato, M.; Bittencourt, C. Dynamic motion of Ru-polyoxometalate ions (POMs) on functionalized few-layer graphene. Small 2013, 9, 3922–3927. [Google Scholar] [CrossRef] [PubMed]
- Padgett, E.; Andrejevic, N.; Liu, Z.; Kongkanand, A.; Gu, W.; Moriyama, K.; Jiang, Y.; Kumaraguru, S.; Moylan, T.E.; Kukreja, R. Connecting fuel cell catalyst nanostructure and accessibility using quantitative cryo-STEM tomography. J. Electrochem. Soc. 2018, 165, F173–F180. [Google Scholar] [CrossRef]
- Hovden, R.; Ercius, P.; Jiang, Y.; Wang, D.; Yu, Y.; Abruña, H.D.; Elser, V.; Muller, D.A. Breaking the Crowther limit: Combining depth-sectioning and tilt tomography for high-resolution, wide-field 3D reconstructions. Ultramicroscopy 2014, 140, 26–31. [Google Scholar] [CrossRef] [PubMed]
- van den Bos, K.H.W.; Altantzis, T.; De Backer, A.; Van Aert, S.; Bals, S. Recent breakthroughs in scanning transmission electron microscopy of small species. Adv. Phys. X 2018, 3, 1480420. [Google Scholar] [CrossRef]
- Arslan Irmak, E.; Liu, P.; Bals, S.; Van Aert, S. 3D Atomic structure of supported metallic nanoparticles estimated from 2D ADF STEM images: A combination of atom-counting and a local minima search algorithm. Small Methods 2021, 5, 2101150. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Irmak, E.A.; De Backer, A.; Lobato, I.; Béché, A.; Van Aert, S.; Bals, S. Three-dimensional atomic structure of supported Au nanoparticles at high temperature. Nanoscale 2021, 13, 1770–1776. [Google Scholar] [CrossRef]
- Albrecht, W.; Van Aert, S.; Bals, S. Three-dimensional nanoparticle transformations captured by an electron microscope. Acc. Chem. Res. 2021, 54, 1189–1199. [Google Scholar] [CrossRef] [PubMed]
- Hodnik, N.; Dehm, G.; Mayrhofer, K.J. Importance and challenges of electrochemical in situ liquid cell electron microscopy for energy conversion research. Acc. Chem. Res. 2016, 49, 2015–2022. [Google Scholar] [CrossRef]
- Bergmann, A.; Roldan Cuenya, B. Operando insights into nanoparticle transformations during catalysis. ACS Catal. 2019, 9, 10020–10043. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, J.; Zhu, F.; Yuan, Y.; Chang, D.J.; Kim, D.S.; Pham, M.; Rana, A.; Tian, X.; Yao, Y.; et al. Determining the three-dimensional atomic structure of an amorphous solid. Nature 2021, 592, 60–64. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Ke, X.; Sui, M. Recent progress on revealing 3D structure of electrocatalysts using advanced 3D electron tomography: A mini review. Front. Chem. 2022, 10, 872117. [Google Scholar] [CrossRef]
- Nicolai, L.; Biermann, K.; Trampert, A. Application of electron tomography for comprehensive determination of III-V interface properties. Ultramicroscopy 2021, 224, 113261. [Google Scholar] [CrossRef]
- Walther, T.; Gerthsen, D. Quantitative characterization of AlAs/GaAs interfaces by high-resolution transmission electron microscopy along the <100> and the <110> projection. Appl. Phys. A 1993, 57, 393–400. [Google Scholar]
- Lichte, H. Performance limits of electron holography. Ultramicroscopy 2008, 108, 256–262. [Google Scholar] [CrossRef]
- Dunin-Borkowski, R. Recent progress in electromagnetic field mapping at the nanoscale. Microscopy 2014, 63, i1. [Google Scholar] [CrossRef]
- Lichte, H.; Lehmann, M. Electron holography—Basics and applications. Rep. Prog. Phys. 2007, 71, 016102. [Google Scholar] [CrossRef]
- Tonomura, A. Fundamentals and applications of electron holography. In Holography, Research and Technologies; INTECH: Vukovar, Croatia, 2011; pp. 441–452. [Google Scholar]
- Hirayama, T.; Anada, S.; Nomura, Y.; Sasaki, H.; Saitoh, K.; Yamamoto, K. Accurate Measurement of Electric Potential Distributions at the Interfaces in Solids Using Phase-shifting Electron Holography. Microsc. Microanal. 2020, 26, 1956–1957. [Google Scholar] [CrossRef]
- Anada, S.; Nomura, Y.; Yamamoto, K. Enhancing performance of electron holography with mathematical and machine learning–based denoising techniques. Microscopy 2023, 72, 461–484. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Cheng, Y.; Liu, Z.; Yan, S.; Li, L.; Wang, J.; Zhang, L.; Gao, Y. Study of structure-property relationship of semiconductor nanomaterials by off-axis electron holography. J. Semicond. 2022, 43, 041103. [Google Scholar] [CrossRef]
- Li, L.; Ketharanathan, S.; Drucker, J.; McCartney, M.R. Study of hole accumulation in individual germanium quantum dots in p-type silicon by off-axis electron holography. Appl. Phys. Lett. 2009, 94, 232108. [Google Scholar] [CrossRef]
- Fry, P.; Itskevich, I.; Mowbray, D.; Skolnick, M.; Finley, J.; Barker, J.; O’Reilly, E.; Wilson, L.; Larkin, I.; Maksym, P. Inverted electron-hole alignment in InAs-GaAs self-assembled quantum dots. Phys. Rev. Lett. 2000, 84, 733. [Google Scholar] [CrossRef] [PubMed]
- Cheng, F.; Li, B.; Li, L.; Wang, X.; Shen, S.; Liu, W.; Zheng, H.; Jia, S.; Yan, X.; Zhang, X. Study of the polarization effect in InAs quantum dots/GaAs nanowires. J. Phys. Chem. C 2019, 123, 4228–4234. [Google Scholar] [CrossRef]
- Yan, Z.; Han, Y.; Lau, K.M. Multi-heterojunction InAs/GaSb nano-ridges directly grown on (001) Si. Nanotechnology 2020, 31, 345707. [Google Scholar] [CrossRef] [PubMed]
- Gourishetty, R.; Shriram, S.R.; Panda, D.P.; Chakrabarti, S. Analytical Model and Experimental Analysis to Estimate the Interdiffusion and Optoelectronic Properties of Coupled InAs Quantum Dots Post Rapid Thermal Processing. IEEE Trans. Electron Devices 2022, 69, 3775–3782. [Google Scholar] [CrossRef]
- Dorfmüller, J.; Vogelgesang, R.; Weitz, R.T.; Rockstuhl, C.; Etrich, C.; Pertsch, T.; Lederer, F.; Kern, K. Fabry-Pérot resonances in one-dimensional plasmonic nanostructures. Nano Lett. 2009, 9, 2372–2377. [Google Scholar] [CrossRef] [PubMed]
- Lovejoy, T.; Corbin, G.; Dellby, N.; Hoffman, M.; Krivanek, O. Advances in ultra-high energy resolution STEM-EELS. Microsc. Microanal. 2018, 24, 446–447. [Google Scholar] [CrossRef]
- Walther, T.; Gerthsen, D.; Carius, R.; Förster, A.; Urban, K. Correlation between the structural and optical properties of AlAs/GaAs quantum well structures. In: Proc. Microscopy of Semiconducting Materials: Oxford, 5—8 April 1993 (ed. by A.G. Cullis, A.E. Staton-Bevan, J.L. Hutchison). Inst. Phys. Conf. Ser. 1993, 134, 449–454. [Google Scholar]
- Yu, Q.; Legros, M.; Minor, A. In situ TEM nanomechanics. MRS Bull. 2015, 40, 62–70. [Google Scholar] [CrossRef]
- Katsuno, H.; Kimura, Y.; Yamazaki, T.; Takigawa, I. Fast improvement of TEM images with low-dose electrons by deep learning. Microsc. Microanal. 2022, 28, 138–144. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Jiang, Y.; Luo, S.; Ying, Y.; Zhang, Q.; Tang, S.; Chen, L.; Xia, J.; Xue, P.; Zhang, J.-J. On-chip gas reaction nanolab for in situ TEM observation. Lab A Chip 2023, 23, 3768–3777. [Google Scholar] [CrossRef] [PubMed]
- Wirth, R. Focused Ion Beam (FIB) combined with SEM and TEM: Advanced analytical tools for studies of chemical composition, microstructure and crystal structure in geomaterials on a nanometre scale. Chem. Geol. 2009, 261, 217–229. [Google Scholar] [CrossRef]
- Haswell, R.; McComb, D.; Smith, W. Preparation of site-specific cross-sections of heterogeneous catalysts prepared by focused ion beam milling. J. Microsc. 2003, 211, 161–166. [Google Scholar] [CrossRef]
- Pan, Y.; Zhao, Y.; Tan, P.K.; Mai, Z.; Rivai, F.; Lam, J. Problems of and solutions for coating techniques for tem sample preparation on ultra low-k dielectric devices after progressive-FIB cross-section analysis. In Proceedings of the 2018 IEEE International Symposium on the Physical and Failure Analysis of Integrated Circuits (IPFA), Singapore, 16–19 July 2018; pp. 1–5. [Google Scholar]
- Jublot, M.; Texier, M. Sample preparation by focused ion beam micromachining for transmission electron microscopy imaging in front-view. Micron 2014, 56, 63–67. [Google Scholar] [CrossRef] [PubMed]
- Novák, L.; Stárek, J.; Vystavěl, T.; Mele, L. MEMS-based heating element for in-situ dynamical experiments on FIB/SEM systems. Microsc. Microanal. 2016, 22, 184–185. [Google Scholar] [CrossRef]
- Saowadee, N.; Agersted, K.; Bowen, J.R. Effects of focused ion beam milling on electron backscatter diffraction patterns in strontium titanate and stabilized zirconia. J. Microsc. 2012, 246, 279–286. [Google Scholar] [CrossRef]
- Ko, D.-S.; Park, Y.M.; Kim, S.-D.; Kim, Y.-W. Effective removal of Ga residue from focused ion beam using a plasma cleaner. Ultramicroscopy 2007, 107, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Stanford, M.G.; Lewis, B.B.; Iberi, V.; Fowlkes, J.D.; Tan, S.; Livengood, R.; Rack, P.D. In situ mitigation of subsurface and peripheral focused ion beam damage via simultaneous pulsed laser heating. Small 2016, 12, 1779–1787. [Google Scholar] [CrossRef]
- Schmied, R.; Chernev, B.; Trimmel, G.; Plank, H. New possibilities for soft matter applications: Eliminating technically induced thermal stress during FIB processing. RSC Adv. 2012, 2, 6932–6938. [Google Scholar] [CrossRef]
- Matsutani, T.; Kawasaki, T.; Kodama, T.; Hisaka, M.; Takai, Y.; Ikuta, T. Development of focused ion beam system attached to floating type low energy ion gun for surface finishing. Vacuum 2014, 110, 228–231. [Google Scholar] [CrossRef]
- Wolff, A.; Klingner, N.; Thompson, W.; Zhou, Y.; Lin, J.; Peng, Y.Y.; Ramshaw, J.A.; Xiao, Y. Modelling of focused ion beam induced increases in sample temperature: A case study of heat damage in biological samples. J. Microsc. 2018, 272, 47–59. [Google Scholar] [CrossRef] [PubMed]
- Gardener, J.; Akey, A.; Alsem, D.H.; Bell, D. Focused ion beam sample preparation for high temperature in-situ transmission electron microscopy experiments: Use carbon for now. Microsc. Microanal. 2020, 26, 3202–3203. [Google Scholar] [CrossRef]
- Zhong, X.; Wade, C.A.; Withers, P.J.; Zhou, X.; Cai, C.; Haigh, S.J.; Burke, M.G. Comparing Xe+ pFIB and Ga+ FIB for TEM sample preparation of Al alloys: Minimising FIB-induced artefacts. J. Microsc. 2021, 282, 101–112. [Google Scholar] [CrossRef] [PubMed]
- Radić, D.; Peterlechner, M.; Bracht, H. Focused ion beam sample preparation for in situ thermal and electrical transmission electron microscopy. Microsc. Microanal. 2021, 27, 828–834. [Google Scholar] [CrossRef] [PubMed]
- Minenkov, A.; Šantić, N.; Truglas, T.; Aberl, J.; Vukušić, L.; Brehm, M.; Groiss, H. Advanced preparation of plan-view specimens on a MEMS chip for in situ TEM heating experiments. MRS Bull. 2022, 47, 359–370. [Google Scholar] [CrossRef] [PubMed]
- Gröger, R.; Marchand, B.; Lookman, T. Dislocations via incompatibilities in phase-field models of microstructure evolution. Phys. Rev. B 2016, 94, 054105. [Google Scholar] [CrossRef]
- Levitas, V.I.; Javanbakht, M. Interaction between phase transformations and dislocations at the nanoscale. Part 1. General phase field approach. J. Mech. Phys. Solids 2015, 82, 287–319. [Google Scholar] [CrossRef]
- Phan, V.-T.; Zhang, X.; Li, Y.; Oskay, C. Microscale modeling of creep deformation and rupture in nickel-based superalloy IN 617 at high temperature. Mech. Mater. 2017, 114, 215–227. [Google Scholar] [CrossRef]
- Aba-Perea, P.-E.; Withers, P.J.; Pirling, T.; Paradowska, A.; Ma, D.; Preuss, M. In situ study of the stress relaxation during aging of nickel-base superalloy forgings. Metall. Mater. Trans. A 2019, 50, 3555–3565. [Google Scholar] [CrossRef]
- Chen, R.; Dayeh, S.A. Recordings and analysis of atomic ledge and dislocation movements in InGaAs to nickelide nanowire phase transformation. Small 2017, 13, 1604117. [Google Scholar] [CrossRef]
- Kröger, A.; Wernhardt, R.; Somsen, C.; Eggeler, G.; Wieck, A. In situ transmission electron microscopy-investigations on the strain-induced B19′-phase in NiTi shape memory alloys structured by focused ion beam. Mater. Sci. Eng. A 2006, 438, 513–516. [Google Scholar] [CrossRef]
- Frick, C.P.; Lang, T.W.; Spark, K.; Gall, K. Stress-induced martensitic transformations and shape memory at nanometer scales. Acta Mater. 2006, 54, 2223–2234. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Zhang, W.; Wang, L.-Y.; Zhuang, Z.; Ma, E.; Li, J.; Shan, Z.-W. In situ TEM study of deformation-induced crystalline-to-amorphous transition in silicon. NPG Asia Mater. 2016, 8, e291. [Google Scholar] [CrossRef]
- Walther, T. What environmental transmission electron microscopy measures and how this links to diffusivity: Thermodynamics versus kinetics. J. Microsc. 2015, 257, 87–91. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Zhu, Y. Perspectives on in situ electron microscopy. Ultramicroscopy 2017, 180, 188–196. [Google Scholar] [CrossRef] [PubMed]
- Straubinger, R.; Beyer, A.; Volz, K. Preparation and loading process of single crystalline samples into a gas environmental cell holder for in situ atomic resolution scanning transmission electron microscopic observation. Microsc. Microanal. 2016, 22, 515–519. [Google Scholar] [CrossRef]
- Wagner, J.B.; Cavalca, F.; Damsgaard, C.D.; Duchstein, L.D.; Hansen, T.W. Exploring the environmental transmission electron microscope. Micron 2012, 43, 1169–1175. [Google Scholar] [CrossRef] [PubMed]
- Persson, A.R.; Tornberg, M.; Sjökvist, R.; Jacobsson, D. Time-resolved compositional mapping during in situ TEM studies. Ultramicroscopy 2021, 222, 113193. [Google Scholar] [CrossRef] [PubMed]









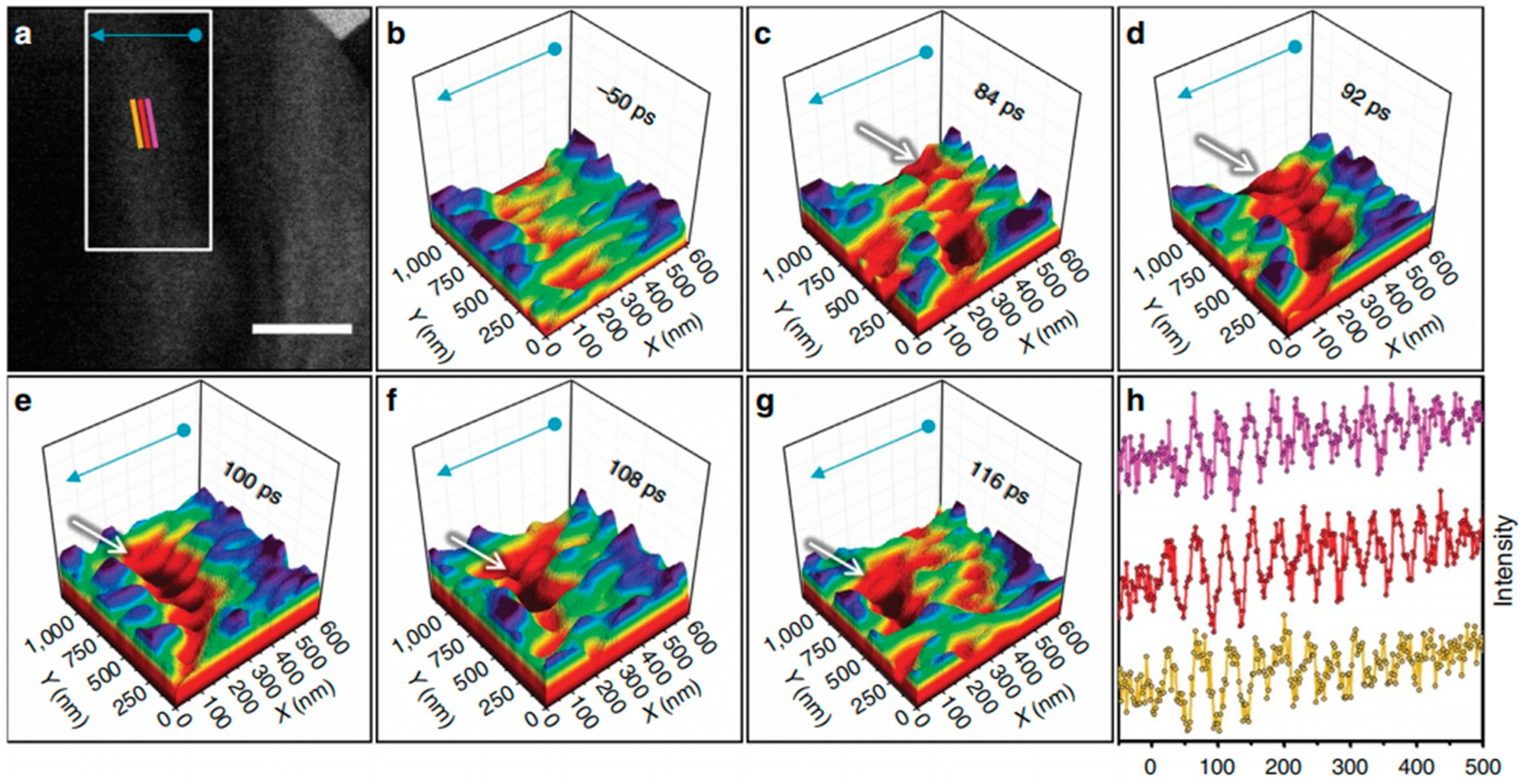


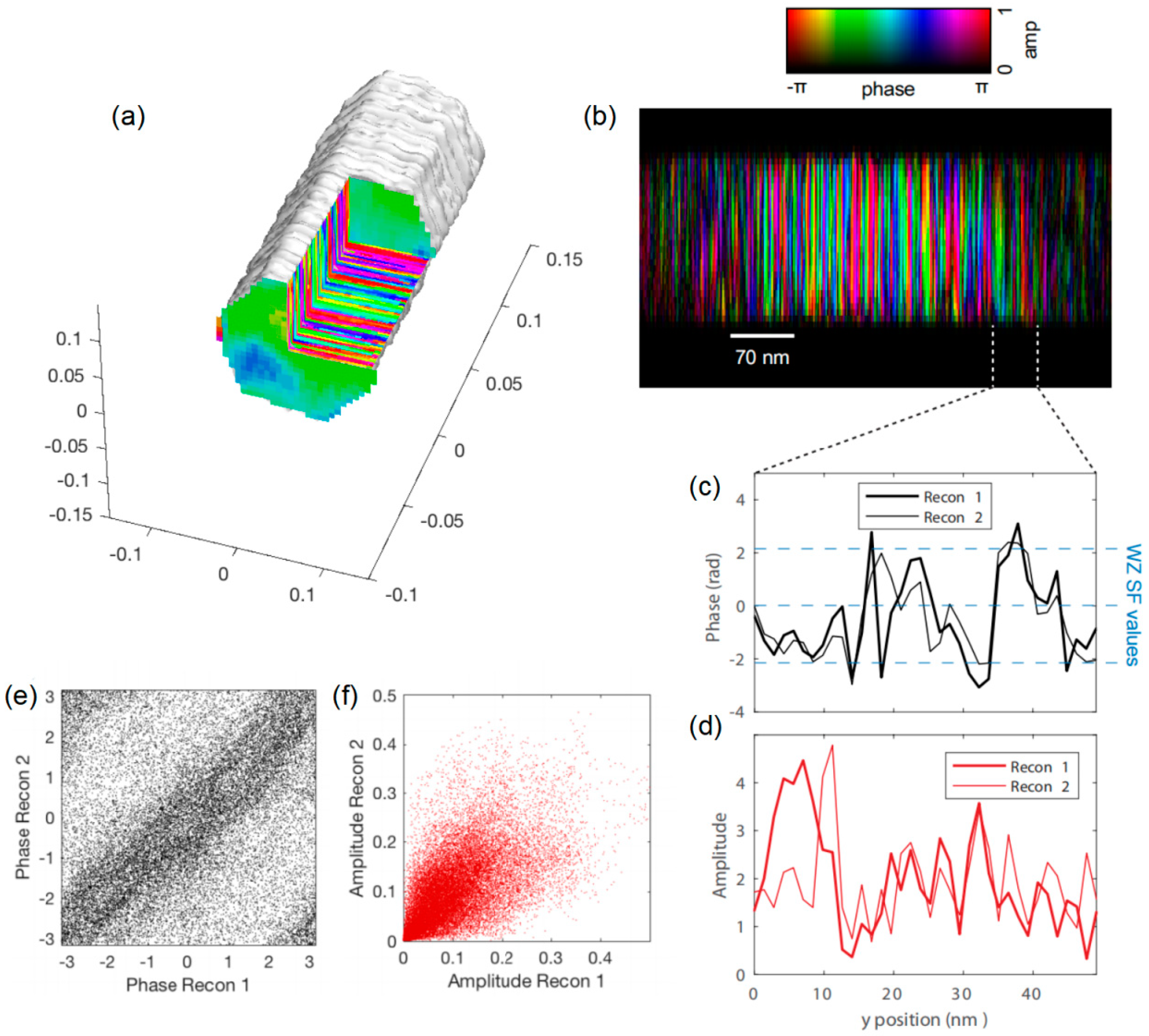
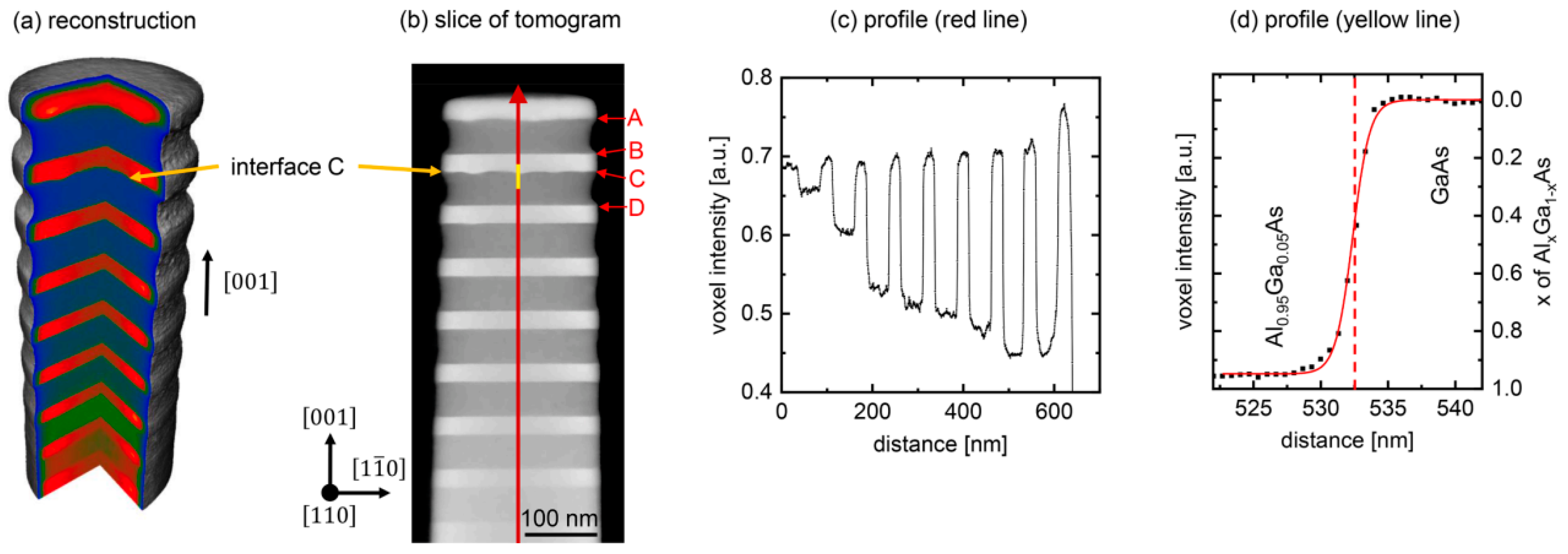
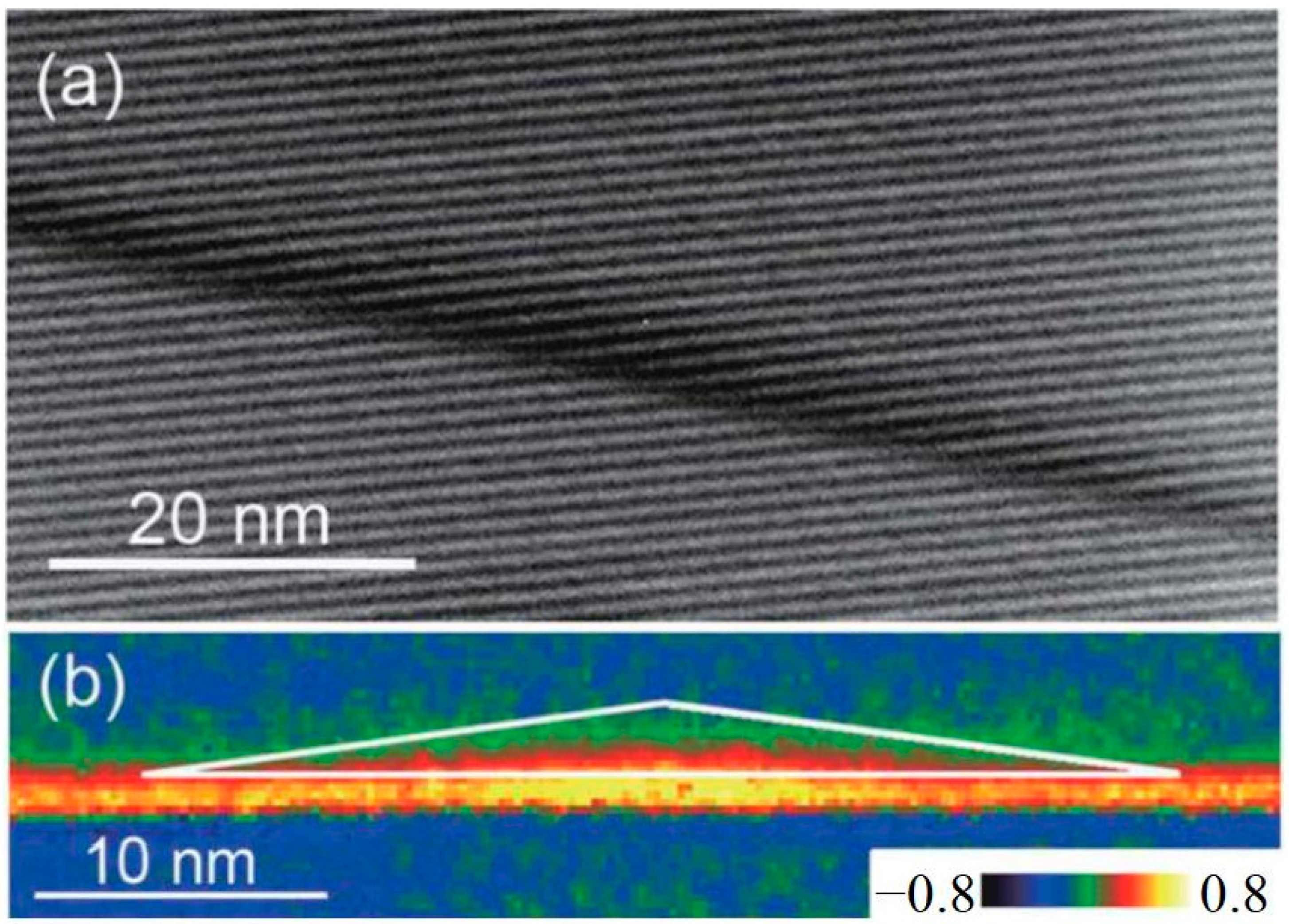

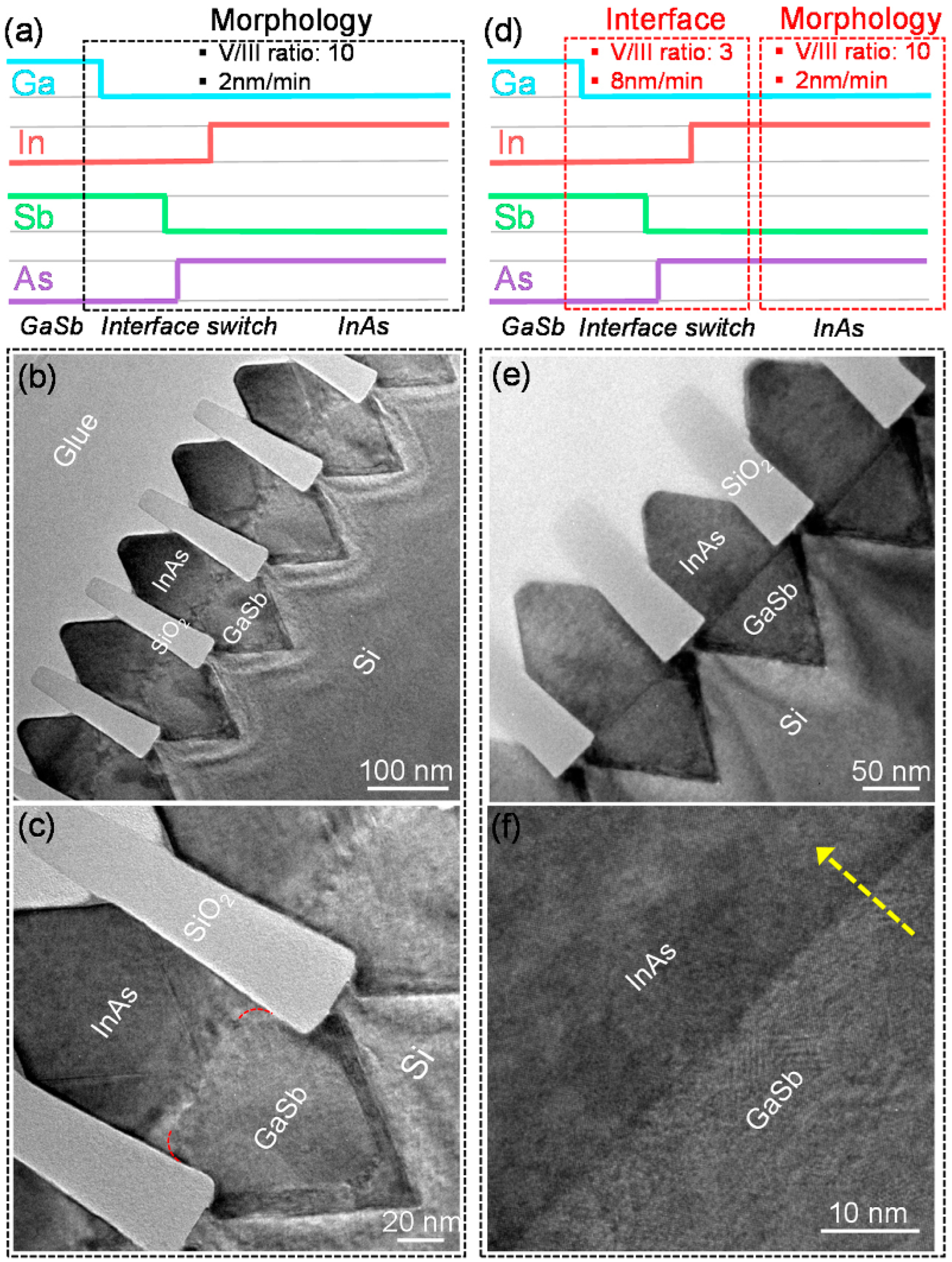



| Feature | Traditional CBED | Improved CBED with Electron Vortex Beams |
|---|---|---|
| Beam type | convergent electron beam | electron vortex beams (with orbital angular momentum) |
| Real space resolution | moderate | improved phase and spatial precision |
| Contrast | standard diffraction contrast | enhanced by selective post-filtering |
| Applications | crystal defects, strain analysis | chirality determination, detailed phase mapping |
| Setup complexity | simple, standard alignment | more complex, requires vortex generation |
| Technique | Advantages | Limitations | Applications |
|---|---|---|---|
| SAED | Simple, quick crystal analysis | Low resolution, limited defect analysis | Basic crystallography, strain study |
| CBED | High-resolution, precise strain data | Sensitive to thickness, complex interpretation | Local strain, crystal symmetry |
| NBD | High-resolution strain mapping | Affected by scattering, thickness limits | Nanoscale and interface studies |
| PED | Averages dynamical effects | Complex data acquisition | Precise lattice and strain analysis |
| Feature | Method 1 [127] | Method 2 [128] | Method 3 [117] |
|---|---|---|---|
| Image Contrast | Good, but some dynamic diffraction persists | Moderate, some image contrast reversal effects | Best contrast, effectively suppresses dynamic background |
| Resolution | Moderate, influenced by thickness fringes | Moderate, minor resolution reduction | Highest resolution, detailed visualization of dislocation core positions |
| Sample Tilting Requirement | High, requires significant sample tilting | Moderate, involves CBED pattern alignment | Low, minimal sample tilting needed |
| Background Noise Suppression | Partially effective | Moderate, residual noise remains present | Most effective, significantly reduced noise from non-defective areas |
| Operational Complexity | High, requires precise optical adjustments | Moderate, involves projector system adjustments | Low, minimal tilting and aperture changes required |
| x | Buffer Layer | TDD (107 cm−2) | TDD Reduction with Respect to x = 0 Wafer (%) for Same Buffer Type |
|---|---|---|---|
| 0 | Ge | 5.9 | 0 |
| 0.1 | Ge | 4.3 | –28 |
| 0.14 | Ge | 3.9 | –34 |
| 0.175 | Ge | 5.0 | –15 |
| 0 | GaAs | 53.4 | 0 |
| 0.14 | GaAs | 17.9 | –66 |
| Technique | Advantages | Limitations | Applications |
|---|---|---|---|
| ptychography | ultra-high resolution, low-dose | computationally intensive | low-dose, detailed imaging |
| tomography | 3D structure visualization | long acquisition time, sampling limitation | porous materials and nanoparticle studies |
| electron holography | measures electric/magnetic fields | complex setup, high stability required | electromagnetic studies |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, T.; Chen, L.; Wang, X.; Qiu, Y.; Liu, H.; Yang, Z.; Walther, T. Recent Developments in Transmission Electron Microscopy for Crystallographic Characterization of Strained Semiconductor Heterostructures. Crystals 2025, 15, 192. https://doi.org/10.3390/cryst15020192
Gong T, Chen L, Wang X, Qiu Y, Liu H, Yang Z, Walther T. Recent Developments in Transmission Electron Microscopy for Crystallographic Characterization of Strained Semiconductor Heterostructures. Crystals. 2025; 15(2):192. https://doi.org/10.3390/cryst15020192
Chicago/Turabian StyleGong, Tao, Longqing Chen, Xiaoyi Wang, Yang Qiu, Huiyun Liu, Zixing Yang, and Thomas Walther. 2025. "Recent Developments in Transmission Electron Microscopy for Crystallographic Characterization of Strained Semiconductor Heterostructures" Crystals 15, no. 2: 192. https://doi.org/10.3390/cryst15020192
APA StyleGong, T., Chen, L., Wang, X., Qiu, Y., Liu, H., Yang, Z., & Walther, T. (2025). Recent Developments in Transmission Electron Microscopy for Crystallographic Characterization of Strained Semiconductor Heterostructures. Crystals, 15(2), 192. https://doi.org/10.3390/cryst15020192







