Next Article in Journal
Particle Size Grading Strategy for Enhanced Performance of Lithium Iron Phosphate Cathode Materials
Next Article in Special Issue
New Discoveries in the Maijishan Grottoes: Identification of Blue-Green Pigments and Insights into Green Pigment Application Techniques
Previous Article in Journal
Experimental Investigation of the Mesostructural Damage in Bedded Rock Salt During Creep Deformation
Previous Article in Special Issue
Study on the Chromogenic Mechanism of Blue Kyanite from Coronel Murta, Minas Gerais, Brazil
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 15
Issue 4
10.3390/cryst15040306
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Discrimination of Thermoluminescent Signals from Natural Quartz and Carbonate Crystals Mixture

by
Rosaria Galvagno
,
Giuseppe Stella
*,
Riccardo Reitano
and
Anna Maria Gueli
Department of Physics and Astronomy “Ettore Majorana”, University of Catania, Via S. Sofia 64, 95123 Catania, Italy
*
Author to whom correspondence should be addressed.
Crystals 2025, 15(4), 306; https://doi.org/10.3390/cryst15040306
Submission received: 23 January 2025 / Revised: 14 March 2025 / Accepted: 22 March 2025 / Published: 26 March 2025
(This article belongs to the Collection Topic Collection: Mineralogical Crystallography)
Browse Figures
Versions Notes

Abstract

:
Luminescence techniques, especially thermoluminescence (TL) and optically stimulated luminescence (OSL), are essential for dating materials in Cultural Heritage. TL is effective for dating bricks by determining their last heating event, but brick reuse can introduce inaccuracies. OSL enhances accuracy by dating the last light exposure of quartz grains in mortars, a material that is coeval with the construction of the building. However, partial bleaching of quartz grains can lead to overestimated ages. A promising solution involves dating the carbonate fraction of mortars, as calcium carbonate experiences bleaching during mortar preparation. This study investigates the feasibility of isolating signals from quartz and calcite in a composite material. Initially, TL signals for quartz and calcite were characterized separately. A laboratory mixture, comprising 75% quartz and 25% calcite, was irradiated to simulate partial bleaching. TL curve deconvolution revealed distinct peaks: quartz displayed four peaks, while calcite had three, notably lacking a low-temperature peak. The mixed sample exhibited peaks at 527 K, 573 K, 618 K, and 690 K, with the first peak being exclusively quartz, the second primarily quartz with minor calcite, and the third showing contributions from both. Dose-response curves indicated that the quartz peaks aligned with the expected 41.40 Gy dose, and the calcite signal matched 10.40 Gy. This confirms the feasibility of separating TL signals from quartz and calcite in mixed samples, offering a potential method for accurately dating the carbonate fraction in mortars and addressing partial bleaching issues. Future work will focus on optimizing detection parameters and applying this method to historically significant mortars to assess its effectiveness.

1. Introduction

Luminescence is now widely applied in the field of Cultural Heritage, with thermo-luminescence (TL) being particularly useful for dating bricks. This technique enables the examination of various phases in a building’s construction by dating the last heating event (above 500 °C) of the material used for the bricks, which typically corresponds to their manufacture phase. However, a significant limitation arises from the fact that the production date and the last heating event can differ from the date of use due to the common practice of reusing bricks [1,2].
To mitigate uncertainties in interpreting results, Optically Stimulated Luminescence (OSL) has been introduced. OSL allows for dating the last exposure to light of quartz grains in the mortar used in construction before they are embedded in masonry and shielded from light [3]. Unlike bricks, mortar cannot be reused, meaning OSL dating can offer a definitive construction date corresponding to when the mortar was applied [4].
OSL works by measuring the luminescence emitted by minerals such as quartz or feldspar that have been exposed to light. These minerals accumulate a “paleodose” as they are exposed to environmental radiation, which can then be measured by stimulating the grains with light. By dividing the paleodose by the annual dose rate (determined by the sample’s radiochemical composition and environmental factors), the age of the sample can be calculated [5,6]. This allows for precise dating of the mortar’s application.
However, a significant challenge in OSL dating arises from the incomplete or partial bleaching of quartz grains during mortar preparation. Full bleaching of grains is essential for accurate dating because grains that are not fully reset retain residual luminescence from previous exposures to light. This leads to mixed luminescent signals, which result in an overestimation of the equivalent dose and inaccurate age estimates [7]. In the context of OSL dating, the issue of incomplete bleaching is critical, as mortars are often composed of grains that have undergone varying degrees of bleaching. Some grains are more effectively reset than others during mortar preparation, leading to heterogeneous luminescence signals.
Consequently, when determining the equivalent dose in incompletely bleached samples, an increase in measured luminescence may lead to an overestimation of the equivalent dose and, consequently, the age of the sample [8]. In the field of stimulated luminescence dating research, partial bleaching remains an ongoing issue.
Researchers have proposed several methods to separate well-bleached grains from those with residual luminescence. The first approach is single-grain OSL dating, which involves measuring individual grains to avoid mixed signals from multiple grains [9]. While this technique can offer more precise results, it presents the challenge of detecting weak luminescence signals emitted by individual grains. Advances in instrumentation and technology have, however, made single-grain analysis more feasible and accurate, enhancing the reliability of OSL dating for mortars [6,10].
Another promising method involves the use of fine-grained quartz fractions (typically between 4 and 11 microns) in the conventional multigrain procedure. This approach has been applied to Mediterranean mortars and has shown promising results that correlate with thermoluminescence dating of adjacent bricks [11,12]. The fine-grain fraction tends to have more consistent bleaching behavior, which can reduce the degree of variability in the luminescence signal. However, bulk measurements of fine grains can obscure individual grain variations, which is a challenge for accurate dating. Researchers recommend combining this method with other techniques, such as TL dating of bricks, to improve the accuracy of mortar age estimates [11,12].
Geographical variations in environmental factors can also influence the effectiveness of OSL dating. For example, mortars from coastal regions, where factors such as sunlight and humidity promote better bleaching, tend to produce more reliable results than mortars from other areas [13]. This highlights the need for further research into how local environmental factors affect bleaching and how these factors can be accounted for in OSL dating methodologies.
Other statistical methods have been designed to analyze data from well-bleached and incompletely bleached grain populations. These methods include the Central Age Model (CAM) [14], Minimum Age Model (MAM) [15], unlogged Minimum Age Model (MAMUL) [16], and Internal-External Consistency Criteria (IEU) [8,17].
A potential new experimental approach is to date the carbonate fraction present in mortars. This fraction is of particular interest for OSL dating because it was formed via the Lime Cycle during the construction of the building.
As shown in Figure 1, during lime mortar production, geological limestone (CaCO3) is heated above 800 °C to produce quicklime (CaO), which is then converted to hydrated lime by adding water. Mixing hydrated lime with aggregate (usually sand) yields mortar, which undergoes a carbonation process as atmospheric CO2 is incorporated, forming anthropogenic lime carbonates [18,19,20]. This process can cause at least two resetting events: the crystallization of calcium carbonate within weeks or months and the bleaching of geological carbonate at high temperatures during limestone heating [21].
The gold standard for absolute dating of mortars is Optically Stimulated Luminescence (OSL) on extracted quartz, where the resetting event corresponds to the last exposure to light during the placement process. However, the high probability of partial bleaching remains a critical limitation, potentially leading to overestimation of the age. An innovative alternative is to explore thermally stimulated luminescence of the carbonate fraction, where the resetting event is intrinsically linked to the crystallization process during mortar manufacture and placement. To date, no documented studies have pursued this approach, making this study the first to preliminarily investigate its feasibility.
Therefore, the ultimate goal is to date historical buildings using the carbonate fraction in mortars.
The current study aims to investigate the feasibility of using the carbonate fraction for dating by distinguishing the luminescence signals of quartz and calcite. Laboratory experiments were conducted in which a mixture of quartz and calcite in known proportions was prepared, and its luminescent response and dosimetric properties were analyzed. This work is significant because it provides a method for addressing the challenge of distinguishing mixed luminescence signals, a problem that has been largely overlooked in the existing literature on luminescence dating. Successfully separating the signals from quartz and calcite would enable more accurate dating of historical mortars, particularly in cases where traditional OSL methods face limitations due to incomplete bleaching. By investigating the potential to distinguish these mixed signals, this study represents an important step forward in the development of more accurate and reliable luminescence dating techniques.

2. Materials and Methods

Calcite and quartz, with a grain size between 180 and 212 microns (180 < Ø < 212), were extracted from a stalagmite and marine sediment, respectively. After resetting the natural luminescence signal (at 450 °C, 5 °C/s), quartz was irradiated with a dose of 41.40 Gy, while calcite received a dose of 10.40 Gy. The artificial irradiation was delivered using a calibrated 90Sr/90Y beta source integrated into a semi-automated Risø TL-DA-15 reader, with a dose rate of 4.14 Gy/min.
The experimental part of this study was divided into two distinct phases. In the first phase, the thermoluminescence signals of quartz and calcite aliquots were separately characterized using deconvolution processes (details in Section 2.1). Deconvolution was conducted, fitting the thermoluminescence (TL) glow curves with multiple peak models to identify and analyze the trapping parameters. For quartz, four high-temperature peaks were identified, while for calcite, the glow curves were best described by the fitting of three peaks [22,23,24]. The goodness of fit was assessed using the χ2 test and Figure of Merit (FOM).
The studies indicate that a constant heating rate was used during the TL curve measurements. Specifically, the TL signal was recorded at a heating rate of 5 °C/s, following preliminary tests conducted at 0.5, 1, 2, and 5 °C/s.
Although the thermal stimulation of quartz typically reaches a maximum temperature of 500 °C, a maximum temperature of 450 °C was chosen to adapt the procedure for a quartz–calcite mixture phase. The measurement conditions for quartz were specifically adjusted to be consistent with those of calcite. Numerous studies indicate that a maximum reading temperature of 450 °C is preferable for calcite, as higher temperatures can induce material degradation, leading to significant variations in sensitivity from a dosimetric perspective [25,26,27,28,29].
To study the dosimetric response of the two materials, a recovery test was performed on 25 aliquots of quartz and 25 aliquots of calcite. This test is critical within the SAR (Single Aliquot Regeneration) protocol, as it helps determine a known dose irradiated under conditions like those following the bleaching of the natural signal during mortar preparation after the last solar exposure [30,31]. The procedure begins by resetting the luminescent signal of the sample without heat treatment. An artificial dose is then delivered through irradiation. The recovery ratio (R) is defined as the ratio between the measured dose using the SAR procedure and the known dose delivered in the laboratory [32], as expressed in Equation (1):
R = M e a s u r e d   d o s e G i v e n   d o s e
The dosimetric response is considered reliable if the test results (R) are close to one. If this is the case, the aliquots are then submitted to the SAR measurement protocol, as outlined in Table 1.
After obtaining the TL curves for all aliquots, deconvolutions were performed on both the artificial and test dose curves, using the method described in Section 2.1. This allowed for the calculation of the ratio Lx/Tx for each deconvolution peak and the construction of an Lx/Tx curve as a function of dose for each peak. The thermoluminescent intensities (L and T values) useful for the analysis were obtained from the integral of the deconvolved single peak. By interpolating Lknown dose/Tknown dose, it is possible to determine the measured dose value for each deconvolution peak of quartz and calcite, which allows for the calculation of the Recovery Test (R) value for both materials.
In the second phase, the irradiated aliquots were combined to create a controlled mixture consisting of 75% quartz and 25% calcite, reflecting typical binder-to-aggregate ratios in historical mortars [11,33,34]. Notably, quartz received a higher irradiation dose than calcite to simulate partial bleaching conditions. To prepare the mixture, 75% quartz and 25% calcite were placed in a beaker, and acetone was added. The solution was mixed in an ultrasonic bath for 5 min and then placed in a G®-Therm 015 drying oven at a controlled temperature of 35 °C for 48 h to ensure complete evaporation of the acetone. These aliquots were then subjected to a measurement protocol, as reported in Table 1.
Based on the results discussed in Section 3.2, the deconvolution process used four peaks: one attributed to quartz (P1), two overlapping between quartz and calcite (P2 and P3), and one last peak that is non-characteristic (P4).
For each aliquot and for each individual deconvolved peak contribution, the total equivalent dose (ED) from the mixture (P3) and the ED of quartz (P1) were calculated, followed by subtraction to obtain the ED of calcite. The experimental ED values for quartz and calcite were then compared with the known irradiation dose using the recovery test method described above.
For all deconvolutions, we used homemade software called Dosimetric Deconvolution Chart, which utilizes a General Order Kinetics (GOK) model to perform the analyses (see Section 2.1) [35].
All measurements in this study were conducted using TL-DA-15 automated Risø readers equipped with EMI 9235QA photomultipliers [5,6]. To optimize the detection of the luminescent signal from calcite, the BG-39 filter was utilized, which is mentioned in the literature for detecting calcite signals [36,37,38,39,40].

2.1. Deconvolution Process

The luminescence intensity in the General Order Kinetics (GOK) model is described by a mathematical formulation that accounts for the number of charge carriers present in a single energy level and their transition rates. This model introduces parameters such as the frequency factor, the order of kinetics (ranging between 1 and 2), and the activation energy, which collectively define the luminescence behavior under thermal stimulation [41,42,43].
In this study, the fitting parameters considered for both quartz and calcite include the peak temperature (Tm), activation energy (E), and the kinetic order (b). The initial values used for fitting are presented in Table 2.
In the assessment of the fit’s quality, the Figure of Merit (FOM) for each deconvolution was calculated. This statistical measure enables an evaluation of the effectiveness of an experimental fit to the data while disregarding experimental discrepancies, such as variations in spectral shapes or techniques [40,44].
The FOM is defined as follows:
F O M = ∑ i = 1 n y i e x p − y i f i t ∑ i = 1 n y i e x p ,     i = 1 … n
where y i e x p is the experimental data, y i f i t is the fitted data, and n is the number of measurements. If FOM < 0.025, it is possible to demonstrate that the fit is good from a statistical point of view [44].

3. Results and Discussion

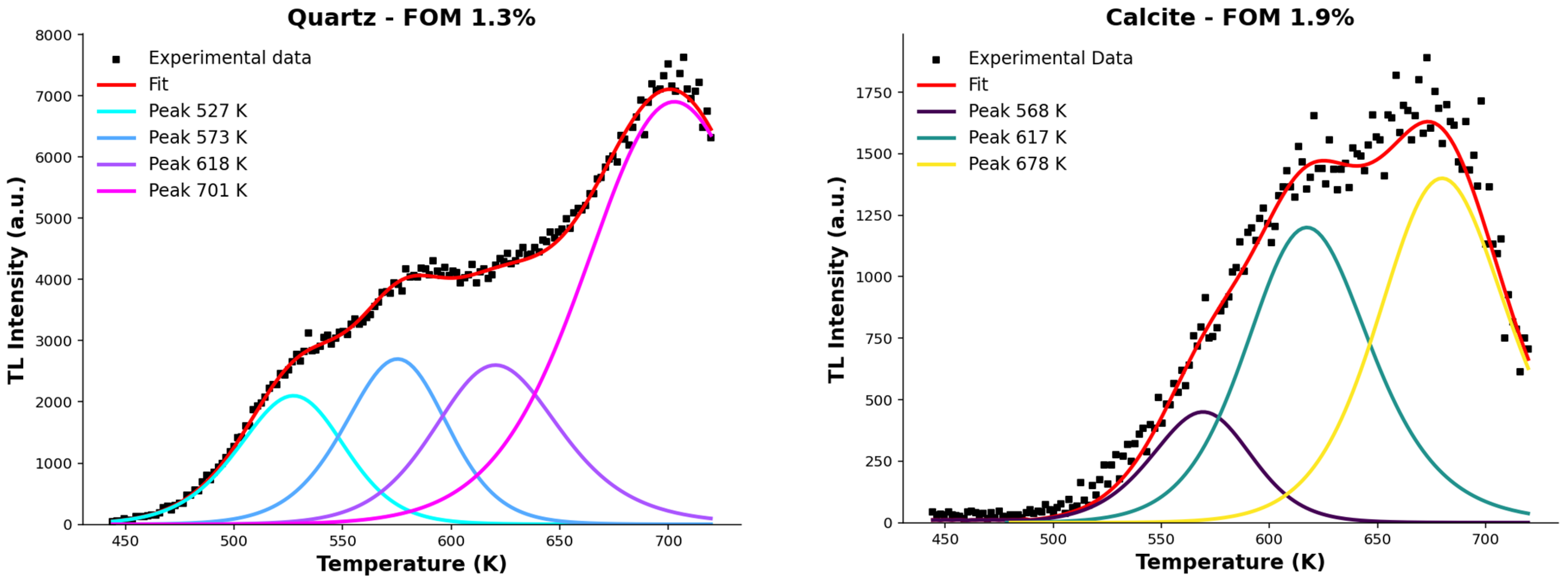
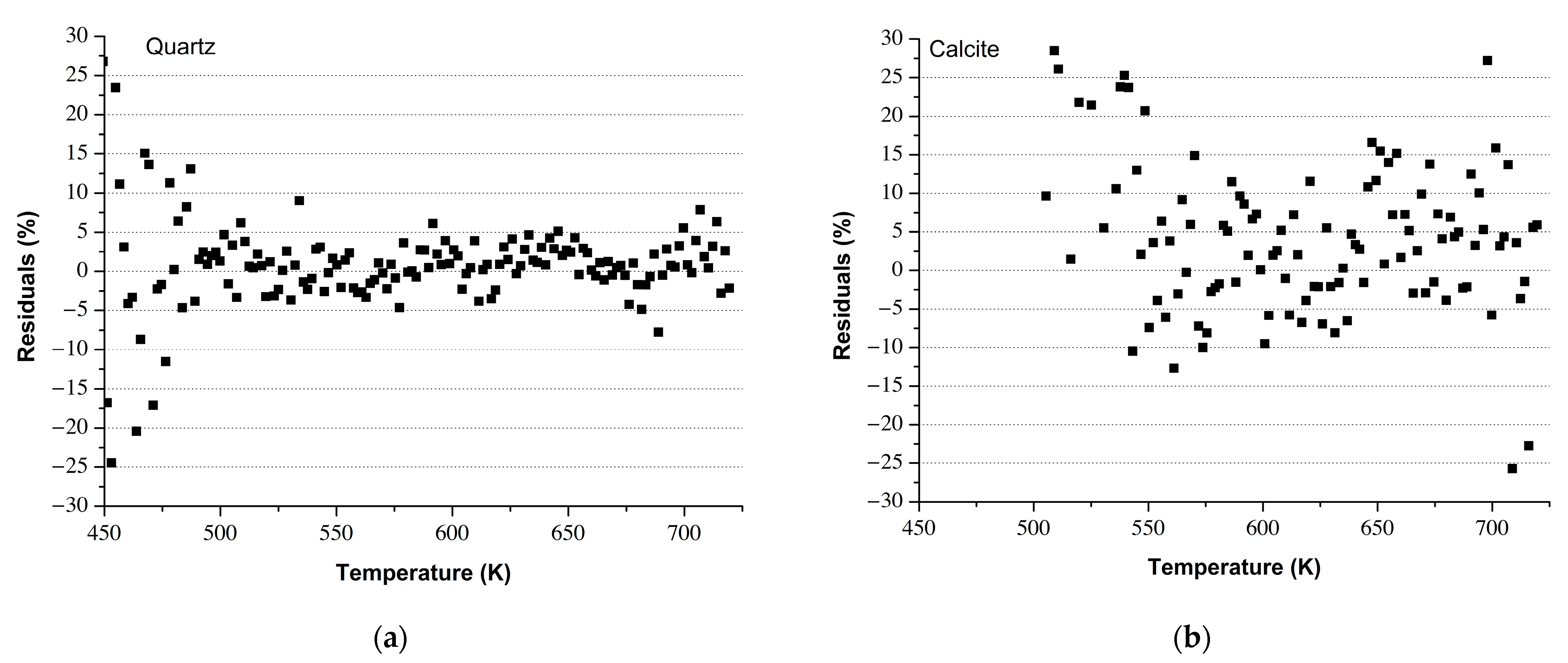
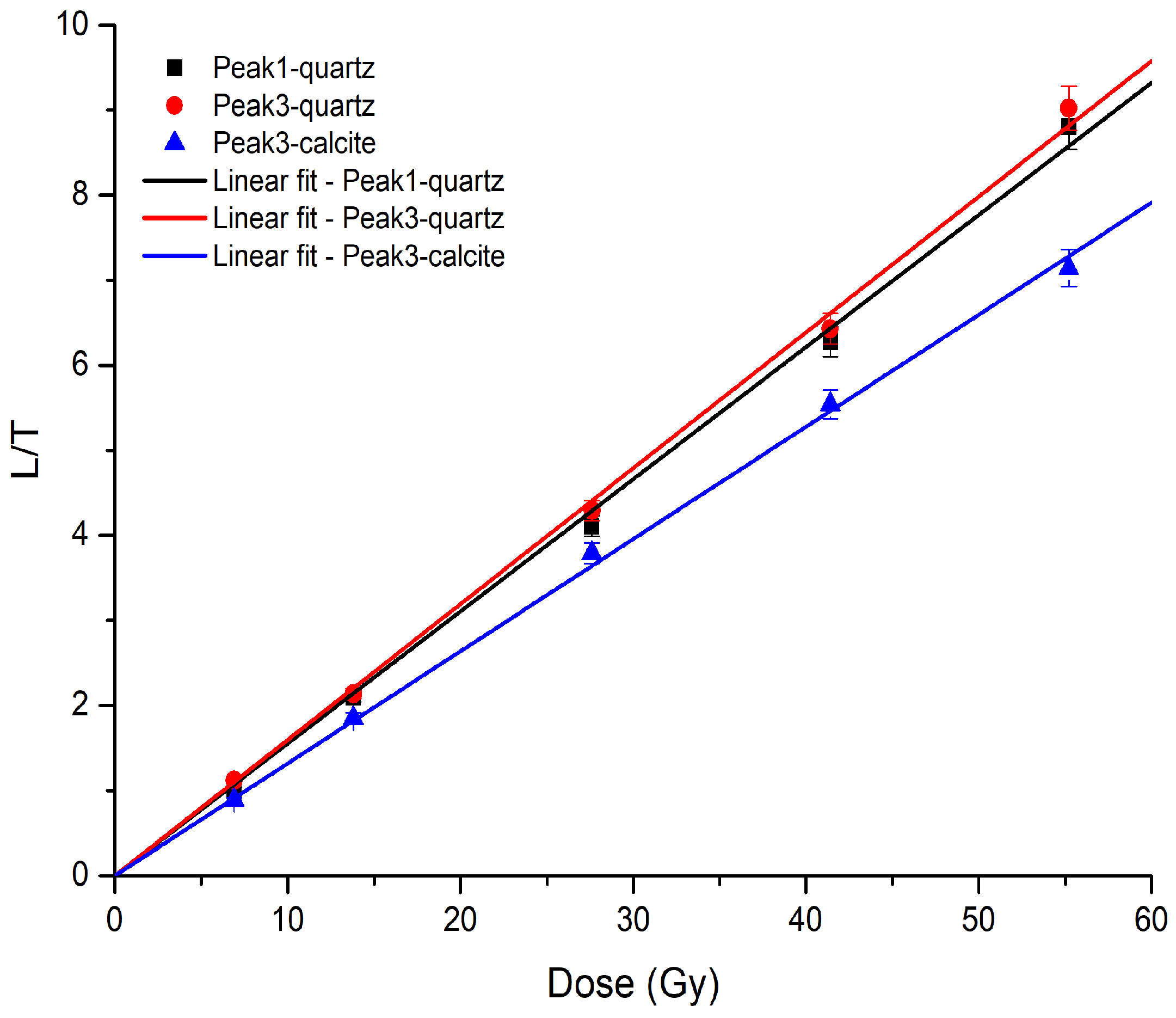
3.1. Analysis of the Individual Thermoluminescent Contributions

Using the measurement sequence outlined in Table 1 and the BG-39 filter, thermoluminescence (TL) curves were obtained. Figure 2 presents an example of the deconvolution results for the TL curve of quartz and calcite aliquots. In particular, the example curves were obtained by irradiating a quartz aliquot and a calcite aliquot at 14 Gy, using a pre-heating condition of 220 °C and a heating rate of 5 °C/s for signal reading.
In Figure 2a, the deconvolution of the quartz TL signal is shown. Quartz displays four deconvolution peaks at different temperatures. In Figure 2b, the deconvolution of the calcite TL signal is presented, revealing three deconvolution peaks. The residuals for each deconvolution are also shown below the corresponding curves.
Unlike quartz, calcite does not exhibit a deconvolution peak at lower temperatures.
For all TL curves of the quartz and calcite aliquots, deconvolutions were performed to minimize the Figure of Merit (FOM). In the deconvolutions shown in Figure 2, the FOM obtained for quartz is 1.3%, while for calcite it is 1.9%. Both values indicate high statistical reliability of the deconvolutions performed. Considering all aliquots on which deconvolution was performed, the average FOM obtained is 1.5 ± 0.4% for quartz and 1.8 ± 0.4% for calcite.
Notably, peak P4 will not be included in subsequent analyses, as background subtraction introduces excessive errors in the deconvolution parameters. This deconvolution peak is not characteristic for studying the luminescent properties of the two materials because it is influenced by the background subtraction process. This illustrates the challenges in accurately modeling TL signals from minerals with overlapping emission bands and emphasizes the importance of refining background correction techniques in such studies.
The deconvolution parameters obtained from the 25 aliquots of quartz and calcite are detailed in Table 3.
Table 3 shows the temperatures associated with the deconvolution peaks. Each temperature value represents the average maximum temperature observed in the TL curves of the aliquots of both quartz and calcite, with the error indicated by the standard deviation of the mean. Additionally, the energy (E in eV) and b parameters of the General Order Kinetics (GOK) model are presented. The luminescent traps in both quartz and calcite are characterized by relatively deep activation energies (ranging from 1.29 eV to 1.59 eV), which are consistent with typical TL behavior for these minerals. Moreover, the parameter b, which falls between 1 and 2, supports the applicability of General Order Kinetics. The data indicate that peaks 2 and 3 for both quartz and calcite overlap at the same temperature, which accounts for the associated experimental errors.
The results presented in Table 3 show that the TL parameters obtained in this study are in good agreement with previously reported values in the literature. A comparison with references [22,23,24] highlights the consistency of the findings, confirming the reliability of the deconvolution process applied to quartz and calcite TL signals.
For the first quartz peak, the measured peak temperature (Tm = 527 ± 4 K) is in good agreement with the values reported in previous studies, which indicate peaks at 549 K ([22]) and at 515 K and 545 K ([23]). The average of these literature values results in Tm = 536 ± 9 K, which is well within the experimental uncertainty of our results. Similarly, the activation energy (E = 1.29 ± 0.04 eV) closely matches the values reported in [22] (E = 1.29 eV) and [23] (E = 1.2 eV and 1.4 eV), leading to an averaged literature value of E = 1.30 ± 0.10 eV. The kinetic order parameter b, although slightly higher in our results (b = 1.52 ± 0.04) compared to the literature values in [22] (b = 1.30) and [23] (b = 1.21 and b = 1.27), remains in reasonable agreement with the averaged literature value of b = 1.24 ± 0.03.
A similar trend is observed for the second quartz peak, where our measured Tm (573 ± 3 K) falls between the values reported in the literature ([22], Tm = 598 K; [23], Tm = 580 K), obtaining an averaged value of 589 ± 9 K. The activation energy found in this study (E = 1.50 ± 0.04 eV) is slightly higher than the values reported in [22] (E = 1.34 eV) and [23] (E = 1.35 eV) but remains consistent within experimental uncertainties. Similarly, the kinetic order parameter (b = 1.57 ± 0.04) aligns well with previous studies, where reported values range from 1.38 ([22]) to 1.51 ([23]), resulting in an averaged value of 1.44 ± 0.1.
For the third quartz peak, the agreement with the literature is again evident. The peak temperature found in this study (Tm = 618 ± 3 K) is consistent with reported values in [23] (Tm = 616 K) and [22] (Tm = 625 K), with an averaged literature value of 620 ± 5 K. The activation energy (E = 1.59 ± 0.04 eV) is slightly higher than the literature-reported values of 1.48 eV ([22]) and 1.45 eV ([23]), with an average of E = 1.46 ± 0.10 eV, but still within an acceptable range. The kinetic order parameter (b = 1.86 ± 0.04) is in good agreement with previous studies, where values of 1.70 ([22]) and 1.93 ([23]) have been reported, leading to an averaged value of b = 1.81 ± 0.10.
Turning to calcite, a strong agreement is also observed. The second calcite peak, identified at Tm = 568 ± 4 K, is well within the range reported in the literature ([24]), where an average peak temperature of Tm = 540 ± 13 K has been found. The activation energy (E = 1.50 ± 0.04 eV) closely matches the literature value of E = 1.53 ± 0.04 eV ([24]), and the kinetic order parameter (b = 1.57 ± 0.04) is compatible with the literature-reported value of b = 1.64 ± 0.16 ([24]).
Finally, for the third calcite peak, results obtained in this study indicate a peak temperature of Tm = 617 ± 4 K, in good agreement with the literature average of Tm = 621 ± 16 K ([24]). The activation energy (E = 1.59 ± 0.04 eV) is slightly lower than the reported literature value of E = 1.76 ± 0.07 eV ([24]), but the difference remains within a reasonable experimental margin. Similarly, the kinetic order parameter (b = 1.86 ± 0.04) is consistent with the literature-reported value of b = 1.90 ± 0.06 ([24]).
Overall, the comparison with literature data confirms the robustness of the followed experimental approach and the accuracy of the deconvolution method used in this study.
To assess the dosimetric response of the materials, a recovery test was conducted on 25 aliquots of quartz and 25 aliquots of calcite. The results, showing the averages of the Recovery Ratio (R) values for all deconvolution peaks, are presented in Table 4.
The R values are close to 1, indicating that the SAR protocol accurately measured the doses delivered. These results suggest that both quartz and calcite are reliable materials for dosimetric purposes, with quartz showing slightly lower recovery ratios, possibly due to the higher dose irradiated.
Figure 3 shows a linear growth of the L/T signal as a function of dose for both peaks 1 and 3 of quartz and peak 3 of calcite. The fit for peak 1 presents a slope coefficient of 0.155 ± 0.001 (R2 = 0.997), the fit for peak 2 has a value of 0.159 ± 0.002 (R2 = 0.997), while the fit for calcite shows a slope coefficient of 0.132 ± 0.001 (R2 = 0.996). While the first two are nearly identical, the lower value for the fit on peak 3 indicates a different behavior, showing reduced sensitivity to dose. This confirms the literature data, which indicate quartz, due to its linearity and dose sensitivity, as the primary dosimeter for optically stimulated luminescence dating of historical buildings.

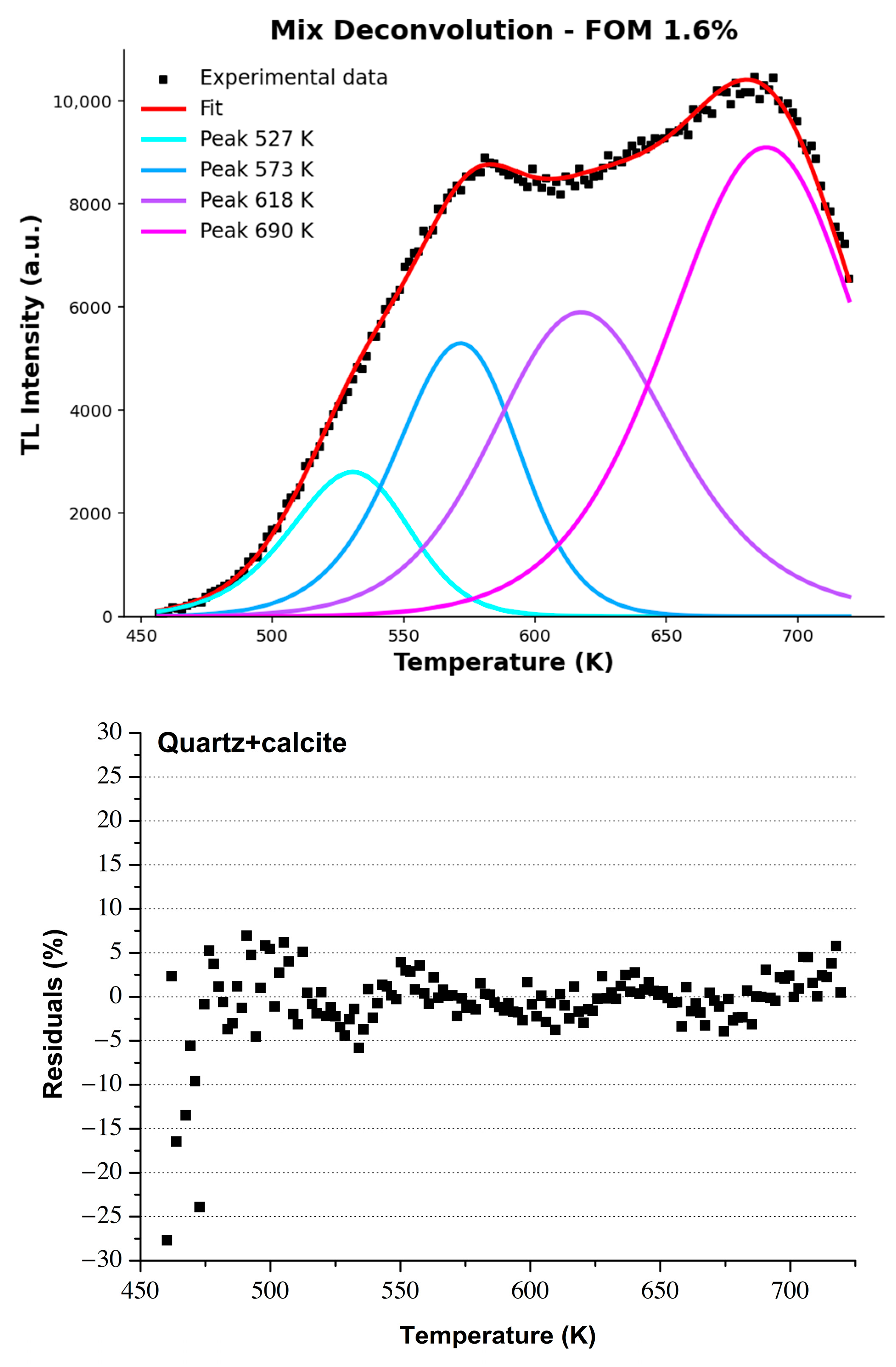
3.2. Analysis of the Thermoluminescent Contribution in the Mixed Phase

A four-peak deconvolution approach was adopted for the deconvolution of the mix, considering the overlaps between the various peaks of quartz and calcite.
Figure 4 illustrates this four-peak deconvolution for one aliquot of the mixture.
Deconvolution of the mixed phase yielded four distinct peaks, including two overlapping peaks (P2 and P3) that represent contributions from both minerals: the peak at 527 K is solely attributed to the quartz signal, while peaks at 573 K and 618 K arise from signals of both materials.
The FOM value of 1.6% for the mixed phase deconvolution suggests that the fitting procedure was effective.
A measurement protocol utilizing the SAR method was conducted on aliquots of the mixture to determine the equivalent dose for each aliquot. Deconvolution was performed on each TL curve obtained through SAR, and integrals under the deconvolution peaks (P1, P2, P3) were calculated. Subsequently, Lx/Tx ratios were determined, and via interpolation, the values of ED (P1) and ED (P3) were obtained. The results are illustrated in the Radial Plots in Figure 5.
In a radial plot, the ED distributions are plotted on a logarithmic scale on the radial axis. The left side depicts the 2-sigma error, with bar width determined by the ED distribution. The bottom scale provides a measure of the error for each ED measurement, allowing relative error and precision assessments.
As shown in Figure 5, the equivalent doses (ED) cluster around a central value of 40.04 ± 0.22 Gy for the first peak, which, within experimental error, aligns with the irradiation dose of quartz prior to mixing, confirming the validity of the deconvolution method for quantifying the dose absorbed by quartz.
For the third peak, P3, the ED values are higher than the one of ED(P1), clustering around 50.02 ± 0.35 Gy, due to a higher contribution from calcite’s signal.
To isolate the ED contribution of quartz from calcite, the differences between the ED values attributed to peak P3, ED(P3), and those attributed to peak P1, ED(P1), were computed. The results are presented in the radial plot shown in Figure 6.
The reference dose indicated corresponds to the irradiation dose of calcite in the analyzed mix, equal to 10.40 ± 0.20 Gy. The points on the radial plot represent ED values obtained by subtracting the ED values from the third and the first deconvolution peaks. All points cluster around the central value, which overlaps within the experimental error with the reference irradiation value of calcite.
This analysis demonstrates that it is possible to determine the irradiation dose absorbed by calcite. By examining the distribution of ED values and comparing them to the reference irradiation value, one can estimate the amount of irradiation received by the mineral.
Finally, the radial plots of ED distributions (Figure 5 and Figure 6) clearly demonstrate the capability of this methodology to differentiate the dosimetric responses of quartz and calcite within the mixture. The ED values for quartz cluster around 40.04 ± 0.22 Gy, which agrees with the initial dose applied, while the ED values for calcite in peak P3 cluster around 50.02 ± 0.35 Gy, reflecting the higher contribution of calcite’s signal due to its lower initial dose and the overlapping nature of the peaks in the mixed phase. The subtraction of the ED values from P1 and P3 effectively isolates the calcite contribution, with the resulting ED distribution aligning with the reference irradiation dose of 10.40 ± 0.20 Gy, confirming the accuracy of the method in distinguishing the two materials.
The equivalent dose (ED) calculated from the peak 1 of quartz corresponds to the dose accumulated from the geological formation of the mineral, reduced by bleaching exposures. In fact, during the transport of quartz sand from the gravel pit to the mortar production site, bleaching occurs. However, it likely stops once the grains are coated with a calcite layer. Given the large quantities of sand being transported, not all grains are exposed to enough light to fully reset the luminescence accumulated over geological time. As a result, the resetting process produces a mixture of grains that are bleached unevenly and incompletely [45].
Optical exposure reduces the measured TL dose in quartz by depleting the shallower electron traps that contribute to the TL signal. This process decreases the number of trapped electrons available to generate measurable luminescence during TL measurement when the sample is heated. The interaction between shallow traps and optical stimulation leads to a reduction in the measured TL dose, as charge is removed from these traps, which would otherwise contribute to the TL response. This phenomenon is supported by the literature, particularly the model proposed by Bøtter-Jensen et al. (1995) [46], which describes a five-level band system: Level 1 (shallow electron traps), Level 2 (optically active traps), Level 3 (deep electron traps), and Levels 4 and 5 (recombination centers). The shallow traps (Level 1) are partially stable at irradiation temperatures and are highly sensitive to optical exposure. When quartz is exposed to light (for example, during an OSL measurement), the electrons in these shallow traps can be optically stimulated and released. This reduces the number of trapped electrons available for subsequent thermoluminescence measurements. Since optically active traps (Level 2) are emptied by optical exposure, electrons that would have contributed to the TL signal (during heating) are no longer available for recombination at the recombination centers (Level 4).
Because the TL signal depends on the release and recombination of electrons from these traps, removing electrons from the shallow traps (which are responsible for the TL peaks) reduces the overall signal intensity. This leads to a reduction in the measured TL dose after optical exposure. The deep traps (Level 3) are not affected by optical exposure and, therefore, do not directly influence the reduction of the TL dose. However, the overall luminescence response is still influenced by the redistribution of charges in the shallower traps.
Another important consideration in our work is that we started with a simple model composed of quartz + calcite, excluding other “luminescent” minerals at this stage. However, the validity of this model is supported by the work of Krbetschek et al. (1997) [47], which provides spectral information from minerals relevant to luminescence dating. This work is foundational for stimulated luminescence dating. Based on this article, here are some considerations made in our work: Feldspars, particularly plagioclase feldspars and alkali feldspars, are the most influential minerals in terms of luminescence signal intensity. However, the strongest signals occur in the blue-violet range (around 420 nm), while weaker signals in the green (560–570 nm) are associated with plagioclase feldspars. Another emission (700–750 nm) is linked to feldspars but occurs at emission temperatures below 200 °C.
Mica and clay minerals generally produce less intense luminescence signals compared to feldspars. Emissions at higher wavelengths, such as red (700–750 nm) or yellow (650 nm), are weak and do not constitute the main part of the signal. Mica can contribute to the red luminescence (700–750 nm), but this signal is only present at low temperatures (<200 °C) and has limited intensity. Clay minerals, such as illite, kaolinite, and montmorillonite, contribute only minimally to luminescence. While they can emit signals, these are much weaker compared to those from quartz. Considering that we use a BG39 signal acquisition filter operating between 390 nm and 600 nm, signals from other minerals are considered negligible at this stage of the experiment.

4. Conclusions

The present study explores the thermoluminescent (TL) properties of quartz and calcite, two prevalent minerals in environmental and archaeological contexts, employing a detailed deconvolution approach. It evaluates the dosimetric responses of quartz and calcite both individually and in mixed phases, determining their equivalent dose (ED) distributions through experimental protocols and advanced analytical techniques.
This research demonstrates the effectiveness of TL signal deconvolution, combined with the SAR protocol, in accurately measuring the equivalent dose absorbed by individual minerals and their mixtures. The findings underscore the potential of this method for dosimetric applications, particularly in analyzing complex mineral mixtures, such as historical mortars, for their luminescent properties.
Moreover, the study emphasizes the importance of precise background subtraction and addressing peak overlap to ensure accurate dose estimation in mixed-phase samples. These results contribute valuable insights to the application of TL in cultural heritage research, enhancing the precision and reliability of luminescence dating for historical mortars and other composite materials.
As an original contribution, this method enables the separation of equivalent dose contributions from quartz and other luminescent mineral fractions, such as calcite, within mixed-phase signals. This capability provides a valuable tool for supporting OSL dating of historical mortars and, by extension, historically significant buildings. The approach represents a promising avenue for advancing the application of luminescence dating in heritage conservation and archaeological research. Furthermore, while this study focuses on dose ranges typically encountered in historical mortar dating, the methodology has the potential to be expanded and optimized for other contexts. Future work could explore different dose ranges to further refine and extend the methodology.
However, at this stage, it does not represent an alternative method to existing ones for dating historical mortars using stimulated luminescence, but rather a guideline for the creation of a supporting method for optically stimulated luminescence dating on quartz extracted using single grain techniques.

Author Contributions

Conceptualization, G.S. and A.M.G.; methodology, G.S. and R.G.; software, R.G.; validation, G.S., A.M.G. and R.R.; formal analysis, R.G. and G.S.; investigation, G.S. and R.G.; resources, A.M.G.; data curation, R.G.; writing—original draft preparation, R.G.; writing—review and editing, R.G., G.S., A.M.G. and R.R.; visualization, A.M.G.; supervision, G.S.; project administration, A.M.G., R.R. and G.S.; funding acquisition, A.M.G. All authors have read and agreed to the published version of the manuscript.

Funding

The research activity was funded by the European Union (NextGeneration EU), through the MUR-PNRR project SAMOTHRACE (Code: ECS00000022; CUP: E63C22000900006) “SiciliAn MicronanOTecH Research and Innovation Center”–Ecosistema dell’innovazione (PNRR, Mission 4, Component 2 Investment 1.5, Avviso n. 3277 del 30 December 2021), Spoke 1–Università di Catania-Work Package 6 Cultural Heritage.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bailiff, I.K. Methodological developments in the Luminescence Dating of brick from English late-medieval and post-medieval buildings. Archaeometry 2007, 49, 827–851. [Google Scholar] [CrossRef]
  2. Galli, A.; Martini, M.; Maspero, F.; Panzeri, L.; Sibilia, E. Surface Dating of Bricks, an Application of Luminescence Techniques. Eur. Phys. J. Plus 2014, 129, 101. [Google Scholar] [CrossRef]
  3. Guibert, P.; Urbanová, P.; Javel, J.-B.; Guérin, G. Modeling Light Exposure of Quartz Grains During Mortar Making: Consequences for Optically Stimulated Luminescence Dating. Radiocarbon 2020, 62, 693–711. [Google Scholar] [CrossRef]
  4. Panzeri, L. Mortar and Surface Dating with Optically Stimulated Luminescence (OSL): Innovative Techniques for the Age Determination of Buildings. Nuovo C. Della 2013, 36, 205–216. [Google Scholar] [CrossRef]
  5. Bøtter-Jensen, L. Luminescence techniques: Instrumentation and methods. Radiat. Meas. 1997, 27, 749–768. [Google Scholar] [CrossRef]
  6. Bøtter-Jensen, L.; Bulur, E.; Duller, G.A.T.; Murray, A.S. Advances in Luminescence Instrument Systems. Radiat. Meas. 2000, 32, 523–528. [Google Scholar] [CrossRef]
  7. Zacharias, N.; Mauz, B.; Michael, C.T. Luminescence Quartz Dating of Lime Mortars: A First Research Approach. Radiat. Prot. Dosim. 2002, 101, 379–382. [Google Scholar] [CrossRef]
  8. Thomsen, K.J.; Murray, A.S.; Bøtter-Jensen, L.; Kinahan, J. Determination of Burial Dose in Incompletely Bleached Fluvial Samples Using Single Grains of Quartz. Radiat. Meas. 2007, 42, 370–379. [Google Scholar] [CrossRef]
  9. Jain, M.; Thomsen, K.J.; Bøtter-Jensen, L.; Murray, A.S. Thermal Transfer and Apparent-Dose Distributions in Poorly Bleached Mortar Samples: Results from Single Grains and Small Aliquots of Quartz. Radiat. Meas. 2004, 38, 101–109. [Google Scholar] [CrossRef]
  10. Duller, G.A.T.; Bøtter-Jensen, L.; Murray, A.S.; Truscott, A.J. Single Grain Laser Luminescence (SGLL) Measurements Using a Novel Automated Reader. Nucl. Instrum. Methods Phys. Res. B 1999, 155, 506–514. [Google Scholar] [CrossRef]
  11. Stella, G.; Fontana, D.; Gueli, A.M.; Troja, S.O. Historical mortars dating from OSL signals of fine grain fraction enriched in quartz. Geochronometria 2013, 40, 153–164. [Google Scholar] [CrossRef]
  12. Stella, G.; Almeida, L.; Basílio, L.; Pasquale, S.; Dinis, J.; Almeida, M.; Gueli, A.M. Historical Building Dating: A Multidisciplinary Study of the Convento de São Francisco (Coimbra, Portugal). Geochronometria 2018, 45, 119–129. [Google Scholar] [CrossRef]
  13. Urbanová, P.; Michel, A.; Bouvier, A.; Cantin, N.; Guibert, P.; Lanos, P.; Dufresne, P.; Garnier, L. Novel Interdisciplinary Approach for Building Archaeology: Integration of Mortar Luminescence Dating into Archaeological Research, an Example of Saint Seurin Basilica, Bordeaux. J. Archaeol. Sci. Rep. 2018, 20, 307–323. [Google Scholar] [CrossRef]
  14. Galbraith, R.F.; Laslett, G.M. Statistical Models for Mixed Fission Track Ages. Nucl. Tracks Radiat. Meas. 1993, 21, 459–470. [Google Scholar] [CrossRef]
  15. Galbraith, R.F.; Roberts, R.G.; Yoshida, H. Error Variation in OSL Palaeodose Estimates from Single Aliquots of Quartz: A Factorial Experiment. Radiat. Meas. 2005, 39, 289–307. [Google Scholar] [CrossRef]
  16. Arnold, L.J.; Roberts, R.G.; Galbraith, R.F.; DeLong, S.B. A Revised Burial Dose Estimation Procedure for Optical Dating of Young and Modern-Age Sediments. Quat. Geochronol. 2009, 4, 306–325. [Google Scholar] [CrossRef]
  17. Thomsen, K.J.; Jain, M.; Bøtter-Jensen, L.; Murray, A.S.; Jungner, H. Variation with Depth of Dose Distributions in Single Grains of Quartz Extracted from an Irradiated Concrete Block. Radiat. Meas. 2003, 37, 315–321. [Google Scholar] [CrossRef]
  18. Hale, J.; Heinemeier, J.; Lindroos, A.; Lancaster, L. Dating Ancient Mortar. Am. Sci. 2003, 91, 130–137. [Google Scholar] [CrossRef]
  19. Daugbjerg, T.S.; Lindroos, A.; Heinemeier, J.; Ringbom, Å.; Barrett, G.; Michalska, D.; Hajdas, I.; Raja, R.; Olsen, J. A Field Guide to Mortar Sampling for Radiocarbon Dating. Archaeometry 2021, 63, 1121–1140. [Google Scholar] [CrossRef]
  20. Wojcieszak, M.; Fontaine, L.; Elsen, J.; Hayen, R.; Lehouck, A.; Boudin, M. Historic Lime Mortars Composition and Terminology for Radiocarbon Dating—Case Studies Based on Thin-Section Petrography and Cathodoluminescence. Radiocarbon 2024, 66, 1814–1834. [Google Scholar] [CrossRef]
  21. Urbanová, P.; Boaretto, E.; Artioli, G. The State-of-the-Art of Dating Techniques Applied to Ancient Mortars and Binders: A Review. Radiocarbon 2020, 62, 503–525. [Google Scholar] [CrossRef]
  22. Gartia, R.K.; Lovedy, L.; Ranita, U. Analysis of Glow Curves of Quartz and Transluminescence Dating; CSIR: Perth, Australia, 2009; pp. 417–419. [Google Scholar]
  23. Gartia, R.K.; Singh, L.L. Evaluation of Trapping Parameter of Quartz by Deconvolution of the Glow Curves. Radiat. Meas. 2011, 46, 664–668. [Google Scholar] [CrossRef]
  24. Kim, K.B.; Hong, D.G. Kinetic Parameters, Bleaching and Radiation Response of Thermoluminescence Glow Peaks Separated by Deconvolution on Korean Calcite. Radiat. Phys. Chem. 2014, 103, 16–21. [Google Scholar] [CrossRef]
  25. Kirsh, Y.; Townsend, P.D.; Shoval, S. Local transitions and charge transport in thermoluminescence of calcite. Int. J. Radiat. Appl. Instrum. Part D Nucl. Tracks Radiat. Meas. 1987, 13, 115–119. [Google Scholar] [CrossRef]
  26. Franklin, A.D.; Hornyak, W.F.; Pagonis, V.; Kristianpoller, N. Thermoluminescence study of annealing a geological calcite. Nucl. Tracks Radiat. Meas. 1990, 17, 517–523. [Google Scholar] [CrossRef]
  27. Dwijen Singh, T.; Dorendrajit Singh, S. Kinetic parameters of thermoluminescence glow curves of γ-irradiated green calcite. Indian J. Pure Appl. Phys. 2009, 47, 409–412. [Google Scholar] [CrossRef]
  28. Cano, N.F.; Etchvarne, C.A.; Munita, C.S.; Rocca, R.R.; Barbosa, R.F.; Watanabe, S. Point defects in calcite used to estimate the date of arrival of first settlers in central region of Brazil. Phys. Status Solidi C 2013, 10, 268–271. [Google Scholar] [CrossRef]
  29. Abdel-Razek, Y.A. Thermoluminescence dosimetry using natural calcite. J. Taibah Univ. Sci. 2016, 10, 286–295. [Google Scholar] [CrossRef]
  30. Murray, A.S.; Wintle, A.G. Luminescence Dating of Quartz Using an Improved Single-Aliquot Regenerative-Dose Protocol. Radiat. Meas. 2000, 32, 57–73. [Google Scholar] [CrossRef]
  31. Murray, A.S.; Wintle, A.G. The Single Aliquot Regenerative Dose Protocol: Potential for Improvements in Reliability. Radiat. Meas. 2003, 37, 377–381. [Google Scholar] [CrossRef]
  32. Murray, A.; Arnold, L.J.; Buylaert, J.P.; Guérin, G.; Qin, J.; Singhvi, A.K.; Thomsen, K.J. Optically stimulated luminescence dating using quartz. Nat. Rev. Methods Primers 2021, 1, 72. [Google Scholar] [CrossRef]
  33. Middendorf, B.; Hughes, J.J.; Callebaut, K.; Baronio, G.; Papayanni, I. 2.3 Chemical Characterisation of Historic Mortars. In Characterisation of Old Mortars with Respect to Their Repair—Final Report of RILEM TC 167-COM; Groot, C., Ashall, G., Hughes, J., Eds.; RILEM Publications: Paris, France, 2004; pp. 39–56. [Google Scholar]
  34. Casadio, F.; Chiari, G.; Simon, S. Evaluation of Binder/Aggregate Ratios in Archaeological Lime Mortars with Carbonate Aggregate: A Comparative Assessment of Chemical, Mechanical and Microscopic Approaches. Archaeometry 2005, 47, 671–689. [Google Scholar] [CrossRef]
  35. Stella, G.; Sallah, A.; Galvagno, R.; D’Anna, A.; Gueli, A.M. Simultaneous Double Dose Measurements Using TLD-100H. Crystals 2024, 14, 603. [Google Scholar] [CrossRef]
  36. Down, J.S.; Flower, R.; Strain, J.A.; Townsend, P.D. Thermoluminescence Emission Spectra of Calcite and Iceland Spar. Nucl. Tracks Radiat. Meas. 1985, 10, 581–589. [Google Scholar] [CrossRef]
  37. Gaft, M.; Nagli, L.; Panczer, G.; Waychunas, G.; Porat, N. The Nature of Unusual Luminescence in Natural Calcite CaCO3. Am. Mineral. 2008, 93, 158–167. [Google Scholar] [CrossRef]
  38. Duller, G.A.T.; Penkman, K.E.H.; Wintle, A.G. Assessing the Potential for Using Biogenic Calcites as Dosemeters for Luminescence Dating. Radiat. Meas. 2009, 44, 429–433. [Google Scholar] [CrossRef]
  39. Zhang, J.; Wang, L. Thermoluminescence Dating of Calcite–Alpha Effectiveness and Measurement Protocols. J. Lumin. 2020, 223, 117205. [Google Scholar] [CrossRef]
  40. Şahiner, E.; Polymeris, G.S.; Öztürk, M.Z.; Kadioğlu, Y.K.; Meriç, N. Component Resolved Equivalent Dose Estimation Using TL Glow Curves of Travertine Samples from Anatolia, Turkey. Geochronometria 2021, 48, 171–178. [Google Scholar] [CrossRef]
  41. May, C.E.; Partridge, J.A. Thermoluminescent kinetics of alpha-irradiated alkali halides. J. Chem. Phys. 1964, 40, 1401–1409. [Google Scholar] [CrossRef]
  42. Randall, J.T.; Wilkins, M.H.F. Phosphorescence and electron traps—I. The study of trap distributions. Proc. R. Soc. Lond. A 1945, 184, 365–389. [Google Scholar] [CrossRef]
  43. Garlick, G.F.J.; Gibson, A.F. The electron trap mechanism of luminescence in sulphide and silicate phosphors. Proc. Phys. Soc. 1948, 60, 574. [Google Scholar] [CrossRef]
  44. Balian, H.G.; Eddy, N.W. Figure-of-Merit (FOM), an Improved Criterion over the Normalized Chi-Squared Test for Assessing Goodness-of-Fit of Gamma-Ray Spectral Peaks. Nucl. Instrum. Methods Phys. Res. 1977, 145, 389–395. [Google Scholar] [CrossRef]
  45. Goedicke, C. Dating historical mortars by blue OSL: Results from known age samples. Radiat. Meas. 2003, 37, 409–415. [Google Scholar] [CrossRef]
  46. Bøtter-Jensen, L.; Larsen, N.A.; Mejdahl, V.; Poolton, N.R.J.; Morris, M.F.; McKeever, S.W.S. Luminescence sensitivity changes in quartz as a result of annealing. Radiat. Meas. 1995, 24, 535–541. [Google Scholar] [CrossRef]
  47. Krbetschek, M.R.; Götze, J.; Dietrich, A.; Trautmann, T. Spectral information from minerals relevant for luminescence dating. Radiat. Meas. 1997, 27, 695–748. [Google Scholar] [CrossRef]
Crystals 15 00306 g001
Figure 1. The Lime Cycle involves a series of chemical reactions in which limestone undergoes transformation, resulting in the formation of calcium carbonate in mortars through the carbonation process.
Figure 1. The Lime Cycle involves a series of chemical reactions in which limestone undergoes transformation, resulting in the formation of calcium carbonate in mortars through the carbonation process.
Crystals 15 00306 g001
Crystals 15 00306 g002aCrystals 15 00306 g002b
Figure 2. Deconvolution of TL curves for (a) quartz and (b) calcite, obtained using the reading conditions specified in Table 1. The graphs display the corresponding FOM values for the deconvolutions of the two TL curves: the FOM for quartz is 1.3%, while the FOM for calcite is 1.9%, indicating statistical significance in the fits. Below each deconvolution, the residuals associated with it are also shown.
Figure 2. Deconvolution of TL curves for (a) quartz and (b) calcite, obtained using the reading conditions specified in Table 1. The graphs display the corresponding FOM values for the deconvolutions of the two TL curves: the FOM for quartz is 1.3%, while the FOM for calcite is 1.9%, indicating statistical significance in the fits. Below each deconvolution, the residuals associated with it are also shown.
Crystals 15 00306 g002aCrystals 15 00306 g002b
Crystals 15 00306 g003
Figure 3. Linear increase in the L/T signal as a function of dose for quartz (peaks 1 and 3) and calcite (peak 3).
Figure 3. Linear increase in the L/T signal as a function of dose for quartz (peaks 1 and 3) and calcite (peak 3).
Crystals 15 00306 g003
Crystals 15 00306 g004
Figure 4. Deconvolution of the mix TL curve. In this case, the deconvolution is made up of four peaks. Below the deconvolution curve of the mix, the residuals are also shown.
Figure 4. Deconvolution of the mix TL curve. In this case, the deconvolution is made up of four peaks. Below the deconvolution curve of the mix, the residuals are also shown.
Crystals 15 00306 g004
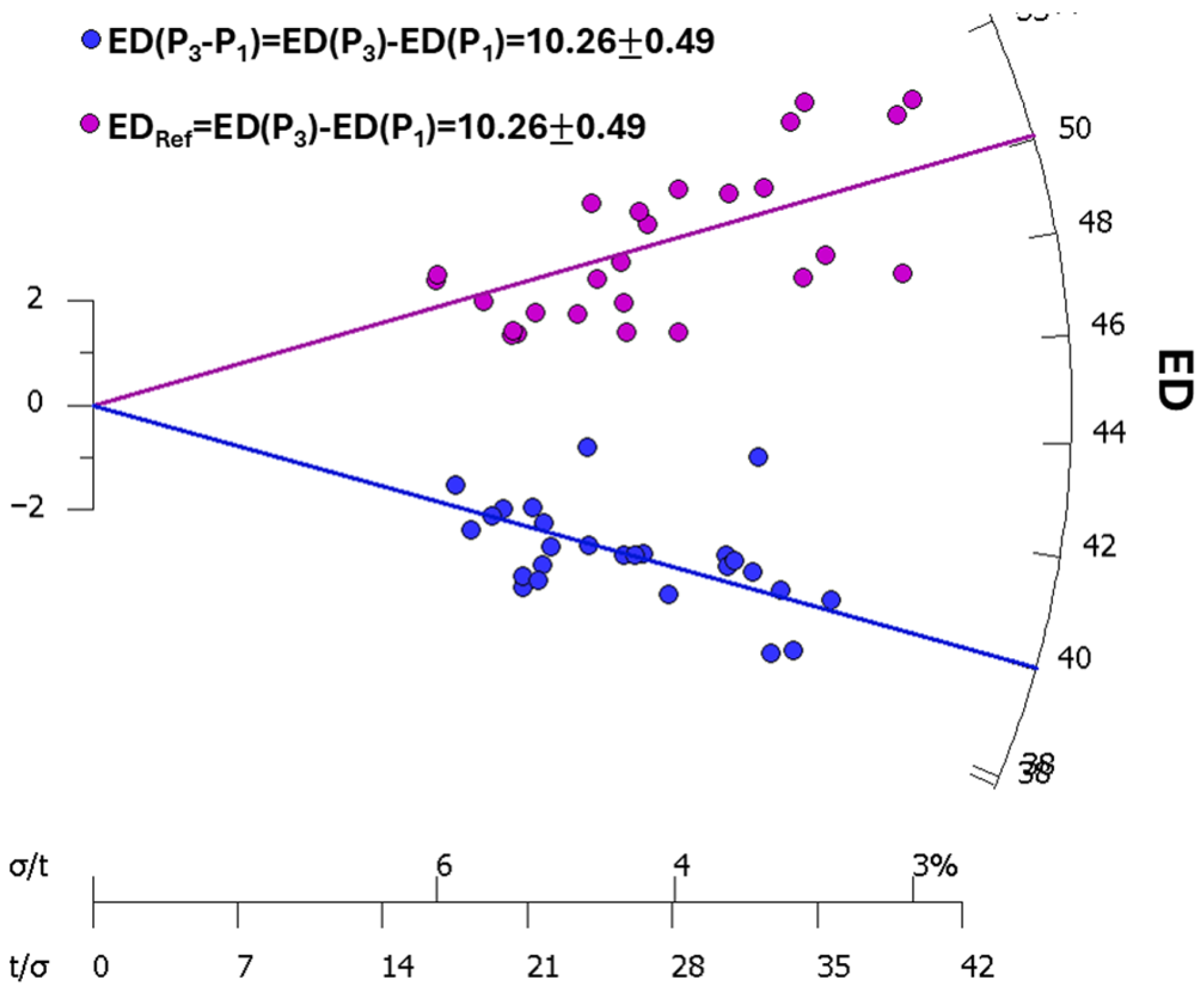
Crystals 15 00306 g005
Figure 5. Radial plot of the ED(P1), and ED(P3) distribution obtained from the samples.
Figure 5. Radial plot of the ED(P1), and ED(P3) distribution obtained from the samples.
Crystals 15 00306 g005
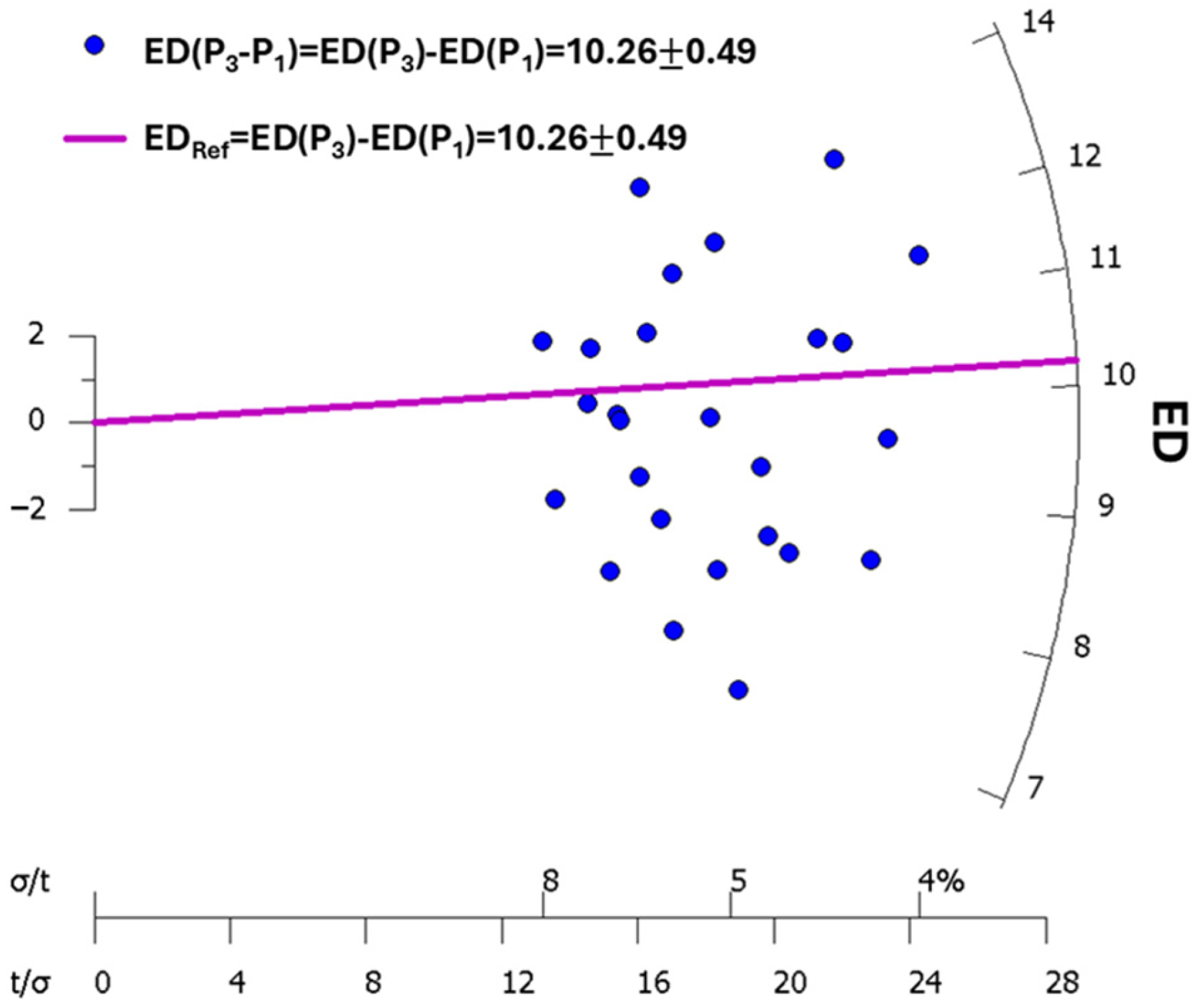
Crystals 15 00306 g006
Figure 6. Radial plot of the dose distribution ED(P3 – P1). Blue dots represent individual ED values, while the magenta line indicates the reference mean value, EDRef = ED(P3) − ED(P1) = 10.26 ± 0.49.
Figure 6. Radial plot of the dose distribution ED(P3 – P1). Blue dots represent individual ED values, while the magenta line indicates the reference mean value, EDRef = ED(P3) − ED(P1) = 10.26 ± 0.49.
Crystals 15 00306 g006
Table 1. SAR measurement protocol.
Table 1. SAR measurement protocol.
StepTreatmentObserved
1Preheating (@220 °C, 10 s)-
2Thermal Stimulation (@450 °C, 5 °C/s)Lknown dose
3Give Test Dose, DT = 7 Gy-
4Cut heat (@180 °C)-
5Thermal Stimulation (@450 °C, 5 °C/s)Tknown dose
6Give Dose, Di-
7Preheating (@220 °C, 10 s)-
8Thermal Stimulation (@450 °C, 5 °C/s)Lx
9Give Test Dose, DT = 7 Gy-
10Cut heat (@180 °C)-
11Thermal Stimulation (@450 °C, 5 °C/s)Tx
12Repeat step 8–13 for the dose value Di = 6.9 Gy, 13.80 Gy, 27.60 Gy, 41.40 Gy, 55.20 Gy-
Table 2. Initial fitting values for both quartz and calcite.
Table 2. Initial fitting values for both quartz and calcite.
QuartzCalcite
Peak NumberTm (K)E (eV)bTm (K)E (eV)b
P15281.201.50---
P25731.501.605681.501.60
P36181.601.806181.601.80
P4698--678--
Table 3. Temperature, energy, b values, frequency factor s, and lifetime τ were used for the deconvolution of TL curves of quartz and calcite aliquots. The missing information pertains to the fourth deconvolution peak, which will not be used for further analysis as this peak is non-characteristic.
Table 3. Temperature, energy, b values, frequency factor s, and lifetime τ were used for the deconvolution of TL curves of quartz and calcite aliquots. The missing information pertains to the fourth deconvolution peak, which will not be used for further analysis as this peak is non-characteristic.
QuartzCalcite
Peak NumberTm (K)E (eV)bs (s−1) τ ( y ) Tm (K)E (eV)bs (s−1) τ ( y )
P1527 ± 41.29 ± 0.041.52 ± 0.041.15 × 10107.94 × 102-----
P2573 ± 31.50 ± 0.041.57 ± 0.047.14 × 10112.73 × 106568 ± 41.50 ± 0.041.57 ± 0.041.01 × 10121.95 × 106
P3618 ± 31.59 ± 0.041.86 ± 0.043.79 × 10111.81 × 108617 ± 41.59 ± 0.041.86 ± 0.044.43 × 10111.55 × 108
P4701 ± 10----678 ± 12----
Table 4. Results of the recovery test conducted on aliquots of quartz and calcite. The displayed recovery ratio values are the mean of the aliquots for each deconvolution peak.
Table 4. Results of the recovery test conducted on aliquots of quartz and calcite. The displayed recovery ratio values are the mean of the aliquots for each deconvolution peak.
Peak RQuartzRCalcite
P10.92 ± 0.30-
P20.94 ± 0.270.97 ± 0.27
P30.96 ± 0.260.99 ± 0.27
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Galvagno, R.; Stella, G.; Reitano, R.; Gueli, A.M. Discrimination of Thermoluminescent Signals from Natural Quartz and Carbonate Crystals Mixture. Crystals 2025, 15, 306. https://doi.org/10.3390/cryst15040306

AMA Style

Galvagno R, Stella G, Reitano R, Gueli AM. Discrimination of Thermoluminescent Signals from Natural Quartz and Carbonate Crystals Mixture. Crystals. 2025; 15(4):306. https://doi.org/10.3390/cryst15040306

Chicago/Turabian Style

Galvagno, Rosaria, Giuseppe Stella, Riccardo Reitano, and Anna Maria Gueli. 2025. "Discrimination of Thermoluminescent Signals from Natural Quartz and Carbonate Crystals Mixture" Crystals 15, no. 4: 306. https://doi.org/10.3390/cryst15040306

APA Style

Galvagno, R., Stella, G., Reitano, R., & Gueli, A. M. (2025). Discrimination of Thermoluminescent Signals from Natural Quartz and Carbonate Crystals Mixture. Crystals, 15(4), 306. https://doi.org/10.3390/cryst15040306

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop