Study on AC Loss of REBCO Tape Encapsulated with Magnetic Materials
Abstract
:1. Introduction
2. Geometric Models and Numerical Method
2.1. Geometric Models of REBCO Tapes Encapsulated with Different Materials
2.2. Numerical Method
2.3. AC Loss Calculation
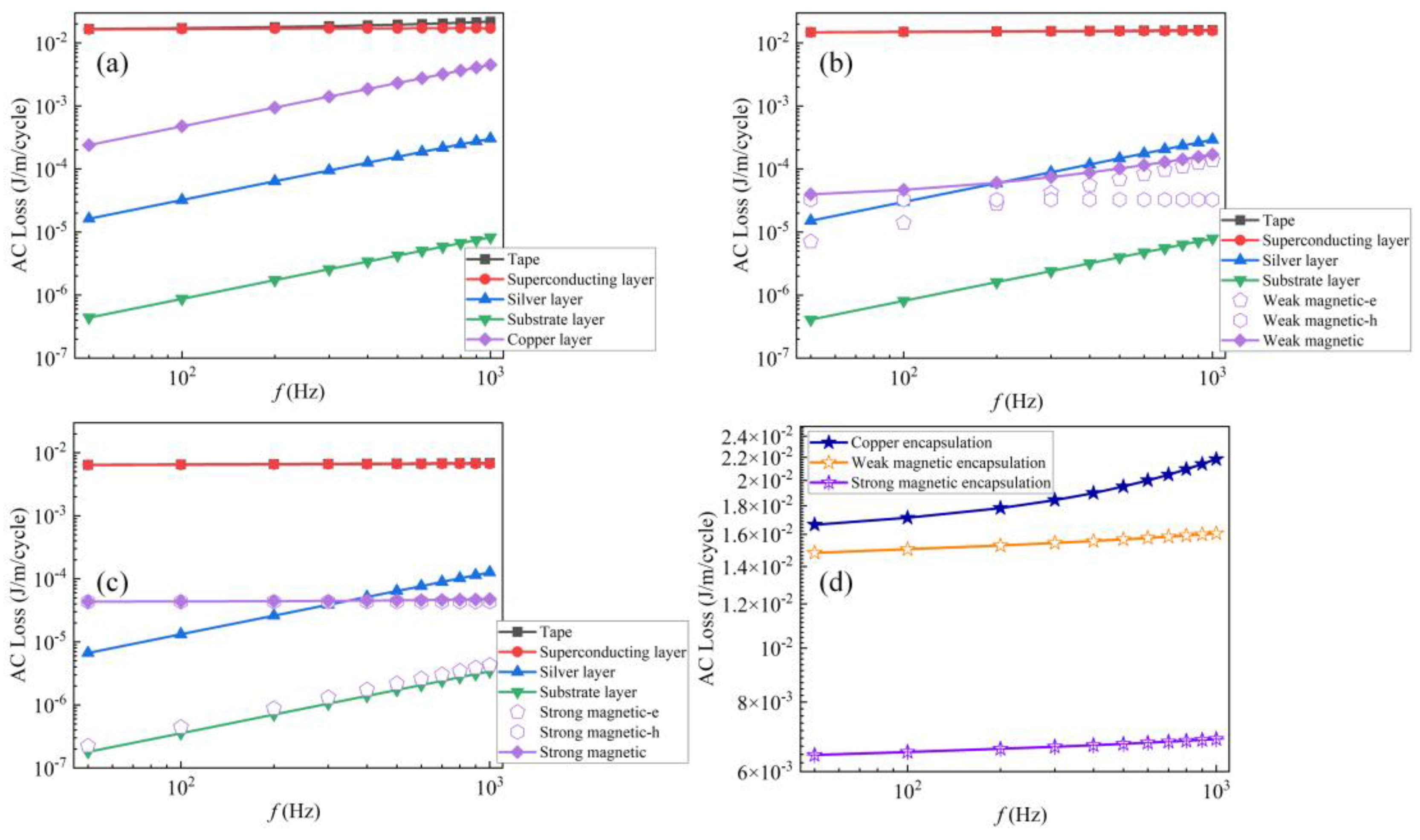
3. Result and Discussion
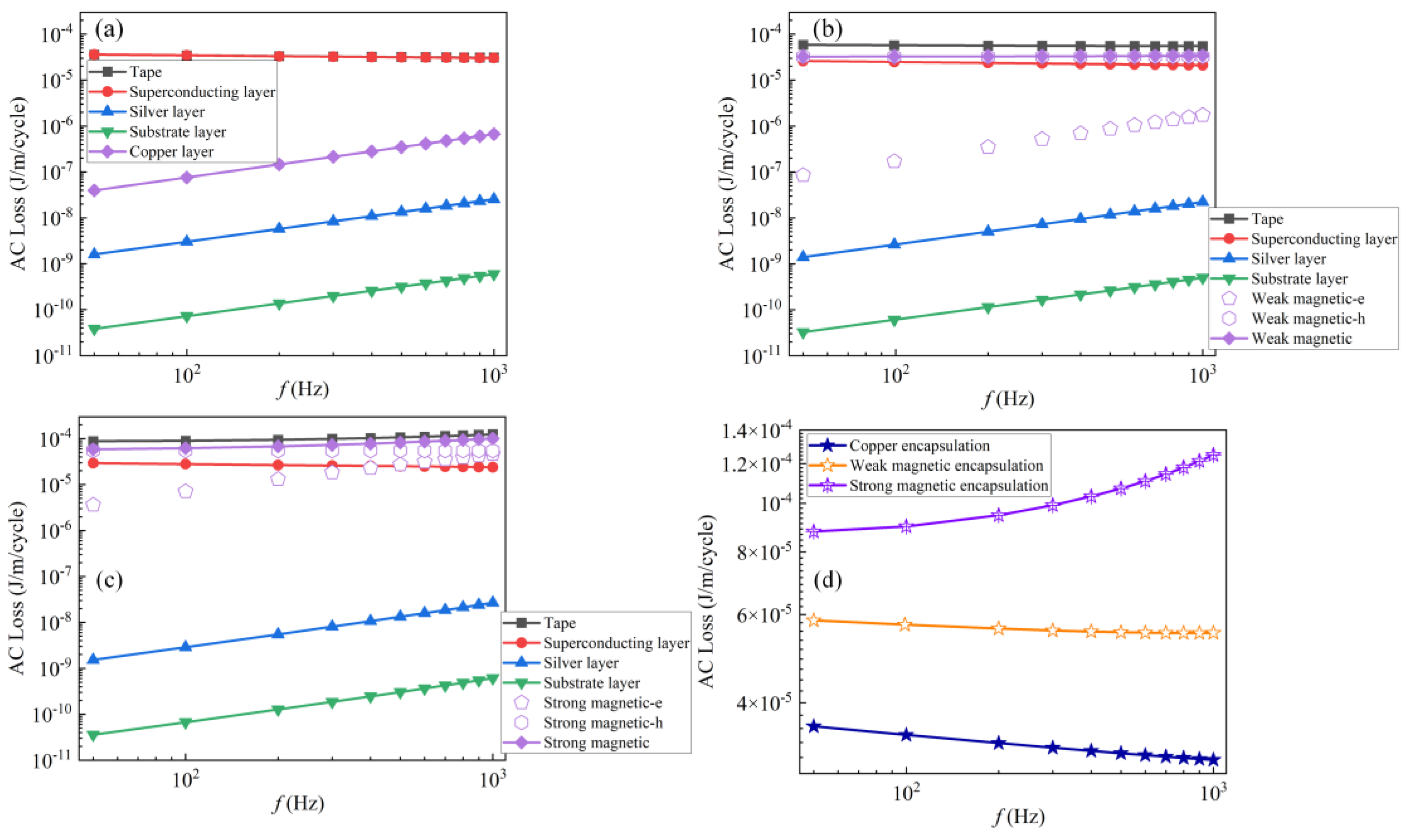
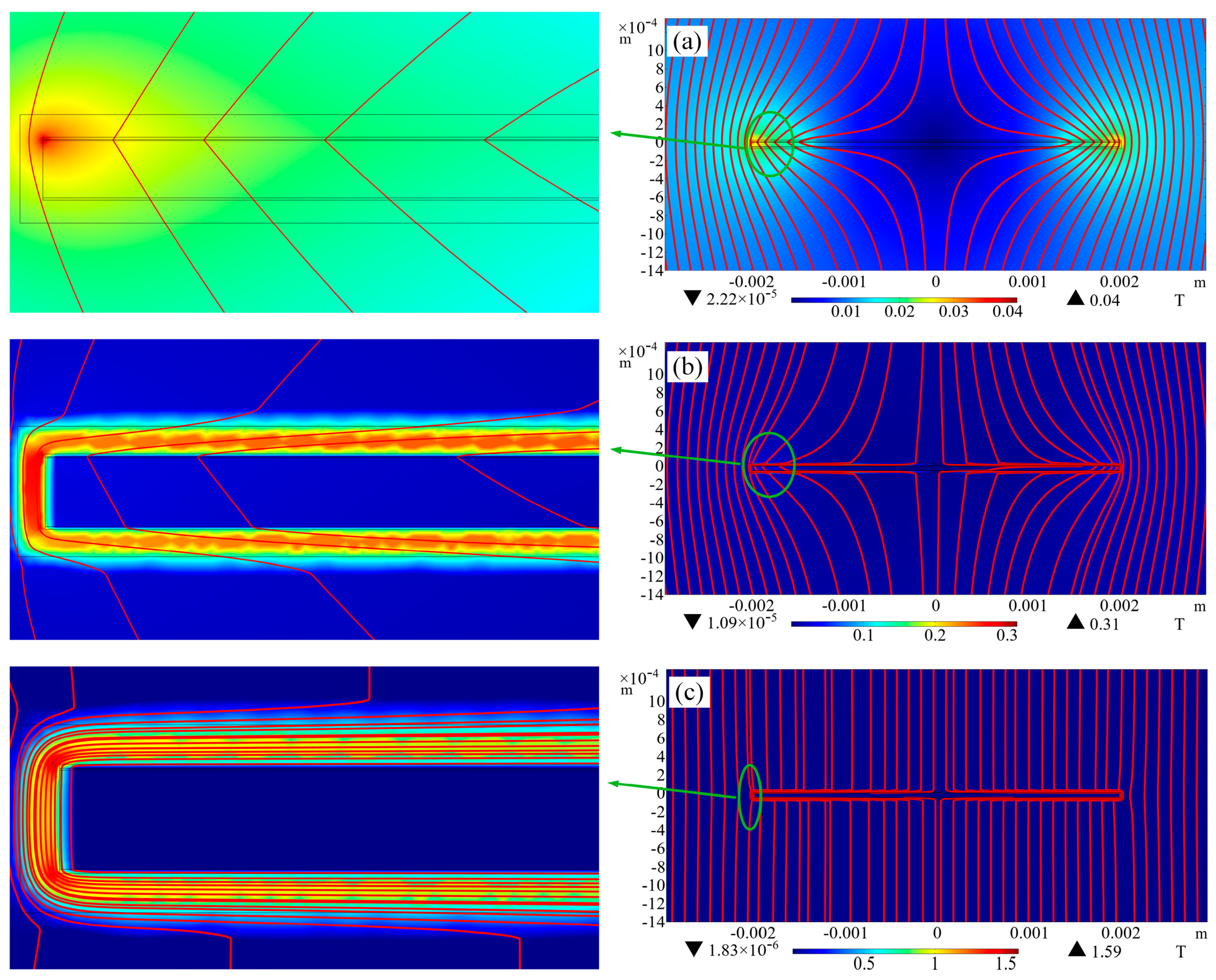
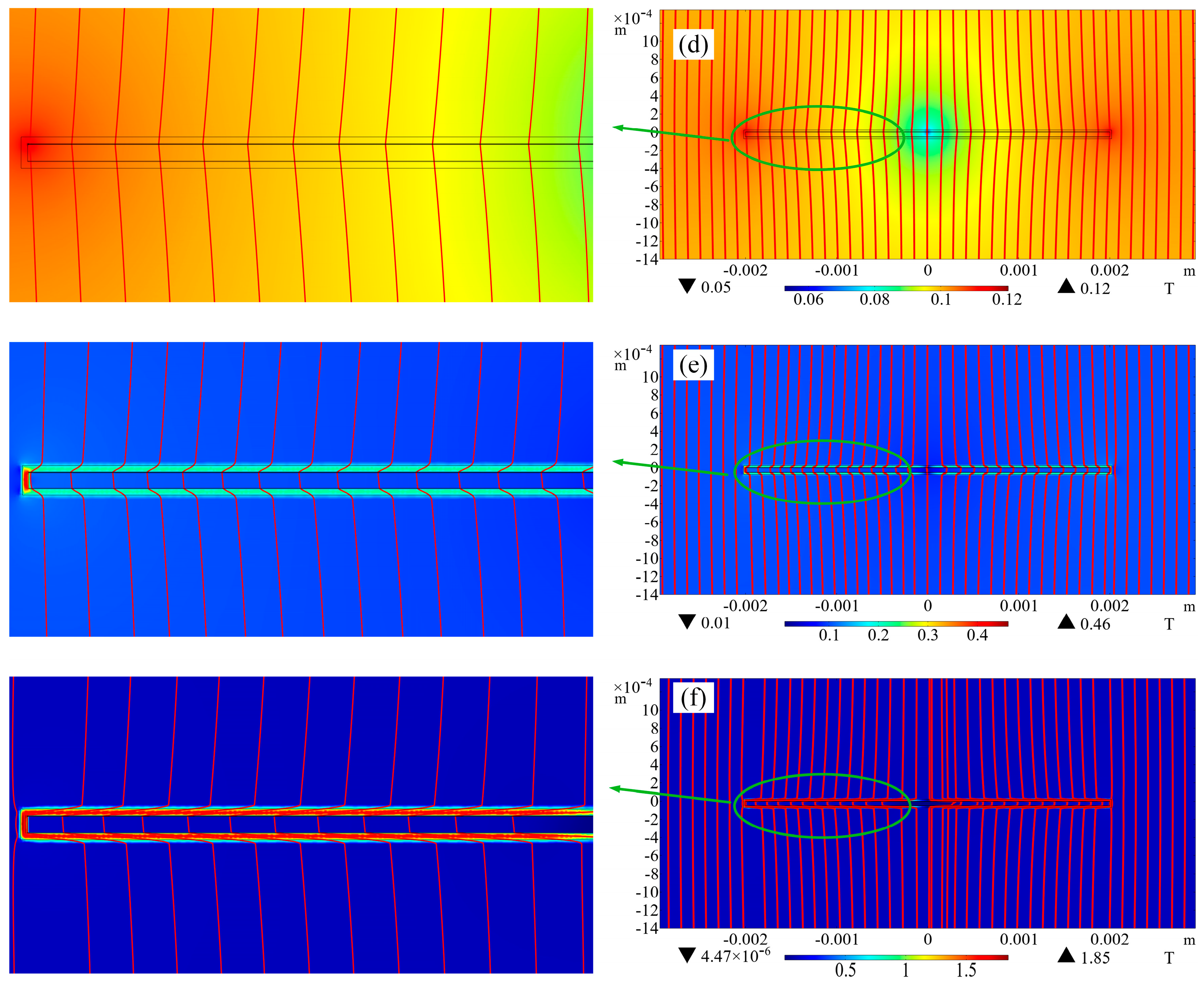
3.1. Transport Loss
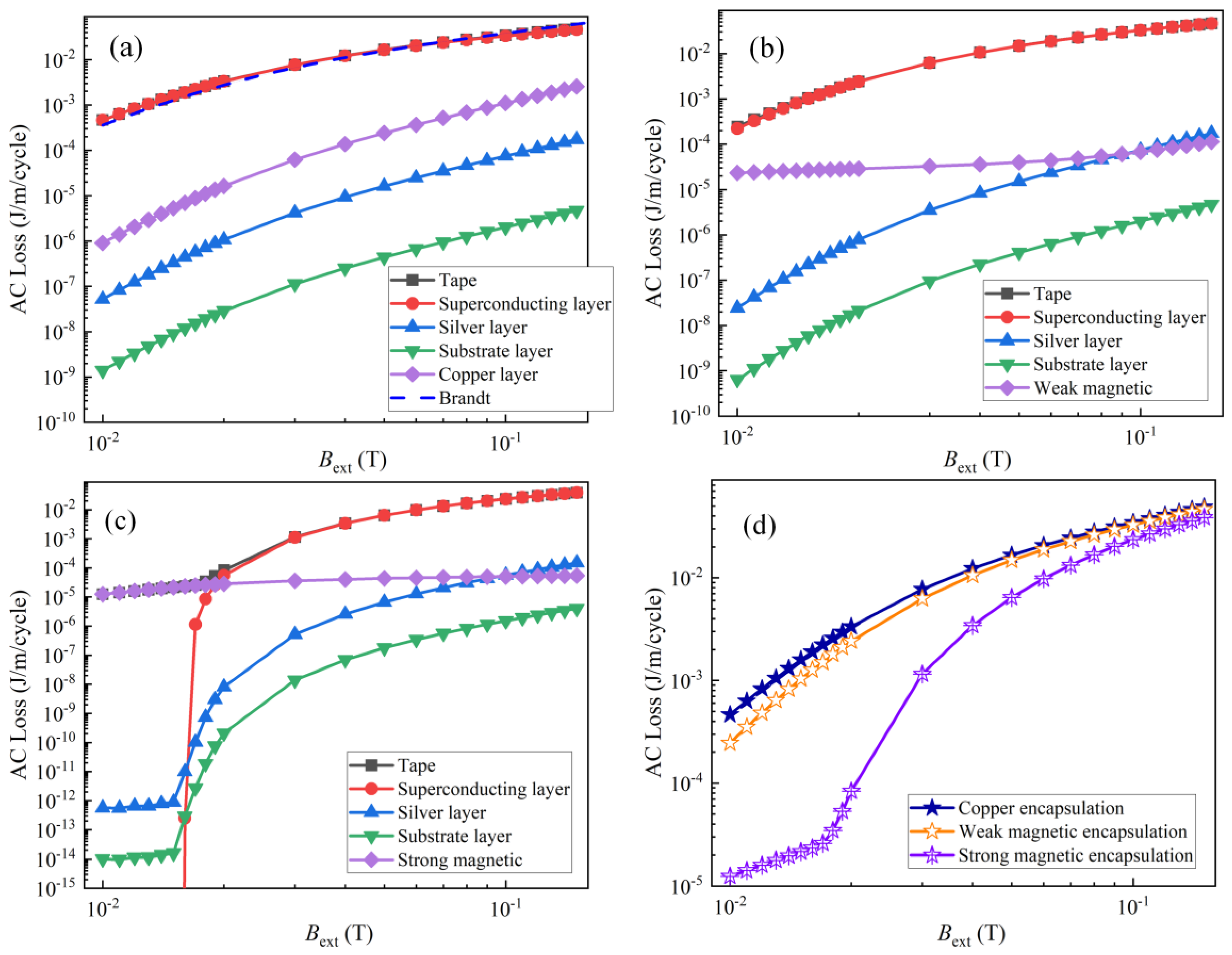
3.2. Magnetization Loss
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, W.; Badcock, R.A.; Long, N.J.; Jiang, Z. AC loss in REBCO coil windings wound with various cables: Effect of current distribution among the cable strands. IEEE Access 2023, 11, 102082–102091. [Google Scholar] [CrossRef]
- Pi, W.; Li, B.; Zhao, Y.; Li, Z.; Guo, L.; Wang, Y.; Shi, Q. Self-Shielding HTS DC Cable Made by REBCO Tapes with Different Widths. IEEE Trans. Appl. Supercond. 2024, 34, 1–6. [Google Scholar] [CrossRef]
- Gao, P.; Guan, M.; Wang, X.; Zhou, Y. Electromagnetic-thermal-structure multi-layer nonlinear elastoplastic modelling study on epoxy-impregnated REBCO pancake coils in high-field magnets. Superconductivity 2022, 1, 100002. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, J.; Haugan, T.; Badcock, R.A.; Storey, J.G.; Jiang, Z. Numerical Simulations on the AC loss of REBCO Stacks under Rotating Magnetic Fields. Superconductivity 2024, 11, 100111. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Z.; Bo, K.; Chen, J. Numerical simulation of AC loss in high-temperature superconducting tapes with strong magnetic field. IEEE Trans. Appl. Supercond. 2024, 34, 1–4. [Google Scholar] [CrossRef]
- Hussain, A.; Dadhich, A.; Pardo, E. Thermal quench modeling of REBCO racetrack coils under either alternating current or short-circuit voltage. Supercond. Sci. Technol. 2024, 37, 115028. [Google Scholar] [CrossRef]
- Otten, S.; Gačnik, D.; Brüggenwirth, S.; Leferink, J.; Dhallé, M.; Kate, H.T.; Dönges, S.; Weiss, J.; Radcliff, K.; van der Laan, D.; et al. Calculation and Measurement of Transport AC Loss of ReBCO CORC Cables for Electric Aircraft. IEEE Trans. Appl. Supercond. 2024, 34, 1–5. [Google Scholar] [CrossRef]
- Luo, X.; Ma, J.; Xiao, H.; Zhang, Z.; Yuan, C. Multiphysics multilayer modelling and simulation of HTS REBCO magnets carrying direct currents under AC magnetic fields. Superconductivity 2025, 14, 100157. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, G.; Jing, L. Experimental and numerical study of the frequency-dependent transport ac losses of the YBa2Cu3O7−δ coil with and without flux diverters. Supercond. Sci. Technol. 2019, 32, 055002. [Google Scholar] [CrossRef]
- Gömöry, F.; Vojenčiak, M.; Pardo, E.; Šouc, J. Magnetic flux penetration and AC loss in a composite superconducting wire with ferromagnetic parts. Supercond. Sci. Technol. 2009, 22, 034017. [Google Scholar] [CrossRef]
- Ma, G.T.; Rauh, H. Thermo-electromagnetic properties of a magnetically shielded superconductor strip: Theoretical foundations and numerical simulations. Supercond. Sci. Technol. 2013, 26, 105001. [Google Scholar] [CrossRef]
- Vojenčiak, M.; Šouc, J.; Gömöry, F. Critical current and AC loss analysis of a superconducting power transmission cable with ferromagnetic diverters. Supercond. Sci. Technol. 2011, 24, 075001. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, G.; Jing, L.; Yu, H. Numerical study on AC loss reduction of stacked HTS tapes by optimal design of flux diverter. Supercond. Sci. Technol. 2017, 30, 125014. [Google Scholar] [CrossRef]
- Chen, W.; Jin, R.; Wang, S.; Xu, M.; Che, T.; Shen, B.; Yang, X.; Zhao, Y. The effect of flux diverters on the AC loss of REBCO coil coupled with iron core. Cryogenics 2022, 128, 103573. [Google Scholar] [CrossRef]
- Wu, Y.; You, S.; Fang, J.; Badcock, R.A.; Long, N.J.; Jiang, Z. AC loss study on a 3-phase HTS 1 MVA transformer coupled with a three-limb iron core. Superconductivity 2024, 10, 100095. [Google Scholar] [CrossRef]
- Wu, Y.; Fang, J.; Miyagi, D.; Amemiya, N.; Badcock, R.A.; Long, N.J.; Jiang, Z. Experimental AC loss study on REBCO coil assemblies coupled with an iron cylinder. Supercond. Sci. Technol. 2024, 37, 055010. [Google Scholar] [CrossRef]
- You, S.; Miyagi, D.; Badcock, R.A.; Long, N.J.; Jiang, Z. Experimental and numerical study on AC loss reduction in a REBCO coil assembly by applying high saturation field powder-core flux diverters. Cryogenics 2022, 124, 103466. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, G.; Liu, G.; Wang, H.; Jing, L. Transport AC loss characteristic of YBa2Cu3 O7-δ coils with and without magnetic substrate up to 10 kHz. IEEE Trans. Appl. Supercond. 2023, 33, 1–8. [Google Scholar]
- Chen, W.; Jin, R.; Chi, F.; Ye, Y.; Wang, W.; Yang, X.; Zhu, Y.; Cai, L.; Sun, X.; Li, X. Study on AC loss of stacked REBCO cable wrapped with magnetic strip. Cryogenics 2024, 144, 103975. [Google Scholar] [CrossRef]
- Jiang, Z.; Song, H.; Song, W.; Badcock, R.A. Optimizing coil configurations for AC loss reduction in REBCO HTS fast-ramping magnets at cryogenic temperatures. Superconductivity 2022, 3, 100024. [Google Scholar] [CrossRef]
- Wu, Y.; Fang, J.; Amemiya, N.; Badcock, R.A.; Long, N.J.; Jiang, Z. AC loss reduction in HTS coil windings coupled with an iron core using flux diverters. IEEE Access 2023, 11, 48826–48840. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, Z.; Grilli, F.; Gyftakis, K.; Mueller, M. Alternating current loss of superconductors applied to superconducting electrical machines. Energies 2021, 14, 2234. [Google Scholar] [CrossRef]
- Shen, B.; Grilli, F.; Coombs, T. Overview of H-formulation: A versatile tool for modeling electromagnetics in high-temperature superconductor applications. IEEE Access 2020, 8, 100403–100414. [Google Scholar] [CrossRef]
- Shen, B.; Grilli, F.; Coombs, T. Review of the AC loss computation for HTS using H formulation. Supercond. Sci. Technol. 2020, 33, 033002. [Google Scholar] [CrossRef]
- Niu, M.; Yong, H.; Xia, J.; Zhou, Y. The effects of ferromagnetic disks on AC losses in HTS pancake coils with nonmagnetic and magnetic substrates. J. Supercond. Nov. Magn. 2019, 32, 499–510. [Google Scholar] [CrossRef]
- Zhou, P.; Ma, G.; Quéval, L. Transition frequency of transport ac losses in high temperature superconducting coated conductors. J. Appl. Phys. 2019, 126, 063901. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, C.; Qian, H.; Quéval, L.; Luo, Z.; Deng, Y. Frequency-dependent transport AC losses of coated superconductors up to tens of kilohertz. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Norris, W.T. Calculation of hysteresis losses in hard superconductors carrying ac: Isolated conductors and edges of thin sheets. J. Phys. D Appl. Phys. 1970, 3, 489–507. [Google Scholar] [CrossRef]
- Gömöry, F.; Šouc, J.; Vojenčiak, M.; Alamgir, A.K.M.; Han, Z.; Gu, C. Reduction of ac transport and magnetization loss of a high-Tc superconducting tape by placing soft ferromagnetic materials at the edges. Appl. Phys. Lett. 2007, 90, 092506. [Google Scholar] [CrossRef]
- Brandt, E.H.; Indenbom, M. Type-II-superconductor strip with current in a perpendicular magnetic field. Phys. Rev. B 1993, 48, 12893. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| Jc0 (77 K, self-field) [A/m2] | 2.85 × 1010 |
| k | 0.25 |
| B0 [mT] | 52.5 |
| α | 0.7 |
| Ec [μV/cm] | 1 |
| n | 32 |
| ρcopper (77 K) [Ω·m] | 1.97 × 10−9 |
| ρsilver (77 K) [Ω·m] | 2.7 × 10−9 |
| ρhastelloy (77 K) [Ω·m] | 1250 × 10−9 |
| ρweak magnetic materials (77 K) [Ω·m] | 63 × 10−9 |
| ρstrong magnetic materials (77 K) [Ω·m] | 1300 × 10−9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Jin, R.; Bai, Y.; Chi, F.; Xu, J.; Yang, X.; Zhu, Y. Study on AC Loss of REBCO Tape Encapsulated with Magnetic Materials. Crystals 2025, 15, 407. https://doi.org/10.3390/cryst15050407
Chen W, Jin R, Bai Y, Chi F, Xu J, Yang X, Zhu Y. Study on AC Loss of REBCO Tape Encapsulated with Magnetic Materials. Crystals. 2025; 15(5):407. https://doi.org/10.3390/cryst15050407
Chicago/Turabian StyleChen, Wei, Rong Jin, Yang Bai, Fei Chi, Jiaqing Xu, Xinsheng Yang, and Yunpeng Zhu. 2025. "Study on AC Loss of REBCO Tape Encapsulated with Magnetic Materials" Crystals 15, no. 5: 407. https://doi.org/10.3390/cryst15050407
APA StyleChen, W., Jin, R., Bai, Y., Chi, F., Xu, J., Yang, X., & Zhu, Y. (2025). Study on AC Loss of REBCO Tape Encapsulated with Magnetic Materials. Crystals, 15(5), 407. https://doi.org/10.3390/cryst15050407








