Elastic Wave Propagation of Two-Dimensional Metamaterials Composed of Auxetic Star-Shaped Honeycomb Structures
Abstract
:1. Introduction
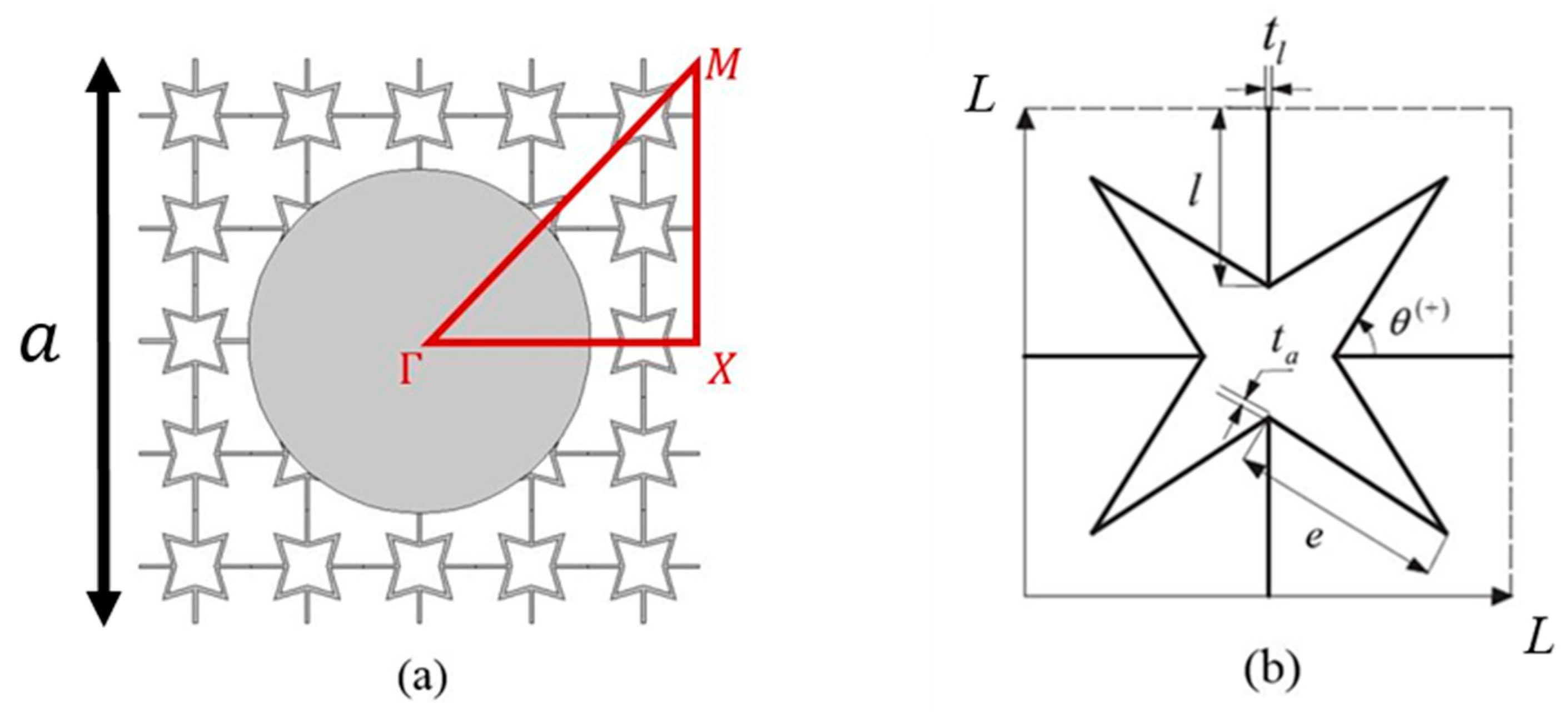
2. Materials and Methods
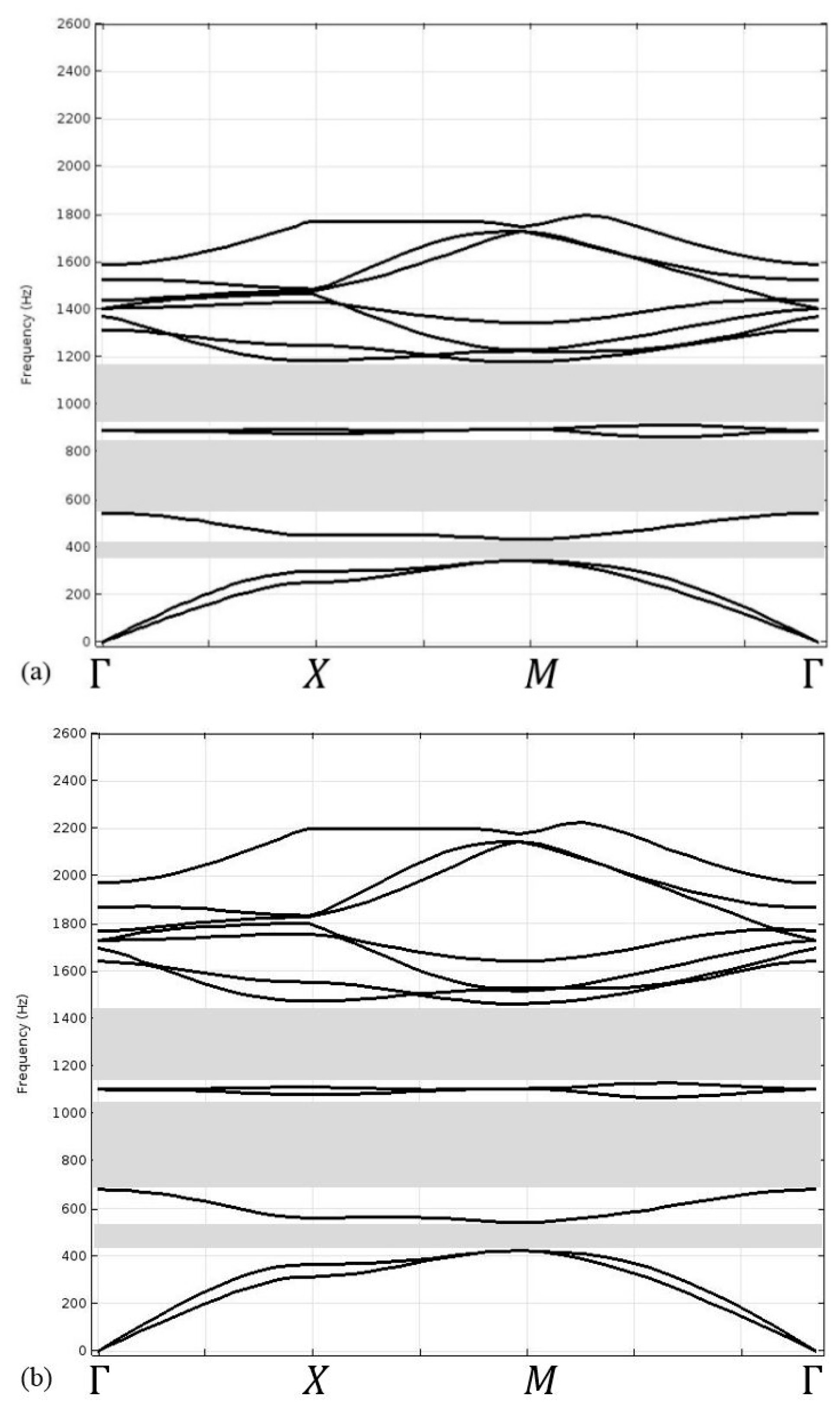
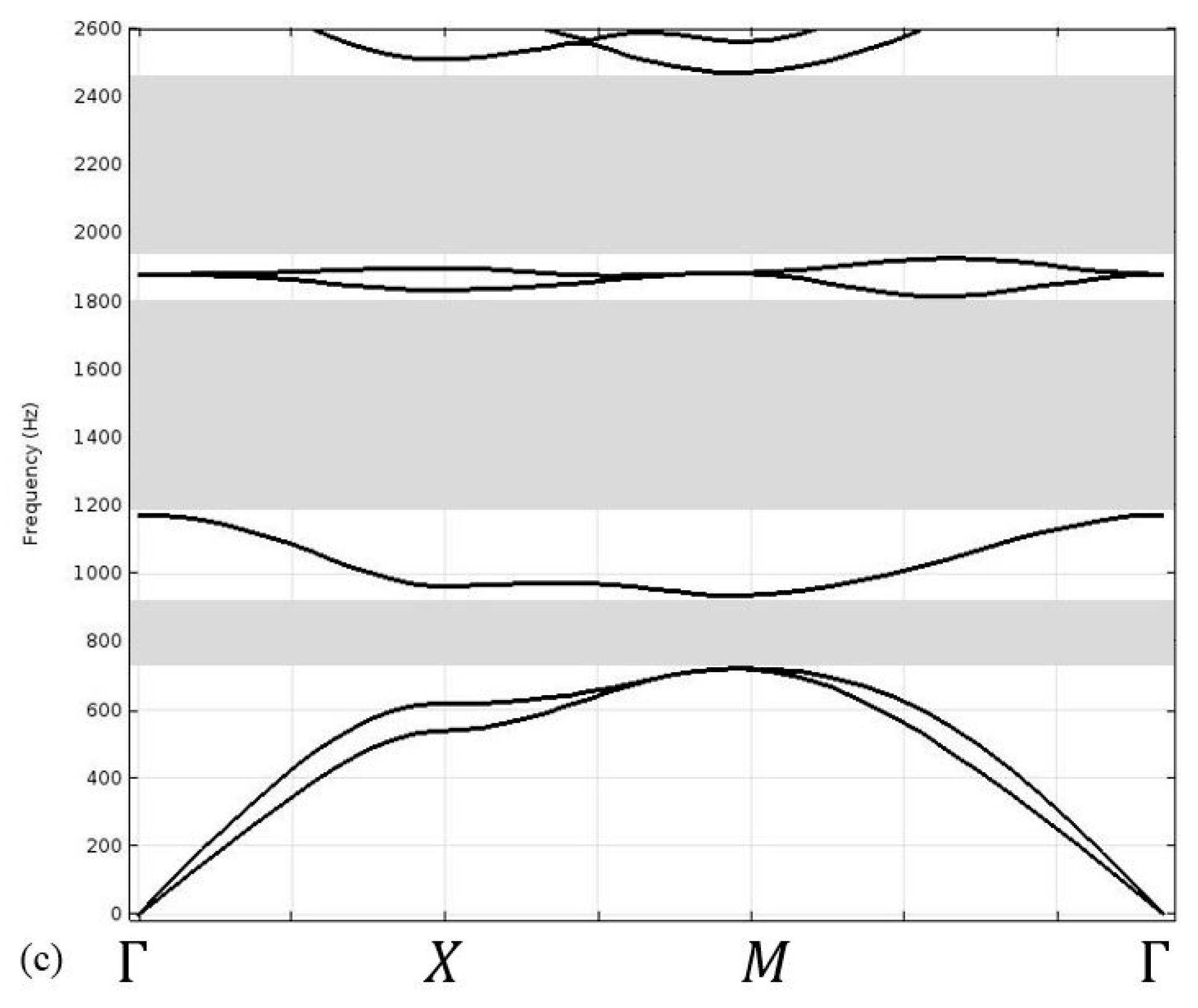
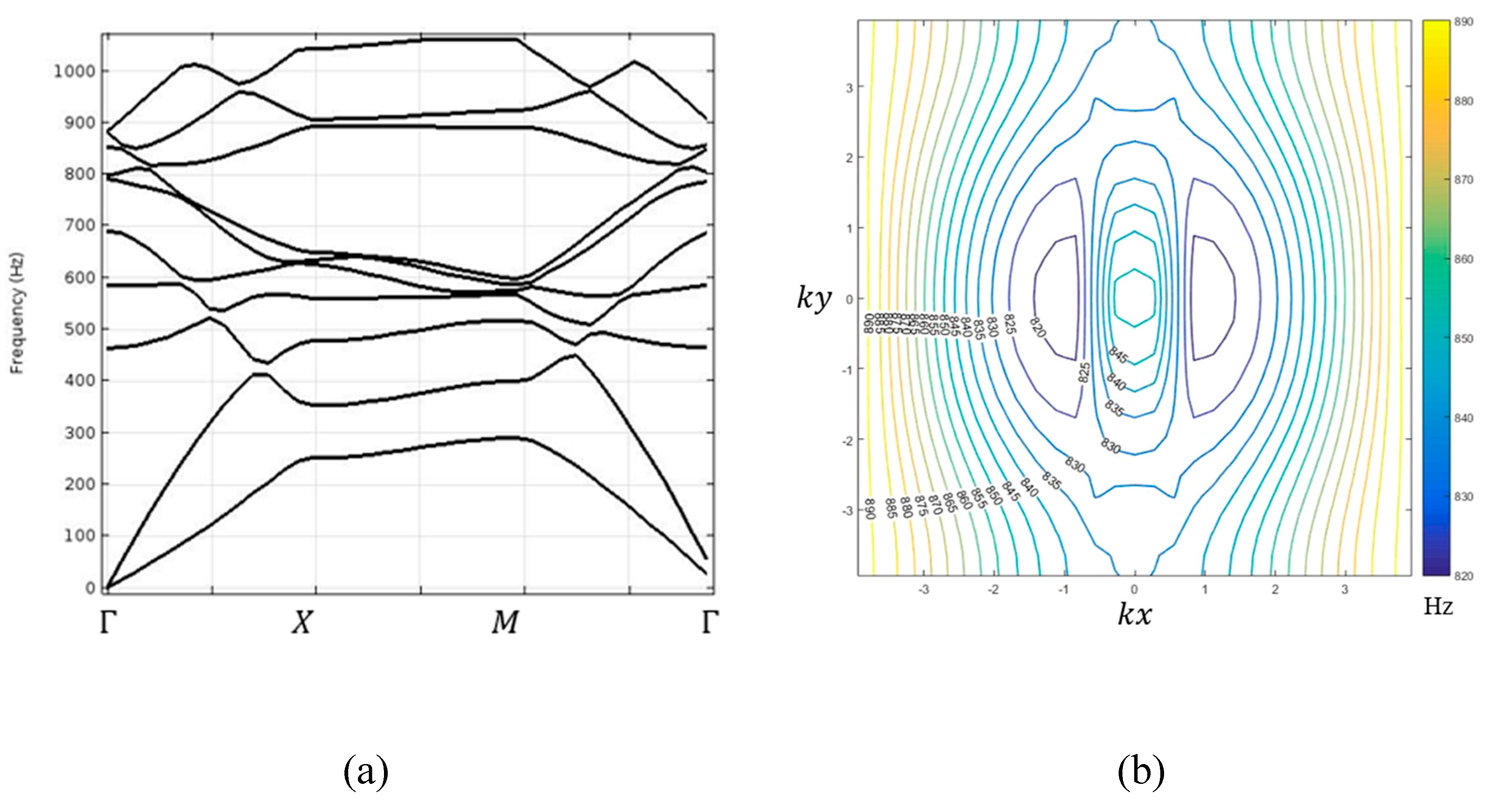
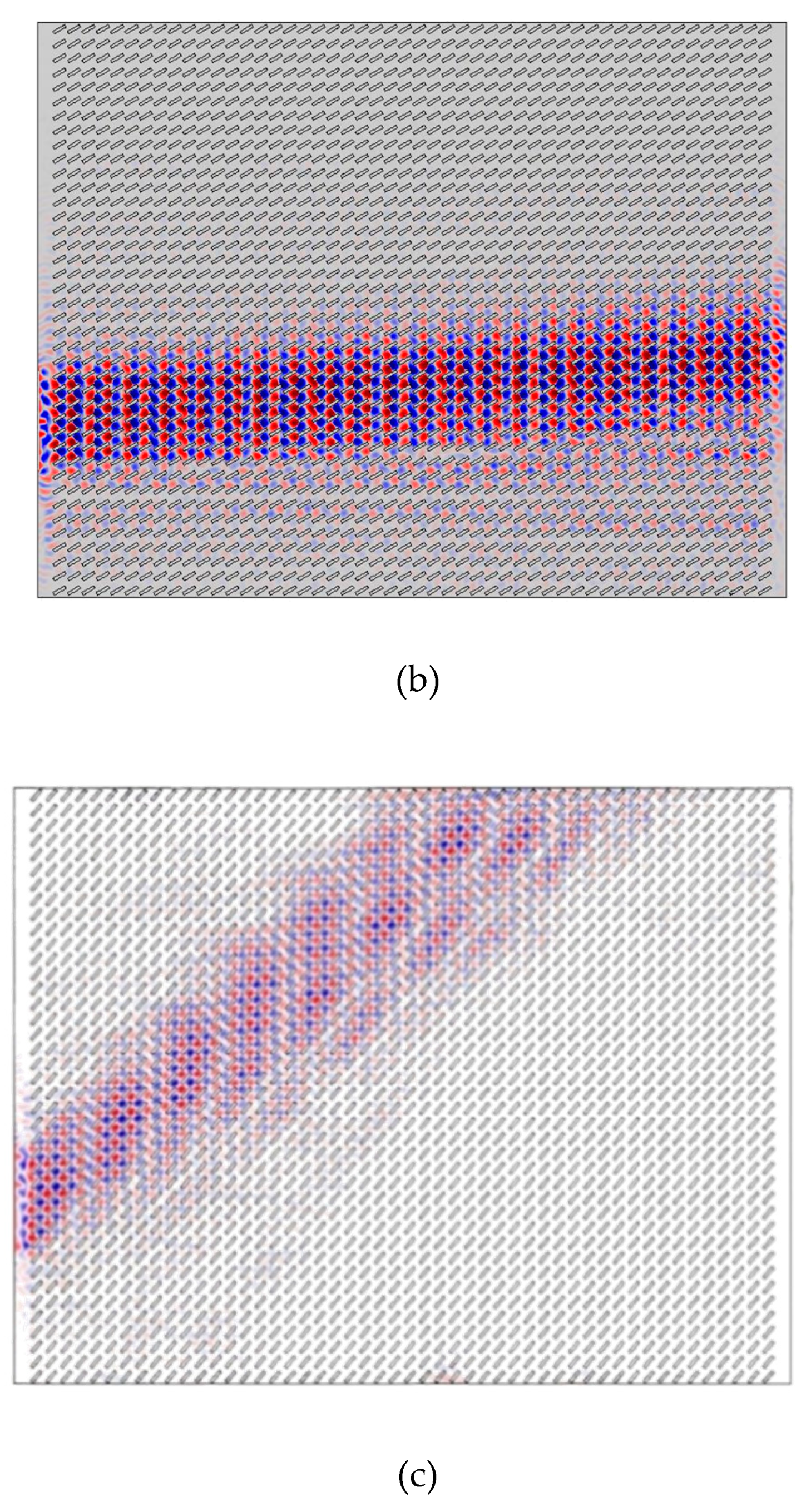
3. Results
4. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sigalas, M.M.; Economou, E.N. Elastic and Acoustic Wave Band Structure. J. Sound Vib. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef] [PubMed]
- Kushwaha, M.S.; Halevi, P.; Martinez, G.; Dobrzynski, L.; Djafari-Rouhani, B. Theory of Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. B 1994, 49, 2313. [Google Scholar] [CrossRef]
- Martinezsala, R.; Sancho, J.; Sanchez, J.V.; Gomez, V.; Llinares, J.; Meseguer, F. Sound Attenuation by Sculpture. Nature 1995, 378, 241. [Google Scholar] [CrossRef]
- Thomas, E.L.; Gorishnyy, T.; Maldovan, M. Colloidal Crystals Go Hypersonic. Nat. Mater. 2006, 5, 773–774. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Wang, G.; Yu, D.; Zhao, H.; Liu, Y. Theoretical and Experimental Investigation of Flexural Wave Propagation in Straight Beams with Periodic Structures: Application to a vibration isolation structure. J. Appl. Phys. 2005, 97, 114907. [Google Scholar] [CrossRef]
- Sigalas, M. Elastic Wave Band Gaps and Defect States in Two-dimensional Composites. J. Acous. Soc. Am. 1997, 101, 1256. [Google Scholar] [CrossRef]
- Wu, F.; Hou, Z.; Liu, Z.; Liu, Y. Point Defect States in Two-dimensional Phononic Crystals. Phys. Lett. A 2001, 292, 198–202. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Liu, Y.; Wu, F. Defect States in 2D Acoustic Band-gap Materials with Bend-shaped Linear Defects. Solid State Commun. 2004, 130, 67–71. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Chan, C.T.; Sheng, P. Three-component Elastic Wave Band-gap Material. Phys. Rev. B 2002, 65, 165116. [Google Scholar] [CrossRef]
- Gang, W.; Li-Hui, S.; Yao-Zong, L.; Ji-Hong, W. Accurate Evaluation of Lowest Band Gaps in Ternary Locally Resonant Phononic Crystals. Chin. Phys. 2006, 15, 1843. [Google Scholar] [CrossRef]
- Larabi, H.; Pennec, Y.; Djafari-Rouhani, B.; Vasseur, J. Multicoaxial Cylindrical Inclusions in Locally Resonant Phononic Crystals. Phys. Rev. E 2007, 75, 066601. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Cheng, J. Existence of Broad Acoustic Bandgaps in Three-Component Composite. Phys. Rev. B 2003, 68, 245101. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Wu, F.; Liu, Z. Large Two-dimensional Band Gaps in Three-component Phononic Crystals. Phys. Lett. A 2003, 317, 144–149. [Google Scholar] [CrossRef]
- Fok, L.; Zhang, X. Negative Acoustic Index Metamaterial. Phys. Rev. B 2011, 83, 214304. [Google Scholar] [CrossRef]
- Wu, Y.; Lai, Y.; Zhang, Z.-Q. Elastic Metamaterials with Simultaneously Negative Effective Shear Modulus and Mass Density. Phys. Rev. Lett. 2011, 107, 105506. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.; Robertson, C.I. The Mechanics of Two-Dimensional Cellular Materials. Proc. R. Soc. Lond. A 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Robert, F.A. An Isotropic Three-dimensional Structure with Poisson’s Ratio = −1. J. Elast. 1985, 15, 427. [Google Scholar]
- Theocaris, P.S.; Stavroulakis, G.E.; Panagiotopoulus, P.D. Negative Poisson’s ratios in composites with star-shaped inclusions: A numerical homogenization approach. Arch. Appl. Mech. 1997, 67, 274–286. [Google Scholar] [CrossRef]
- Gonella, S.; Ruzzene, M. Analysis of In-plane Wave Propagation in Hexagonal and Re-entrant Lattices. J. Sound Vib. 2008, 312, 125–139. [Google Scholar] [CrossRef]
- Liebold-Ribeiro, Y.; Körner, C. Phononic Band Gaps in Periodic Cellular Materials. Adv. Eng. Mater. 2014, 16, 328–334. [Google Scholar] [CrossRef]
- Meng, J.; Deng, Z.; Zhang, K.; Xu, X.; Wen, F. Band Gap Analysis of Star-shaped Honeycombs with Varied Poisson’s Ratio. Smart Mater. Struct. 2015, 24, 095011. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Scarpa, F.; Grima, J.N. Auxetics and Other Systems of Anomalous Characteristics. Phys. Status Solidi B-Basic Solid Status Phys. 2017, 254, 1770266. [Google Scholar] [CrossRef] [Green Version]
- Qiu, C.; Liu, Z.; Shi, J.; Chan, C. Directional Acoustic Source Based on the Resonant Cavity of Two-dimensional Phononic Crystals. Appl. Phys. Lett. 2005, 86, 224105. [Google Scholar] [CrossRef]
- Liu, W.; Su, X. Collimation and Enhancement of Elastic Transverse Waves in Two-dimensional Solid Phononic Crystals. Phys. Lett. A 2010, 374, 29682971. [Google Scholar] [CrossRef]
- Cicek, A.; Kaya, O.A.; Ulug, B. Wide-band All-angle Acoustic Self-collimation by Rectangular Sonic Crystals with Elliptical Bases. J. Phys. D Appl. Phys. 2011, 44, 205104. [Google Scholar] [CrossRef]
- Cicek, A.; Kaya, O.A.; Ulug, B. Impacts of Uniaxial Elongation on the Bandstructures of Two-dimensional Sonic Crystals and Associated Applications. Appl. Acoust. 2012, 73, 28–36. [Google Scholar] [CrossRef]
- Cebrecos, A.; Romero-Garcia, V.; Pico, R.; Perez-Arjona, I.; Espinosa, V.; Sanchez-Morcillo, V.; Staliunas, K. Formation of Collimated Sound Beams by Three-dimensional Sonic Crystals. J. Appl. Phys. 2012, 111, 104910. [Google Scholar] [CrossRef]
- Morvan, B.; Tinel, A.; Vasseur, J.; Sainidou, R.; Rembert, P.; Hladky-Hennion, A.-C.; Swinteck, N.; Deymier, P. Ultra-directional Source of Longitudinal Acoustic Waves Based on a Two-dimensional Solid/solid Phononic Crystal. J. Appl. Phys. 2014, 116, 214901. [Google Scholar] [CrossRef]
- Soliveres, E.; Espinosa, V.; Pérez-Arjona, I.; Sánchez-Morcillo, V.J.; Staliunas, K. Self Collimation of Ultrasound in a Three-dimensional Sonic Crystal. Appl. Phys. Lett. 2009, 94, 164101. [Google Scholar] [CrossRef]
- Liu, G.-T.; Tsai, C.-N.; Chang, I.-L.; Chen, L.-W. Elastic Dispersion Analysis of Two Dimensional Phononic Crystals Composed of Auxetic Materials. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015; American Society of Mechanical Engineers: New York, NY, USA; p. V013T16A021. [Google Scholar]
- Tsai, C.-N.; Chen, L.-W. The manipulation of self-collimated beam in phononic crystals composed of orientated rectangular inclusions. Appl. Phys. A 2016, 122, 659. [Google Scholar] [CrossRef]
- Graff, K.F. Wave Motion in Elastic Solids; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Tang, H.-W.; Chou, W.-D.; Chen, L.-W. Wave propagation in the polymer-filled star-shaped honeycomb periodic structure. Appl. Phys. A 2017, 123, 523. [Google Scholar] [CrossRef]







| Young’s module | 0.5124 | 0.3123 | 0.2305 | 0.1806 |
| Poisson’s ratio | −0.53 | −0.35 | −0.15 | 0.05 |
| Mass density | 921 | 921 | 921 | 921 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, S.-Y.; Chen, C.-D.; Yeh, J.-Y.; Chen, L.-W. Elastic Wave Propagation of Two-Dimensional Metamaterials Composed of Auxetic Star-Shaped Honeycomb Structures. Crystals 2019, 9, 121. https://doi.org/10.3390/cryst9030121
Chang S-Y, Chen C-D, Yeh J-Y, Chen L-W. Elastic Wave Propagation of Two-Dimensional Metamaterials Composed of Auxetic Star-Shaped Honeycomb Structures. Crystals. 2019; 9(3):121. https://doi.org/10.3390/cryst9030121
Chicago/Turabian StyleChang, Shu-Yeh, Chung-De Chen, Jia-Yi Yeh, and Lien-Wen Chen. 2019. "Elastic Wave Propagation of Two-Dimensional Metamaterials Composed of Auxetic Star-Shaped Honeycomb Structures" Crystals 9, no. 3: 121. https://doi.org/10.3390/cryst9030121
APA StyleChang, S. -Y., Chen, C. -D., Yeh, J. -Y., & Chen, L. -W. (2019). Elastic Wave Propagation of Two-Dimensional Metamaterials Composed of Auxetic Star-Shaped Honeycomb Structures. Crystals, 9(3), 121. https://doi.org/10.3390/cryst9030121





