Fuzzy Optimization on the Synthesis of Chitosan-Graft-Polyacrylic Acid with Montmorillonite as Filler Material: A Case Study
Abstract
1. Introduction
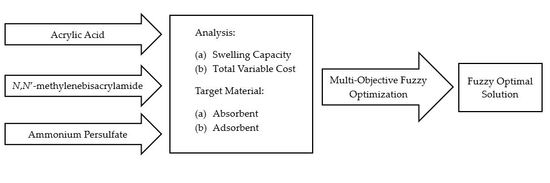
2. Methodology
2.1. Materials
2.2. Experimental Method
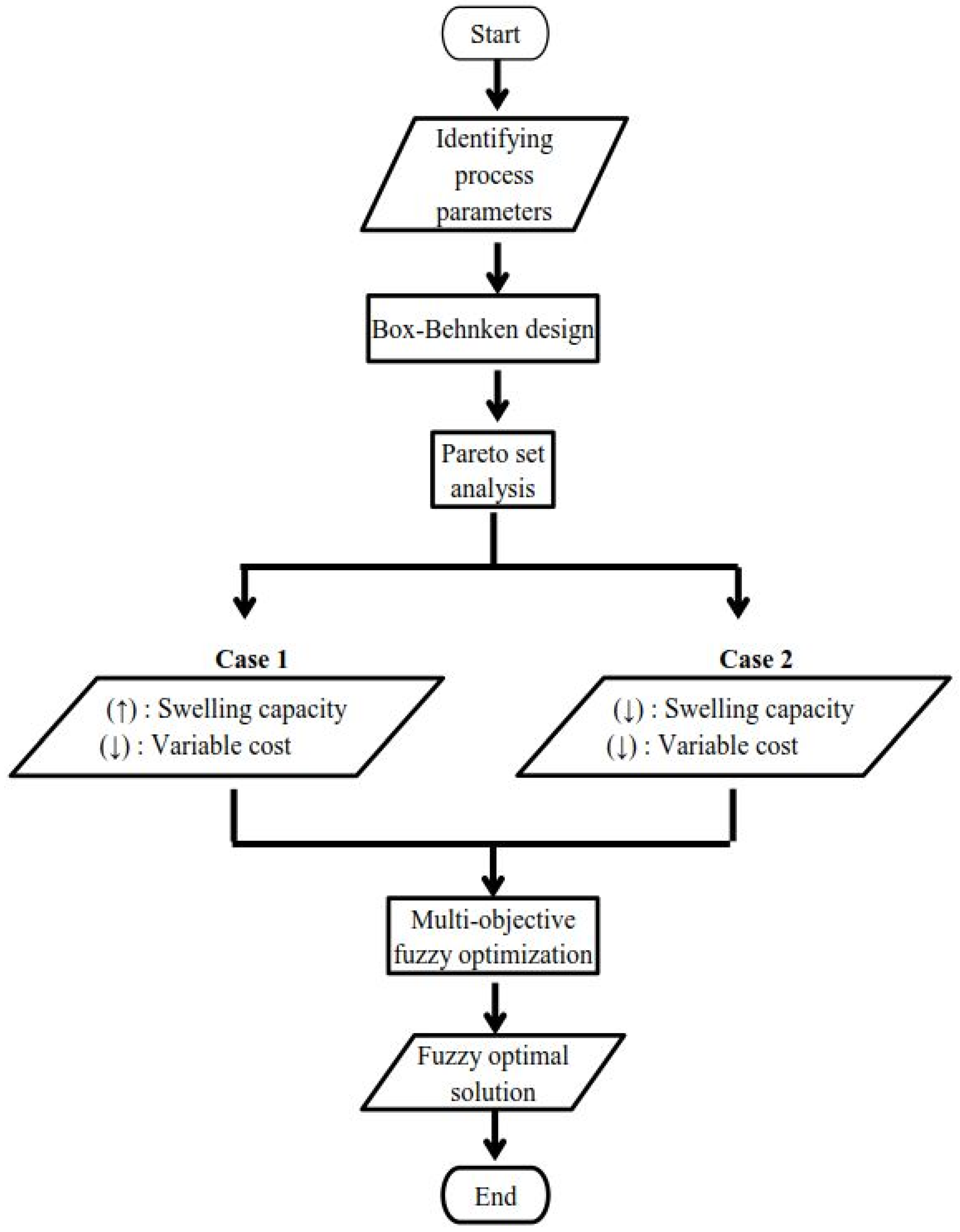
2.3. Fuzzy Multi-Objective Optimization Method
2.3.1. Determination of Boundary Limits through the Pareto Optimality
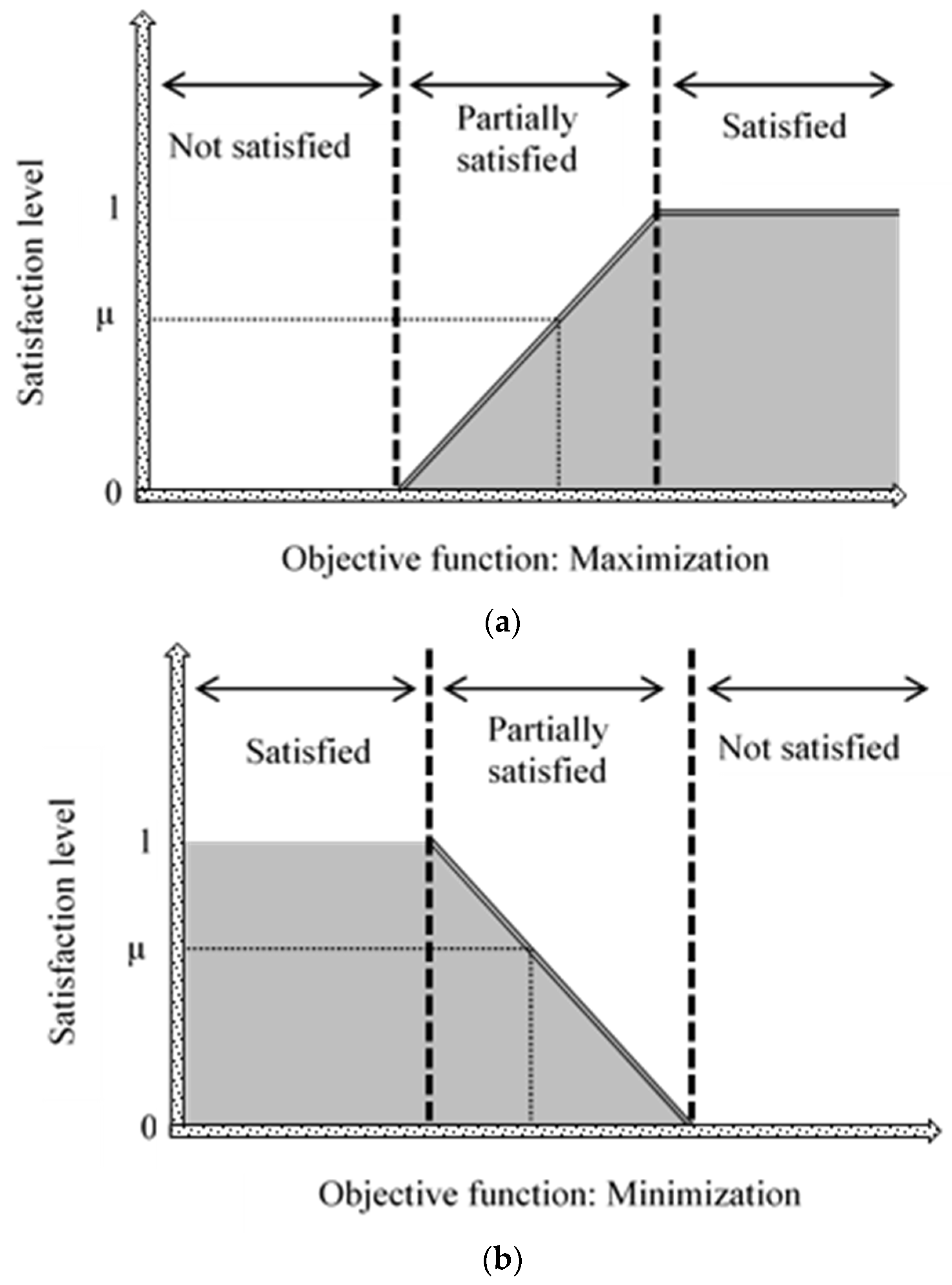
2.3.2. Multi-Objective Decision Making through Fuzzy Logic
3. Results and Discussion
3.1. Effect of AA/Ch Molar Ratio on the Swelling Capacity and Its Variable Cost
3.2. Effect of N,N′-methylenebisacrylamide on the Swelling Capacity and Its Variable Cost
3.3. Effect of Ammonium Persulfate on the Swelling Capacity and Its Variable Cost
3.4. Pareto Set Result
3.4.1. Case 1: Absorbent Material
3.4.2. Case 2: Adsorbent Material
3.5. Multi-Objective Fuzzy Optimization Result
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Wang, Q.; Wang, A. Synthesis and characterization of chitosan-g-poly(acrylic acid)/attapulgite superabsorbent composites. Carbohydr. Polym. 2007, 68, 367–374. [Google Scholar] [CrossRef]
- Kabiri, K.; Roshanfekr, S. Converting water absorbent polymer to alcohol absorbent polymer. Polym. Adv. Technol. 2013, 24, 28–33. [Google Scholar] [CrossRef]
- Ghazy, M.B.M.; El-Hai, F.A.; Mohamed, M.F.; Essawy, H.A. Potassium fulvate as co-interpenetrating agent during graft polymerization of acrylic acid from cellulose. Int. J. Biol. Macromol. 2016, 91, 1206–1214. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Hua, S.; Wang, A. Adsorption behavior of Cu2+ from aqueous solutions onto starch-g-poly (acrylic acid)/sodium humate hydrogels. Desalination 2010, 263, 170–175. [Google Scholar] [CrossRef]
- Kabiri, K.; Omidian, H.; Hashemi, S.A.; Zohuriaan-Mehr, M.J. Synthesis of fast-swelling superabsorbent hydrogels: Effect of crosslinker type and concentration on porosity and absorption rate. Eur. Polym. J. 2003, 39, 1341–1348. [Google Scholar] [CrossRef]
- Singh, J.; Dhaliwal, A.S. Synthesis, characterization and swelling behavior of silver nanoparticles containing superabsorbent based on grafted copolymer of polyacrylic acid/Guar gum. Vacuum 2018, 157, 51–60. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Kang, Y.; Wang, A. Synthesis, swelling and responsive properties of a new composite hydrogel based on hydroxyethyl cellulose and medicinal stone. Compos. Part B Eng. 2011, 42, 809–818. [Google Scholar] [CrossRef]
- Pourjavadi, A.; Fakoorpoor, S.M.; Hosseini, P.; Khaloo, A. Interactions between superabsorbent polymers and cement-based composites incorporating colloidal silica nanoparticles. Cem. Concr. Compos. 2013, 37, 196–204. [Google Scholar] [CrossRef]
- Bao, Y.; Ma, J.; Li, N. Synthesis and swelling behaviors of sodium carboxymethyl cellulose-g-poly(AA-co-AM-co-AMPS)/MMT superabsorbent hydrogel. Carbohydr. Polym. 2011, 84, 76–82. [Google Scholar] [CrossRef]
- Bhattacharyya, R.; Ray, S.K. Micro- and nano-sized bentonite filled composite superabsorbents of chitosan and acrylic copolymer for removal of synthetic dyes from water. Appl. Clay Sci. 2014, 101, 510–520. [Google Scholar] [CrossRef]
- Fang, S.; Wang, G.; Li, P.; Xing, R.; Liu, S.; Qin, Y.; Yu, H.; Chen, X.; Li, K. Synthesis of chitosan derivative graft acrylic acid superabsorbent polymers and its application as water retaining agent. Int. J. Biol. Macromol. 2018, 115, 754–761. [Google Scholar] [CrossRef]
- Gao, J.; Yang, Q.; Ran, F.; Ma, G.; Lei, Z. Preparation and properties of novel eco-friendly superabsorbent composites based on raw wheat bran and clays. Appl. Clay Sci. 2016, 132–133, 739–747. [Google Scholar] [CrossRef]
- Da Costa, M.P.M.; De Mello Ferreira, I.L.; De Macedo Cruz, M.T. New polyelectrolyte complex from pectin/chitosan and montmorillonite clay. Carbohydr. Polym. 2016, 146, 123–130. [Google Scholar] [CrossRef]
- Jayakumar, R.; Nagahama, H.; Furuike, T.; Tamura, H. Synthesis of phosphorylated chitosan by novel method and its characterization. Int. J. Biol. Macromol. 2008, 42, 335–339. [Google Scholar] [CrossRef]
- Fazli, Y.; Shariatinia, Z. Controlled release of cefazolin sodium antibiotic drug from electrospun chitosan-polyethylene oxide nanofibrous Mats. Mater. Sci. Eng. C 2017, 71, 614–652. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Wang, A. Removal of methylene blue from aqueous solution using chitosan-g-poly(acrylic acid)/montmorillonite superadsorbent nanocomposite. Colloids Surf. A Physicochem. Eng. Asp. 2008, 322, 47–53. [Google Scholar] [CrossRef]
- Je, J.Y.; Kim, S.K. Antimicrobial action of novel chitin derivative. Biochim. Biophys. Acta Gen. Subj. 2006, 1760, 104–109. [Google Scholar] [CrossRef]
- Pelissari, F.M.; Yamashita, F.; Garcia, M.A.; Martino, M.N.; Zaritzky, N.E.; Grossmann, M.V.E. Constrained mixture design applied to the development of cassava starch-chitosan blown films. J. Food Eng. 2012, 108, 262–267. [Google Scholar] [CrossRef]
- Gao, X.; Cao, Y.; Song, X.; Zhang, Z.; Zhuang, X.; He, C.; Chen, X. Biodegradable, pH-responsive carboxymethyl cellulose/poly(acrylic acid) hydrogels for oral insulin delivery. Macromol. Biosci. 2014, 14, 565–575. [Google Scholar] [CrossRef]
- Yadav, M.; Rhee, K.Y. Superabsorbent nanocomposite (alginate-g-PAMPS/MMT): Synthesis, characterization and swelling behavior. Carbohydr. Polym. 2012, 90, 165–173. [Google Scholar] [CrossRef]
- Feng, E.; Ma, G.; Wu, Y.; Wang, H.; Lei, Z. Preparation and properties of organic-inorganic composite superabsorbent based on xanthan gum and loess. Carbohydr. Polym. 2014, 111, 463–468. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Wang, W.; Kang, Y.; Wang, A. Enhanced swelling properties of a novel sodium alginate-based superabsorbent composites: NaAlg-g-poly(NaA-co-St)/APT. J. Appl. Polym. Sci. 2012, 125, 1822–1832. [Google Scholar] [CrossRef]
- Spagnol, C.; Rodrigues, F.H.A.; Pereira, A.G.B.; Fajardo, A.R.; Rubira, A.F.; Muniz, E.C. Superabsorbent hydrogel composite made of cellulose nanofibrils and chitosan-graft-poly(acrylic acid). Carbohydr. Polym. 2012, 87, 2038–2045. [Google Scholar] [CrossRef]
- Murray, H.H. Overview—Clay mineral applications. Appl. Clay Sci. 1991, 5, 379–395. [Google Scholar] [CrossRef]
- Kotal, M.; Bhowmick, A.K. Polymer nanocomposites from modified clays: Recent advances and challenges. Prog. Polym. Sci. 2015, 51, 127–187. [Google Scholar] [CrossRef]
- Mansoori, Y.; Atghia, S.V.; Zamanloo, M.R.; Imanzadeh, G.; Sirousazar, M. Polymer-clay nanocomposites: Free-radical grafting of polyacrylamide onto organophilic montmorillonite. Eur. Polym. J. 2010, 9, 1844–1853. [Google Scholar] [CrossRef]
- Abdel Aziz, M.S.; Salama, H.E. Effect of vinyl montmorillonite on the physical, responsive and antimicrobial properties of the optimized polyacrylic acid/chitosan superabsorbent via Box-Behnken model. Int. J. Biol. Macromol. 2018, 116, 840–848. [Google Scholar] [CrossRef]
- Nie, X.; Adalati, A.; Du, J.; Liu, H.; Xu, S.; Wang, J. Preparation of amphoteric nanocomposite hydrogels based on the exfoliation of montmorillonite via in-situ intercalative polymerization of hydrophilic cationic and anionic monomers. Appl. Clay Sci. 2014, 97, 132–137. [Google Scholar] [CrossRef]
- Oyekanmi, A.A.; Ahmad, A.; Hossain, K.; Rafatullah, M. Statistical optimization for adsorption of Rhodamine B dye from aqueous solutions. J. Mol. Liq. 2019, 281, 48–58. [Google Scholar] [CrossRef]
- Singh, K.P.; Gupta, S.; Singh, A.K.; Sinha, S. Optimizing adsorption of crystal violet dye from water by magnetic nanocomposite using response surface modeling approach. J. Hazard. Mater. 2011, 186, 1462–1473. [Google Scholar] [CrossRef]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef] [PubMed]
- Metternicht, G.; Gonzalez, S. FUERO: Foundations of a fuzzy exploratory model for soil erosion hazard prediction. Environ. Model. Softw. 2005, 20, 715–728. [Google Scholar] [CrossRef]
- Jiang, H.; Eastman, J.R. Application of fuzzy measures in multi-criteria evaluation in GIS. Int. J. Geogr. Inf. Sci. 2000, 14, 173–184. [Google Scholar] [CrossRef]
- Kangas, A.; Kangas, J.; Laukkanen, S. Fuzzy multicriteria approval method and its application to two forest planning problems. For. Sci. 2006, 52, 232–242. [Google Scholar]
- Nagarpita, M.V.; Roy, P.; Shruthi, S.B.; Sailaja, R.R.N. Synthesis and swelling characteristics of chitosan and CMC grafted sodium acrylate-co-acrylamide using modified nanoclay and examining its efficacy for removal of dyes. Int. J. Biol. Macromol. 2017, 102, 1226–1240. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Chen, Y.; Zhao, J.; Tong, Z.; Jin, S. Preparation of SA-g-(PAA-co-PDMC) polyampholytic superabsorbent polymer and its application to the anionic dye adsorption removal from effluents. Sep. Purif. Technol. 2017, 188, 329–340. [Google Scholar] [CrossRef]
- Shah, L.A.; Khan, M.; Javed, R.; Sayed, M.; Khan, M.S.; Khan, A.; Ullah, M. Superabsorbent polymer hydrogels with good thermal and mechanical properties for removal of selected heavy metal ions. J. Clean. Prod. 2018, 201, 78–87. [Google Scholar] [CrossRef]
- Kyzas, G.Z.; Kostoglou, M. Swelling—Adsorption interactions during mercury and nickel ions removal by chitosan derivatives. Sep. Purif. Technol. 2015, 149, 92–102. [Google Scholar] [CrossRef]
- Naguib, H.F.; Abdel Aziz, M.S.; Saad, G.R. Synthesis, Characterization, and Microbial Activity of Nanocomposites of Chitosan-Graft-Poly(4-vinyl pyridine) Copolymer/Organophilic Montmorillonite. Polym. Plast. Technol. Eng. 2015, 54, 1270–1279. [Google Scholar] [CrossRef]
- Zhang, F.; Cheng, J. Verification of fuzzy UML models with fuzzy Description Logic. Appl. Soft Comput. J. 2018, 73, 134–152. [Google Scholar] [CrossRef]
- Pirouzan, D.; Yahyaei, M.; Banisi, S. Pareto based optimization of flotation cells configuration using an oriented genetic algorithm. Int. J. Miner. Process. 2014, 126, 107–116. [Google Scholar] [CrossRef]
- Aviso, K.B.; Tan, R.R.; Culaba, A.B.; Cruz, J.B. Bi-level fuzzy optimization approach for water exchange in eco-industrial parks. Process Saf. Environ. Prot. 2010, 88, 31–40. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy mathematical programming. Comput. Oper. Res. 1983, 10, 291–298. [Google Scholar] [CrossRef]
- Czogala, E.; Zimmermann, H.-J. Decision making in uncertain environments. Eur. J. Oper. Res. 1986, 23, 202–212. [Google Scholar] [CrossRef]
- Aviso, K.B.; Tan, R.R.; Culaba, A.B. Designing eco-industrial water exchange networks using fuzzy mathematical programming. Clean Technol. Environ. Policy 2010, 12, 353–363. [Google Scholar] [CrossRef]
- Tapia, J.F.D.; Tan, R.R. Fuzzy optimization of multi-period carbon capture and storage systems with parametric uncertainties. Process Saf. Environ. Prot. 2014, 92, 545–554. [Google Scholar] [CrossRef]
- Choi, A.E.S.; Roces, S.; Dugos, N.; Wan, M.W. Operating cost study through a Pareto-optimal fuzzy analysis using commercial ferrate (VI) in an ultrasound-assisted oxidative desulfurization of model sulfur compounds. Clean Technol. Environ. Policy 2016, 18, 1433–1441. [Google Scholar] [CrossRef]
- Ge, H.; Wang, S. Thermal preparation of chitosan-acrylic acid superabsorbent: Optimization, characteristic and water absorbency. Carbohydr. Polym. 2014, 113, 296–303. [Google Scholar] [CrossRef]
- Bukhari, S.M.H.; Khan, S.; Rehanullah, M.; Ranjha, N.M. Synthesis and Characterization of Chemically Cross-Linked Acrylic Acid/Gelatin Hydrogels: Effect of pH and Composition on Swelling and Drug Release. Int. J. Polym. Sci. 2015, 2015, 187961. [Google Scholar] [CrossRef]
- Grisdanurak, N.; Akewaranugulsiri, S.; Futalan, C.M.; Tsai, W.; Kan, C.; Hsu, C.; Wan, M. The Study of Copper Adsorption from Aqueous Solution Using Crosslinked Chitosan Immobilized on Bentonite. J. Appl. Polym. Sci. 2012, 125, E132–E142. [Google Scholar] [CrossRef]
- Kumar, P.; Kundu, P.P. Formation of semi-IPN membrane composed of crosslinked SPS-[PVdF-co-HFP/Nafion] for application in DMFC: A fine tuning between crosslinker and initiator. Mater. Chem. Phys. 2015, 164, 188–197. [Google Scholar] [CrossRef]
- Wang, W.; Yu, Y.; Wang, P.; Wang, Q.; Li, Y.; Yuan, J.; Fan, X. Controlled graft polymerization on the surface of filter paper via enzyme-initiated RAFT polymerization. Carbohydr. Polym. 2019, 207, 239–245. [Google Scholar] [CrossRef] [PubMed]
- Singhal, R.; Tomar, R.S.; Nagpal, A.K. Effect of cross-linker and initiator concentration on the swelling behaviour and network parameters of superabsorbent hydrogels based on acrylamide and acrylic acid. Int. J. Plast. Technol. 2009, 13, 22–37. [Google Scholar] [CrossRef]
- Lim, S.; Zhu, J. Integrated data envelopment analysis: Global vs. local optimum. Eur. J. Oper. Res. 2013, 229, 276–278. [Google Scholar] [CrossRef]
- Omidian, H.; Hashemi, S.A.; Sammes, P.G.; Meldrum, I. A model for the swelling of superabsorbent polymers. Polymer 1998, 39, 6697–6704. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Individual Decision Making in Fuzzy Environments. In Fuzzy Sets, Decision Making, and Expert Systems; Springer: Dordrecht, The Netherlands, 1987; pp. 15–44. ISBN 978-0-89838-149-8. [Google Scholar]
- Wen, B.; Li, H. An approach to formulation of FNLP with complex piecewise linear membership functions. Chin. J. Chem. Eng. 2014, 22, 411–417. [Google Scholar] [CrossRef]




| (a) Process Parameters | Unit | Range |
| AA/Ch (A) | 5–10 | |
| N,N′-methylenebisacrylamide (B) | wt % | 1–3 |
| Ammonium persulfate (C) | wt % | 1–3 |
| (b) Chemicals | Unit | * Material Cost |
| AA | USD/g | 0.44 |
| N,N′-methylenebisacrylamide | USD/g | 0.41 |
| Ammonium persulfate | USD/g | 0.39 |
| Run | AA/Ch (A) | N,N′-methylenebisacrylamide (B: wt %) | Ammonium Persulfate (C: wt %) | Predicted Swelling Capacity (g/g) | * Cumulative Uncertainty (g/g) |
|---|---|---|---|---|---|
| 1 | 5 | 2 | 1 | 74 | 19 |
| 2 | 5 | 3 | 2 | 66 | 14 |
| 3 | 5 | 1 | 2 | 232 | 17 |
| 4 | 5 | 2 | 3 | 164 | 14 |
| 5 | 7.5 | 3 | 3 | 192 | 9 |
| 6 | 7.5 | 2 | 2 | 220 | 13 |
| 7 | 7.5 | 2 | 2 | 220 | 13 |
| 8 | 7.5 | 3 | 1 | 91 | 17 |
| 9 | 7.5 | 2 | 2 | 220 | 13 |
| 10 | 7.5 | 1 | 3 | 322 | 13 |
| 11 | 7.5 | 1 | 1 | 221 | 19 |
| 12 | 7.5 | 2 | 2 | 220 | 13 |
| 13 | 7.5 | 2 | 2 | 220 | 13 |
| 14 | 10 | 3 | 2 | 226 | 10 |
| 15 | 10 | 2 | 1 | 186 | 17 |
| 16 | 10 | 1 | 2 | 320 | 13 |
| 17 | 10 | 2 | 3 | 299 | 8 |
| Parameters | Unit | Goal | |
|---|---|---|---|
| Absorbent : Swelling Capacity : Variable Cost | Adsorben : Swelling Capacity : Variable Cost | ||
| % | 67.2 | 52.3 | |
| % | 67.2 | 52.3 | |
| % | 67.2 | 52.3 | |
| Swelling capacity | g/g | 2 | 78 |
| Cumulative uncertainty | g/g | 15 | 19 |
| Overall | g/g | 305 | 97 |
| Costing: | |||
| Arylic acid | USD/kg | 1.0 | 0.5 |
| N,N′-methylenebisacrylamide | USD/kg | 4.1 | 8.0 |
| Ammonium persulfate | USD/kg | 5.7 | 3.8 |
| Total variable cost | USD/kg | 10.8 | 12.3 |
| Process Parameters: | |||
| AA/Ch | 10.0 | 5.0 | |
| N,N′-methylenebisacrylamide | wt % | 1.0 | 1.9 |
| Ammonium persulfate | wt % | 1.6 | 1.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, A.E.S.; Futalan, C.M.; Yee, J.-J. Fuzzy Optimization on the Synthesis of Chitosan-Graft-Polyacrylic Acid with Montmorillonite as Filler Material: A Case Study. Polymers 2019, 11, 738. https://doi.org/10.3390/polym11040738
Choi AES, Futalan CM, Yee J-J. Fuzzy Optimization on the Synthesis of Chitosan-Graft-Polyacrylic Acid with Montmorillonite as Filler Material: A Case Study. Polymers. 2019; 11(4):738. https://doi.org/10.3390/polym11040738
Chicago/Turabian StyleChoi, Angelo Earvin Sy, Cybelle Morales Futalan, and Jurng-Jae Yee. 2019. "Fuzzy Optimization on the Synthesis of Chitosan-Graft-Polyacrylic Acid with Montmorillonite as Filler Material: A Case Study" Polymers 11, no. 4: 738. https://doi.org/10.3390/polym11040738
APA StyleChoi, A. E. S., Futalan, C. M., & Yee, J.-J. (2019). Fuzzy Optimization on the Synthesis of Chitosan-Graft-Polyacrylic Acid with Montmorillonite as Filler Material: A Case Study. Polymers, 11(4), 738. https://doi.org/10.3390/polym11040738