A Dissipative Particle Dynamics Study of Flow Behaviors in Ultra High Molecular Weight Polyethylene/Polyamide 6 Blends Based on Souza-Martins Method
Abstract
:1. Introduction
2. Theoretical Background and Simulation Details
2.1. The Interfacial Properties between Immiscible Polymers
2.2. Construction Basis in Flow Field
2.3. Simulation Details
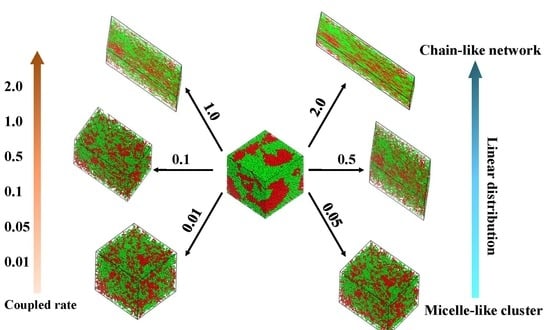
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Elemans, P.M.; Janssen, J.H.; Meijer, H.H. The measurement of interfacial tension in polymer/polymer systems: The breaking thread method. J. Rheol. 1990, 34, 1311–1325. [Google Scholar] [CrossRef] [Green Version]
- Tufano, C.; Peters, G.M.; Meijer, H.H.; Anderson, P.D. Effects of partial miscibility on drop-wall and drop-drop interactions. J. Rheol. 2010, 54, 159–183. [Google Scholar] [CrossRef]
- Meijer, H.; Keestra, B.J.; Anderson, P.D.; Puyvelde, P.V. Diffuse interface modelling of the rheology of immiscible polymer blends. Phys. Fluids 2003, 15, 2567–2575. [Google Scholar]
- Tufano, C.; Peters, G.; Anderson, P.; Meijer, H.; Anderson, P. Transient interfacial tension of partially miscible polymers. J. Colloid Interface Sci. 2008, 325, 130–140. [Google Scholar] [CrossRef] [PubMed]
- Khatavkar, V.V.; Anderson, P.D.; Meijer, H.E.H. On scaling of diffuse-interface models. Chem. Eng. Sci. 2006, 61, 2364–2378. [Google Scholar] [CrossRef]
- Helfand, E.; Tagami, Y. Theory of the interface between immiscible polymers. J. Chem. Phys. 1972, 56, 3592. [Google Scholar] [CrossRef]
- Singh, M.K.; Kang, T.G.; Anderson, P.D.; Han, E.M.; Hrymak, A.N. Analysis and optimization of low-pressure drop static mixers. Aiche J. 2010, 55, 2208–2216. [Google Scholar] [CrossRef]
- Broseta, D.; Fredrickson, G.H.; Helfand, E.; Leibler, L. Molecular-weight and polydispersity effects at polymer polymer interfaces. Macromolecules 1990, 23, 132–139. [Google Scholar] [CrossRef]
- Qu, J.P.; Chen, H.Z.; Liu, S.R.; Tan, B.; Liu, L.M.; Yin, X.C.; Liu, Q.J.; Guo, R.B. Morphology study of immiscible polymer blends in a vane extruder. J. Appl. Polym. Sci. 2013, 128, 3576–3585. [Google Scholar] [CrossRef]
- Qu, J.P.; Zhao, X.Q.; Li, J.B.; Cai, S.Q. Power consumption in the compacting process of polymer particulate solids in a vane extruder. J. Appl. Polym. Sci. 2013, 127, 3923–3932. [Google Scholar] [CrossRef]
- Yin, X.C.; Li, S.; He, G.J.; Zhang, G.Z.; Qu, J.P. Experimental study of the extrusion characteristic of a vane extruder based on extensional flow. Adv. Polym. Technol. 2015, 35, 215–220. [Google Scholar]
- Cao, C.L.; Chen, X.C.; Wang, J.X.; Lin, Y.; Guo, Y.Y.; Qian, Q.R.; Chen, Q.H.; Feng, Y.H.; Yu, D.S.; Chen, X.D. Structure and properties of ultrahigh molecular weight polyethylene processed under a consecutive elongational flow. J. Polym. Res. 2018, 25, 16. [Google Scholar] [CrossRef]
- Fu, Y.; Song, J.-H. Large deformation mechanism of glassy polyethylene polymer nanocomposites: Coarse grain molecular dynamics study. Comput. Mater. Sci. 2015, 96, 485–494. [Google Scholar] [CrossRef]
- Zhou, B.; Luo, W.; Yang, J.; Duan, X.; Wen, Y.; Zhou, H.; Chen, R.; Shan, B. Simulation of dispersion and alignment of carbon nanotubes in polymer flow using dissipative particle dynamics. Comput. Mater. Sci. 2017, 126, 35–42. [Google Scholar] [CrossRef]
- Fu, Y.; Michopoulos, J.G.; Song, J.H. On investigating the thermomechanical properties of Cross-linked epoxy via molecular dynamics analysis. Nanoscale Microscale Thermophys. Eng. 2017, 21, 8–25. [Google Scholar] [CrossRef]
- Gai, J.-G.; Li, H.-L.; Schrauwen, C.; Hu, G.H. Dissipative particle dynamics study on the phase morphologies of the ultrahigh molecular weight polyethylene/polypropylene/poly(ethylene glycol) blends. Polymer 2009, 50, 336–346. [Google Scholar] [CrossRef]
- Gai, J.G.; Hu, G.H.; Li, H.L.; Zhu, S.P.; Sandrine, H. Dissipative particle dynamics and flory-huggins theories for predicting the rheological behavior of ultrahigh molecular weight polyethylene blends. Ind. Eng. Chem. Res. 2010, 49, 11137–11369. [Google Scholar] [CrossRef]
- Wang, J.X.; Cao, C.L.; Chen, X.C.; Yu, D.S.; Chen, X.D. Phase behavior and alignment transition of ultra high molecular weight polyethylene/polyamide 6 blends under extensional and shear flow. Comput. Mater. Sci. 2018, 149, 21–27. [Google Scholar] [CrossRef]
- Wang, J.X.; Cao, C.L.; Yu, D.S.; Chen, X.D. Deformation and stress response of carbon nanotubes/uhmwpe composites under extensional-shear coupling flow. Appl. Compos. Mater. 2017, 25, 35–43. [Google Scholar] [CrossRef]
- Fu, Y.; Song, J.H. On computing stress in polymer systems involving multi-body potentials from molecular dynamics simulation. J. Chem. Phys. 2014, 141, 54108. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Song, J.-H. Heat flux expressions that satisfy the conservation laws in atomistic system involving multibody potentials. J. Comput. Phys. 2015, 294, 191–207. [Google Scholar] [CrossRef]
- Souzajos, I.; Martins, J.L. Metric tensor as the dynamical variable for variable-cell-shape molecular dynamics. Phys. Rev. B 1997, 55, 8733–8742. [Google Scholar] [Green Version]
- Lees, A.W.; Edwards, S.F. The computer study of transport processes under extreme conditions. J. Phys. C Solid State Phys. 1972, 5, 1921. [Google Scholar] [CrossRef]
- Cohen, E.D. Transport coefficients and Lyapunov exponents. Physica A 1995, 213, 293–314. [Google Scholar] [CrossRef]
- Robert, D.G.; Patrick, B.W. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar]
- Spyriouni, A.T.; Caroll, V. A molecular modeling study of binary blend compatibility of polyamide 6 and poly(vinyl acetate) with different degrees of hydrolysis: An atomistic and mesoscopic approach. Macromolecules 2001, 34, 5306–5316. [Google Scholar] [CrossRef]
- Hassan, E.; Ahmad, R.A.; Ali, K.H. Predictions of some internal microstructural models for polymer melts and solutions in shear and elongational flows. Macromol. Theor. Simul. 2004, 13, 655–664. [Google Scholar]
- Byron, B.R.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids: Fluid Mechanics, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1987. [Google Scholar]
- Matin, M.L.; Daivis, P.J.; Todd, B.D. Comparison of planar shear flow and planar elongational flow for systems of small molecules. J. Chem. Phys. 2001, 115, 5338. [Google Scholar] [CrossRef]
- Tang, Y.H.; He, Y.D.; Wang, X.L. Investigation on the membrane formation process of polymer–diluent system via thermally induced phase separation accompanied with mass transfer across the interface: Dissipative particle dynamics simulation and its experimental verification. J. Membr. Sci. 2015, 474, 196–206. [Google Scholar] [CrossRef]
- Lin, H.H.; Tang, Y.H.; Matsuyama, H.; Wang, X.L. Dissipative particle dynamics simulation on the membrane formation of polymer–solvent system via nonsolvent induced phase separation. J. Membr. Sci. 2018, 548, 288–297. [Google Scholar] [CrossRef]









© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, P.; Cao, C.; Ren, S.; Yu, D. A Dissipative Particle Dynamics Study of Flow Behaviors in Ultra High Molecular Weight Polyethylene/Polyamide 6 Blends Based on Souza-Martins Method. Polymers 2019, 11, 1275. https://doi.org/10.3390/polym11081275
Wang J, Li P, Cao C, Ren S, Yu D. A Dissipative Particle Dynamics Study of Flow Behaviors in Ultra High Molecular Weight Polyethylene/Polyamide 6 Blends Based on Souza-Martins Method. Polymers. 2019; 11(8):1275. https://doi.org/10.3390/polym11081275
Chicago/Turabian StyleWang, Junxia, Ping Li, Changlin Cao, Shijie Ren, and Dingshan Yu. 2019. "A Dissipative Particle Dynamics Study of Flow Behaviors in Ultra High Molecular Weight Polyethylene/Polyamide 6 Blends Based on Souza-Martins Method" Polymers 11, no. 8: 1275. https://doi.org/10.3390/polym11081275
APA StyleWang, J., Li, P., Cao, C., Ren, S., & Yu, D. (2019). A Dissipative Particle Dynamics Study of Flow Behaviors in Ultra High Molecular Weight Polyethylene/Polyamide 6 Blends Based on Souza-Martins Method. Polymers, 11(8), 1275. https://doi.org/10.3390/polym11081275