Injectability of Thermosensitive, Low-Concentrated Chitosan Colloids as Flow Phenomenon through the Capillary under High Shear Rate Conditions
Abstract
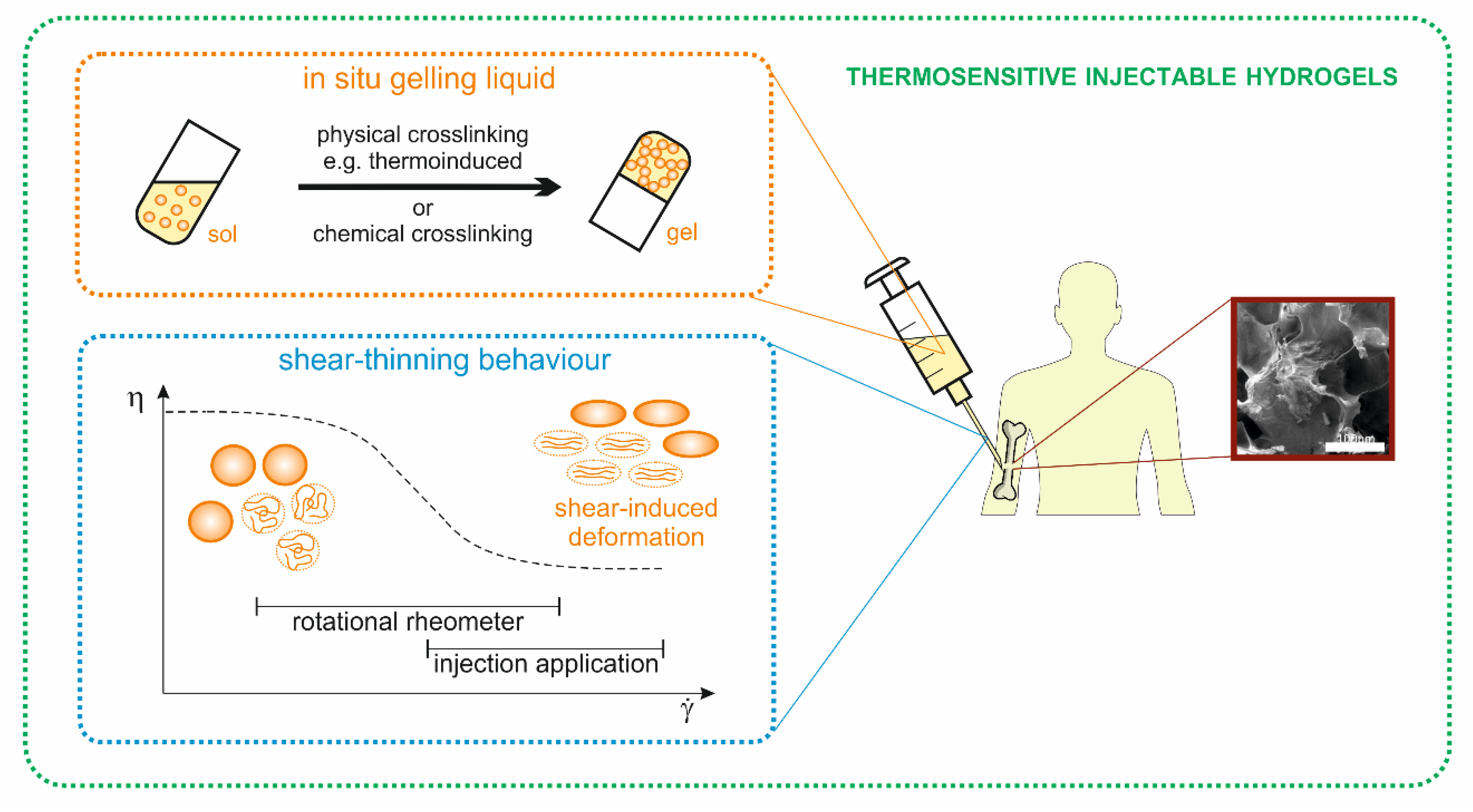
:1. Introduction
2. Materials and Methods
2.1. Preparation of Injectable Chitosan Hydrogels
2.2. Instrumental Injectability Studies
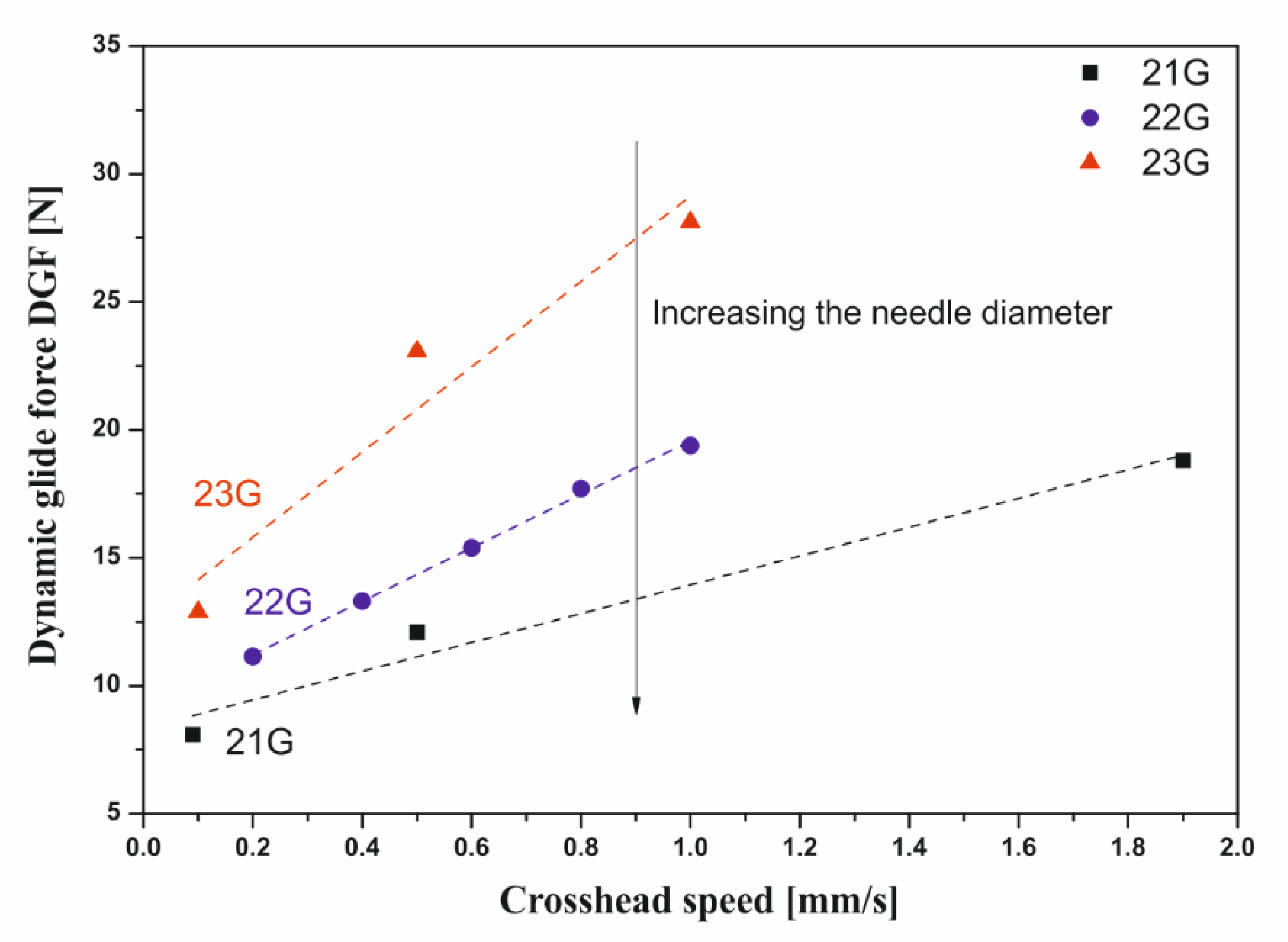
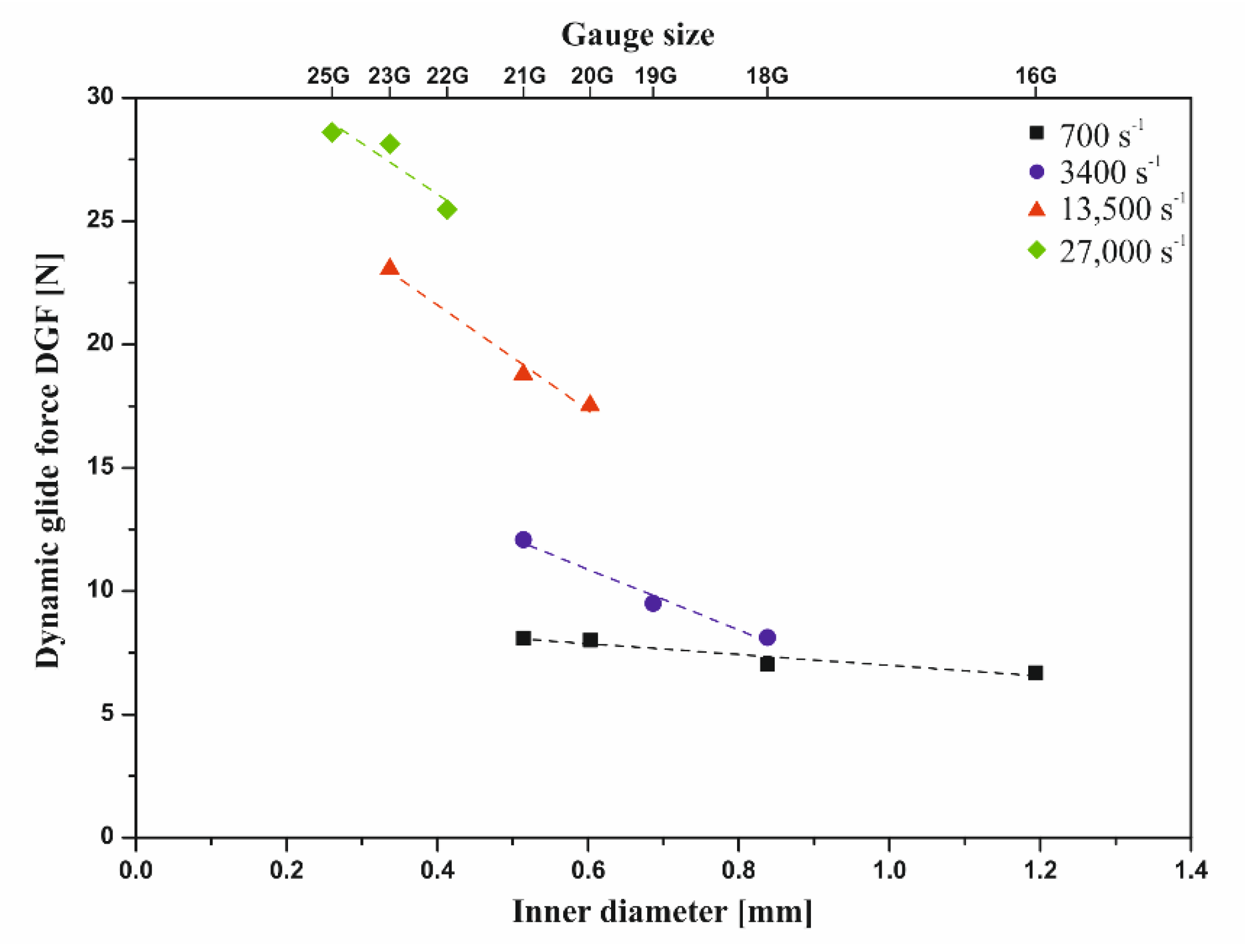
2.2.1. Influence of the Injection Needle Used (Diameter and Length)
2.2.2. Influence of the Injection Rate
2.2.3. Injection under Constant Shear Conditions in the Needle
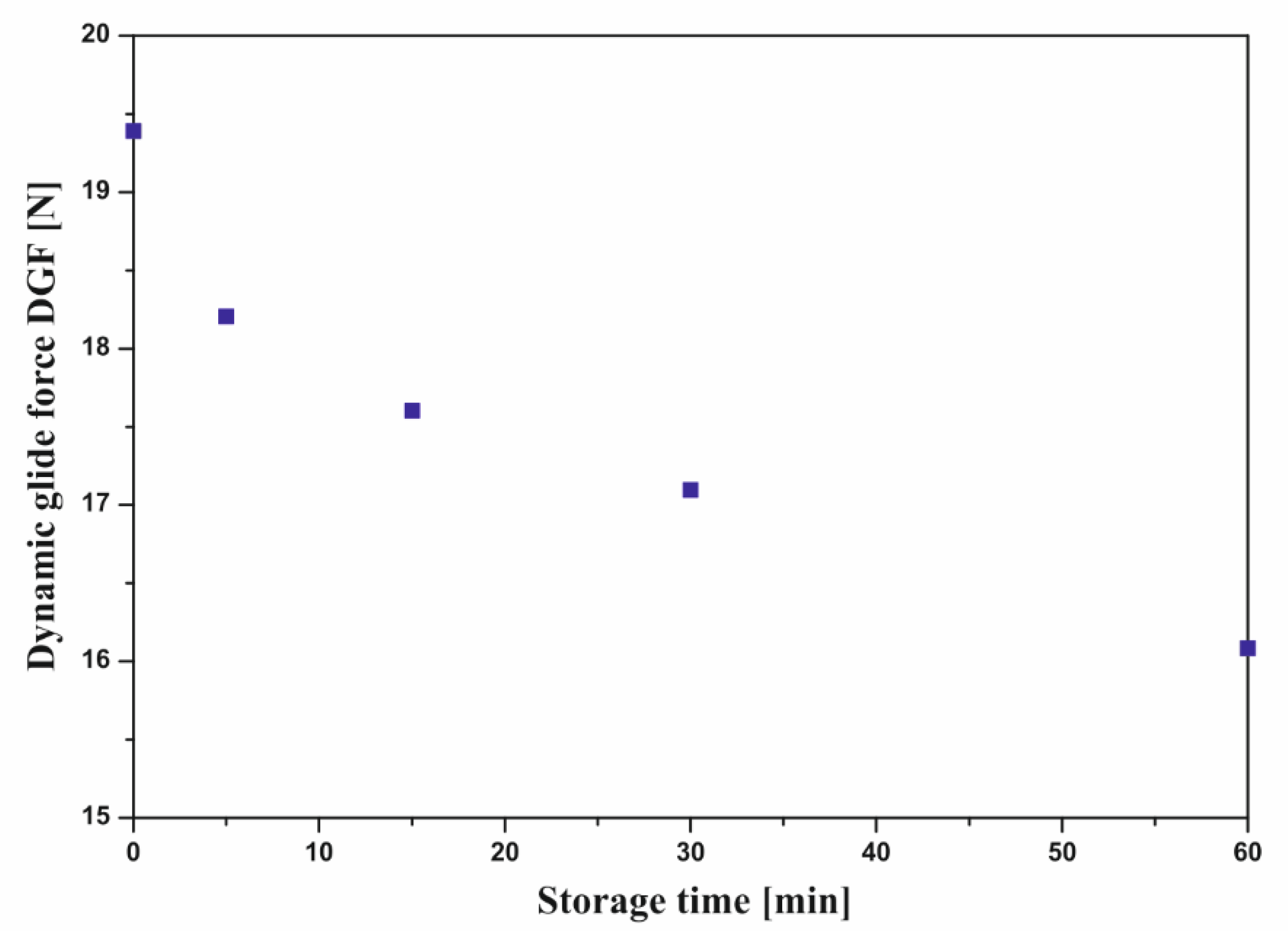
2.2.4. Effect of Uncontrolled Storage at Room Temperature
2.3. Rheological Characterization
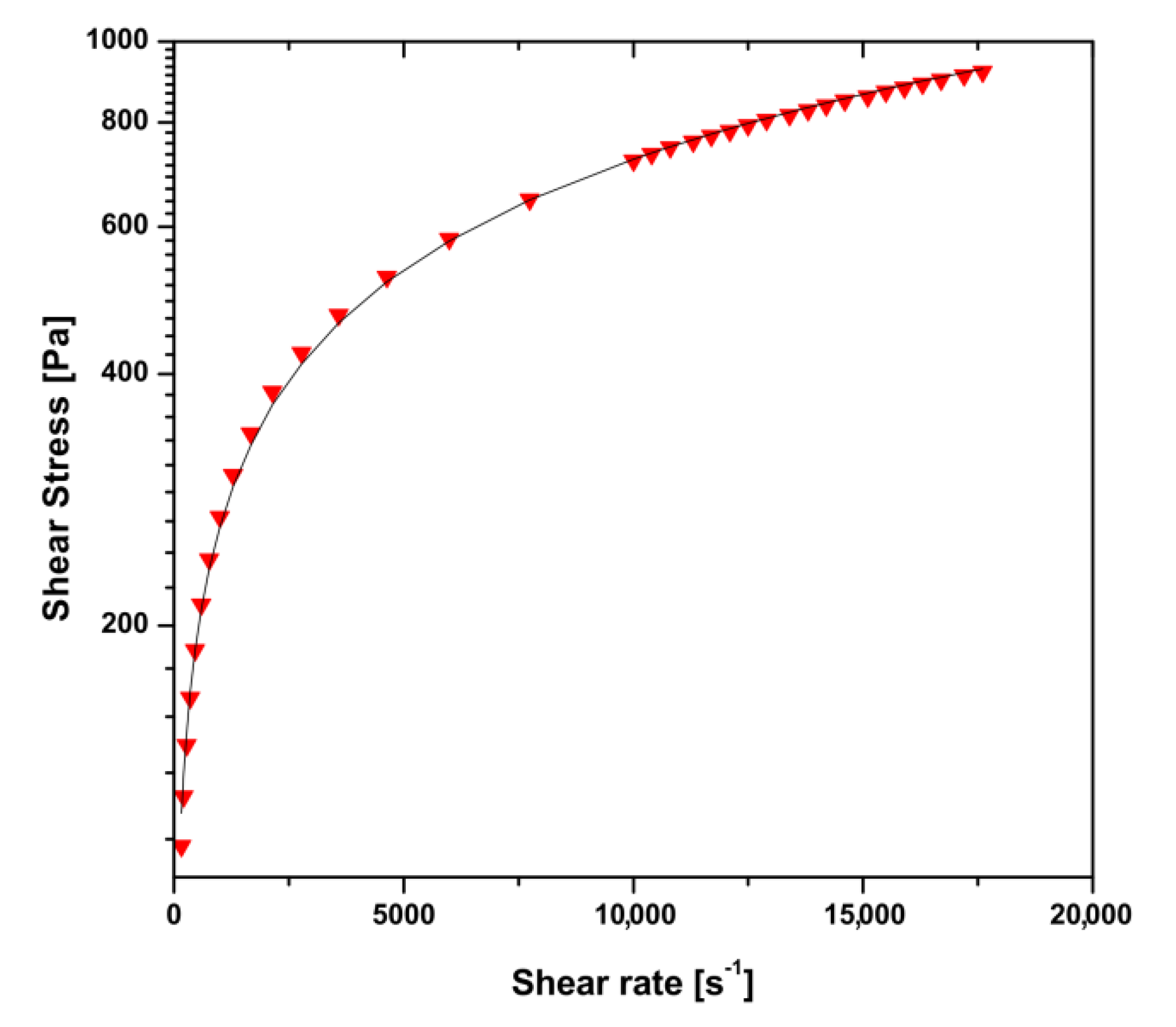
2.3.1. Flow Curve in the Range of High Shear Rates
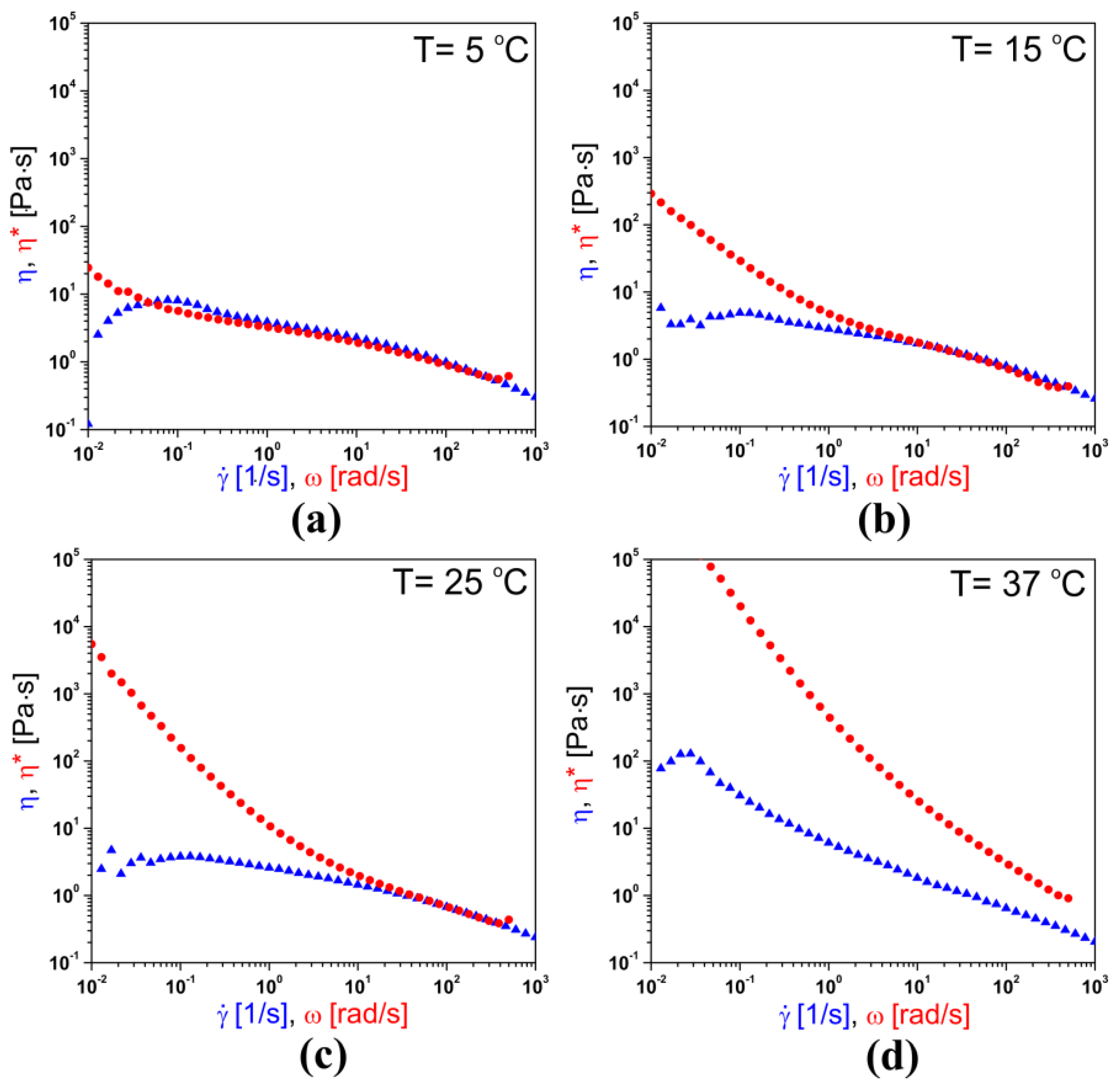
2.3.2. The Cox–Merz Rule
2.3.3. Three-Interval Thixotropic Tests
3. Results
3.1. Rheological Characterization of Chitosan Sol
3.2. Theoretical Analysis of Flow Conditions in an Injection Needle
3.3. Instrumental Injectability Tests
3.4. Influence of the Injection Application on the Conformation of Chitosan Molecules
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Sivashanmugam, A.; Arun Kumar, R.; Vishnu Priya, M.; Nair, S.V.; Jayakumar, R. An overview of injectable polymeric hydrogels for tissue engineering. Eur. Polym. J. 2015, 72, 543–565. [Google Scholar] [CrossRef]
- Sun, Y.; Nan, D.; Jin, H.; Qu, X. Recent advances of injectable hydrogels for drug delivery and tissue engineering applications. Polym. Test. 2020, 81, 106283. [Google Scholar] [CrossRef]
- Yu, L.; Ding, J. Injectable hydrogels as unique biomedical materials. Chem. Soc. Rev. 2008, 37, 1473–1481. [Google Scholar] [CrossRef] [PubMed]
- González-Díaz, E.C.; Varghese, S. Hydrogels as Extracellular Matrix Analogs. Gels 2016, 2, 20. [Google Scholar] [CrossRef] [PubMed]
- Tibbitt, M.W.; Anseth, K.S. Hydrogels as extracellular matrix mimics for 3D cell culture. Biotechnol. Bioeng. 2009, 103, 655–663. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.H. Injectable hydrogels delivering therapeutic agents for disease treatment and tissue engineering. Biomater. Res. 2018, 22, 27. [Google Scholar] [CrossRef] [Green Version]
- Guvendiren, M.; Lu, H.D.; Burdick, J.A. Shear-thinning hydrogels for biomedical applications. Soft Matter 2011, 8, 260–272. [Google Scholar] [CrossRef]
- Yang, J.-A.; Yeom, J.; Hwang, B.W.; Hoffman, A.S.; Hahn, S.K. In situ-forming injectable hydrogels for regenerative medicine. Prog. Polym. Sci. 2014, 39, 1973–1986. [Google Scholar] [CrossRef]
- Watt, R.P.; Khatri, H.; Dibble, A.R.G. Injectability as a function of viscosity and dosing materials for subcutaneous administration. Int. J. Pharm. 2019, 554, 376–386. [Google Scholar] [CrossRef]
- Qiu, Y.; Park, K. Environment-sensitive hydrogels for drug delivery. Adv. Drug Deliv. Rev. 2012, 64, 49–60. [Google Scholar] [CrossRef]
- Taylor, M.J.; Tomlins, P.; Sahota, T.S. Thermoresponsive Gels. Gels 2017, 3, 4. [Google Scholar] [CrossRef] [PubMed]
- Lavertu, M.; Filion, D.; Buschmann, M.D. Heat-induced transfer of protons from chitosan to glycerol phosphate produces chitosan precipitation and gelation. Biomacromolecules 2008, 9, 640–650. [Google Scholar] [CrossRef]
- Filion, D.; Lavertu, M.; Buschmann, M.D. Ionization and Solubility of Chitosan Solutions Related to Thermosensitive Chitosan/Glycerol-Phosphate Systems. Biomacromolecules 2007, 8, 3224–3234. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Yang, Y.; Wang, L.; Lu, S.; Shao, Z.; Chen, X. Synergistic interactions during thermosensitive chitosan-β-glycerophosphate hydrogel formation. RSC Adv. 2011, 1, 282–289. [Google Scholar] [CrossRef]
- Owczarz, P.; Ziółkowski, P.; Modrzejewska, Z.; Kuberski, S.; Dziubiński, M. Rheo-Kinetic Study of Sol-Gel Phase Transition of Chitosan Colloidal Systems. Polymers 2018, 10, 47. [Google Scholar] [CrossRef] [Green Version]
- Supper, S.; Anton, N.; Seidel, N.; Riemenschnitter, M.; Schoch, C.; Vandamme, T. Rheological Study of Chitosan/Polyol-phosphate Systems: Influence of the Polyol Part on the Thermo-Induced Gelation Mechanism. Langmuir 2013, 29, 10229–10237. [Google Scholar] [CrossRef] [PubMed]
- Cho, J.; Heuzey, M.-C.; Bégin, A.; Carreau, P.J. Physical gelation of chitosan in the presence of beta-glycerophosphate: The effect of temperature. Biomacromolecules 2005, 6, 3267–3275. [Google Scholar] [CrossRef]
- Chenite, A.; Chaput, C.; Wang, D.; Combes, C.; Buschmann, M.D.; Hoemann, C.D.; Leroux, J.C.; Atkinson, B.L.; Binette, F.; Selmani, A. Novel injectable neutral solutions of chitosan form biodegradable gels in situ. Biomaterials 2000, 21, 2155–2161. [Google Scholar] [CrossRef]
- Aliaghaie, M.; Mirzadeh, H.; Dashtimoghadam, E.; Taranejoo, S. Investigation of gelation mechanism of an injectable hydrogel based on chitosan by rheological measurements for a drug delivery application. Soft Matter 2012, 8, 7128–7137. [Google Scholar] [CrossRef]
- Douglas, T.E.L.; Skwarczynska, A.; Modrzejewska, Z.; Balcaen, L.; Schaubroeck, D.; Lycke, S.; Vanhaecke, F.; Vandenabeele, P.; Dubruel, P.; Jansen, J.A.; et al. Acceleration of gelation and promotion of mineralization of chitosan hydrogels by alkaline phosphatase. Int. J. Biol. Macromol. 2013, 56, 122–132. [Google Scholar] [CrossRef]
- Kim, S.; Nishimoto, S.K.; Bumgardner, J.D.; Haggard, W.O.; Gaber, M.W.; Yang, Y. A chitosan/β-glycerophosphate thermo-sensitive gel for the delivery of ellagic acid for the treatment of brain cancer. Biomaterials 2010, 31, 4157–4166. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.Y.; Jiang, L.J.; Cao, P.P.; Li, J.B.; Chen, X.G. Glycerophosphate-based chitosan thermosensitive hydrogels and their biomedical applications. Carbohydr. Polym. 2015, 117, 524–536. [Google Scholar] [CrossRef] [PubMed]
- Martins, E.A.; Michelacci, Y.M.; Baccarin, R.Y.; Cogliati, B.; Silva, L.C. Evaluation of chitosan-GP hydrogel biocompatibility in osteochondral defects: An experimental approach. BMC Vet. Res. 2014, 10, 197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hastings, C.L.; Kelly, H.M.; Murphy, M.J.; Barry, F.P.; O′Brien, F.J.; Duffy, G.P. Development of a thermoresponsive chitosan gel combined with human mesenchymal stem cells and desferrioxamine as a multimodal pro-angiogenic therapeutic for the treatment of critical limb ischaemia. J. Control. Release 2012, 161, 73–80. [Google Scholar] [CrossRef] [Green Version]
- Lisková, J.; Bačaková, L.; Skwarczyńska, A.L.; Musial, O.; Bliznuk, V.; De Schamphelaere, K.; Modrzejewska, Z.; Douglas, T.E.L. Development of thermosensitive hydrogels of chitosan, sodium and magnesium glycerophosphate for bone regeneration applications. J. Funct. Biomater. 2015, 6, 192–203. [Google Scholar] [CrossRef] [Green Version]
- Ngoenkam, J.; Faikrua, A.; Yasothornsrikul, S.; Viyoch, J. Potential of an injectable chitosan/starch/β-glycerol phosphate hydrogel for sustaining normal chondrocyte function. Int. J. Pharm. 2010, 391, 115–124. [Google Scholar] [CrossRef]
- Huang, C.-L.; Chen, Y.-B.; Lo, Y.-L.; Lin, Y.-H. Development of chitosan/β-glycerophosphate/glycerol hydrogel as a thermosensitive coupling agent. Carbohydr. Polym. 2016, 147, 409–414. [Google Scholar] [CrossRef]
- Mellati, A.; Akhtari, J. Injectable Hydrogels: A Review of Injectability Mechanisms and Biomedical Applications. Res. Mol. Med. 2019, 6, 1–14. [Google Scholar] [CrossRef]
- Cilurzo, F.; Selmin, F.; Minghetti, P.; Adami, M.; Bertoni, E.; Lauria, S.; Montanari, L. Injectability Evaluation: An Open Issue. AAPS Pharmscitech 2011, 12, 604–609. [Google Scholar] [CrossRef]
- Rungseevijitprapa, W.; Bodmeier, R. Injectability of biodegradable in situ forming microparticle systems (ISM). Eur. J. Pharm. Sci. 2009, 36, 524–531. [Google Scholar] [CrossRef]
- Zhang, Q.; Fassihi, M.A.; Fassihi, R. Delivery Considerations of Highly Viscous Polymeric Fluids Mimicking Concentrated Biopharmaceuticals: Assessment of Injectability via Measurement of Total Work Done “WT”. AAPS PharmSciTech 2018, 19, 1520–1528. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allmendinger, A.; Fischer, S.; Huwyler, J.; Mahler, H.-C.; Schwarb, E.; Zarraga, I.E.; Mueller, R. Rheological characterization and injection forces of concentrated protein formulations: An alternative predictive model for non-Newtonian solutions. Eur. J. Pharm. Biopharm. 2014, 87, 318–328. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.H.; Wang, L.L.; Chung, J.J.; Kim, Y.-H.; Atluri, P.; Burdick, J.A. Methods To Assess Shear-Thinning Hydrogels for Application As Injectable Biomaterials. ACS Biomater. Sci. Eng. 2017, 3, 3146–3160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rathore, N.; Pranay, P.; Bernacki, J.; Eu, B.; Ji, W.; Walls, E. Characterization of protein rheology and delivery forces for combination products. J. Pharm. Sci. 2012, 101, 4472–4480. [Google Scholar] [CrossRef]
- Allahham, A.; Mainwaring, D.; Stewart, P.; Marriott, J. Development and application of a micro-capillary rheometer for in-vitro evaluation of parenteral injectability. J. Pharm. Pharmacol. 2004, 56, 709–716. [Google Scholar] [CrossRef]
- Owczarz, P.; Rył, A.; Dziubiński, M.; Sielski, J. Injectable Chitosan Scaffolds with Calcium β-Glycerophosphate as the Only Neutralizing Agent. Processes 2019, 7, 297. [Google Scholar] [CrossRef] [Green Version]
- Ji, Q.X.; Deng, J.; Xing, X.M.; Yuan, C.Q.; Yu, X.B.; Xu, Q.C.; Yue, J. Biocompatibility of a chitosan-based injectable thermosensitive hydrogel and its effects on dog periodontal tissue regeneration. Carbohydr. Polym. 2010, 82, 1153–1160. [Google Scholar] [CrossRef]
- Parameswaran-Thankam, A.; Parnell, C.M.; Watanabe, F.; RanguMagar, A.B.; Chhetri, B.P.; Szwedo, P.K.; Biris, A.S.; Ghosh, A. Guar-Based Injectable Thermoresponsive Hydrogel as a Scaffold for Bone Cell Growth and Controlled Drug Delivery. ACS Omega 2018, 3, 15158–15167. [Google Scholar] [CrossRef]
- Kolawole, O.M.; Lau, W.M.; Khutoryanskiy, V.V. Chitosan/β-glycerophosphate in situ gelling mucoadhesive systems for intravesical delivery of mitomycin-C. Int. J. Pharm. X 2019, 1, 100007. [Google Scholar] [CrossRef]
- Shavandi, A.; Bekhit, A.E.-D.A.; Sun, Z.; Ali, M.A. Injectable gel from squid pen chitosan for bone tissue engineering applications. J. Sol-Gel Sci. Technol. 2016, 77, 675–687. [Google Scholar] [CrossRef]
- Yasmeen, S.; Lo, M.K.; Bajracharya, S.; Roldo, M. Injectable Scaffolds for Bone Regeneration. Langmuir 2014, 30, 12977–12985. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doench, I.; Torres-Ramos, M.E.W.; Montembault, A.; Nunes de Oliveira, P.; Halimi, C.; Viguier, E.; Heux, L.; Siadous, R.; Thiré, R.M.S.M.; Osorio-Madrazo, A. Injectable and Gellable Chitosan Formulations Filled with Cellulose Nanofibers for Intervertebral Disc Tissue Engineering. Polymers 2018, 10, 1202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Snijkers, F.; Pasquino, R.; Olmsted, P.D.; Vlassopoulos, D. Perspectives on the viscoelasticity and flow behavior of entangled linear and branched polymers. J. Phys. Condens. Matter 2015, 27, 473002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Colby, R.H.; Boris, D.C.; Krause, W.E.; Dou, S. Shear thinning of unentangled flexible polymer liquids. Rheol. Acta 2007, 46, 569–575. [Google Scholar] [CrossRef]
- Xu, X.; Chen, J.; An, L. Shear thinning behavior of linear polymer melts under shear flow via nonequilibrium molecular dynamics. J. Chem. Phys. 2014, 140, 174902. [Google Scholar] [CrossRef] [PubMed]
- Owczarz, P.; Ziółkowski, P.; Dziubiński, M. The Application of Small-Angle Light Scattering for Rheo-Optical Characterization of Chitosan Colloidal Solutions. Polymers 2018, 10, 431. [Google Scholar] [CrossRef] [Green Version]
- Kume, T.; Hashimoto, T.; Takahashi, T.; Fuller, G.G. Rheo-Optical Studies of Shear-Induced Structures in Semidilute Polystyrene Solutions. Macromolecules 1997, 30, 7232–7236. [Google Scholar] [CrossRef]
- Saito, S.; Hashimoto, T.; Morfin, I.; Lindner, P.; Boué, F. Structures in a Semidilute Polymer Solution Induced under Steady Shear Flow as Studied by Small-Angle Light and Neutron Scattering. Macromolecules 2002, 35, 445–459. [Google Scholar] [CrossRef]
- Bair, S.; Tsuyoshi, Y.; Ludwig, B.; Hubert, S.; Vergne, P.; Gerhard, P. Oscillatory and Steady Shear Viscosity of Liquid Lubricants: The Cox-Merz Rule, Superposition, and Application to EHL Friction. In Proceedings of the 41st Leeds-Lyon Symposium on Tribology “Integrated Tribology”, Leeds, UK, 2–5 September 2014. [Google Scholar]
- Toker, O.S.; Karasu, S.; Yilmaz, M.T.; Karaman, S. Three interval thixotropy test (3ITT) in food applications: A novel technique to determine structural regeneration of mayonnaise under different shear conditions. Food Res. Int. 2015, 70, 125–133. [Google Scholar] [CrossRef]
- Owczarz, P.; Rył, A.; Modrzejewska, Z.; Dziubiński, M. The influence of the addition of collagen on the rheological properties of chitosan chloride solutions. Prog. Chem. Appl. Chitin Deriv. 2017, 22, 176–189. [Google Scholar] [CrossRef] [Green Version]
- Rył, A.; Owczarz, P. Thermoinduced Aggregation of Chitosan Systems in Perikinetic and Orthokinetic Regimes. manuscript in preparation.
- Chen, H.; Liu, W.; Hong, M.; Zhang, E.; Dai, X.; Chen, Q.; Yang, W.; Xue, Y.; Qiu, X.; Ji, X. Associative behavior of polyimide/cyclohexanone solutions. RSC Adv. 2019, 9, 27455–27463. [Google Scholar] [CrossRef] [Green Version]
- Fernández Farrés, I.; Moakes, R.J.A.; Norton, I.T. Designing biopolymer fluid gels: A microstructural approach. Food Hydrocoll. 2014, 42, 362–372. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Ruvalcaba, A.; Chornet, E.; Rodrigue, D. Dynamic Rheological Properties of Concentrated Chitosan Soltions. Appl. Rheol. 2004, 14, 140–147. [Google Scholar] [CrossRef]


| Needle | Outer Diameter (OD) (mm) | Inner Diameter (ID) (mm) | Length (mm) | Actual Length (mm) | Actual Length/ID (-) | Shear Rate (s−1) | Real Shear Rate (s−1) | ReMR 1 (−) |
|---|---|---|---|---|---|---|---|---|
| 14G × 1½’’ | 2.108 | 1.6 | 40 | 37 | 23.1 | 186 | 245 | 0.10 |
| 15G × 1½’’ | 1.829 | 1.372 | 40 | 38 | 27.7 | 294 | 388 | 0.15 |
| 16G × 1½’’ | 1.651 | 1.194 | 40 | 41 | 34.3 | 447 | 589 | 0.22 |
| 18G × 1½’’ | 1.270 | 0.838 | 40 | 41 | 48.9 | 1292 | 1703 | 0.57 |
| 19G × 1½’’ | 1.067 | 0.686 | 40 | 41 | 59.8 | 2356 | 3104 | 0.97 |
| 20G × 1½’’ | 0.908 | 0.603 | 40 | 41 | 68.0 | 3469 | 4571 | 1.37 |
| 21G × 1½’’ | 0.819 | 0.514 | 40 | 41 | 79.8 | 5600 | 7380 | 2.09 |
| 22G × 1¼’’ | 0.718 | 0.413 | 30 | 37 | 89.6 | 10,796 | 14,226 | 3.76 |
| 23G × 1¼’’ | 0.641 | 0.337 | 30 | 37 | 109.8 | 19,871 | 26,185 | 6.49 |
| 23G × 1′’ | 25 | 31 | 92.0 | |||||
| 25G × 1′’ | 0.514 | 0.26 | 25 | 31 | 119.2 | 43,269 | 57,020 | 13.00 |
| Needle | Assumed Shear Rate at the Injection Needle (s−1) | |||
|---|---|---|---|---|
| 700 | 3400 | 13,500 | 27,000 | |
| 15G | 1.8 | |||
| 16G | 1.2 | |||
| 18G | 0.4 | 2.0 | ||
| 19G | 1.1 | |||
| 20G | 0.2 | 3.0 | ||
| 21G | 0.09 | 0.5 | 1.9 | |
| 22G | 1.9 | |||
| 23G | 0.5 | 1 | ||
| 25G | 0.5 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rył, A.; Owczarz, P. Injectability of Thermosensitive, Low-Concentrated Chitosan Colloids as Flow Phenomenon through the Capillary under High Shear Rate Conditions. Polymers 2020, 12, 2260. https://doi.org/10.3390/polym12102260
Rył A, Owczarz P. Injectability of Thermosensitive, Low-Concentrated Chitosan Colloids as Flow Phenomenon through the Capillary under High Shear Rate Conditions. Polymers. 2020; 12(10):2260. https://doi.org/10.3390/polym12102260
Chicago/Turabian StyleRył, Anna, and Piotr Owczarz. 2020. "Injectability of Thermosensitive, Low-Concentrated Chitosan Colloids as Flow Phenomenon through the Capillary under High Shear Rate Conditions" Polymers 12, no. 10: 2260. https://doi.org/10.3390/polym12102260
APA StyleRył, A., & Owczarz, P. (2020). Injectability of Thermosensitive, Low-Concentrated Chitosan Colloids as Flow Phenomenon through the Capillary under High Shear Rate Conditions. Polymers, 12(10), 2260. https://doi.org/10.3390/polym12102260






