Analysis of Viscoelastic Behavior of Polypropylene/Carbon Nanotube Nanocomposites by Instrumented Indentation
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Manufacturing
2.2. SEM Analysis
2.3. Indentation Experiments
- (a)
- 2-step indentation test (Figure 1a) that consists of linear loading to 1000 mN and unloading back to zero with the same rate of 2000 mN/min.
- (b)
- 3-step indentation test (Figure 1b) that consists of loading, holding, and unloading. Both loading and unloading steps were carried out with the same rate of 2000 mN/min. A holding step of 40 s at constant force of 1000 mN was added at the end of the loading step. The 3-step indentation test is carried out in order to evaluate the mechanical properties based on the O and P method [32].
- (c)
- 2-cycle indentation test (Figure 1c), which combines a 2-step indentation test with loading and unloading at the same rate (2000 m N/min) with a 3-step indentation test (loading/unloading with 2000 N/min, and a 300 s holding at 1000 mN). The interval time between the two cycles was set to 0 s and the tests were carried out on the same surface position.
3. Results and Discussion
3.1. Morphology of PP/MWCNT Nanocomposites
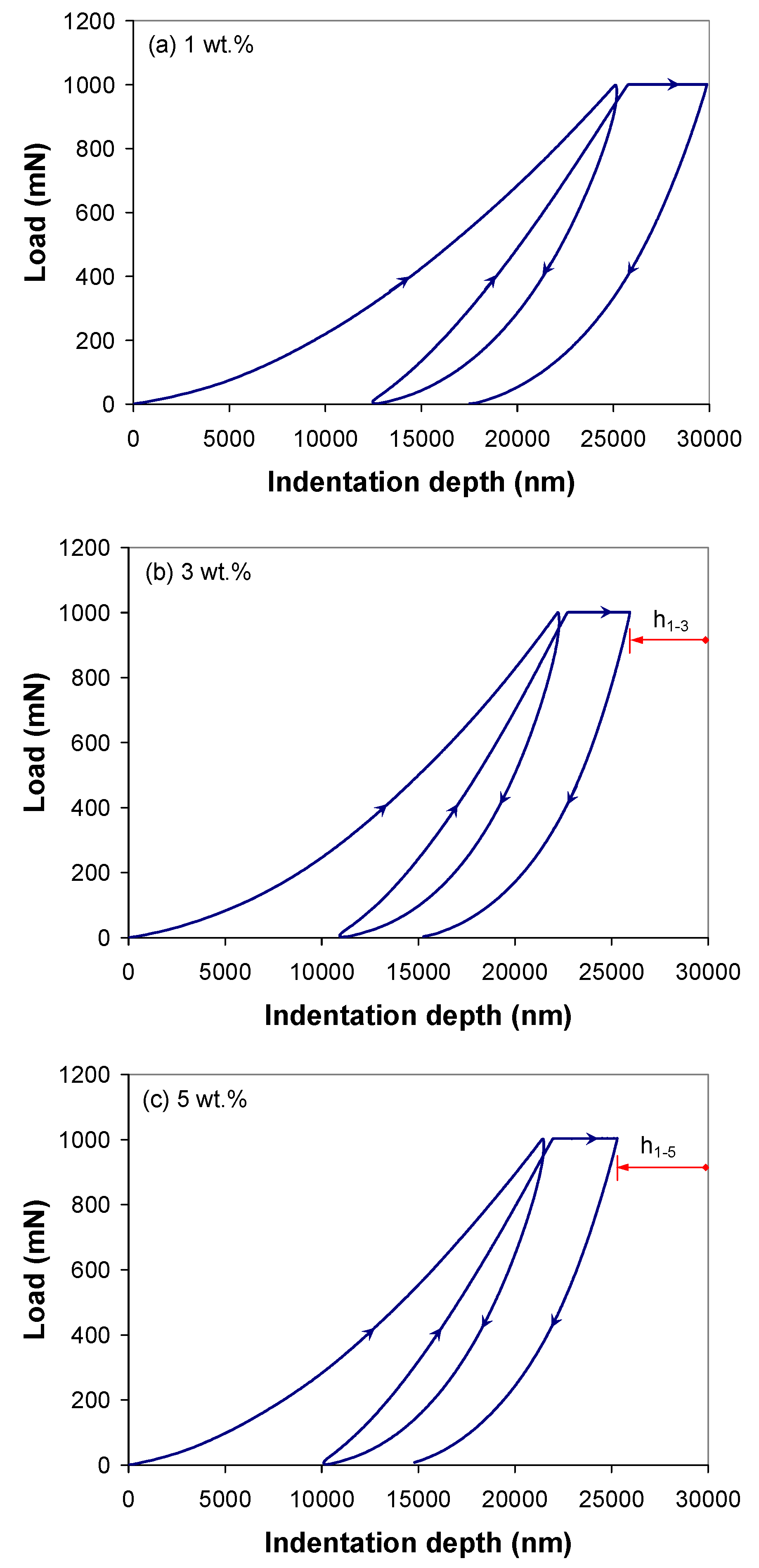
3.2. Load Displacement Curves
3.3. Indentation Modulus and Hardness
3.4. Creep of PP/MWCNT Nanocomposites
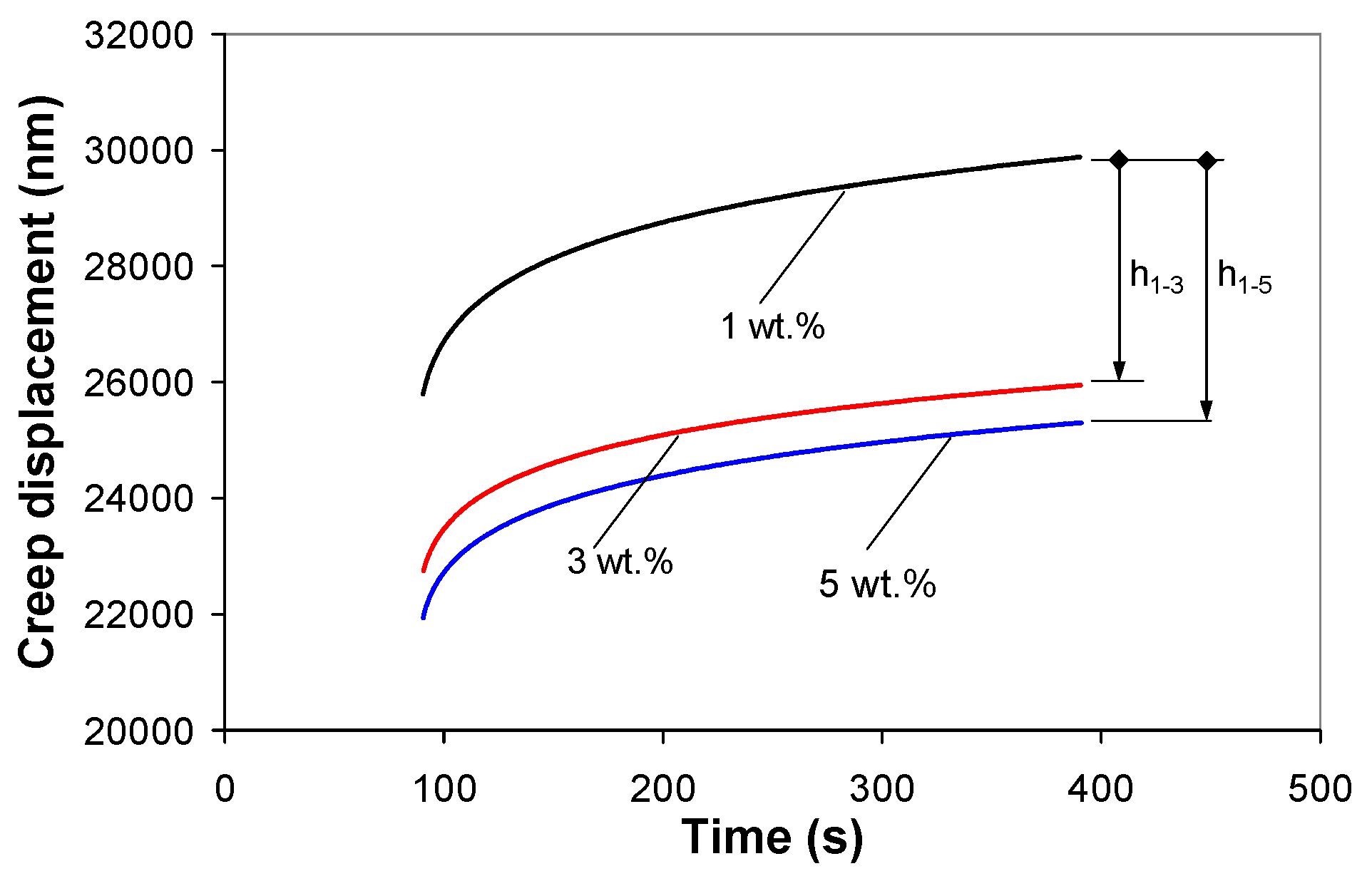
3.4.1. Indentation Creep Displacement
3.4.2. Creep Compliance Function
4. Conclusions
- At micro-scale level, the addition of nanotubes into the polypropylene has a positive effect on the mechanical properties of the PP/MWCNT nanocomposites. The indentation hardness and elastic modulus increased significantly with increasing MWCNT loading, without statistically significant differences among different regions.
- The creep resistance of the PP/MWCNT nanocomposites improved with the addition of MWCNTs, with creep displacement reduced by up to 20% with increasing MWCNT loading from 1 to 5 wt %. It is suggested that the creep deformation of the PP/MWCNT nanocomposites would proceed by deformation of the matrix and the role of the nanotubes would be to increase the creep resistance by restricting the polymer chain movement.
- The Maxwell–Voigt–Kelvin model accurately predicted the shear creep indentation behavior of PP/MWCNT nanocomposites and its change with increasing MWCNT loading, providing an indirect method to estimate the equivalent indentation modulus. However, the equivalent indentation modulus was found to be sensitive to the number of Voigt–Kelvin units: the more Voigt–Kelvin units used, the better the model predicts the equivalent indentation modulus.
Author Contributions
Funding
Conflicts of Interest
References
- McClory, C.; Chin, S.J.; McNally, T. Polymer/Carbon Nanotube Composites. Aust. J. Chem. 2009, 62, 762–785. [Google Scholar] [CrossRef]
- McNally, T.; Pötschke, P. Polymer-Carbon Nanotube Composites: Preparation, Properties and Applications, 1st ed.; Woodhead Publishing: Cambridge, UK, 2011; ISBN 9780857091390. [Google Scholar]
- Grady, B.P. Carbon Nanotube-Polymer Composites Manufacture, Properties, and Applications; John Wiley and Sons: New York, NY, USA, 2011. [Google Scholar]
- Choudhary, V.; Gupta, A. Polymer/Carbon Nanotube Nanocomposites, Carbon Nanotubes-Polymer Nanocomposites; Yellampalli, S., Ed.; IntechOpen: London, UK, 2011. [Google Scholar] [CrossRef]
- Coleman, J.N.; Khan, U.; Blau, W.J.; Gun’ko, Y.K. Small but strong: A review of the mechanical properties of carbon nanotube-polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Bauhofer, W.; Kovacs, J.Z. A review and analysis of electrical percolation in carbon nanotube polymer composites. Compos. Sci. Technol. 2009, 69, 1486–1498. [Google Scholar] [CrossRef]
- Byrne, M.T.; Gun’ko, Y.K. Recent Advances in Research on Carbon Nanotube-Polymer Composites. Adv. Mater. 2010, 22, 1672–1688. [Google Scholar] [CrossRef]
- Spitalsky, Z.; Tasis, D.; Papagelis, K.; Galiotis, C. Carbon nanotube-polymer composites: Chemistry, processing, mechanical and electrical properties. Prog. Polym. Sci 2010, 35, 357–401. [Google Scholar] [CrossRef]
- Yaodong, L.; Satish, K. Polymer/Carbon Nanotube Nano Composite Fibers—A Review. ACS Appl. Mater. Interfaces 2014, 6, 6069–6087. [Google Scholar]
- Mittal, G.; Dhand, V.; Rhee, K.Y.; Park, S.-J.; Lee, W.R. A review on carbon nanotubes and graphene as fillers in reinforced polymer nanocomposites. J. Ind. Eng. Chem. 2015, 21, 11–25. [Google Scholar] [CrossRef]
- Bhattacharya, M. Polymer Nanocomposites—A Comparison between Carbon Nanotubes, Graphene, and Clay as Nanofillers. Materials 2016, 9, 262. [Google Scholar] [CrossRef] [PubMed]
- Sabu, T.; Rene, M.; Jiji, A. Rheology and Processing of Polymer Nanocomposites; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; ISBN 9781118969793. [Google Scholar]
- Chen, J.; Yan, L.; Song, W.; Xu, D. Interfacial characteristics of carbon nanotube-polymer composites: A review. Compos. Part A Appl. Sci. Manuf. 2018, 114, 149–169. [Google Scholar] [CrossRef]
- Cadek, M.; Coleman, J.N.; Barron, V. Morphological and mechanical properties of carbon nanotube-reinforced semicrystalline and amorphous polymer composites. Appl. Phys. Lett. 2002, 81, 27. [Google Scholar] [CrossRef]
- Li, X.; Gao, H.; Scrivens, W.A.; Fei, D.; Xu, X.; Sutton, M.A.; Reynolds, A.P.; Myrick, M.L. Nanomechanical characterization of single-walled carbon nanotube reinforced epoxy composites. Nanotechnology 2004, 15, 1416–1423. [Google Scholar] [CrossRef]
- Lu, H.; Gang, H.; Wang, B.; Mamedov, A.; Gupta, S. Characterization of the linear visco-elastic behavior of single-wall nanotube/polyelectrolyte multilayer nanocomposite film using nanoindentation. Thin Solid Films 2006, 500, 197–202. [Google Scholar] [CrossRef]
- Nagy, P.M.; Aranyi, D.; Horváth, P.; Pötschke, P.; Pegel, S.; Kálmán, E. Nanoindentation Investigation of Carbon Nanotube–Polymer Composites. Internet Electron J. Mol. Des. 2006, 5, 135–143. [Google Scholar]
- Lee, H.; Mall, S.; He, P.; Shi, D.; Narasimhadevara, S.; Yeo-Heung, Y.; Shanov, V.; Schulz, M.J. Characterization of carbon nanotube/nanofiber-reinforced polymer composites using an instrumented indentation technique. Compos. Part B Eng. 2007, 38, 58–65. [Google Scholar] [CrossRef]
- Tehrani, M.; Safdari, M.; Al-Haik, M.S. Nanocharacterization of creep behavior of multiwall carbon nanotubes/epoxy nanocomposite. Int. J. Plast. 2011, 27, 887–901. [Google Scholar] [CrossRef]
- Gibson, R.F. A review of recent research on nanoindentation of polymer composites and their constituents. Compos. Sci. Technol. 2014, 105, 51–65. [Google Scholar] [CrossRef]
- Prashant, J.; Meenakshi, G.; Navin, K. Mechanical characterization of multiwalled carbon nanotubes-polycarbonate composites. Mater. Des. 2014, 54, 864–868. [Google Scholar]
- Cantaragiu, A.M.; Stan, F.; Fetecau, C.; Sandu, L.I. Effect of the Injection Moulding Parameters on the Creep Properties in Polypropylene/Carbon Nanotubes Composites. Appl. Mech. Mater. 2015, 809–810, 253–258. [Google Scholar] [CrossRef]
- Diez-Pascual, A.M.; Gómez-Fatou, M.A.; Ania, F.; Flores, A. Nanoindentation in polymer nanocomposites. Prog. Mater. Sci. 2015, 67, 1–94. [Google Scholar] [CrossRef]
- Koumoulos, E.P.; Jagdale, P.; Koklioti, M.A.; Kartsonakis, I.A.; Giorcelli, M.; Tagliaferro, A.; Charitidis, C.A. Carbon nanotube/polymer nanocomposites: A study on mechanical integrity through nanoindentation. Polym. Compos. 2015, 36, 1432–1446. [Google Scholar] [CrossRef]
- Gayle, A.J.; Cook, R.F. Mapping Viscoelastic and Plastic Properties of Polymers and Polymer-Nanotube Composites using Instrumented Indentation. J. Mater. Res. 2016, 31, 2347–2360. [Google Scholar] [CrossRef] [PubMed]
- El Moumen, A.; Tarfaoui, M.; Lafdi, K. Mechanical characterization of carbon nanotubes based polymer composites using indentation tests. Compos. B 2017, 114, 1–7. [Google Scholar] [CrossRef]
- Ekici, R. Effects of random particle dispersion and size on the indentation behavior of SiC particle reinforced metal matrix composites. Mater. Des. 2010, 31, 2818–2833. [Google Scholar] [CrossRef]
- Lorenzo, V.; Orden, M.U.; Muñoz, C.; Serrano, C.; Martínez Urreaga, J. Mechanical characterisation of virgin and recovered polycarbonate based nanocomposites by means of Depth Sensing Indentation measurements. Eur. Polym. J. 2014, 55, 1–8. [Google Scholar] [CrossRef]
- Nardi, T.; Hammerquist, C.; Nairn, J.A.; Karimi, A.; Månson, J.-A.E.; Leterrier, Y. Nanoindentation of functionally graded polymer nanocomposites: Assessment of the strengthening parameters through experiments and modeling. Front. Mater. 2015, 2, 57. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Samadi-Dooki, A.; Malekmotiei, L. Nanoindentation of high performance semicrystalline polymers: A case study on PEEK. Polym. Test. 2017, 61, 57–64. [Google Scholar] [CrossRef]
- Karimzadeh, A.; Koloor, S.S.R.; Ayatollahi, M.R.; Bushroa, A.R.; Yahya, M.Y. Assessment of Nano-Indentation Method in Mechanical Characterization of Heterogeneous Nanocomposite Materials Using Experimental and Computational Approaches. Sci. Rep. 2019, 9, 15763. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Briscoe, B.J.; Fiori, L.; Pelillo, E. Nano-indentation of polymeric surfaces. J. Phys. D Appl. Phys. 1998, 31, 2395–2405. [Google Scholar] [CrossRef]
- Chudoba, T.; Richter, F. Investigation of creep behaviour under load during indentation experiments and its influence on hardness and modulus results. Surf. Coat. Technol. 2001, 148, 191–198. [Google Scholar] [CrossRef]
- Oyen, M.L.; Cook, R.F. Load-displacement behavior during sharp indentation of viscous-elastic-plastic materials. J. Mater. Res. 2003, 18, 139–150. [Google Scholar] [CrossRef]
- Tang, B.; Ngan, A.H.W. Accurate measurement of tip–sample contact size during nanoindentation of viscoelastic materials. J. Mater. Res. 2003, 18, 1141–1148. [Google Scholar] [CrossRef]
- Cheng, Y.T.; Cheng, C. Relationships between initial unloading slope, contact depth, and mechanical properties for spherical indentation in linear viscoelastic solids. Mater. Sci. Eng. A 2005, 409, 93–99. [Google Scholar] [CrossRef]
- Cheng, Y.T.; Ni, W.; Cheng, C.-M. Determining the instantaneous modulus of viscoelastic solids using instrumented indentation measurements. J. Mater. Res. 2005, 20, 3061–3071. [Google Scholar] [CrossRef]
- Oyen, M.L. Analytical techniques for indentation of viscoelastic materials. Philos. Mag. 2006, 86, 5625–5641. [Google Scholar] [CrossRef]
- Vandamme, M.; Ulm, F.-J. Viscoelastic solutions for conical indentation. Int. J. Solids Struct. 2006, 43, 3142–3165. [Google Scholar] [CrossRef]
- Alisafaei, F.; Han, C.-S.; Lakhera, N. Characterization of indentation size effects in epoxy. Polym. Test. 2014, 40, 70–78. [Google Scholar] [CrossRef]
- Herbert, E.G.; Sudharshan Phani, P.; Kurt, E.J. Nanoindentation of viscoelastic solids: A critical assessment of experimental methods. Curr. Opin. Solid State Mater. Sci. 2015, 19, 334–339. [Google Scholar] [CrossRef]
- Mencik, J.; He, L.H.; Swain, M.V. Determination of viscoelastic–plastic material parameters of biomaterials by instrumented indentation. J. Mech. Behav. Biomed. Mater. 2009, 2, 318–325. [Google Scholar] [CrossRef]
- Mencík, J.; He, L.H.; Nemecek, J. Characterization of viscoelasticplastic properties of solid polymers by instrumented indentation. Polym. Test. 2011, 30, 101–109. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Zhang, Y.W.; Zeng, K.Y.; Shen, L. Nanoindentation of Polymers with a Sharp Indenter. J. Mater. Res. 2005, 20, 1597–1605. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Zhang, Y.W.; Zeng, K.Y.; Shen, L. Characterization of mechanical properties of polymers by nanoindentation tests. Philos. Mag. 2006, 86, 4487–4506. [Google Scholar] [CrossRef]
- Vandamme, M.; Tweedie, C.A.; Constantinides, G.; Ulm, F.-J.; Van Vliet, K.J. Quantifying plasticity-independent creep compliance and relaxation of viscelastoplastic materials under contact load. J. Mater. Res. 2012, 27, 302–312. [Google Scholar] [CrossRef]
- Braunsmann, C.; Proksch, R.; Revenko, I.; Schäffer, T.E. Creep compliance mapping by atomic force microscopy. Polymer 2014, 55, 219–225. [Google Scholar] [CrossRef]
- Stan, F.; Fetecau, C. Characterization of viscoelastic properties of molybdenum disulphide filled polyamide by indentation. Mech. Time-Depend. Mater. 2013, 17, 205–221. [Google Scholar] [CrossRef]
- Kato, K.; Kishibe, S.; Sakaue, K.; Yoshimoto, T. Multicycle Indentation for Evaluation of Polymer Material Viscoelastic Characteristics. Exp. Mech. 2018, 58, 759–766. [Google Scholar] [CrossRef]
- Peng, G.; Zhang, T.; Feng, Y.; Huan, Y. Determination of shear creep compliance of linear visco-elastic-plastic solids by instrumented indentation. Polym. Test. 2012, 31, 1038–1044. [Google Scholar] [CrossRef]
- Peng, G.; Zhang, T.; Feng, Y.; Huan, Y.; Zang, T. Characterization of the viscoelastic-plastic properties of UPVC by instrumented sharp indentation. Polym. Test. 2013, 32, 1358–1367. [Google Scholar] [CrossRef]
- Peng, G. Nanoindentation creep of nonlinear viscoelastic polypropylene. Polym. Test. 2015, 43, 38–43. [Google Scholar] [CrossRef]
- Nanocyl Technical Data Sheet: PLASTICYL™ PP2001. Available online: http://www.nanocyl.com/. (accessed on 12 September 2012).
- Stan, F.; Sandu, I.L.; Fetecau, C. Effect of processing parameters and strain rate on mechanical properties of carbon nanotube-filled polypropylene nanocomposites. Compos. B. Eng. 2014, 59, 109–122. [Google Scholar] [CrossRef]
- Xu, H.; Zhong, G.; Fu, Q.; Lei, J.; Jiang, W.; Hsiao, B. Formation of shish-kebabs in injection-molded poly (l-lactic acid) by application of an intense flow field. ACS Appl. Mater. Interfaces 2012, 4, 6774–6784. [Google Scholar] [CrossRef]
- Wang, X.; Pan, Y.; Qin, Y.; Voigt, M.; Liu, X.; Zheng, G.; Chen, Q.; Schubert, D.W.; Liu, C.; Shen, C. Creep and recovery behavior of injection-molded isotactic polypropylene with controllable skin-core structure. Polym. Test. 2018, 69, 478–484. [Google Scholar] [CrossRef]
- Tang, L.; Wang, X.; Gong, L.; Peng, K.; Zhao, L.; Chen, Q. Creep and recovery of polystyrene composites filled with graphene additives. Compos. Sci. Technol. 2014, 91, 63–70. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Yuan, H.; Liu, H.; Liu, C.; Li, C.T.; Yan, C.; Yan, X.; Shen, C.; Guo, Z. Non-covalently functionalized graphene strengthened poly (vinyl alcohol). Mater. Des. 2018, 139, 372–379. [Google Scholar] [CrossRef]
- Lu, Z.; Pan, Y.; Liu, X.; Zheng, G.; Schubert, D.; Liu, C. Molar mass and temperature dependence of rheological properties of polymethylmethacrylate melt. Mater. Lett. 2018, 221, 62–65. [Google Scholar] [CrossRef]
- Pan, Y.; Liu, X.; Kaschta, J.; Hao, X.; Liu, C.; Schubert, D. Viscoelastic and electrical behavior of poly (methyl methacrylate)/carbon black composites prior to and after annealing. Polymer 2017, 113, 34–38. [Google Scholar] [CrossRef]
- Qu, M.; Nilsson, F.; Qin, Y.; Yang, G.; Pan, Y.; Liu, X.; Rodriguez, G.; Chen, J.; Zhang, C.; Schubert, D. Electrical conductivity and mechanical properties of melt-spun ternary composites comprising PMMA, carbon fibers and carbon black. Compos. Sci. Technol. 2017, 15, 24–31. [Google Scholar] [CrossRef]
- Lee, E.H.; Radok, J.R.M. The contact problem for viscoelastic. J. Appl. Mech. 1960, 27, 438–444. [Google Scholar] [CrossRef]
- Graham, G.A.C. The contact problem in the linear theory of viscoelasticity. Int. J. Eng. Sci. 1965, 3, 27–46. [Google Scholar] [CrossRef]
- Ting, T.C.T. The contact stresses between a rigid indenter and a viscoelastic half-space. J. Appl. Mech. 1966, 33, 845–854. [Google Scholar] [CrossRef]
- Christensen, R.M. Theory of Viscoelastitcity, 2nd ed.; Dover: Mineola, NY, USA, 2003. [Google Scholar]
- Lu, H.; Wang, B.; Ma, J.; Huang, G.; Viswanathan, H. Measurement of creep compliance of solid polymers by nanoindentation. Mech. Time-Depend. Mat. 2003, 7, 189–207. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, L.; Zhang, P.; Yan, X.; Zhang, K.; Do, S.; Zhao, J.; Li, Y. Measurement of viscoelastic properties for polymers by nanoindentation. Polym. Test. 2020, 83, 106353. [Google Scholar] [CrossRef]
- Lee, S.; Knauss, W.G. A note on the determination of relaxation and creep data from ramp tests. Mech. Time-Depend. Mater. 2000, 4, 1–7. [Google Scholar] [CrossRef]
- Gavin, H.P. The Levenberg-Marquardt Method for Nonlinear Least Squares Curve-Fitting Problems. 2007. Available online: http://people.duke.edu/~hpgavin/ce281/lm.pdf. (accessed on 15 November 2019).







| MWCNTs (wt %) | HIT (MPa) | EIT (GPa) |
|---|---|---|
| 1 | 85.33 (± 3.58) | 1.71 (± 0.05) |
| 3 | 99.52 (± 8.22) | 1.99 (± 0.09) |
| 5 | 122.09 (± 5.28) | 2.21 (± 0.05) |
| Number of VK Units | 1 wt % | 3 wt % | 5 wt % | ||||
|---|---|---|---|---|---|---|---|
| i | Ji (MPa) | τi (s) | Ji (MPa) | τi (s) | Ji (MPa) | τi (s) | |
| 3 | 0 | 1.757 | - | 1.439 | - | 1.234 | - |
| 1 | 0.505 | 5.70 | 0.360 | 6.77 | 0.405 | 4.92 | |
| 2 | 0.685 | 30.89 | 0.251 | 36.18 | 0.266 | 28.30 | |
| 3 | 0.374 | 235.54 | 0.450 | 252.97 | 0.474 | 223.29 | |
| SSq | 1.61 × 10−1 | 1.07 × 10−1 | 1.39 × 10−1 | ||||
| RMSE | 0.004 | 0.003 | 0.003 | ||||
| MPE (%) | 1.03 × 10−2 | 9.2 × 10−3 | 1.12 × 10−2 | ||||
| 5 | 0 | 1.198 | - | 1.003 | - | 0.878 | - |
| 1 | 0.950 | 2.09 | 0.589 | 1.28 | 0.584 | 1.42 | |
| 2 | 0.444 | 22.69 | 0.273 | 11.96 | 0.275 | 10.89 | |
| 3 | 0.693 | 201.20 | 0.219 | 48.68 | 0.210 | 43.26 | |
| 4 | 1.04 × 10−4 | 200.05 | 6.53 × 10−7 | 199.63 | 0.111 | 194.59 | |
| 5 | 6.28 × 10−5 | 300.04 | 0.443 | 301.26 | 0.366 | 321.70 | |
| SSq | 6.58 × 10−1 | 1.31 × 10−1 | 1.07 × 10−1 | ||||
| RMSE | 0.007 | 0.003 | 0.003 | ||||
| MPE (%) | 2.02 × 10−2 | 9.96 × 10−3 | 9.24 × 10−3 | ||||
| Number of VK Units | Modulus (GPa) | MWCNTs | ||
|---|---|---|---|---|
| 1 wt % | 3 wt % | 5 wt % | ||
| 3 | G0 | 0.285 | 0.348 | 0.405 |
| G∞ | 0.602 | 0.800 | 0.841 | |
| 5 | G0 | 0.417 | 0.499 | 0.570 |
| G∞ | 0.609 | 0.792 | 0.825 | |
| MWCNTs wt % | Methodology | |||
|---|---|---|---|---|
| S + nVK Model | Oliver and Pharr [32] | |||
| 4G0 (GPa) | EIT (GPa) | M (GPa) | ||
| S + 3VK | S + 5VK | |||
| 1 | 1.14 | 1.67 | 1.71 (±0.05) | 1.91 |
| 3 | 1.39 | 1.99 | 1.99 (±0.09) | 2.19 |
| 5 | 1.62 | 2.28 | 2.21 (±0.05) | 2.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stan, F.; Turcanu, A.-M.; Fetecau, C. Analysis of Viscoelastic Behavior of Polypropylene/Carbon Nanotube Nanocomposites by Instrumented Indentation. Polymers 2020, 12, 2535. https://doi.org/10.3390/polym12112535
Stan F, Turcanu A-M, Fetecau C. Analysis of Viscoelastic Behavior of Polypropylene/Carbon Nanotube Nanocomposites by Instrumented Indentation. Polymers. 2020; 12(11):2535. https://doi.org/10.3390/polym12112535
Chicago/Turabian StyleStan, Felicia, Adriana-Madalina Turcanu (Constantinescu), and Catalin Fetecau. 2020. "Analysis of Viscoelastic Behavior of Polypropylene/Carbon Nanotube Nanocomposites by Instrumented Indentation" Polymers 12, no. 11: 2535. https://doi.org/10.3390/polym12112535
APA StyleStan, F., Turcanu, A.-M., & Fetecau, C. (2020). Analysis of Viscoelastic Behavior of Polypropylene/Carbon Nanotube Nanocomposites by Instrumented Indentation. Polymers, 12(11), 2535. https://doi.org/10.3390/polym12112535





