Self-Healing in Mobility-Restricted Conditions Maintaining Mechanical Robustness: Furan–Maleimide Diels–Alder Cycloadditions in Polymer Networks for Ambient Applications
Abstract
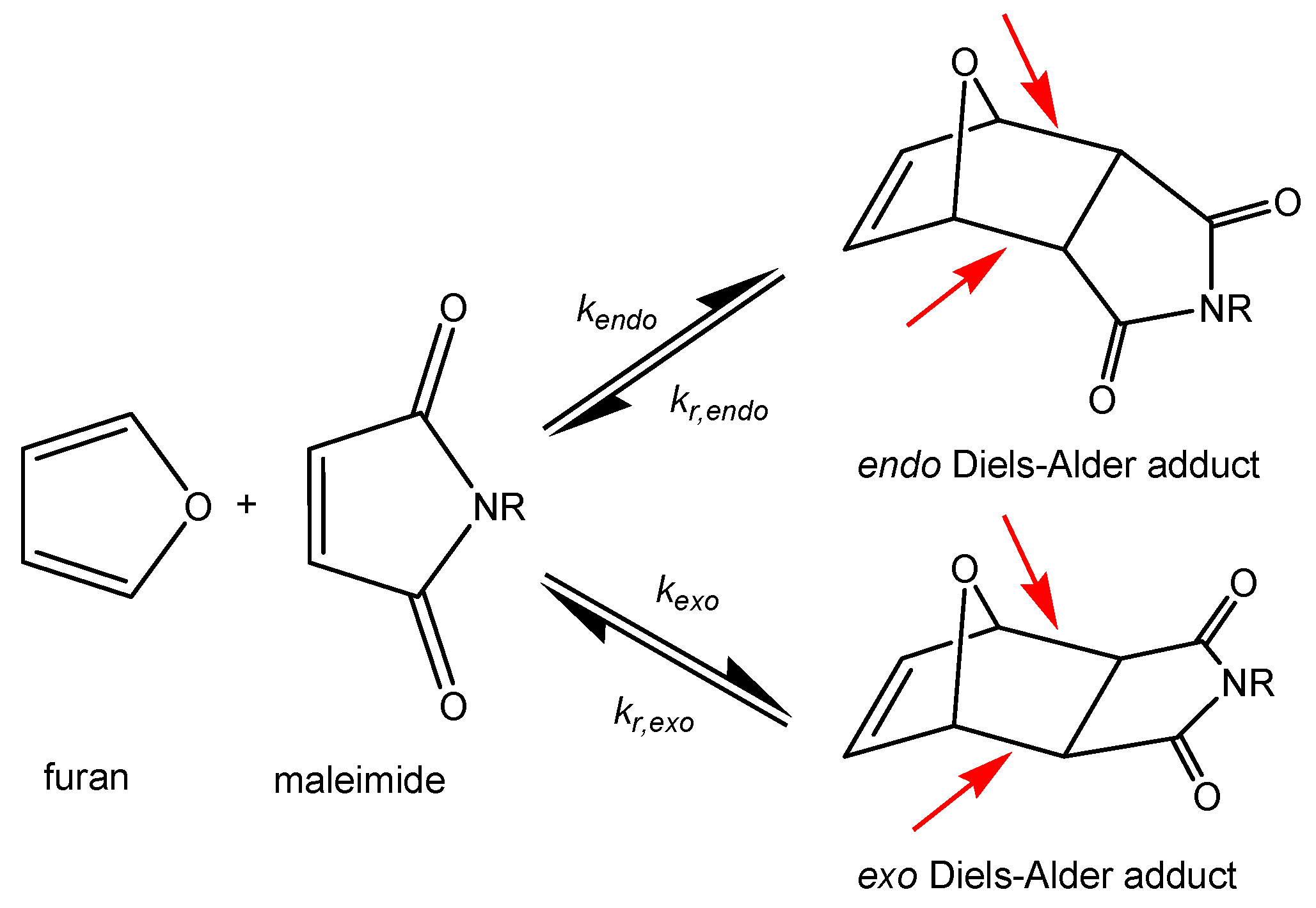
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Synthesis
2.3. Methods
3. Results and Discussion
3.1. Vitrification and Gelation during Cure of Reversible Network 3M-3F630 in Ambient Conditions
3.1.1. Vitrification Study Based on Modulated Temperature Differential Scanning Calorimetry
3.1.2. Dynamic Rheometry as Proof of Gelation and Vitrification
3.2. Proof of Progress of Cure in Diffusion-Controlled Conditions at 20 °C in Reversible Network 3M-3F630
3.2.1. Tg–x Relationship
3.2.2. Cure in Diffusion-Controlled Conditions at 20 °C
3.3. De-Gelation
3.4. Proof of Self-Healing of the Reversible Network 3M-F375PMA at Ambient Temperature
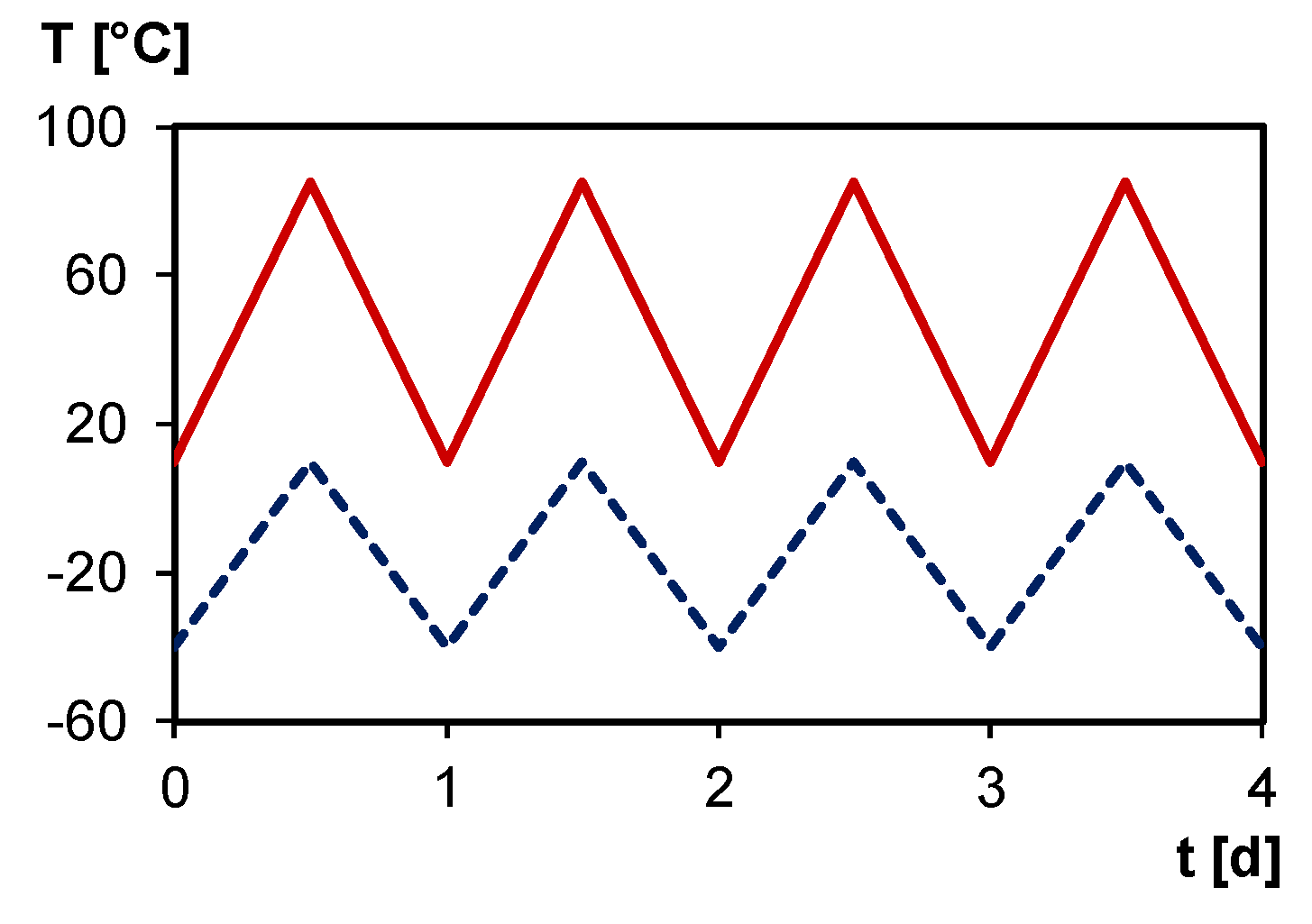
3.4.1. Reversibility of the Poly(methacrylate) Network 3M-F375PMA
3.4.2. Structural Integrity and Mechanical Robustness of the Reversible Poly(methacrylate) Network 3M-F375PMA
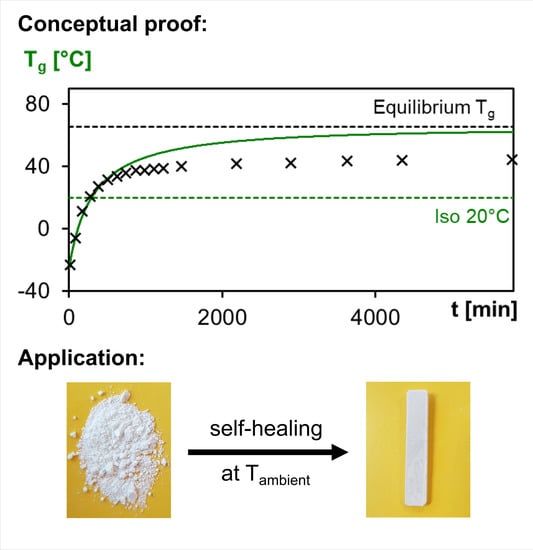
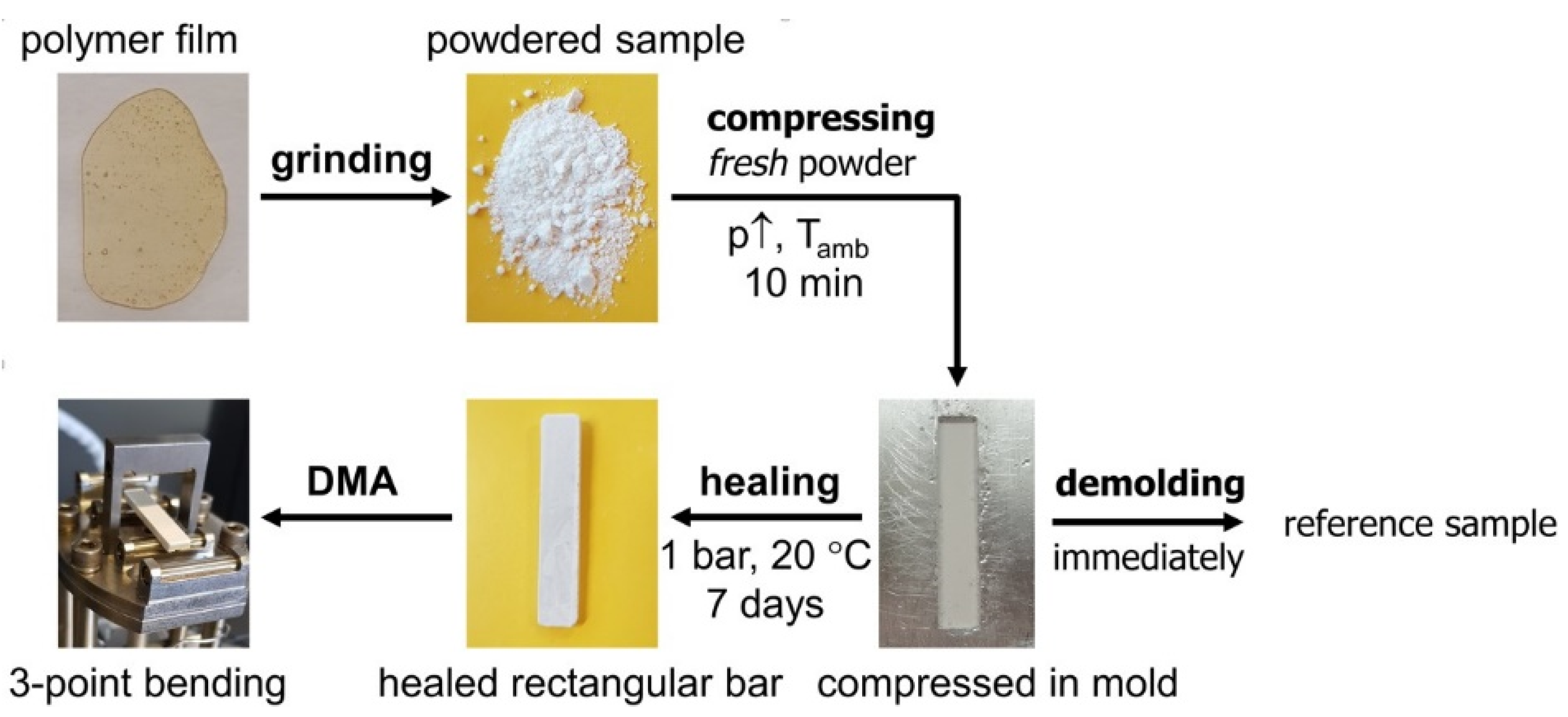
3.4.3. Self-Healing of 3M-F375PMA Powder Rectangular Bar Samples at Ambient Temperature
3.5. Ambient-Temperature Healing Application: Encapsulant in Photovoltaics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Van der Zwaag, S. An introduction to material design principles: Damage prevention versus damage management. In Self-Healing Materials: An Alternative Approach to 20 Centuries of Materials Science; Springer: Dordrecht, The Netherlands, 2007; pp. 1–18. ISBN 97 8-1-4020-6250-6. [Google Scholar]
- Ando, K.; Barbero, E.J.; Ford, K.J.; Joseph, C.; Kalista, S.J.; Ghosh, S.K.; Manuel, M.V.; Mayugo, J.A.; Nakao, W.; Rong, M.Z.; et al. Self-Healing Materials: Fundamentals, Design Strategies, and Applications, 1st ed.; Gosh, S.K., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2009; ISBN 978-3-527-31829-2. [Google Scholar]
- Wu, D.Y.; Meure, S.; Solomon, D. Self-Healing polymeric materials: A review of recent developments. Prog. Polym. Sci. 2008, 33, 479–522. [Google Scholar] [CrossRef]
- Hager, M.D.; Greil, P.; Leyens, C.; van der Zwaag, S.; Schubert, U.S. Self-Healing materials. Adv. Mater. 2010, 22, 5424–5430. [Google Scholar] [CrossRef] [PubMed]
- Billiet, S.; Hillewaere, X.K.D.; Teixeira, R.F.A.; Du Prez, F.E. Chemistry of crosslinking processes for self-healing polymers. Macromol. Rapid Commun. 2013, 34, 290–309. [Google Scholar] [CrossRef] [PubMed]
- Lyon, G.B.; Baranek, A.; Bowman, C.N. Scaffolded thermally remendable hybrid polymer networks. Adv. Funct. Mater. 2016, 26, 1477–1485. [Google Scholar] [CrossRef]
- Kötteritzsch, J.; Stumpf, S.; Hoeppener, S.; Vitz, J.; Hager, M.D.; Schubert, U.S. One-component intrinsic self-healing coatings based on reversible crosslinking by Diels-Alder cycloadditions. Macromol. Chem. Phys. 2013, 214, 1636–1649. [Google Scholar] [CrossRef]
- Biggs, P.; Jones, L.; Lewis, G. An autonomically-healed PMMA bone cement: Influence of the crystal size of Grubbs’ catalyst on fracture toughness and polymerisation rate. Int. J. Nano Biomater. 2009, 2, 494–504. [Google Scholar] [CrossRef]
- Xing, R.Y.; Zhang, Q.Y.; Sun, J.L. Preparation and properties of self-healing microcapsules containing an UV-curable oligomers of silicone. Polym. Polym. Compos. 2012, 20, 77–82. [Google Scholar] [CrossRef]
- Tippabhotla, S.K.; Song, W.J.R.; Tay, A.A.O.; Budiman, A.S. Effect of encapsulants on the thermomechanical residual stress in the back-contact silicon solar cells of photovoltaic modules–A constrained local curvature model. Sol. Energy 2019, 182, 134–147. [Google Scholar] [CrossRef]
- Dry, C. Procedures developed for self-repair of polymer matrix composite materials. Compos. Struct. 1996, 35, 263–269. [Google Scholar] [CrossRef]
- Cuvellier, A.; Torre-Muruzabal, A.; Van Assche, G.; De Clerck, K.; Rahier, H. Selection of healing agents for a vascular self-healing application. Polym. Test. 2017, 62, 302–310. [Google Scholar] [CrossRef] [Green Version]
- Toohey, K.S.; Sottos, N.R.; White, S.R. Characterization of microvascular-based self-healing coatings. Exp. Mech. 2009, 49, 707–717. [Google Scholar] [CrossRef]
- Hansen, C.J.; Wu, W.; Toohey, K.S.; Sottos, N.R.; White, S.R.; Lewis, J.A. Self-healing materials with interpenetrating microvascular networks. Adv. Mater. 2009, 21, 4143–4147. [Google Scholar] [CrossRef]
- Maeda, T.; Otsuka, H.; Takahara, A. Dynamic covalent polymers: Reorganizable polymers with dynamic covalent bonds. Prog. Polym. Sci. 2009, 34, 581–604. [Google Scholar] [CrossRef]
- Davis, D.A.; Hamilton, A.; Yang, J.; Cremar, L.D.; Van Gough, D.; Potisek, S.L.; Ong, M.T.; Braun, P.V.; Martínez, T.J.; White, S.R.; et al. Force-induced activation of covalent bonds in mechanoresponsive polymeric materials. Nature 2009, 459, 68–72. [Google Scholar] [CrossRef]
- Capelot, M.; Montarnal, D.; Tournilhac, F.; Leibler, L. Metal-catalyzed transesterification for healing and assembling of thermosets. J. Am. Chem. Soc. 2012, 134, 7664–7667. [Google Scholar] [CrossRef]
- Kloxin, C.J.; Bowman, C.N. Covalent adaptable networks: Smart, reconfigurable and responsive network systems. Chem. Soc. Rev. 2013, 42, 7161–7173. [Google Scholar] [CrossRef] [Green Version]
- Kuhl, N.; Bode, S.; Hager, M.D.; Schubert, U.S. Self-Healing polymers based on reversible covalent bonds. Adv. Polym. Sci. 2015, 273, 1–58. [Google Scholar] [CrossRef]
- Van Damme, J.; Vlaminck, L.; Van Assche, G.; Van Mele, B.; van den Berg, O.; Du Prez, F. Synthesis and evaluation of 9-substituted anthracenes with potential in reversible polymer systems. Tetrahedron 2016, 72, 4303–4311. [Google Scholar] [CrossRef]
- Van Damme, J.; Van Den Berg, O.; Brancart, J.; Vlaminck, L.; Huyck, C.; Van Assche, G.; Van Mele, B.; Du Prez, F. Anthracene-Based thiol-ene networks with thermo-degradable and photo-reversible properties. Macromolecules 2017, 50, 1930–1938. [Google Scholar] [CrossRef]
- McBride, M.K.; Worrell, B.T.; Brown, T.; Cox, L.M.; Sowan, N.; Wang, C.; Podgorski, M.; Martinez, A.M.; Bowman, C.N. Enabling applications of covalent adaptable networks. Annu. Rev. Chem. Biomol. Eng. 2019, 10, 175–198. [Google Scholar] [CrossRef]
- Winne, J.M.; Leibler, L.; Du Prez, F.E. Dynamic covalent chemistry in polymer networks: A mechanistic perspective. Polym. Chem. 2019, 10, 6091–6108. [Google Scholar] [CrossRef]
- Alabiso, W.; Schlögl, S. The impact of vitrimers on the industry of the future: Chemistry, properties and sustainable forward-looking applications. Polymers 2020, 12, 1660. [Google Scholar] [CrossRef]
- Brunsveld, L.; Folmer, B.J.B.; Meijer, E.W.; Sijbesma, R.P. Supramolecular polymers. Chem. Rev. 2001, 101, 4071–4097. [Google Scholar] [CrossRef]
- Lehn, J.M. Supramolecular polymer chemistry-Scope and perspective. Polym. Int. 2002, 51, 825–839. [Google Scholar] [CrossRef]
- Bosman, A.W.; Sijbesma, R.P.; Meijer, E.W. Supramolecular polymers at work. Mater. Today 2004, 7, 34–39. [Google Scholar] [CrossRef]
- Burnworth, M.; Tang, L.; Kumpfer, J.R.; Duncan, A.J.; Beyer, F.L.; Fiore, G.L.; Rowan, S.J.; Weder, C. Optically healable supramolecular polymers. Nature 2011, 472, 334–337. [Google Scholar] [CrossRef] [Green Version]
- Herbst, F.; Döhler, D.; Michael, P.; Binder, W.H. Self-healing polymers via supramolecular forces. Macromol. Rapid Commun. 2013, 34, 203–220. [Google Scholar] [CrossRef]
- Adzima, B.J.; Aguirre, H.A.; Kloxin, C.J.; Scott, T.F.; Bowman, C.N. Rheological and chemical analysis of reverse gelation in a covalently cross-linked diels-alder polymer network. Macromolecules 2008, 41, 9112–9117. [Google Scholar] [CrossRef] [Green Version]
- Scheltjens, G.; Brancart, J.; De Graeve, I.; Van Mele, B.; Terryn, H.; Van Assche, G. Self-healing property characterization of reversible thermoset coatings. J. Therm. Anal. Calorim. 2011, 105, 805–809. [Google Scholar] [CrossRef]
- Scheltjens, G.; Diaz, M.M.; Brancart, J.; Van Assche, G.; Van Mele, B. A self-healing polymer network based on reversible covalent bonding. React. Funct. Polym. 2013, 73, 413–420. [Google Scholar] [CrossRef]
- Mineo, P.; Barbera, V.; Romeo, G.; Ghezzo, F.; Scamporrino, E.; Spitaleri, F.; Chiacchio, U. Thermally reversible highly cross-linked polymeric materials based on furan/maleimide Diels-Alder adducts. J. Appl. Polym. Sci. 2015, 132, 1–9. [Google Scholar] [CrossRef]
- Diaz, M.M.; Van Assche, G.; Maurer, F.H.J.; Van Mele, B. Thermophysical characterization of a reversible dynamic polymer network based on kinetics and equilibrium of an amorphous furan-maleimide Diels-Alder cycloaddition. Polymer 2017, 120, 176–188. [Google Scholar] [CrossRef]
- Terryn, S.; Brancart, J.; Lefeber, D.; Van Assche, G.; Vanderborght, B. Self-healing soft pneumatic robots. Sci. Robot. 2017, 2, 1–13. [Google Scholar] [CrossRef]
- Diaz, M.M.; Brancart, J.; Van Assche, G.; Van Mele, B. Room-temperature versus heating-mediated healing of a Diels-Alder crosslinked polymer network. Polymer 2018, 153, 453–463. [Google Scholar] [CrossRef]
- Cuvellier, A.; Verhelle, R.; Brancart, J.; Vanderborght, B.; Van Assche, G.; Rahier, H. The influence of stereochemistry on the reactivity of the Diels-Alder cycloaddition and the implications for reversible network polymerization. Polym. Chem. 2019, 10, 473–485. [Google Scholar] [CrossRef]
- Mangialetto, J.; Cuvellier, A.; Verhelle, R.; Brancart, J.; Van Assche, G.; Van den Brande, N.; Van Mele, B. Diffusion-and mobility-controlled self-healing polymer networks with dynamic covalent bonding. Macromolecules 2019, 52, 8440–8452. [Google Scholar] [CrossRef]
- Ehrhardt, D.; Van Durme, K.; Jansen, J.F.G.A.; Van Mele, B.; Van den Brande, N. Self-healing UV-curable polymer network with reversible Diels-Alder bonds for applications in ambient conditions. Polymer 2020, 203, 122762. [Google Scholar] [CrossRef]
- Mangialetto, J.; Verhelle, R.; Van Assche, G.; Van Mele, B.; Van den Brande, N. Time-Temperature-Transformation, Temperature-conversion-Transformation, and Continuous-Heating-Transformation diagram of reversible polymer networks. Macromolecules 2020. in publication. [Google Scholar]
- Fringuelli, F.; Taticchi, A. Diels-Alder reaction: General remarks. In The Diels-Alder Reaction: Selected Practical Methods; John Wiley & Sons, Ltd.: Chichester, UK, 2002; pp. 3–28. ISBN 0-471-80343-X. [Google Scholar]
- Chen, X.; Dam, M.A.; Ono, K.; Mal, A.; Shen, H.; Nutt, S.R.; Sheran, K.; Wudl, F. A Thermally remendable cross-linked polymeric material. Science 2002, 295, 1698–1702. [Google Scholar] [CrossRef]
- Jung, S.; Liu, J.T.; Hong, S.H.; Arunbabu, D.; Noh, S.M.; Oh, J.K. A new reactive polymethacrylate bearing pendant furfuryl groups: Synthesis, thermoreversible reactions, and self-healing. Polymer 2017, 109, 58–65. [Google Scholar] [CrossRef]
- Padhan, A.K.; Mandal, D. Thermo-reversible self-healing in a fluorous crosslinked copolymer. Polym. Chem. 2018, 9, 3248–3261. [Google Scholar] [CrossRef]
- Fortunato, G.; Tatsi, E.; Rigatelli, B.; Turri, S.; Griffini, G. Highly transparent and colorless self-healing polyacrylate coatings based on Diels–Alder chemistry. Macromol. Mater. Eng. 2020, 305, 1900652. [Google Scholar] [CrossRef]
- Diaz Acevedo, M.M. Physical Chemical and Thermomechanical Characterization of Reversible and Partially Reversible Dynamic Polymer Networks for Self-Healing Applications. Ph.D. Thesis, Vrije Universiteit Brussel, Brussels, Belgium, 2016. ISBN 978-9-4619735-6-6. [Google Scholar]
- Van Assche, G.; Van Hemelrijck, A.; Rahier, H.; Van Mele, B. Modulated differential scanning calorimetry: Isothermal cure and vitrification of thermosetting systems. Thermochim. Acta 1995, 268, 121–142. [Google Scholar] [CrossRef]
- Van Assche, G.; Van Hemelrijck, A.; Rahier, H.; Van Mele, B. Modulated differential scanning calorimetry: Non-isothermal cure, vitrification, and devitrification of thermosetting systems. Thermochim. Acta 1996, 286, 209–224. [Google Scholar] [CrossRef]
- Van Assche, G.; Van Hemelrijck, A.; Rahier, H.; Van Mele, B. Modulated temperature differential scanning calorimetry: Cure, vitrification, and devitrification of thermosetting systems. Thermochim. Acta 1997, 304–305, 317–334. [Google Scholar] [CrossRef]
- Winter, H.H. Can the gel point of a cross-linking polymer be detected by the G’-G’’ crossover? Polym. Eng. Sci. 1987, 27, 1698–1702. [Google Scholar] [CrossRef]
- Winter, H.H. Evolution of rheology during chemical gelation. Prog. Colloid Polym. Sci. 1987, 75, 104–110. [Google Scholar] [CrossRef]
- Winter, H.H. The solidification rheology of amorphous polymers−Vitrification as compared to gelation. Macromol. Symp. 2017, 374, 1600113. [Google Scholar] [CrossRef]
- Fang, H.; Ye, W.; Ding, Y.; Winter, H.H. Rheology of the critical transition state of an epoxy vitrimer. Macromolecules 2020, 53, 4855–4862. [Google Scholar] [CrossRef]
- DiBenedetto, A.T. Prediction of the glass transition temperature of polymers: A model based on the principle of corresponding states. J. Polym. Sci. Part B Polym. Phys. 1987, 25, 1949–1969. [Google Scholar] [CrossRef]
- Couchman, P.R. Thermodynamics and the compositional variation of glass. Macromolecules 1987, 20, 1712–1717. [Google Scholar] [CrossRef]
- Pascault, J.P.; Williams, R.J.J. Relationships between glass transition temperature and conversion-Analyses of limiting cases. Polym. Bull. 1990, 24, 115–121. [Google Scholar] [CrossRef]
- Grenier-Loustalot, M.F.; Gouarderes, F.; Joubert, F.; Grenier, P. Synthesis, mechanism and kinetics of radical polymerization of bismaleimide-type telechelic oligomers in solvent and in the solid state. Polymer 1993, 34, 3848–3859. [Google Scholar] [CrossRef]
- Sharma, B.K.; Desai, U.; Singh, A.; Singh, A. Effect of vinyl acetate content on the photovoltaic-encapsulation performance of ethylene vinyl acetate under accelerated ultra-violet aging. J. Appl. Polym. Sci. 2020, 137, 48268. [Google Scholar] [CrossRef]
- Eitner, U.; Kajari-Schröder, S.; Köntges, M.; Altenbach, H. Thermal stress and strain of solar cells in photovoltaic modules. In Shell-Like Structures; Springer: Berlin, Germany, 2011; pp. 453–468. ISBN 9783642218545. [Google Scholar]














Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ehrhardt, D.; Mangialetto, J.; Bertouille, J.; Van Durme, K.; Van Mele, B.; Van den Brande, N. Self-Healing in Mobility-Restricted Conditions Maintaining Mechanical Robustness: Furan–Maleimide Diels–Alder Cycloadditions in Polymer Networks for Ambient Applications. Polymers 2020, 12, 2543. https://doi.org/10.3390/polym12112543
Ehrhardt D, Mangialetto J, Bertouille J, Van Durme K, Van Mele B, Van den Brande N. Self-Healing in Mobility-Restricted Conditions Maintaining Mechanical Robustness: Furan–Maleimide Diels–Alder Cycloadditions in Polymer Networks for Ambient Applications. Polymers. 2020; 12(11):2543. https://doi.org/10.3390/polym12112543
Chicago/Turabian StyleEhrhardt, Dorothee, Jessica Mangialetto, Jolien Bertouille, Kurt Van Durme, Bruno Van Mele, and Niko Van den Brande. 2020. "Self-Healing in Mobility-Restricted Conditions Maintaining Mechanical Robustness: Furan–Maleimide Diels–Alder Cycloadditions in Polymer Networks for Ambient Applications" Polymers 12, no. 11: 2543. https://doi.org/10.3390/polym12112543
APA StyleEhrhardt, D., Mangialetto, J., Bertouille, J., Van Durme, K., Van Mele, B., & Van den Brande, N. (2020). Self-Healing in Mobility-Restricted Conditions Maintaining Mechanical Robustness: Furan–Maleimide Diels–Alder Cycloadditions in Polymer Networks for Ambient Applications. Polymers, 12(11), 2543. https://doi.org/10.3390/polym12112543