Compressive Behaviour of Lattice Structures Manufactured by Polyjet Technologies
Abstract
1. Introduction
- Vat Photo Polymerization—uses a liquid photopolymer resin, located in the printer tank (composed of a liquid photopolymer to which a special hardener is added) which solidifies (polymerizes) in successive layers, under the influence of a laser with ultraviolet light, for obtaining the solid three-dimensional model. e.g., stereolithography (SLA), digital light processing (DLP).
- Material Jetting—works similarly to 2D printers. A print-head deposits droplets of a photosensitive material (photopolymer), which solidifies under ultraviolet (UV) light, for building the object layer by layer. e.g., PolyJet technology.
- Binder Jetting—uses a bed of powder, on which the nozzles spray micro fine drops of a liquid, which glues the powder particles to build a section of the piece. e.g., 3D Printing.
2. Materials and Methods
2.1. The Geometry of the Samples
2.2. Parts Manufacturing and the Equipment that Was Used to Perform Compression Tests
3. Experimental Method
- The platform moving speed, during the tests: vpm = 6 mm/min;
- The loading force: Fl = 3000 N;
- Height of the punch, after finishing the charging amounts (above the piece): hp = 5 mm;
- The chosen load method: comprehensive Strain;
- Geometry of the samples: overall cubic shape with the dimensions: 30 mm × 30 mm × 30 mm.
4. Results
5. Discussion
- Fi-j is the maximum compressive force of the sample j that is a member of the i group;
- Mi-j is the mass of the sample j that is a member of the i group.
- Rci max—the compressive strength to mass ratio at initial failure
- Fci med—the average of compression force at initial failure
- Mi med—the average mass
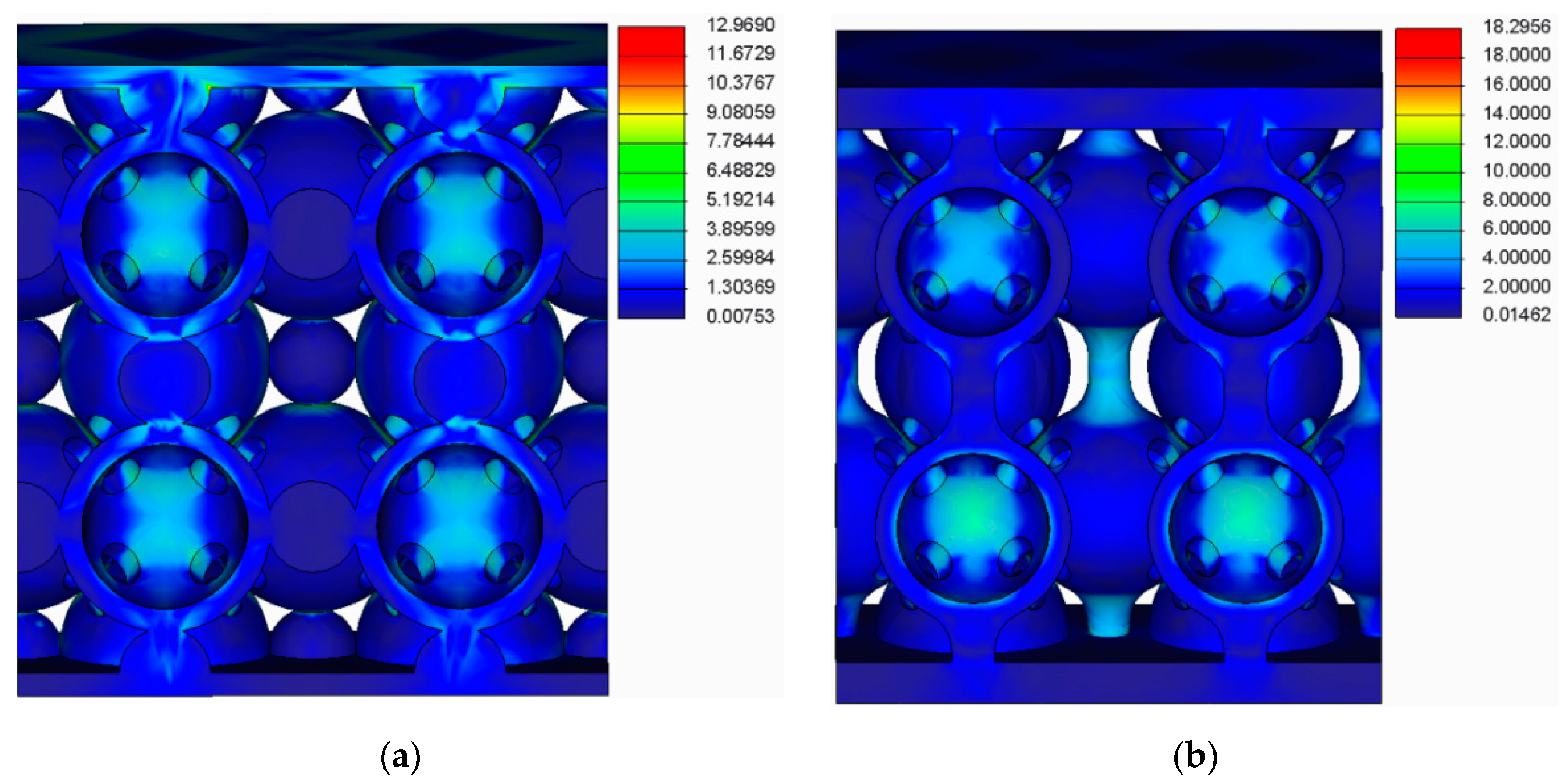
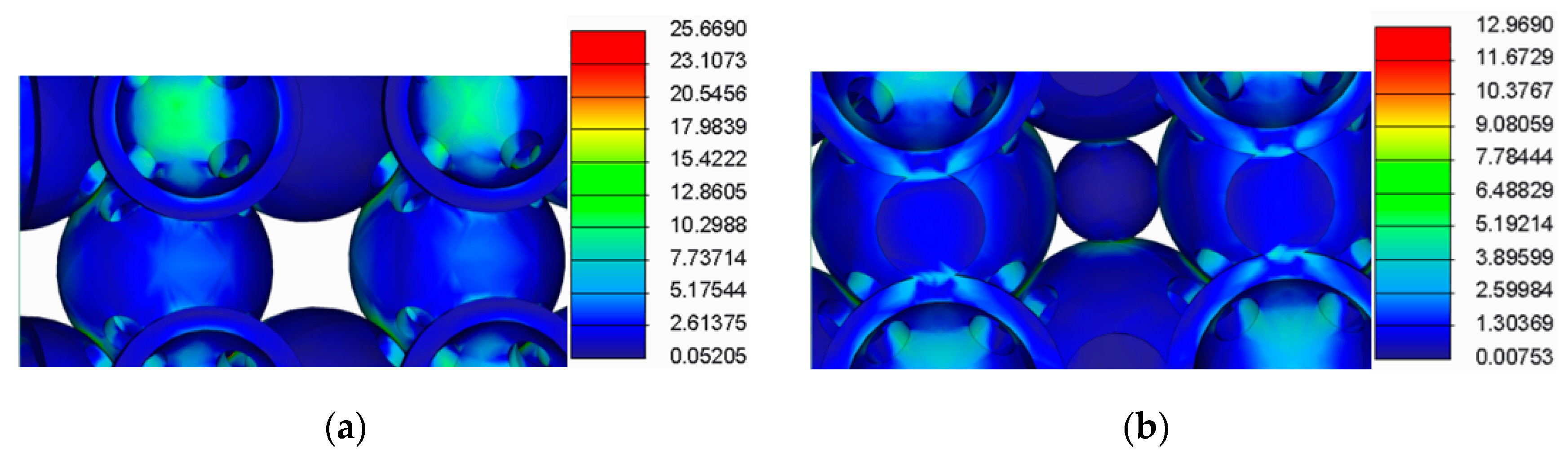
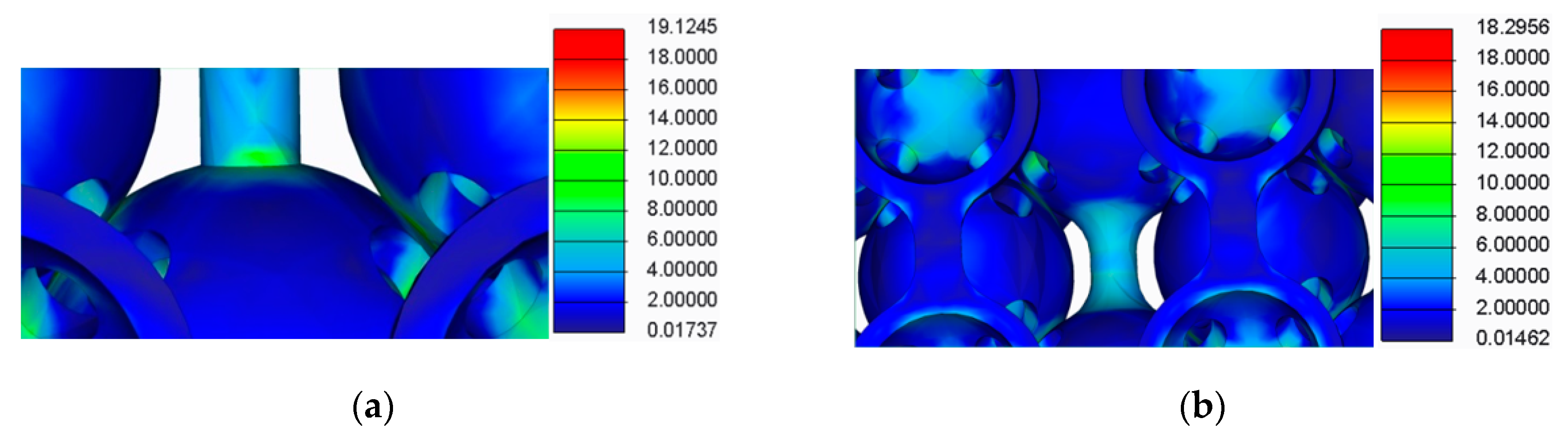
- The spherical supports penetrated the spheres in the main structure of the samples;
- For the samples with double supports, the supports failed before the spheres in the main structure failed;
- The samples with a lower number of supports had a more uniform stress distribution across the supports and the main structure.
- Rci max—the compressive strength to mass ratio at initial failure
- Fci med—the average of compression force at initial failure
- S (mm2)—the area of the critical section.
6. Conclusions
- The compressive strength of the spherical lattice structures increases when link elements are added;
- After analysing all the samples, it was found that the structures with spherical link elements offer the optimal structure to be used for parts subjected to compression;
- In the case of single directional loads, doubling the number of link elements had little influence on the compressive strength of the samples;
- After comparing the information obtained from the loading graphs with the FEA results, it was found that for the structures with double the number of supports, the supports crushed before the destruction of the spheres in the main structure. For the other cases (the samples with spherical supports and the samples with a smaller number of supports) the structure compactness was increased and failure of the supports occurred simultaneously with the failure of the spheres in the main structure;
- Due to the much lower manufacturing cost of the polymer parts, compared to the price of the metal alloy parts, the results of these tests can be an important starting point for substantially reducing the testing costs of the metal parts, produced by SLM technology.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fernandes, F.; Jardin, R.; Pereira, A.; De Sousa, R.J.A. Comparing the mechanical performance of synthetic and natural cellular materials. Mater. Des. 2015, 82, 335–341. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge Solid State Science Series; Cambridge University Press: Cambridge, UK, 2014; ISBN 100521499119. [Google Scholar]
- Zangana, S.; Epaarachchi, J.; Ferdous, W.; Leng, J. A novel hybridised composite sandwich core with Glass, Kevlar and Zylon fibres—Investigation under low-velocity impact. Int. J. Impact Eng. 2020, 137, 103430. [Google Scholar] [CrossRef]
- Park, S.-I.; Rosen, D.W.; Choi, S.-K.; Duty, C.E. Effective mechanical properties of lattice material fabricated by material extrusion additive manufacturing. Addit. Manuf. 2014, 1, 12–23. [Google Scholar]
- Mahshid, R.; Hansen, H.N.; Højbjerre, K.L. Strength analysis and modeling of cellular lattice structures manufactured using selective laser melting for tooling applications. Mater. Des. 2016, 104, 276–283. [Google Scholar] [CrossRef]
- Moroni, L.; De Wijn, J.; Van Blitterswijk, C. 3D fiber-deposited scaffolds for tissue engineering: Influence of pores geometry and architecture on dynamic mechanical properties. Biomaterials 2006, 27, 974–985. [Google Scholar] [CrossRef] [PubMed]
- Kadkhodapour, J.; Montazerian, H.; Raeisi, S. Investigating internal architecture effect in plastic deformation and failure for TPMS-based scaffolds using simulation methods and experimental procedure. Mater. Sci. Eng. C 2014, 43, 587–597. [Google Scholar] [CrossRef]
- Siddika, A.; Al Mamun, A.; Ferdous, W.; Alyousef, R. Performances, challenges and opportunities in strengthening reinforced concrete structures by using FRPs—A state-of-the-art review. Eng. Fail. Anal. 2020, 137, 104480. [Google Scholar] [CrossRef]
- Singh, S.; Ramakrishna, S.; Singh, R. Material issues in additive manufacturing: A review. J. Manuf. Process. 2017, 25, 185–200. [Google Scholar] [CrossRef]
- Chu, C.; Graf, G.; Rosen, D.W. Design for Additive Manufacturing of Cellular Structures. Comput. Des. Appl. 2013, 5, 686–696. [Google Scholar] [CrossRef]
- Conner, B.; Manogharan, G.P.; Martof, A.N.; Rodomsky, L.M.; Rodomsky, C.M.; Jordan, D.C.; Limperos, J.W. Making sense of 3-D printing: Creating a map of additive manufacturing products and services. Addit. Manuf. 2014, 1, 64–76. [Google Scholar] [CrossRef]
- Thompson, M.K.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for Additive Manufacturing: Trends, opportunities, considerations, and constraints. CIRP Ann. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Türk, D.A.; Kussmaul, R.; Zogg, M.; Klahn, C.; Leutenecker-Twelsiek, B.; Meboldt, M. Composites Part Production with Additive Manufacturing Technologies. Procedia CIRP 2017, 66, 306–311. [Google Scholar] [CrossRef]
- Van Eijnatten, M.; Berger, F.H.; De Graaf, P.; Koivisto, J.; Forouzanfar, T.; Wolff, J. Influence of CT parameters on STL model accuracy. Rapid Prototyp. J. 2017, 23, 678–685. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.; Aremu, A.; Tuck, C.; Ashcroft, I.; Wildman, R.D.; Hague, R.J. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef]
- Choy, S.Y.; Sun, C.-N.; Leong, K.F.; Wei, J. Compressive properties of functionally graded lattice structures manufactured by selective laser melting. Mater. Des. 2017, 131, 112–120. [Google Scholar] [CrossRef]
- Kadkhodapour, J.; Montazerian, H.; Darabi, A.C.; Zargarian, A.; Schmauder, S. The relationships between deformation mechanisms and mechanical properties of additively manufactured porous biomaterials. J. Mech. Behav. Biomed. Mater. 2017, 70, 28–42. [Google Scholar] [CrossRef]
- Türk, D.-A.; Brenni, F.; Zogg, M.; Meboldt, M. Mechanical characterization of 3D printed polymers for fiber reinforced polymers processing. Mater. Des. 2017, 118, 256–265. [Google Scholar] [CrossRef]
- Lancea, C.; Chicoș, L.A.; Zaharia, S.M.; Pop, M.A. Microstructure and micro-hardness analyses of titanium alloy Ti6Al4V parts manufactured by selective laser melting. MATEC Web Conf. 2017, 94, 3009. [Google Scholar] [CrossRef]
- Buican, G.R.; Oancea, G.; Lancea, C.; Pop, M.A. Influence of Layer Thickness on Internal Structure of Parts Manufactured from 316-L Steel Using SLM Technology. Appl. Mech. Mater. 2015, 809, 369–374. [Google Scholar] [CrossRef]
- Buican, G.R.; Oancea, G.; Lancea, C.; Pop, M.A. Some Considerations Regarding Micro Hardness of Parts Manufactured from 316-L Steel Using SLM Technology. Appl. Mech. Mater. 2015, 760, 515–520. [Google Scholar] [CrossRef]
- Lancea, C.; Chicos, L.A.; Zaharia, S.M. Researches about the Corrosion Resistance of Different Materials used for Building Sustainable Energy Systems. In Proiect SFERA—Solar Facilities for the European Research Area—Grant Agreement; 228296; European Commission: Casaccia, Italy, 2013; Available online: https://cordis.europa.eu/project/id/228296 (accessed on 15 November 2020).
- ASTM Standards. Standard Test Method for Compressive Properties of Polymer Matrix Composite Materials D 3410/D 3410M–03; ASTM: West Conshohocken, PA, USA, 2003. [Google Scholar]
- Langrand, B.; Casadei, F.; Marcadon, V.; Portemont, G.; Kruch, S. Experimental and finite element analysis of cellular materials under large compaction levels. Int. J. Solids Struct. 2017, 128, 99–116. [Google Scholar] [CrossRef]
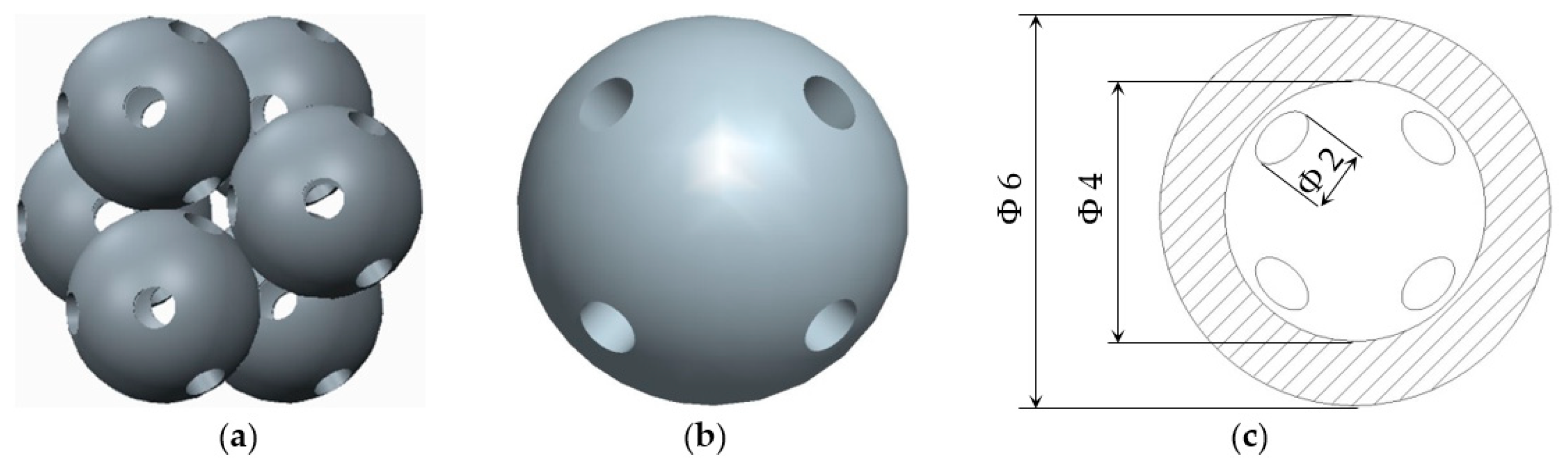
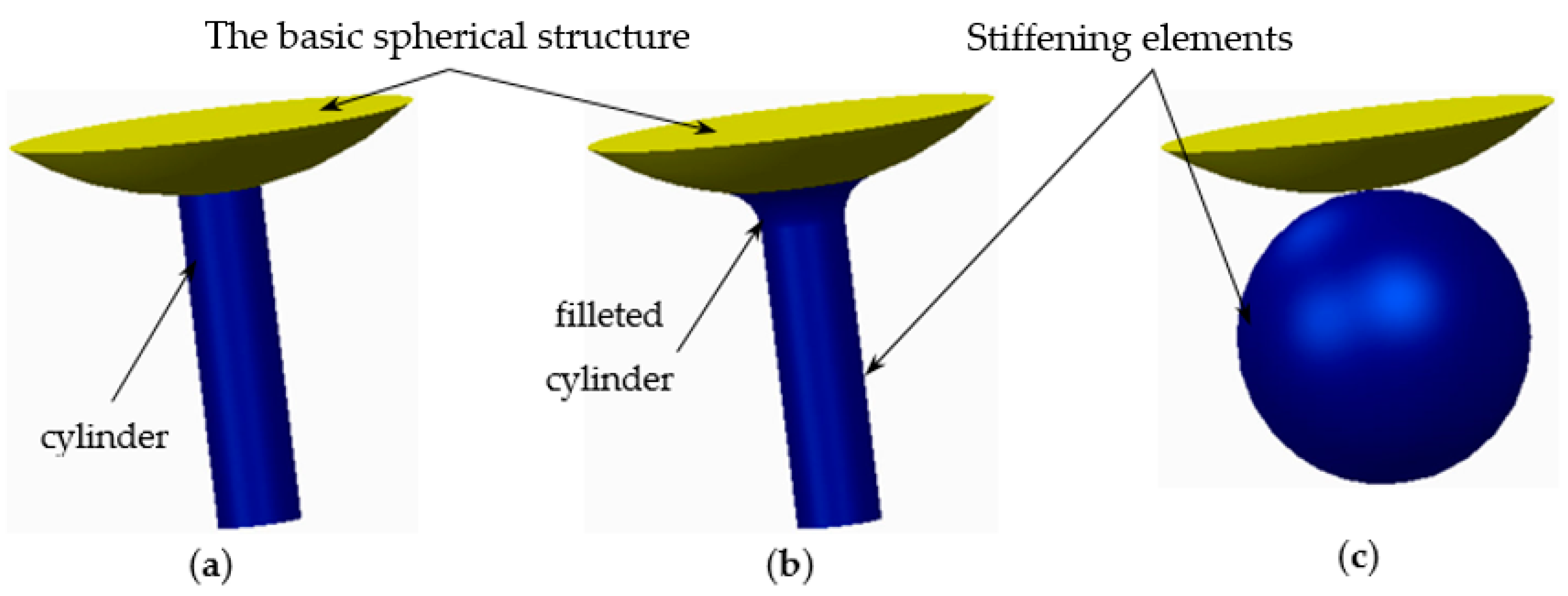
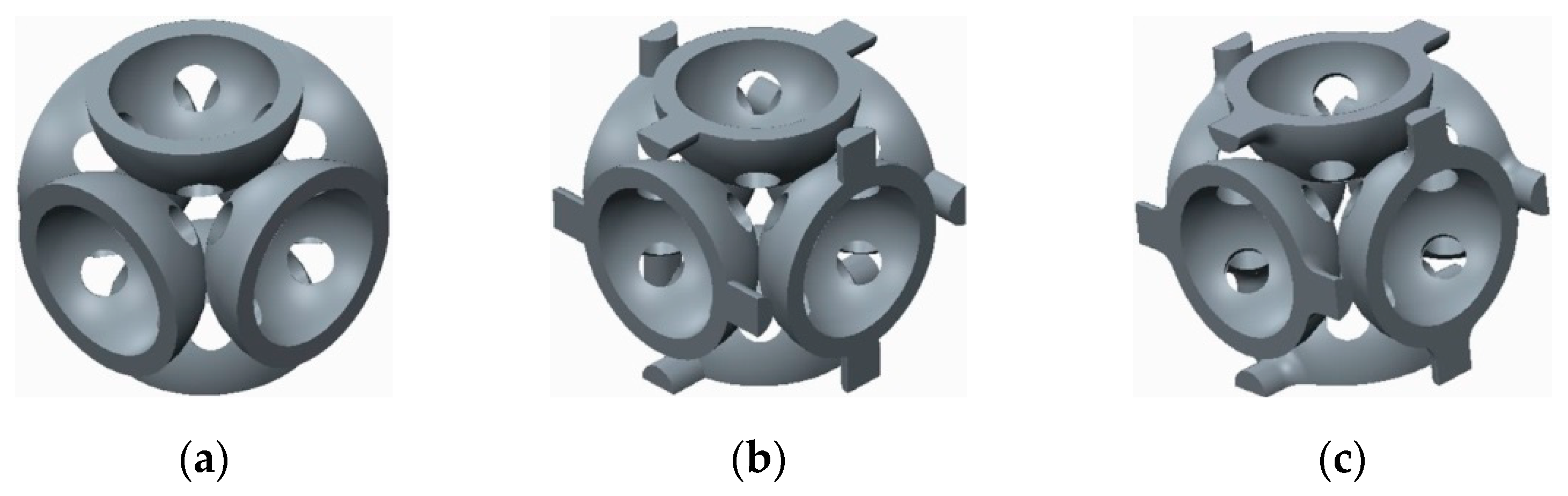
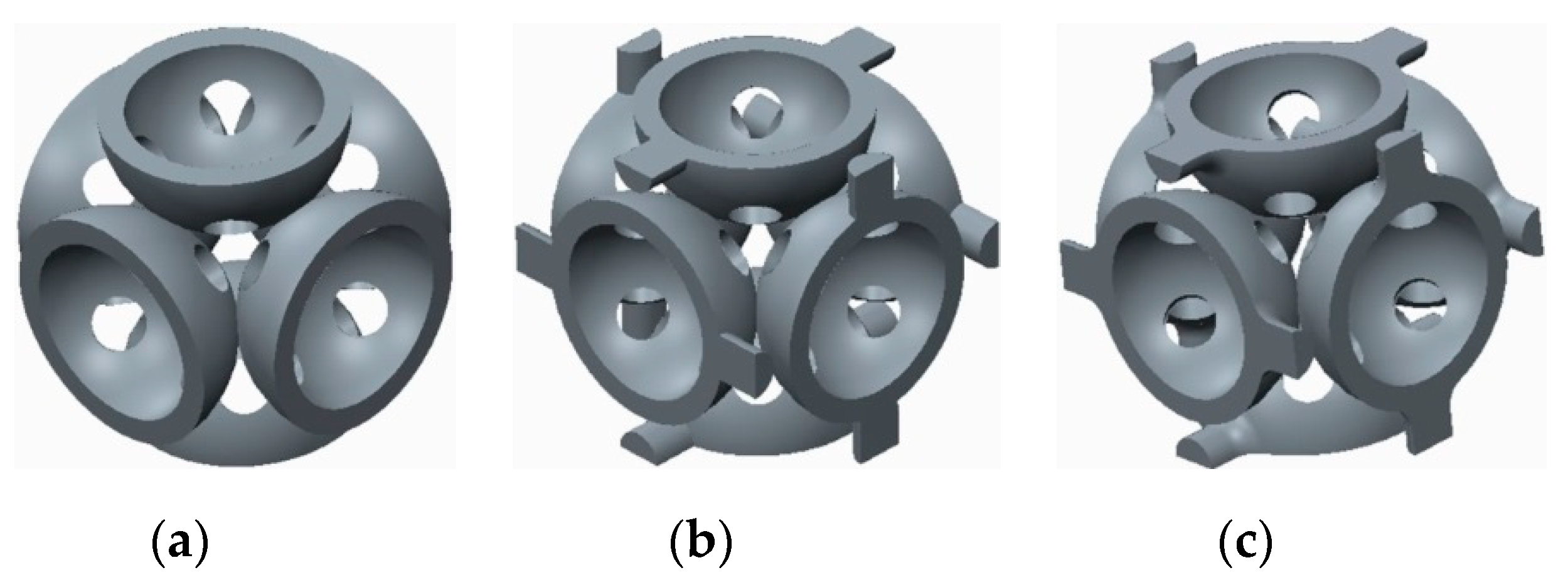


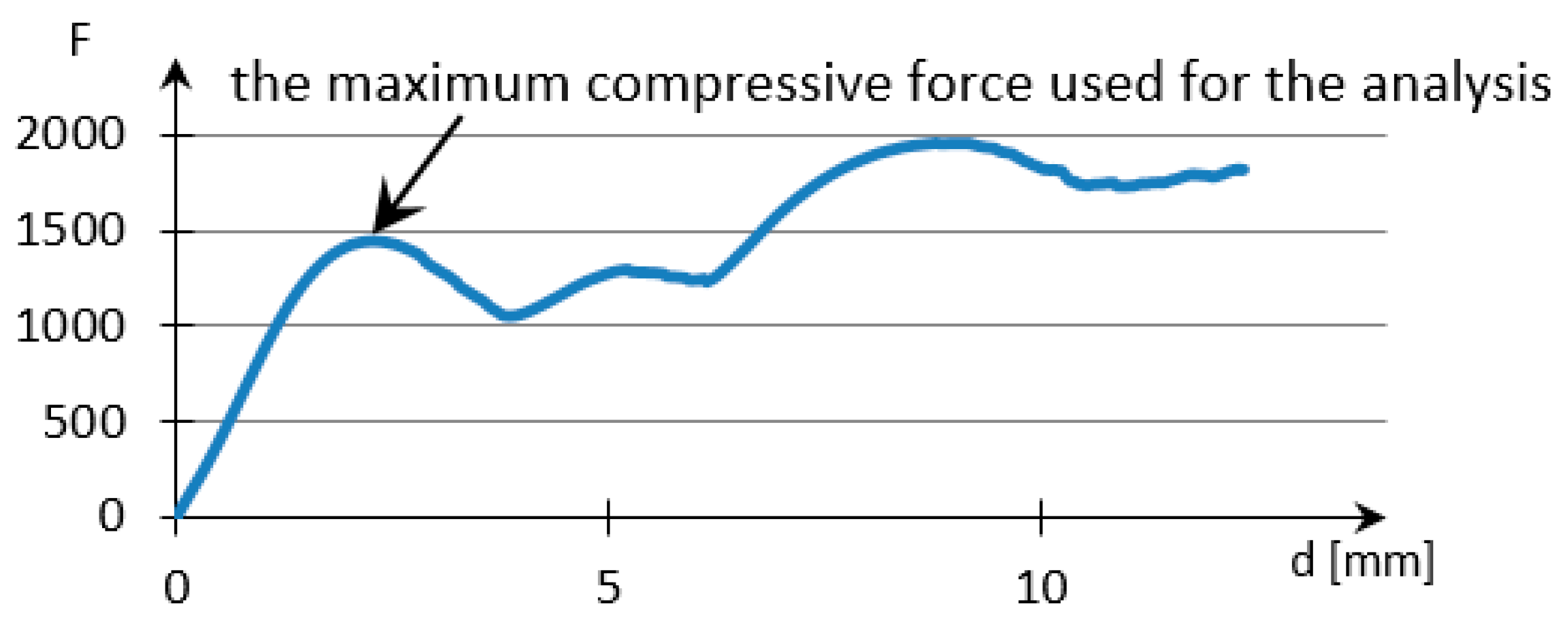



| Structures with Stiffening Elements | Structures with Doubled Stiffening Elements | ||
|---|---|---|---|
| Lattice cell geometry | The loading force (N) × displacement (mm) graph | Lattice cell geometry | The loading force (N) × displacement (mm) graph |
 Without stiffening supports | 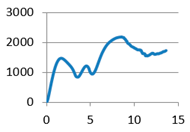 |  With spherical supports | 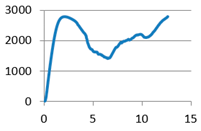 |
| Part mass average: 11.82 g | Part mass average: 13.601 g | ||
 With cylindrical supports | 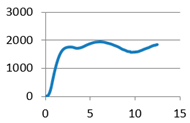 |  With cylindrical supports |  |
| Part mass average: 12.225 g | Part mass average: 12.018 g | ||
 With filleted cylindrical supports | 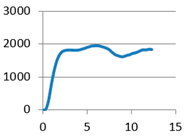 |  With doubled filleted cylindrical supports | 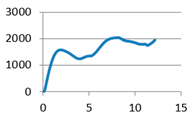 |
| Part mass average: 12.306 g | Part mass average: 12.044 g | ||
| Lattice Cell Geometry | Maximum Compressive Force (N) | Mass (g) | Lattice Cell Geometry | Maximum Compressive Force (N) | Mass (g) |
|---|---|---|---|---|---|
 Without stiffening supports | F1-1: 1415.089 F1-2: 1404.516 F1-3: 1456.453 F1-4: 1147.601 F1-5: 1311.217 F1-6: 1338.975 | m1-1: 12.172 m1-2: 11.703 m1-3: 12.117 m1-4: 11.951 m1-5: 11.610 m1-6: 11.365 |  With cylindrical supports | F2-1: 1696.994 F2-2: 1783.833 F2-3: 1896.945 F2-4: 1765.031 F2-5: 1698.578 F2-6: 1782.309 | m2-1: 12.725 m2-2: 12.058 m2-3: 11.512 m2-4: 11.886 m2-5: 12.618 m2-6: 12.548 |
| Average value | 1345.642 | 11.82 | Average value | 1770.615 | 12.225 |
| Standard deviation | 110.47 | 0.314 | Standard deviation | 73.364 | 0.482 |
 With filleted cylindrical supports | F3-1: 2120.697 F3-2: 1779.39 F3-3: 1808.261 F3-4: 1863.207 F3-5: 1710.604 F3-6: 1886.721 | m3-1: 12.586 m3-2: 12.042 m3-3: 12.305 m3-4: 11.852 m3-5: 12.801 m3-6: 12.250 |  With doubled cylindrical supports | F4-1: 1523.174 F4-2: 1703.174 F4-3: 1655.9434 F4-4: 1591.677 F4-5: 1442.222 F4-6: 1495.113 | m4-1: 11.479 m4-2: 12.254 m4-3: 12.518 m4-4: 12.650 m4-5: 11.687 m4-6: 11.520 |
| Average value | 1861.48 | 12.306 | Average value | 1568.55 | 12.018 |
| Standard deviation | 141.54 | 0.347 | Standard deviation | 99.706 | 0.52 |
 With doubled filleted cylindrical supports | F5-1: 1568.214 F5-2: 1552.337 F5-3: 1631.017 F5-4: 1607.449 F5-5: 1651.441 F5-6: 1593.386 | m5-1: 12.215 m5-2: 12.399 m5-3: 12.541 m5-4: 11.364 m5-5: 11.511 m5-6: 12.231 |  With spherical supports | F6-1: 2619.124 F6-2: 2644.336 F6-3: 2603.658 F6-4: 2795.897 F6-5: 2567.721 F6-6: 2484.217 | m6-1: 14.379 m6-2: 12.789 m6-3: 14.192 m6-4: 13.755 m6-5: 12.594 m6-6: 13.899 |
| Average value | 1600.641 | 12.044 | Average value | 2619.159 | 13.601 |
| Standard deviation | 37.382 | 0.487 | Standard deviation | 102.9223 | 0.740 |
| Samples Type | Rcimax (N/g) |
|---|---|
| Samples without supports | Rc1max = 1345.642/11.82 = 113.845 N/g |
| Samples with spherical supports | Rc2max = 2619.159/13.601 = 192.571 N/g |
| Samples with cylindrical supports | Rc3max = 1770.615/12.225 = 144.836 N/g |
| Samples filleted cylindrical supports | Rc4 max = 1861.48/12.306 = 151.266 N/g |
| Samples doubled cylindrical supports | Rc5 max = 1568.55/12.018 = 130.517 N/g |
| Samples doubled filleted cylindrical supports | Rc6 max = 1600.641/12.044 = 132.899 N/g |
| Samples Type | Calculated Rcimax (MPa) | Rcimax by FEA (MPa) |
|---|---|---|
| Samples without supports | Rc1max = 25.05 | Rc1max = 25.67 |
| Samples with spherical supports | Rc2max = 12.87 | Rc2max = 12.97 |
| Samples with cylindrical supports | Rc3max = 19.04 | Rc3max = 19.12 |
| Samples filleted cylindrical supports | Rc4 max = 18.11 | Rc4 max = 18.30 |
| Samples doubled cylindrical supports | Rc5 max = 21.49 | Rc5 max = 21.33 |
| Samples doubled filleted cylindrical supports | Rc6 max = 21.06 | Rc6 max = 22.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lancea, C.; Campbell, I.; Chicos, L.-A.; Zaharia, S.-M. Compressive Behaviour of Lattice Structures Manufactured by Polyjet Technologies. Polymers 2020, 12, 2767. https://doi.org/10.3390/polym12122767
Lancea C, Campbell I, Chicos L-A, Zaharia S-M. Compressive Behaviour of Lattice Structures Manufactured by Polyjet Technologies. Polymers. 2020; 12(12):2767. https://doi.org/10.3390/polym12122767
Chicago/Turabian StyleLancea, Camil, Ian Campbell, Lucia-Antoneta Chicos, and Sebastian-Marian Zaharia. 2020. "Compressive Behaviour of Lattice Structures Manufactured by Polyjet Technologies" Polymers 12, no. 12: 2767. https://doi.org/10.3390/polym12122767
APA StyleLancea, C., Campbell, I., Chicos, L.-A., & Zaharia, S.-M. (2020). Compressive Behaviour of Lattice Structures Manufactured by Polyjet Technologies. Polymers, 12(12), 2767. https://doi.org/10.3390/polym12122767





