Correlation Between the Structure and Compressive Property of PMMA Microcellular Foams Fabricated by Supercritical CO2 Foaming Method
Abstract
:1. Introduction
2. Experimental
2.1. Chemicals and Foaming Production
2.2. Characterization and Testing
2.2.1. Density Determining
2.2.2. Microstructural Observation
2.2.3. Compressive Property Testing
2.2.4. FEM Simulation
3. Results and Discussion
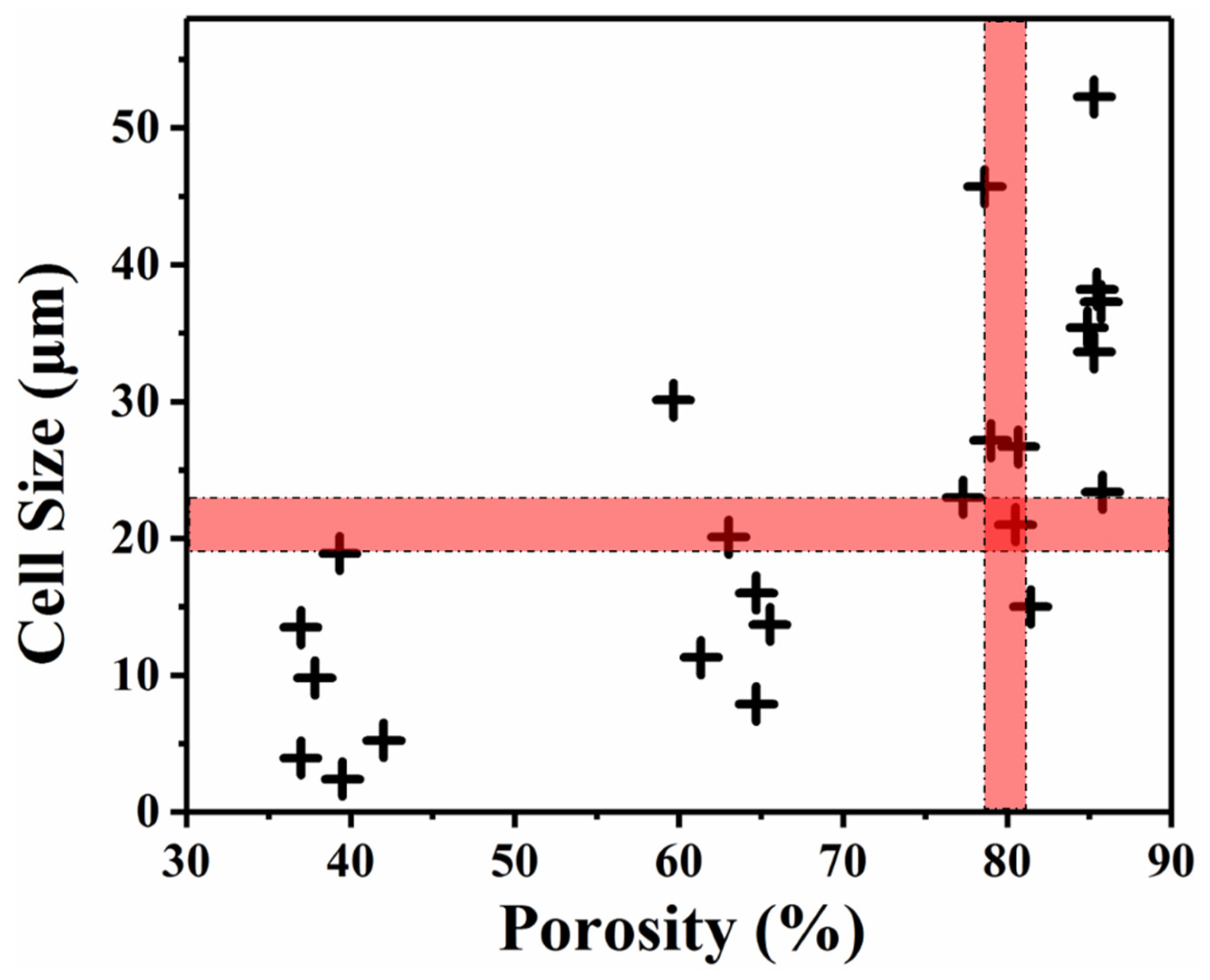
3.1. Foam Porosity
3.2. Foam Microstructure
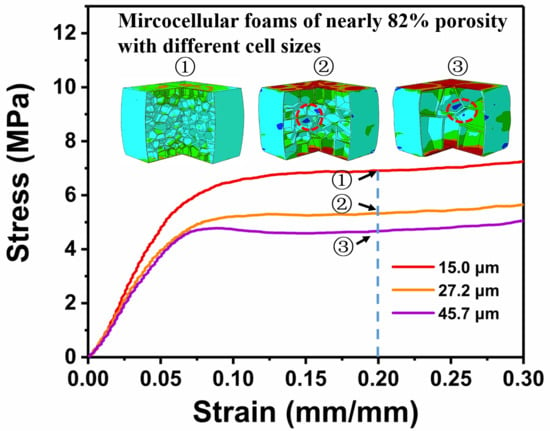
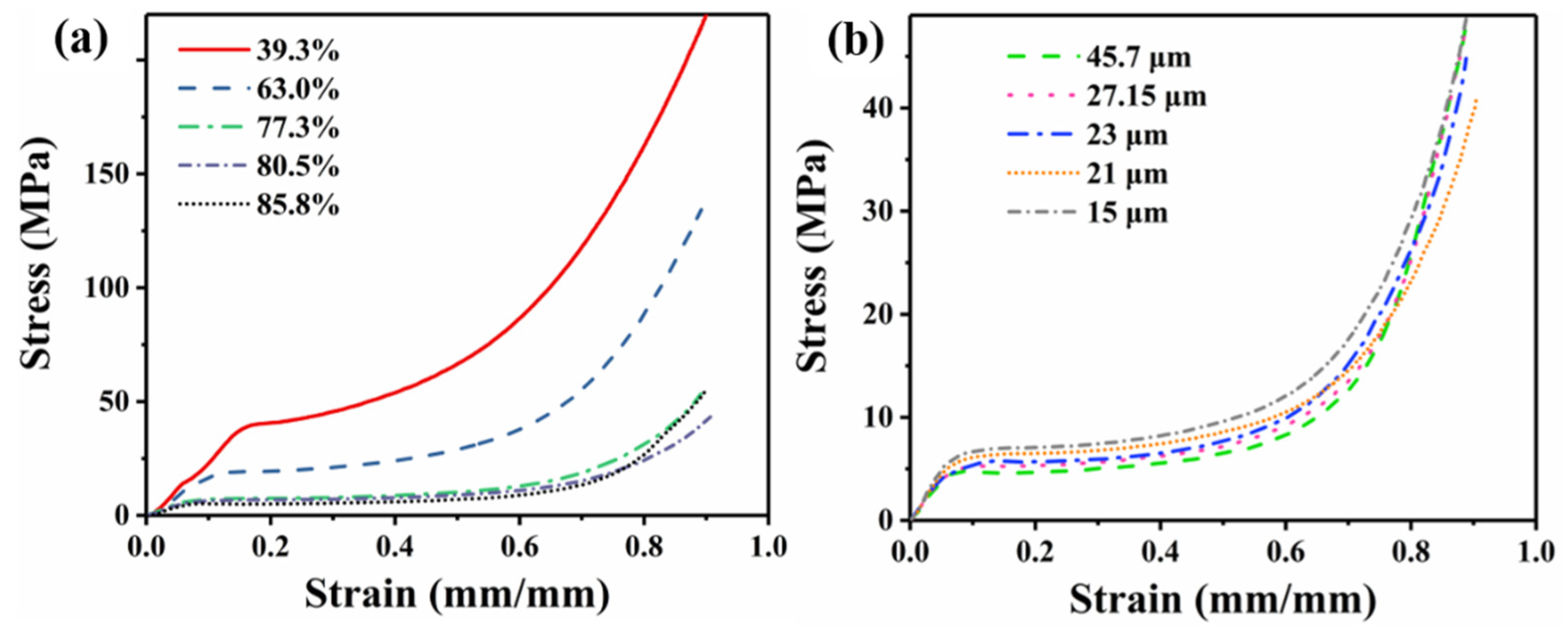
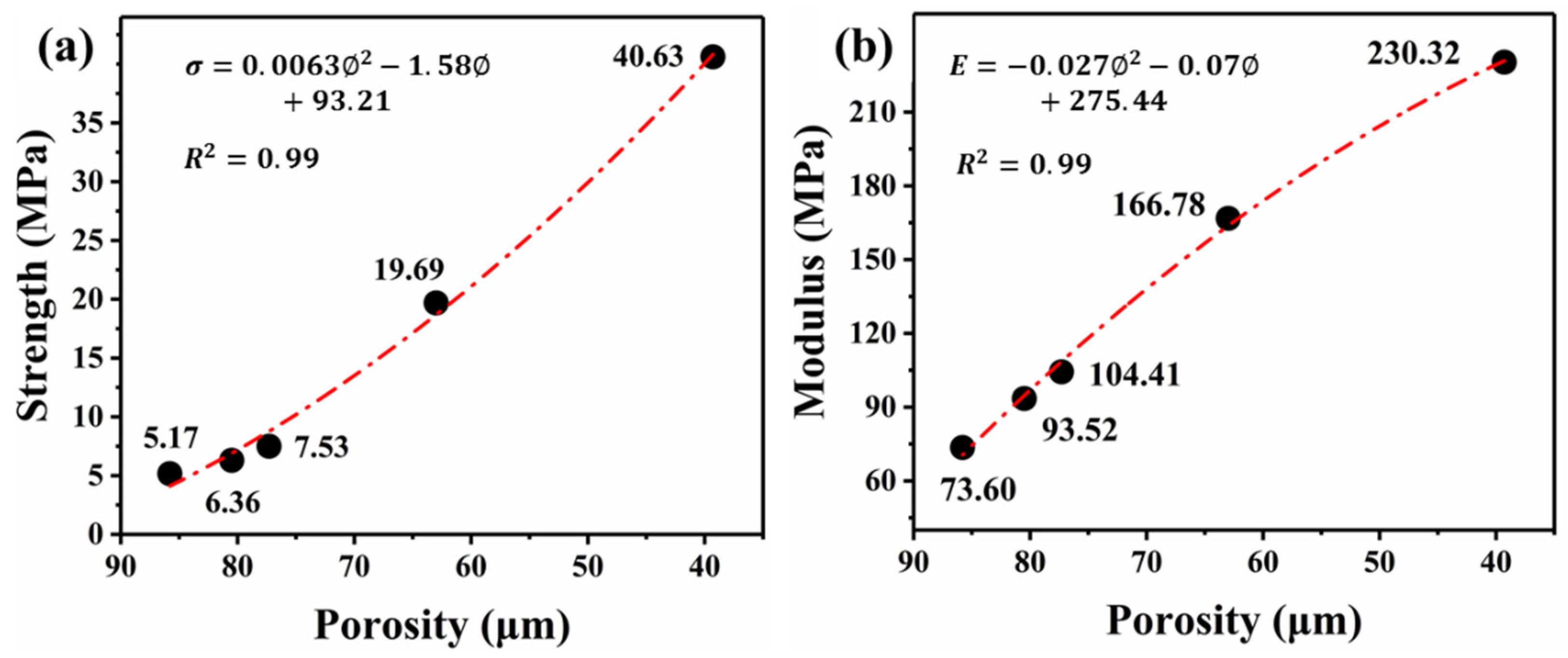
3.3. Mechanical Properties
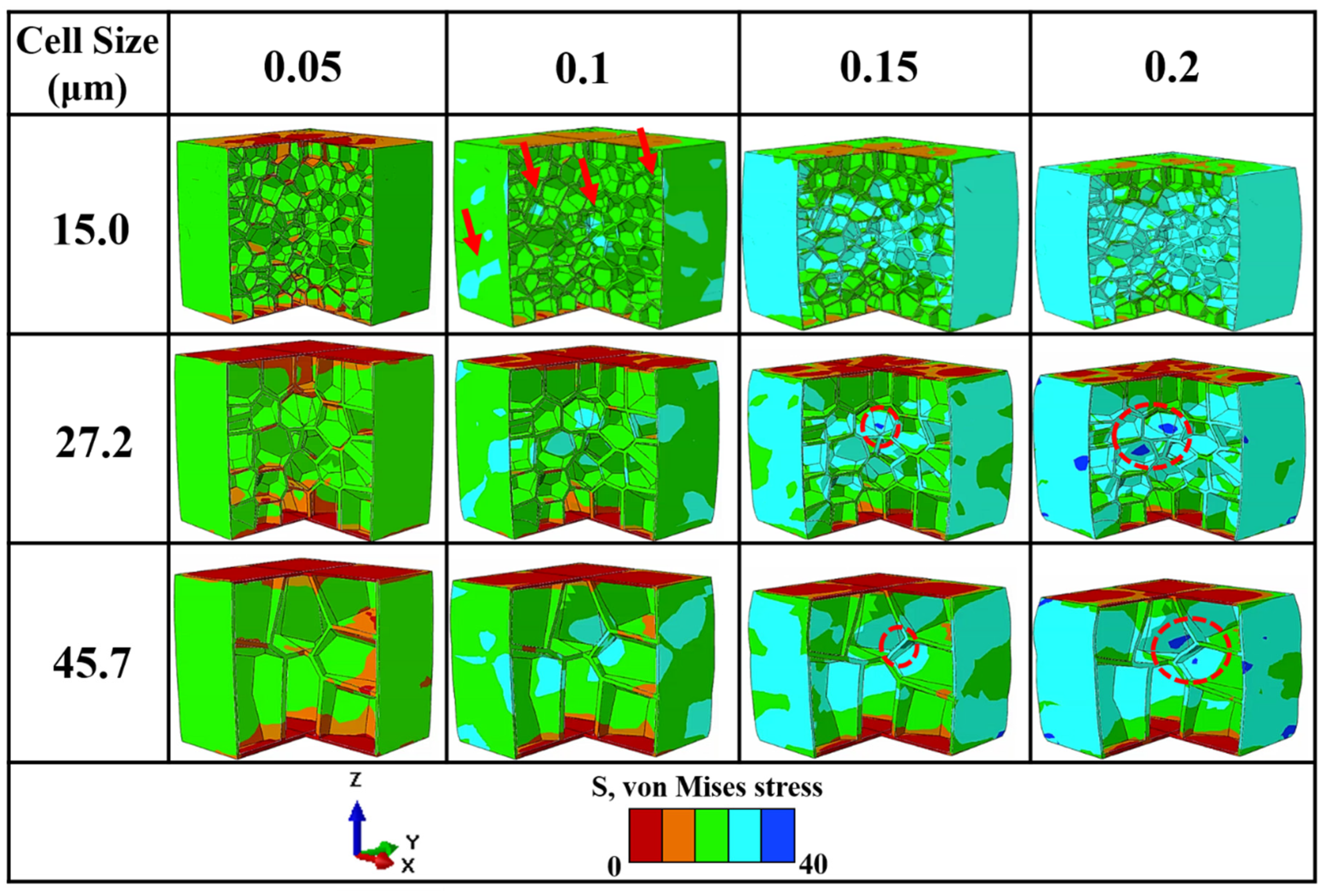
3.4. Numerical Simulation on Mechanical Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Meyers, M.A.; McKittrick, J.; Chen, P.-Y. Structural Biological Materials: Critical Mechanics-Materials Connections. Science 2013, 339, 773–779. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gibson, L.J. Biomechanics of cellular solids. J. Biomech. 2005, 38, 377–399. [Google Scholar] [CrossRef] [PubMed]
- Yeo, S.J.; Oh, M.J.; Yoo, P.J. Structurally Controlled Cellular Architectures for High-Performance Ultra-Lightweight Materials. Adv. Mater. 2019, 31, 26. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Yang, Q.; Mao, H.J.; Meng, Z.H.; Hua, L.; He, B. A Combined In-Mold Decoration and Microcellular Injection Molding Method for Preparing Foamed Products with Improved Surface Appearance. Polymers 2019, 11, 778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Collias, D.I.; Baird, D.G.; Borggreve, R.J.J.P. Impact toughening of polycarbonate by microcellular foaming. Polymer 1994, 35, 3978–3983. [Google Scholar] [CrossRef]
- Fei, Y.P.; Fang, W.; Zhong, M.Q.; Jin, J.M.; Fan, P.; Yang, J.T.; Fei, Z.D.; Xu, L.X.; Chen, F. Extrusion Foaming of Lightweight Polystyrene Composite Foams with Controllable Cellular Structure for Sound Absorption Application. Polymers 2019, 11, 106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Volpe, V.; Lanzillo, S.; Affinita, G.; Villacci, B.; Macchiarolo, I.; Pantani, R. Lightweight High-Performance Polymer Composite for Automotive Applications. Polymers 2019, 11, 326. [Google Scholar] [CrossRef] [Green Version]
- Brydon, A.D.; Bardenhagen, S.G.; Miller, E.A.; Seidler, G.T. Simulation of the densification of real open-celled foam microstructures. J. Mech. Phys. Solids 2005, 53, 2638–2660. [Google Scholar] [CrossRef]
- Gibson, L.; Ashby, M.; Kumar, K. Cellular Solids: Structure and Properties, 2nd ed. Mrs Bull. Mater. Res. Soc. 1999, 23, 69. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ashby, M. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2005, 364, 15–30. [Google Scholar] [CrossRef]
- Alvarez, P.; Mendizabal, A.; Petite, M.; Rodríguez-Pérez, M.; Echeverria, A. Finite element modelling of compressive mechanical behaviour of high and low density polymeric foams. Mater. Werkst. 2009, 40, 126–132. [Google Scholar] [CrossRef]
- Solórzano, E.; Rodriguez-Perez, M.A. Polymeric Foams. Struct. Mater. Process. Transp. 2013, 375–413. [Google Scholar]
- Chen, L.; Schadler, L.S.; Ozisik, R. An experimental and theoretical investigation of the compressive properties of multi-walled carbon nanotube/poly(methyl methacrylate) nanocomposite foams. Polymer 2011, 52, 2899–2909. [Google Scholar] [CrossRef]
- Tomasko, D.L.; Li, H.B.; Liu, D.H.; Han, X.M.; Wingert, M.J.; Lee, L.J.; Koelling, K.W. A review of CO(2) applications in the processing of polymers. Ind. Eng. Chem. Res. 2003, 42, 6431–6456. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, J.; Wang, G.; Lun, H.M.; Park, C.B.; Zhao, G.J.E.P.J. Low-density and structure-tunable microcellular PMMA foams with improved thermal-insulation and compressive mechanical properties. Eur. Polym. J. 2017, 95, 382–393. [Google Scholar] [CrossRef]
- Saha, M.C.; Mahfuz, H.; Chakravarty, U.K.; Uddin, M.; Kabir, M.E.; Jeelani, S. Effect of density, microstructure, and strain rate on compression behavior of polymeric foams. Mater. Sci. Eng. A 2005, 406, 328–336. [Google Scholar] [CrossRef]
- Reglero Ruiz, J.A.; Viot, P.; Dumon, M. Microcellular foaming of polymethylmethacrylate in a batch supercritical CO2 process: Effect of microstructure on compression behavior. J. Appl. Polym. Sci. 2010, 118, 320–331. [Google Scholar] [CrossRef] [Green Version]
- Brezny, R.; Green, D.J. The effect of cell size on the mechanical behavior of cellular materials. Acta Metall. Et Mater. 1990, 38, 2517–2526. [Google Scholar] [CrossRef]
- Weller, J.E.; Kumar, V.J. Solid-state microcellular polycarbonate foams. II. The effect of cell size on tensile properties. Polym. Eng. Sci. 2010, 50, 2170–2175. [Google Scholar] [CrossRef]
- Doroudiani, S.; Kortschot, M.T. Polystyrene foams. III. Structure–tensile properties relationships. J. Appl. Polym. Sci. 2003, 90, 1427–1434. [Google Scholar] [CrossRef]
- Mao, H.J.; He, B.; Guo, W.; Hua, L.; Yang, Q. Effects of Nano-CaCO3 Content on the Crystallization, Mechanical Properties, and Cell Structure of PP Nanocomposites in Microcellular Injection Molding. Polymers 2018, 10, 1160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, Y.X.; Luo, G.Q.; Zhang, R.Z.; Liu, Q.W.; Sun, Y.; Zhang, J.; Shen, Q.; Zhang, L.M. Investigation of the Constitutive Model of W/PMMA Composite Microcellular Foams. Polymers 2019, 11, 1136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, J.; Jo, C.; Naguib, H.E. Effect of processing parameters on cellular structures and mechanical properties of PMMA microcellular foams. Cell. Polym. 2005, 24, 177–195. [Google Scholar] [CrossRef]
- Wang, G.; Wan, G.; Chai, J.; Li, B.; Zhao, G.; Mu, Y.; Park, C.B. Structure-tunable thermoplastic polyurethane foams fabricated by supercritical carbon dioxide foaming and their compressive mechanical properties. J. Supercrit. Fluids 2019, 149, 127–137. [Google Scholar] [CrossRef]
- Wong, A.; Guo, H.; Kumar, V.; Park, C.B.; Suh, N.P. Microcellular Plastics. Encycl. Polym. Sci. Technol. 2016, 1–57. [Google Scholar]
- Shulmeister, V.; Van der Burg, M.W.D.; Van der Giessen, E.; Materials, R. A numerical study of large deformations of low-density elastomeric open-cell foams. Mech. Mater. 1998, 30, 125–140. [Google Scholar] [CrossRef] [Green Version]
- Roszkos, C.S.; Bocko, J.; Kula, T.; Sarlosi, J. Static and dynamic analyses of aluminum foam geometric models using the homogenization procedure and the FEA. Compos. Part B Eng. 2019, 171, 361–374. [Google Scholar] [CrossRef]
- Zhang, R.Z.; Zhang, L.M.; Zhang, J.; Luo, G.Q.; Xiao, D.W.; Song, Z.F.; Li, M.J.; Xiong, Y.L.; Shen, Q. Compressive response of PMMA microcellular foams at low and high strain rates. J. Appl. Polym. Sci. 2018, 135, 10. [Google Scholar] [CrossRef]
- Guo, H.; Kumar, V. Solid-state poly (methyl methacrylate)(PMMA) nanofoams. Part I: Low-temperature CO2 sorption, diffusion, and the depression in PMMA glass transition. Polymer 2015, 57, 157–163. [Google Scholar] [CrossRef]
- Condo, P.; Johnston, K. Retrograde vitrification of polymers with compressed fluid diluents: Experimental confirmation. Macromolecules 1992, 25, 6730–6732. [Google Scholar] [CrossRef]
- Handa, Y.P.; Zhang, Z. A new technique for measuring retrograde vitrification in polymer–gas systems and for making ultramicrocellular foams from the retrograde phase. J. Polym. Sci. Part B Polym. Phys. 2000, 38, 716–725. [Google Scholar] [CrossRef]
- Goel, S.K.; Beckman, E.J. Generation of microcellular polymeric foams using supercritical carbon dioxide. I: Effect of pressure and temperature on nucleation. Polym. Eng. Sci. 1994, 34, 1137–1147. [Google Scholar] [CrossRef]
- Zhou, D.; Xiong, Y.; Yuan, H.; Luo, G.; Zhang, J.; Shen, Q.; Zhang, L. Synthesis and compressive behaviors of PMMA microporous foam with multi-layer cell structure. Compos. Part B Eng. 2019, 165, 272–278. [Google Scholar] [CrossRef]
- Bai, J.; Liao, X.; Huang, E.; Luo, Y.; Yang, Q.; Li, G. Control of the cell structure of microcellular silicone rubber/nanographite foam for enhanced mechanical performance. Mater. Des. 2017, 133, 288–298. [Google Scholar] [CrossRef]
- Smits, G.F. Envelopes, B. Effect of cellsize reduction on polyurethane foam physical properties. J. Insul. Build. Env. 1994, 17, 309–329. [Google Scholar]


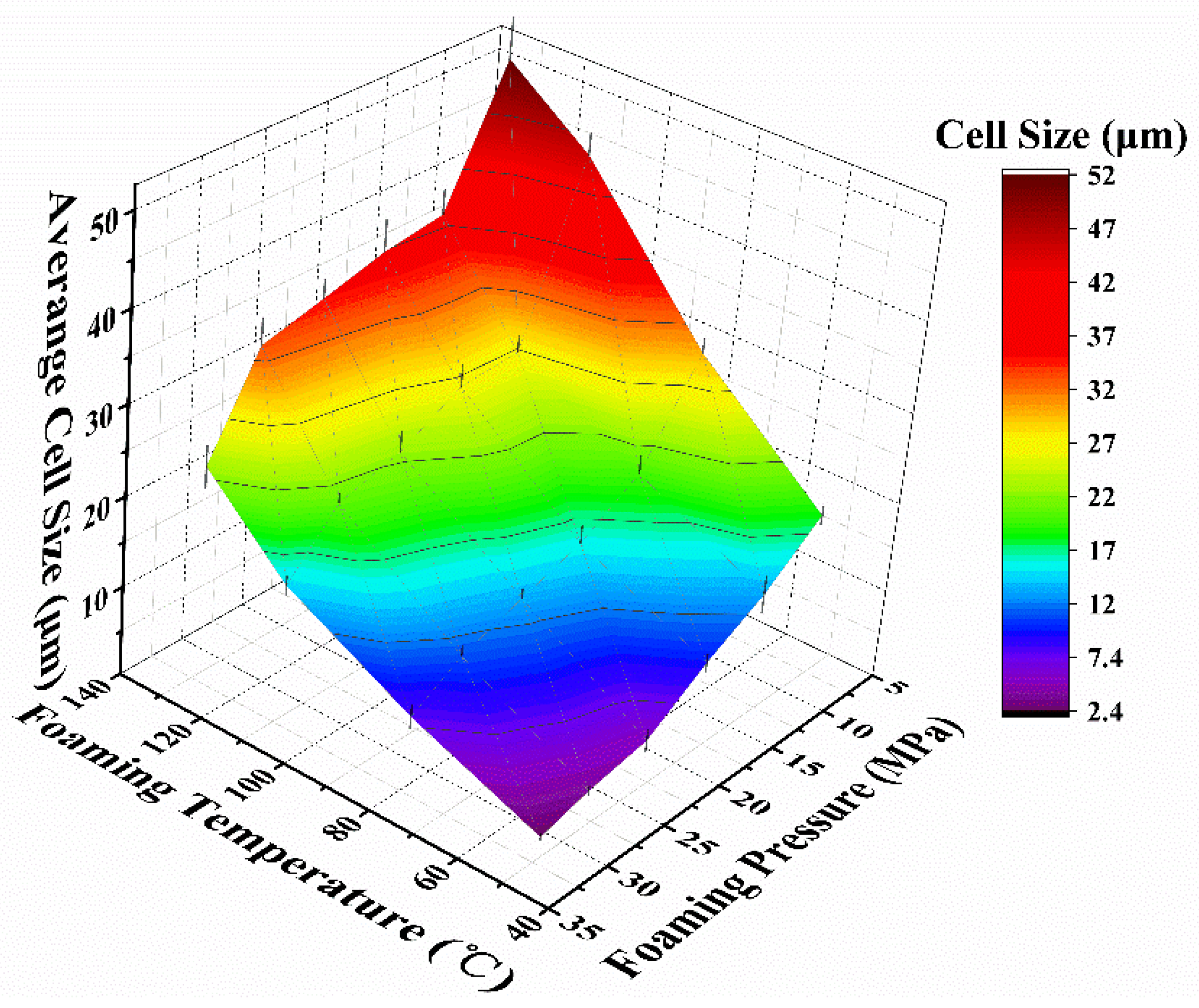
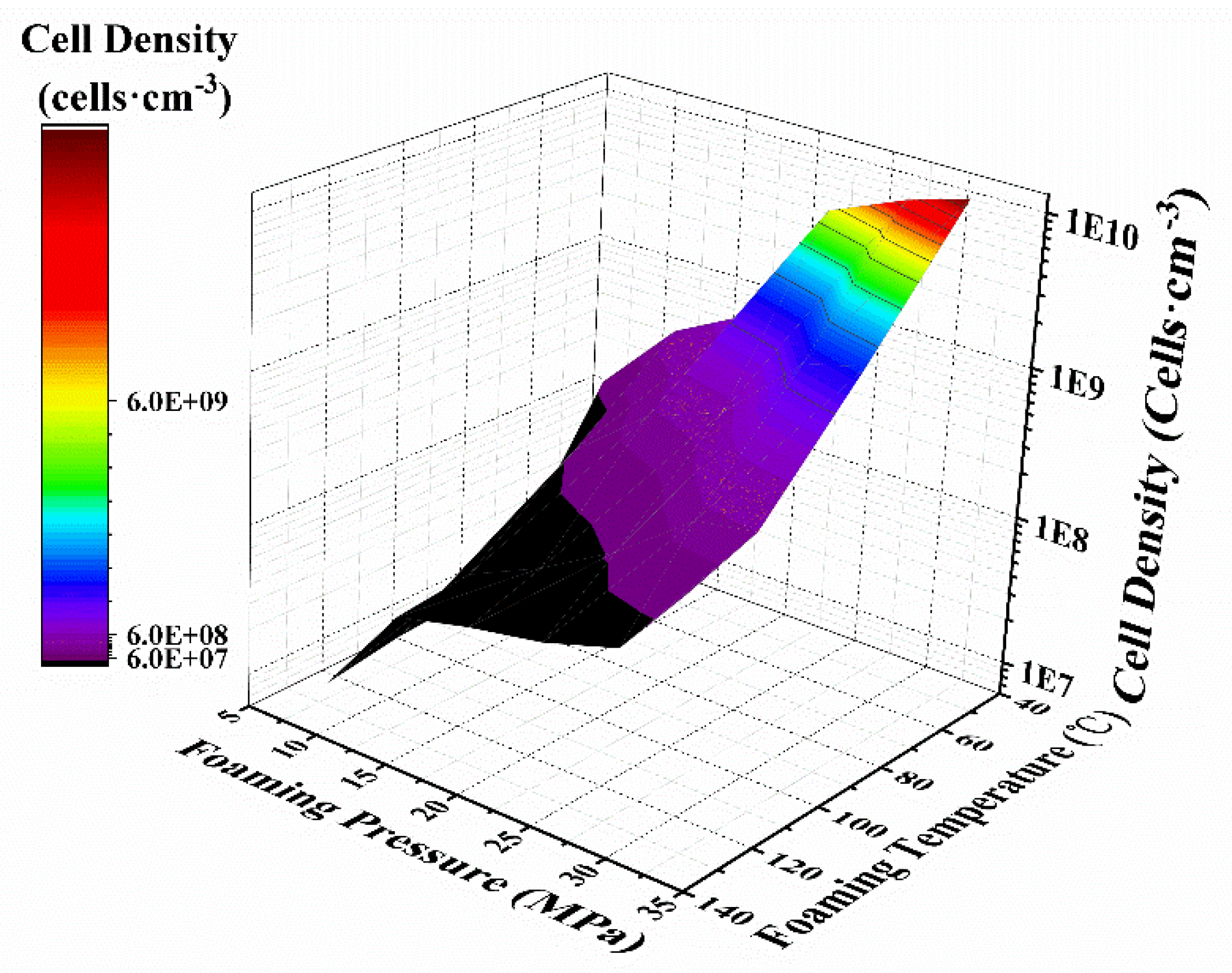


| Foaming Temperature (°C) | Saturation Pressure (MPa) | ρ (kg/m3) | Porosity (%) | Cell Size (μm) | Cell Density (cells·cm−3) |
|---|---|---|---|---|---|
| 50 | 8 | 0.722 ± 0.039 | 39.3 ± 3.26 | 18.6 ± 3.01 | (1.41 ± 0.34) E08 |
| 13 | 0.751 ± 0.027 | 36.9 ± 2.31 | 13.5 ± 2.13 | (4.55 ± 0.26) E08 | |
| 18 | 0.740 ± 0.025 | 37.8 ± 2.12 | 9.80 ± 3.05 | (8.30 ± 0.97) E08 | |
| 23 | 0.690 ± 0.038 | 42.0 ± 3.21 | 5.24 ± 2.28 | (5.74 ± 0.86) E09 | |
| 28 | 0.755 ± 0.013 | 36.5 ± 1.13 | 3.96 ± 0.53 | (9.29 ± 0.53) E09 | |
| 32 | 0.719 ± 0.027 | 39.5 ± 2.31 | 2.42 ± 0.42 | (1.22 ± 0.83) E10 | |
| 80 | 8 | 0.481 ± 0.052 | 59.6 ± 4.35 | 30.1 ± 2.74 | (1.13 ± 0.33) E07 |
| 13 | 0.440 ± 0.064 | 63.0 ± 5.42 | 20.1 ± 2.08 | (1.36 ± 0.15) E08 | |
| 18 | 0.421 ± 0.052 | 64.7 ± 4.33 | 16.0 ± 2.12 | (3.40 ± 0.29) E08 | |
| 23 | 0.409 ± 0.035 | 65.6 ± 2.98 | 13.7 ± 1.06 | (5.23 ± 0.38) E08 | |
| 28 | 0.460 ± 0.049 | 61.3 ± 4.15 | 11.3 ± 2.25 | (1.56 ± 0.64) E09 | |
| 32 | 0.422 ± 0.012 | 64.7 ± 1.05 | 7.90 ± 1.32 | (1.99 ± 0.13) E09 | |
| 110 | 8 | 0.260 ± 0.043 | 78.2 ± 3.62 | 45.7 ± 8.41 | (1.01 ± 0.25) E07 |
| 13 | 0.254 ± 0.059 | 78.7 ± 4.96 | 27.2 ± 1.89 | (4.15 ± 0.42) E07 | |
| 18 | 0.232 ± 0.014 | 80.5 ± 1.21 | 26.7 ± 2.46 | (6.93 ± 0.68) E07 | |
| 23 | 0.270 ± 0.063 | 77.3 ± 5.32 | 23.0 ± 2.35 | (1.34 ± 0.17) E08 | |
| 28 | 0.232 ± 0.040 | 80.5 ± 3.34 | 21.1 ± 1.20 | (3.18 ± 0.26) E08 | |
| 32 | 0.221 ± 0.051 | 81.4 ± 4.32 | 15.2 ± 1.15 | (3.73 ± 0.35) E08 | |
| 130 | 8 | 0.175 ± 0.024 | 85.3 ± 2.02 | 52.4 ± 8.52 | (8.39 ± 0.33) E06 |
| 13 | 0.173 ± 0.014 | 85.5 ± 1.17 | 38.3 ± 2.84 | (3.68 ± 0.28) E07 | |
| 18 | 0.170 ± 0.034 | 85.7 ± 2.98 | 37.3 ± 7.46 | (4.82 ± 0.17) E07 | |
| 23 | 0.183 ± 0.043 | 84.6 ± 3.58 | 35.4 ± 7.12 | (5.92 ± 0.55) E07 | |
| 28 | 0.175 ± 0.024 | 85.3 ± 2.05 | 33.6 ± 6.02 | (8.39 ± 0.48) E07 | |
| 32 | 0.169 ± 0.033 | 85.8 ± 2.81 | 23.4 ± 5.34 | (2.56 ± 0.97) E08 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Chen, J.; Zhu, Y.; Zhang, J.; Luo, G.; Cao, P.; Shen, Q.; Zhang, L. Correlation Between the Structure and Compressive Property of PMMA Microcellular Foams Fabricated by Supercritical CO2 Foaming Method. Polymers 2020, 12, 315. https://doi.org/10.3390/polym12020315
Zhang R, Chen J, Zhu Y, Zhang J, Luo G, Cao P, Shen Q, Zhang L. Correlation Between the Structure and Compressive Property of PMMA Microcellular Foams Fabricated by Supercritical CO2 Foaming Method. Polymers. 2020; 12(2):315. https://doi.org/10.3390/polym12020315
Chicago/Turabian StyleZhang, Ruizhi, Ju Chen, Yuxuan Zhu, Jian Zhang, Guoqiang Luo, Peng Cao, Qiang Shen, and Lianmeng Zhang. 2020. "Correlation Between the Structure and Compressive Property of PMMA Microcellular Foams Fabricated by Supercritical CO2 Foaming Method" Polymers 12, no. 2: 315. https://doi.org/10.3390/polym12020315
APA StyleZhang, R., Chen, J., Zhu, Y., Zhang, J., Luo, G., Cao, P., Shen, Q., & Zhang, L. (2020). Correlation Between the Structure and Compressive Property of PMMA Microcellular Foams Fabricated by Supercritical CO2 Foaming Method. Polymers, 12(2), 315. https://doi.org/10.3390/polym12020315