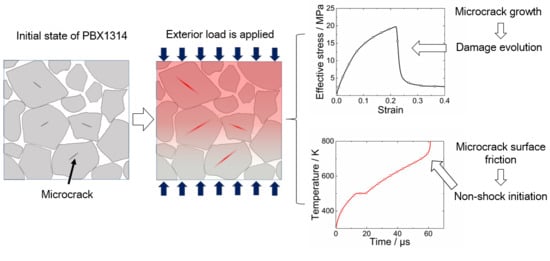
Dynamic Mechanical Damage and Non-Shock initiation of a New Polymer Bonded Explosive during Penetration
Abstract
:1. Introduction
2. Materials and Experiments
2.1. PBX1314 Composition
2.2. Penetration Experiment
3. Dynamic Damage Model of PBX1314
3.1. Dynamic Damage Model
3.2. Effects of the Microcracks and Binder on Dynamic Mechanical Properties of PBX1314
4. Non-Shock Initiation Model of PBX1314
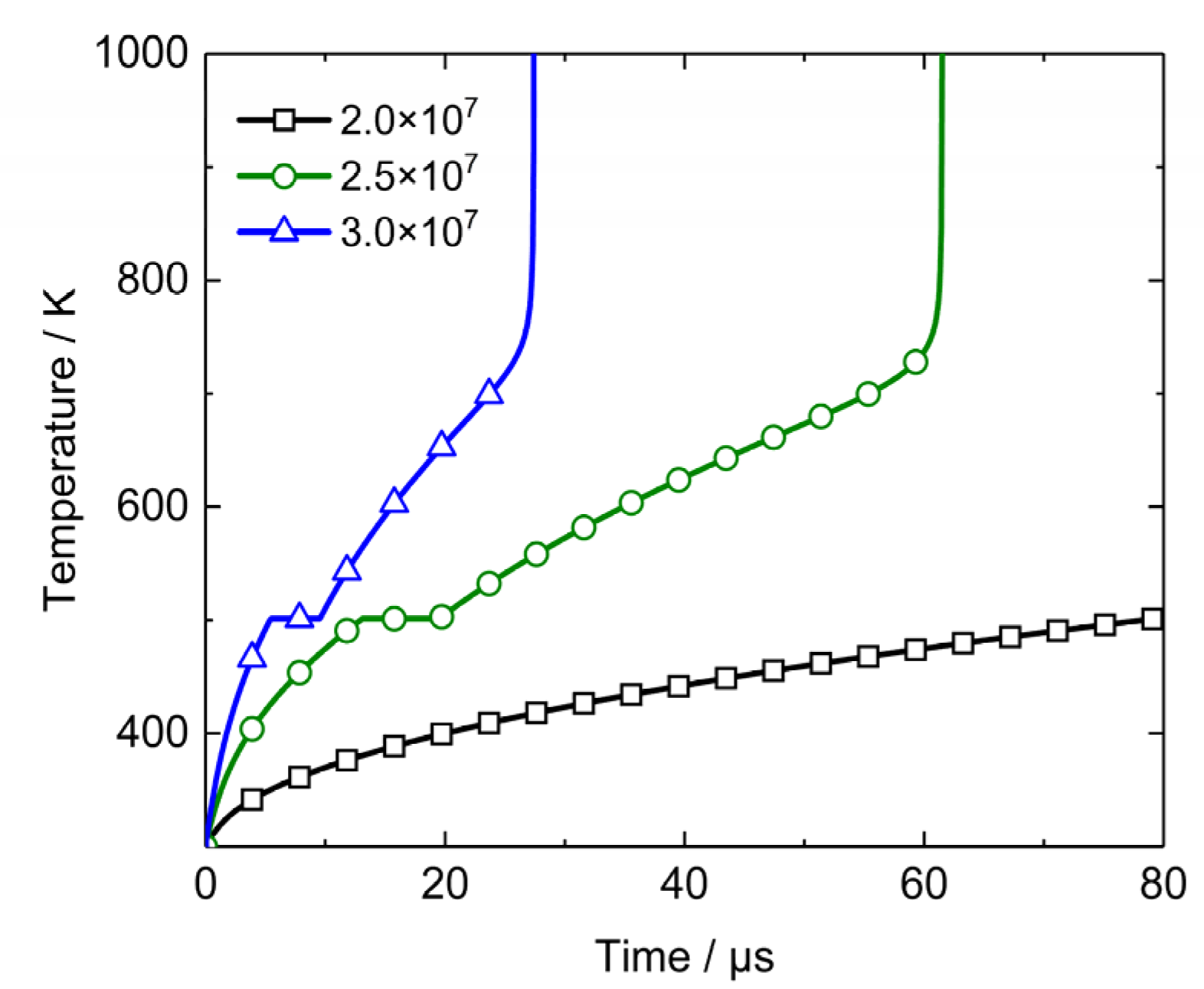
4.1. Bulk Temperature Increase in PBX1314
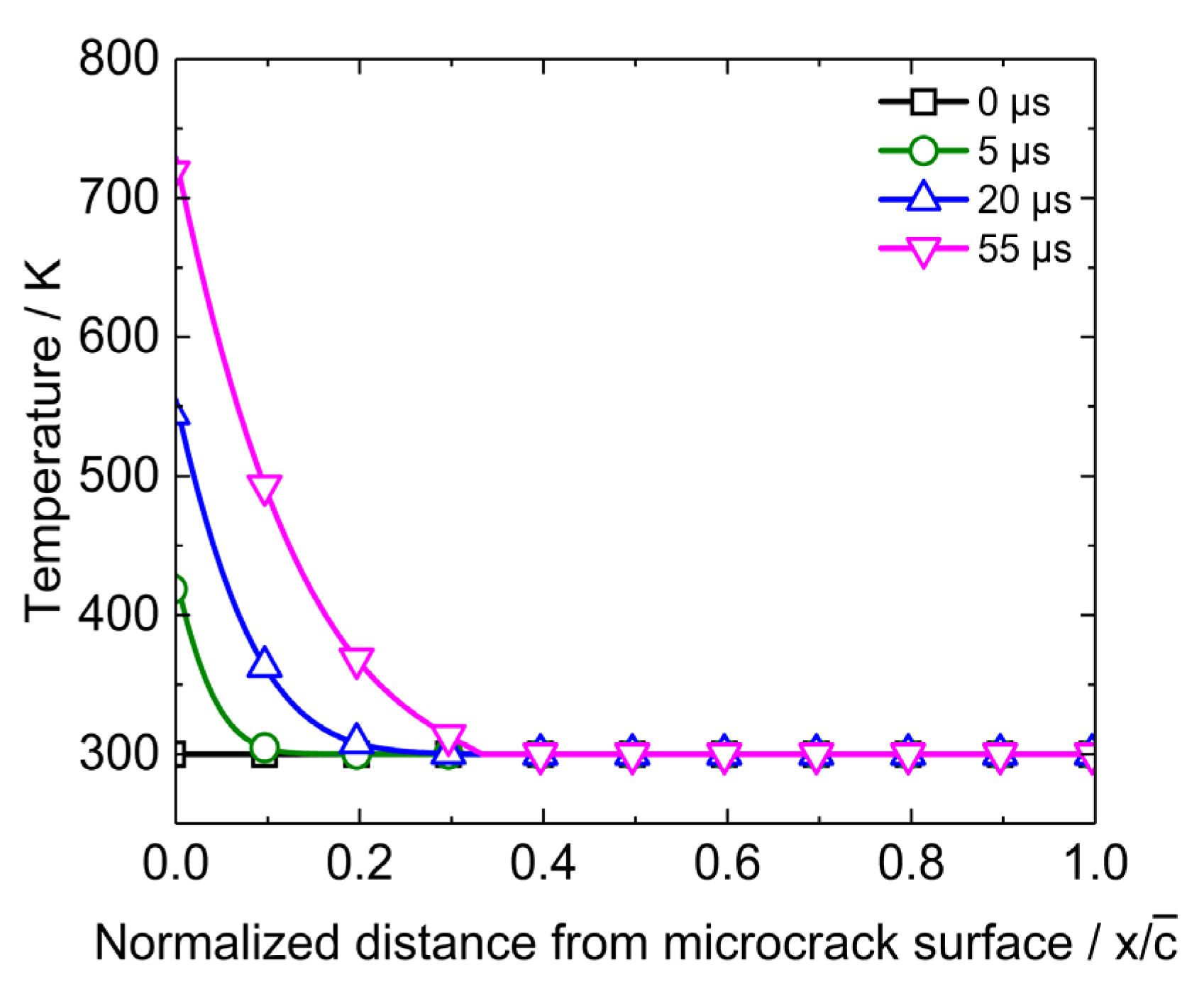
4.2. Energy Dissipation and Accumulation Near Microcracks
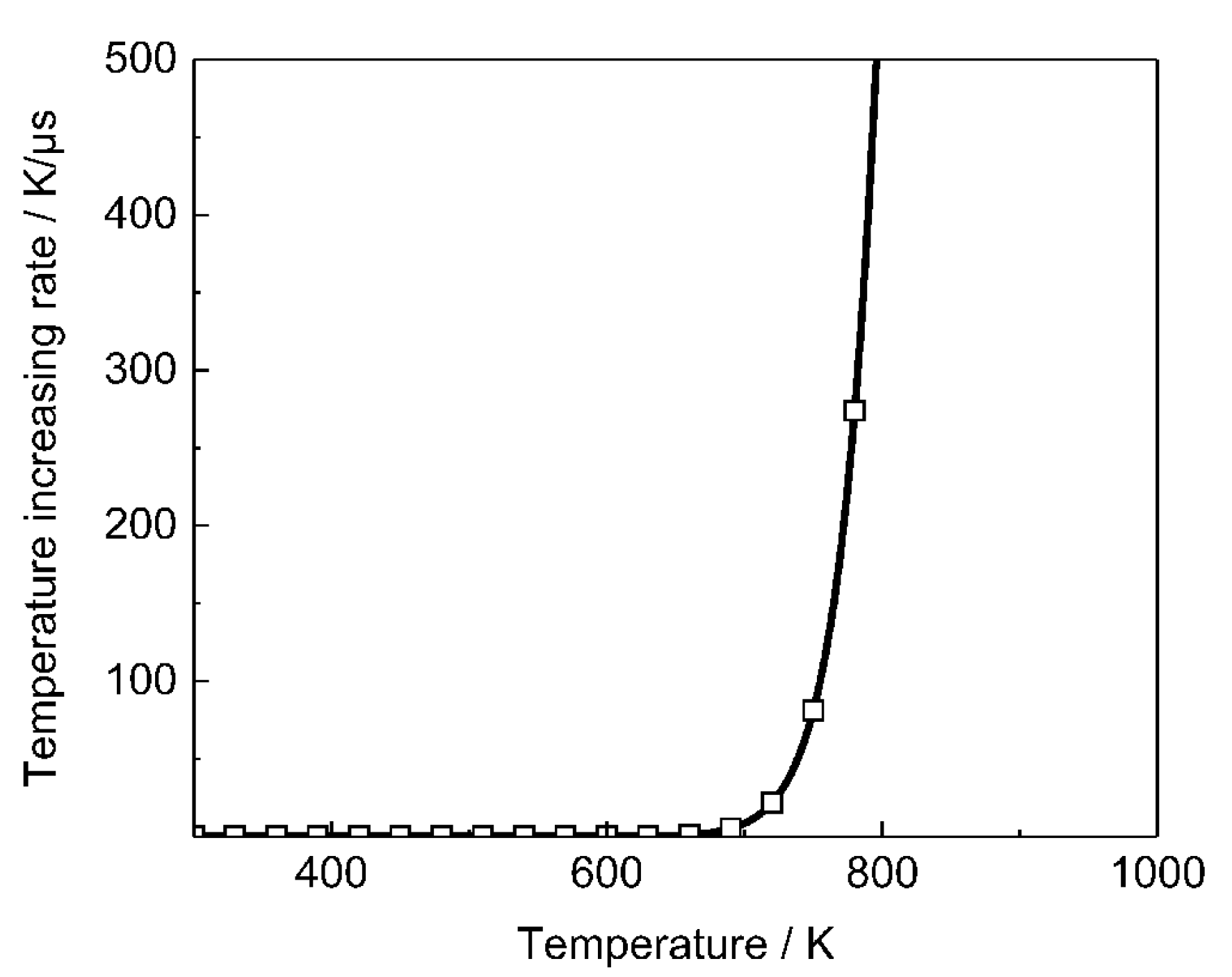
4.3. Temperature Increase in PBX1314 under Dynamic Loads
4.4. Non-Uniform Initiation Criterion
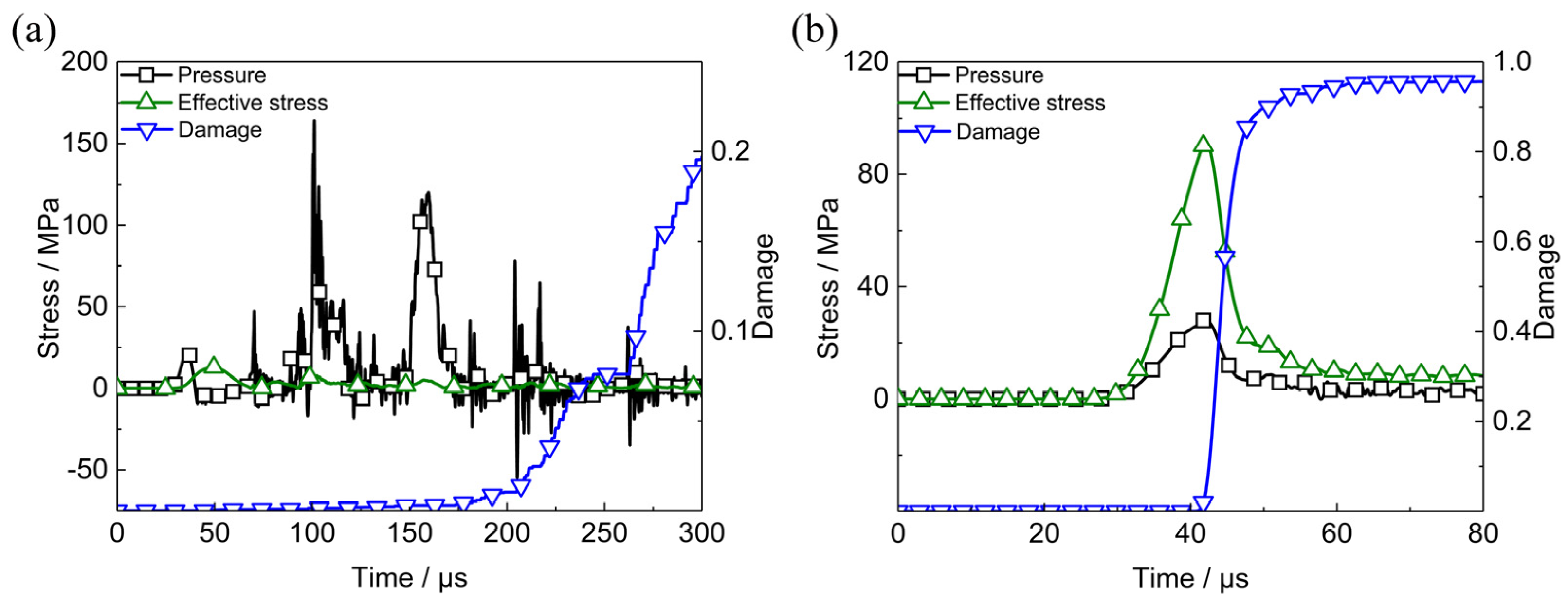
5. Damage and Initiation of PBX1314 during Penetration
5.1. Finite Element Model
5.2. Results of the Model that the Friction between Projectile Shell and PBX1314 Is Not Considered
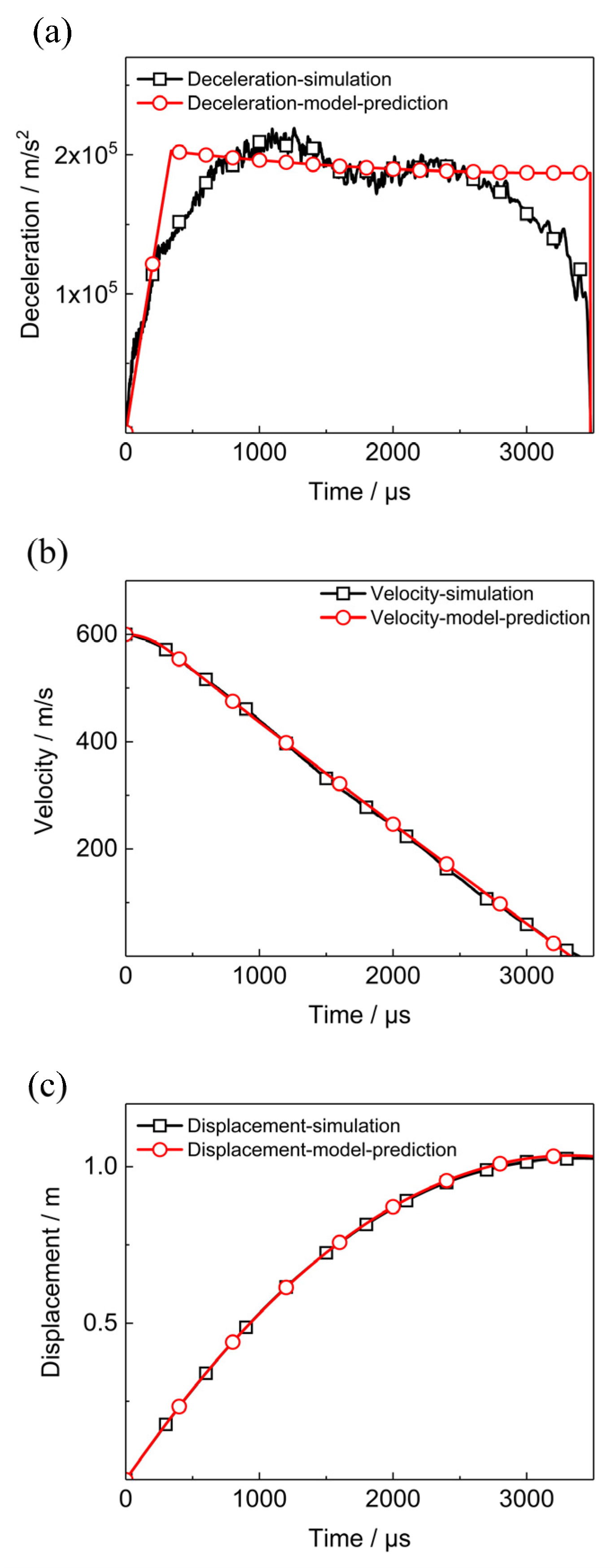
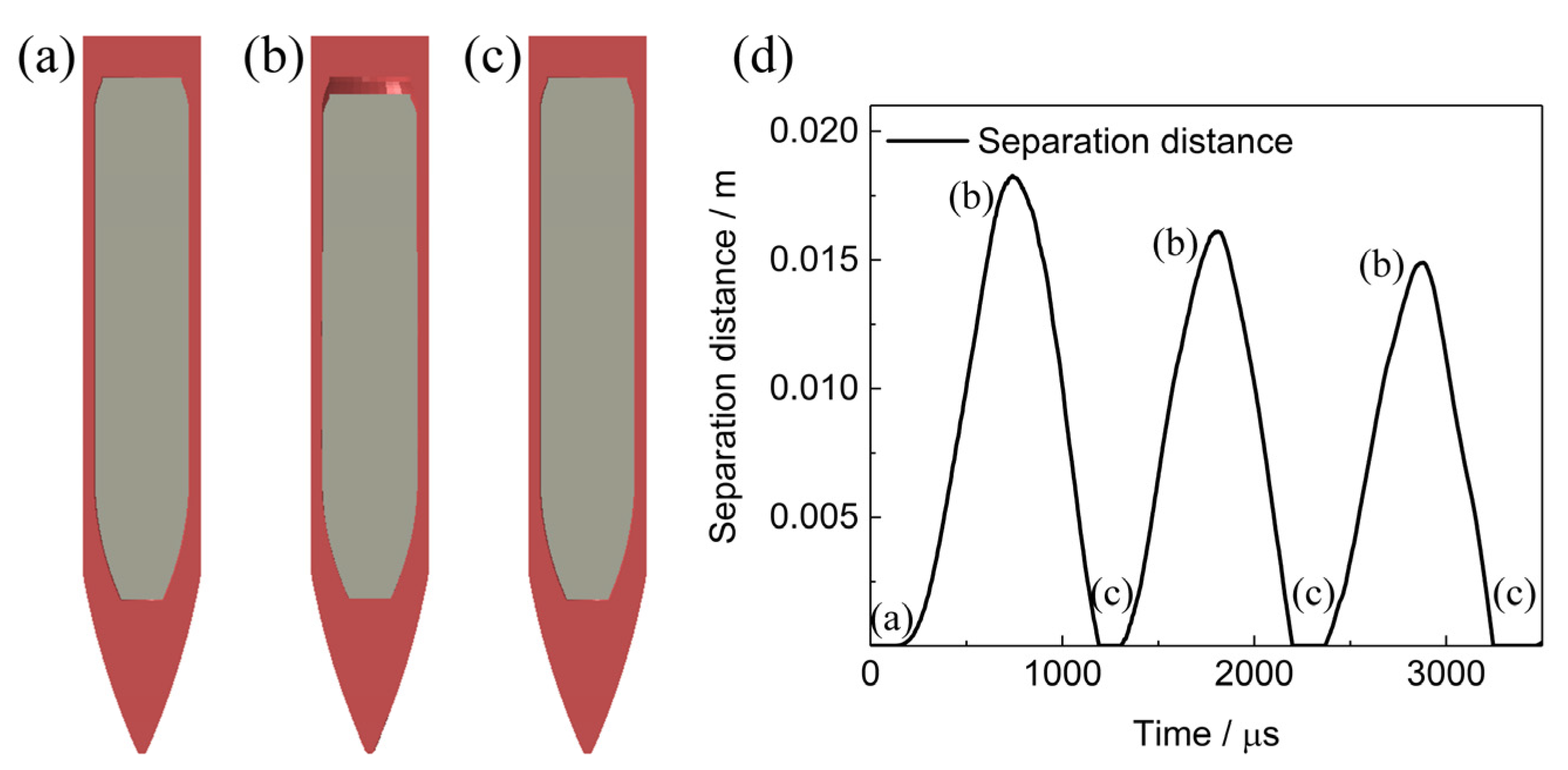
5.2.1. Deformation of PBX1314 Main Explosive during Penetration
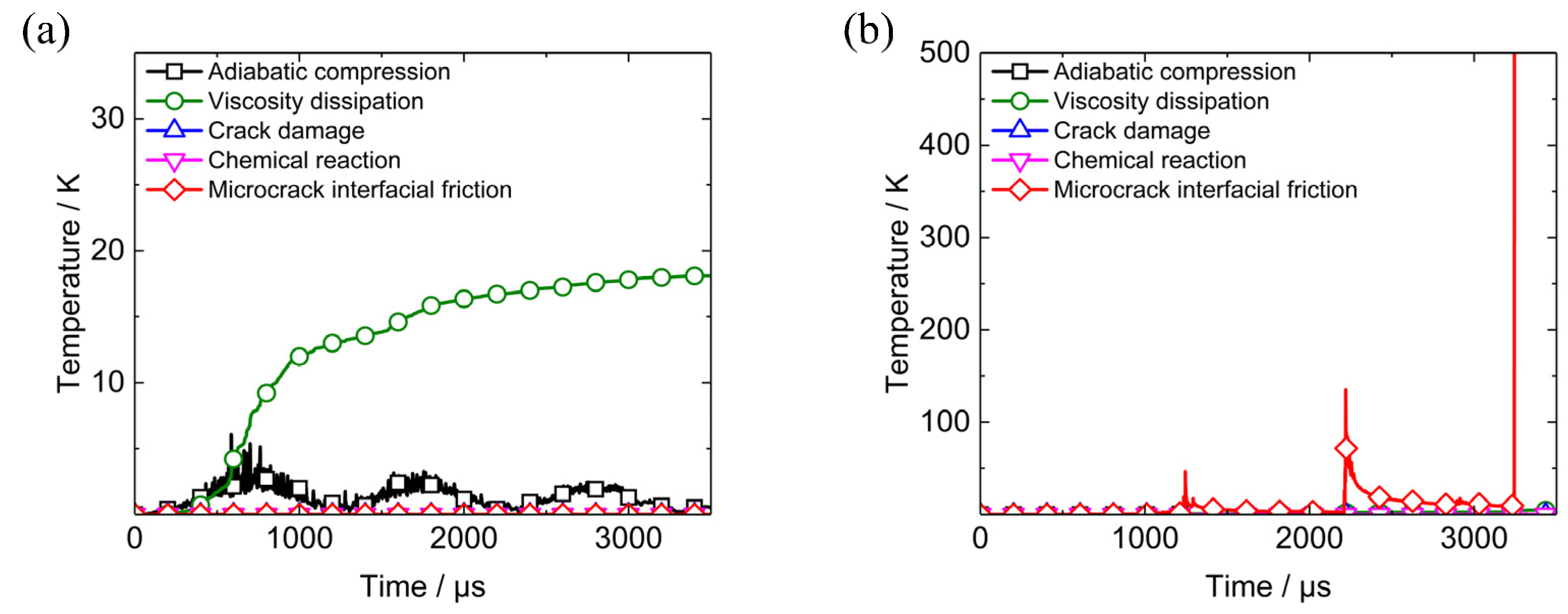
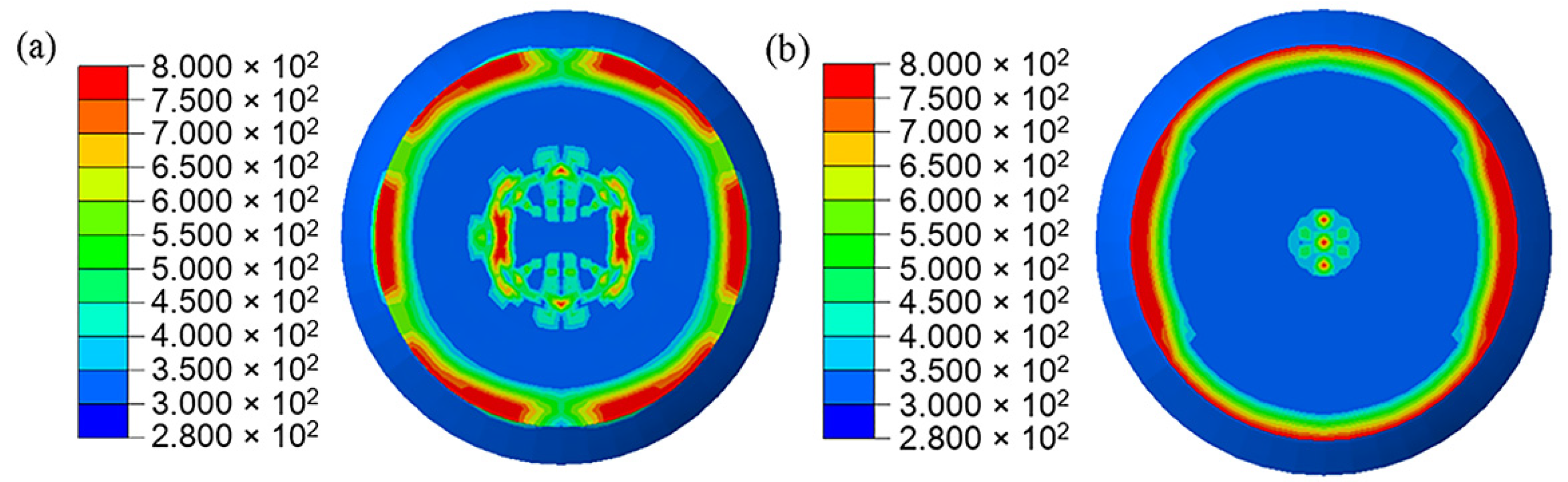
5.2.2. Damage Evolution and Heat Localization in PBX1314
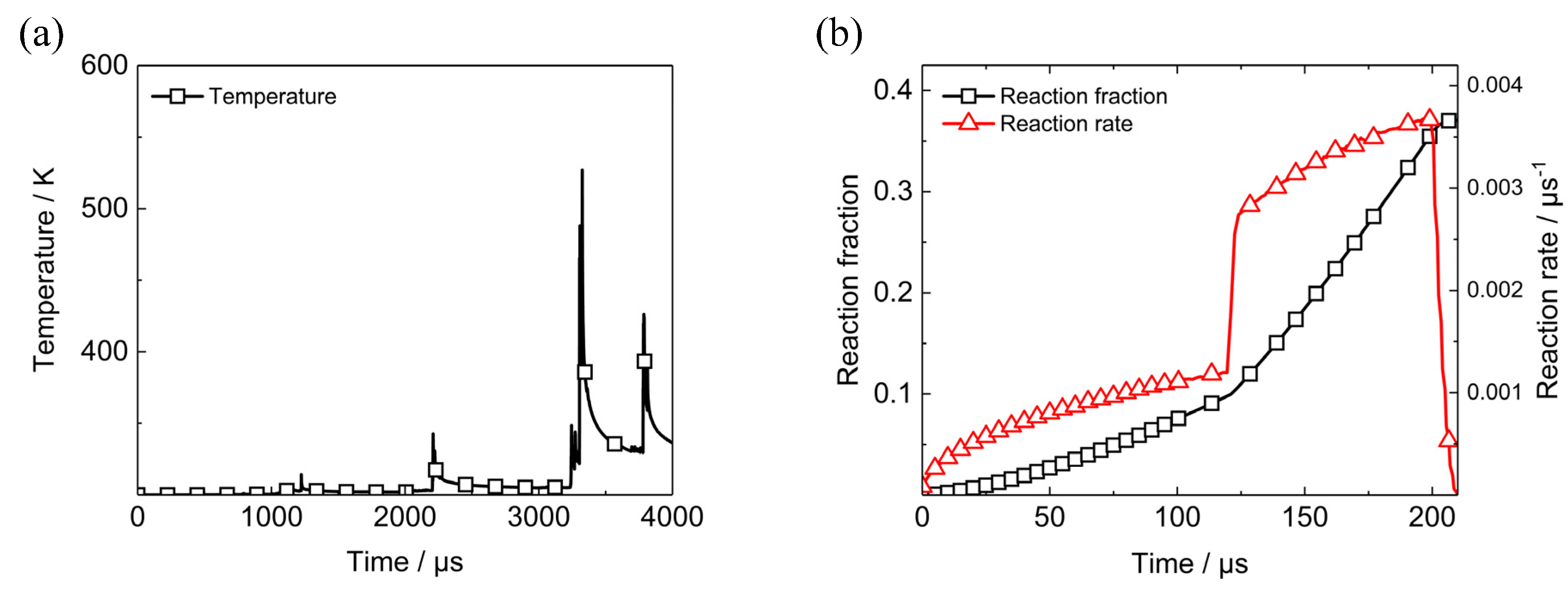
5.2.3. Reaction Process after Initiation of PBX1314
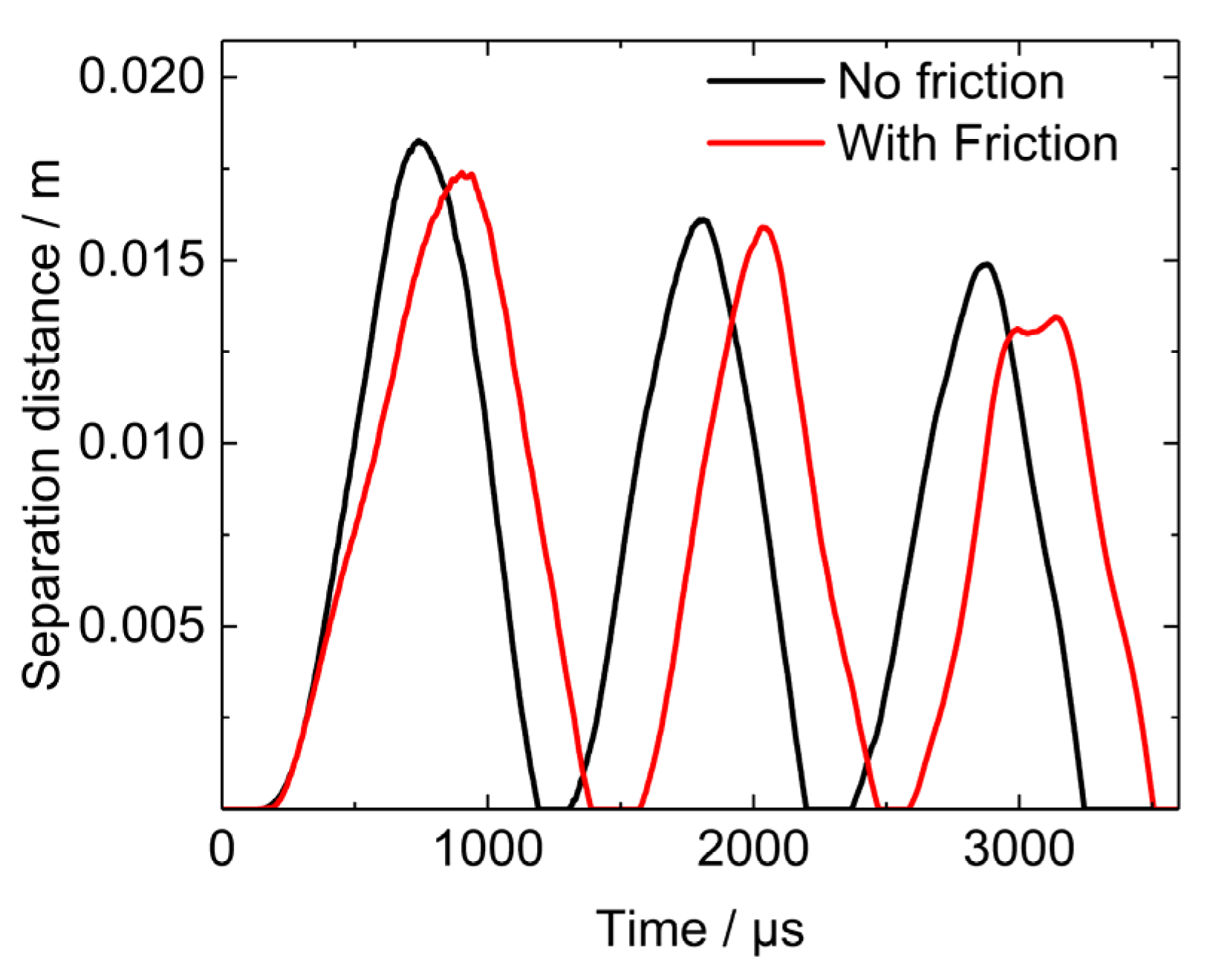
5.3. Effects of Friction between Projectile Shell and PBX1314
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Menikoff, R.; Shaw, M.S. Review of the Forest fire model for high explosives. Combust. Theory Model. 2008, 12, 569–604. [Google Scholar] [CrossRef]
- Johnson, J.N.; Tang, P.K.; Forest, C.A. Shock-wave initiation of heterogeneous reactive solids. J. Appl. Phys. 1985, 57, 4323–4334. [Google Scholar] [CrossRef]
- Lee, E.L.; Tarver, C.M. Phenomenological model of shock initiation in heterogeneous explosives. Phys. Fluids 1980, 23, 2362–2372. [Google Scholar] [CrossRef]
- Bennett, J.G.; Haberman, K.S.; Johnson, J.N.; Asay, B.W. A constitutive model for the non-shock ignition and mechanical response of high explosives. J. Mech. Phys. Solids 1998, 46, 2303–2322. [Google Scholar] [CrossRef]
- Dienes, J.; Zuo, Q.; Kershner, J. Impact initiation of explosives and propellants via statistical crack mechanics. J. Mech. Phys. Solids 2006, 54, 1237–1275. [Google Scholar] [CrossRef]
- Field, J.E. Hot spot ignition mechanisms for explosives. Acc. Chem. Res. 1992, 25, 489–496. [Google Scholar] [CrossRef]
- Barua, A.; Horie, Y.; Zhou, M. Energy localization in HMX-Estane polymer-bonded explosives during impact loading. J. Appl. Phys. 2012, 111, 054902. [Google Scholar] [CrossRef] [Green Version]
- Barua, A.; Zhou, M. A Lagrangian framework for analyzing microstructural level response of polymer-bonded explosives. Model. Simul. Mater. Sci. Eng. 2011, 19, 055001. [Google Scholar] [CrossRef]
- Barua, A.; Kim, S.; Horie, Y.; Zhou, M. Ignition criterion for heterogeneous energetic materials based on hotspot size-temperature threshold. J. Appl. Phys. 2013, 113, 064906. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wu, Y.; Huang, F. Numerical mesoscopic investigations of dynamic damage and failure mechanisms of polymer bonded explosives. Int. J. Solids Struct. 2017, 129, 28–39. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Huang, F. Thermal–mechanical–chemical responses of polymer-bonded explosives using a mesoscopic reactive model under impact loading. J. Hazard. Mater. 2017, 321, 256–267. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wu, Y.; Huang, F.; Jiao, T.; Clifton, R.J. Mesoscale thermal-mechanical analysis of impacted granular and polymer-bonded explosives. Mech. Mater. 2016, 99, 68–78. [Google Scholar] [CrossRef]
- LaBarbera, D.; Zikry, M. Dynamic fracture and local failure mechanisms in heterogeneous RDX-Estane energetic aggregates. J. Mater. Sci. 2015, 50, 5549–5561. [Google Scholar] [CrossRef]
- LaBarbera, D.; Zikry, M. Heterogeneous thermo-mechanical behavior and hot spot formation in RDX–estane energetic aggregates. Int. J. Solids Struct. 2015, 62, 91–103. [Google Scholar] [CrossRef]
- Duarte, C.A.; Kohler, R.; Koslowski, M. Dynamic fracture and frictional heating due to periodic excitation in energetic materials. J. Appl. Phys. 2018, 124, 165109. [Google Scholar] [CrossRef]
- Grilli, N.; Duarte, C.A.; Koslowski, M. Dynamic fracture and hot-spot modeling in energetic composites. J. Appl. Phys. 2018, 123, 065101. [Google Scholar] [CrossRef]
- Dienes, J.K. A statistical theory of fragmentatio0n processes. Mech. Mater. 1985, 4, 325–335. [Google Scholar] [CrossRef] [Green Version]
- Dienes, J.K.; Kershner, J. Multiple-Shock Initiation Via Statistical Crack Mechanics; Los Alamos National Lab.: Los Alamos, NM, USA, 1998. [Google Scholar]
- Yang, K.; Wu, Y.; Huang, F. Numerical simulations of microcrack-related damage and ignition behavior of mild-impacted polymer bonded explosives. J. Hazard. Mater. 2018, 356, 34–52. [Google Scholar] [CrossRef]
- Hackett, R.M.; Bennett, J.G. An implicit finite element material model for energetic particulate composite materials. Int. J. Numer. Methods Eng. 2000, 49, 1191–1209. [Google Scholar] [CrossRef]
- Liu, R.; Chen, P. Modeling ignition prediction of HMX-based polymer bonded explosives under low velocity impact. Mech. Mater. 2018, 124, 106–117. [Google Scholar] [CrossRef]
- Xiao, Y.C.; Sun, Y.; Li, X.; Zhang, Q.; Liu, S.; Yang, H. Dynamic mechanical behavior of PBX. Propellants Explos. Pyrotech. 2016, 41, 629–636. [Google Scholar] [CrossRef]
- Xiao, Y.; Sun, Y.; Wang, Z. Investigating the static and dynamic tensile mechanical behaviour of polymer-bonded explosives. Strain 2018, 54, e12262. [Google Scholar] [CrossRef]
- Xiao, Y.; Sun, Y.; Li, X.; Zhang, Q. Dynamic compressive properties of polymer bonded explosives under confining pressure. Propellants Explos. Pyrotech. 2017, 42, 873–882. [Google Scholar] [CrossRef]
- Li, X.; Sun, Y.; Zhao, H.; Xiao, Y.; Cai, X.; Zhang, Q.; Zhang, W. A Systematic Method to Determine and Test the Ignition and Growth Reactive Flow Model Parameters of a Newly Designed Polymer-Bonded Explosive. Propellants Explos. Pyrotech. 2018, 43, 948–954. [Google Scholar] [CrossRef]
- Xiao, Y.; Sun, Y.; Zhen, Y.; Guo, L.; Yao, L. Characterization, modeling and simulation of the impact damage for polymer bonded explosives. Int. J. Impact Eng. 2017, 103, 149–158. [Google Scholar] [CrossRef]
- Vandersall, K.S.; Tarver, C.M.; Garcia, F.; Chidester, S.K. On the low pressure shock initiation of octahydro-1, 3, 5, 7–tetranitro-1, 3, 5, 7-tetrazocine based plastic bonded explosives. J. Appl. Phys. 2010, 107, 094906. [Google Scholar] [CrossRef]
- Addessio, F.L.; Johnson, J.N. A constitutive model for the dynamic response of brittle materials. J. Appl. Phys. 1990, 67, 3275–3286. [Google Scholar] [CrossRef]
- Zuo, Q.; Addessio, F.; Dienes, J.; Lewis, M. A rate-dependent damage model for brittle materials based on the dominant crack. Int. J. Solids Struct. 2006, 43, 3350–3380. [Google Scholar] [CrossRef] [Green Version]
- Zuo, Q.; Dienes, J. On the stability of penny-shaped cracks with friction: The five types of brittle behavior. Int. J. Solids Struct. 2005, 42, 1309–1326. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R. A computational constitutive model for glass subjected to large strains, high strain rates and high pressures. J. Appl. Mech. 2011, 78, 051003. [Google Scholar] [CrossRef]
- Forrestal, M.; Altman, B.; Cargile, J.; Hanchak, S. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets. Ini. J. Impact Egn. 1994, 15, 395–405. [Google Scholar] [CrossRef]
- Perry, W.L.; Gunderson, J.A.; Balkey, M.M.; Dickson, P.M. Impact-induced friction ignition of an explosive: Infrared observations and modeling. J. Appl. Phys. 2010, 108, 084902. [Google Scholar] [CrossRef]
- Dienes. Frictional Hot-Spots and Propellant Sensitivity. Proc. Mater. Res. Soc. Symp. 1984, 24, 373–381. [Google Scholar]
- Ma, D.; Chen, P.; Qiang, Z.; Dai, K. Ignition criterion and safety prediction of explosives under low velocity impact. J. Appl. Phys. 2013, 114, 113505. [Google Scholar] [CrossRef]













| Parameter | Value | Parameter | Value |
|---|---|---|---|
| G(1) (MPa) | 472 | vmax (m/s) | 300 |
| G(2) (MPa) | 115.94 | c0 (m) | 0.00003 |
| G(3) (MPa) | 83.56 | γ0 (J·m−2) | 50 |
| G(4) (MPa) | 4.27 | ρ (kg·m−3) | 1690 |
| G(5) (MPa) | 35 | μs | 0.5 |
| τ(1)(μs) | 0.75 | μd | 0.2 |
| τ(2) (μs) | 7.5 | CV (J·Kg−1·K−1) | 970 |
| τ(3) (μs) | 75 | k (J·m−1·s−1·K−1) | 0.292 |
| τ(4) (μs) | 750 | ||
| τ(5) (μs) | ∞ | Tm (K) | 501.9 |
| ν | 0.49 | Qr (J·Kg−1) | 2.09 × 106 |
| m | 10 | E (J·mol−1) | 2.37 × 105 |
| a (m) | 0.002 |
| Coefficient | Value | Coefficient | Value |
|---|---|---|---|
| P1 | 6.834 × 10−12 | P5 | 9.711 × 10−6 |
| P2 | 1.422 × 10−3 | P6 | 2.010 × 10−2 |
| P3 | 2.849 × 10−19 | P7 | −1.931 |
| P4 | 3.550 × 10−2 | P8 | −1.639 × 10−4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Liu, Y.; Sun, Y. Dynamic Mechanical Damage and Non-Shock initiation of a New Polymer Bonded Explosive during Penetration. Polymers 2020, 12, 1342. https://doi.org/10.3390/polym12061342
Li X, Liu Y, Sun Y. Dynamic Mechanical Damage and Non-Shock initiation of a New Polymer Bonded Explosive during Penetration. Polymers. 2020; 12(6):1342. https://doi.org/10.3390/polym12061342
Chicago/Turabian StyleLi, Xiao, Yizhi Liu, and Yi Sun. 2020. "Dynamic Mechanical Damage and Non-Shock initiation of a New Polymer Bonded Explosive during Penetration" Polymers 12, no. 6: 1342. https://doi.org/10.3390/polym12061342
APA StyleLi, X., Liu, Y., & Sun, Y. (2020). Dynamic Mechanical Damage and Non-Shock initiation of a New Polymer Bonded Explosive during Penetration. Polymers, 12(6), 1342. https://doi.org/10.3390/polym12061342