A New Polymer-Based Mechanical Metamaterial with Tailorable Large Negative Poisson’s Ratios
Abstract
:1. Introduction
2. Methodology
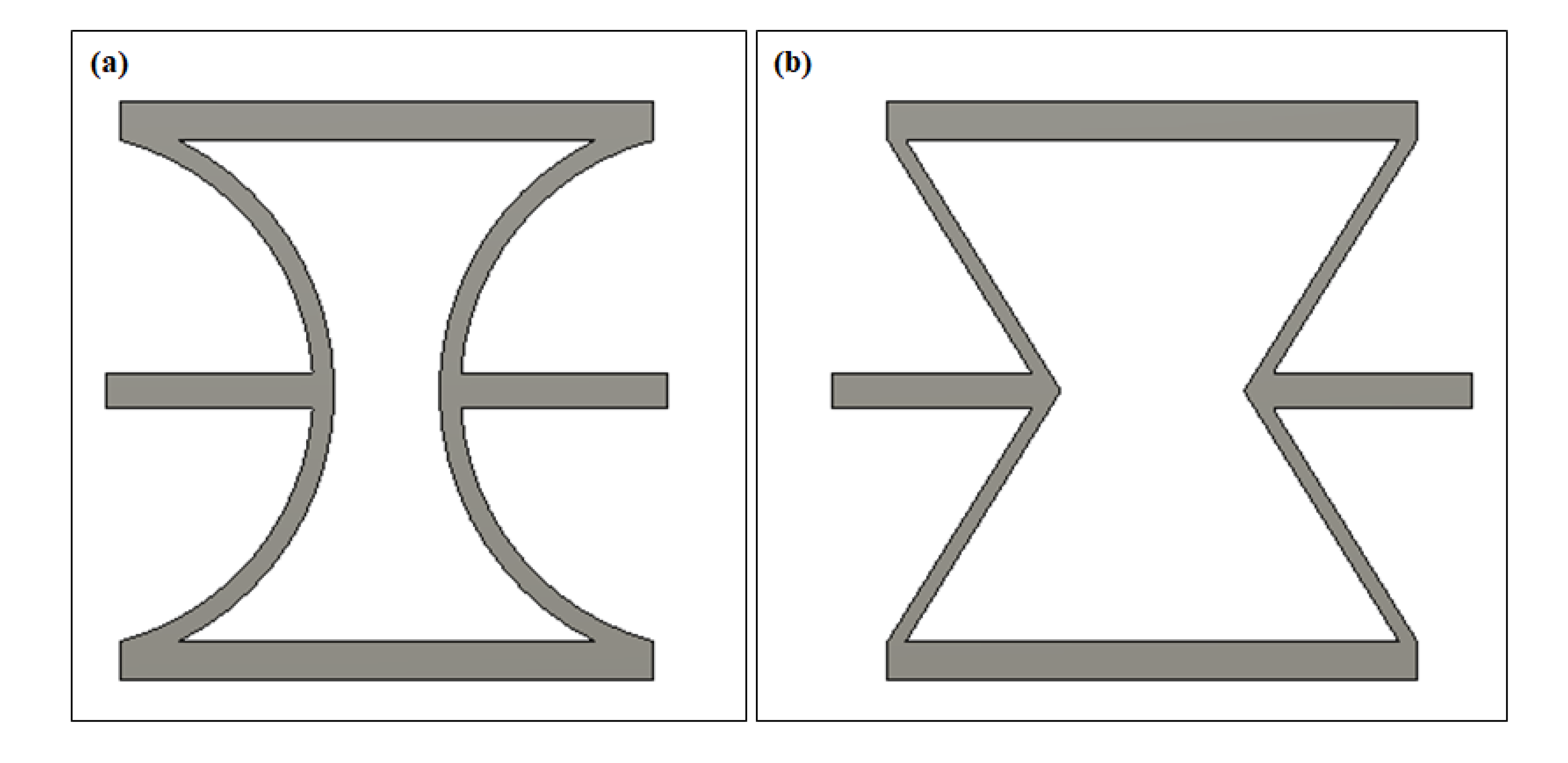
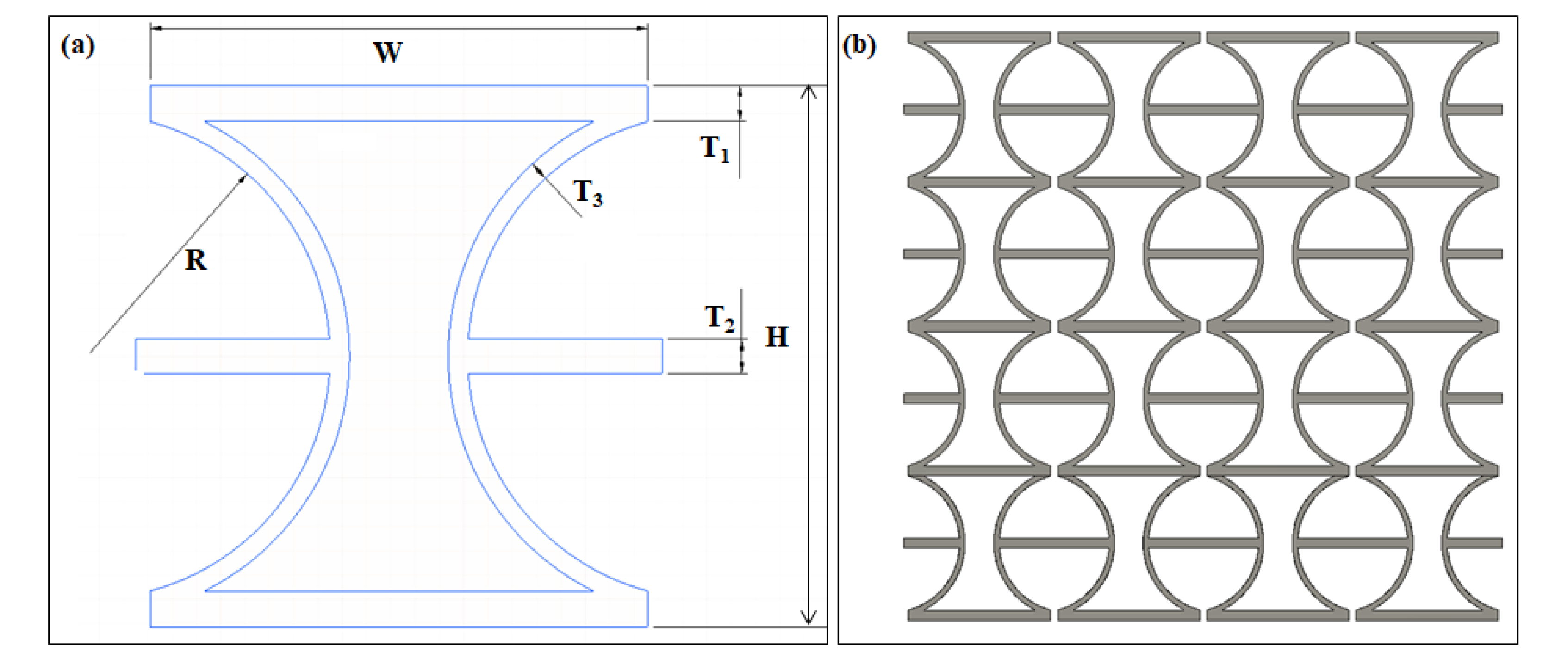
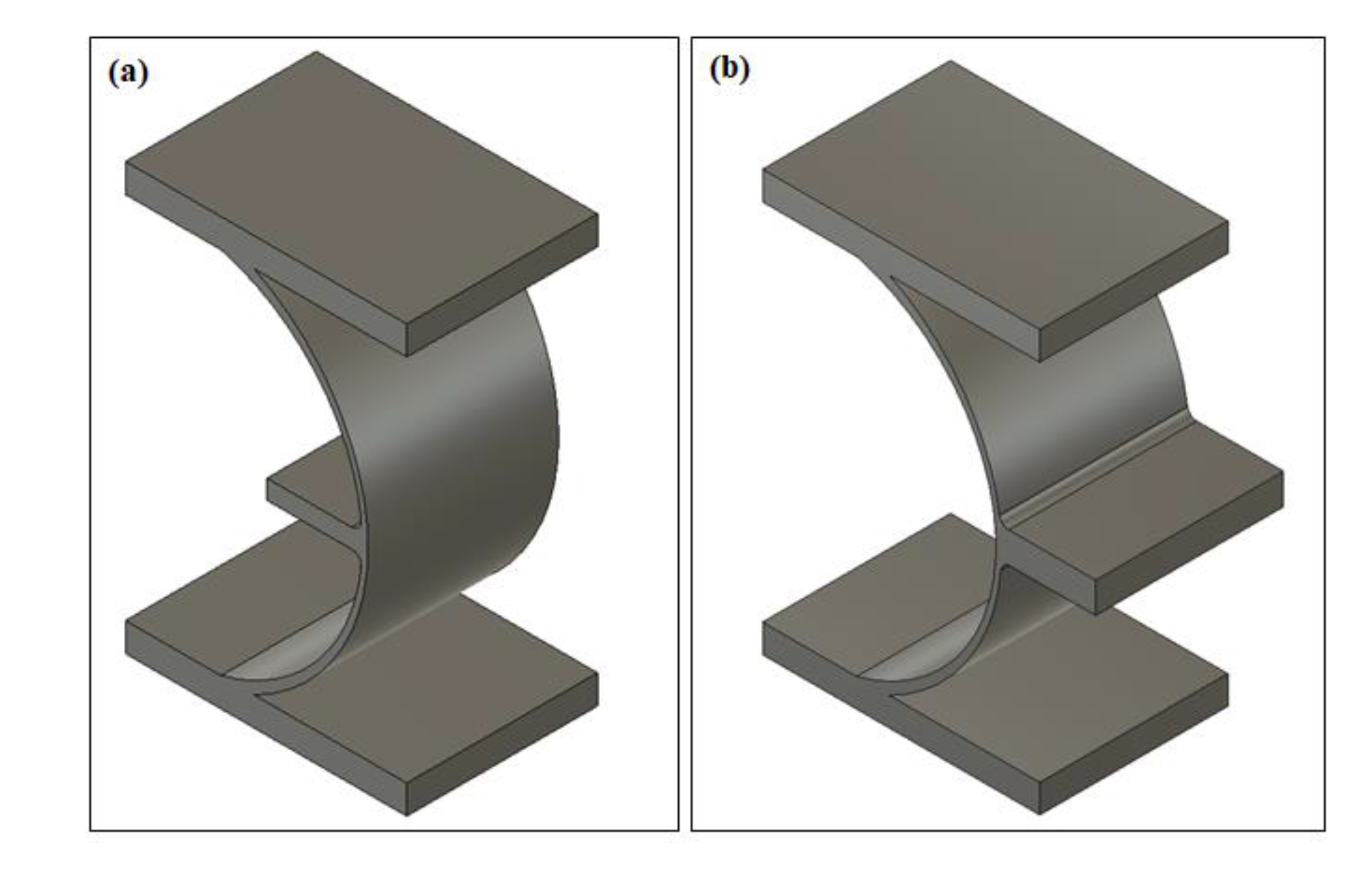
2.1. Microstructural Design
2.2. Finite Element Analysis
- Geometries of the specimens are assumed to be perfect. Surface and internal defects by the manufacturing process are negligible.
- The raw material applied to this design is isotropic, the possible anisotropy of structure due to 3D printing technique is neglected.
- Fixed boundaries are applied onto the bottom surface as a simplification. Loadings are displacement-controlled and applied to the top surface of the specimen.
- There is no out-plane distortion during compression.
2.3. 3D-Printing and Uniaxial Tensile/Compressive Tests
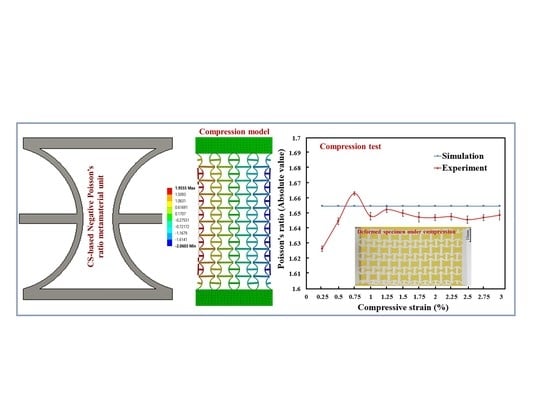
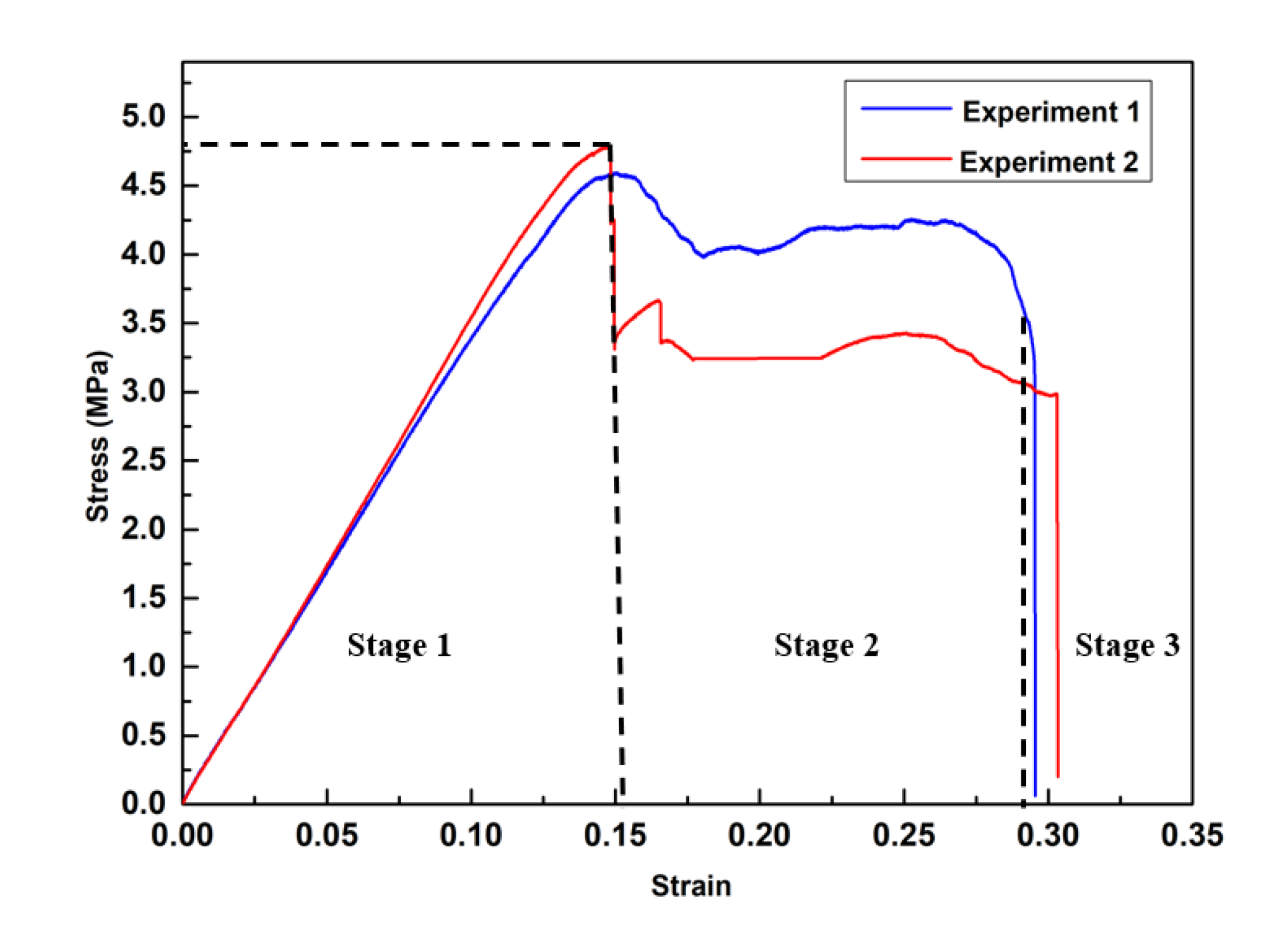
3. Results
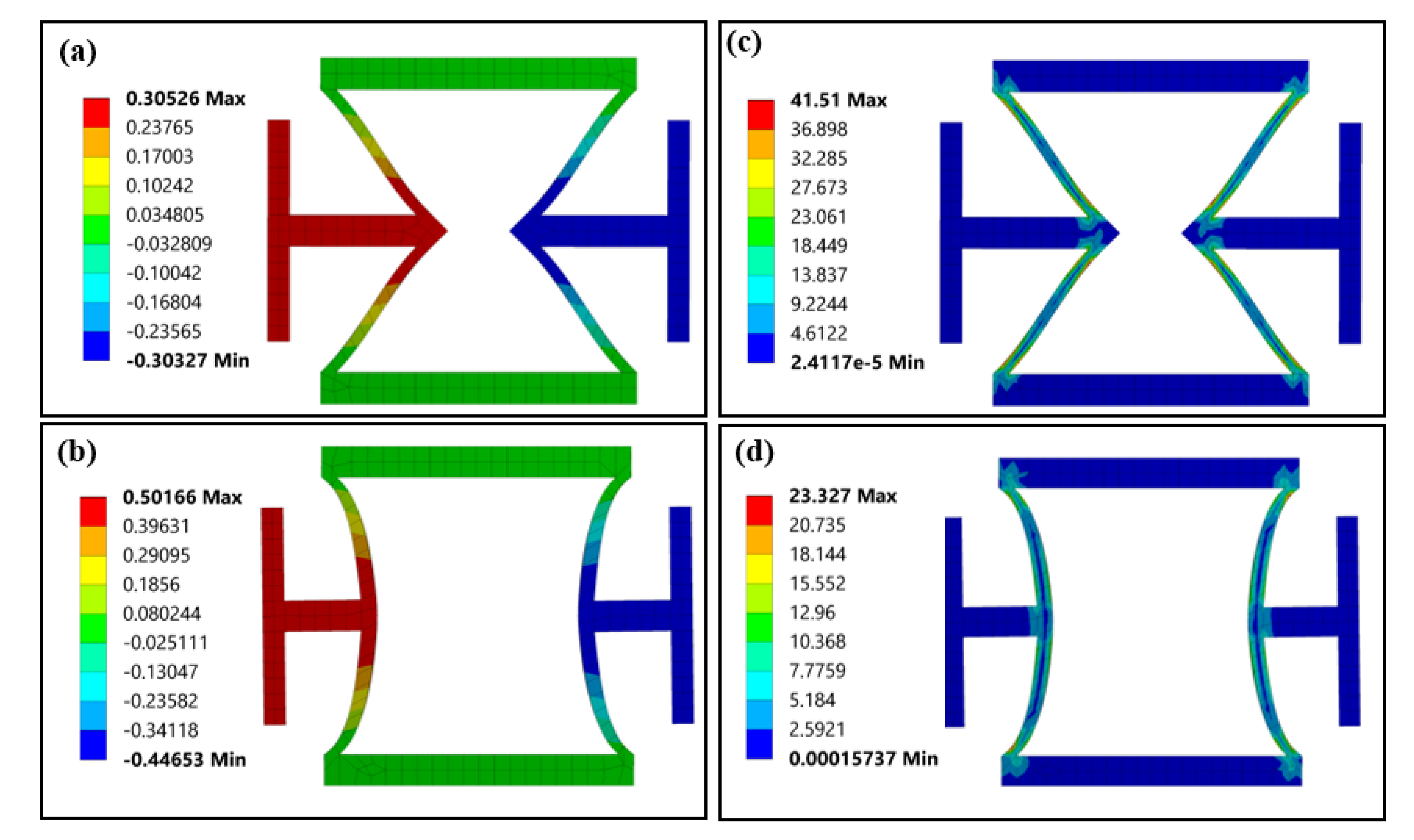
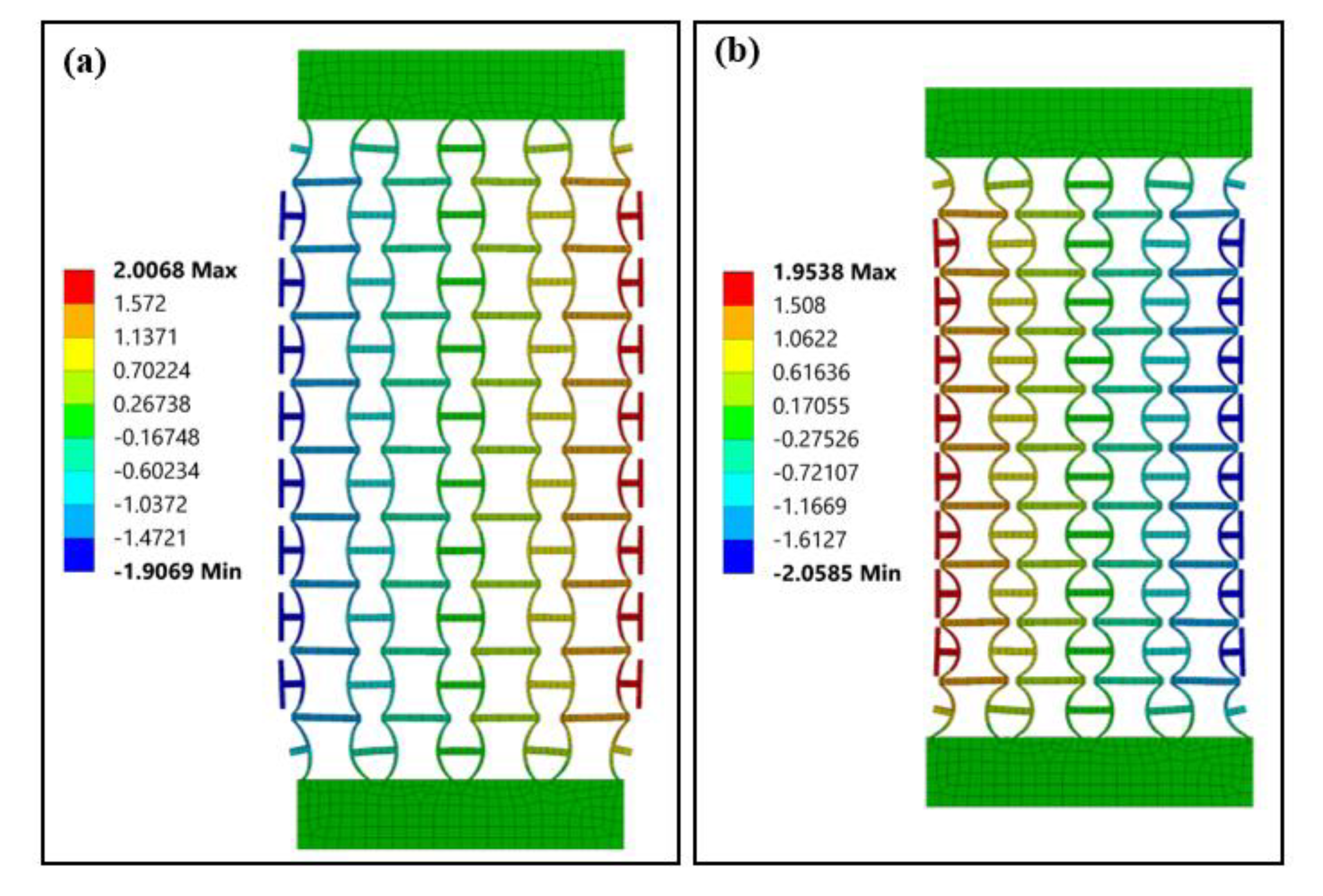
3.1. Finite Element Analysis Results
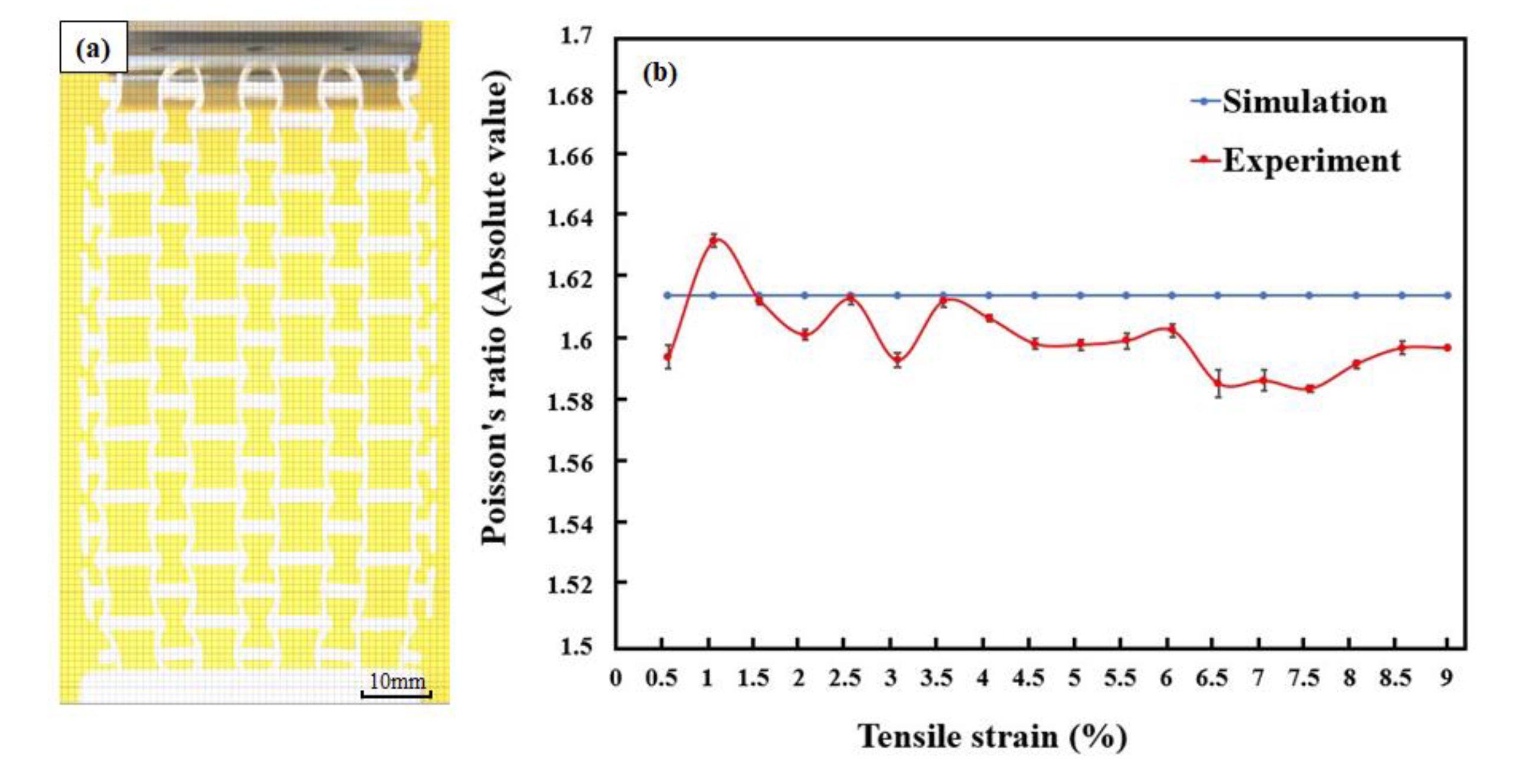
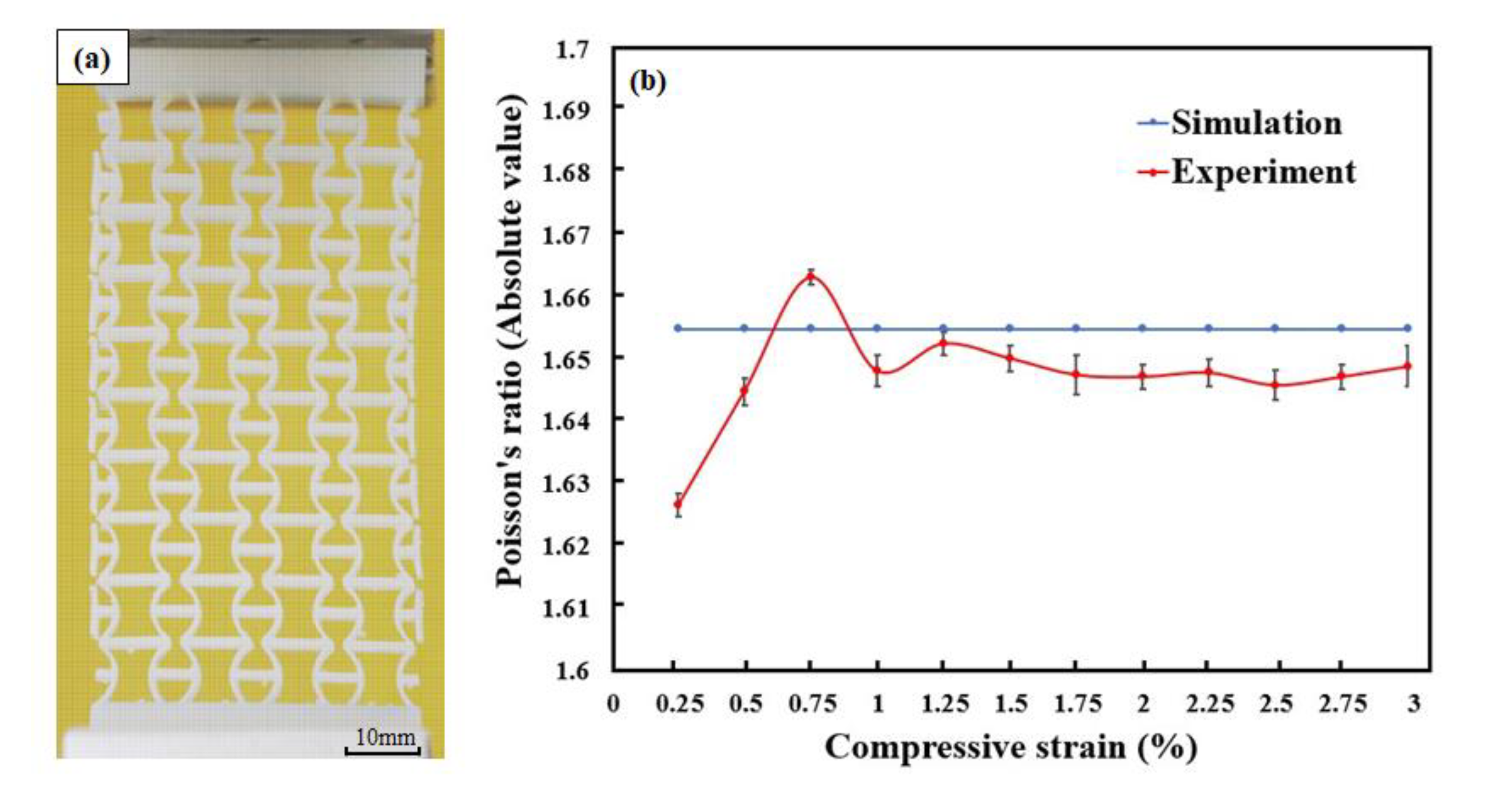
3.2. Experimental Test Results
4. Discussion
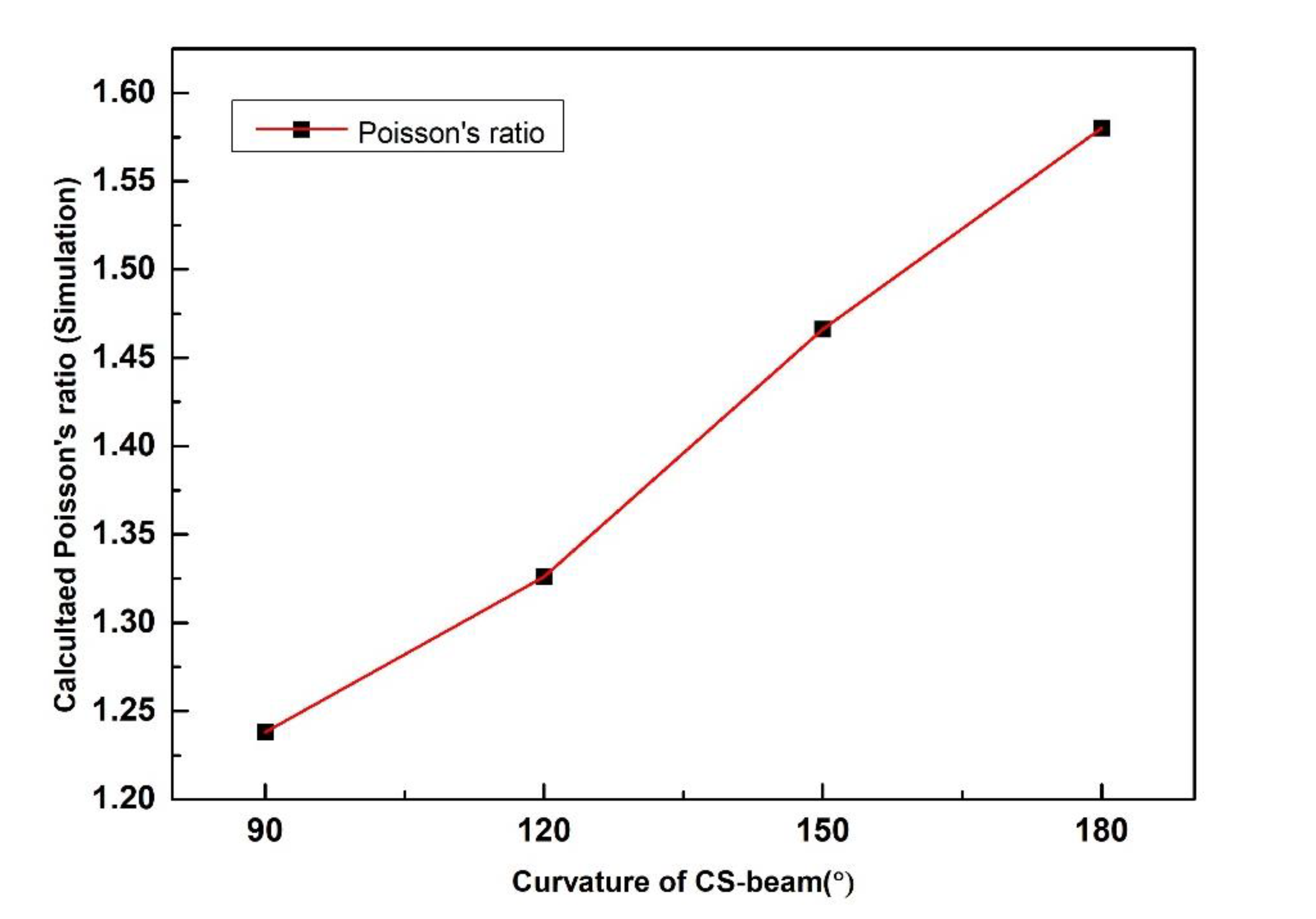
4.1. Universality of Cylindrical-Shell-Based Structures
4.2. Wearable Generator Based on Cylindrical-Shell-Based NPR Metamaterial
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Ren, C.; Yang, D.; Qin, H. Mechanical performance of multidirectional buckling-based ngative stiffness metamaterials: An analytical and numerical study. Materials. 2018, 11, 1078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zadpoor, A.A. Mechanical meta-materials. Mater. Horiz. 2016, 3, 371–381. [Google Scholar] [CrossRef] [Green Version]
- Miller, W.; Smith, C.W.; Mackenzie, D.S.; Evans, K.E. Negative thermal expansion: A review. J. Mater. Sci. 2009, 44, 5441–5451. [Google Scholar] [CrossRef]
- Li, S.; Hassanin, H.; Attallah, M.M.; Adkins, N.J.E.; Essa, K. The development of TiNi-based negative Poisson’s ratio structure using selective laser melting. Acta Mater. 2016, 105, 75–83. [Google Scholar] [CrossRef] [Green Version]
- Schwerdtfeger, J.; Heinl, P.; Singer, R.F.; Körner, C. Auxetic cellular structures through selective electron-beam melting. Phys. Status Solidi B Basic Res. 2010, 247, 269–272. [Google Scholar] [CrossRef]
- Bose, P.; Pandey, K.M. Desirability and Assessment of Mechanical Strength Characteristics of Solid Propellant for Use in Multi Barrel Rocket Launcher. Int. J Chem. Eng. 2012, 5, 114–124. [Google Scholar] [CrossRef]
- Zhang, L. Solid Mechanics for Engineers; Palgrave: Basingstoke, UK, 2001. [Google Scholar]
- Lakes, R.J. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Mizzi, L.; Mahdi, E.M.; Titov, K.; Gatt, R.; Attard, D.; Evans, K.E.; Grima, J.N.; Tan, J.C. Mechanical metamaterials with star-shaped pores exhibiting negative and zero Poisson’s ratio. Mater. Des. 2018, 146, 28–37. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Gambarotta, L. Homogenization of periodic hexa- and tetrachiral cellular solids. Compos. Struct. 2014, 116, 461–476. [Google Scholar] [CrossRef] [Green Version]
- Alderson, A.; Alderson, K.L.; Attatd, D.; Evans, K.E.; Gatt, R.; Grima, J.N.; Miller, W.; Ravirala, N.; Smith, C.W.; Zied, K. Elastic constants of 3-, 4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading. Compos. Sci. Technol. 2010, 70, 1042–1048. [Google Scholar] [CrossRef] [Green Version]
- Nežerka, V.; Somr, M.; Vorel, J.; Doskar, M.; Antos, J.; Zeman, J.; Novak, J. A jigsaw puzzle metamaterial concept. Compos. Struct. 2018, 202, 1275–1279. [Google Scholar] [CrossRef] [Green Version]
- Taylor, M.; Francesconi, L.; Gerendas, M.; Shanian, A.; Carson, C.; Bertoldi, K. Low porosity metallic periodic structures with negative Poisson’s ratio. Adv. Mater. 2014, 26, 65–70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hewage, T.; Alderson, K.; Alderson, A.; Scarpa, F. Double—Negative Mechanical Metamaterials Displaying Simultaneous Negative Stiffness and Negative Poisson’s Ratio Properties. Adv. Mater. 2016, 28, 10323–10332. [Google Scholar] [CrossRef]
- Yang, H.; Ma, L. Multi-stable mechanical metamaterials with shape-reconfiguration and zero Poisson’s ratio. Mater. Des. 2018, 152, 181–190. [Google Scholar] [CrossRef]
- Qiu, J.; Lang, J.H.; Slocum, A.H. A Curved-Beam Bistable Mechanism. J. Microelectromech. Syst. 2004, 13, 137–146. [Google Scholar] [CrossRef]
- Larsen, U.D.; Signund, S.; Bouwsta, S. Design and fabrication of compliant micromechanisms and structures with negative Poisson’s ratio. J. Microelectromech. Syst. 1997, 6, 99–106. [Google Scholar] [CrossRef] [Green Version]
- Rafsanjani, A.; Akbarzadeh, A.; Pasini, D. Snapping mechanical metamaterials under tension. Adv. Mater. 2015, 27, 5931–5935. [Google Scholar] [CrossRef] [Green Version]
- Shan, S.; Kang, S.H.; Raney, J.R.; Wang, P.; Fang, L.; Candido, F.; Lewis, J.A.; Bertoldi, K. Multistable Architected Materials for Trapping Elastic Strain Energy. Adv. Mater. 2015, 27, 4296–4301. [Google Scholar] [CrossRef]
- Neville, R.; Scarpa, F.; Pirrera, A. Shape morphing Kirigami mechanical metamaterials. Sci. Rep. 2016, 6, 31067. [Google Scholar] [CrossRef] [Green Version]
- Olympio, K.R.; Gandhi, F. Zero Poisson’s Ratio Cellular Honeycombs for Flex Skins Undergoing One-Dimensional Morphing. J. Intell. Mater. Syst. 2009, 21, 1737–1753. [Google Scholar] [CrossRef]
- Broccolo, S.D.; Laurenzi, S.; Scarpa, F. AUXHEX – A Kirigami inspired zero Poisson’s ratio cellular structure. Compos. Struct. 2017, 176, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Evans, K.; Kansah, M.; Hutchinson, I. Modelling negative Poisson ratio effects in network-embedded composites. Acta Mater. 1992, 40, 2463–2469. [Google Scholar] [CrossRef]
- Li, D.; Yin, J.; Dong, L.; Lakes, R. Strong re-entrant cellular structures with negative Poisson’s ratio. J. Mater. Sci. 2018, 53, 3493–3499. [Google Scholar] [CrossRef]
- Fu, M.; Chen, Y.; Hu, L. A novel auxetic honeycomb with enhanced in-plane stiffness and buckling strength. Compo. Struct. 2017, 160, 574–585. [Google Scholar] [CrossRef]
- Li, D.; Gao, R.; Dong, L.; Lam, W.; Zhang, F. A novel 3D re-entrant unit cell structure with negative Poisson’s ratio and tunable stiffness. Smart Mater. Struct. 2019, 29, 045015. [Google Scholar] [CrossRef]
- Jiang, W.; Ma, H.; Wang, J.; Feng, M.; Qu, S. Mechanical metamaterial with negative Poisson’s ratio based on circular honeycomb core. Chin. Sci. Bull. 2016, 61, 1421–1427. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Ma, L. Multi-stable mechanical metamaterials by elastic buckling instability. J. Mater. Sci. 2019, 54, 3509–3526. [Google Scholar] [CrossRef]
- Liu, J.; Tang, J.; Ahmad, R.; Ma, Y. Meta-Material Topology Optimization with Geometric Control. Comput. Aided Des. Appl. 2019, 16, 951–961. [Google Scholar] [CrossRef]
- Lira, C.; Scarpa, F.; Tai, Y.H.; Yates, J.R. Transverse shear modulus of SILICOMB cellular structures. Comps. Sci. Technol. 2011, 71, 1236–1241. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Scarpa, F.; Remillat, C.; Farrow, I.; Liu, Y.; Leng, J. Curved Kirigami SILICOMB cellular structures with zero Poisson’s ratio for large deformations and morphing. J. Intell. Mater. Syst. Struct. 2013, 25, 731–743. [Google Scholar] [CrossRef]
- Durable Resin Technical. Available online: https://formlabs-media.formlabs.com/datasheets/1801084-TDS-ENUS-0P.pdf (accessed on 5 March 2020).
- Xu, T.; Yoo, J.H.; Babu, S.; Roy, S.; Lee, J.B.; Lu, H. Characterization of the mechanical behaviour of SU-8 at microscale by viscoelastic analysis. J. Micromech. Microeng. 2016, 26, 105001. [Google Scholar] [CrossRef] [Green Version]
- ASTM. D638-14 Standard Test Methods for Tensile Properties of Plastics; ASTM International: West Conshohocken, USA, 2014. [Google Scholar]
- ASTM. D695-15 Standard Test Method for Compressive Properties of Rigid Plastics; ASTM International: West Conshohocken, USA, 2015. [Google Scholar]
- Zuo, Z.; Gong, J.; Huang, Y.; Zhan, Y.; Gong, M.; Zhang, L. Experimental research on transition from scale 3D printing to full-size printing in construction. Constr. Build Mater. 2019, 208, 350–360. [Google Scholar] [CrossRef]
- Weng, Z.; Zhou, Y.; Lin, W.; Senthil, T.; Wu, L. Structure-property relationship of nano enhanced stereolithography resin for desktop SLA 3D printer. Compos. Part A Appl. Sci. Manuf. 2016, 88, 234–242. [Google Scholar] [CrossRef]
- Borrello, J.; Nasser, P.; Iatridis, J.C.; Costa, K.D. 3D printing a mechanically-tunable acrylate resin on a commercial DLP-SLA printer. Addit. Manuf. 2018, 23, 374–380. [Google Scholar] [CrossRef] [PubMed]
- Hou, X.; Silberschmidt, V. Metamaterials with Negative Poisson’s Ratio: A Review of Mechanical Properties and Deformation Mechanisms. Mech. Adv. Mater. 2015, 7, 155–179. [Google Scholar]
- Ling, B.; Wei, K.; Wang, Z.; Yang, X.; Qu, Z.; Fang, D. Experimentally program large magnitude of Poisson’s ratio in additively manufactured mechanical metamaterials. Int. J. Mech. Sci. 2020, 173, 105466. [Google Scholar] [CrossRef]
- Wang, F. Systematic design of 3D auxetic lattice materials with programmable Poisson’s ratio for finite strains. J. Mech. Phys. Solids 2018, 114, 303–318. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Zhang, Q.; Scarpa, F.; Liu, Y.; Leng, J. Bending and benchmark of zero Poisson’s ratio cellular structures. Compos Struct 2016, 152, 729–736. [Google Scholar] [CrossRef] [Green Version]
- Levy, O.; Krylov, S.; Goldfarb, I. Design considerations for negative Poisson ratio structures under large deflection for MEMS applications. Smart Mater. Struct. 2006, 15, 1459–1466. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Li, X.; Ma, L. Interlocking assembled 3D auxetic cellular structures. Mater. Des. 2016, 99, 467–476. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Gu, D.; Chen, H.; Dai, D.; Shi, Q. Structural optimization of re-entrant negative Poisson’s ratio structure fabricated by selective laser melting. Mater. Des. 2017, 120, 307–316. [Google Scholar] [CrossRef]
- Turkmen, A.C.; Celik, C. Energy harvesting with the piezoelectric material integrated shoe. Energy 2018, 150, 556–564. [Google Scholar] [CrossRef]


| Name | Advantage | Limitation |
|---|---|---|
| Star-shaped-pore metamaterials [10] | Large negative Poisson’s ratio (Poisson’s ratio: −1) | Soft substrate materials, flat structure. |
| Bistable bridge metamaterials [16] | Unlimited extension with almost zero Poisson’s ratio | Introduce impulse to the structure. |
| Kirigami cellulars [21] | Customized Poisson’s ratio with simple internal structures | Stress concentration. |
| Paper-folding inspired metamaterials [22] | Customized Poisson’s ratio with a continues deformation | Poor structural stability with thin beams. |
| Length (mm) | Width (mm) | Thickness (mm) | |
|---|---|---|---|
| Maximum measured value | 90.54 | 48.73 | 10.30 |
| Minimum measured value | 89.50 | 48.20 | 9.95 |
| Average measured value | 89.90 | 48.49 | 10.07 |
| Standard deviation | 0.329 | 0.175 | 0.101 |
| Sizes of the digital model | 90.00 | 48.40 | 10.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Liu, W.; Zhang, L.; Gain, A.K. A New Polymer-Based Mechanical Metamaterial with Tailorable Large Negative Poisson’s Ratios. Polymers 2020, 12, 1492. https://doi.org/10.3390/polym12071492
Gao S, Liu W, Zhang L, Gain AK. A New Polymer-Based Mechanical Metamaterial with Tailorable Large Negative Poisson’s Ratios. Polymers. 2020; 12(7):1492. https://doi.org/10.3390/polym12071492
Chicago/Turabian StyleGao, Shanshi, Weidong Liu, Liangchi Zhang, and Asit Kumar Gain. 2020. "A New Polymer-Based Mechanical Metamaterial with Tailorable Large Negative Poisson’s Ratios" Polymers 12, no. 7: 1492. https://doi.org/10.3390/polym12071492
APA StyleGao, S., Liu, W., Zhang, L., & Gain, A. K. (2020). A New Polymer-Based Mechanical Metamaterial with Tailorable Large Negative Poisson’s Ratios. Polymers, 12(7), 1492. https://doi.org/10.3390/polym12071492