Master Curve Establishment and Complex Modulus Evaluation of SBS-Modified Asphalt Mixture Reinforced with Basalt Fiber Based on Generalized Sigmoidal Model
Abstract
1. Introduction
2. Formulations of Complex Modulus
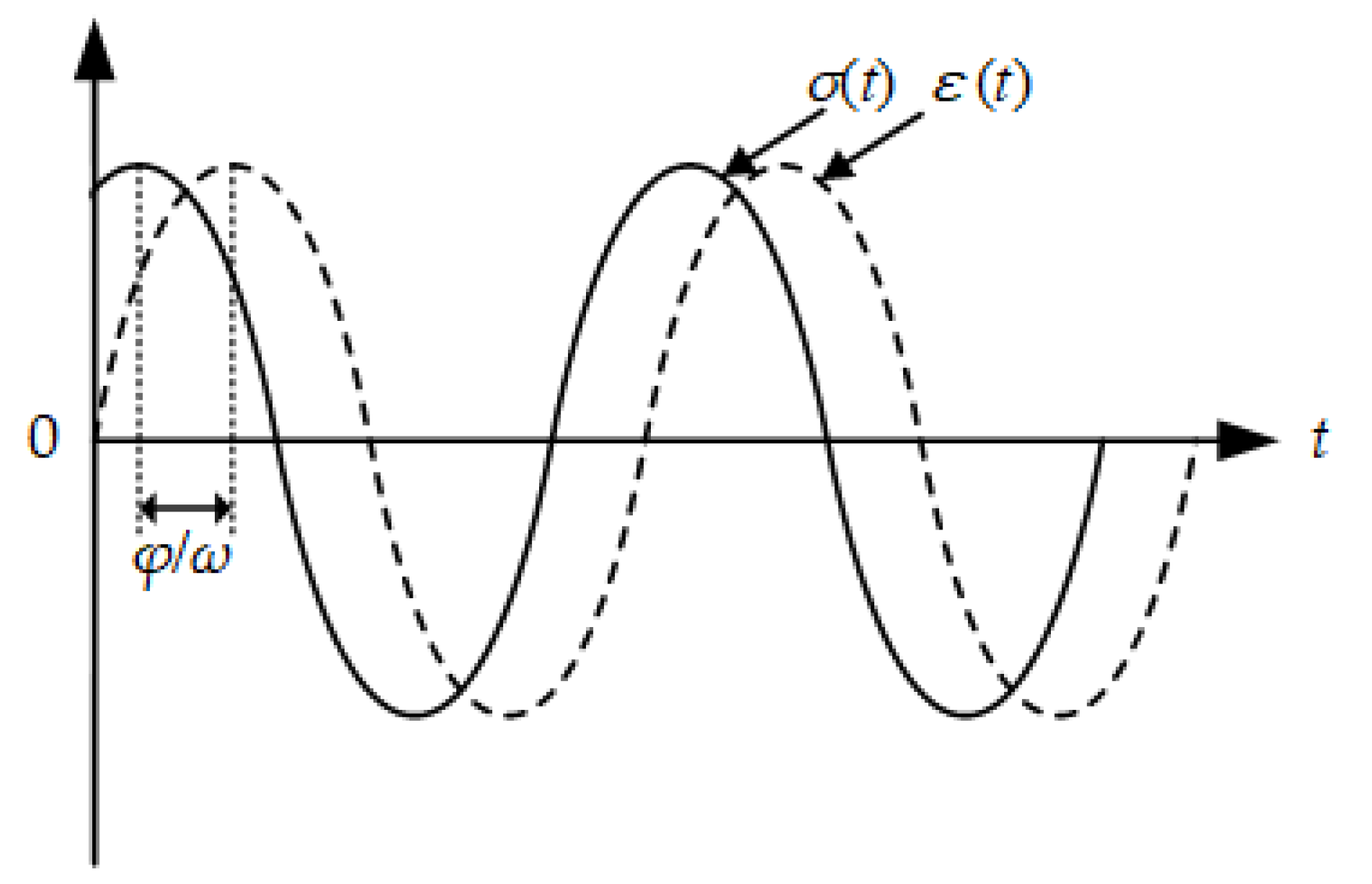
2.1. Dynamic Mechanical Response of Viscoelastic Materials
2.2. Time-Temperature Superposition Principle
2.3. Construction of Master Curves Based on Generalized Sigmoidal Model
3. Experimental Procedures
3.1. Raw Materials and Specimen Preparation
3.1.1. Raw Materials
3.1.2. Specimen Preparation
3.2. Test Configuration and Protocol
4. Results and Discussion
4.1. Determination of Dynamic Modulus of Asphalt Mixture Reinforced with Basalt Fiber
4.1.1. Influence Analysis of Temperature and Frequency on Dynamic Modulus
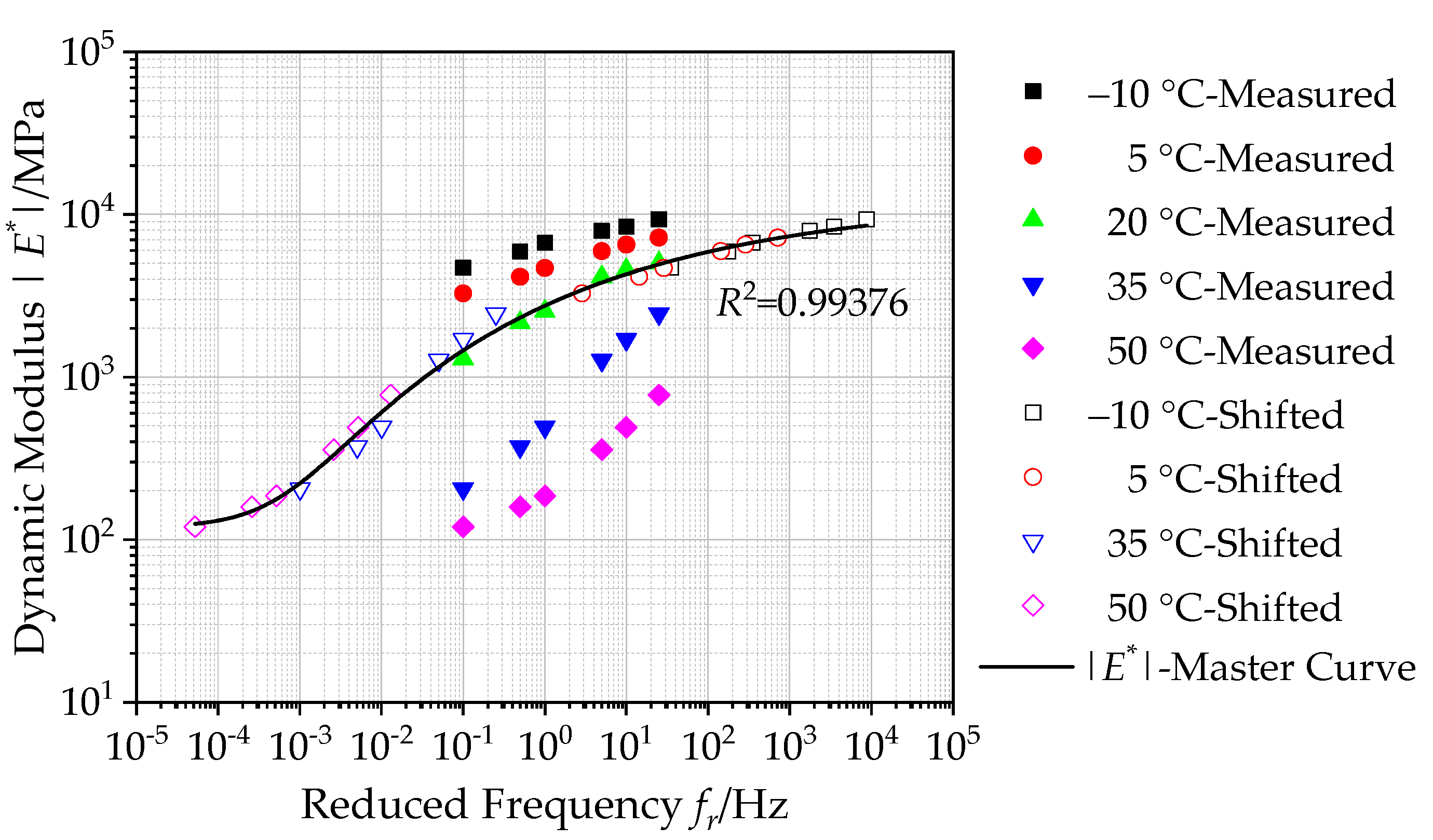
4.1.2. Construction of Master Curves of Dynamic Modulus
4.2. Determination of Phase Angle of Asphalt Mixture Reinforced with Basalt Fiber
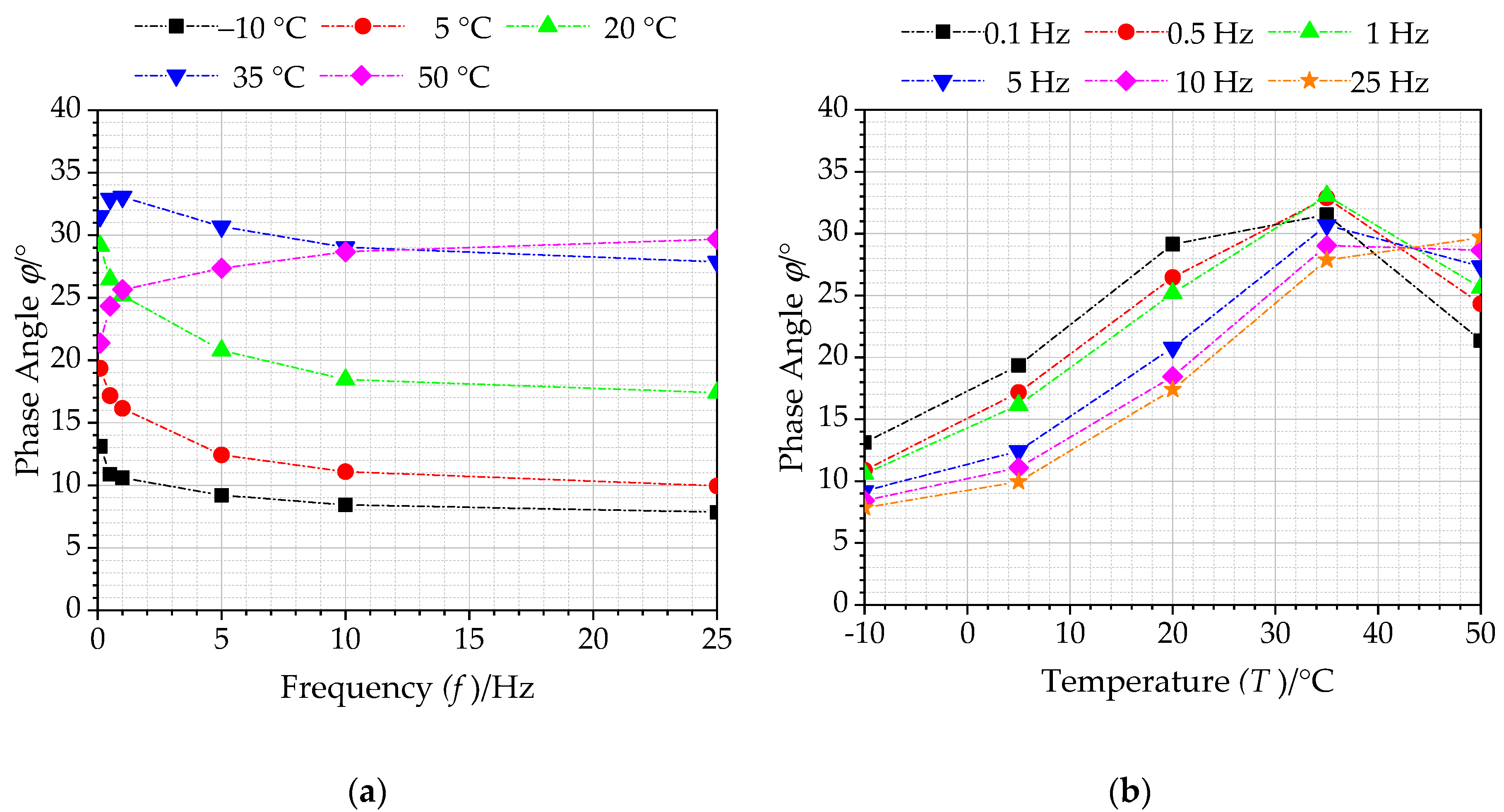
4.2.1. Influence Analysis of Temperature and Frequency on Phase Angle
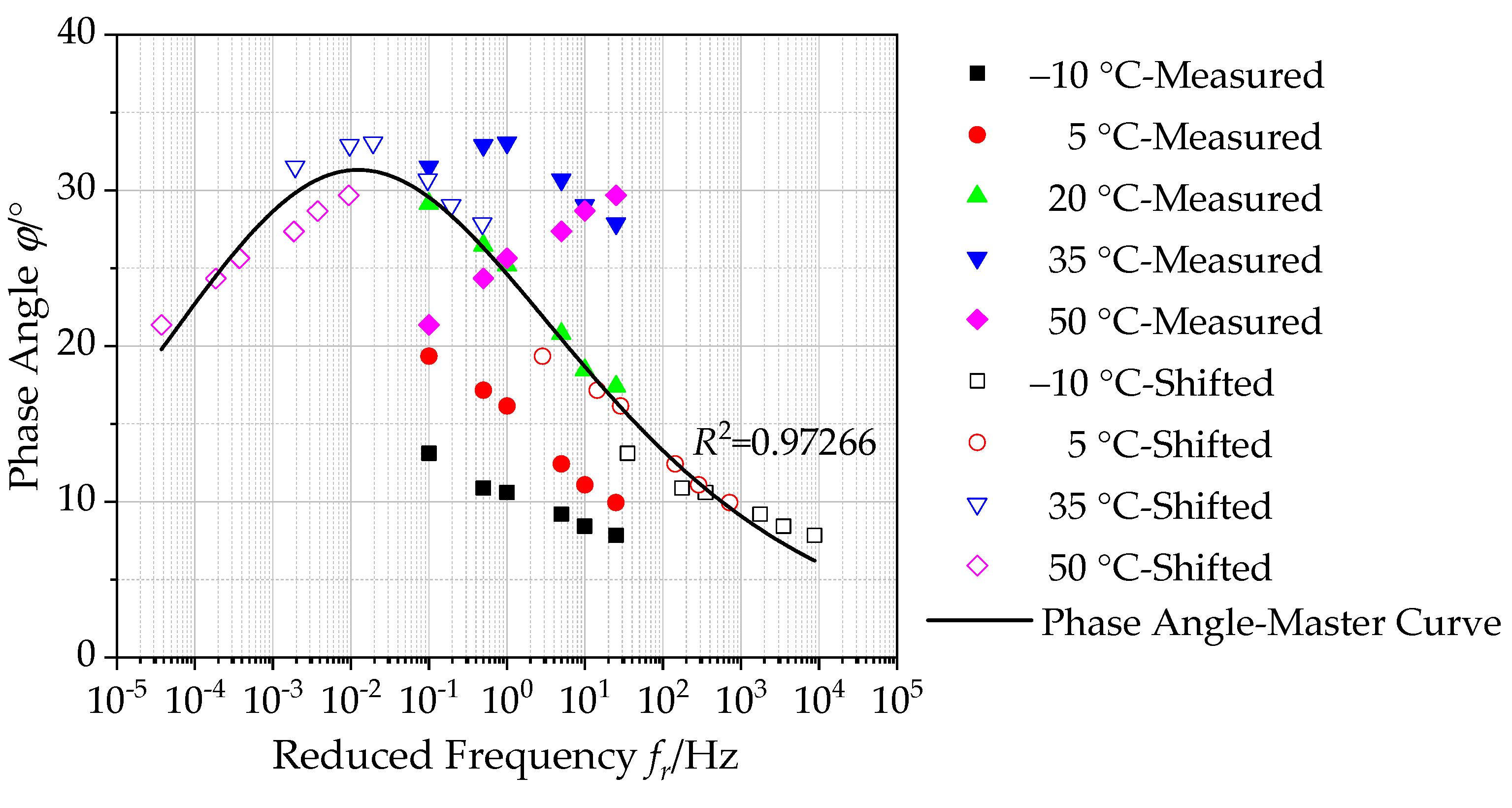
4.2.2. Construction of Master Curves of Phase Angle
4.3. Determination of Storage Modulus and Loss Modulus of Asphalt Mixture Reinforced with Basalt Fiber
4.3.1. Storage Modulus and Master Curve of Asphalt Mixture with Basalt Fiber
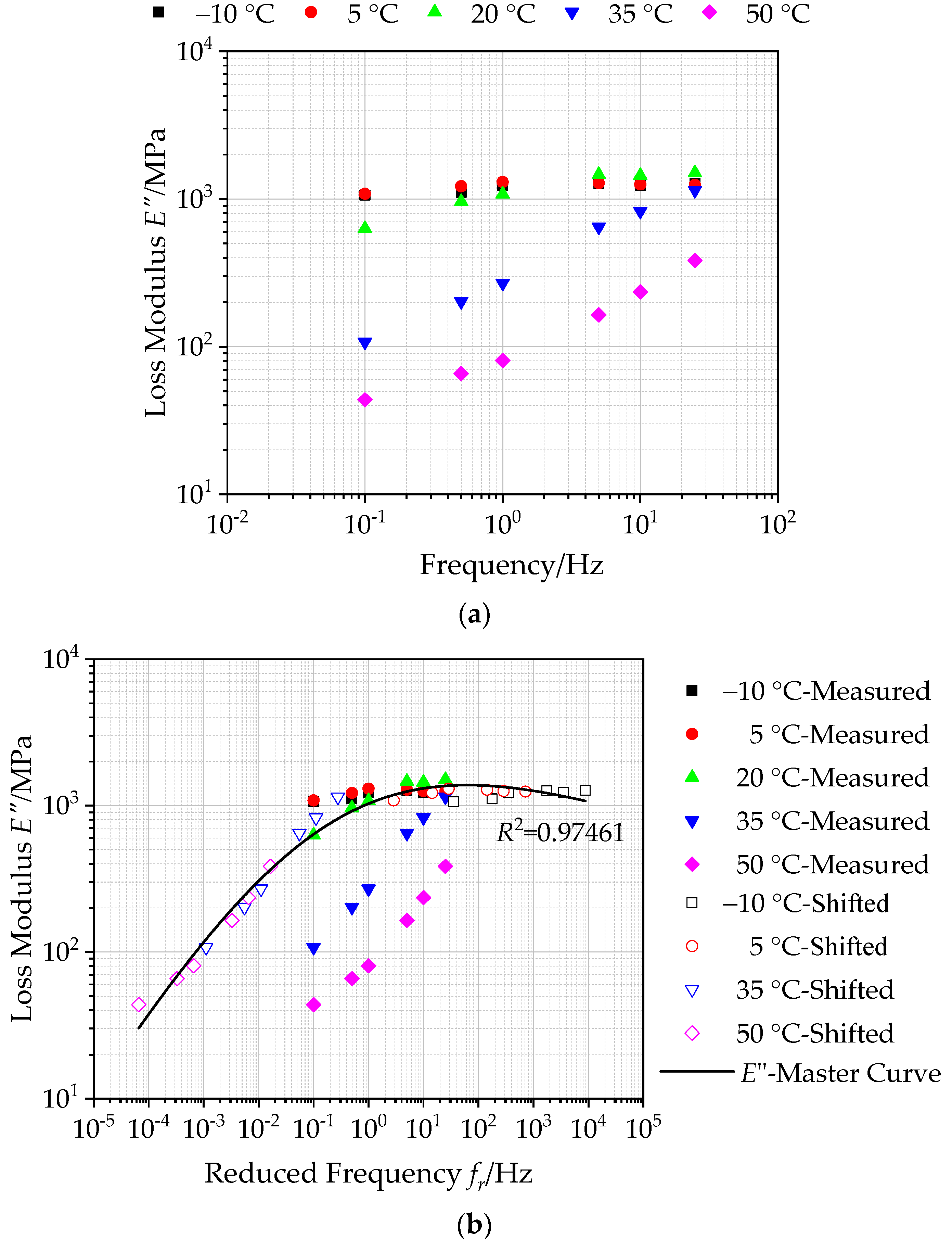
4.3.2. Loss Modulus and Master Curve of Asphalt Mixture with Basalt Fiber
5. Conclusions
- Dynamic modulus values of asphalt mixture specimens exhibit an increasing trend with loading frequency. Under the same load, the dynamic deformation response would change with loading frequency, affecting the dynamic modulus.
- The dynamic modulus of asphalt mixture with basalt fiber decreases with the increasing of the test temperature. Asphalt mixture is closer to a linear elastomer at lower temperature, and it is prone to cracking and failure under a long-term load. While asphalt mixture would be prone to a large permanent deformation under the heavy load at higher temperature, due to the viscoelastic composition change. This could explain the rutting destruction for basalt fiber modified asphalt pavement.
- The phase angle varies with test temperature for different loading frequencies, but phase angle at each loading frequency would increase first and then decrease as test temperature increases. For different loading frequencies, the corresponding temperatures at which the phase angle appears peak are different.
- The storage modulus of asphalt mixture exhibits a similar variation trend with dynamic modulus. The storage modulus gradually decreases with increasing temperature, while the value increases with increasing loading frequency. With respect to loss modulus, it exhibits an increasing trend with the loading frequency at low temperatures. While, at high temperature, loss modulus increases first and then decreases. These moduli also show the variation trends of elastic and viscous behaviors of asphalt mixture.
- The generalized Sigmoidal model is proved to characterize the dynamic modulus, phase angle, storage modulus and loss modulus of asphalt mixture with basalt fiber with correlation coefficients above 0.97, which is utilized to predict the dynamic mechanical performances accurately. The established master curves can extend over a broader reduced frequency range at an arbitrary reference temperature accurately. The developed dynamic modulus model could provide a guidance for the repair and maintenance of basalt fiber reinforced asphalt pavement.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ding, X.H.; Ma, T.; Gu, L.H.; Zhang, Y. Investigation of surface micro-crack growth behavior of asphalt mortar based on the designed innovative mesoscopic test. Mater. Des. 2020, 185, 108238. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, Y.; Zhang, D.Y.; Yan, J.H.; Ye, Q. Influences by air voids on fatigue life of asphalt mixture based on discrete element method. Constr. Build. Mater. 2016, 126, 785–799. [Google Scholar] [CrossRef]
- Jiao, Y.B.; Zhang, L.D.; Guo, Q.L.; Guo, M.; Zhang, Y. Acoustic Emission-Based Reinforcement Evaluation of Basalt and Steel Fibers on Low-Temperature Fracture Resistance of Asphalt Concrete. J. Mater. Civ. Eng. 2020, 32, 5. [Google Scholar] [CrossRef]
- Guo, Q.L.; Wang, H.Y.; Gao, Y.; Jiao, Y.B.; Liu, F.C.; Dong, Z.Z. Investigation of the low-temperature properties and cracking resistance of fiber-reinforced asphalt concrete using the DIC technique. Eng. Fract. Mech. 2020, 229, 106951. [Google Scholar] [CrossRef]
- Razmi, A.; Mirsayar, M.M. Fracture resistance of asphalt concrete modified with crumb rubber at low temperatures. Int. J. Pavement Res. Technol. 2018, 11, 265–273. [Google Scholar] [CrossRef]
- Guo, Q.L.; Li, L.L.; Cheng, Y.C.; Jiao, Y.B.; Xu, C. Laboratory evaluation on performance of diatomite and glass fiber compound modified asphalt mixture. Mater. Des. 2015, 66, 51–59. [Google Scholar] [CrossRef]
- Wang, W.S.; Cheng, Y.C.; Tan, G.J. Design optimization of SBS-modified asphalt mixture reinforced with eco-friendly basalt fiber based on response surface methodology. Materials 2018, 11, 1311. [Google Scholar] [CrossRef]
- Wang, W.S.; Cheng, Y.C.; Zhou, P.L.; Tan, G.J.; Wang, H.T.; Liu, H.B. Performance Evaluation of Styrene-Butadiene-Styrene-Modified Stone Mastic Asphalt with Basalt Fiber Using Different Compaction Methods. Polymers 2019, 11, 1006. [Google Scholar] [CrossRef]
- Karakas, A.S.; Kuloglu, N.; Kok, B.V.; Yilmaz, M. The evaluation of the field performance of the neat and SBS modified hot mixture asphalt. Constr. Build. Mater. 2015, 98, 678–684. [Google Scholar] [CrossRef]
- Wu, S.P.; Ye, Q.S.; Li, N. Investigation of rheological and fatigue properties of asphalt mixtures containing polyester fibers. Constr. Build. Mater. 2008, 22, 2111–2115. [Google Scholar] [CrossRef]
- Guo, M.; Tan, Y.Q.; Luo, D.S.; Li, Y.F.; Farooq, A.; Mo, L.T.; Jiao, Y.B. Effect of Recycling Agents on Rheological and Micromechanical Properties of SBS-Modified Asphalt Binders. Adv. Mater. Sci. Eng. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Yu, H.; Bai, X.; Qian, G.; Wei, H.; Gong, X.; Jin, J.; Li, Z. Impact of Ultraviolet Radiation on the Aging Properties of SBS-Modified Asphalt Binders. Polymers 2019, 11, 1111. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.Q.; Huang, W.D.; Ma, J.M.; Xu, J.; Lv, Q.; Lin, P. Characterizing the SBS polymer degradation within high content polymer modified asphalt using ATR-FTIR. Constr. Build. Mater. 2019, 233, 117708. [Google Scholar] [CrossRef]
- Imaninasab, R. Effect of granular polymers on rutting performance of SMA with respect to modification process. Constr. Build. Mater. 2017, 130, 64–72. [Google Scholar] [CrossRef]
- Wang, Y.H.; Chong, D.; Wen, Y. Quality verification of polymer-modified asphalt binder used in hot-mix asphalt pavement construction. Constr. Build. Mater. 2017, 150, 157–166. [Google Scholar] [CrossRef]
- Hajikarimi, P.; Tehrani, F.F.; Nejad, F.M.; Absi, J.; Rahi, M.; Khodaii, A.; Petit, C. Mechanical Behavior of Polymer-Modified Bituminous Mastics. I: Experimental Approach. J. Mater. Civ. Eng. 2019, 31, 04018337. [Google Scholar] [CrossRef]
- Hajikarimi, P.; Tehrani, F.F.; Nejad, F.M.; Absi, J.; Khodaii, A.; Rahi, M.; Petit, C. Mechanical Behavior of Polymer-Modified Bituminous Mastics. II: Numerical Approach. J. Mater. Civ. Eng. 2019, 31, 04018338. [Google Scholar] [CrossRef]
- Zhang, J.W.; Huang, W.D.; Zhang, Y.; Lv, Q.; Yan, C.Q. Evaluating four typical fibers used for OGFC mixture modification regarding drainage, raveling, rutting and fatigue resistance. Constr. Build. Mater. 2020, 253, 119131. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Gu, X.Y.; Lv, J.X. Effect of basalt fiber distribution on the flexural–tensile rheological performance of asphalt mortar. Constr. Build. Mater. 2018, 179, 307–314. [Google Scholar] [CrossRef]
- Morova, N. Investigation of usability of basalt fibers in hot mix asphalt concrete. Constr. Build. Mater. 2013, 47, 175–180. [Google Scholar] [CrossRef]
- Sun, X.L.; Qin, X.; Chen, Q.; Ma, Q. Investigation of enhancing effect and mechanism of basalt fiber on toughness of asphalt material. Pet. Sci. Technol. 2018, 36, 1710–1717. [Google Scholar] [CrossRef]
- Qin, X.; Shen, A.Q.; Guo, Y.C.; Li, Z.N.; Lv, Z.H. Characterization of asphalt mastics reinforced with basalt fibers. Constr. Build. Mater. 2018, 159, 508–516. [Google Scholar] [CrossRef]
- Li, Z.N.; Shen, A.Q.; Wang, H.; Guo, Y.C.; Wu, H. Effect of basalt fiber on the low-temperature performance of an asphalt mixture in a heavily frozen area. Constr. Build. Mater. 2020, 253, 119080. [Google Scholar] [CrossRef]
- Gu, X.Y.; Xu, T.T.; Ni, F.J. Rheological behavior of basalt fiber reinforced asphalt mastic. J. Wuhan. Univ. Technol. 2014, 29, 950–955. [Google Scholar] [CrossRef]
- Tanzadeh, R.; Tanzadeh, J.; Honarmand, M.; Tahami, S.A. Experimental study on the effect of basalt and glass fibers on behavior of open-graded friction course asphalt modified with nano-silica. Constr. Build. Mater. 2019, 212, 467–475. [Google Scholar] [CrossRef]
- Miao, Y.; Wang, T.; Wang, L. Influences of Interface Properties on the Performance of Fiber-Reinforced Asphalt Binder. Polymers 2019, 11, 542. [Google Scholar] [CrossRef]
- Luo, Y.F.; Zhang, K.; Xie, X.B.; Yao, X.G. Performance evaluation and material optimization of Micro-surfacing based on cracking and rutting resistance. Constr. Build. Mater. 2019, 206, 193–200. [Google Scholar] [CrossRef]
- Kou, C.; Wu, X.; Xiao, P.; Liu, Y.; Wu, Z. Physical, Rheological, and Morphological Properties of Asphalt Reinforced by Basalt Fiber and Lignin Fiber. Materials 2020, 13, 2520. [Google Scholar] [CrossRef]
- Badeli, S.; Carter, A.; Dore, G.; Saliani, S. Evaluation of the durability and the performance of an asphalt mix involving Aramid Pulp Fiber (APF): Complex modulus before and after freeze-thaw cycles, fatigue, and TSRST tests. Constr. Build. Mater. 2018, 174, 60–71. [Google Scholar] [CrossRef]
- Xu, H.N.; Guo, W.; Tan, Y.Q. Permeability of asphalt mixtures exposed to freeze-thaw cycles. Cold Reg. Sci. Technol. 2016, 123, 99–106. [Google Scholar] [CrossRef]
- Guo, Q.L.; Li, G.Y.; Gao, Y.; Wang, K.Y.; Dong, Z.Z.; Liu, F.C.; Zhu, H. Experimental investigation on bonding property of asphalt-aggregate interface under the actions of salt immersion and freeze-thaw cycles. Constr. Build. Mater. 2019, 206, 590–599. [Google Scholar] [CrossRef]
- Badeli, S.; Carter, A.; Dore, G. Complex Modulus and Fatigue Analysis of Asphalt Mix after Daily Rapid Freeze-Thaw Cycles. J. Mater. Civ. Eng. 2018, 4, 04018056. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, W.; Gong, Y.; Wang, S.; Yang, S.; Sun, X. Comparative Study on the Damage Characteristics of Asphalt Mixtures Reinforced with an Eco-Friendly Basalt Fiber under Freeze-thaw Cycles. Materials 2018, 11, 2488. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, Y.; Ma, G.; Tan, G.; Sun, X.; Yang, S. Further Investigation on Damage Model of Eco-Friendly Basalt Fiber Modified Asphalt Mixture under Freeze-Thaw Cycles. Appl. Sci. 2019, 9, 60. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, H.; Wang, W.; Li, L.; Wang, H. Laboratory Evaluation on the Performance Degradation of Styrene-Butadiene-Styrene-Modified Asphalt Mixture Reinforced with Basalt Fiber under Freeze–Thaw Cycles. Polymers 2020, 12, 1092. [Google Scholar] [CrossRef]
- Tarefder, R.; Faisal, H.; Barlas, G. Freeze-thaw effects on fatigue LIFE of hot mix asphalt and creep stiffness of asphalt binder. Cold Reg. Sci. Technol. 2018, 153, 197–204. [Google Scholar] [CrossRef]
- Levenberg, E.; Shah, A. Interpretation of complex modulus test results for asphalt-aggregate mixes. J. Test. Eval. 2008, 36, 326–334. [Google Scholar]
- Walubita, L.F.; Martin, A.E.; Cleveland, G.S.; Lytton, R.L. Computation of pseudo strain energy and Paris law fracture coefficients from surface energy and uniaxial strain-controlled tension test data. Int. J. Pavement Eng. 2006, 7, 167–178. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, R.; Lytton, R.L. Anisotropic viscoelastic properties of undamaged asphalt mixtures. J. Transp. Eng. 2012, 138, 75–89. [Google Scholar] [CrossRef]
- Liu, H.Q.; Luo, R. Development of master curve models complying with linear viscoelastic theory for complex moduli of asphalt mixtures with improved accuracy. Constr. Build. Mater. 2017, 152, 259–268. [Google Scholar] [CrossRef]
- Parot, J.M.; Duperray, B. Applications of exact causality relationships to materials dynamic analysis. Mech. Mater. 2007, 39, 419–433. [Google Scholar] [CrossRef]
- Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering; JTG E20-2011; Ministry of Transport of the People’s Republic of China: Beijing, China, 2011. (In Chinese)
- Standard Method of Test for Determining the Dynamic Modulus and Flow Number for Asphalt Mixtures Using the Asphalt Mixture Performance Tester (AMPT); AASHTO TP 79; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2015.





| Test Parameters | Unit | Standards | Requirements | Values |
|---|---|---|---|---|
| Penetration | 0.1 mm (@ 25 °C, 100 g, 5 s) | T0604 | 60~80 | 71 |
| Ductility | cm (@ 15 °C, 5 cm/min) | T0605 | ≥30 | 45 |
| Softening point | °C | T0606 | ≥55 | 60.5 |
| Density | g/cm3 | T0603 | — | 1.018 |
| Flash point | °C | T0611 | ≥230 | 262 |
| RTFOT | ||||
| Mass loss | % | T0609 | ±1.0 | −0.094 |
| Penetration ratio | % (@ 25 °C) | T0609 | ≥60 | 66.9 |
| Test Parameters | Unit | Standards | Requirements | Values | |
|---|---|---|---|---|---|
| Crushing value | % | T0316 | ≤26 | 13.6 | |
| Los Angeles abrasion value | % | T0317 | ≤28 | 17.9 | |
| Apparent specific gravity | 13.2 mm | — | T0304 | ≥2.6 | 2.836 |
| 9.5 mm | 2.805 | ||||
| 4.75 mm | 2.726 | ||||
| Water absorption | 13.2 mm | % | T0304 | ≤2.0 | 0.6 |
| 9.5 mm | 0.28 | ||||
| 4.75 mm | 0.7 | ||||
| Soundness | % | T0314 | ≤12 | 5 | |
| Elongated particle content | % | T0312 | ≤15 | 9.2 | |
| Passing 0.075 mm sieve | % | T0310 | ≤1 | 0.3 | |
| Test Parameters | Unit | Standards | Requirements | Values |
|---|---|---|---|---|
| Apparent specific gravity | — | T0328 | ≥2.5 | 2.723 |
| Water absorption | % | T0304 | — | 0.64 |
| Angularity (flow time) | s | T0345 | ≥30 | 39.9 |
| Sand equivalent | % | T0334 | ≥60 | 68 |
| Test Parameters | Unit | Standards | Requirements | Values | |
|---|---|---|---|---|---|
| Apparent density | t/m3 | T0352 | ≥2.5 | 2.712 | |
| Hydrophilic coefficient | — | T0353 | <1 | 0.63 | |
| Water content | % | T0103 | ≤1 | 0.3 | |
| Plastic index | % | T0354 | <4 | 2 | |
| Granular composition | <0.6 mm | % | T0351 | 100 | 100 |
| <0.15 mm | 90~100 | 92.5 | |||
| <0.075 mm | 75~100 | 81.8 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, G.; Wang, W.; Cheng, Y.; Wang, Y.; Zhu, Z. Master Curve Establishment and Complex Modulus Evaluation of SBS-Modified Asphalt Mixture Reinforced with Basalt Fiber Based on Generalized Sigmoidal Model. Polymers 2020, 12, 1586. https://doi.org/10.3390/polym12071586
Tan G, Wang W, Cheng Y, Wang Y, Zhu Z. Master Curve Establishment and Complex Modulus Evaluation of SBS-Modified Asphalt Mixture Reinforced with Basalt Fiber Based on Generalized Sigmoidal Model. Polymers. 2020; 12(7):1586. https://doi.org/10.3390/polym12071586
Chicago/Turabian StyleTan, Guojin, Wensheng Wang, Yongchun Cheng, Yong Wang, and Zhiqing Zhu. 2020. "Master Curve Establishment and Complex Modulus Evaluation of SBS-Modified Asphalt Mixture Reinforced with Basalt Fiber Based on Generalized Sigmoidal Model" Polymers 12, no. 7: 1586. https://doi.org/10.3390/polym12071586
APA StyleTan, G., Wang, W., Cheng, Y., Wang, Y., & Zhu, Z. (2020). Master Curve Establishment and Complex Modulus Evaluation of SBS-Modified Asphalt Mixture Reinforced with Basalt Fiber Based on Generalized Sigmoidal Model. Polymers, 12(7), 1586. https://doi.org/10.3390/polym12071586








