Investigation of the Shape-Memory Properties of 3D Printed PLA Structures with Different Infills †
Abstract
:1. Introduction
2. Materials and Methods
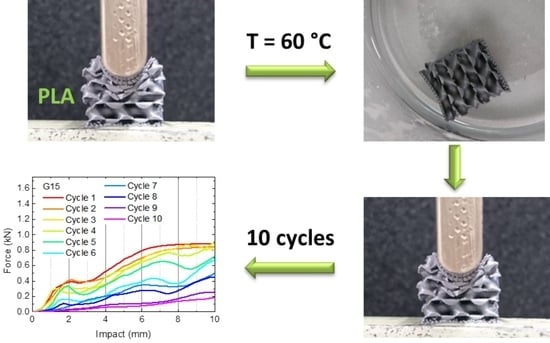
3. Results and Discussion
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Szykiedans, K.; Credo, W. Mechanical properties of FDM and SLA low-cost 3-D prints. Proc. Eng. 2016, 136, 257–262. [Google Scholar] [CrossRef] [Green Version]
- Moreno, R.; Carou, D.; Carazo-Alvarez, D.; Gupta, M.K. Statistical models for the mechanical properties of 3D printed external medical aids. Rapid Prototyp. J. 2020. early access. [Google Scholar] [CrossRef]
- Han, S.H.; Cha, M.; Jin, Y.Z.; Lee, K.M.; Lee, J.H. BMP-2 and hMSC dual delivery onto 3D printed PLA-Biogel scaffold for critical-size bone defect regeneration in rabbit tibia. Biomed. Mater. 2021, 16, 015019. [Google Scholar] [CrossRef] [PubMed]
- Sölmann, S.; Rattenholl, A.; Blattner, H.; Ehrmann, G.; Gudermann, F.; Lütkemeyer, D.; Ehrmann, A. Mammalian cell adhesion on different 3D printed polymers with varying sterilization methods and acidic treatment. AIMS Bioeng. 2021, 8, 25–35. [Google Scholar]
- Wan, M.L.; Liu, S.F.; Huang, D.; Qu, Y.; Hu, Y.; Su, Q.S.; Zheng, W.X.; Dong, X.M.; Zhang, H.W.; Wei, Y.; et al. Biocompatible heterogeneous bone incorporated with polymeric biocomposites for human bone repair by 3D printing technology. J. Appl. Polym. Sci. 2020. early access. [Google Scholar] [CrossRef]
- Horst, J.D.; de Andreade, P.P.; Duvoisin, C.A.; Vieira, R.D. Fabrication of conductive filaments for 3D-printing: Polymer nanocomposites. Biointerface Res. Appl. Chem. 2020, 10, 6577–6586. [Google Scholar]
- Junpha, J.; Wisitsoraat, A.; Prathumwan, R.; Chaengsawang, W.; Khomungkhun, K.; Subannajui, K. Electronic tongue and cyclic voltammetric sensors based on carbon nanotube/polylactic composites fabricated by fused deposition modelling 3D printing. Mater. Sci. Eng. C Mater. Biol. Appl. 2020, 117, 111319. [Google Scholar] [CrossRef]
- Le Duigou, A.; Chabaud, G.; Matsuzaki, R.; Castro, M. Tailoring the mechanical properties of 3D-printed continuous flax/PLA biocomposites by controlling the slicing parameters. Compos. B Eng. 2020, 203, 108474. [Google Scholar] [CrossRef]
- Jing, H.S.; He, H.; Liu, H.; Huang, B.; Zhang, C. Study on properties of polylactic acid/lemongrass fiber biocomposites prepared by fused deposition modeling. Polym. Compos. 2020. [Google Scholar] [CrossRef]
- Pinho, A.C.; Amaro, A.M.; Piedade, A.P. 3D printing goes greener: Study of the properties of post-consumer recycles polymers for the manufacturing of engineering components. Waste Manag. 2020, 118, 426–434. [Google Scholar] [CrossRef]
- Wach, R.A.; Wolszczak, P.; Adamus-Wlodarczyk, A. Enhancement of mechanical properties of FDM-PLA Parts via thermal annealing. Macromol. Mater. Eng. 2018, 303, 1800169. [Google Scholar] [CrossRef]
- Fafenrot, S.; Grimmelsmann, N.; Wortmann, M.; Ehrmann, A. Three-Dimensional (3D) printing of polymer-metal hybrid materials by fused deposition modeling. Materials 2017, 10, 1199. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kozior, T.; Mamun, A.; Trabelsi, M.; Sabantina, L.; Ehrmann, A. Quality of the surface texture and mechanical properties of FDM printed samples after thermal and chemical treatment. Stroj. Vestn. 2020, 66, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Schiovone, N.; Verney, V.; Askanian, H. Effect of 3D printing temperature profile on polymer materials behavior. 3D Print. Add. Manufact. 2020. [Google Scholar] [CrossRef]
- Ivanov, E.; Kotsilkova, R.; Xia, H.S.; Chen, Y.H.; Donato, R.K.; Donato, K.; Godoy, A.P.; di Maio, R.; Silvestre, C.; Cimmino, S.; et al. PLA/Graphene/MWCNT composites with improved electrical and thermal properties suitable for FDM 3D printing applications. Appl. Sci. 2019, 9, 1209. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Singh, R.; Singh, M.; Kumar, P. ZnO nanoparticle-grafted PLA thermoplastic composites for 3D printing applications: Tuning of thermal, mechanical, morphological and shape memory effect. J. Thermoplast. Compos. Mater. 2020. [Google Scholar] [CrossRef]
- Wickramasinghe, S.; Do, T.; Tran, P. FDM-based 3D printing of polymer and associated composite: A review on mechanical properties, defects and treatments. Polymers 2020, 12, 1529. [Google Scholar] [CrossRef]
- Grothe, T.; Brockhagen, B.; Storck, J.L. Three-dimensional printing resin on different textile substrates using stereolithography: A proof of concept. J. Eng. Fibers Fabrics 2020, 15, 1558925020933440. [Google Scholar] [CrossRef]
- Korger, M.; Glogowsky, A.; Sanduloff, S.; Steinem, C.; Huysman, S.; Horn, B.; Ernst, M.; Rabe, M. Testing thermoplastic elastomers selected as flexible three-dimensional printing materials for functional garment and technical textile applications. J. Eng. Fibers Fabrics 2020, 15, 1558925020924599. [Google Scholar] [CrossRef]
- Kozior, T.; Blachowicz, T.; Ehrmann, A. Adhesion of three-dimensional printing on textile fabrics: Inspiration from and for other research areas. J. Eng. Fibers Fabrics 2020, 15, 1558925020910875. [Google Scholar] [CrossRef] [Green Version]
- Senatov, F.S.; Zadorozhnyy, M.Y.; Niaza, K.V.; Medvedev, V.V.; Kaloshkin, S.D.; Anisimova, N.Y.; Kiselevskiy, M.V.; Yang, K.-C. Shape memory effect in 3D-printed scaffolds for self-fitting implants. Eur. Polym. J. 2017, 93, 222–231. [Google Scholar] [CrossRef]
- Senatov, F.S.; Niaza, N.K.; Zadorozhnyy, M.Y.; Maksimkin, A.V.; Kaloshkin, S.D.; Estrin, Y.Z. Mechanical properties and shape memory effect of 3D-printed PLA-based porous scaffolds. J. Mech. Behav. Biomedic. Mater. 2016, 57, 139–148. [Google Scholar] [CrossRef] [PubMed]
- Lendlein, A.; Langer, R. Biodegradable, elastic shape-memory polymers for potential biomedical applications. Science 2002, 296, 1673–1676. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.Z.; Ye, W.L.; Wu, Z.C.; Geng, P.; Wang, Y.L.; Zhao, J. Influence of layer thickness, raster angle, deformation temperature and recovery temperature on the shape-memory effect of 3D-printed polylactic acid samples. Materials 2017, 10, 970. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, T.T.; Kim, J.Y. 4D-printing—Fused deposition modeling printing and PolyJet printing with shape memory polymers composite. Fibers Polym. 2020, 21, 2364–2372. [Google Scholar] [CrossRef]
- Kabir, S.; Lee, S.H. Study of shape memory and tensile property of 3D printed sinusoidal sample/nylon composite focused on various thicknesses and shape memory cycles. Polymers 2020, 12, 1600. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; He, H.; Huang, B. Favorable thermoresponsive shape memory effects of 3D printed poly(lactic acid/poly(ε-caprolactone) blends fabricated by fused deposition modeling. Macromol. Mater. Eng. 2020, 305, 2000295. [Google Scholar] [CrossRef]
- Melocchi, A.; Uboldi, M.; Inverardi, N.; Briatico-Vangosa, F.; Baldi, F.; Pandini, S.; Scalet, G.; Auricchio, F.; Cerea, M.; Foppoli, A.; et al. Expandable drug delivery system for gastric retention based on shape memory polymers: Development via 4D printing and extrusion. Int. J. Pharmac. 2019, 571, 118700. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, L.; Guo, Y.; Zhang, H.; Zhang, Z. Multi-responsive shape memory polymer printed by fused deposition modeling technique. Express Polym. Lett. 2020, 14, 348–357. [Google Scholar] [CrossRef]
- Ehrmann, G.; Ehrmann, A. Shape-memory properties of 3D printed PLA structures. Proceedings 2021. accepted. [Google Scholar]
- Grimmelsmann, N.; Meissner, H.; Ehrmann, A. 3D printed auxetic forms on knitted fabrics for adjustable permeability and mechanical properties. IOP Conf. Series Mater. Sci. Eng. 2016, 137, 012011. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Chen, Y.H.; Wei, Y.; Li, Y.T. 3D printing of shape memory polymer for functional part fabrication. Int. J. Adv. Manufact. Technol. 2016, 84, 2079–2095. [Google Scholar] [CrossRef]
- Blachowicz, T.; Pajak, K.; Recha, P.; Ehrmann, A. 3D printing for microsatellites—Material requirements and recent developments. AIMS Mater. Sci. 2020, 7, 926–938. [Google Scholar] [CrossRef]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ehrmann, G.; Ehrmann, A. Investigation of the Shape-Memory Properties of 3D Printed PLA Structures with Different Infills. Polymers 2021, 13, 164. https://doi.org/10.3390/polym13010164
Ehrmann G, Ehrmann A. Investigation of the Shape-Memory Properties of 3D Printed PLA Structures with Different Infills. Polymers. 2021; 13(1):164. https://doi.org/10.3390/polym13010164
Chicago/Turabian StyleEhrmann, Guido, and Andrea Ehrmann. 2021. "Investigation of the Shape-Memory Properties of 3D Printed PLA Structures with Different Infills" Polymers 13, no. 1: 164. https://doi.org/10.3390/polym13010164
APA StyleEhrmann, G., & Ehrmann, A. (2021). Investigation of the Shape-Memory Properties of 3D Printed PLA Structures with Different Infills. Polymers, 13(1), 164. https://doi.org/10.3390/polym13010164