Creep and Recovery Behavior of Continuous Fiber-Reinforced 3DP Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and 3DP Conditions
2.2. 3D Printing Process
2.3. Creep and Recovery Experiments
2.4. Modeling Viscoelasticity
3. Results and Discussion
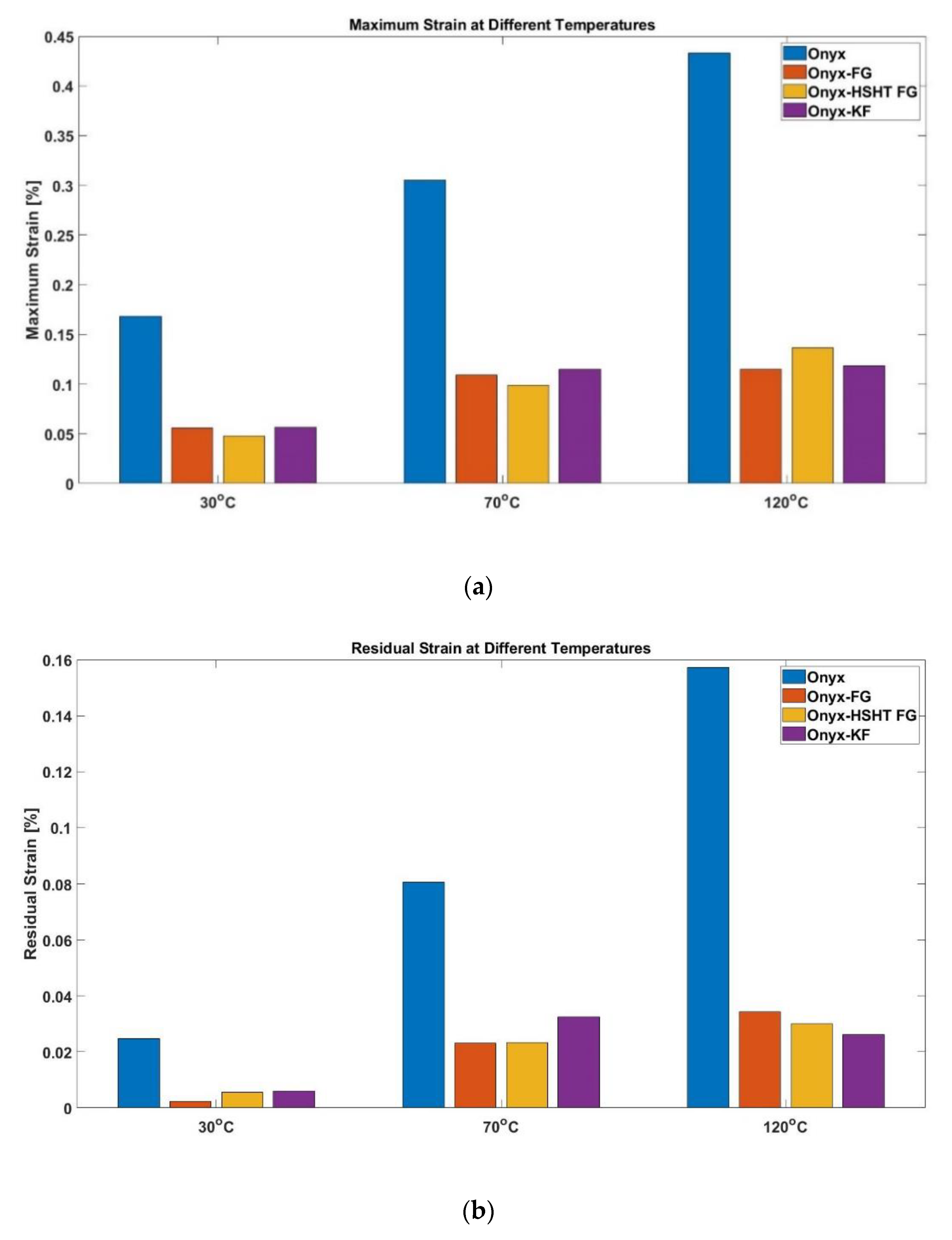
3.1. Creep and Recovery Analysis
3.2. Creep and Recovery Modeling
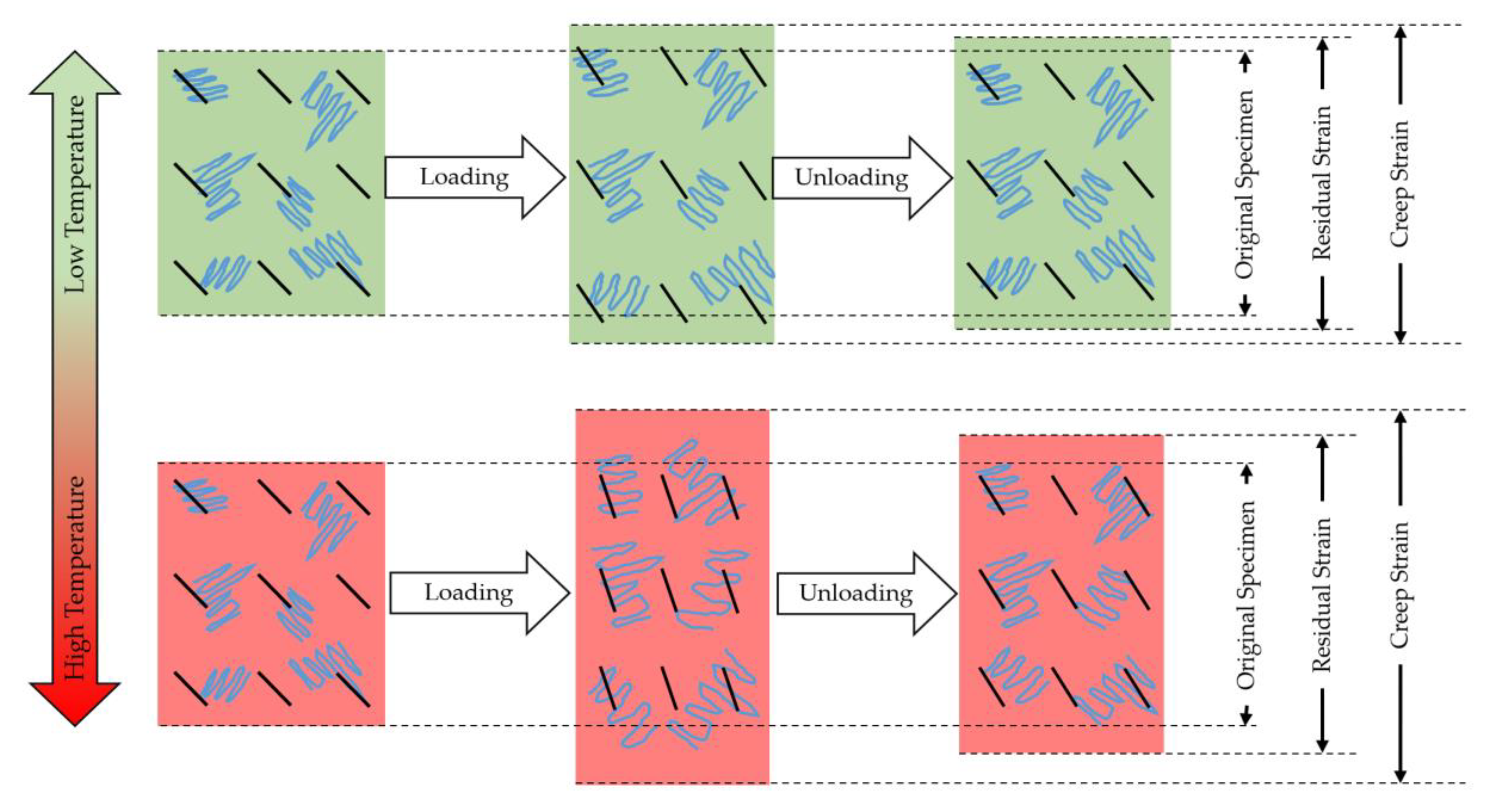
3.3. Possible Mechanism in Creep and Recovery
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Al Rashid, A.; Khan, S.A.; Al-Ghamdi, S.G.; Koç, M. Additive manufacturing: Technology, applications, markets, and opportunities for the built environment. Autom. Constr. 2020, 118, 103268. [Google Scholar] [CrossRef]
- Tofail, S.A.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; O’Donoghue, L.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2018, 21, 22–37. [Google Scholar] [CrossRef]
- González-Henríquez, C.M.; Sarabia-Vallejos, M.A.; Rodriguez-Hernandez, J. Polymers for additive manufacturing and 4D-printing: Materials, methodologies, and biomedical applications. Prog. Polym. Sci. 2019, 94, 57–116. [Google Scholar] [CrossRef]
- Sánchez, D.M.; de la Mata, M.; Delgado, F.J.; Casal, V.; Molina, S.I. Development of carbon fiber acrylonitrile styrene acrylate composite for large format additive manufacturing. Mater. Des. 2020, 191, 108577. [Google Scholar] [CrossRef]
- Khalid, M.Y.; Nasir, M.A.; Ali, A.; Al Rashid, A.; Khan, M.R. Experimental and numerical characterization of tensile property of jute/carbon fabric reinforced epoxy hybrid composites. SN Appl. Sci. 2020, 2, 577. [Google Scholar] [CrossRef] [Green Version]
- Karakoç, A.; Rastogi, V.K.; Isoaho, T.; Tardy, B.; Paltakari, J.; Rojas, O.J. Comparative Screening of the Structural and Thermomechanical Properties of FDM Filaments Comprising Thermoplastics Loaded with Cellulose, Carbon and Glass Fibers. Materials 2020, 13, 422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malas, A.; Isakov, D.; Couling, K.; Gibbons, G.J. Fabrication of High Permittivity Resin Composite for Vat Photopolymerization 3D Printing: Morphology, Thermal, Dynamic Mechanical and Dielectric Properties. Materials 2019, 12, 3818. [Google Scholar] [CrossRef] [Green Version]
- Al Rashid, A.; Khalid, M.Y.; Imran, R.; Ali, U.; Koc, M. Utilization of Banana Fiber-Reinforced Hybrid Composites in the Sports Industry. Materials 2020, 13, 3167. [Google Scholar] [CrossRef] [PubMed]
- Spinelli, G.; Lamberti, P.; Tucci, V.; Kotsilkova, R.; Ivanov, E.; Menseidov, D.; Naddeo, C.; Romano, V.; Guadagno, L.; Adami, R.; et al. Nanocarbon/Poly(Lactic) Acid for 3D Printing: Effect of Fillers Content on Electromagnetic and Thermal Properties. Materials 2019, 12, 2369. [Google Scholar] [CrossRef] [Green Version]
- Van de Werken, N.; Tekinalp, H.; Khanbolouki, P.; Ozcan, S.; Williams, A.; Tehrani, M. Additively manufactured carbon fiber-reinforced composites: State of the art and perspective. Addit. Manuf. 2020, 31, 100962. [Google Scholar] [CrossRef]
- Blok, L.; Longana, M.; Yu, H.; Woods, B. An investigation into 3D printing of fibre reinforced thermoplastic composites. Addit. Manuf. 2018, 22, 176–186. [Google Scholar] [CrossRef]
- Al Rashid, A.; Imran, R.; Khalid, M.Y. Determination of opening stresses for railway steel under low cycle fatigue using digital image correlation. Theor. Appl. Fract. Mech. 2020, 108, 102601. [Google Scholar] [CrossRef]
- Xiao, B.; Huang, Q.; Chen, H.; Chen, X.; Long, G. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29. [Google Scholar] [CrossRef]
- Mohammadizadeh, M.; Imeri, A.; Fidan, I.; Elkelany, M. 3D printed fiber reinforced polymer composites—Structural analysis. Compos. Part B Eng. 2019, 175, 107112. [Google Scholar] [CrossRef]
- Kaur, M.; Yun, T.G.; Han, S.M.; Thomas, E.L.; Kim, W.S. 3D printed stretching-dominated micro-trusses. Mater. Des. 2017, 134, 272–280. [Google Scholar] [CrossRef]
- Korkees, F.; Allenby, J.; Dorrington, P. 3D printing of composites: Design parameters and flexural performance. Rapid Prototyp. J. 2020, 26, 699–706. [Google Scholar] [CrossRef]
- Bárnik, F.; Vaško, M.; Handrik, M.; Dorčiak, F.; Majko, J. Comparing mechanical properties of composites structures on Onyx base with different density and shape of fill. Transp. Res. Procedia 2019, 40, 616–622. [Google Scholar] [CrossRef]
- Bárnik, F.; Vaško, M.; Sága, M.; Handrik, M.; Sapietová, A. Mechanical properties of structures produced by 3D printing from composite materials. MATEC Web Conf. 2019, 254, 01018. [Google Scholar] [CrossRef]
- Sága, M.; Bárnik, F.; Vaško, M.; Handrik, M.; Kopas, P. Identification of Physical Characteristic of Composite Materials Produced by Additive Technology from Perspective of Selected Mechanical Properties. Acta Phys. Pol. A 2020, 138, 249–252. [Google Scholar] [CrossRef]
- Dorčiak, F.; Vaško, M.; Handrik, M.; Bárnik, F.; Majko, J. Tensile test for specimen with different size and shape of inner structures created by 3D printing. Transp. Res. Procedia 2019, 40, 671–677. [Google Scholar] [CrossRef]
- Sága, M.; Majko, J.; Handrik, M.; Vaško, M.M.; Sapietová, A. Proposal of Physical Model for Damage Simulation of Composite Structures Produced by 3D Printing. Acta Phys. Pol. A 2020, 138, 245–248. [Google Scholar] [CrossRef]
- Yang, P.; Hu, N.; Guo, X.; Dong, L.; Chen, Y.; Guo, Z. An ultra-simple universal model for the effective elastic properties of isotropic 3D closed-cell porous materials. Compos. Struct. 2020, 249, 112531. [Google Scholar] [CrossRef]
- Nayak, S.M.; Shetty, P.B.; Mishra, R.K.; Reddy, S.; Viraj, G.R. Failure Analysis of Additive Manufactured Fiber-Reinforced Thermoplastics. J. Fail. Anal. Prev. 2019, 19, 471–475. [Google Scholar] [CrossRef]
- Zhang, Y.; Purssell, C.; Mao, K.; Leigh, S. A physical investigation of wear and thermal characteristics of 3D printed nylon spur gears. Tribol. Int. 2020, 141, 105953. [Google Scholar] [CrossRef]
- Cuesta, I.; Martinez-Pañeda, E.; Díaz, A.; Alegre, J. The Essential Work of Fracture parameters for 3D printed polymer sheets. Mater. Des. 2019, 181, 1–9. [Google Scholar] [CrossRef]
- Liu, C.; Liu, P.; Zhao, Z.; Northwood, D.O. Room temperature creep of a high strength steel. Mater. Des. 2001, 22, 325–328. [Google Scholar] [CrossRef]
- Wilshire, B. Microscopic Models and Macroscopic Constitutive Laws for High Temperature Creep and Creep Fracture of Metallic and Ceramic Materials. In Mechanics of Creep Brittle Materials 2; Cocks, A.C.F., Ponter, A.R.S., Eds.; Springer: Dordrecht, The Netherlands, 1991; pp. 112–123. [Google Scholar]
- Beaulieu, A.; Linden, A.Z.; Phillips, J.; Arroyo, L.G.; Koenig, J.; Monteith, G. Various 3D printed materials mimic bone ultrasonographically: 3D printed models of the equine cervical articular process joints as a simulator for ultrasound guided intra-articular injections. PLoS ONE 2019, 14, e0220332. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, X.; Koomson, C.; Doddamani, M.; Behera, R.K.; Gupta, N. Extracting elastic modulus at different strain rates and temperatures from dynamic mechanical analysis data: A study on nanocomposites. Compos. Part. B Eng. 2019, 159, 346–354. [Google Scholar] [CrossRef]
- Zeltmann, S.E.; Prakash, K.A.; Doddamani, M.; Gupta, N. Prediction of modulus at various strain rates from dynamic mechanical analysis data for polymer matrix composites. Compos. Part. B Eng. 2017, 120, 27–34. [Google Scholar] [CrossRef]
- Kabir, S.M.F.; Mathur, K.; Seyam, A.-F.M. A critical review on 3D printed continuous fiber-reinforced composites: History, mechanism, materials and properties. Compos. Struct. 2020, 232, 111476. [Google Scholar] [CrossRef]
- Markforged. Available online: https://markforged.com/ (accessed on 1 January 2021).
- ASTM International. ASTM D4065-20—Standard Practice for Plastics: Dynamic Mechanical Properties; ASTM International: West Conshohocken, PA, USA, 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Zhong, W.; Li, F.; Zhang, Z.; Song, L.; Li, Z. Short fiber reinforced composites for fused deposition modeling. Mater. Sci. Eng. A 2001, 301, 125–130. [Google Scholar] [CrossRef]
- Brenken, B.; Barocio, E.; Favaloro, A.; Kunc, V.; Pipes, R.B. Fused filament fabrication of fiber-reinforced polymers: A review. Addit. Manuf. 2018, 21, 1–16. [Google Scholar] [CrossRef]
- Dai, Z.; Gao, Y.; Liu, L.; Pötschke, P.; Yang, J.; Zhang, Z. Creep-resistant behavior of MWCNT-polycarbonate melt spun nanocomposite fibers at elevated temperature. Polymer 2013, 54, 3723–3729. [Google Scholar] [CrossRef]
- Jia, Y.; Jiang, Z.; Peng, J.; Gong, X.; Zhang, Z. Resistance to time-dependent deformation of polystyrene/carbon nanotube composites under cyclic tension. Compos. Part. A Appl. Sci. Manuf. 2012, 43, 1561–1568. [Google Scholar] [CrossRef]





| Specimen Dimensions | 60 × 12 × 3 mm³ (L × W × T) |
| Printing Resolution | 0.10 mm |
| Fill Pattern | Solid Fill |
| Fill Density | 100% |
| Wall Layers | 2 |
| Printing Orientation (Onyx) | ±45° |
| Fiber Volume Fraction | ~38% |
| Reinforcement Fill Type | Hybrid (Concentric + Isotropic) |
| Concentric Rings | 2 |
| Isotropic Reinforcement Angle | 0ᴼ |
| Stacking Sequence | [4O/4F/2O/4F/1O]s |
| Printing Temperature (Onyx) | 275 °C |
| Printing Temperature (Reinforcements) | 252 °C |
| Temperature | Material | ||||
|---|---|---|---|---|---|
| 30 °C | Onyx | 342,409 | 7.26 | 2.09 | 126 |
| Onyx-FG | 342,457 | 19.79 | 3.33 | 687 | |
| Onyx-HSHT-FG | 342,483 | 23.09 | 4.80 | 821 | |
| Onyx-KF | 342,457 | 20.10 | 3.84 | 528 | |
| 70 °C | Onyx | 342,449 | 3.52 | 0.84 | 171 |
| Onyx-FG | 342,500 | 10.00 | 2.27 | 393 | |
| Onyx-HSHT-FG | 342,511 | 10.94 | 2.71 | 479 | |
| Onyx-KF | 342,439 | 9.77 | 2.50 | 287 | |
| 120 °C | Onyx | 342,534 | 2.43 | 0.66 | 181 |
| Onyx-FG | 342,530 | 9.68 | 2.33 | 321 | |
| Onyx-HSHT-FG | 342,532 | 7.87 | 2.03 | 379 | |
| Onyx-KF | 342,470 | 8.95 | 2.54 | 543 |
| Temperature | Material | ԐV(%) | ηr (s) | βr | ԐP(%) |
|---|---|---|---|---|---|
| 30 °C | Onyx | 0.113 | 250.43 | 0.253 | 0.009 |
| Onyx-FG | 0.023 | 201.90 | 0.252 | 0 | |
| Onyx-HSHT-FG | 0.024 | 955.99 | 0.298 | 0 | |
| Onyx-KF | 0.026 | 520.63 | 0.213 | 0 | |
| 70 °C | Onyx | 0.124 | 3971.48 | 0.248 | 0.035 |
| Onyx-FG | 0.047 | 15,062.15 | 0.249 | 0 | |
| Onyx-HSHT-FG | 0.039 | 3505.37 | 0.202 | 0.009 | |
| Onyx-KF | 0.042 | 3536.11 | 0.206 | 0.017 | |
| 120 °C | Onyx | 0.171 | 8371.30 | 0.293 | 0.081 |
| Onyx-FG | 0.041 | 15,483.37 | 0.252 | 0.014 | |
| Onyx-HSHT-FG | 0.064 | 10,196.39 | 0.357 | 0 | |
| Onyx-KF | 0.044 | 4210.91 | 0.435 | 0.011 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Rashid, A.; Koҫ, M. Creep and Recovery Behavior of Continuous Fiber-Reinforced 3DP Composites. Polymers 2021, 13, 1644. https://doi.org/10.3390/polym13101644
Al Rashid A, Koҫ M. Creep and Recovery Behavior of Continuous Fiber-Reinforced 3DP Composites. Polymers. 2021; 13(10):1644. https://doi.org/10.3390/polym13101644
Chicago/Turabian StyleAl Rashid, Ans, and Muammer Koҫ. 2021. "Creep and Recovery Behavior of Continuous Fiber-Reinforced 3DP Composites" Polymers 13, no. 10: 1644. https://doi.org/10.3390/polym13101644
APA StyleAl Rashid, A., & Koҫ, M. (2021). Creep and Recovery Behavior of Continuous Fiber-Reinforced 3DP Composites. Polymers, 13(10), 1644. https://doi.org/10.3390/polym13101644







