Leakage-Flow Models for Screw Extruders
Abstract
:1. Introduction
1.1. Analysis of Flow in Metering Channels
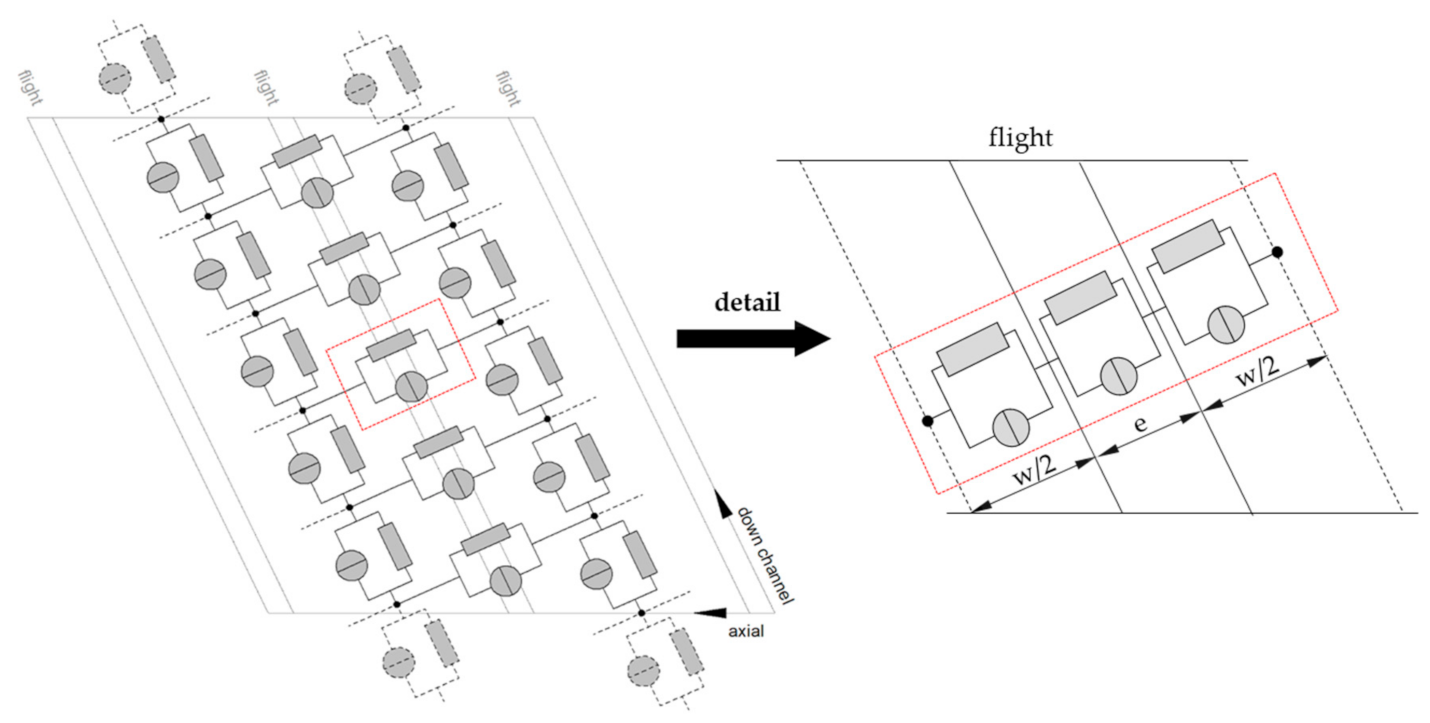
1.2. Analysis of Leakage Flow
1.3. Research Approach
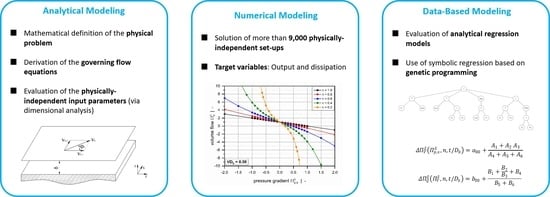
2. Model Development
2.1. Analytical Modeling
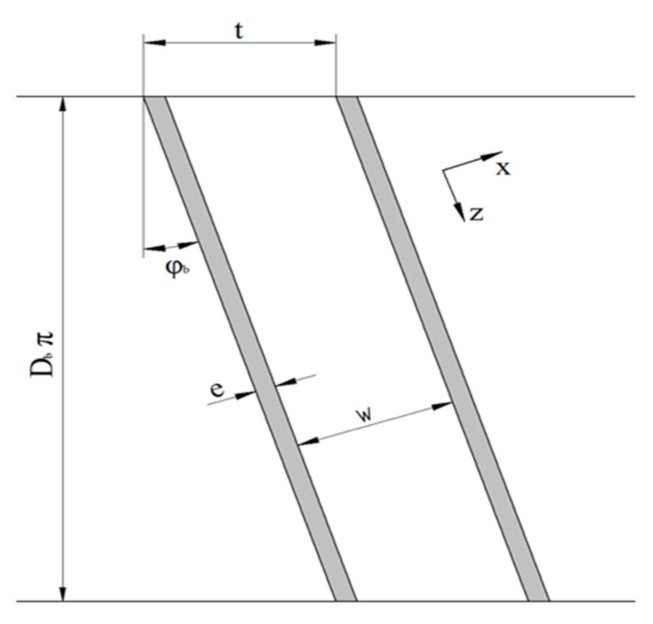
2.1.1. Problem Definition
2.1.2. Governing Equations
2.1.3. Theory of Similarity
2.1.4. Set-Up of Parametric Study
2.2. Numerical Modeling
2.2.1. Numerical Solution Procedure
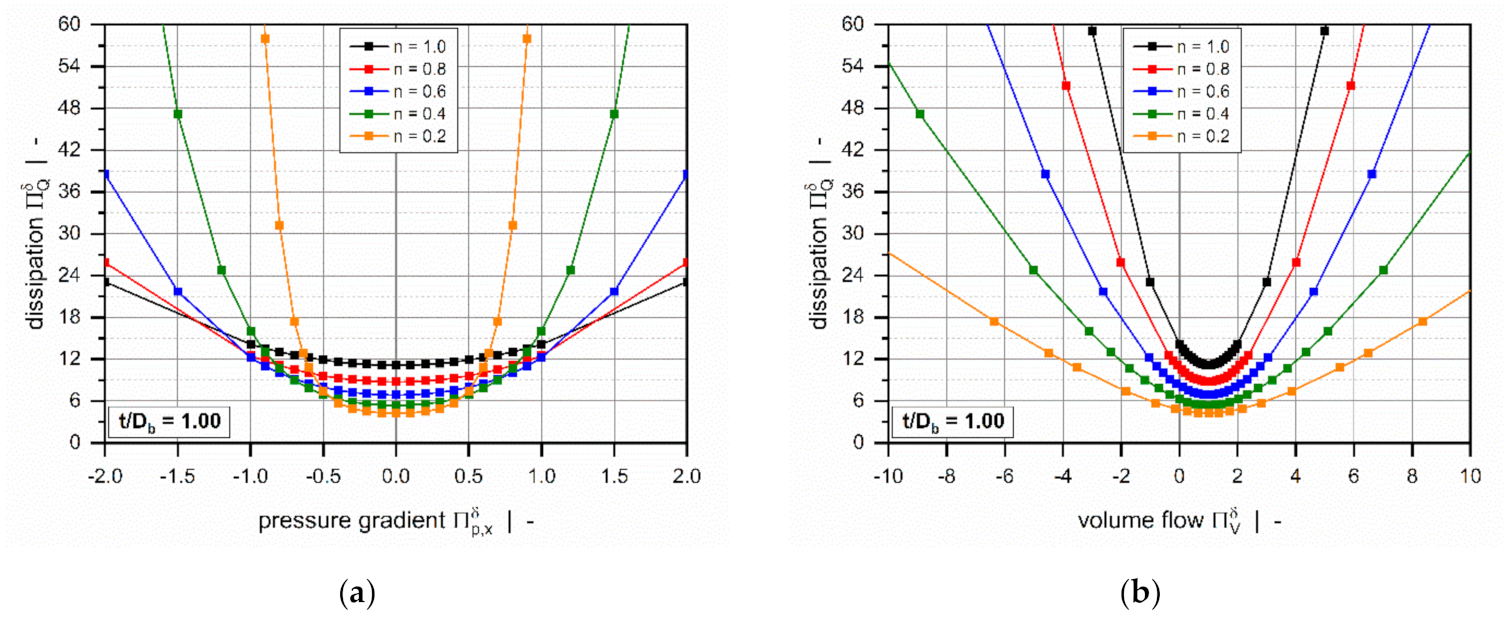
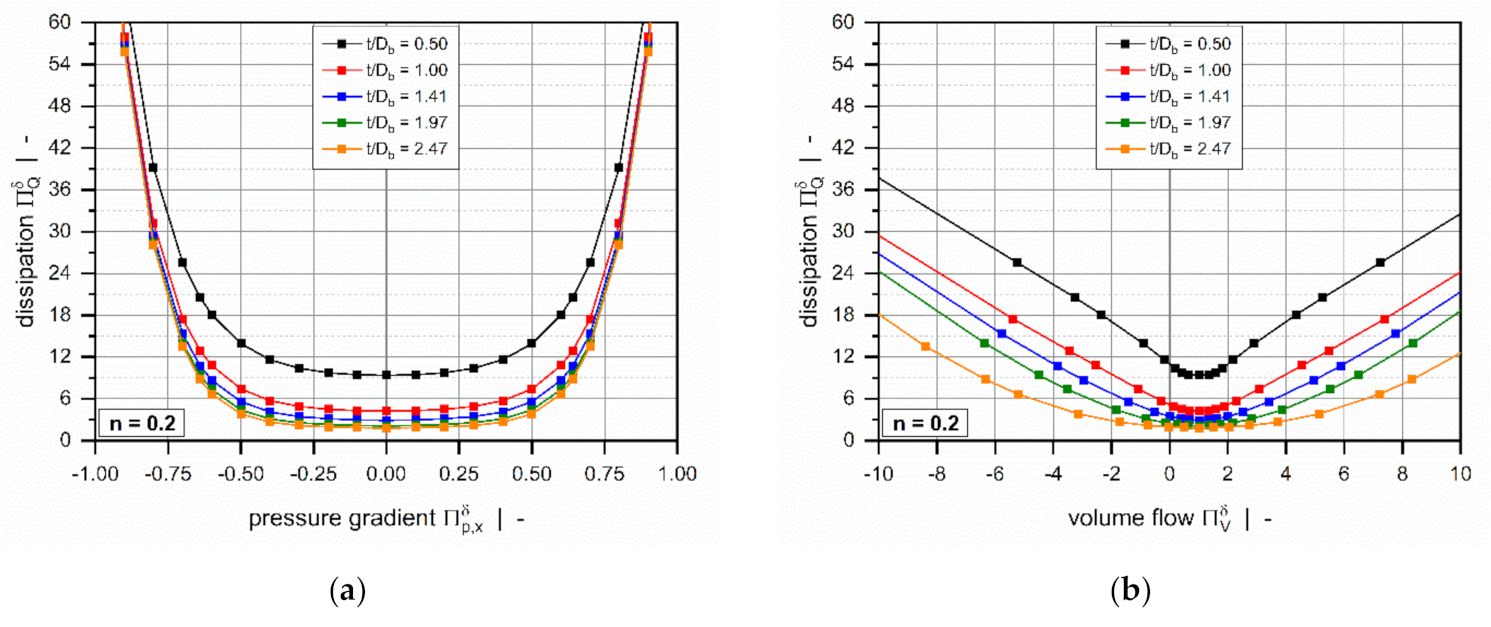
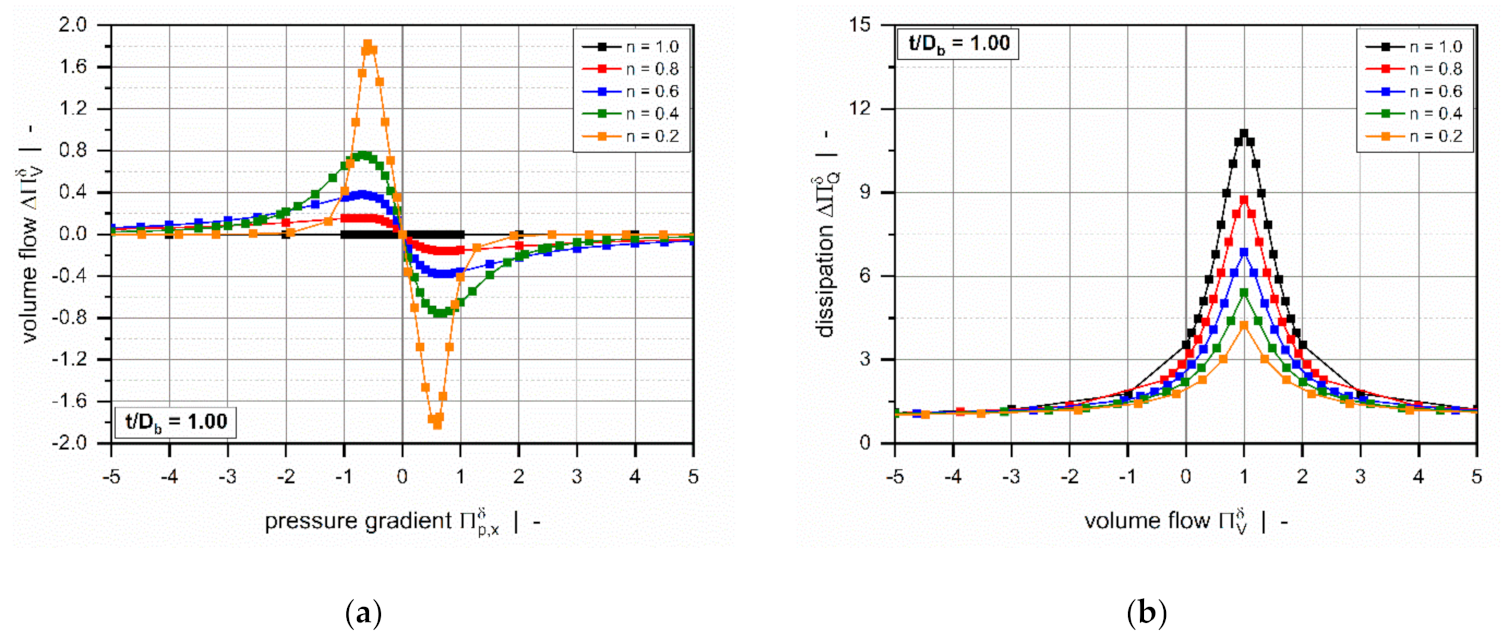
2.2.2. Numerical Results
2.3. Data-Based Modeling
2.3.1. Symbolic Regression Analysis
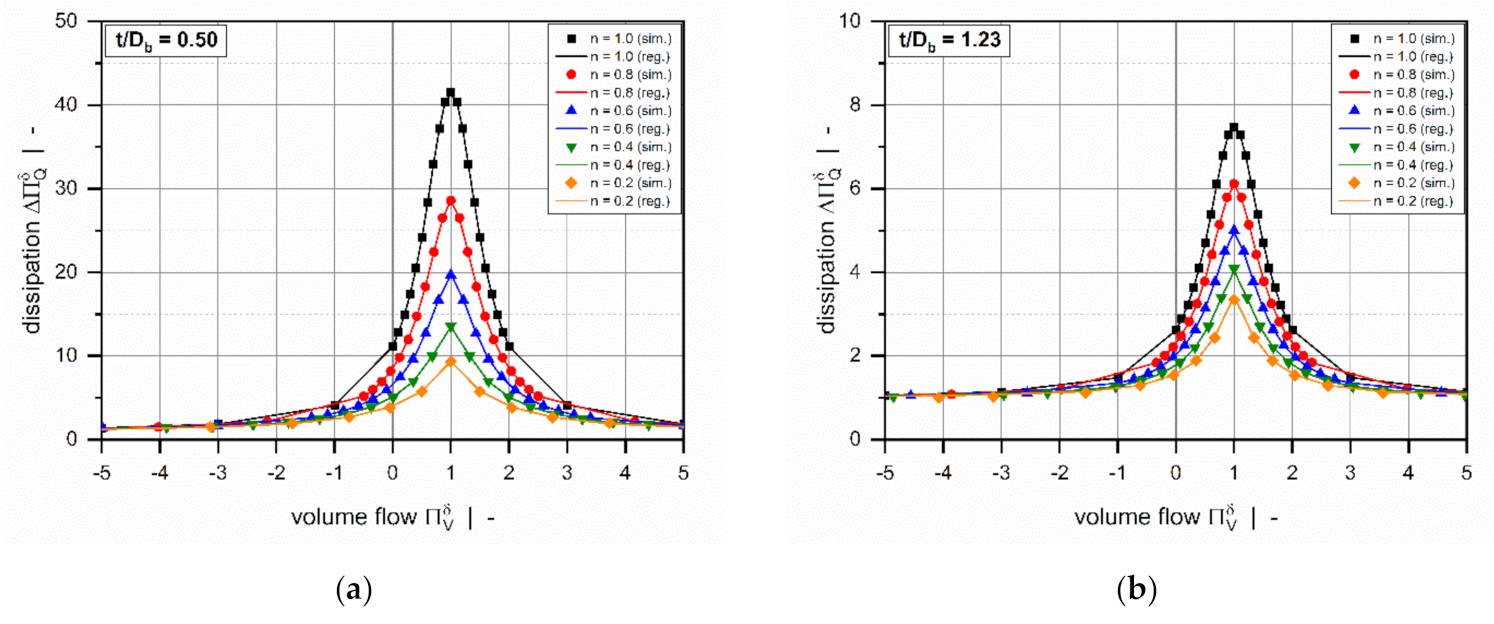
2.3.2. Symbolic Regression Results
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Subfunctions of Equations (44) and (45)
Appendix A.2. Model Coefficients
| 0.0000413479 | 0.998487 | ||
| −2.97497 | −11.4595 | ||
| 390.644 | 9.75142 | ||
| −1.00056 | 1.69836 | ||
| −0.121986 | −0.775636 | ||
| −0.394801 | −0.533892 | ||
| −0.317506 | 0.1505 | ||
| −0.093065 | 0.063818 | ||
| 0.762303 | 0.910203 | ||
| 0.11879 | −0.148087 | ||
| 0.121586 | 0.169683 | ||
| 4.04094 | −0.471171 | ||
| 11.6959 | 0.015469 | ||
| 89.2206 | 0.30448 | ||
| −0.147822 | 1.74533 | ||
| 0.0113796 | 0.343839 | ||
| −0.0381859 | −3.1969 | ||
| 0.0171605 | 1.597370 | ||
| 791.442 | −67815.8 | ||
| −1.01937 | 67789.9 | ||
| 0.209565 | 0.00156 | ||
| 4118.38 | 1.01936 | ||
| −0.26066 | 1.45018 | ||
| 0.00593881 | 17.2059 | ||
| 0.26419 | −13.3529 | ||
| 6.68431 | |||
| 0.35355 | |||
| −2.15945 | |||
| −0.00005 | |||
| 0.99991 | |||
| −0.368 |
| coefficients of regression model | volume flow rate | ||
| subfunctions of regression model | channel width | ||
| maximum absolute error | cross-channel coordinate | ||
| mean absolute error | vector of unknowns | ||
| coefficients of regression model | up-channel coordinate | ||
| subfunctions of regression model | numerical result | ||
| constants | approximated result | ||
| barrel diameter | mean value of numerical results | ||
| rate-of-deformation tensor | down-channel coordinate | ||
| flight width | temperature coefficient | ||
| vector of boundary conditions | flight clearance | ||
| number of parallel screw flights | shear rate | ||
| Jacobian | dimensionless shear rate | ||
| consistency | viscosity | ||
| velocity gradient tensor | dimensionless viscosity | ||
| mass-flow rate | dimensionless velocities | ||
| power-law index | dimensionless height direction | ||
| screw speed | dimensionless pressure gradients | ||
| coefficient of correlation | dimensionless dissipation | ||
| maximum relative error | approximated dimensionless dissipation | ||
| mean relative error | corrected dimensionless dissipation | ||
| pressure | dimensionless flow rate | ||
| screw pitch | approximated dimensionless flow rate | ||
| velocities | corrected dimensionless flow rate | ||
| barrel velocity | melt density | ||
| barrel velocity in x-direction | shear stresses | ||
| barrel velocity in z-direction | stress tensor | ||
| velocity vector | pitch angle |
References
- Tadmor, Z.; Klein, I. Engineering Principles of Plasticating Extrusion; Van Nostrand Reinhold, Co.: New York, NY, USA; ISBN 9780442156350.
- White, J.L.; Potente, H. Screw Extrusion; Hanser Publishers: Munich, Germany, 2001; ISBN 9783446196247. [Google Scholar]
- Tadmor, Z.; Gogos, Z.G. Principles of Polymer Processing, 2nd ed.; Wiley and Sons: Hoboken, NJ, USA, 2002; ISBN 9780471387701. [Google Scholar]
- Campbell, G.A.; Spalding, M. Analyzing and Troubleshooting Single-Screw Extruders; Hanser Publishers: Munich, Germany, 2013; ISBN 9783446413719. [Google Scholar]
- Rauwendaal, C. Polymer Extrusion, 5th ed.; Hanser Publishers: Munich, Germany, 2014; ISBN 9783446217744. [Google Scholar]
- Agassant, J.F.; Avenas, P.; Carreau, P.J.; Vergnes, B.; Vincent, M. Polymer Processing. Principles and Modelling, 2nd ed.; Hanser Publishers: Munich, Germany, 2017; ISBN 9781569906057. [Google Scholar]
- Wilczyńnski, K.; Nastaj, A.; Lewandowski, A.; Wilczyńnski, K.J.; Buziak, K. Fundamentals of global modeling for polymer extrusion. Polymers 2019, 11, 2106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anonymous. Screw Viscosity Pumps. Engineering 1922, 114, 606–607. [Google Scholar]
- Rowell, H.S.; Finlayson, D. Screw viscosity pumps. Engineering 1928, 126, 249–250, 385–387. [Google Scholar]
- Carley, J.F.; Mallouk, R.S.; McKelvey, J.M. Simplified flow theory for screw extruder. Ind. Eng. Chem. 1953, 45, 974–978. [Google Scholar] [CrossRef]
- Mohr, W.D.; Saxton, R.L.; Jepson, C.H. Theory of mixing in the single-screw extruder. Ind. Eng. Chem. 1957, 49, 1857–1862. [Google Scholar] [CrossRef]
- Mohr, W.D.; Mallouk, R.S. Flow, power requirement, and pressure distribution of fluid in a screw extruder. Ind. Eng. Chem. 1959, 51, 765–770. [Google Scholar] [CrossRef]
- Rotem, Z.; Shinnar, R. Non-newtonian flow between parallel boundaries in linear movements. Chem. Eng. Sci. 1961, 15, 130–149. [Google Scholar] [CrossRef]
- Griffith, R.M. Fully developed flow in screw extruders. Ind. Eng. Chem. Fundam. 1962, 1, 180–187. [Google Scholar] [CrossRef]
- Zamodits, H.J.; Pearson, J.R.A. Flow of polymer melts in extruders. Part I. The effect of transverse flow and of a superpose steady temperature profile. Trans. Soc. Rheol. 1969, 13, 357–385. [Google Scholar] [CrossRef]
- Karwe, M.V.; Jaluria, Y. Numerical simulation of fluid flow and heat transfer in a single-screw extruder for non-newtonian fluids. Numer. Heat Transf. Part. A 1990, 17, 167–190. [Google Scholar] [CrossRef]
- Spalding, M.A.; Dooley, J.; Hyun, K.S.; Strand, S.R. Three-Dimensional Numerical Analysis of a Single-Screw Extruder; SPE ANTEC Technical Papers; Society of Plastics Engineers: New Orleans, LA, USA, 1993; pp. 1533–1541. [Google Scholar]
- Ghoreishy, M.H.R.; Razavi-Nouri, M.; Naderi, G. Finite element analysis of a thermoplastic elastomer melt flow in the metering region of a single screw extruder. Comp. Mater. Sci. 2005, 34, 389–396. [Google Scholar] [CrossRef]
- Polychronopoulos, N.D.; Vlachopoulos, J. Computer flow simulation of moffat eddies in single screw extrusion. Int. Polym. Process. 2018, 5, 662–668. [Google Scholar] [CrossRef]
- Vachagina, E.K.; Kadyirov, A.; Karaeva, J. Simulation of Giesekus fluid flow in extruder using helical coordinate system. IOP Conf. Ser. Mater. Sci. Eng. 2020, 733, 1–5. [Google Scholar] [CrossRef]
- Booy, M.L. The influence of non-newtonian flow on effective viscosity and channel efficiency in screw pumps. Polym. Eng. Sci. 1981, 21, 93–99. [Google Scholar] [CrossRef]
- Rauwendaal, C. Throughput-pressure relationships for power law fluids in single screw extruders. Polym. Eng. Sci. 1986, 26, 1240. [Google Scholar] [CrossRef]
- Spalding, M.A.; Campbell, G.A. An Engineering Approach to the Correction of Rotational Flow Calculations for Single-Screw Extruders-Equation Correction; SPE ANTEC Technical Paper; Society of Plastics Engineers: New Orleans, LA, USA, 2011; pp. 1211–1216. [Google Scholar]
- Pachner, S.; Löw-Baselli, B.; Affenzeller, M.; Miethlinger, J. A Generalized 2d output model of polymer melt flow in single-screw extrusion. Int. Polym. Process. 2017, 32, 209. [Google Scholar] [CrossRef]
- Roland, W.; Miethlinger, J. Heuristic analysis of viscous dissipation in single-screw extruders. Polym. Eng. Sci. 2018, 58, 2055–2070. [Google Scholar] [CrossRef] [Green Version]
- Roland, W.; Kommenda, M.; Marschik, C.; Miethlinger, J. extended regression models for predicting the pumping capability and viscous dissipation of two-dimensional flows in single-screw extrusion. Polymers 2019, 11, 334. [Google Scholar] [CrossRef] [Green Version]
- Marschik, C.; Roland, W.; Loew-Baselli, B.; Miethlinger, J. Modeling Three-Dimensional Non-Newtonian Flows in Single-Screw Extruders; SPE ANTEC Technical Papers; Society of Plastics Engineers: New Orleans, LA, USA, 2017; pp. 1125–1130. [Google Scholar]
- Marschik, C.; Roland, W.; Loew-Baselli, B.; Miethlinger, J. A heuristic method for modeling three-dimensional non-Newtonian flows of polymer melts in single-screw extruders. J. Non Newt. Fluid Mech. 2017, 248, 27–39. [Google Scholar] [CrossRef]
- Marschik, C.; Osswald, T.; Roland, W.; Loew-Baselli, B.; Miethlinger, J. A Heuristic Model for Predicting Three-Dimensional Non-Newtonian Flows in Metering Channels; SPE ANTEC Technical Papers; Society of Plastics Engineers: New Orleans, LA, USA, 2018. [Google Scholar]
- Roland, W.; Marschik, C.; Krieger, M.; Löw-Baselli, B.; Miethlinger, J. Symbolic regression models for predicting viscous dissipation of three-dimensional non-Newtonian flows in single-screw extruders. J. Non Newt. Fluid Mech. 2019, 268, 12–19. [Google Scholar] [CrossRef]
- Gore, W.L.; McKelvey, J.M. Theory of Screw Extruders. In Rheology: Theory and Applications, 3rd ed.; Eirich, F.R., Ed.; Academic Press: New York, NY, USA, 1959. [Google Scholar]
- Rauwendaal, C.; Ingen Housz, J.F. Leakage flow of an isothermal power law fluid. Adv. Polym. Tech. 1988, 8, 290. [Google Scholar] [CrossRef]
- Meyer, H.E.H.; Ingen Housz, J.F.; Gorissen, W.C.M. temperature development in the leakage flow of screw extruders. Polym. Eng. Sci. 1978, 18, 288. [Google Scholar] [CrossRef] [Green Version]
- Pittman, J.F.T.; Rashid, K. Heat transfer in recirculating extruder channel flow. J. Polym. Eng. 1985, 5, 1. [Google Scholar] [CrossRef]
- Rauwendaal, C. Finite element studies of flow and temperature evolution in single screw extruder. Plast. Rubber Comp. 2004, 33, 390. [Google Scholar] [CrossRef]
- Aigner, M. Computational and Experimental Modelling of Transport Phenomena in Single Screw Plasticating Units under Consideration of the Melt Quality. Ph.D. Thesis, Johannes Kepler University, Linz, Austria, 2014. [Google Scholar]
- Marschik, C.; Roland, W.; Miethlinger, J. A network-theory-based comparative study of melt-conveying models in single-screw extrusion: A. Isothermal flow. Polymers 2018, 10, 929. [Google Scholar] [CrossRef] [Green Version]
- Marschik, C.; Dörner, M.; Roland, W.; Miethlinger, J.; Schöppner, V.; Steinbichler, G. Application of network analysis to flow systems with alternating wave channels: Part A (pressure flows). Polymers 2019, 11, 1488. [Google Scholar] [CrossRef] [Green Version]
- Marschik, C.; Roland, W.; Dörner, M.; Schaufler, S.; Schöppner, V.; Steinbichler, G. Application of network analysis to flow systems with alternating wave channels: Part B (superimposed drag-pressure flows in extrusion). Polymers 2020, 12, 1900. [Google Scholar] [CrossRef]
- Roland, W.; Marschik, C.; Hammer, A.; Steinbichler, G. Modeling The Non-Isothermal Conveying Characteristics in Single-Screw Extrusion by Application of Network Analysis; SPE ANTEC Technical Papers; Society of Plastics Engineers: New Orleans, LA, USA, 2020. [Google Scholar]
- Luger, H.J. High-Performance Extrusion under Consideration of Extensional and Wedge Flows. Ph.D. Thesis, Johannes Kepler University, Linz, Austria, 2020. [Google Scholar]
- Marschik, C.; Roland, W.; Loew-Baselli, B.; Steinbichler, G. Application of Hybrid Modeling in Polymer Processing; SPE ANTEC Technical Papers; Society of Plastics Engineers: New Orleans, LA, USA, 2020. [Google Scholar]
- Sun, J.; Rauwendaal, C. Analysis of Flow in Single Screw Extruders; SPE ANTEC Technical Papers; Society of Plastics Engineers: New Orleans, LA, USA, 2002. [Google Scholar]
- Roland, W.; Marschik, C.; Loew-Baselli, B.; Miethlinger, J. The Effect of Channel Curvature on the Flow Rate and Viscous Dissipation of Power-Law Fluids; SPE ANTEC Technical Papers; Society of Plastics Engineers: New Orleans, LA, USA, 2018. [Google Scholar]
- Wagner, S.; Kronberger, G.; Beham, A.; Kommenda, M.; Scheibenpflug, A.; Pitzer, E.; Vonolefen, S.; Kofler, M.; Winkler, S.; Dorfer, V.; et al. Architecture and Design of the Heuristic Lab Optimization Environment. In Advanced Methods and Applications in Computational Intelligence; Klempous, R., Nikodem, J., Jacak, W., Chaczko, Z., Eds.; Springer: Heidelberg, Germany, 2014; Volume 6, pp. 197–261. ISBN 9783319014364. [Google Scholar]
- Poli, R.; Langdon, W.B.; McPhee, N.F. A Field Guide to Genetic Programming; Lulu Press: Morrisville, NC, USA, 2008; ISBN 9781409200734. [Google Scholar]
- Affenzeller, M.; Wagner, S.; Winkler, S.; Beham, A. Genetic Algorithms and Genetic Programming: Modern Concepts and Practical Applications; Chapman & Hall/CRC Press: New York, NY, USA, 2018; ISBN 978-1-58488-629-7. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comp. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]





| Parameter | Unit | Screw Channel | Flight Clearance |
|---|---|---|---|
| Pasn | 1000 | 1000 | |
| - | 0.3 | 0.3 | |
| mm | 45 | 45 | |
| rpm | 100 | 100 | |
| or | mm | 3.5 | 0.075 |
| Pa/m | 50·105 | 50·105 | |
| or | - | 0.82 | 0.006 |
| Variable | Min | Max | Delta |
|---|---|---|---|
| 0.50 | 2.47 | variable | |
| 0.2 | 1.0 | 0.1 | |
| -1.0 | 1.0 | 0.1 |
| Variable | Min | Max | Delta |
|---|---|---|---|
| 0.50 | 2.47 | variable | |
| 0.2 | 1.0 | 0.1 |
| Data Set 2 | Data Set 3 | Data Set 4 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Delta | Min | Max | Delta | Min | Max | Delta | |
| −2000 | 2000 | 200 | −40 | 40 | 4 | −20 | 20 | 2 | |
| −2000 | 2000 | 200 | −20 | 20 | 2 | −10 | 10 | 1 | |
| 0.8 | −1000 | 1000 | 100 | −20 | 20 | 2 | −10 | 10 | 1 |
| 0.7 | −400 | 400 | 40 | −20 | 20 | 2 | −10 | 10 | 1 |
| 0.6 | −200 | 200 | 20 | −10 | 10 | 1 | −5 | 5 | 0.5 |
| 0.5 | −80 | 80 | 8 | −10 | 10 | 1 | −5 | 5 | 0.5 |
| 0.4 | −32 | 32 | 3.2 | −5 | 5 | 0.5 | −3 | 3 | 0.3 |
| 0.3 | −12.8 | 12.8 | 1.28 | −3 | 3 | 0.3 | - | - | - |
| 0.2 | −6.4 | 6.4 | 0.64 | - | - | - | - | - | - |
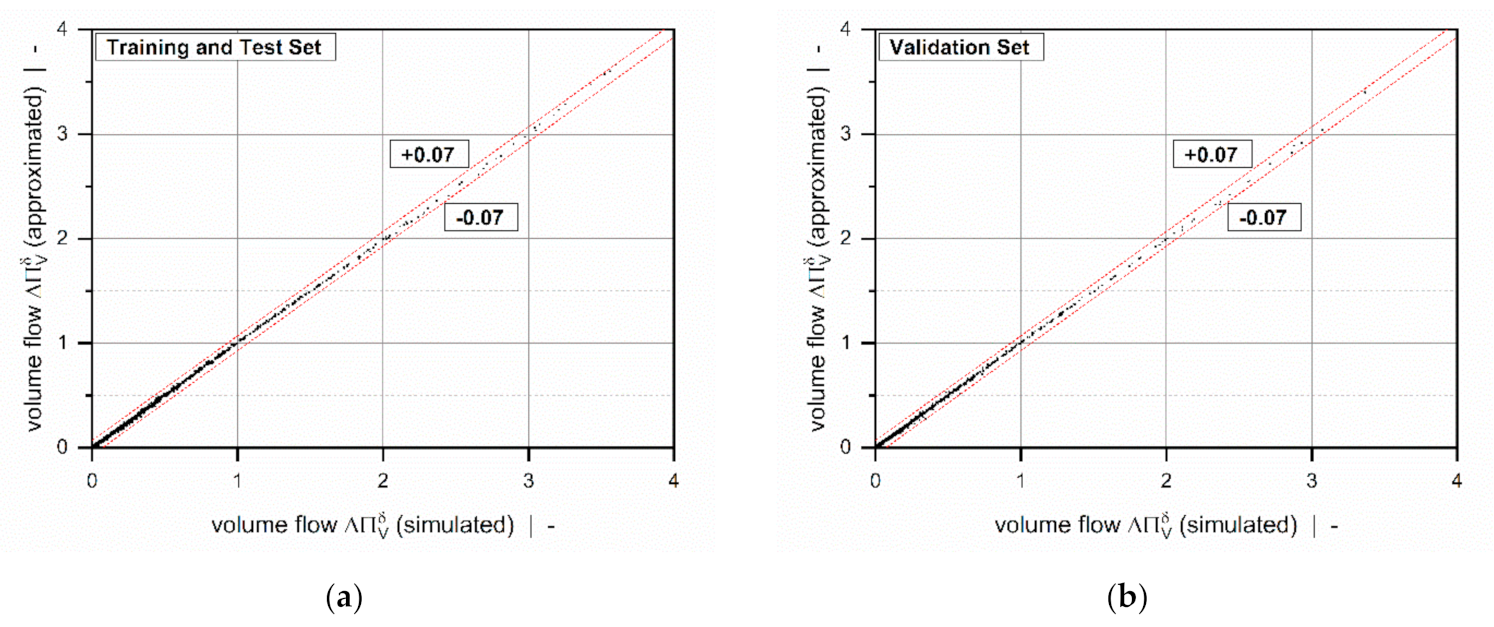
| Quality Measure | Unit | Training Set | Test Set | Validation Set |
|---|---|---|---|---|
| - | 0.99985 | 0.99983 | 0.99986 | |
| - | 0.00536 | 0.00543 | 0.00545 | |
| - | 0.04511 | 0.06068 | 0.06735 |
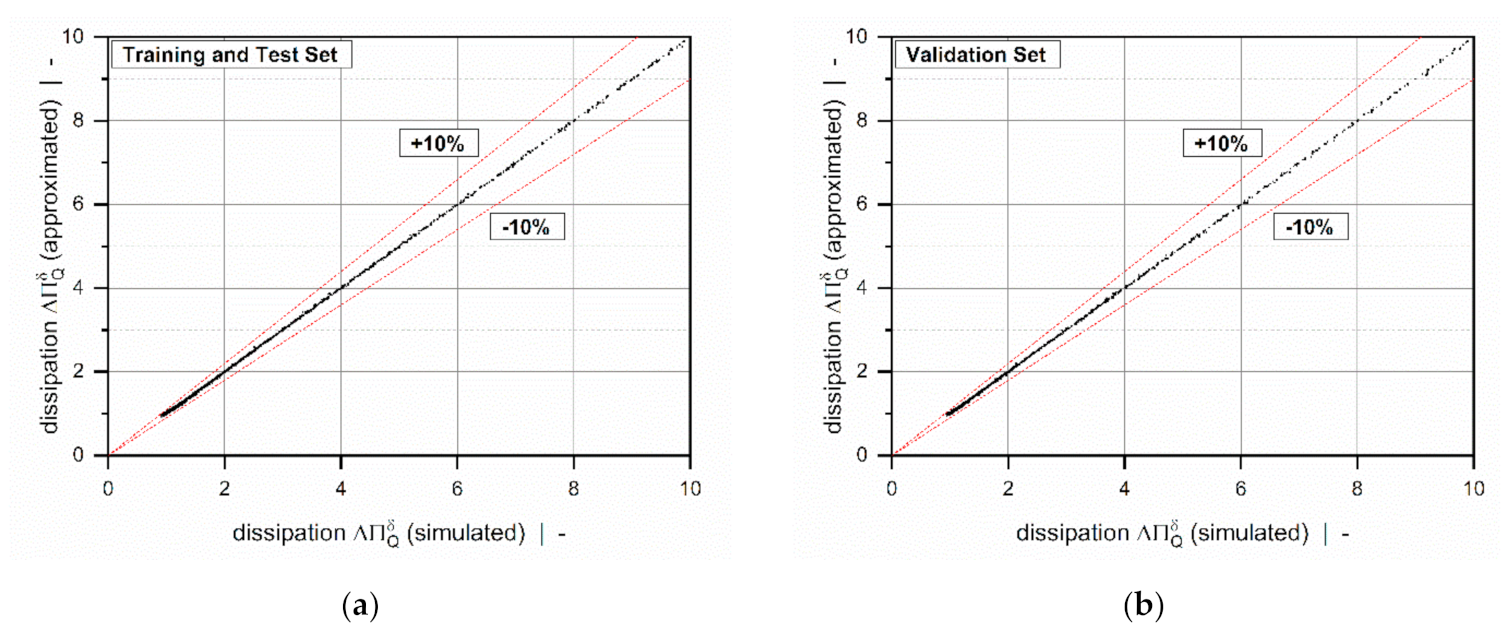
| Quality Measure | Unit | Training Set | Test Set | Validation Set |
|---|---|---|---|---|
| - | 0.99999 | 0.99999 | 0.99999 | |
| - | 0.00638 | 0.00698 | 0.00634 | |
| - | 00.15041 | 0.17306 | 0.20197 | |
| % | 0.31 | 0.33 | 0.3 | |
| % | 6.65 | 6.29 | 6.64 |
| Quality Measure | Unit | ||
|---|---|---|---|
| - | 0.99985 | 0.99999 | |
| - | 0.00513 | 1047.77 | |
| - | 0.06735 | 30270.9 | |
| % | - | 0.31 | |
| % | - | 6.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marschik, C.; Roland, W.; Dörner, M.; Steinbichler, G.; Schöppner, V. Leakage-Flow Models for Screw Extruders. Polymers 2021, 13, 1919. https://doi.org/10.3390/polym13121919
Marschik C, Roland W, Dörner M, Steinbichler G, Schöppner V. Leakage-Flow Models for Screw Extruders. Polymers. 2021; 13(12):1919. https://doi.org/10.3390/polym13121919
Chicago/Turabian StyleMarschik, Christian, Wolfgang Roland, Marius Dörner, Georg Steinbichler, and Volker Schöppner. 2021. "Leakage-Flow Models for Screw Extruders" Polymers 13, no. 12: 1919. https://doi.org/10.3390/polym13121919
APA StyleMarschik, C., Roland, W., Dörner, M., Steinbichler, G., & Schöppner, V. (2021). Leakage-Flow Models for Screw Extruders. Polymers, 13(12), 1919. https://doi.org/10.3390/polym13121919