A Multi-Rheology Design Method of Sheeting Polymer Extrusion Dies Based on Flow Network and the Winter–Fritz Design Equation
Abstract
:1. Introduction
2. Methodology
- Isothermal incompressible flow
- Streamlined flow
- Steady and fully-developed flows in both slit and manifold
- Uniform pressure at the exit of the slit
- Unidirectional flow in both manifold and slit network segments (ignoring traverse flow in the manifold)
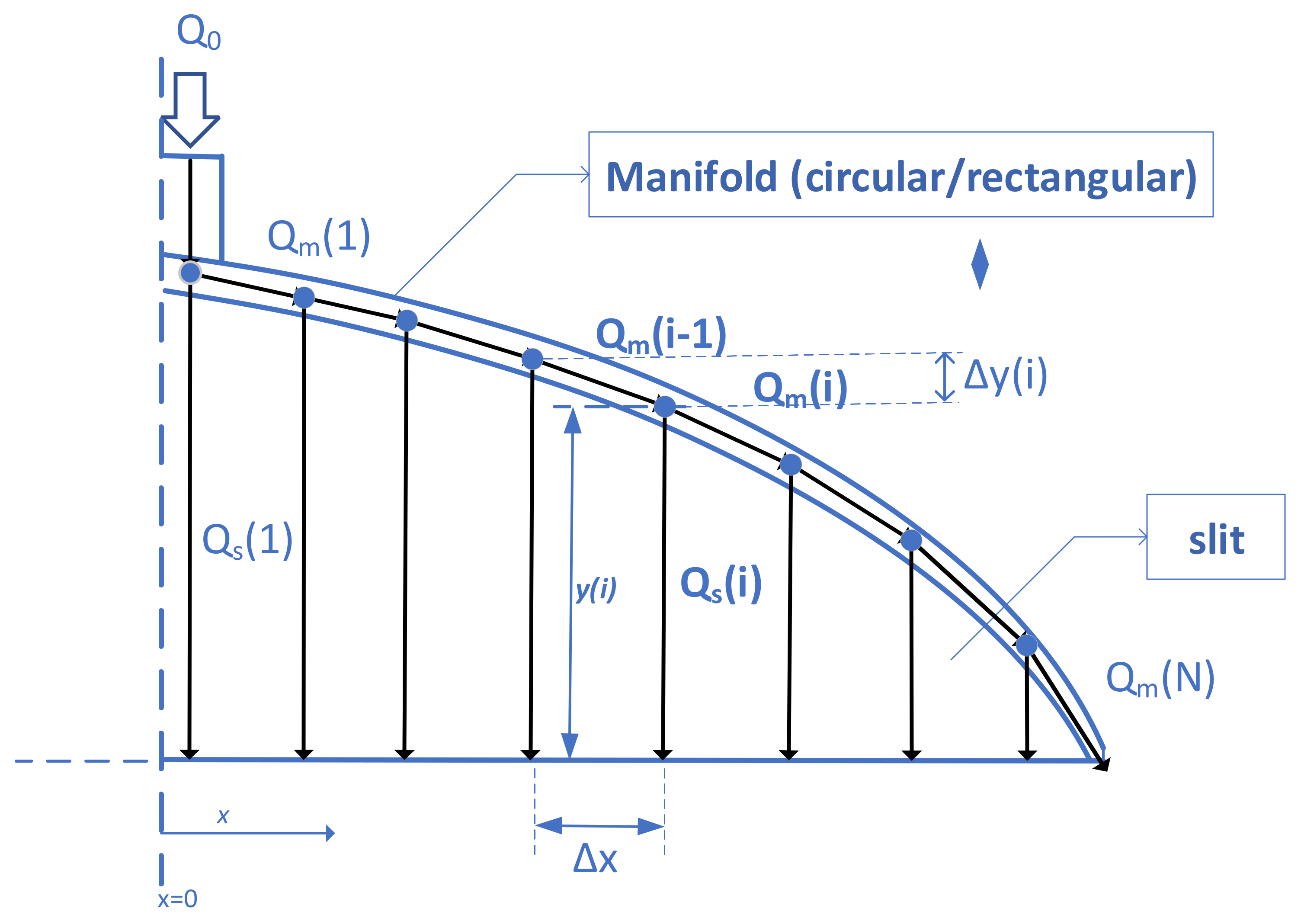
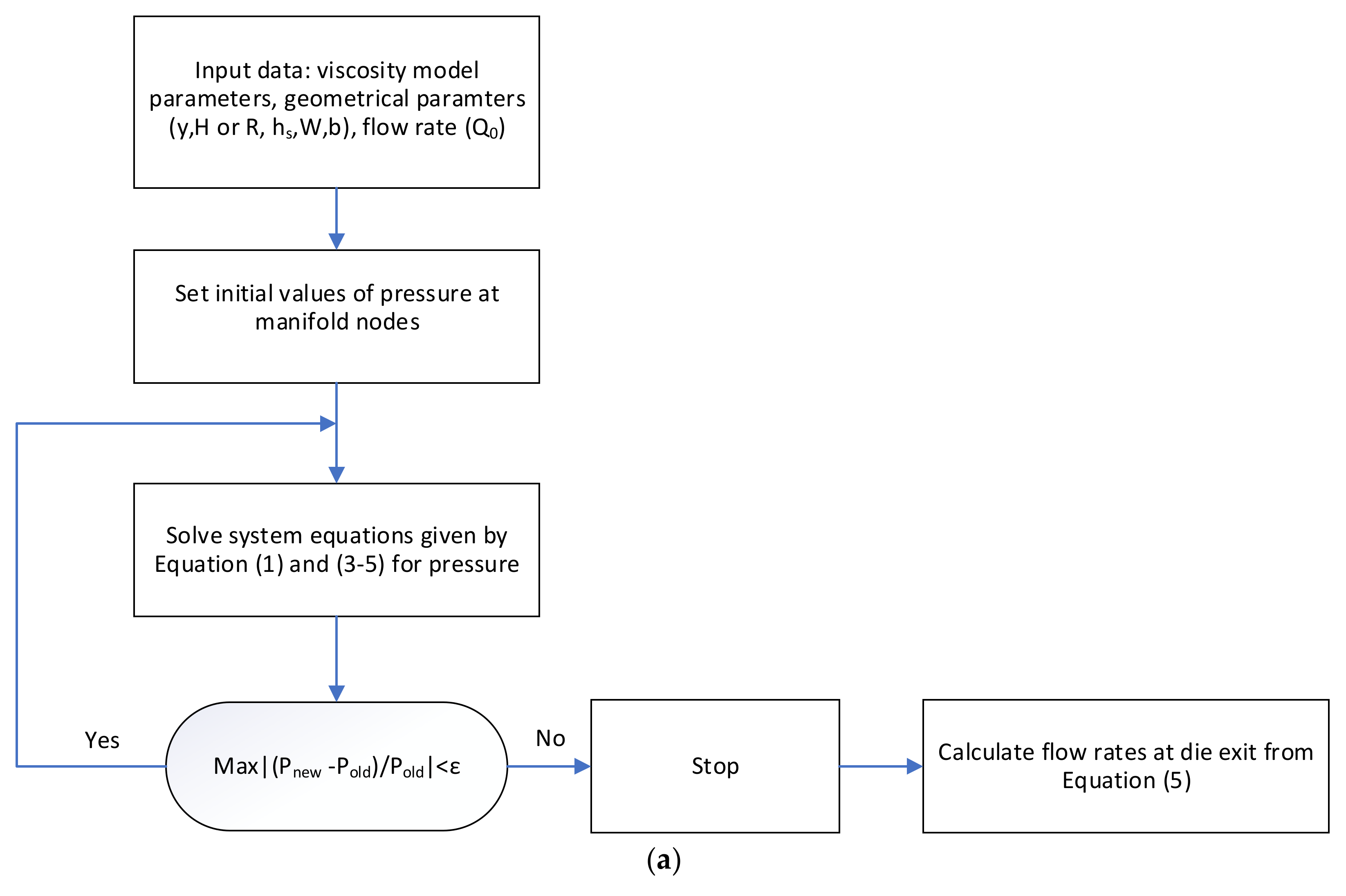
2.1. Calculation of the Flow Distribution
2.2. Design of the Manifold Curve
- Constant shear rates between the slit and the manifold and
- Uniform velocity distribution at the exit of the slit.
2.3. Calculation of Wall Shear Rates and Pressure Gradients
3. Results and Discussion
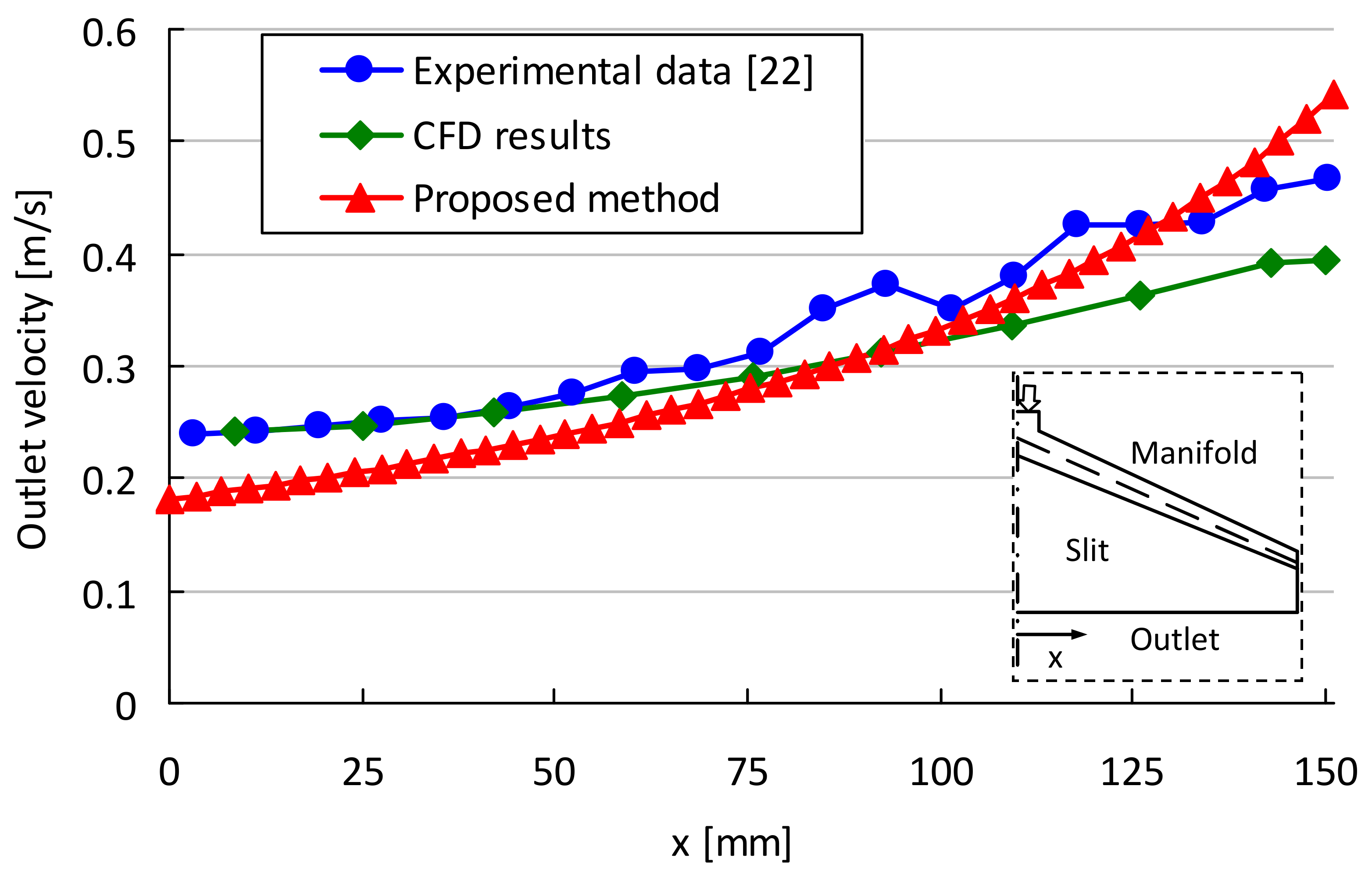
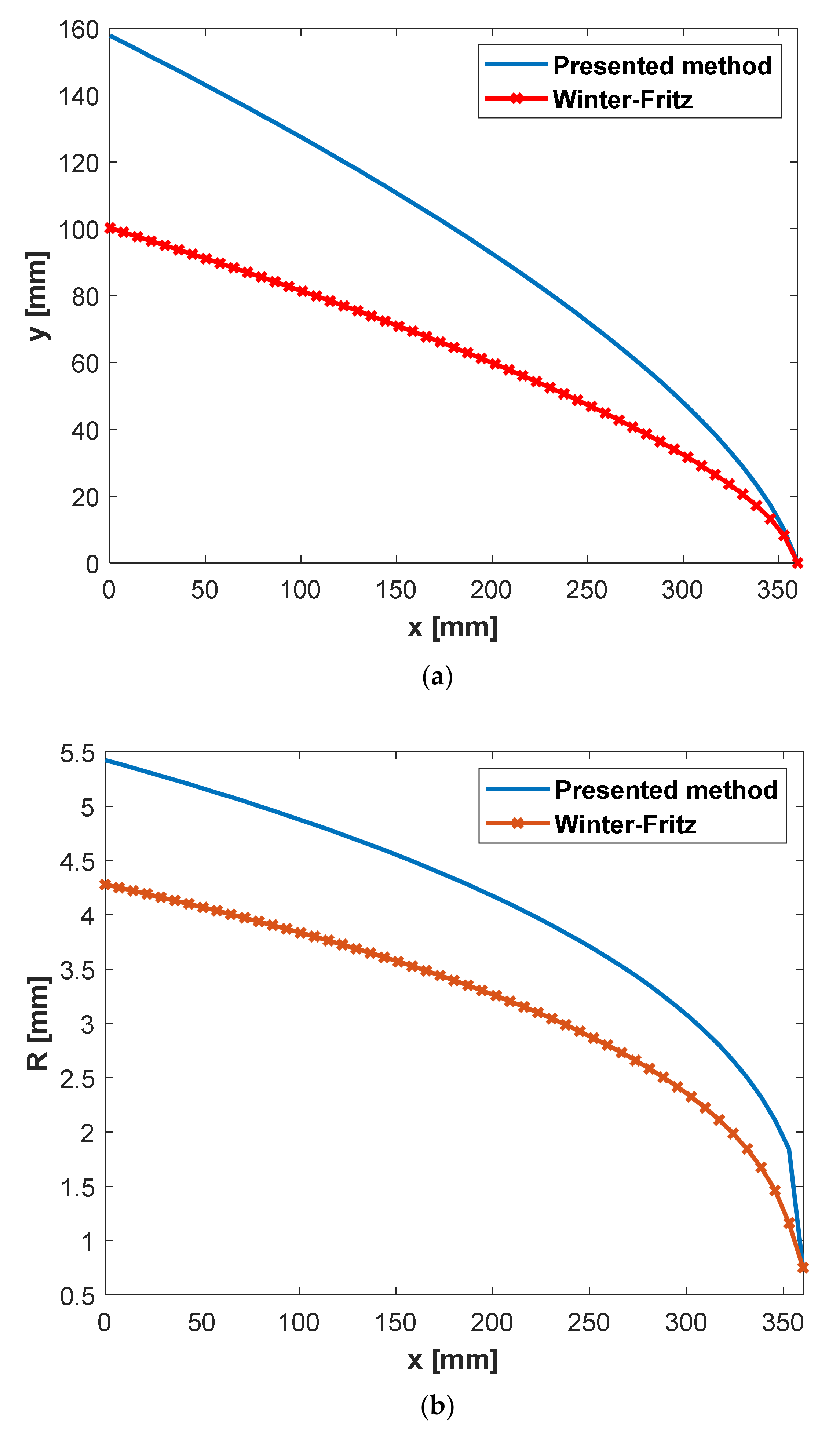
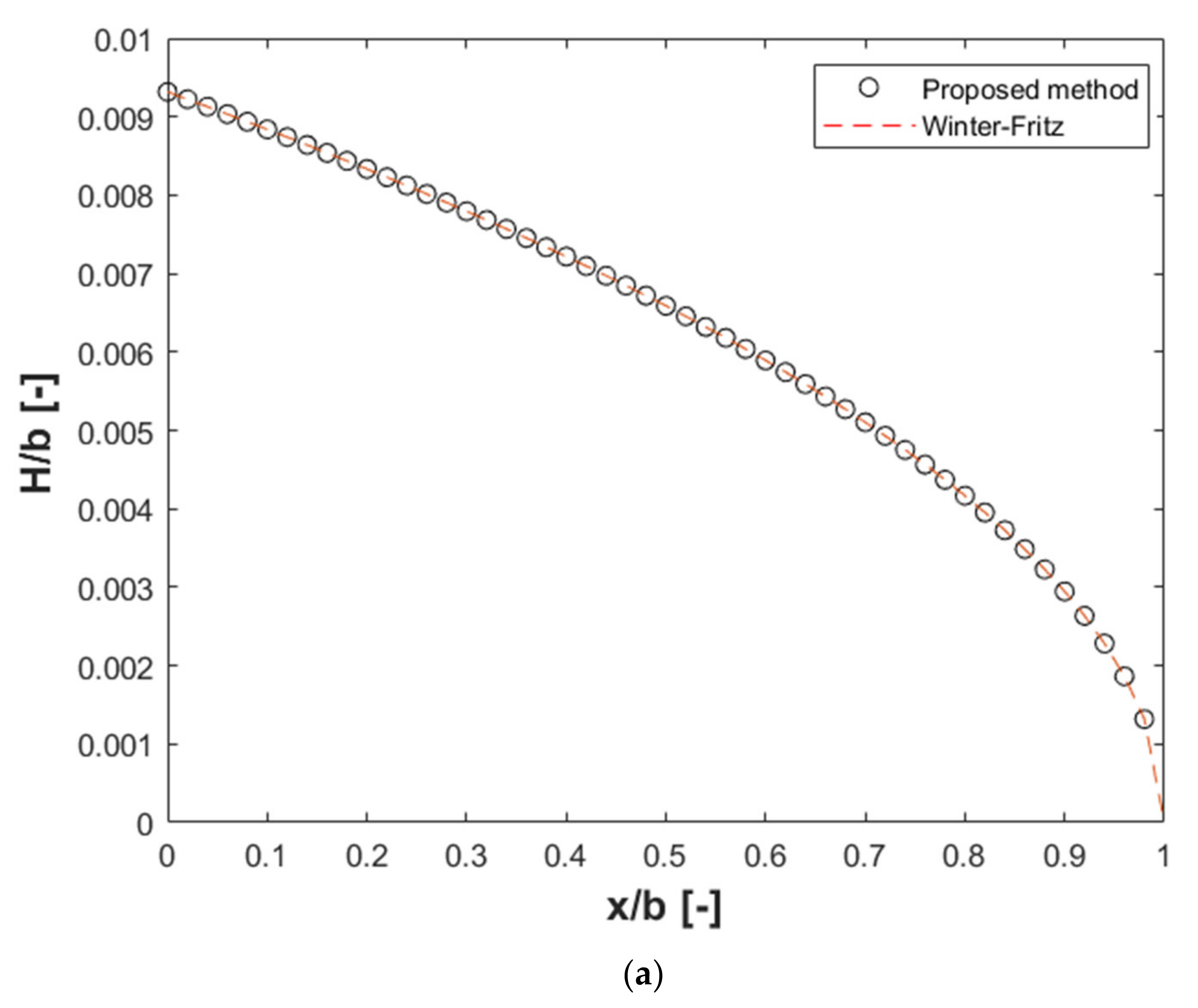
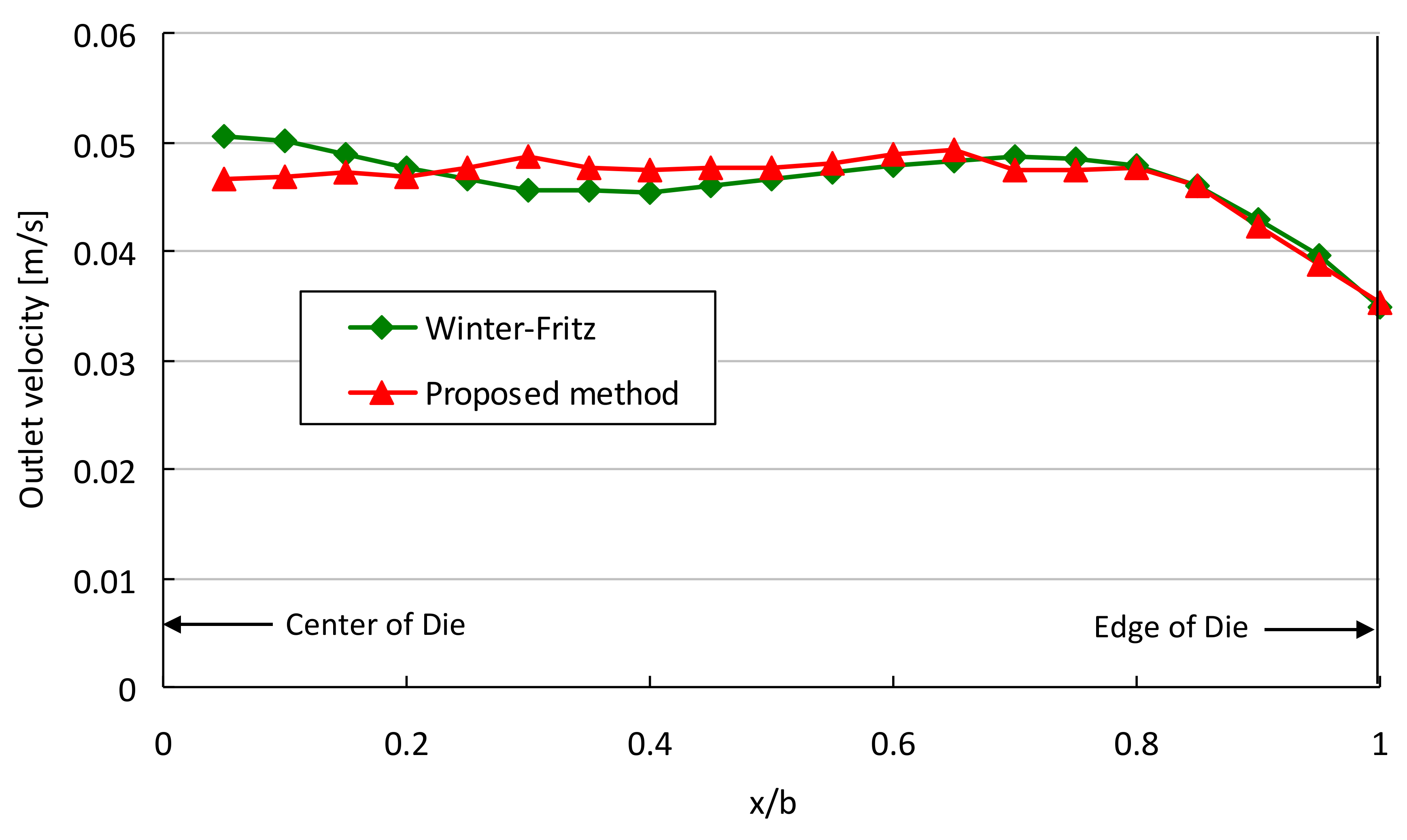
3.1. Validation
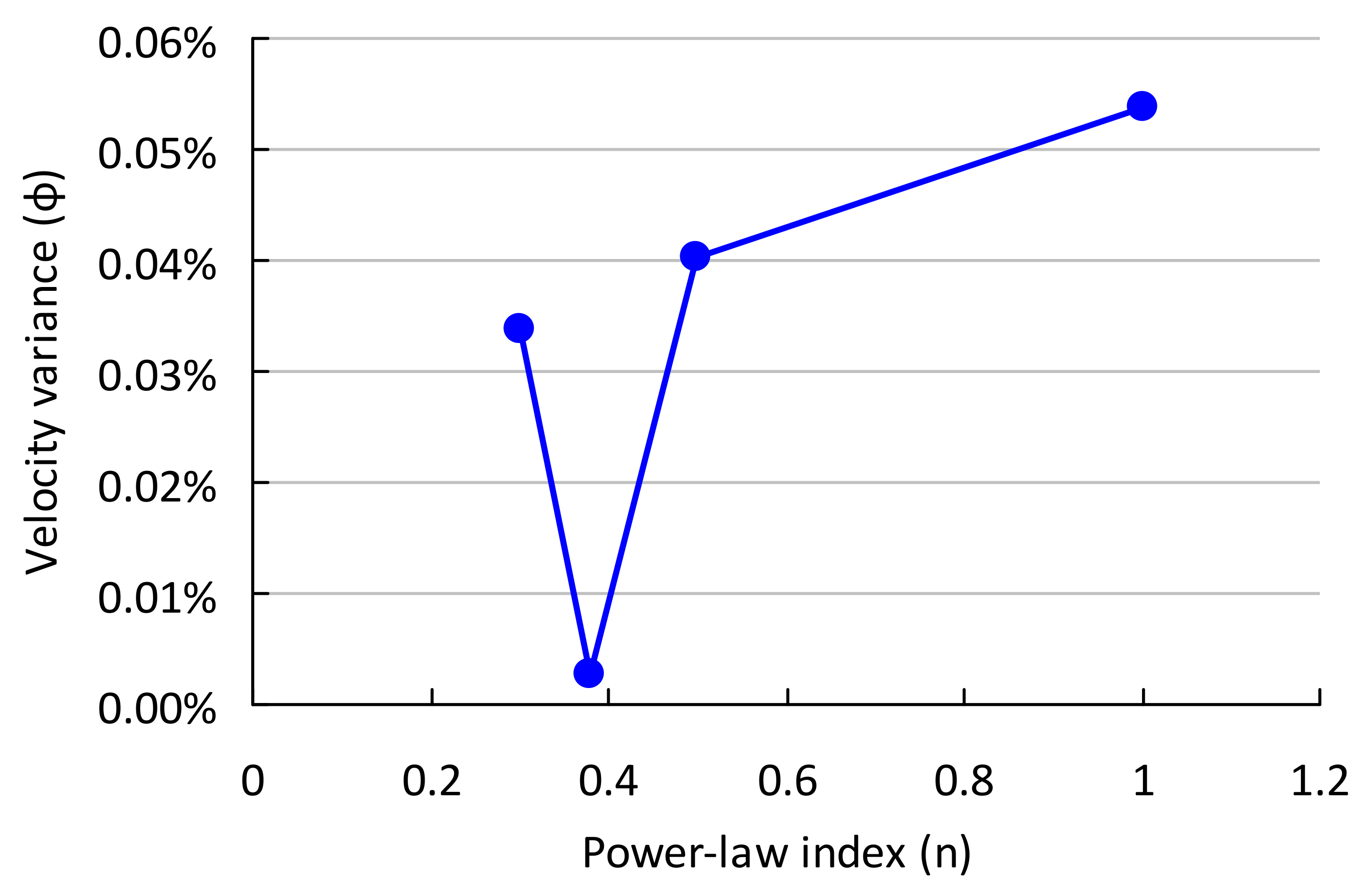
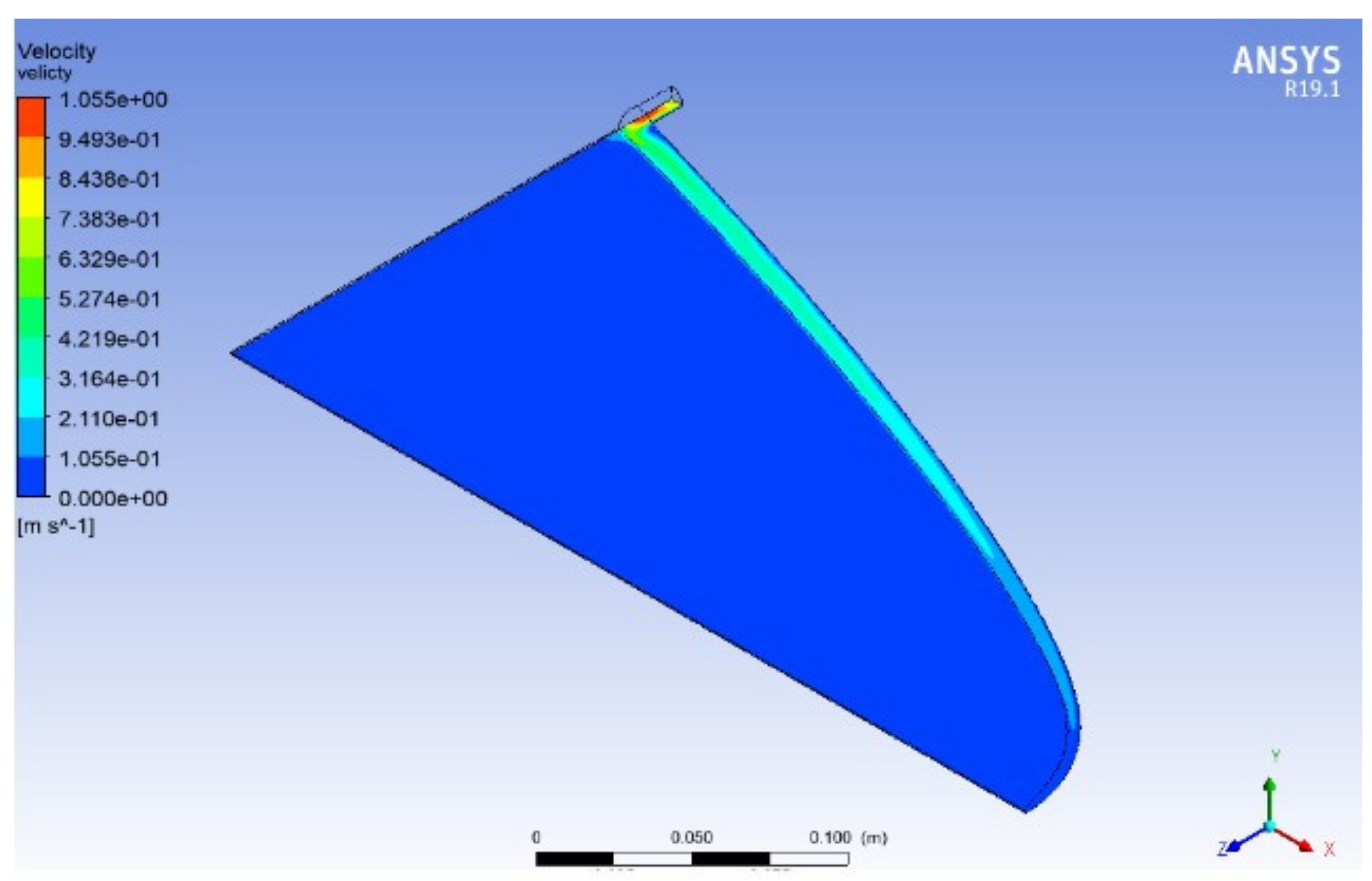
3.2. Sensitivity Analysis
3.3. Design of a Power-Law Fluid with Circular Manifold
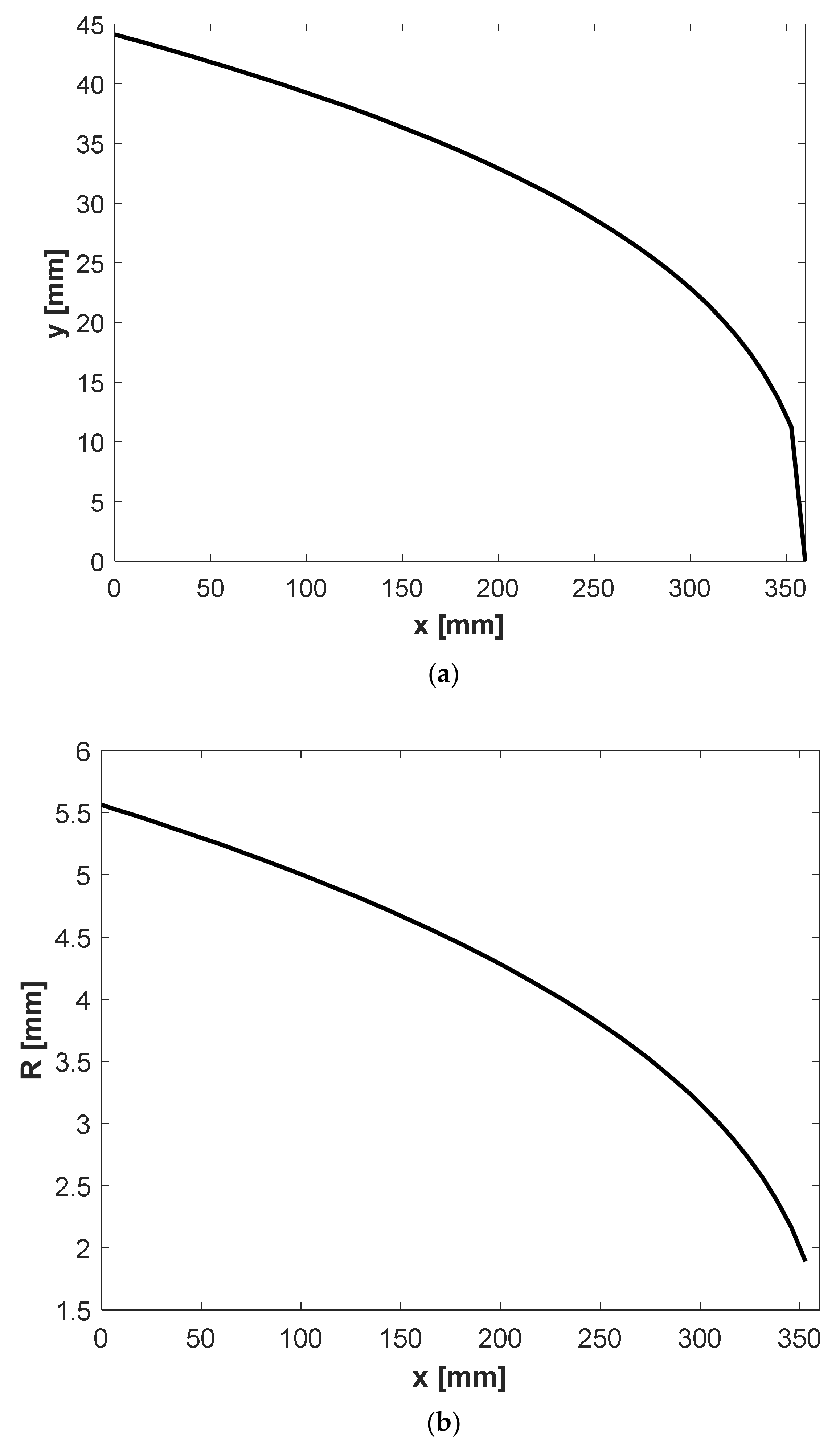
3.4. Design of a Carreau-Yasuda Fluid
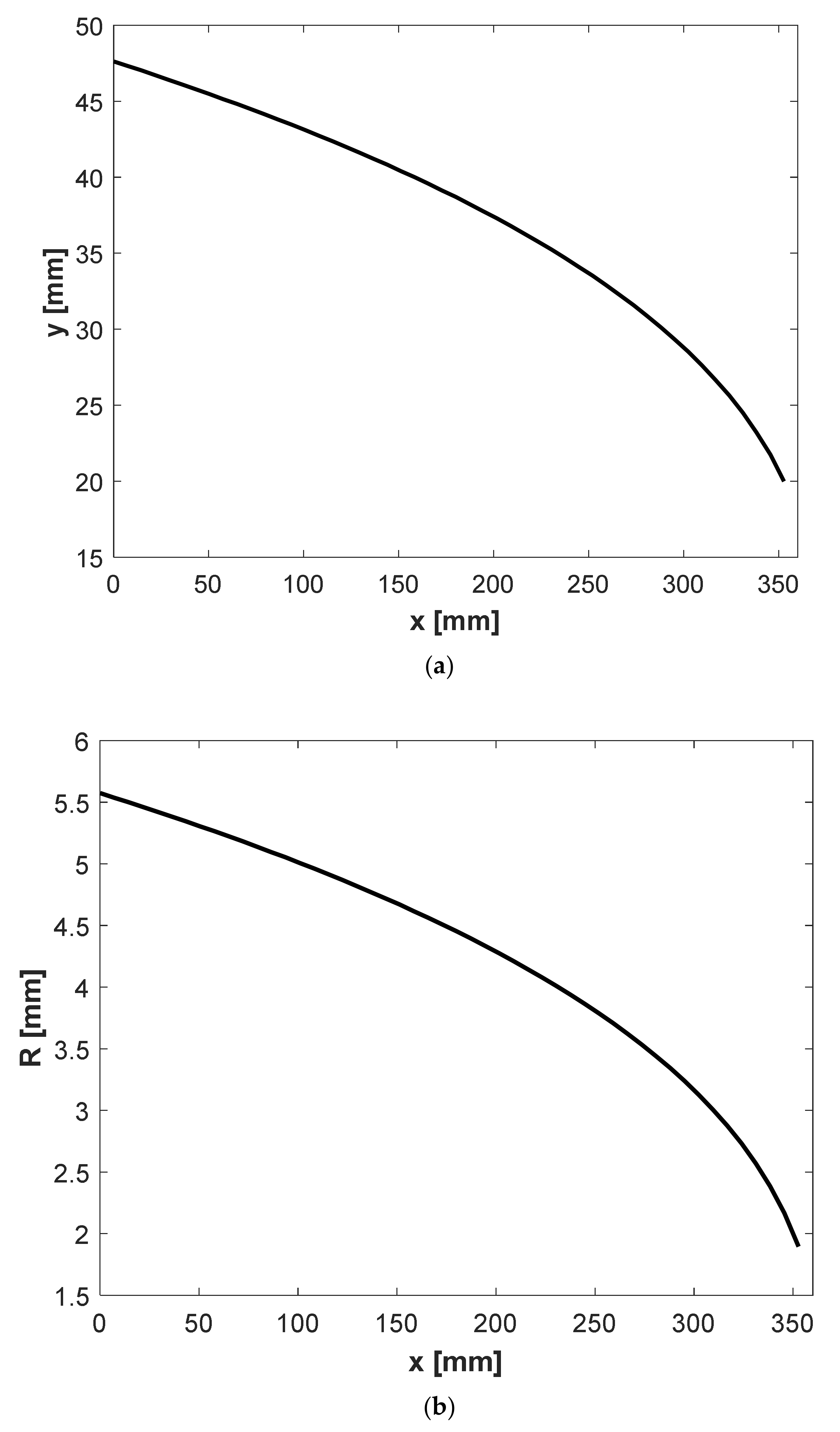
3.5. Design of a Cross Fluid
3.6. Desgin of a Power-Law Fluid with Rectangular Manifold
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Ratio of manifold width to half die thickness (W/b) |
| b | Half die thickness [m] |
| B | Parameter in Winter–Fritz equation |
| fp | Shape factor in Winter–Fritz model |
| g | Parameter in Winter–Fritz equation |
| H | Manifold height [m] |
| hs | Slit height [m] |
| I | Identity tensor |
| Ic | Definite integral definition for circular duct in Equation (22) [Pa3 s−1] |
| Ipp | Definite integral definition for parallel plates Equation (19) [Pa2 s−1] |
| k | Power-law consistency factor |
| m | Cross model parameter |
| n | Power-law index |
| N | Number of manifold and slit segments |
| Q0 | Flow rate in entry [m3/s] |
| Qm | Flow rate in the manifold [m3/s] |
| Qs | Flow rate in the slit [m3/s] |
| R | Radius of manifold [m] |
| v | Velocity [m/s] |
| φ | Velocity variance |
| W | Width of channel [m] |
| x | Coordinate along die [m] |
| y | Distance between manifold and die outlet [m] |
| ΔPm | Incremental pressure drops in manifold [Pa] |
| ΔPs | Incremental pressure drops in slit [Pa] |
| µ | Apparent viscosity [Pa s] |
| µ0 | Rheological parameter in Cross and Carreau–Yasuda models [Pa s] |
| µ∞ | Rheological parameter in Cross and Carreau–Yasuda models [Pa s] |
| γm | Shear rate in manifold [1/s] |
| γs | Shear rate in slit [1/s] |
| γw | Shear rate at wall [1/s] |
| ζ | Coordinate in direction of manifold [m] |
| λ | Rheological parameter in Cross and Carreau–Yasuda models [s] |
| τ | Shear stress [Pa] |
| τw | Shear stress at wall [Pa] |
| φ | Velocity variance [m2/s2] |
| dPm | Differential pressure drops in manifold [Pa] |
| dPs | Differential pressure drops in slit [Pa] |
References
- Hopmann, C.; Michaeli, W. Extrusion Dies for Plastics and Rubber: Design and Engineering Computations; Carl Hanser Verlag GmbH Co KG: Munich, Germany, 2016. [Google Scholar]
- Reid, J.; Campanella, O.; Corvalan, C.; Okos, M. The influence of power-law rheology on flow distribution in coathanger manifolds. Polym. Eng. Sci. 2003, 43, 693–703. [Google Scholar] [CrossRef]
- Winter, H.; Fritz, H. Design of dies for the extrusion of sheets and annular parisons: The distribution problem. Polym. Eng. Sci. 1986, 26, 543–553. [Google Scholar] [CrossRef]
- Awe, T.J.; Eligindi, M.; Langer, R. Internal Design of Uniform Shear Rate Dies. Morehead Electron. J. Appl. Math. 2005. [Google Scholar]
- Igali, D.; Perveen, A.; Zhang, D.; Wei, D. Shear Rate Coat-Hanger Die Using Casson Viscosity Model. Processes 2020, 8, 1524. [Google Scholar] [CrossRef]
- Han, W.; Wang, X. Multi-objective optimization of the coat-hanger die for melt-blowing process. Fibers Polym. 2012, 13, 626–631. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, J.; Xia, C.; Zhou, W. A finite piece method for simulating polymer melt flows in extrusion sheet dies. J. Appl. Polym. Sci. 2012, 123, 3189–3198. [Google Scholar] [CrossRef]
- Smith, D.E.; Wang, Q. Optimization-based design of polymer sheeting dies using generalized Newtonian fluid models. Polym. Eng. Sci. 2005, 45, 953–965. [Google Scholar] [CrossRef]
- Smith, D.E. Design sensitivity analysis and optimization for polymer sheet extrusion and mold filling processes. Int. J. Numer. Methods Eng. 2003, 57, 1381–1411. [Google Scholar] [CrossRef]
- Nadhir, L.; Fabrice, S.; Stephan, P. Design and optimization of three-dimensional extrusion dies, using constraint optimization algorithm. Finite Elem. Anal. Des. 2009, 45, 333–340. [Google Scholar]
- Lebaal, N.; Puissant, S.; Schmidt, F. Application of a response surface method to the optimal design of the wall temperature profiles in extrusion die. Int. J. Mater. Form. 2010, 3, 47–58. [Google Scholar] [CrossRef]
- Lebaal, N.; Puissant, S.; Schmidt, F. Rheological parameters identification using in situ experimental data of a flat die extrusion. J. Mater. Process. Technol. 2005, 164, 1524–1529. [Google Scholar] [CrossRef] [Green Version]
- Razeghiyadaki, A.; Zhang, D.; Wei, D.; Perveen, A. Optimization of Polymer Extrusion Die Based on Response Surface Method. Processes 2020, 8, 1043. [Google Scholar] [CrossRef]
- Oh, K.W.; Lee, K.; Ahn, B.; Furlani, E.P. Design of pressure-driven microfluidic networks using electric circuit analogy. Lab A Chip 2012, 12, 515–545. [Google Scholar] [CrossRef]
- Yilmaz, O.; Kirkkopru, K. Inverse Design and Flow Distribution Analysis of Carreau Type Fluid Flow through Coat-Hanger Die. Fibers Polym. 2020, 21, 204–215. [Google Scholar] [CrossRef]
- Michaeli, W.; Kaul, S.; Wolff, T. Computer-aided optimization of extrusion dies. J. Polym. Eng. 2001, 21, 225–238. [Google Scholar] [CrossRef]
- Liu, T.J.; Liu, L.D.; Tsou, J.D. A unified lubrication approach for the design of a coat-hanger die. Polym. Eng. Sci. 1994, 34, 541–550. [Google Scholar] [CrossRef]
- Dealy, J.M.; Wissbrun, K.F. Melt Rheology and Its Role in Plastics Processing: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Rudolph, N.; Osswald, T.A. Polymer Rheology: Fundamentals and Applications; Carl Hanser Verlag GmbH Co KG: Berlin, Germany, 2014. [Google Scholar]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Amangeldi, M.; Wei, D.; Perveen, A.; Zhang, D. Numerical Modeling of Thermal Flows in Entrance Channels for Polymer Extrusion: A Parametric Study. Processes 2020, 8, 1256. [Google Scholar] [CrossRef]
- Meng, K.; Wang, X.; Chen, Q. Fluid flow in coat-hanger die of melt blowing process: Comparison of numerical simulations and experimental measurements. Text. Res. J. 2011, 81, 1686–1693. [Google Scholar] [CrossRef]
- Kozicki, W.; Chou, C.; Tiu, C. Non-Newtonian flow in ducts of arbitrary cross-sectional shape. Chem. Eng. Sci. 1966, 21, 665–679. [Google Scholar] [CrossRef]
- Xiao, B.; Huang, Q.; Chen, H.; Chen, X.; Long, G. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29, 2150017. [Google Scholar] [CrossRef]
- Xiao, B.; Liu, Y.; Chen, H.; Chen, X.; Long, G. A Novel Fractal Solution for Laminar Flow Resistance in Roughened Cylindrical Microchannels. Fractals 2020, 28, 2050097–2050968. [Google Scholar] [CrossRef]
- Sochi, T. Analytical solutions for the flow of Carreau and Cross fluids in circular pipes and thin slits. Rheol. Acta 2015, 54, 745–756. [Google Scholar] [CrossRef] [Green Version]




| Rheology Model | Equation | Parameters |
|---|---|---|
| Power-law | k = 8.125 × 103 Pa sn n = 0.38 | |
| Carreau–Yasuda | µ0 = 1326 Pa sn µ∞ = 0 λ = 0.12 s n = 0.35 | |
| Cross | µ0 = 564.4 Pa sn µ∞ = 0 λ = 0.017 s m = 0.749 |
| Parameter | Value |
|---|---|
| Flow rate in the entry of the die, Q0 | 5 × 10−5 m3/s |
| Land height, hs | 1.5 mm |
| Total die width at exit, b | 360 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razeghiyadaki, A.; Wei, D.; Perveen, A.; Zhang, D. A Multi-Rheology Design Method of Sheeting Polymer Extrusion Dies Based on Flow Network and the Winter–Fritz Design Equation. Polymers 2021, 13, 1924. https://doi.org/10.3390/polym13121924
Razeghiyadaki A, Wei D, Perveen A, Zhang D. A Multi-Rheology Design Method of Sheeting Polymer Extrusion Dies Based on Flow Network and the Winter–Fritz Design Equation. Polymers. 2021; 13(12):1924. https://doi.org/10.3390/polym13121924
Chicago/Turabian StyleRazeghiyadaki, Amin, Dongming Wei, Asma Perveen, and Dichuan Zhang. 2021. "A Multi-Rheology Design Method of Sheeting Polymer Extrusion Dies Based on Flow Network and the Winter–Fritz Design Equation" Polymers 13, no. 12: 1924. https://doi.org/10.3390/polym13121924
APA StyleRazeghiyadaki, A., Wei, D., Perveen, A., & Zhang, D. (2021). A Multi-Rheology Design Method of Sheeting Polymer Extrusion Dies Based on Flow Network and the Winter–Fritz Design Equation. Polymers, 13(12), 1924. https://doi.org/10.3390/polym13121924







