Going Beyond the Carothers, Flory and Stockmayer Equation by Including Cyclization Reactions and Mobility Constraints
Abstract
:1. Introduction
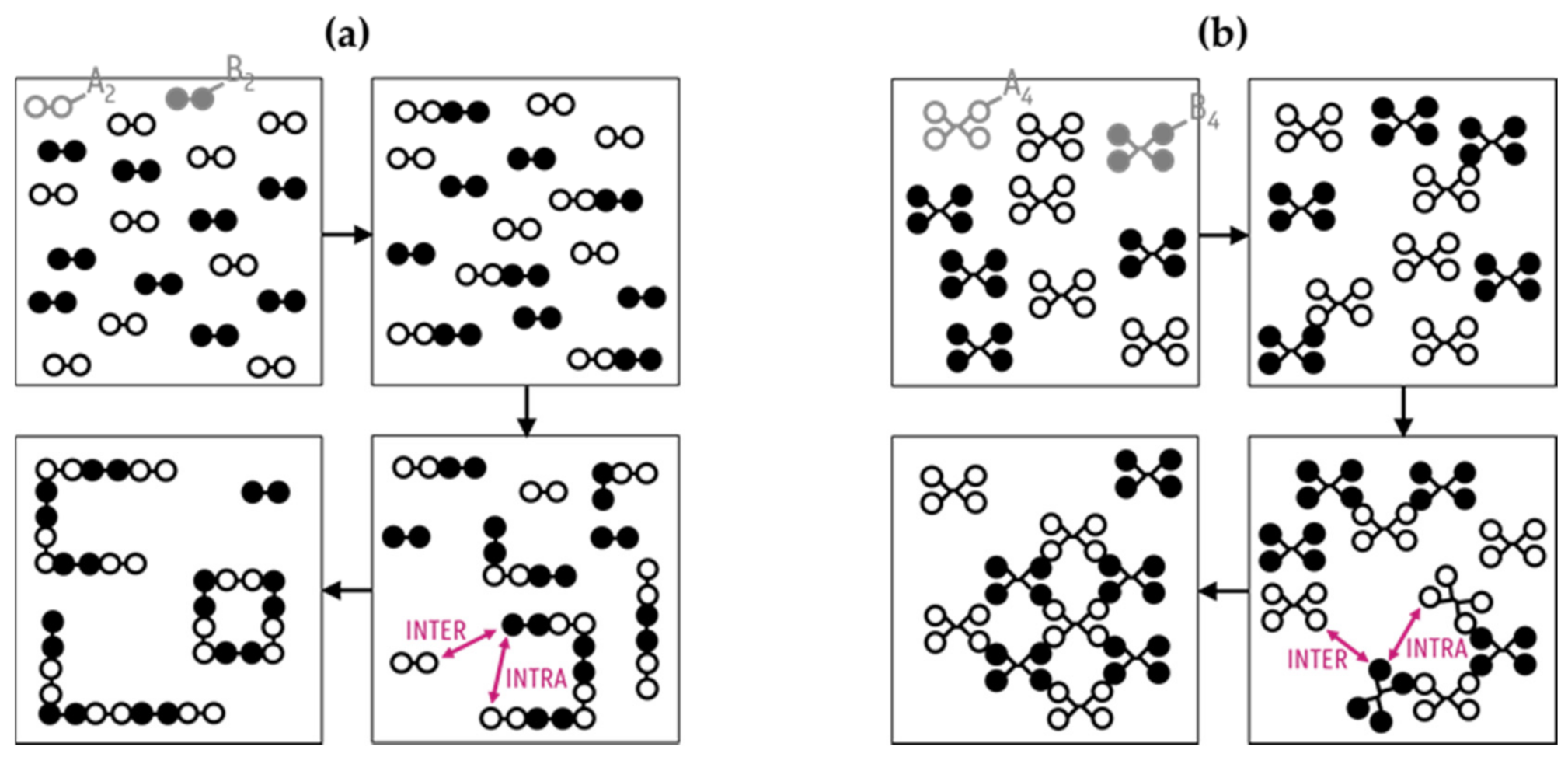
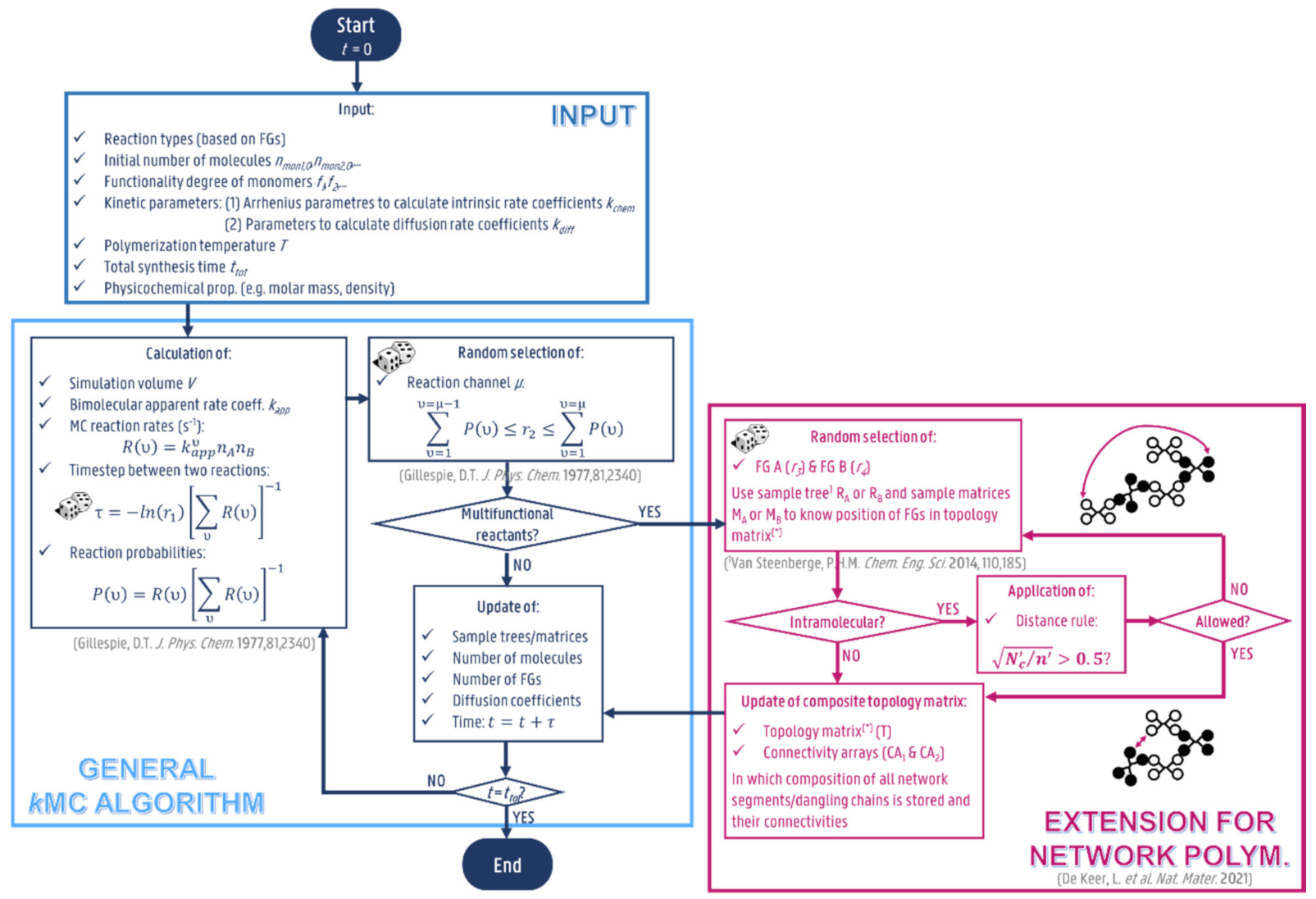
2. Kinetic Monte Carlo Modeling Details
3. Results and Discussion
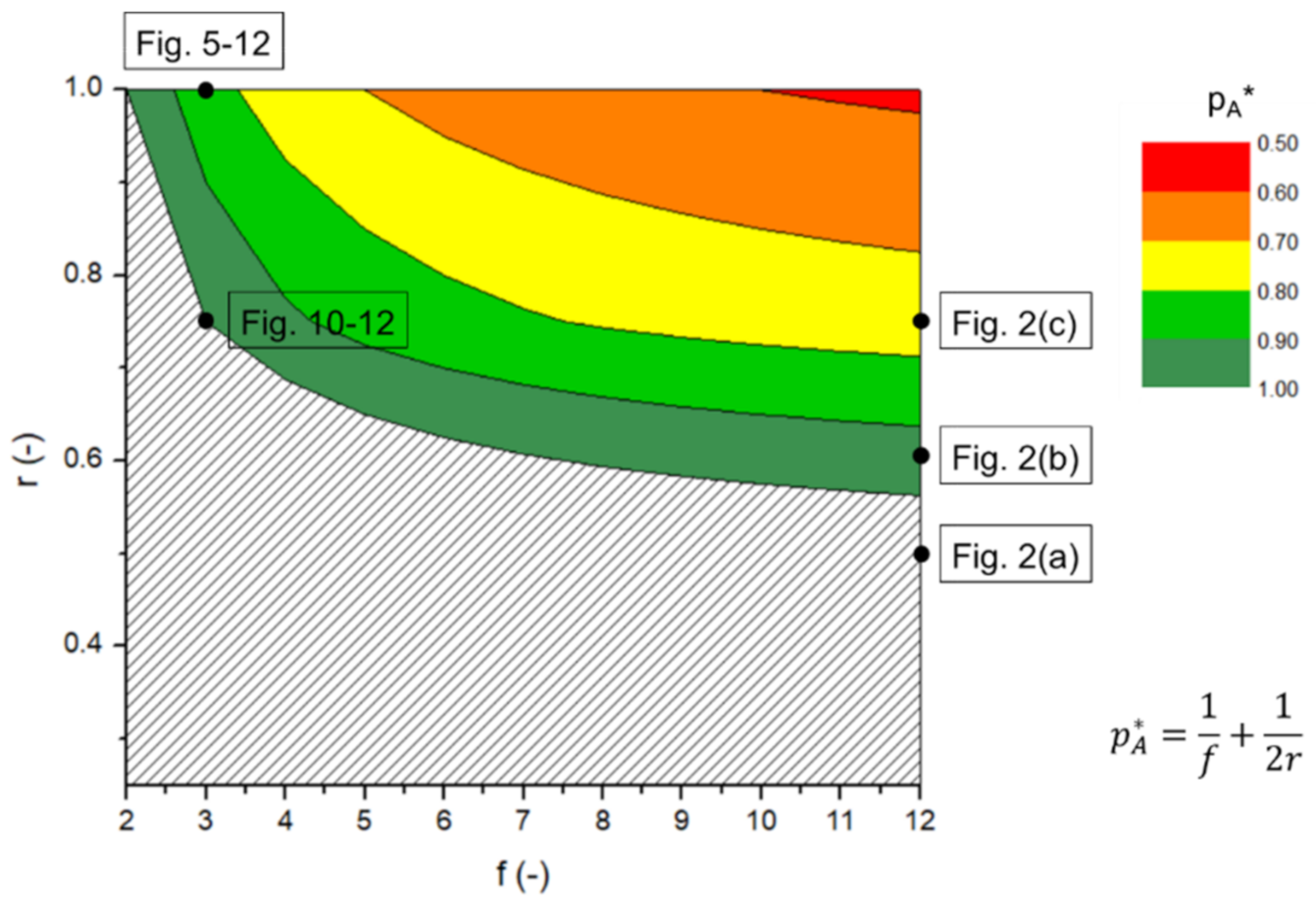
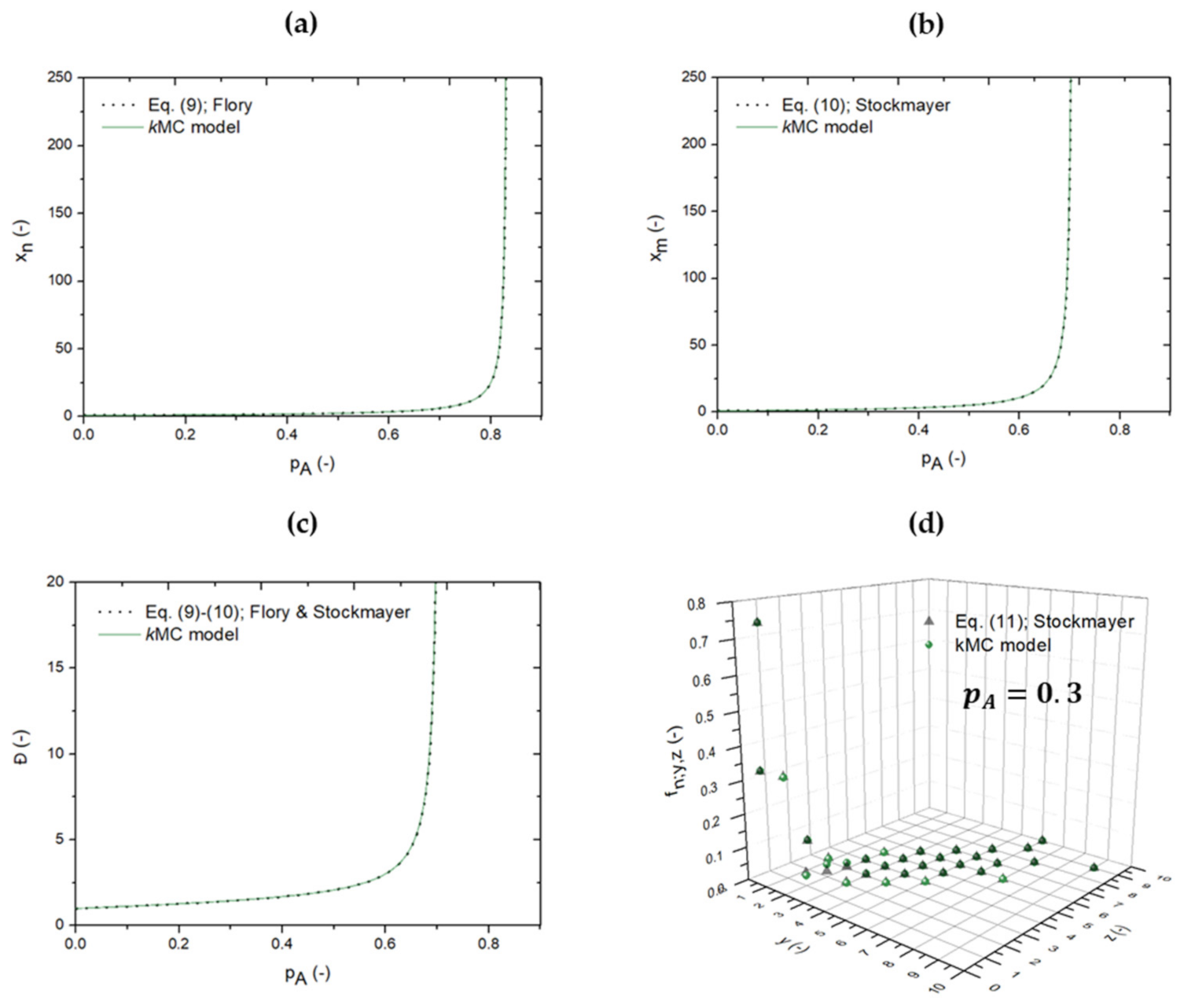
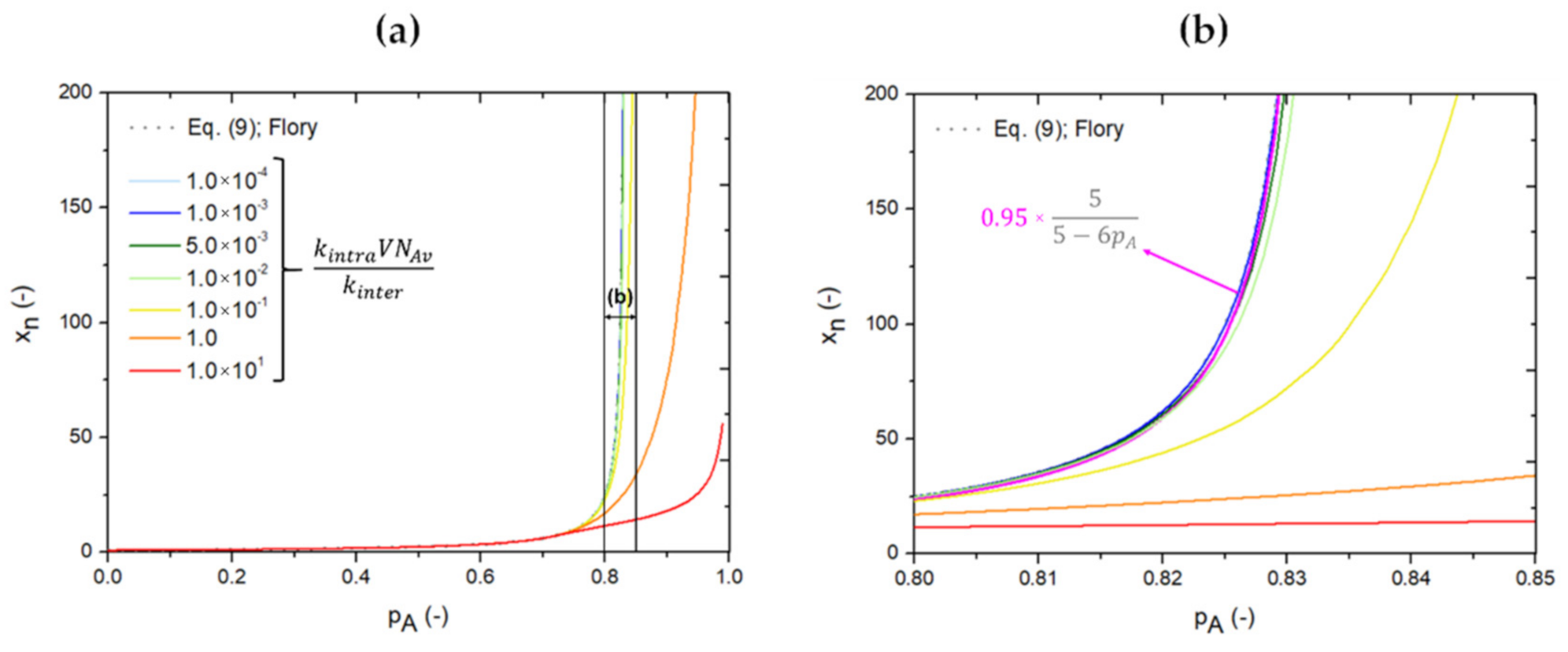
3.1. From Flory(-Stockmayer) Analytical Equations to kMC Prediction of the “Inter-Intra Competition”
3.2. Reverse Engineering and Dimensionless Analysis for (Pseudo-)Analytical Descriptions
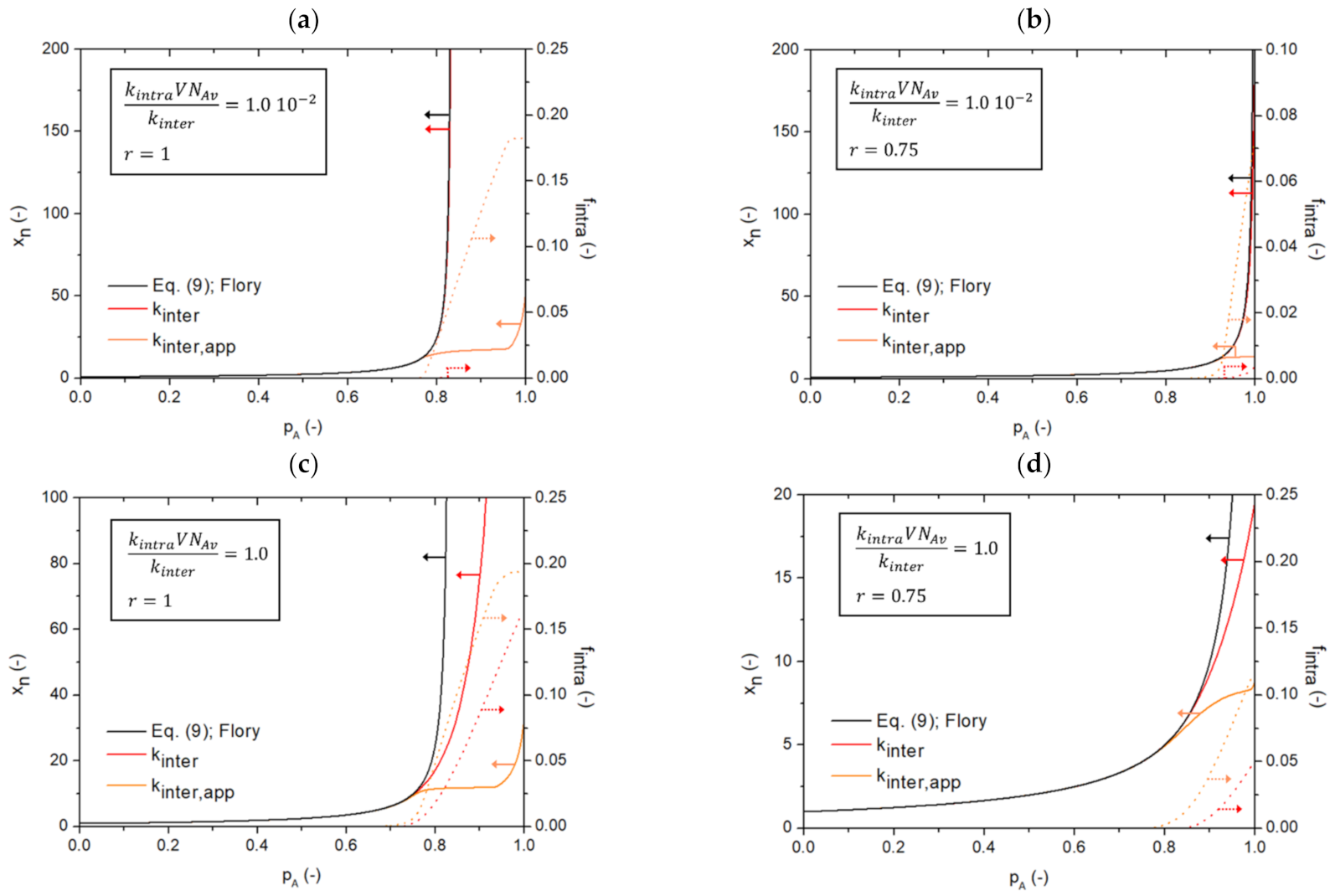
3.3. Competitive Inter- and Intramolecular Reactions Accounting for Restrictions in Mobility
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choi, K.Y.; McAuley, K.B. Step-Growth Polymerization. In Polymer Reaction Engineering; Asua, J.M., Ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2008; pp. 273–314. [Google Scholar]
- Ravve, A. Naturally Occurring Polymers. In Principles of Polymer Chemistry; Springer: Berlin/Heidelberg, Germany, 2013; pp. 449–475. [Google Scholar]
- Nabae, Y.; Kakimoto, M.-A. Design and Synthesis of Hyperbranched Aromatic Polymers for Catalysis. Polymers 2018, 10, 1344. [Google Scholar] [CrossRef] [Green Version]
- Boonlert-uthai, T.; Samthong, C.; Somwangthanaroj, A. Synthesis, Thermal Properties and Curing Kinetics of Hyperbranched BPA/PEG Epoxy Resin. Polymers 2019, 11, 1545. [Google Scholar] [CrossRef] [Green Version]
- Tuten, B.T.; De Keer, L.; Wiedbrauk, S.; Van Steenberge, P.H.M.; D’hooge, D.R.; Barner-Kowollik, C. Visible-Light-Induced Passerini Multicomponent Polymerization. Angew. Chem. Int. Ed. 2019, 58, 5672–5676. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baekeland, L.H. The Synthesis, Constitution, and Uses of Bakelite. J. Ind. Eng. Chem. 1909, 1, 149–161. [Google Scholar] [CrossRef] [Green Version]
- Weber, J.N. Kirk-Othmer Encyclopedia of Chemical Technology; Wiley-Interscience: New York, NY, USA, 1996; pp. 1–54. [Google Scholar]
- McKee, M.G.; Unal, S.; Wilkes, G.L.; Long, T.E. Branched polyesters: Recent advances in synthesis and performance. Prog. Polym. Sci. 2005, 30, 507–539. [Google Scholar] [CrossRef]
- Marchildon, K. Polyamides–Still Strong After Seventy Years. Macromol. React. Eng. 2011, 5, 22–54. [Google Scholar] [CrossRef]
- Daelemans, L.; Van Paepegem, W.; D’hooge, D.R.; De Clerck, K. Composite Materials: Excellent Nanofiber Adhesion for Hybrid Polymer Materials with High Toughness Based on Matrix Interdiffusion During Chemical Conversion. Adv. Funct. Mater. 2019, 29, 1970051. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.R.P.F.N.; Bachmann, R. Polycondensation. In Handbook of Polymer Reaction Engineering; Meyer, T., Keurentjes, J., Eds.; Wiley-VCH: Weinheim, Germany, 2005; Volume 1, pp. 57–151. [Google Scholar]
- Brunelle, D.J. Polycarbonates. In Encyclopedia of Polymer Science and Technology; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Oertel, G. Polyurethane Handbook: Chemistry, Raw Materials, Processing, Application Properties, 2nd ed.; Hanser: New York, NY, USA, 1993. [Google Scholar]
- Stille, J.K. Step-growth polymerization. J. Chem. Educ. 1981, 58, 862. [Google Scholar] [CrossRef] [Green Version]
- Mallon, F.K.; Ray, W.H. Modeling of solid-state polycondensation. I. Particle models. J. Appl. Polym. Sci. 1998, 69, 1233–1250. [Google Scholar] [CrossRef]
- Gantillon, B.; Spitz, R.; McKenna, T.F. The Solid State Postcondensation of PET, 2. Macromol. Mater. Eng. 2004, 289, 106–112. [Google Scholar] [CrossRef]
- Goodner, M.D.; Gross, S.M.; Desimone, J.M.; Roberts, G.W.; Kiserow, D.J. Broadening of molecular-weight distribution in solid-state polymerization resulting from condensate diffusion. J. Appl. Polym. Sci. 2001, 79, 928–943. [Google Scholar] [CrossRef]
- Carothers, W.H. Polymers and polyfunctionality. Trans. Faraday Soc. 1936, 32, 39–49. [Google Scholar] [CrossRef]
- Tobita, H.; Ohtani, Y. Control of molecular weight distribution in step-growth polymerization by an intermediate monomer feed method: Effect of interchange reactions. Polymer 1992, 33, 2194–2202. [Google Scholar] [CrossRef]
- Flory, P.J. Kinetics of Polyesterification: A Study of the Effects of Molecular Weight and Viscosity on Reaction Rate. J. Am. Chem. Soc. 1939, 61, 3334–3340. [Google Scholar] [CrossRef]
- Flory, P.J. A Comparison of Esterification and Ester Interchange Kinetics. J. Am. Chem. Soc. 1940, 62, 2261–2264. [Google Scholar] [CrossRef]
- Flory, P.J. Molecular Size Distribution in Three Dimensional Polymers. I. Gelation1. J. Am. Chem. Soc. 1941, 63, 3083–3090. [Google Scholar] [CrossRef]
- Harshe, Y.M.; Storti, G.; Morbidelli, M.; Gelosa, S.; Moscatelli, D. Polycondensation Kinetics of Lactic Acid. Macromol. React. Eng. 2007, 1, 611–621. [Google Scholar] [CrossRef]
- Kryven, I.; Duivenvoorden, J.; Hermans, J.; Iedema, P.D. Random Graph Approach to Multifunctional Molecular Networks. Macromol. Theory Simul. 2016, 25, 449–465. [Google Scholar] [CrossRef]
- Zhao, Y.R.; Buren, B.D.; Puskas, J.E.; McAuley, K.B. A Simple Monte Carlo Method for Modeling Arborescent Polymer Production in Continuous Stirred Tank Reactor. Macromol. React. Eng. 2018, 12, 1800020. [Google Scholar] [CrossRef]
- Gegenhuber, T.; De Keer, L.; Goldmann, A.S.; Van Steenberge, P.H.M.; Mueller, J.O.; Reyniers, M.-F.; Menzel, J.P.; D’hooge, D.R.; Barner-Kowollik, C. Fusing Light-Induced Step-Growth Processes with RAFT Chemistry for Segmented Copolymer Synthesis: A Synergetic Experimental and Kinetic Modeling Study. Macromolecules 2017, 50, 6451–6467. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Theory of Molecular Size Distribution and Gel Formation in Branched-Chain Polymers. J. Chem. Phys. 1943, 11, 45–55. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Theory of Molecular Size Distribution and Gel Formation in Branched Polymers II. General Cross Linking. J. Chem. Phys. 1944, 12, 125–131. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Molecular distribution in condensation polymers. J. Polym. Sci. 1952, 9, 69–71. [Google Scholar] [CrossRef]
- Gordon, M. Good’s Theory of Cascade Processes Applied to the Statistics of Polymer Distributions. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1962, 268, 240–256. [Google Scholar]
- Good, I.J. The joint distribution for the sizes of the generations in a cascade process. Math. Proc. Camb. Philos. Soc. 1955, 51, 240–242. [Google Scholar] [CrossRef]
- Good, I.J. Generalizations to several variables of Lagrange’s expansion, with applications to stochastic processes. Math. Proc. Camb. Philos. Soc. 1960, 56, 367–380. [Google Scholar] [CrossRef]
- Beginn, U.; Drohmann, C.; Möller, M. Conversion Dependence of the Branching Density for the Polycondensation of ABn Monomers. Macromolecules 1997, 30, 4112–4116. [Google Scholar] [CrossRef]
- Cheng, K.-C. Kinetic model of diepoxides with reactive diluents cured with amines. J. Polym. Sci. Part B Polym. Phys. 1998, 36, 2339–2348. [Google Scholar] [CrossRef]
- Cheng, K.-C.; Wang, L.Y. Kinetic Model of Hyperbranched Polymers Formed in Copolymerization of AB2 Monomers and Multifunctional Core Molecules with Various Reactivities. Macromolecules 2002, 35, 5657–5664. [Google Scholar] [CrossRef]
- Hillegers, L.T.; Slot, J.J.M. Step-Growth Polymerized Systems of Type “A1+A2+A3”: A Method to Calculate the Bivariate (Molecular Size) × (Path Length) Distribution. Macromol. Theory Simul. 2021, 30, 2000082. [Google Scholar] [CrossRef]
- Macosko, C.W.; Miller, D.R. A New Derivation of Average Molecular Weights of Nonlinear Polymers. Macromolecules 1976, 9, 199–206. [Google Scholar] [CrossRef] [Green Version]
- Miller, D.R.; Macosko, C.W. A New Derivation of Post Gel Properties of Network Polymers. Macromolecules 1976, 9, 206–211. [Google Scholar] [CrossRef]
- Stanford, J.L.; Stepto, R.F.T. Rate theory of irreversible linear random polymrisation. Part 1.—Basic theory. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1975, 71, 1292–1307. [Google Scholar] [CrossRef]
- Ziff, R.M. Kinetics of polymerization. J. Stat. Phys. 1980, 23, 241–263. [Google Scholar] [CrossRef]
- Stafford, J.W. Multifunctional polycondensation and gelation: A kinetic approach. J. Polym. Sci. Polym. Chem. Ed. 1981, 19, 3219–3236. [Google Scholar] [CrossRef]
- Stafford, J.W. Multifunctional polycondensation distributions: A kinetic approach to mixed monomer systems. J. Polym. Sci. Polym. Chem. Ed. 1984, 22, 365–381. [Google Scholar] [CrossRef]
- Pis’men, L.M.; Kuchanov, S.I. Multifunctional polycondensation and gelation. Polym. Sci. USSR 1971, 13, 890–903. [Google Scholar] [CrossRef]
- Dušek, K. Correspondence between the theory of branching processes and the kinetic theory for random crosslinking in the post-gel stage. Polym. Bull. 1979, 1, 523–528. [Google Scholar] [CrossRef]
- Jackson, R.A.; Small, P.A.; Whiteley, K.S. Prediction of molecular weight distributions in branched polymers. J. Polym. Sci. Polym. Chem. Ed. 1973, 11, 1781–1809. [Google Scholar] [CrossRef]
- Cozewith, C.; Graessley, W.W.; Ver Strate, G. Polymer crosslinking in continuous flow stirred reactors. Chem. Eng. Sci. 1979, 34, 245–248. [Google Scholar] [CrossRef]
- Müller, A.H.E.; Yan, D.; Wulkow, M. Molecular Parameters of Hyperbranched Polymers Made by Self-Condensing Vinyl Polymerization. 1. Molecular Weight Distribution. Macromolecules 1997, 30, 7015–7023. [Google Scholar] [CrossRef]
- Yan, D.; Müller, A.H.E.; Matyjaszewski, K. Molecular Parameters of Hyperbranched Polymers Made by Self-Condensing Vinyl Polymerization. 2. Degree of Branching. Macromolecules 1997, 30, 7024–7033. [Google Scholar] [CrossRef]
- Yan, D.; Zhou, Z. Molecular Weight Distribution of Hyperbranched Polymers Generated from Polycondensation of AB2 Type Monomers in the Presence of Multifunctional Core Moieties. Macromolecules 1999, 32, 819–824. [Google Scholar] [CrossRef]
- Zhou, Z.; Yan, D. Kinetic analysis of the polycondensation of ABg type monomer with a multifunctional core. Polymer 2000, 41, 4549–4558. [Google Scholar] [CrossRef]
- Zhou, Z.; Jia, Z.; Yan, D. Kinetic analysis of AB2 polycondensation in the presence of multifunctional cores with various reactivities. Polymer 2012, 53, 3386–3391. [Google Scholar] [CrossRef]
- Hao, T.; Zhou, Z.; Yan, D. Kinetic theory of A2+B3+B2 type hyperbranched polymerization. Polymer 2019, 185, 121985. [Google Scholar] [CrossRef]
- Hao, T.; Zhou, Z.; Nie, N. Theoretical Methods of the Size Distribution Function for the Products of Hyperbranched Polymerization. Macromol. Theory Simul. 2021, 30, 2000039. [Google Scholar] [CrossRef]
- Vo, A.-D.D.; Cui, W.J.; McAuley, K.B. An Improved PO3G Model–Accounting for Cyclic Oligomers. Macromol. Theory Simul. 2020, 29, 2000023. [Google Scholar] [CrossRef]
- Schamboeck, V.; Iedema, P.D.; Kryven, I. Dynamic Networks that Drive the Process of Irreversible Step-Growth Polymerization. Sci. Rep. 2019, 9, 2276. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor & Francis: London, UK, 1992. [Google Scholar]
- Stepto, R.F.T.; Waywell, D.R. A study of intramolecular reaction during linear polyurethane formation. Die Makromol. Chem. 1972, 152, 263–275. [Google Scholar] [CrossRef]
- Costa, M.R.N.; Villermaux, J. Mathematical and experimental foundations of linear polycondensation modeling. 3. Experimental study of catalyzed polyesterification of adipic acid and triethylene glycol: Equilibrium and kinetics. Ind. Eng. Chem. Res. 1989, 28, 711–719. [Google Scholar] [CrossRef]
- Kricheldorf, H.R.; Schwarz, G. Cyclic Polymers by Kinetically Controlled Step-Growth Polymerization. Macromol. Rapid Commun. 2003, 24, 359–381. [Google Scholar] [CrossRef]
- Kricheldorf, H.R.; Vakhtangishvili, L.; Schwarz, G.; Schulz, G.; Kruger, R.P. Macrocycles 25. Cyclic poly(ether sulfone)s derived from 4-tert-butylcatechol. Polymer 2003, 44, 4471–4480. [Google Scholar] [CrossRef]
- Wiesecke, J.; Rehahn, M. [2.2]Paracyclophanes with Defined Substitution Pattern—Key Compounds for the Mechanistic Understanding of the Gilch Reaction to Poly(p-phenylene vinylene)s. Angew. Chem. Int. Ed. 2003, 42, 567–570. [Google Scholar] [CrossRef]
- Zaquen, N.; Van Steenberge, P.H.M.; D’hooge, D.R.; Reyniers, M.-F.; Marin, G.B.; Vandenbergh, J.; Lutsen, L.; Vanderzande, D.J.M.; Junkers, T. Improved Mechanistic Insights into Radical Sulfinyl Precursor MDMO-PPV Synthesis by Combining Microflow Technology and Computer Simulations. Macromolecules 2015, 48, 8294–8306. [Google Scholar] [CrossRef]
- Stanford, J.L.; Stepto, R.F.T. A study of intramolecular reaction and gelation during non-linear polyurethane formation. Br. Polym. J. 1977, 9, 124–132. [Google Scholar] [CrossRef]
- Stepto, R.F.T. Theoretical and experimental studies of network formation and properties. Polymer 1979, 20, 1324–1326. [Google Scholar] [CrossRef]
- Fasina, A.B.; Stepto, R.F.T. Formation and properties of triol-based polyester networks. Die Makromol. Chem. 1981, 182, 2479–2493. [Google Scholar] [CrossRef]
- Smith, R.S.; Stepto, R.F.T. Gelation in the reactions of dicarboxylic acid dichlorides with triols. Die Makromol. Chem. 1974, 175, 2365–2373. [Google Scholar] [CrossRef]
- Peters, R.H.; Stepto, R.F.T. The Chemistry of Polymerisation Processes; Monograph No. 20; Society of Chemical Industry: London, UK, 1966. [Google Scholar]
- Xu, X.; Wang, Q. Direct characterization of a polymer network through its retainable units. Polym. Chem. 2019, 10, 4837–4843. [Google Scholar] [CrossRef]
- Gordon, M.; Scantlebury, G.R. Statistical kinetics of polyesterification of adipic acid with pentaerythritol or trimethylol ethane. J. Chem. Soc. B Phys. Org. 1967, 1–13. [Google Scholar] [CrossRef]
- Dušek, K.; Gordon, M.; Ross-Murphy, S.B. Graphlike State of Matter. 10. Cyclization and Concentration of Elastically Active Network Chains in Polymer Networks. Macromolecules 1978, 11, 236–245. [Google Scholar] [CrossRef]
- Jacobson, H.; Stockmayer, W.H. Intramolecular Reaction in Polycondensations. I. The Theory of Linear Systems. J. Chem. Phys. 1950, 18, 1600–1606. [Google Scholar] [CrossRef]
- Temple, W.B. The graph-like state of matter. IV. Ring-chain competition kinetics in a branched polymerisation reaction. Die Makromol. Chem. 1972, 160, 277–289. [Google Scholar] [CrossRef]
- Kumar, A.; Wahal, S.; Sastri, S.; Gupta, S.K. Modelling of intramolecular reactions in the step-growth polymerization of multifunctional monomers. Polymer 1986, 27, 583–591. [Google Scholar] [CrossRef]
- Kumar, A.; Khandelwal, P.K. Modelling of multifunctional step growth polymerization in presence of cyclization. Chem. Eng. Sci. 1988, 43, 1819–1824. [Google Scholar] [CrossRef]
- Fastrez, J. Cyclization versus polymerization in polycondensation reactions under continuous addition of two symmetrical monomers. Tetrahedron Lett. 1987, 28, 419–422. [Google Scholar] [CrossRef]
- Fastrez, J. Macrocyclization versus polymerization in polycondensation reactions under high-dilution conditions: A theoretical study. J. Phys. Chem. 1989, 93, 2635–2642. [Google Scholar] [CrossRef]
- Yuan, X.-F.; Masters, A.J.; Nicholas, C.V.; Booth, C. Ring-chain competition in kinetically-controlled condensation polymerization. Die Makromol. Chem. 1988, 189, 823–832. [Google Scholar] [CrossRef]
- Sarmoria, C.; Valles, E.M.; Miller, D.R. Validity of some approximations used to model intramolecular reaction in irreversible polymerization. Macromolecules 1990, 23, 580–589. [Google Scholar] [CrossRef]
- Szymanski, R. The Molar Mass Distribution of Polymers in Step-Growth Polymerization is Influenced by Cyclization Reactions. The Simplified Case of Irreversible Reactions with Cyclizations is Independent of the Ring Size. Macromol. Theory Simul. 2013, 22, 335–343. [Google Scholar] [CrossRef]
- Romero-Hernández, J.E.; Cruz-Rosado, A.; Vivaldo-Lima, E.; Palacios-Alquisira, J.; Zolotukhin, M.G. Analysis of the Competition between Cyclization and Linear Chain Growth in Kinetically Controlled A2 + B2 Step-Growth Polymerizations Using Modeling Tools. Macromol. Theory Simul. 2020, 29, 2000050. [Google Scholar] [CrossRef]
- Mikes, J.; Dusek, K. Simulation of polymer network formation by the Monte Carlo method. Macromolecules 1982, 15, 93–99. [Google Scholar] [CrossRef]
- Fawcett, A.H.; Mee, R.A.W.; McBride, F.V. A Monte-Carlo Study of Ring Formation and Molecular Configurations during Step Growth on a Lattice in Three Dimensions. Macromolecules 1995, 28, 1481–1490. [Google Scholar] [CrossRef]
- Cameron, C.; Fawcett, A.H.; Hetherington, C.R.; Mee, R.A.W.; McBride, F.V. Cycles frustrating fractal formation in an AB2 step growth polymerization. Chem. Commun. 1997, 1801–1802. [Google Scholar] [CrossRef]
- Cameron, C.; Fawcett, A.H.; Hetherington, C.R.; Mee, R.A.W.; McBride, F.V. Step growth of an AB2 monomer, with cycle formation. J. Chem. Phys. 1998, 108, 8235–8251. [Google Scholar] [CrossRef]
- Arraez, F.J.; Van Steenberge, P.H.M.; D’hooge, D.R. Conformational Distributions near and on the Substrate during Surface-Initiated Living Polymerization: A Lattice-Based Kinetic Monte Carlo Approach. Macromolecules 2020, 53, 4630–4648. [Google Scholar] [CrossRef]
- Arraez, F.J.; Van Steenberge, P.H.M.; D’hooge, D.R. The Competition of Termination and Shielding to Evaluate the Success of Surface-Initiated Reversible Deactivation Radical Polymerization. Polymers 2020, 12, 1409. [Google Scholar] [CrossRef] [PubMed]
- D’hooge, D.R.; Van Steenberge, P.H.M.; Reyniers, M.-F.; Marin, G.B. The strength of multi-scale modeling to unveil the complexity of radical polymerization. Prog. Polym. Sci. 2016, 58, 59–89. [Google Scholar] [CrossRef]
- Mastan, E.; Li, X.; Zhu, S. Modeling and theoretical development in controlled radical polymerization. Prog. Polym. Sci. 2015, 45, 71–101. [Google Scholar] [CrossRef]
- Achilias, D.S. A Review of Modeling of Diffusion Controlled Polymerization Reactions. Macromol. Theory Simul. 2007, 16, 319–347. [Google Scholar] [CrossRef]
- D’hooge, D.R.; Reyniers, M.-F.; Marin, G.B. The Crucial Role of Diffusional Limitations in Controlled Radical Polymerization. Macromol. React. Eng. 2013, 7, 362–379. [Google Scholar] [CrossRef]
- Tripathi, A.K.; Tsavalas, J.G.; Sundberg, D.C. Monte Carlo Simulations of Free Radical Polymerizations with Divinyl Cross-Linker: Pre- and Postgel Simulations of Reaction Kinetics and Molecular Structure. Macromolecules 2015, 48, 184–197. [Google Scholar] [CrossRef]
- D’Hooge, D.R.; Van Steenberge, P.H.M.; Derboven, P.; Reyniers, M.-F.; Marin, G.B. Model-based design of the polymer microstructure: Bridging the gap between polymer chemistry and engineering. Polym. Chem. 2015, 6, 7081–7096. [Google Scholar] [CrossRef]
- D’hooge, D.R. In Silico Tracking of Individual Species Accelerating Progress in Macromolecular Engineering and Design. Macromol. Rapid Commun. 2018, 39, 1800057. [Google Scholar] [CrossRef]
- Brandão, A.L.T.; Soares, J.B.P.; Pinto, J.C.; Alberton, A.L. When Polymer Reaction Engineers Play Dice: Applications of Monte Carlo Models in PRE. Macromol. React. Eng. 2015, 9, 141–185. [Google Scholar] [CrossRef]
- Lemos, T.; Melo, P.A.; Pinto, J.C. Stochastic Modeling of Polymer Microstructure From Residence Time Distribution. Macromol. React. Eng. 2015, 9, 259–270. [Google Scholar] [CrossRef]
- Van Steenberge, P.H.M.; Verbraeken, B.; Reyniers, M.-F.; Hoogenboom, R.; D’hooge, D.R. Model-Based Visualization and Understanding of Monomer Sequence Formation in Gradient Copoly(2-oxazoline)s On the basis of 2-Methyl-2-oxazoline and 2-Phenyl-2-oxazoline. Macromolecules 2015, 48, 7765–7773. [Google Scholar] [CrossRef]
- Van Steenberge, P.H.M.; D’hooge, D.R.; Reyniers, M.F.; Marin, G.B. Improved kinetic Monte Carlo simulation of chemical composition-chain length distributions in polymerization processes. Chem. Eng. Sci. 2014, 110, 185–199. [Google Scholar] [CrossRef]
- Hernández-Ortiz, J.C.; Van Steenberge, P.H.M.; Reyniers, M.-F.; Marin, G.B.; D’hooge, D.R.; Duchateau, J.N.E.; Remerie, K.; Toloza, C.; Vaz, A.L.; Schreurs, F. Modeling the reaction event history and microstructure of individual macrospecies in postpolymerization modification. AlChE J. 2017, 63, 4944–4961. [Google Scholar] [CrossRef]
- Cavalli, F.; De Keer, L.; Huber, B.; Van Steenberge, P.H.M.; D’Hooge, D.R.; Barner, L. A kinetic study on the para-fluoro-thiol reaction in view of its use in materials design. Polym. Chem. 2019, 10, 2781–2791. [Google Scholar] [CrossRef]
- Trigilio, A.D.; Marien, Y.W.; Van Steenberge, P.H.M.; D’hooge, D.R. Gillespie-Driven kinetic Monte Carlo Algorithms to Model Events for Bulk or Solution (Bio)Chemical Systems Containing Elemental and Distributed Species. Ind. Eng. Chem. Res. 2020, 59, 18357–18386. [Google Scholar] [CrossRef]
- De Keer, L.; Kilic, K.I.; Van Steenberge, P.H.M.; Daelemans, L.; Kodura, D.; Frisch, H.; De Clerck, K.; Reyniers, M.-F.; Barner-Kowollik, C.; Dauskardt, R.H.; et al. Computational predicition of the molecular configuration of three-dimensional network polymers. Nat. Mater. 2021. [Google Scholar] [CrossRef]
- De Kock, J.B.L.; Van Herk, A.M.; German, A.L. Bimolecular free-radical termination at low conversion. J. Macromol. Sci. Rev. Macromol. Chem. Phys. 2001, 41, 199–252. [Google Scholar] [CrossRef]
- Mueller, P.A.; Storti, G.; Morbidelli, M. Detailed modelling of MMA dispersion polymerization in supercritical carbon dioxide. Chem. Eng. Sci. 2005, 60, 1911–1925. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Vilgis, T.A.; Boué, F. Brownian motion of chains and crosslinks in a permanently linked network: The dynamic form factor. J. Polym. Sci. Part B Polym. Phys. 1988, 26, 2291–2302. [Google Scholar] [CrossRef]
- Zhou, Y.-N.; Luo, Z.-H. State-of-the-Art and Progress in Method of Moments for the Model-Based Reversible-Deactivation Radical Polymerization. Macromol. React. Eng. 2016, 10, 516–534. [Google Scholar] [CrossRef]
- Mastan, E.; Zhu, S. Method of moments: A versatile tool for deterministic modeling of polymerization kinetics. Eur. Polym. J. 2015, 68, 139–160. [Google Scholar] [CrossRef]
- Constales, D.; Yablonsky, G.; D’hooge, D.R.; Thybaut, J.; Marin, G.B. Advanced Data Analysis and Modelling in Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Keer, L.; Van Steenberge, P.H.M.; Reyniers, M.-F.; D’hooge, D.R. Going Beyond the Carothers, Flory and Stockmayer Equation by Including Cyclization Reactions and Mobility Constraints. Polymers 2021, 13, 2410. https://doi.org/10.3390/polym13152410
De Keer L, Van Steenberge PHM, Reyniers M-F, D’hooge DR. Going Beyond the Carothers, Flory and Stockmayer Equation by Including Cyclization Reactions and Mobility Constraints. Polymers. 2021; 13(15):2410. https://doi.org/10.3390/polym13152410
Chicago/Turabian StyleDe Keer, Lies, Paul H. M. Van Steenberge, Marie-Françoise Reyniers, and Dagmar R. D’hooge. 2021. "Going Beyond the Carothers, Flory and Stockmayer Equation by Including Cyclization Reactions and Mobility Constraints" Polymers 13, no. 15: 2410. https://doi.org/10.3390/polym13152410






