Multi-Objective Optimization of Resistance Welding Process of GF/PP Composites
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Materials
2.2. Mechanical Properties
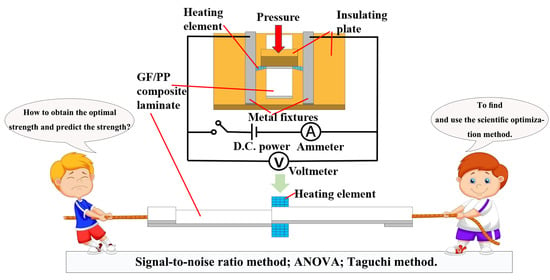
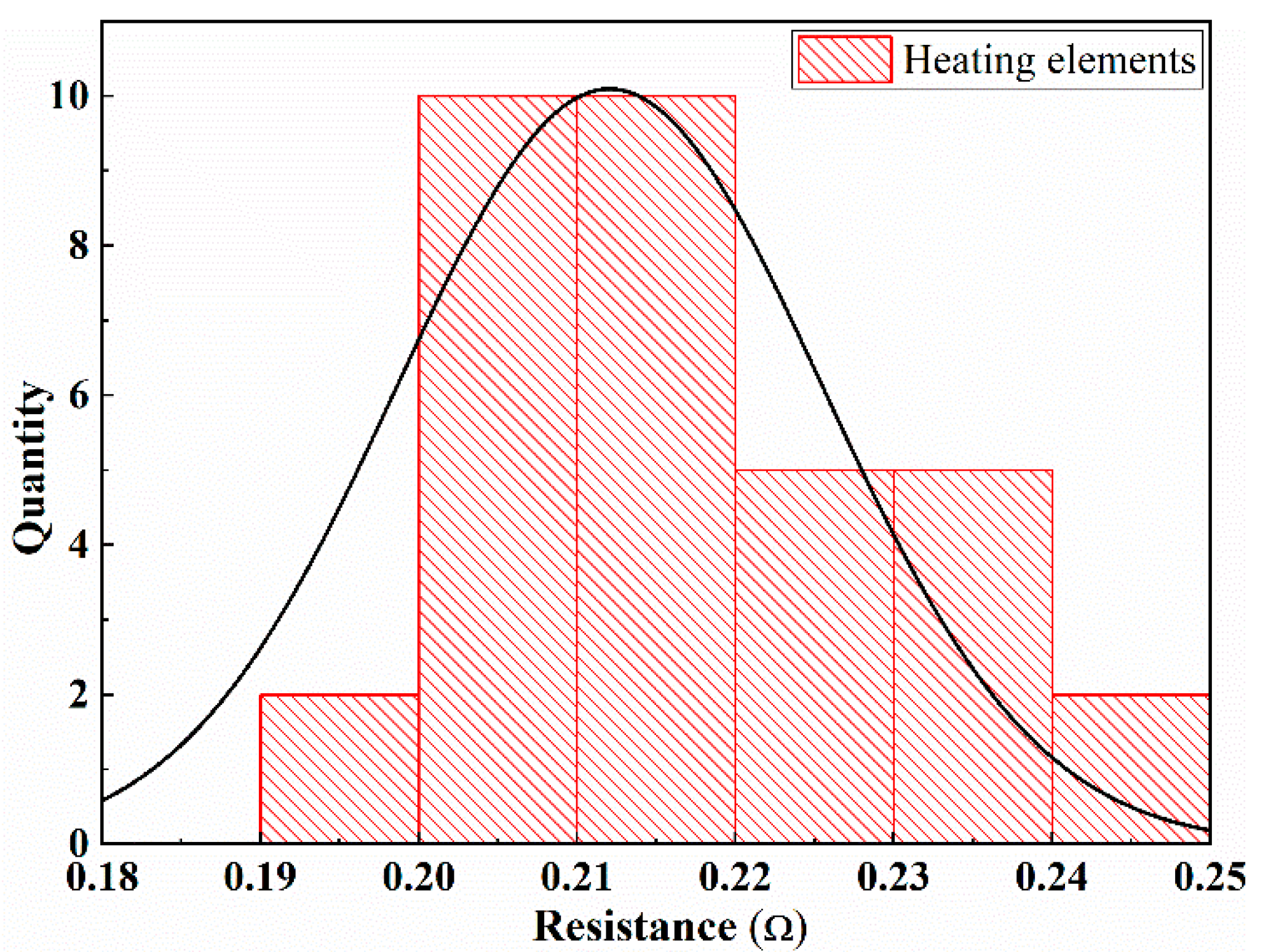
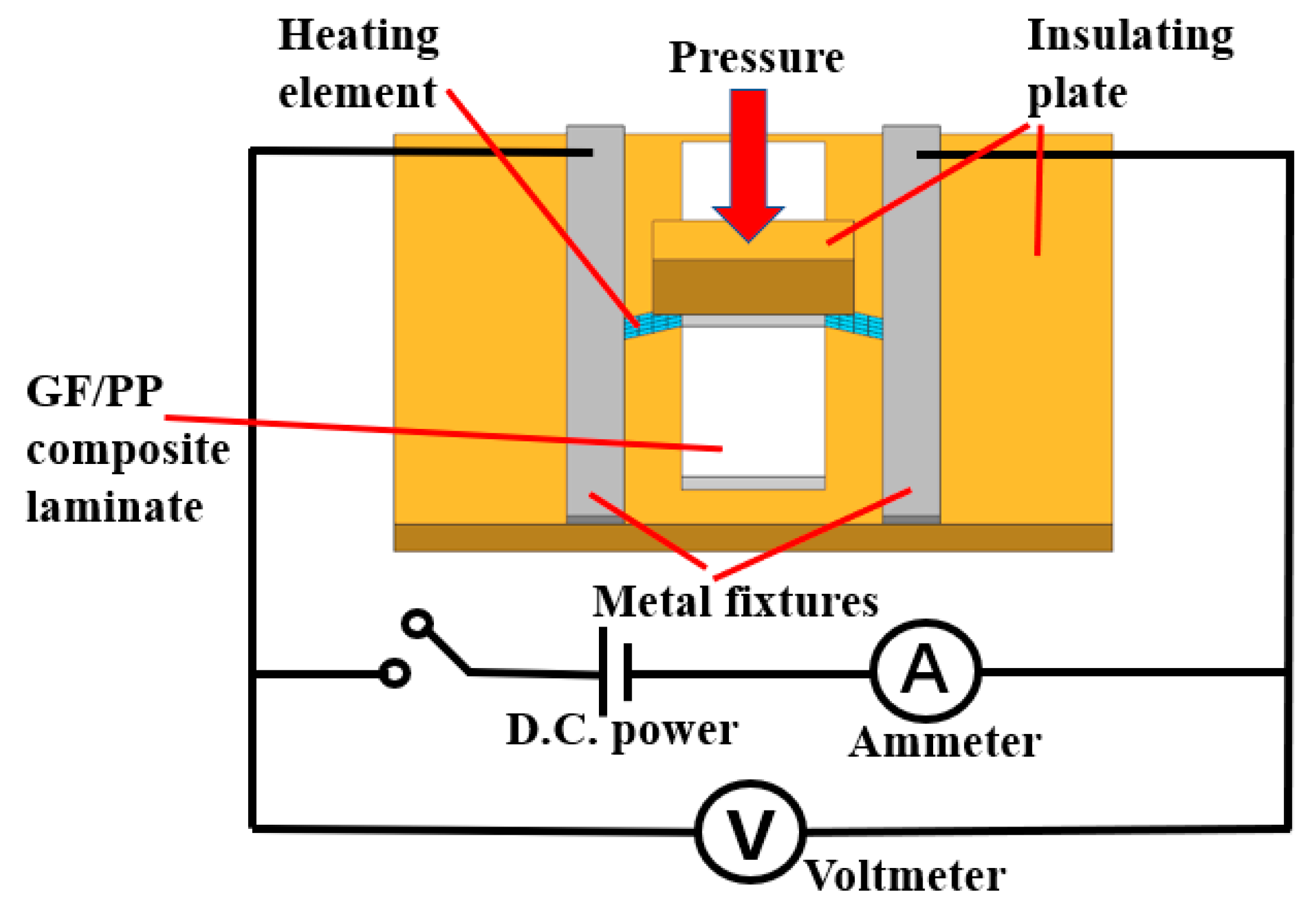
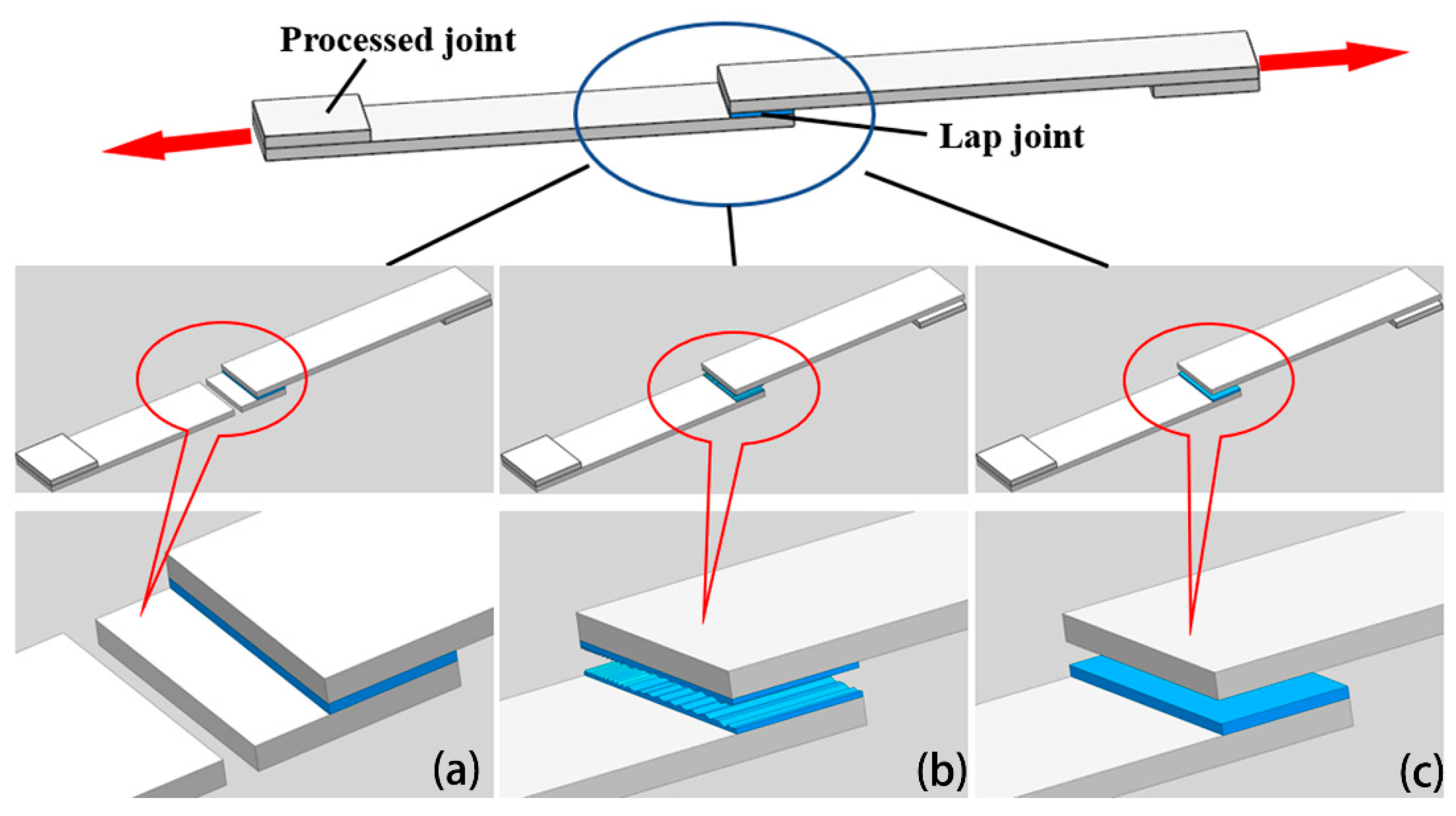
2.3. Heating Element
2.4. Experiments
3. Parameter Setting and Orthogonal Table Construction
3.1. Evaluation and Prediction Method
3.2. Orthogonal Experimental Design
3.3. ANOVA
4. Results and Discussion
4.1. Study Regarding PROCESS Parameters
4.2. Destruction MODE Analysis
5. Conclusions
- A self-designed resistance welding platform containing a DC power supply, an electrode, a heating element, an adherend, an insulation board, and a pressure control unit was established. The resistance values of the heating elements for the resistance welding process conformed to the normal distribution.
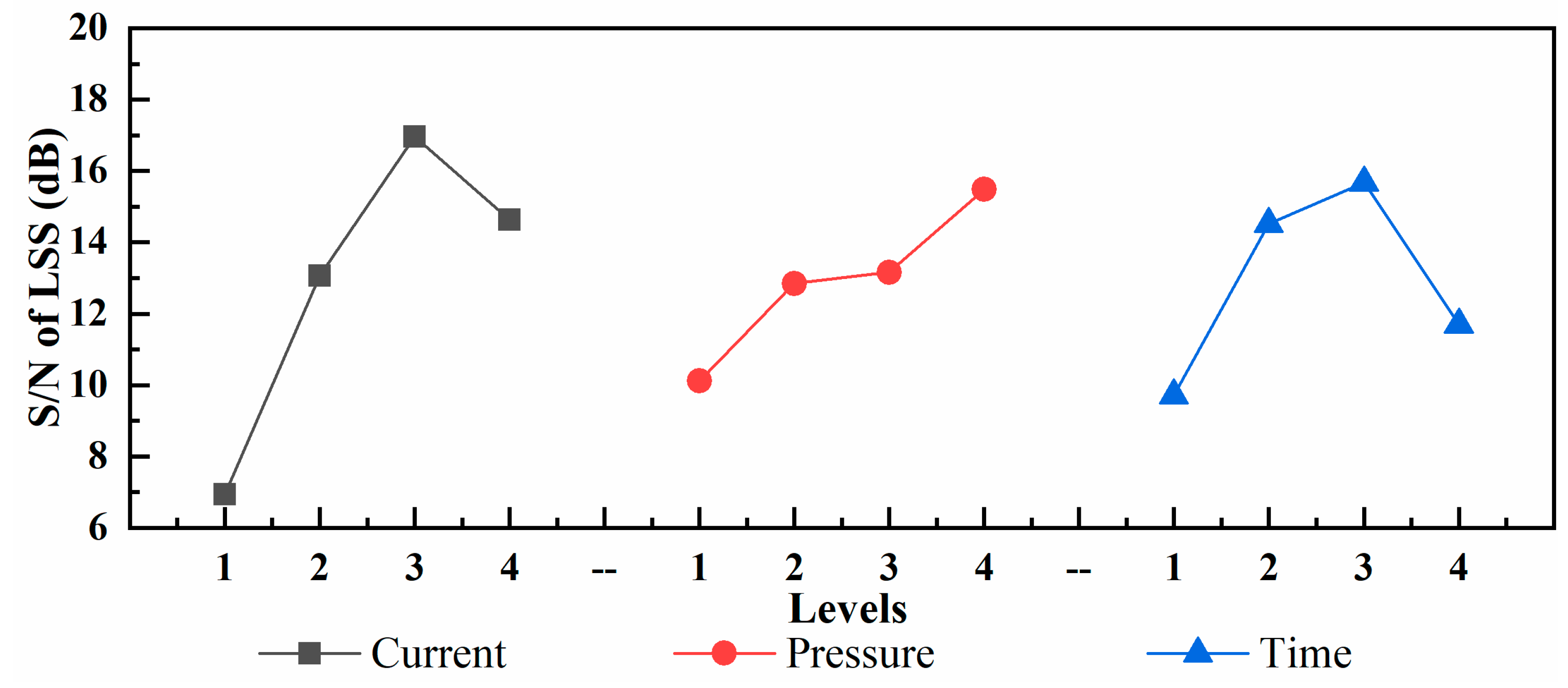
- Using the Taguchi method and ANOVA, it was discovered that among the three process factors (welding current, welding pressure, and welding time) of the GF/PP resistance welding process, current was the main factor affecting the resistance welding quality of GF/PP TPCs, with a contribution rate of 58.12%. The contribution rates of time, pressure, and experimental error were 23.07%, 15.29%, and 3.51%, respectively.
- The S/N method was used to establish a relationship between the LSS and process factors to optimize the LSS. Among the different level combinations of various factors, the optimal process parameters were a current of 12.5 A, pressure of 2.5 MPa, and time of 540 s. The error between the experimental and predicted LSS values was 6.76%.
- The primary failure mode was intralaminar failure, which was primarily caused by fiber fracture and pull-out, and the damaged surface of the sample indicated that the heating element can be well implanted in the laminate, revealing good bonding at the interface.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kropka, M.; Muehlbacher, M. From UD-tape to Final Part—A Comprehensive Approach towards Thermoplastic Composites. Procedia CIRP 2017, 66, 96–100. [Google Scholar] [CrossRef]
- Yang, Y.; Boom, R. Recycling of composite materials. Chem. Eng. Process. 2012, 51, 53–68. [Google Scholar] [CrossRef]
- Li, H.; Englund, K. Recycling of carbon fiber-reinforced thermoplastic composite wastes from the aerospace industry. J. Compos. Mater. 2016, 51, 1265–1273. [Google Scholar] [CrossRef]
- Benoit, N.; González-Núñez, R.; Rodrigue, D. Long-term closed-loop recycling of high-density polyethylene/flax composites. Prog. Rubber Plast. Recycl. Technol. 2018, 34, 171–199. [Google Scholar] [CrossRef]
- Thoppul, S.D.; Finegan, J. Mechanics of mechanically fastened joints in polymer–matrix composite structures—A review. Compos. Sci. Technol. 2009, 69, 301–329. [Google Scholar] [CrossRef]
- Xiong, J.J.; Shenoi, R.A. General aspects on structural integrity. Chin. J. Aeronaut. 2019, 32, 114–132. [Google Scholar] [CrossRef]
- Bersee, D. Resistance welding of thermoplastic composites-an overview. Compos. Part A Appl. Sci. Manuf. 2005, 36, 39–54. [Google Scholar] [CrossRef]
- Budhe, S.; Banea, M.D. An updated review of adhesively bonded joints in composite materials. Int. J. Adhes. Adhes. 2016, 72, 30–42. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, X. Effect of curing condition on bonding quality of scarf-repaired composite laminates. Chin. J. Aeronaut. 2020, 33, 2257–2267. [Google Scholar] [CrossRef]
- Ageorges, C.; Ye, L. Advances in fusion bonding techniques for joining thermoplastic matrix composites: A review. Compos. Part A Appl. Sci. Manuf. 2001, 32, 839–857. [Google Scholar] [CrossRef]
- Yousefpour, A.; Hojjati, M. Fusion Bonding/Welding of Thermoplastic Composites. J. Thermoplast. Compos. Mater. 2004, 17, 303–341. [Google Scholar] [CrossRef]
- Hou, M.; Ye, L. An Experimental Study of Resistance Welding of Carbon Fibre Fabric Reinforced Polyetherimide (CF Fabric/PEI) Composite Material. Appl. Compos. Mater. 1999, 6, 35–49. [Google Scholar] [CrossRef]
- Ageorges, C.; Ye, L. Experimental investigation of the resistance welding for thermoplastic-matrix composites. Part I: Heating element and heat transfer. Compos. Sci. Technol. 2000, 60, 1027–1039. [Google Scholar] [CrossRef]
- Li, X.; Zhang, T. The Effect of Cooling Rate on Resistance-Welded CF/PEEK Joints. J. Mater. Res. Technol. 2021, 12, 52–63. [Google Scholar] [CrossRef]
- Vincent, R.; Louis, L.L. Effects of environmental conditions on the lap shear strength of resistance-welded carbon fibre/thermoplastic composite joints. Compos. Part B Eng. 2020, 198, 108239. [Google Scholar] [CrossRef]
- Barbosa, L.; Souza, S.D. Fractographic evaluation of welded joints of PPS/glass fiber thermoplastic composites. Eng. Fail. Anal. 2019, 102, 60–68. [Google Scholar] [CrossRef]
- Ageorges, C.; Ye, L. Experimental investigation of the resistance welding of thermoplastic-matrix composites. Part II: Optimum processing window and mechanical performance. Compos. Sci. Technol. 2000, 60, 1191–1202. [Google Scholar] [CrossRef]
- Stavrov, D.; Bersee, H.E.N.; Beukers, A. The Influence of the Heating Element on Resistance Welding of Thermoplastic Composite Materials. In Proceedings of the ICCM-14 Conference, San Diego, CA, USA, 14–18 July 2003. [Google Scholar]
- Tanabe, D.; Nishiyabu, K.; Kurashiki, T. Effects of processing parameters on electro-fusion joining of CF/PPS composites using carbon fiber heating elements. Trans. JSME 2015, 81, 15-00005. [Google Scholar] [CrossRef]
- Tanabe, D.; Kubohori, F. Effects of Dimension of Joining Part on Welding Behavior of Carbon Fiber Reinforced Thermoplastics using Spread and Woven Carbon Fiber Resistance Heating Element. J. Soc. Mater. Sci. 2019, 68, 162–169. [Google Scholar] [CrossRef] [Green Version]
- Meng, H.; Yang, M. Resistance welding of carbon fibre reinforced thermoplastic composite using alternative heating element. Compos. Struct. 1999, 47, 667–672. [Google Scholar] [CrossRef]
- Yousefpour, A.; Simard, M. Effects of Mesh Size on Resistance Welding of Thermoplastic Composites using Metal Mesh Heating Elements. In Proceedings of the SAMPE-Europe, Paris, France, 1 April 2004. [Google Scholar]
- Souza, S.D.; Abrah, A.B. Experimental Investigation of Processing Welding Parameters for PPS/Carbon Fiber Laminates for Aeronautical Applications. Adv. Mater. Res. 2016, 1135, 62–74. [Google Scholar] [CrossRef]
- Dubé, M.; Chazerain, A. Characterization of resistance-welded thermoplastic composite double-lap joints under static and fatigue loading. J. Thermoplast. Compos. Mater. 2013, 28, 762–776. [Google Scholar] [CrossRef]
- Koutras, N.; Villegas, I.F.; Benedictus, R. Influence of temperature on the strength of resistance welded glass fibre reinforced PPS joints. Compos. Part A Appl. Sci. Manuf. 2017, 105, 57–67. [Google Scholar] [CrossRef]
- Khaw, J.; Lim, B.S. Optimal design of neural networks using the Taguchi method. Neurocomputing 1995, 7, 225–245. [Google Scholar] [CrossRef]
- Yang, W.H.; Tarng, Y.S. Design optimization of cutting parameters for turning operations based on the Taguchi method. J. Mater. Process. Technol. 1998, 84, 122–129. [Google Scholar] [CrossRef]
- Ko, D.C.; Kim, D.H. Application of artificial neural network and Taguchi method to preform design in metal forming considering workability. Int. J. Mach. Tools Manuf. 1999, 39, 771–785. [Google Scholar] [CrossRef]
- Shaji, S.; Radhakrishnan, V. Analysis of process parameters in surface grinding with graphite as lubricant based on the Taguchi method. J. Mater. Process. Technol. 2003, 141, 51–59. [Google Scholar] [CrossRef]
- Sathiya, P.; Panneerselvam, K. Optimization of laser welding process parameters for super austenitic stainless steel using artificial neural networks and genetic algorithm. Mater. Des. 2012, 36, 490–498. [Google Scholar] [CrossRef]
- Bilici, M.K. Application of Taguchi approach to optimize friction stir spot welding parameters of polypropylene. Mater. Des. 2012, 35, 113–119. [Google Scholar] [CrossRef]
- Li, M.; Hong, S.M. Optimal parameter design for chip-on-film technology using the Taguchi method. Int. J. Adv. Manuf. Technol. 2005, 25, 145–153. [Google Scholar] [CrossRef]
- Li, B.; Nye, T.J. Multi-objective optimization of forming parameters for tube hydroforming process based on the Taguchi method. Int. J. Adv. Manuf. Technol. 2006, 28, 23–30. [Google Scholar] [CrossRef]
- Bagci, E.; Ozcelik, B. Analysis of temperature changes on the twist drill under different drilling conditions based on Taguchi method during dry drilling of Al 7075-T651. Int. J. Adv. Manuf. Technol. 2006, 29, 629–636. [Google Scholar] [CrossRef]
- Lin, T.R. Optimisation Technique for Face Milling Stainless Steel with Multiple Performance Characteristics. Int. J. Adv. Manuf. Technol. 2002, 19, 330–335. [Google Scholar] [CrossRef]
- Tong, L.I.; Wang, C.H. Optimizing processes based on censored data obtained in repetitious experiments using grey prediction. Int. J. Adv. Manuf. Technol. 2006, 27, 990–998. [Google Scholar] [CrossRef]
- Onwubolu, G.C.; Kumar, S. Response surface methodology-based approach to CNC drilling operations. J. Mater. Process. Technol. 2006, 171, 41–47. [Google Scholar] [CrossRef]
- Panneerselvam, K.; Aravindan, S. Study on resistance welding of glass fiber reinforced thermoplastic composites. Mater. Des. 2012, 41, 453–459. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Thickness | 2.4 mm |
| Layup | [0/90/90/0]2 |
| Fiber weight content | 60% |
| Properties | Value |
|---|---|
| 0° Tensile strength | 479.26 MPa |
| 0° Tensile modulus | 29.64 GPa |
| 90° Tensile strength | 13.71 MPa |
| 90° Tensile modulus | 3.53 GPa |
| No. | Factor A (Current) | Factor B (Pressure) | Factor C (Time) |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 |
| 3 | 1 | 3 | 3 |
| 4 | 1 | 4 | 4 |
| 5 | 2 | 1 | 2 |
| 6 | 2 | 2 | 1 |
| 7 | 2 | 3 | 4 |
| 8 | 2 | 4 | 3 |
| 9 | 3 | 1 | 3 |
| 10 | 3 | 2 | 4 |
| 11 | 3 | 3 | 1 |
| 12 | 3 | 4 | 2 |
| 13 | 4 | 1 | 4 |
| 14 | 4 | 2 | 3 |
| 15 | 4 | 3 | 2 |
| 16 | 4 | 4 | 1 |
| Factors | Levels | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Current/A | 10.5 | 11.5 | 12.5 | 13.5 |
| Pressure/MPa | 1 | 1.5 | 2.0 | 2.5 |
| Time/s | 180 | 360 | 540 | 720 |
| No. | Parameters | Performance Characteristics | |||
|---|---|---|---|---|---|
| Factor A (Current/A) | Factor B (Pressure/MPa) | Factor C (Time/s) | Mean LSS (MPa) | S/N Value (dB) | |
| 1 | 1(10.5) | 1(1) | 1(180) | 1.01 | 0.09 |
| 2 | 1(10.5) | 2(1.5) | 2(360) | 2.4 | 7.60 |
| 3 | 1(10.5) | 3(2) | 3(540) | 3.42 | 10.68 |
| 4 | 1(10.5) | 4(2.5) | 4(720) | 2.93 | 9.34 |
| 5 | 2(11.5) | 1(1) | 2(360) | 4.21 | 12.49 |
| 6 | 2(11.5) | 2(1.5) | 1(180) | 3.54 | 10.98 |
| 7 | 2(11.5) | 3(2) | 4(720) | 3.16 | 9.99 |
| 8 | 2(11.5) | 4(2.5) | 3(540) | 8.73 | 18.82 |
| 9 | 3(12.5) | 1(1) | 3(540) | 6.85 | 16.71 |
| 10 | 3(12.5) | 2(1.5) | 4(720) | 6.57 | 16.35 |
| 11 | 3(12.5) | 3(2) | 1(180) | 5.25 | 14.40 |
| 12 | 3(12.5) | 4(2.5) | 2(360) | 10.47 | 20.40 |
| 13 | 4(13.5) | 1(1) | 4(720) | 3.6 | 11.13 |
| 14 | 4(13.5) | 2(1.5) | 3(540) | 6.65 | 16.46 |
| 15 | 4(13.5) | 3(2) | 2(360) | 7.57 | 17.58 |
| 16 | 4(13.5) | 4(2.5) | 1(180) | 4.65 | 13.35 |
| ηm | 12.90 | ||||
| Variables | Level-1 | Level-2 | Level-3 | Level-4 | SS | df | Mean Variance | F-Test | P |
|---|---|---|---|---|---|---|---|---|---|
| Current | 6.93 | 13.07 | 16.97 | 14.63 | 220.87 | 3 | 73.622 | 33.109 | 58.12 |
| Pressure | 10.11 | 12.85 | 13.16 | 15.48 | 58.11 | 3 | 19.37 | 8.711 | 15.29 |
| Time | 9.71 | 14.52 | 15.67 | 11.70 | 87.67 | 3 | 29.223 | 13.142 | 23.07 |
| Errors | 13.34 | 6 | 2.224 | 3.51 | |||||
| Total | 379.99 | 15 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Lin, T.; Luo, L.; Zhang, B.; Qu, Y.; Meng, B. Multi-Objective Optimization of Resistance Welding Process of GF/PP Composites. Polymers 2021, 13, 2560. https://doi.org/10.3390/polym13152560
Zhang G, Lin T, Luo L, Zhang B, Qu Y, Meng B. Multi-Objective Optimization of Resistance Welding Process of GF/PP Composites. Polymers. 2021; 13(15):2560. https://doi.org/10.3390/polym13152560
Chicago/Turabian StyleZhang, Guowei, Ting Lin, Ling Luo, Boming Zhang, Yuao Qu, and Bangke Meng. 2021. "Multi-Objective Optimization of Resistance Welding Process of GF/PP Composites" Polymers 13, no. 15: 2560. https://doi.org/10.3390/polym13152560
APA StyleZhang, G., Lin, T., Luo, L., Zhang, B., Qu, Y., & Meng, B. (2021). Multi-Objective Optimization of Resistance Welding Process of GF/PP Composites. Polymers, 13(15), 2560. https://doi.org/10.3390/polym13152560