Multi-Scale Study of the Small-Strain Damping Ratio of Fiber-Sand Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Materials
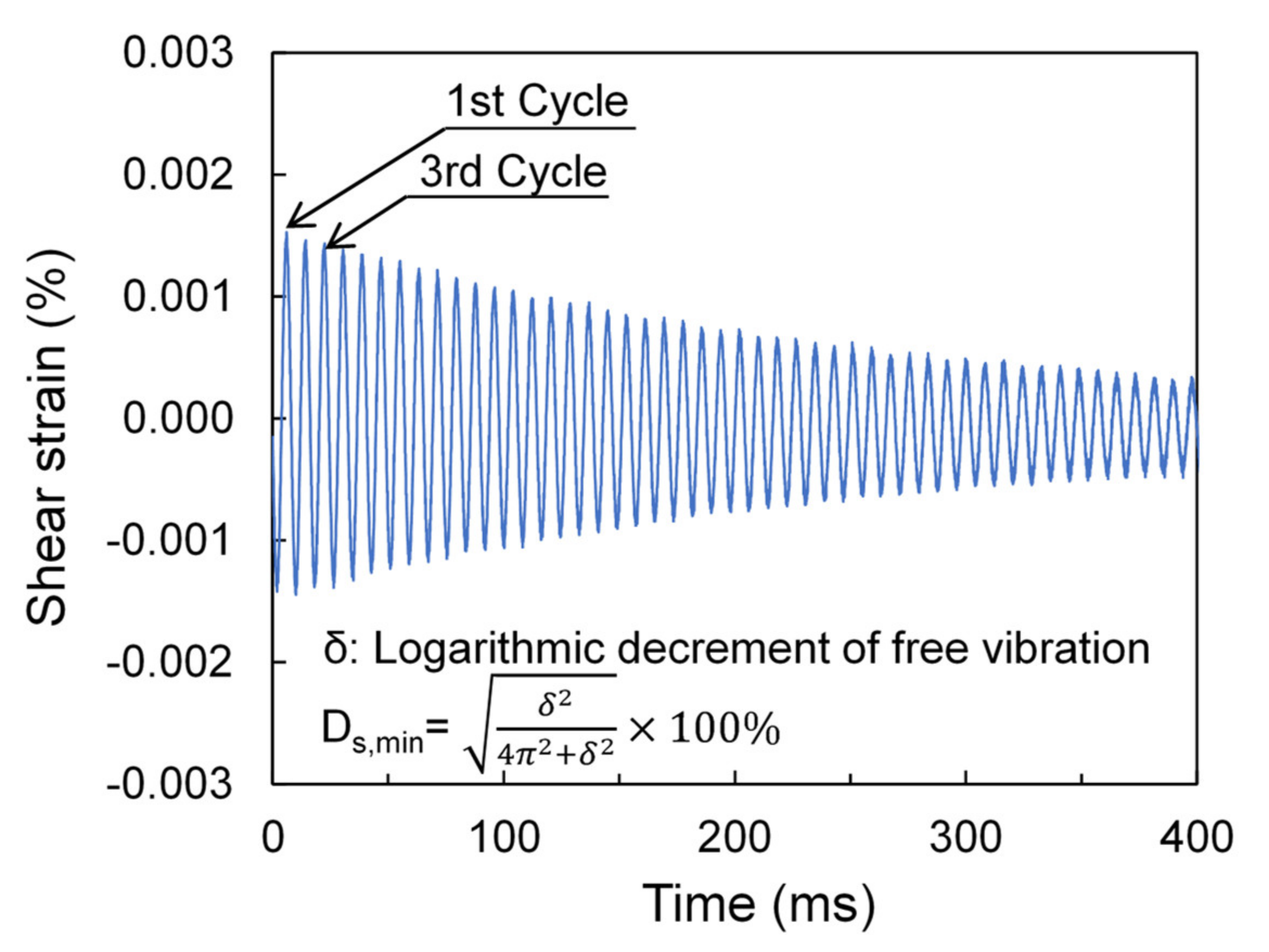
2.2. Resonant Column Tests: Sample Preparation, Experimental Setup and Testing Program
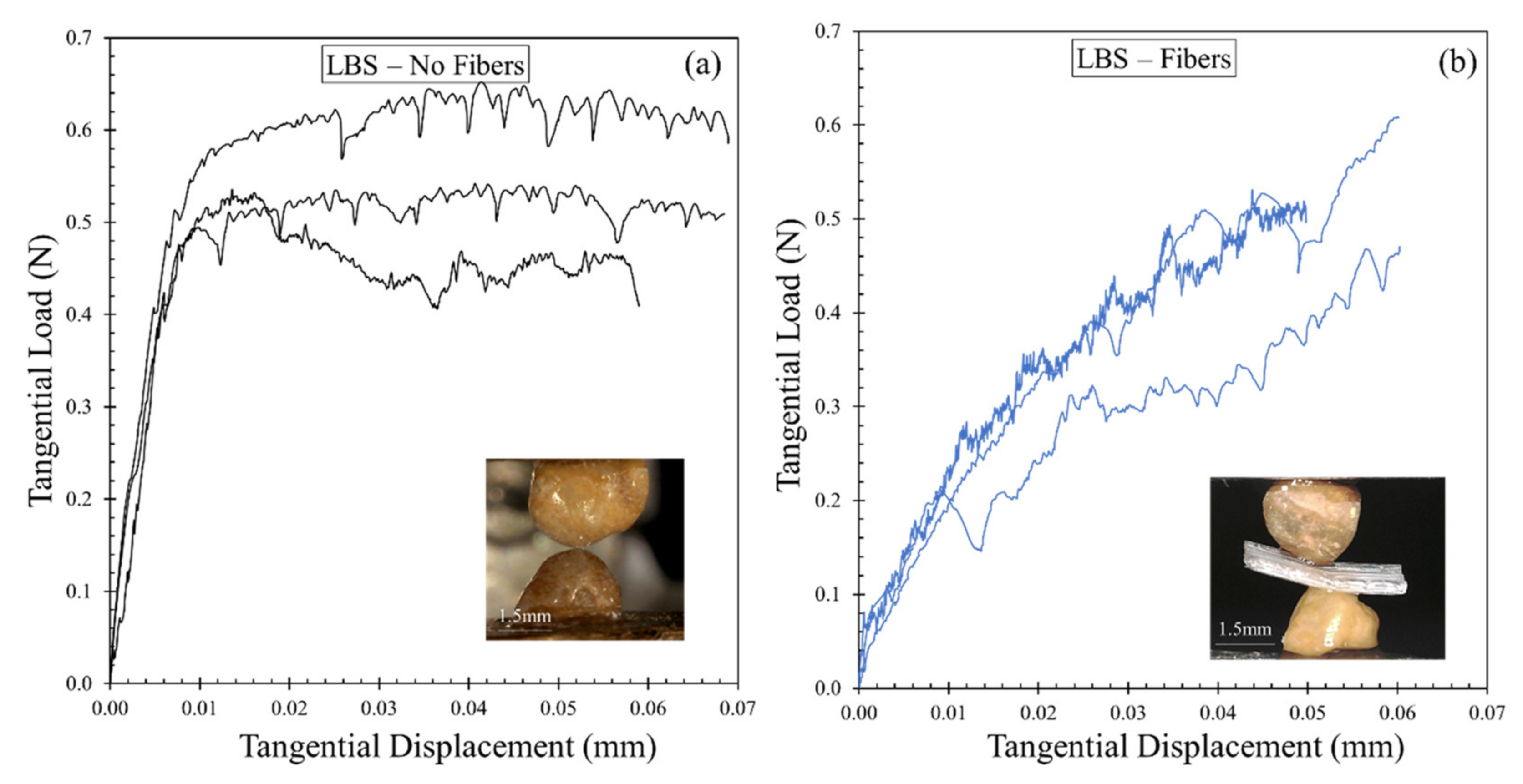
2.3. Grain-Scale Tests: Sample Preparation, Experimental Setup and Testing Program
3. Results and Discussion
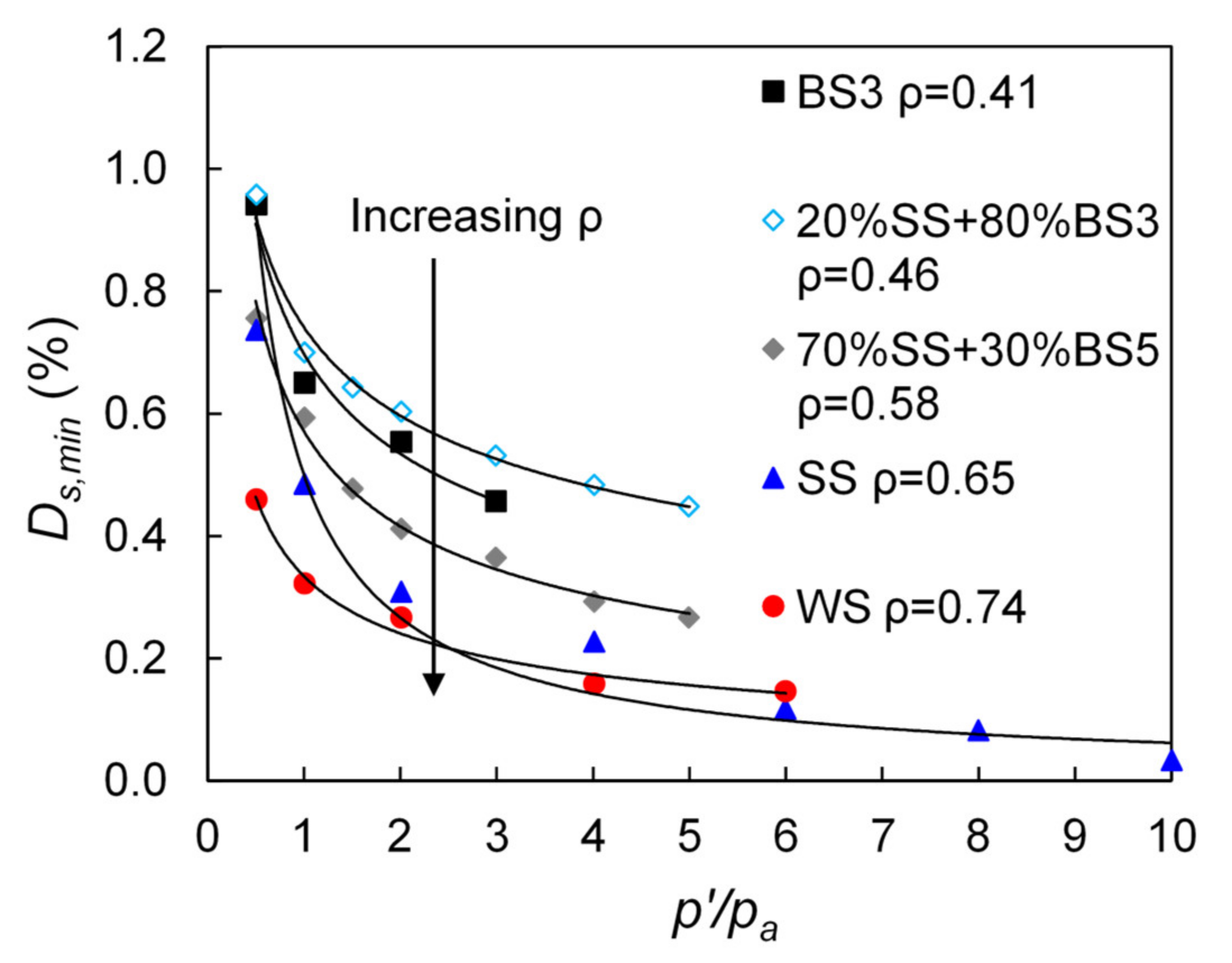
3.1. Small-Strain Damping Ratio of Pure Sand
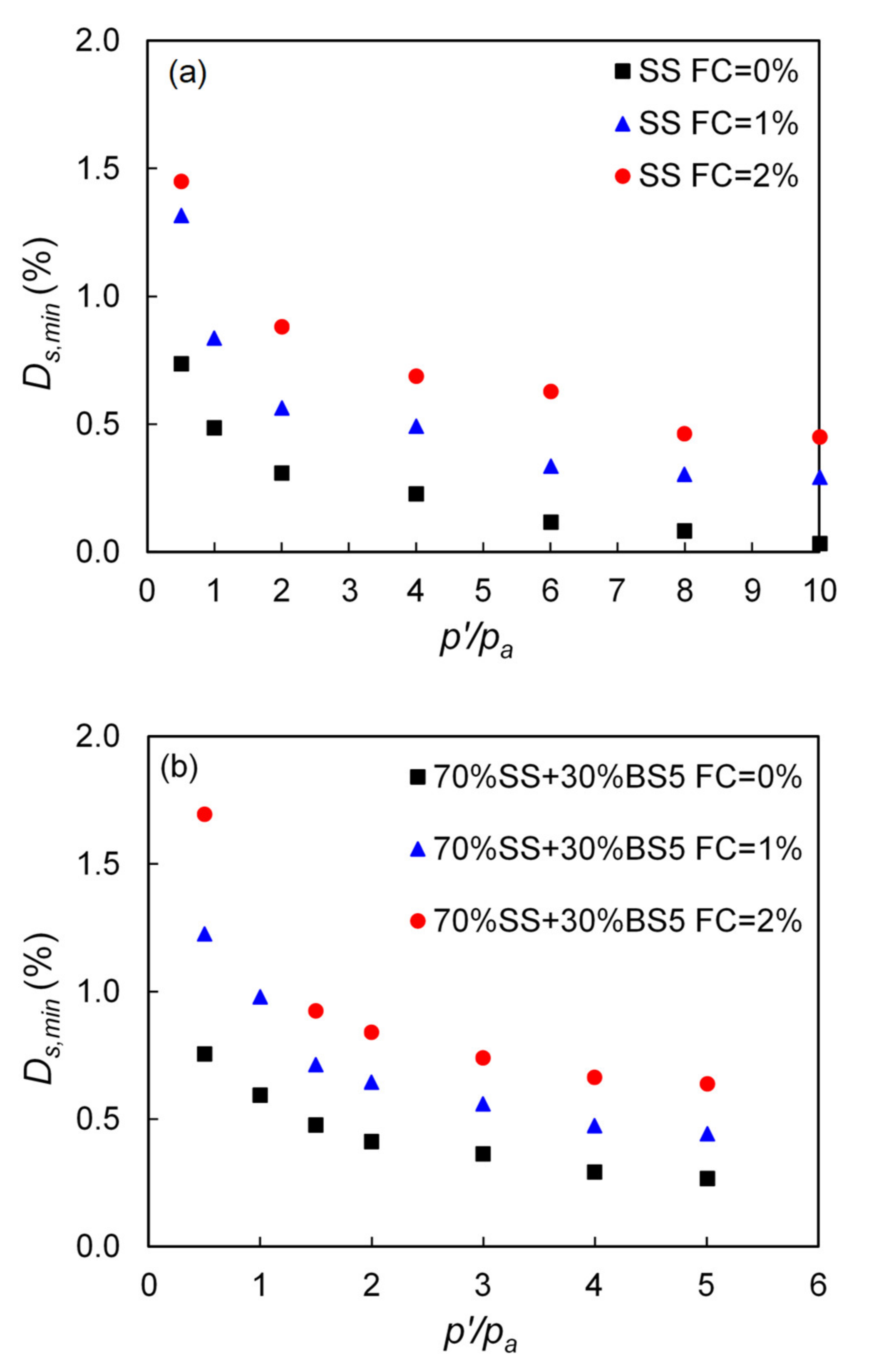
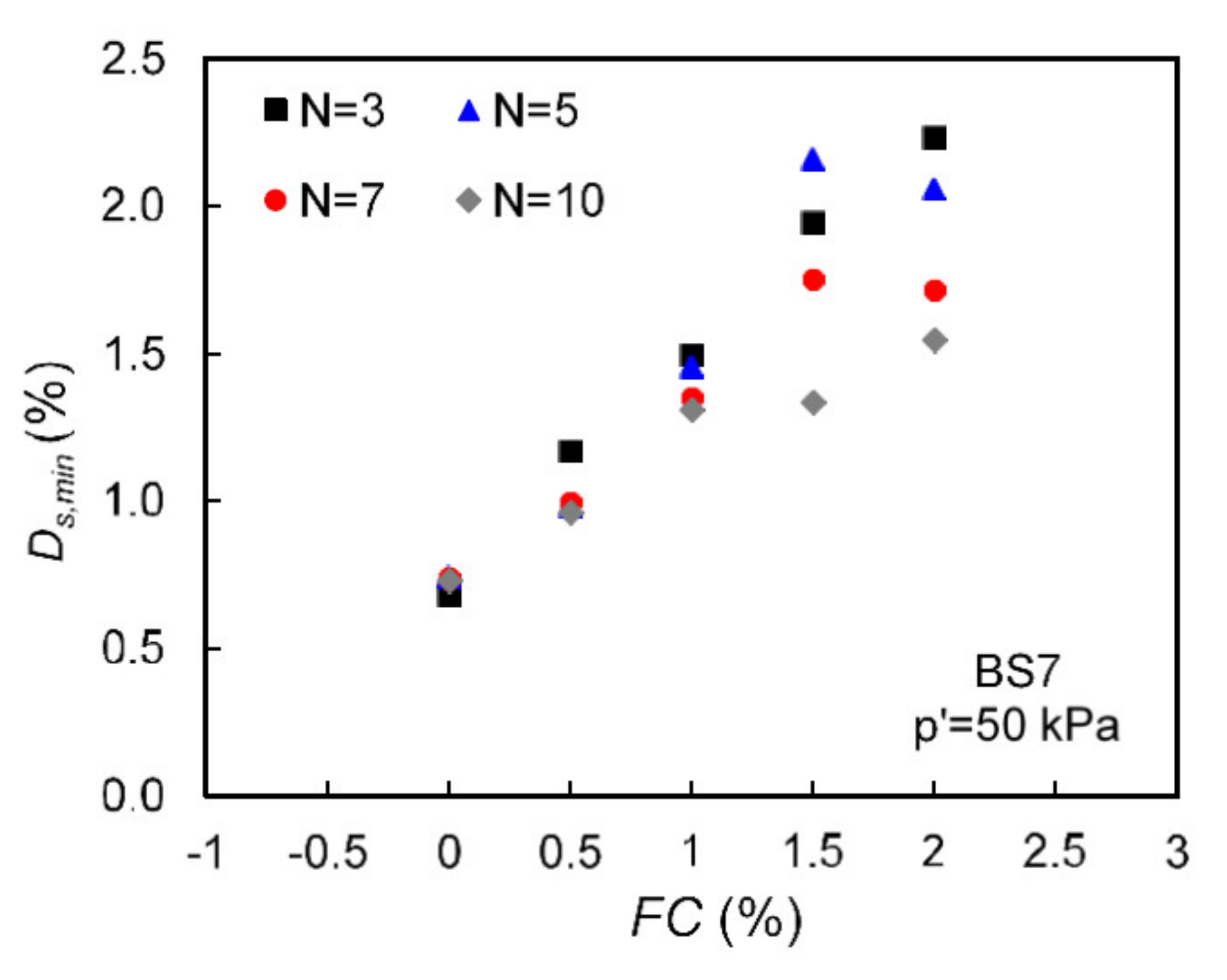
3.2. Small-Strain Damping Ratio of Fiber-Sand Mixtures
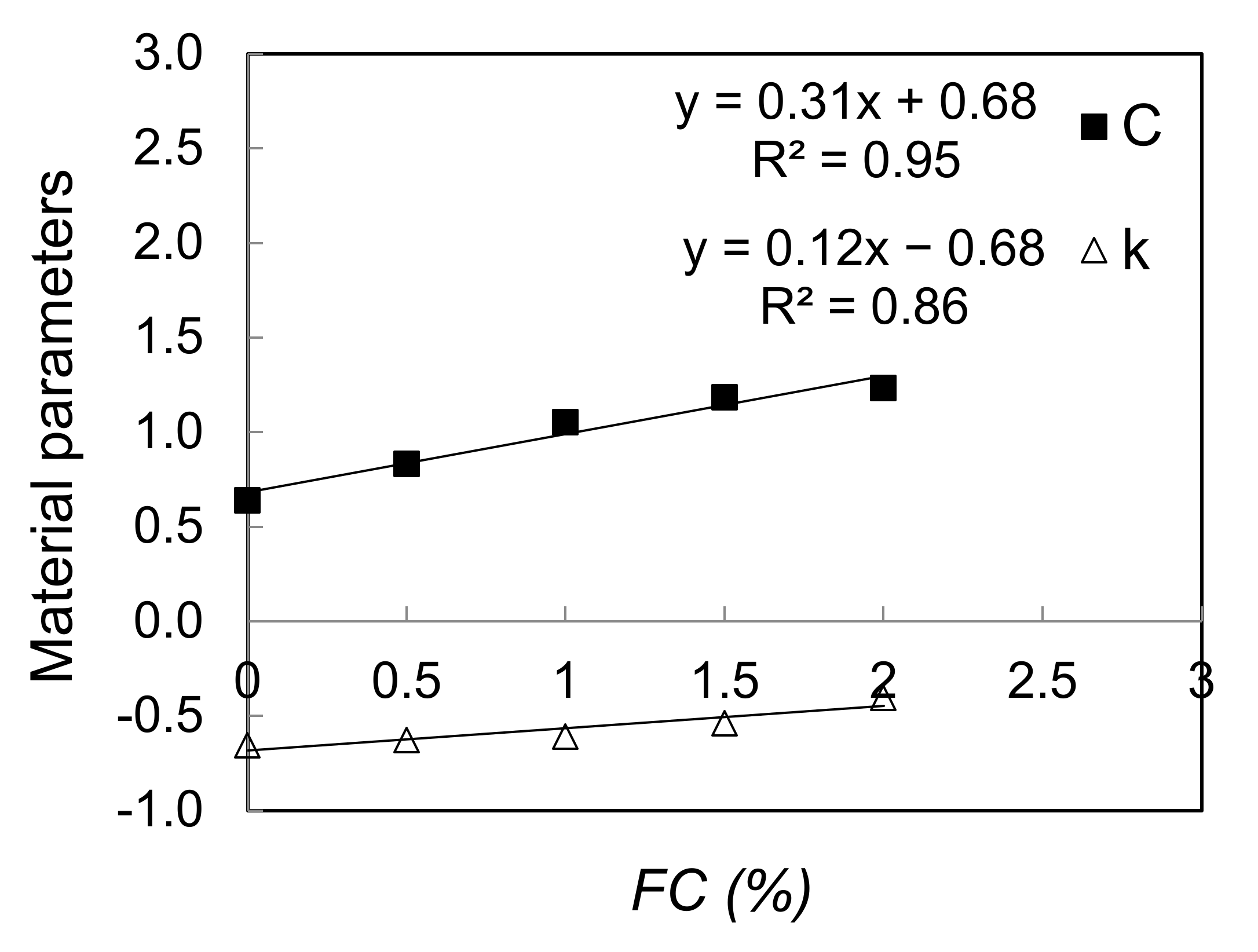
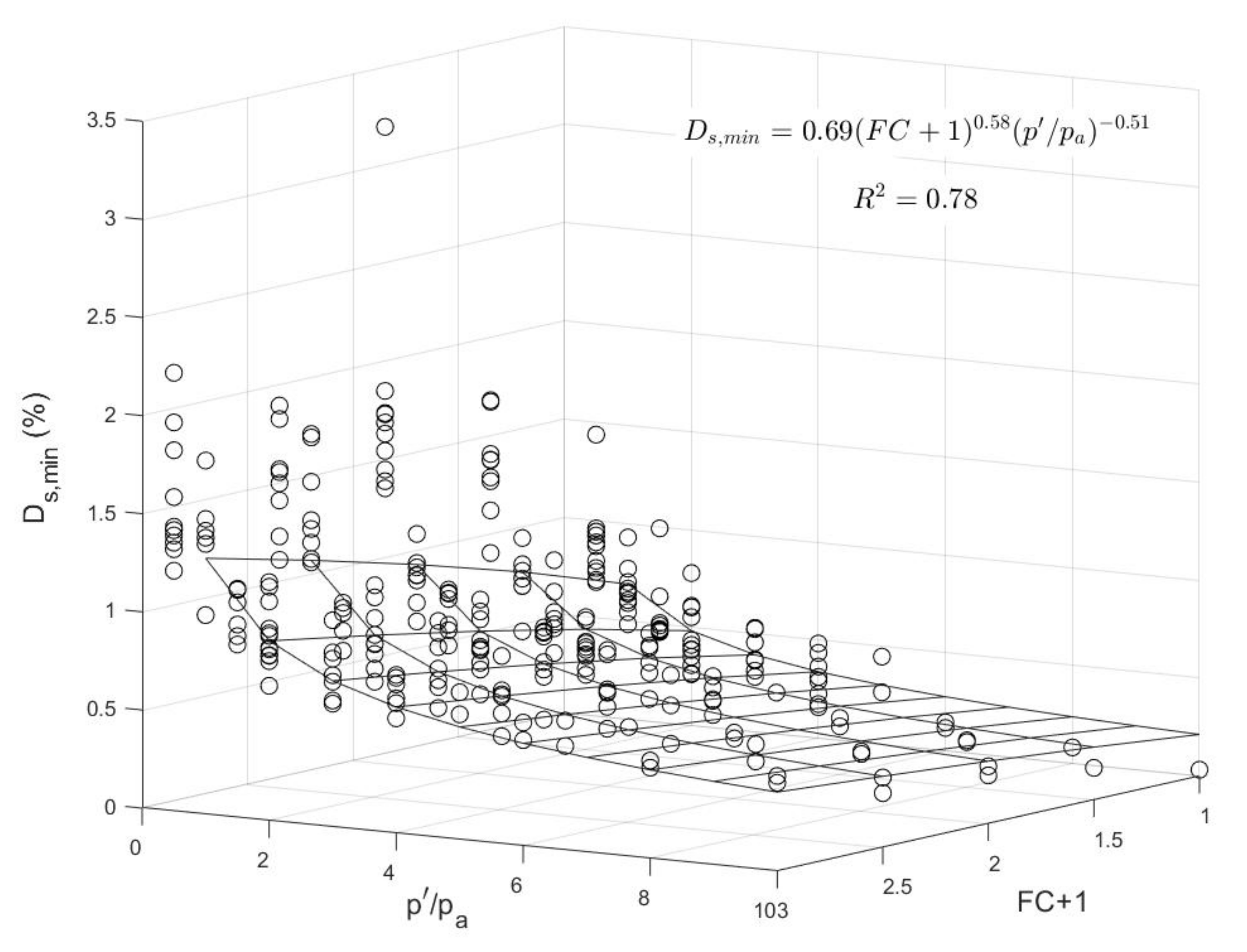
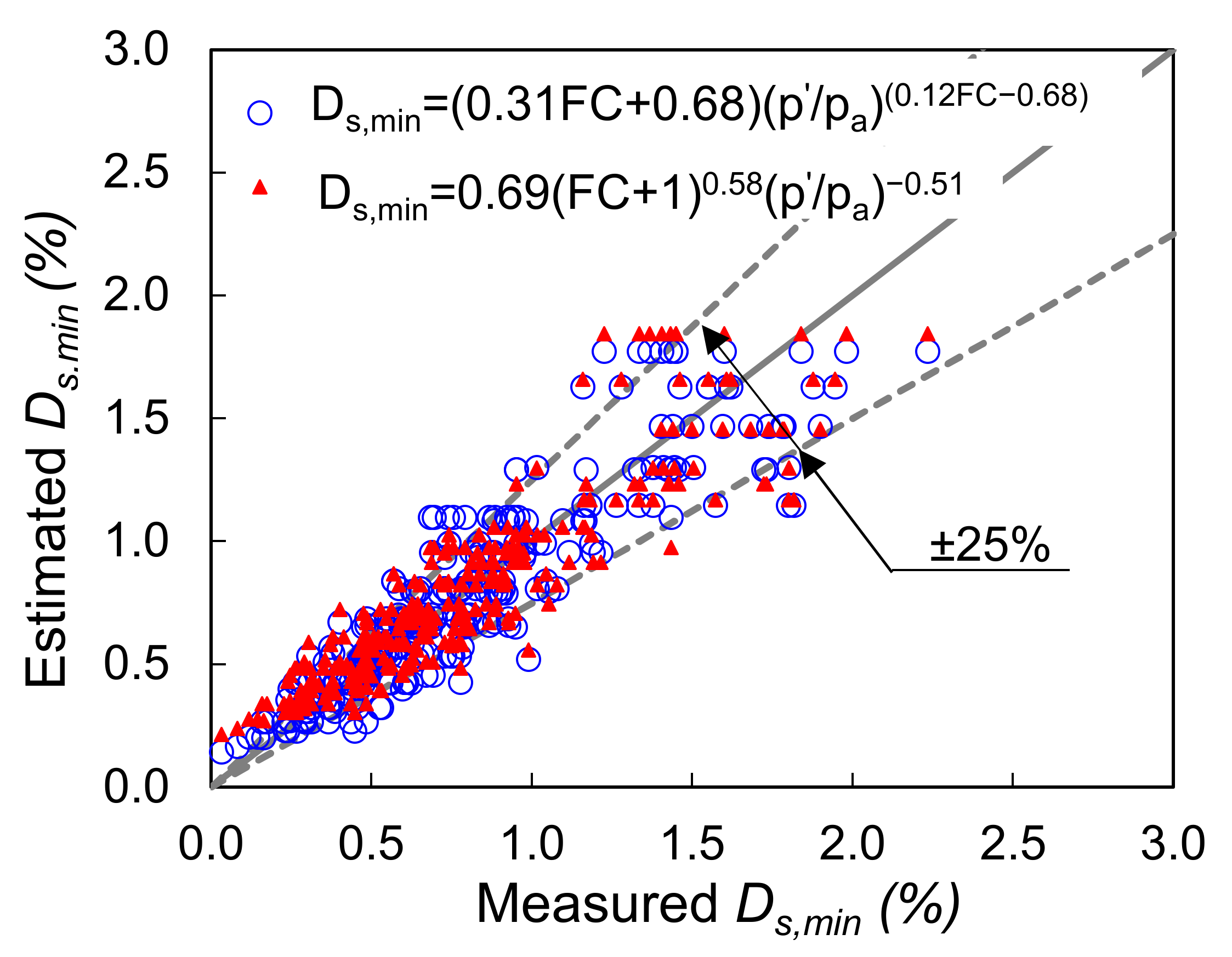
3.3. Development of a New Expression for Small-Strain Damping Ratio of Fiber-Sand Mixtures
3.4. Multi-Scale Insights
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Senetakis, K.; Coop, M.R. Medium-strain dynamic behavior of fiber-reinforced sand subjected to stress anisotropy. Soil Dyn. Earthq. Eng. 2019, 126, 105764. [Google Scholar] [CrossRef]
- Collins, R.; Zhang, M.; Zhang, X.; Hulsey, L.; Ravens, T.; Van Veldhuizen, R. Evaluation of geofibers and nontraditional liquid additives on erodible slopes in Interior Alaska. Geotext. Geomembr. 2015, 43, 412–423. [Google Scholar] [CrossRef]
- Hosney, M.S.; Rowe, R.K. Performance of polymer-enhanced bentonite–sand mixture for covering arsenic-rich gold mine tailings for up to 4 years. Can. Geotech. J. 2017, 54, 588–599. [Google Scholar] [CrossRef]
- Jamshidi, R.; Towhata, I.; Ghiassian, H.; Tabarsa, A. Experimental evaluation of dynamic deformation characteristics of sheet pile retaining walls with fiber reinforced backfill. Soil Dyn. Earthq. Eng. 2010, 30, 438–446. [Google Scholar] [CrossRef]
- Liu, J.; Wang, G.; Kamai, T.; Zhang, F.; Yang, J.; Shi, B. Static liquefaction behavior of saturated fiber reinforced sand in un-drained ring-shear tests. Geotext. Geomembr. 2011, 29, 462–471. [Google Scholar] [CrossRef]
- Mirzababaei, M.; Mohamed, M.; Miraftab, M. Analysis of Strip Footings on Fiber-Reinforced Slopes with the Aid of Particle Image Velocimetry. J. Mater. Civ. Eng. 2017, 29, 04016243. [Google Scholar] [CrossRef] [Green Version]
- Pino, L.F.M.; Baudet, B.A. The effect of the particle size distribution on the mechanics of fiber reinforced sands under one-dimensional compression. Geotext. Geomembr. 2015, 43, 250–258. [Google Scholar] [CrossRef]
- Sahu, S.A.; Saroj, P.K.; Paswan, B. Shear Waves in a Heterogeneous Fiber-Reinforced Layer over a Half-Space under Gravity. Int. J. Geomech. 2015, 15, 04014048. [Google Scholar] [CrossRef]
- Santoni, R.L.; Tingle, J.S.; Webster, S.L. Engineering Properties of Sand-Fiber Mixtures for Road Construction. J. Geotech. Geoenviron. Eng. 2001, 127, 258–268. [Google Scholar] [CrossRef]
- Tang, C.-S.; Shi, B.; Cui, Y.-J.; Liu, C.; Gu, K. Desiccation cracking behavior of polypropylene fiber–reinforced clayey soil. Can. Geotech. J. 2012, 49, 1088–1101. [Google Scholar] [CrossRef]
- Viswanadham, B.V.S.; Rajesh, S.; Divya, P.V.; Gourc, J.P.; Sathiyamoorthy, R. Influence of randomly distributed geofibers on the integrity of clay-based landfill covers: A centrifuge study. Geosynth. Int. 2011, 18, 255–271. [Google Scholar] [CrossRef]
- Yetimoglu, T.; Inanir, M.; Esatinanir, O. A study on bearing capacity of randomly distributed fiber-reinforced sand fills overlying soft clay. Geotext. Geomembr. 2005, 23, 174–183. [Google Scholar] [CrossRef]
- Zornberg, J. Discrete framework for limit equilibrium analysis of fiber reinforced soil. Géotechnique 2002, 52, 593–604. [Google Scholar] [CrossRef]
- Ibraim, E.; Diambra, A.; Wood, D.M.; Russell, A. Static liquefaction of fibre reinforced sand under monotonic loading. Geotext. Geomembr. 2010, 28, 374–385. [Google Scholar] [CrossRef]
- Wang, K.; Brennanb, A. Behaviour of saturated fibre-reinforced sand in centrifuge model tests. Soil Dyn. Earthq. Eng. 2019, 125, 105749. [Google Scholar] [CrossRef]
- Zhang, X.; Russell, A.R. Assessing Liquefaction Resistance of Fiber-Reinforced Sand Using a New Pore Pressure Ratio. J. Geotech. Geoenviron. Eng. 2020, 146, 04019125. [Google Scholar] [CrossRef]
- Li, H.; Senetakis, K. Dynamic properties of polypropylene fibre-reinforced silica quarry sand. Soil Dyn. Earthq. Eng. 2017, 100, 224–232. [Google Scholar] [CrossRef]
- Li, H.; Senetakis, K.; Khoshghalb, A. On the small-strain stiffness of polypropylene fibre-sand mixtures. Geosynth. Int. 2019, 26, 66–80. [Google Scholar] [CrossRef]
- Maher, M.H.; Gray, D.H. Static Response of Sands Reinforced with Randomly Distributed Fibers. J. Geotech. Eng. 1990, 116, 1661–1677. [Google Scholar] [CrossRef]
- Vettorelo, P.V.; Clariá, J.J. Modeling the Fiber Addition Influence on the Small Strain Shear Modulus of Sand. Indian Geotech. J. 2017, 48, 196–204. [Google Scholar] [CrossRef]
- Li, M.; He, H.; Senetakis, K. Behavior of carbon fiber reinforced recycled concrete. Geosynth. Int. 2017, 24, 480–490. [Google Scholar] [CrossRef]
- Senetakis, K.; Li, H. Influence of stress anisotropy on small-strain stiffness of reinforced sand with polypropylene fibres. Soils Found. 2017, 57, 1076–1082. [Google Scholar] [CrossRef]
- Li, H.; Senetakis, K. Modulus Reduction and Damping Increase of Two Sands Reinforced with Polypropylene Fibers. J. Mater. Civ. Eng. 2018, 30, 04017299. [Google Scholar] [CrossRef]
- Richart, F.E.; Hall, J.R.; Woods, R.D. Vibrations of Soils and Foundations; Prentice Hall: Englewood Cliffs, NJ, USA, 1970. [Google Scholar]
- Ishihara, K. Soil Behaviour in Earthquake Geotechnics; Clarendon Press, Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice-Hall: New York, NY, USA, 1996. [Google Scholar]
- Stokoe, K.; Darendeli, M.; Andrus, R.; Brown, L.T. Dynamic soil properties: Laboratory, field and correlation studies. In Proceedings of the 2nd International Conference on Earthquake Geotechnical Engineering, Lisbon, Portugal, 21–25 June 1999; pp. 811–845. [Google Scholar]
- Darendeli, M.B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2001. [Google Scholar]
- Menq, F.-Y. Dynamic Properties of Sandy and Gravelly Soils. Ph.D. Thesis, University of Texas, Austin, TX, USA, 2003. [Google Scholar]
- Cascante, G.; Santamarina, C. Interparticle contact behavior and wave propagation. J. Geotech. Geoenviron. Eng. ASCE 1996, 122, 831–839. [Google Scholar] [CrossRef]
- Senetakis, K.; Anastasiadis, A.; Pitilakis, K. The Small-Strain Shear Modulus and Damping Ratio of Quartz and Volcanic Sands. Geotech. Test. J. 2012, 35, 20120073. [Google Scholar] [CrossRef]
- Senetakis, K.; Anastasiadis, A.; Pitilakis, K. Normalized shear modulus reduction and damping ratio curves of quartz sand and rhyolitic crushed rock. Soils Found. 2013, 53, 879–893. [Google Scholar] [CrossRef] [Green Version]
- Senetakis, K.; Anastasiadis, A.; Pitilakis, K.; Coop, M.R. The dynamics of a pumice granular soil in dry state under isotropic resonant column testing. Soil Dyn. Earthq. Eng. 2013, 45, 70–79. [Google Scholar] [CrossRef]
- Senetakis, K.; Madhusudhan, B.N. Dynamics of potential fill–backfill material at very small strains. Soils Found. 2015, 55, 1196–1210. [Google Scholar] [CrossRef] [Green Version]
- Payan, M.; Senetakis, K.; Khoshghalb, A.; Khalili, N. Influence of particle shape on small-strain material damping of dry sand. Geotechnique 2016, 66, 610–616. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Senetakis, K. Effects of Particle Grading and Stress State on Strain-Nonlinearity of Shear Modulus and Damping Ratio of Sand Evaluated by Resonant-Column Testing. J. Earthq. Eng. 2018, 24, 1886–1912. [Google Scholar] [CrossRef]
- Payan, M.; Khoshghalb, A.; Senetakis, K.; Khalili, N. Effect of particle shape and validity of Gmax models for sand: A critical review and a new model. Comput. Geotech. 2016, 72, 28–41. [Google Scholar] [CrossRef]
- Schnabel, P.B.; Lysmer, J.; Seed, H.B. SHAKE: A Computer Program for Earthquake Response Analysis of Horizontally Layered Sites; Rep. No. EERC 72-12; Earthquake Engineering Research Center University of California: Berkeley, CA, USA, 1972. [Google Scholar]
- Idriss, I.; Lysmer, J.; Hwang, R.; Seed, H. QUAD4: A Computer Program for Evaluating the Seismic Response of Soil Structures by Variable Damping Finite Element Procedures; EERC Report 73-16; University of California: Berkeley, CA, USA, 1973. [Google Scholar]
- Hudson, M.; Idriss, I.; Beikae, M. User’s Manual for QUAD4M: A Computer Program to Evaluate the Seismic Response of Soil Structures Using Finite Element Procedures and Incorporating a Compliant Base; University of California: Davis, CA, USA, 1994. [Google Scholar]
- Bardet, J.P.; Ichii, K.; Lin, C.H. EERA: A Computer Program for Equivalent-Linear Earthquake Site Response Analyses of Layered Soil Deposits; University of Southern California, Department of Civil Engineering: Los Angeles, CA, USA, 2000. [Google Scholar]
- Clayton, C.R.I. Stiffness at small strain: Research and practice. Géotechnique 2011, 61, 5–37. [Google Scholar] [CrossRef] [Green Version]
- Zoback, M.D.; Kohli, A.H. Unconventional Reservoir Geomechanics: Shale Gas, Tight Oil, and Induced Seismicity; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Soriano, I.; Ibraim, E.; Andò, E.; Diambra, A.; Laurencin, T.; Moro, P.; Viggiani, G. 3D fibre architecture of fibre-reinforced sand. Granul. Matter 2017, 19, 75. [Google Scholar] [CrossRef] [Green Version]
- Cho, G.C.; Dodds, J.; Santamarina, J.C. Particle shape effects on packing density, stiffness and strength: Natural and crushed sands. J. Geotech. Geoenviron. Eng. ASCE 2006, 132, 591–602. [Google Scholar] [CrossRef] [Green Version]
- Almajid, A.; Walter, R.; Kroos, T.; Junaedi, H.; Gurka, M.; Khalil, K. The Multiple Uses of Polypropylene/Polyethylene Terephthalate Microfibrillar Composite Structures to Support Waste Management—Composite Processing and Properties. Polymers 2021, 13, 1296. [Google Scholar] [CrossRef]
- Burgada, F.; Fages, E.; Quiles-Carrillo, L.; Lascano, D.; Ivorra-Martinez, J.; Arrieta, M.; Fenollar, O. Upgrading Recycled Polypropylene from Textile Wastes in Wood Plastic Composites with Short Hemp Fiber. Polymers 2021, 13, 1248. [Google Scholar] [CrossRef]
- Kůdelová, T.; Bartuli, E.; Strunga, A.; Hvožďa, J.; Dohnal, M. Fully Polymeric Distillation Unit Based on Polypropylene Hollow Fibers. Polymers 2021, 13, 1031. [Google Scholar] [CrossRef]
- Kim, J.; Cho, D. Effects of Waste Expanded Polypropylene as Recycled Matrix on the Flexural, Impact, and Heat Deflection Temperature Properties of Kenaf Fiber/Polypropylene Composites. Polymers 2020, 12, 2578. [Google Scholar] [CrossRef] [PubMed]
- Jabir, H.A.; Abid, S.R.; Murali, G.; Ali, S.H.; Klyuev, S.; Fediuk, R.; Vatin, N.; Promakhov, V.; Vasilev, Y. Experimental Tests and Reliability Analysis of the Cracking Impact Resistance of UHPFRC. Fibers 2020, 8, 74. [Google Scholar] [CrossRef]
- Signorini, C.; Volpini, V. Mechanical Performance of Fiber Reinforced Cement Composites Including Fully-Recycled Plastic Fibers. Fibers 2021, 9, 16. [Google Scholar] [CrossRef]
- Guo, H.; Jiang, L.; Tao, J.; Chen, Y.; Zheng, Z.; Jia, B. Influence of a hybrid combination of steel and polypropylene fibers on concrete toughness. Constr. Build. Mater. 2021, 275, 122132. [Google Scholar] [CrossRef]
- Li, Y.; Su, Y.; Tan, K.H.; Zheng, X.; Sheng, J. Pore structure and splitting tensile strength of hybrid Basalt–Polypropylene fiber reinforced concrete subjected to carbonation. Constr. Build. Mater. 2021, 297, 123779. [Google Scholar] [CrossRef]
- Liu, Z.; Worley, R., II; Du, F.; Huston, D.; Dewoolkar, M.; Tan, T. Measurement of stress-time avalanches inside polypropylene fiber reinforced concrete beams during flexure. Constr. Build. Mater. 2021, 270, 121428. [Google Scholar] [CrossRef]
- Meng, K.; Xu, L.; Chi, Y. Experimental investigation on the mechanical behavior of hybrid steel-polypropylene fiber reinforced concrete under conventional triaxial cyclic compression. Constr. Build. Mater. 2021, 291, 123262. [Google Scholar] [CrossRef]
- Sandeep, C.S.; Senetakis, K. Effect of Young’s Modulus and Surface Roughness on the Inter-Particle Friction of Granular Materials. Materials 2018, 11, 217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sandeep, C.S.; Senetakis, K. An experimental investigation of the microslip displacement of geological materials. Comput. Geotech. 2019, 107, 55–67. [Google Scholar] [CrossRef]
- Tian, Y.; Senetakis, K. Influence of creep on the small-strain stiffness of sand-rubber mixtures. Geotechnique 2021. ahead of print. [Google Scholar] [CrossRef]
- Tian, Y.; Kasyap, S.; Senetakis, K. Influence of Loading History and Soil Type on the Normal Contact Behavior of Natural Sand Grain-Elastomer Composite Interfaces. Polymers 2021, 13, 1830. [Google Scholar] [CrossRef]
- Li, H.; He, H.; Senetakis, K. Calibration exercise of a Hardin-type resonant column. Géotechnique 2018, 68, 171–176. [Google Scholar] [CrossRef]
- Senetakis, K.; He, H. Dynamic characterization of a biogenic granular soil with a resonant column of fixed-partly fixed boundary conditions. Soil Dyn. Earthq. Eng. 2017, 95, 180–187. [Google Scholar] [CrossRef]
- Kasyap, S.S.; Senetakis, K.; Coop, M.R.; Zhao, J. Micromechanical behaviour in shearing of reproduced flat LBS grains with strong and weak artificial bonds. Acta Geotech. 2020, 16, 1355–1376. [Google Scholar] [CrossRef]
- Li, W.; Kwok, C.Y.; Sandeep, C.S.; Senetakis, K. Sand type effect on the behaviour of sand-granulated rubber mixtures: Integrated study from micro- to macro-scales. Powder Technol. 2019, 342, 907–916. [Google Scholar] [CrossRef]
- Marzulli, V.; Sandeep, C.S.; Senetakis, K.; Cafaro, F.; Pöschel, T. Scale and water effects on the friction angles of two granular soils with different roughness. Powder Technol. 2021, 377, 813–826. [Google Scholar] [CrossRef]
- ASTM. Standard Test Methods for Modulus and Damping of Soils by Fixed-Base Resonant-Column Devices; D4015-15: Annual Book of ASTM Standards; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Senetakis, K.; Anastasiadis, A. Effects of state of test sample, specimen geometry and sample preparation on dynamic properties of rubber-sand mixtures. Geosynth. Int. 2015, 22, 301–310. [Google Scholar] [CrossRef] [Green Version]
- Santamarina, C.; Cascante, G. Effect of surface roughness on wave propagation parameters. Geotechnique 1998, 48, 129–136. [Google Scholar] [CrossRef]
- Anastasiadis, A.; Senetakis, K.; Pitilakis, K.; Gargala, C.; Karakasi, I. Dynamic Behavior of Sand/Rubber Mixtures, Part I: Effect of Rubber Content and Duration of Confinement on Small-Strain Shear Modulus and Damping Ratio; ASTM International: West Conshohocken, PA, USA, 2012; Volume 9, Paper ID JAI103680. [Google Scholar]
- Senetakis, K.; Anastasiadis, A.; Pitilakis, K. Dynamic properties of dry sand/rubber (SRM) and gravel/rubber (GRM) mixtures in a wide range of shearing strain amplitudes. Soil Dyn. Earthq. Eng. 2012, 33, 38–53. [Google Scholar] [CrossRef]
- He, H.; Senetakis, K.; Coop, M.R. An investigation of the effect of shearing velocity on the inter-particle behavior of granular and composite materials with a new micromechanical dynamic testing apparatus. Tribol. Int. 2019, 134, 252–263. [Google Scholar] [CrossRef] [Green Version]








| Sand Type | Sand Name | Grain Size Distribution | Particle Shape Descriptors * | ||||
|---|---|---|---|---|---|---|---|
| d50(mm) | Cu | Cc | R | S | ρ | ||
| Sydney Sand | SS | 0.33 | 2.18 | 0.89 | 0.63 | 0.68 | 0.65 |
| Blue Sand 1 | BS 1 | 0.99 | 5.84 | 1.22 | 0.28 | 0.54 | 0.41 |
| Blue Sand 2 | BS 2 | 0.96 | 2.98 | 0.88 | 0.28 | 0.54 | 0.41 |
| Blue Sand 3 | BS 3 | 1.00 | 1.66 | 0.90 | 0.28 | 0.54 | 0.41 |
| Blue Sand 4 | BS 4 | 3.35 | 1.42 | 0.93 | 0.28 | 0.54 | 0.41 |
| Blue Sand 5 | BS 5 | 0.42 | 1.41 | 0.93 | 0.28 | 0.54 | 0.41 |
| Blue Sand 6 | BS 6 | 1.67 | 1.41 | 0.93 | 0.28 | 0.54 | 0.41 |
| Blue Sand 7 | BS 7 | 2.5 | 2.08 | 0.89 | 0.28 | 0.54 | 0.41 |
| 50% SS + 50% BS 3 | 50SS-50BS3 | 0.63 | 3.75 | 0.91 | 0.46 | 0.61 | 0.53 |
| 20% SS + 80% BS 5 | 20SS-80BS5 | 0.41 | 1.47 | 0.93 | 0.35 | 0.57 | 0.46 |
| White sand | WS | 0.24 | 1.66 | 0.90 | 0.71 | 0.76 | 0.74 |
| 70% SS + 30% BS5 | 70SS-30BS5 | 0.37 | 2.2 | 1.18 | 0.53 | 0.64 | 0.58 |
| Sample No. | Sand Type | Fiber Content (%) | Initial Dry Density γd (kN/m3) | Initial Void Ratio (e) |
|---|---|---|---|---|
| 1 | WS | 0 | 16.74 | 0.553 |
| 2 | WS | 0.5 | 15.03 | 0.733 |
| 3 | WS | 1 | 14.72 | 0.732 |
| 4 | WS | 1.5 | 14.14 | 0.787 |
| 5 | WS | 2 | 13.94 | 0.796 |
| 6 | 70SS-30BS5 | 0 | 16.18 | 0.607 |
| 7 | 70SS-30BS5 | 0.5 | 14.50 | 0.776 |
| 8 | 70SS-30BS5 | 1 | 13.92 | 0.833 |
| 9 | 70SS-30BS5 | 1.5 | 13.49 | 0.874 |
| 10 | 70SS-30BS5 | 2 | 13.38 | 0.872 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Kasyap, S.S.; Senetakis, K. Multi-Scale Study of the Small-Strain Damping Ratio of Fiber-Sand Composites. Polymers 2021, 13, 2476. https://doi.org/10.3390/polym13152476
Li H, Kasyap SS, Senetakis K. Multi-Scale Study of the Small-Strain Damping Ratio of Fiber-Sand Composites. Polymers. 2021; 13(15):2476. https://doi.org/10.3390/polym13152476
Chicago/Turabian StyleLi, Haiwen, Sathwik S. Kasyap, and Kostas Senetakis. 2021. "Multi-Scale Study of the Small-Strain Damping Ratio of Fiber-Sand Composites" Polymers 13, no. 15: 2476. https://doi.org/10.3390/polym13152476






