Review of Strain Rate Effects of Fiber-Reinforced Polymer Composites
Abstract
1. Introduction
2. Rate-Dependent Deformation and Failure
- inertia effects characterized as inertia resistance against rapid deformation, damage formation and crack propagation. Due to material heterogeneity, micro-inertia effects also arise as a result of wave reflection occurring at the interfaces between the constituents, which can result in complex spatiotemporal scenarios of damage and failure evolution, initiated at multiple spots [56,57,58,59];
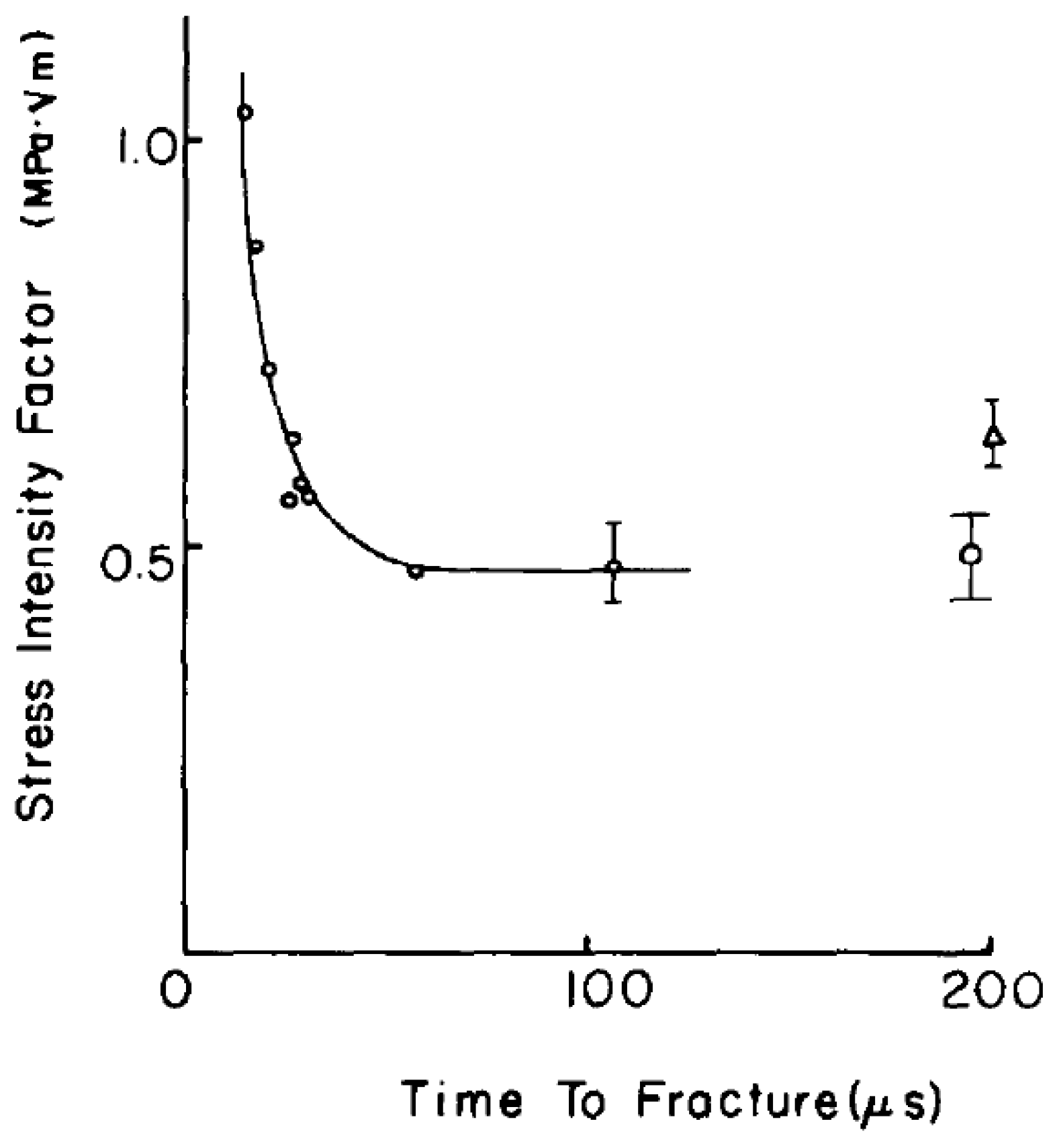
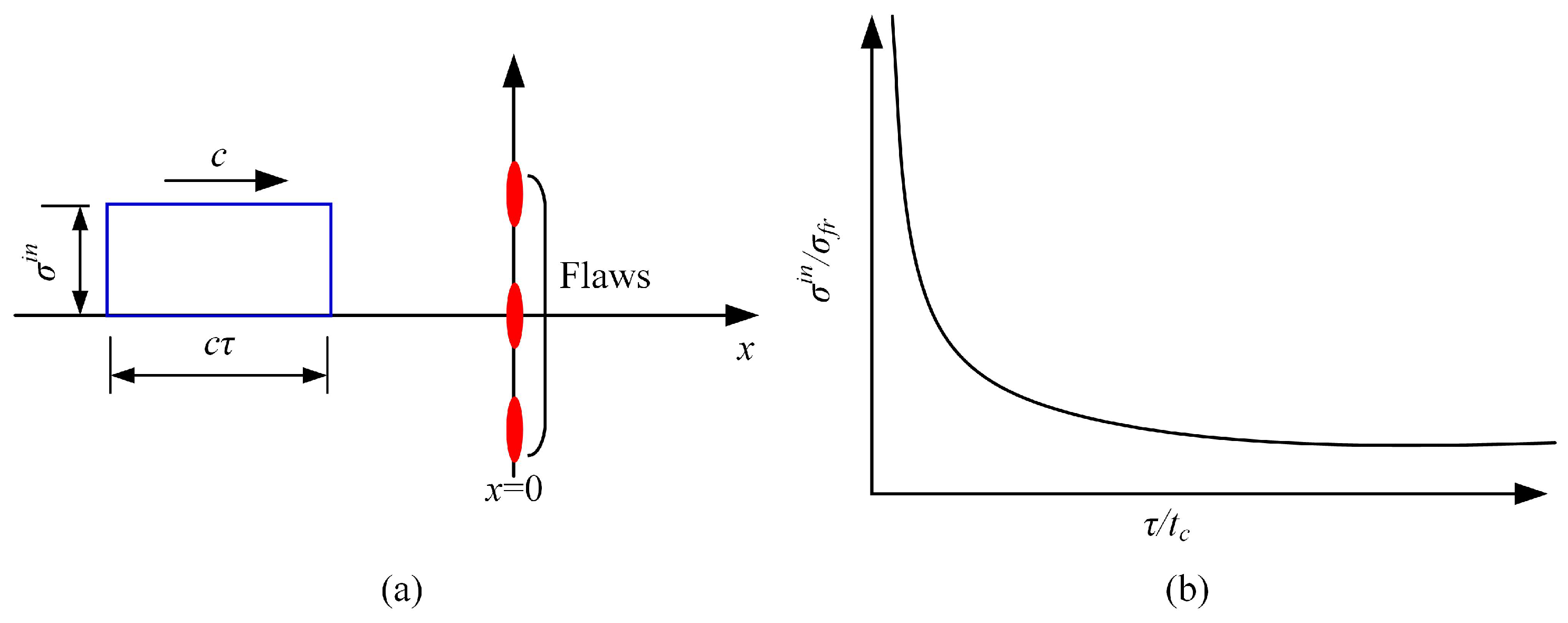
- the characteristic fracture time, as there is a threshold time (characteristic fracture time) required to activate cracks [48].
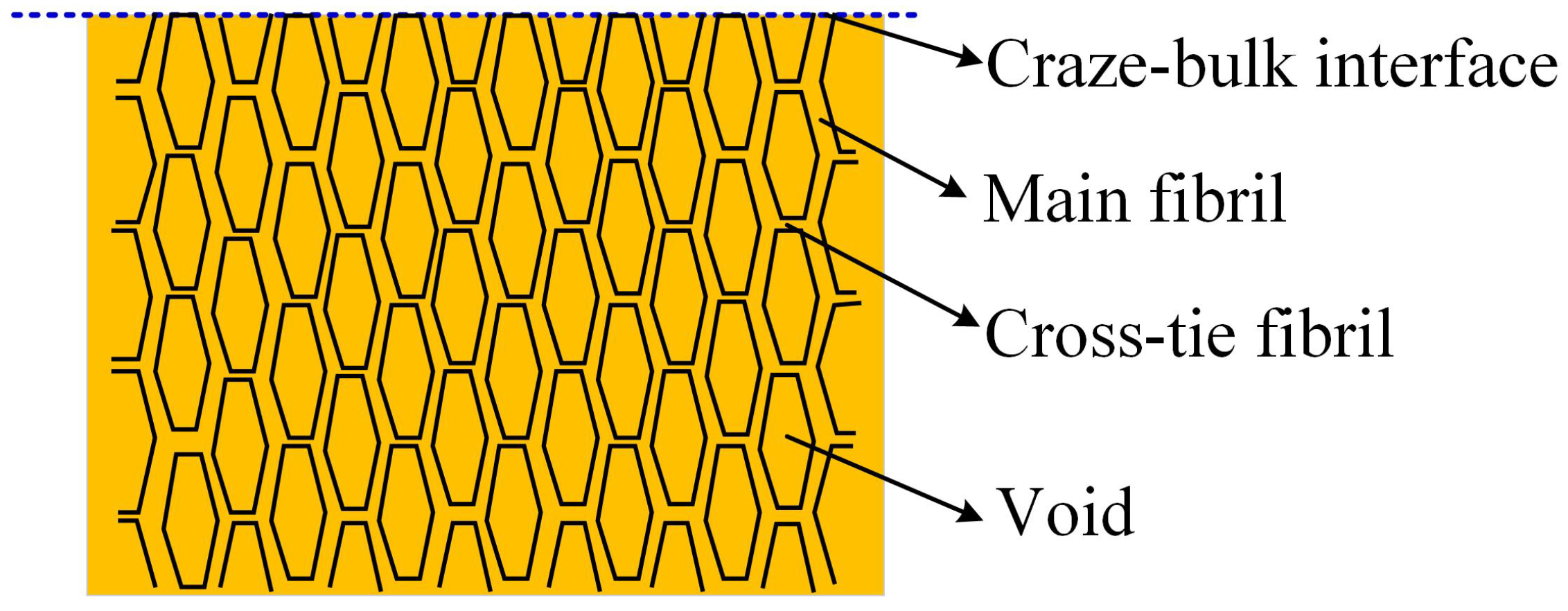
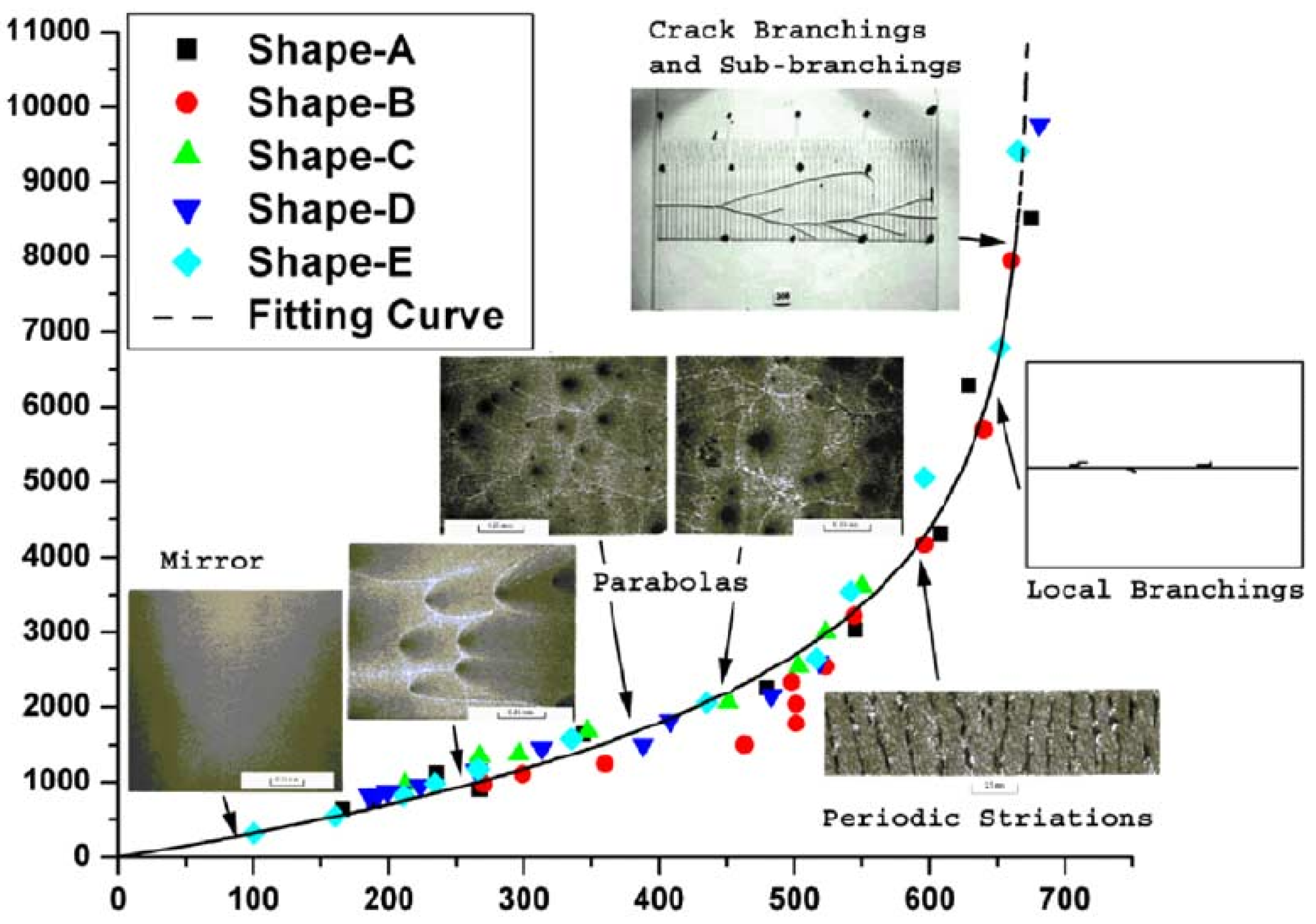
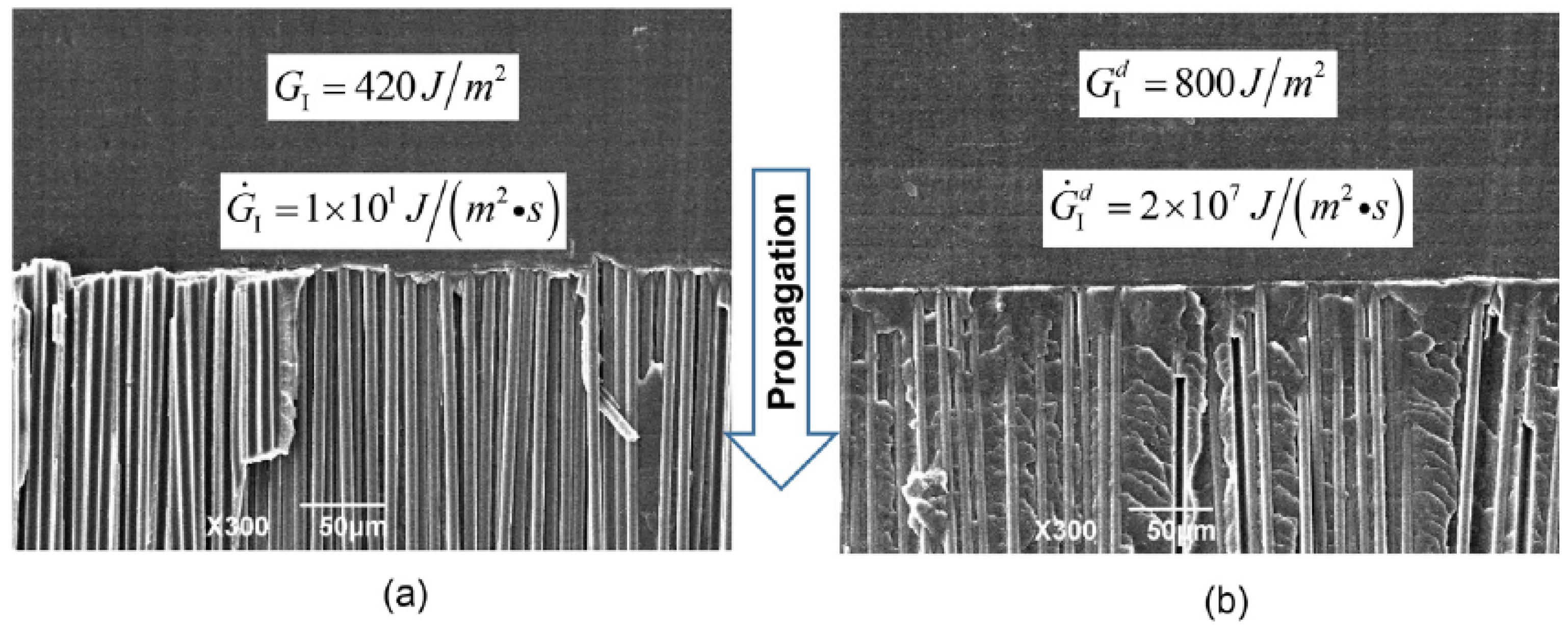
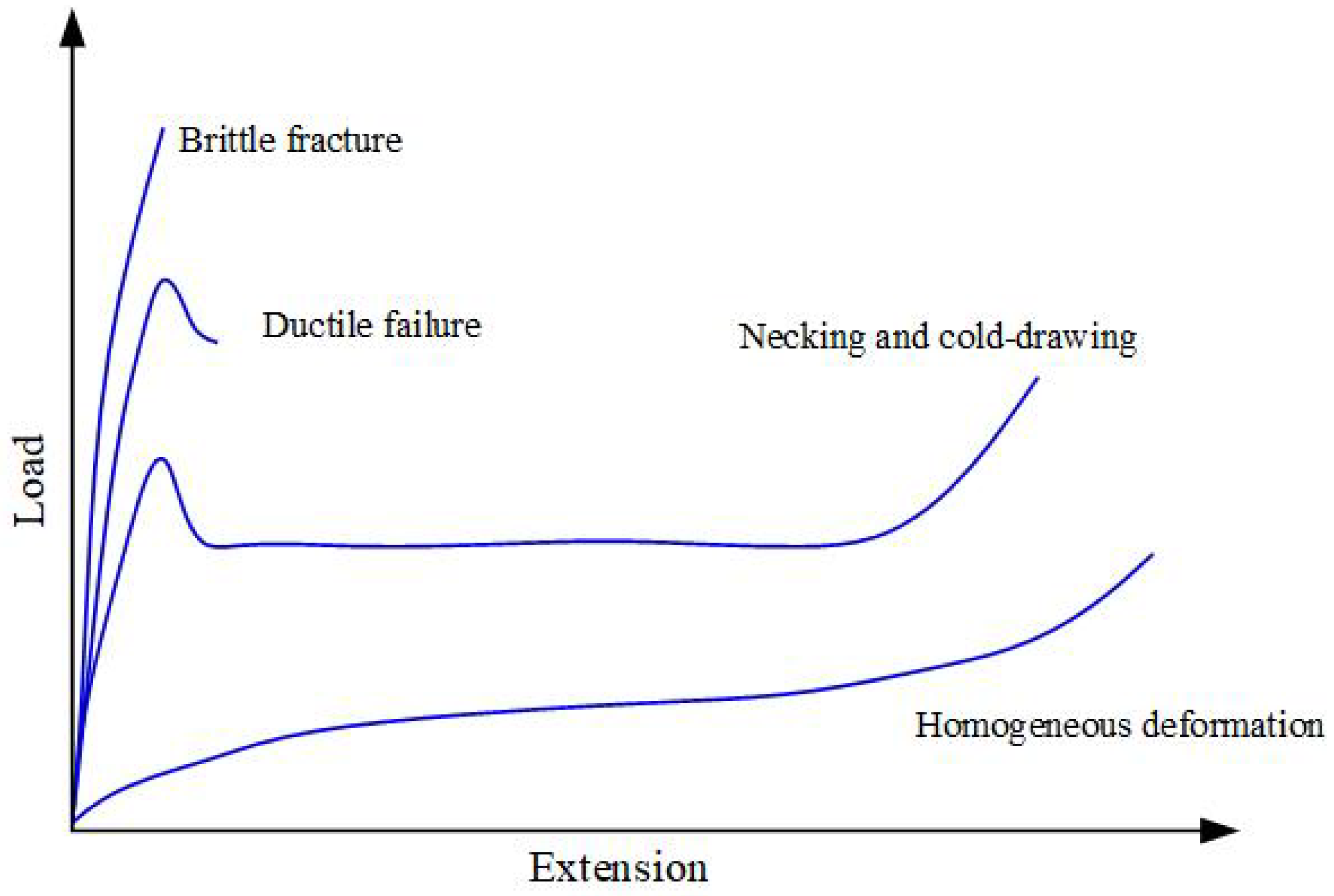
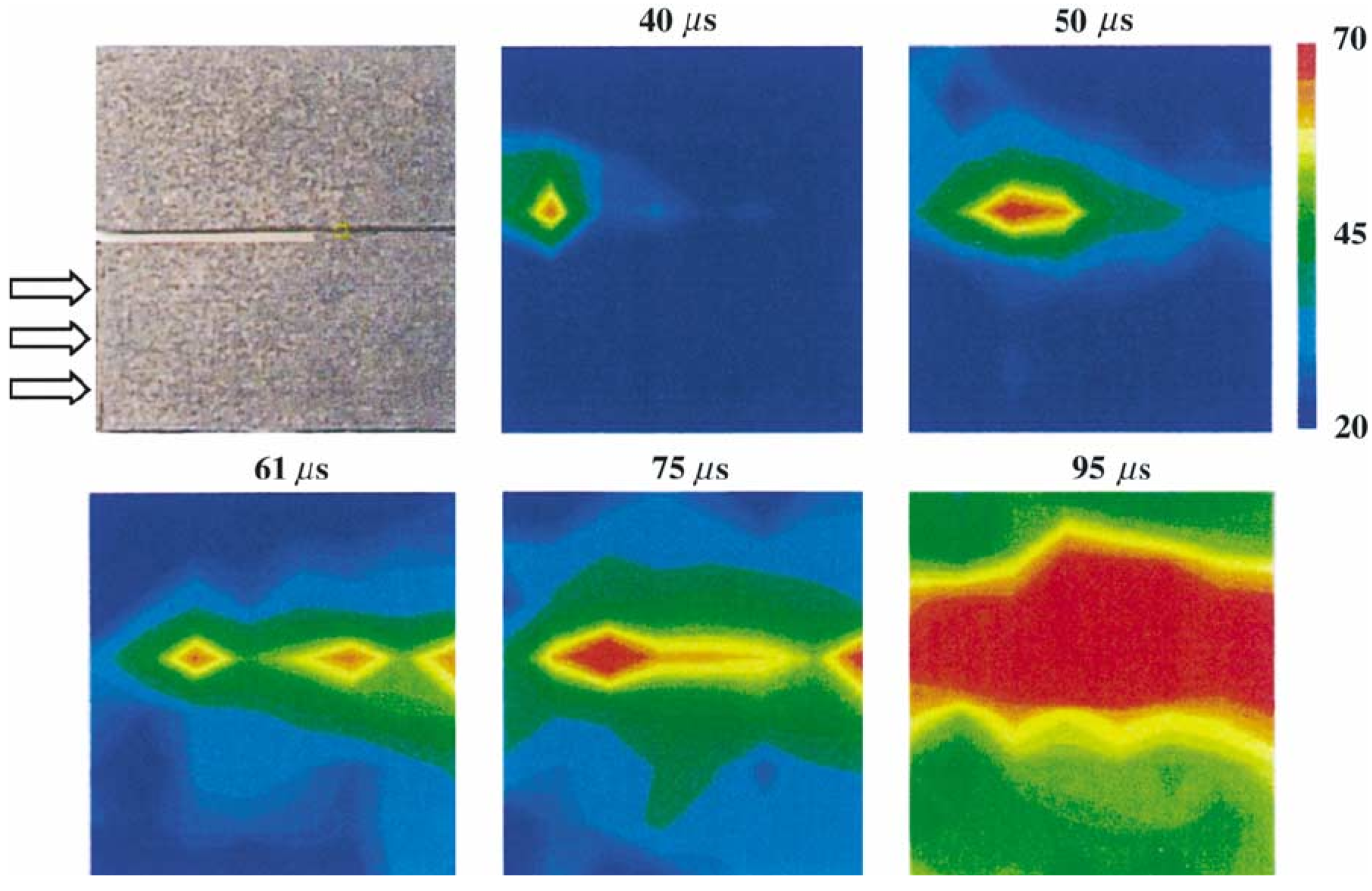
2.1. Rate-Dependent Fracture
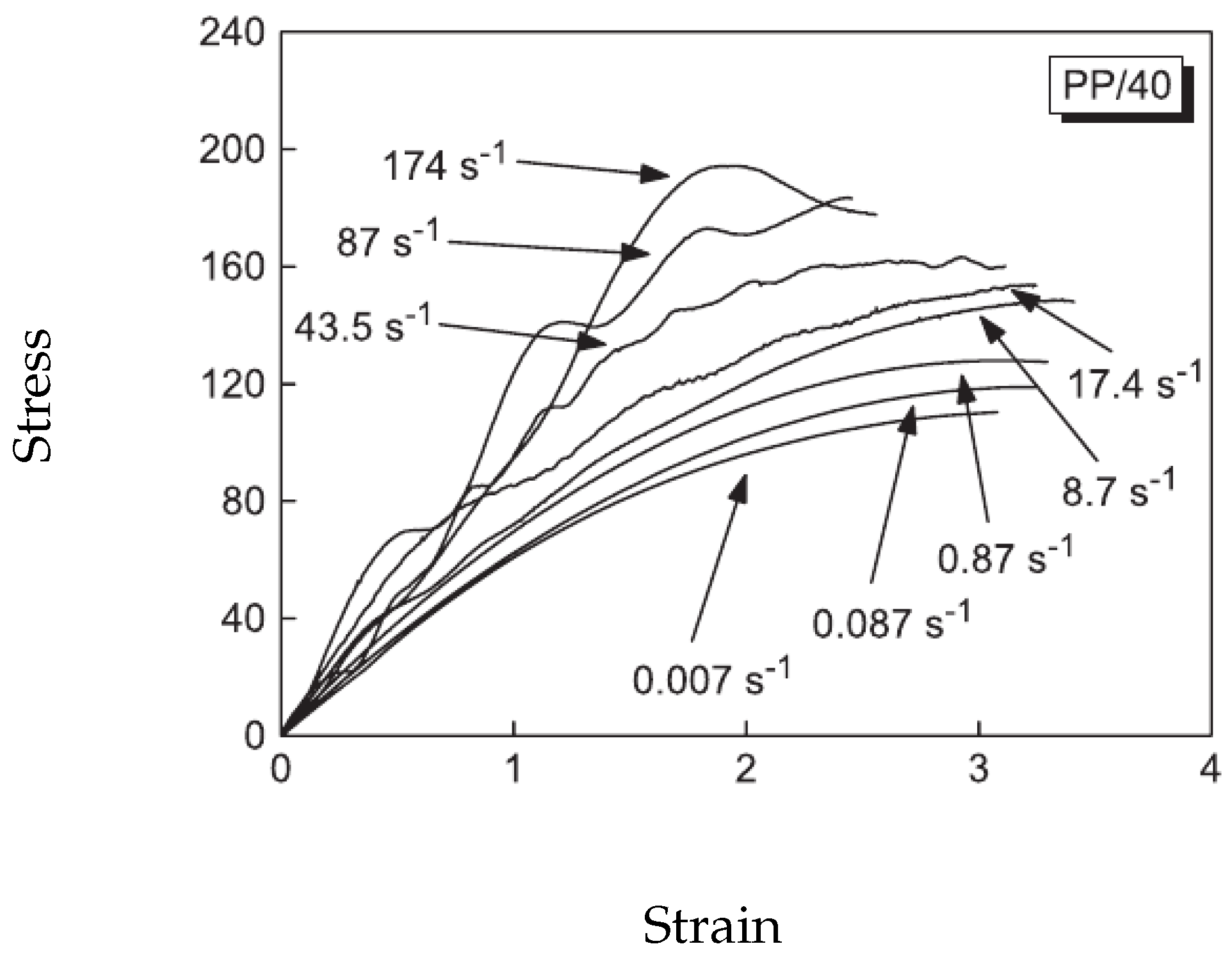
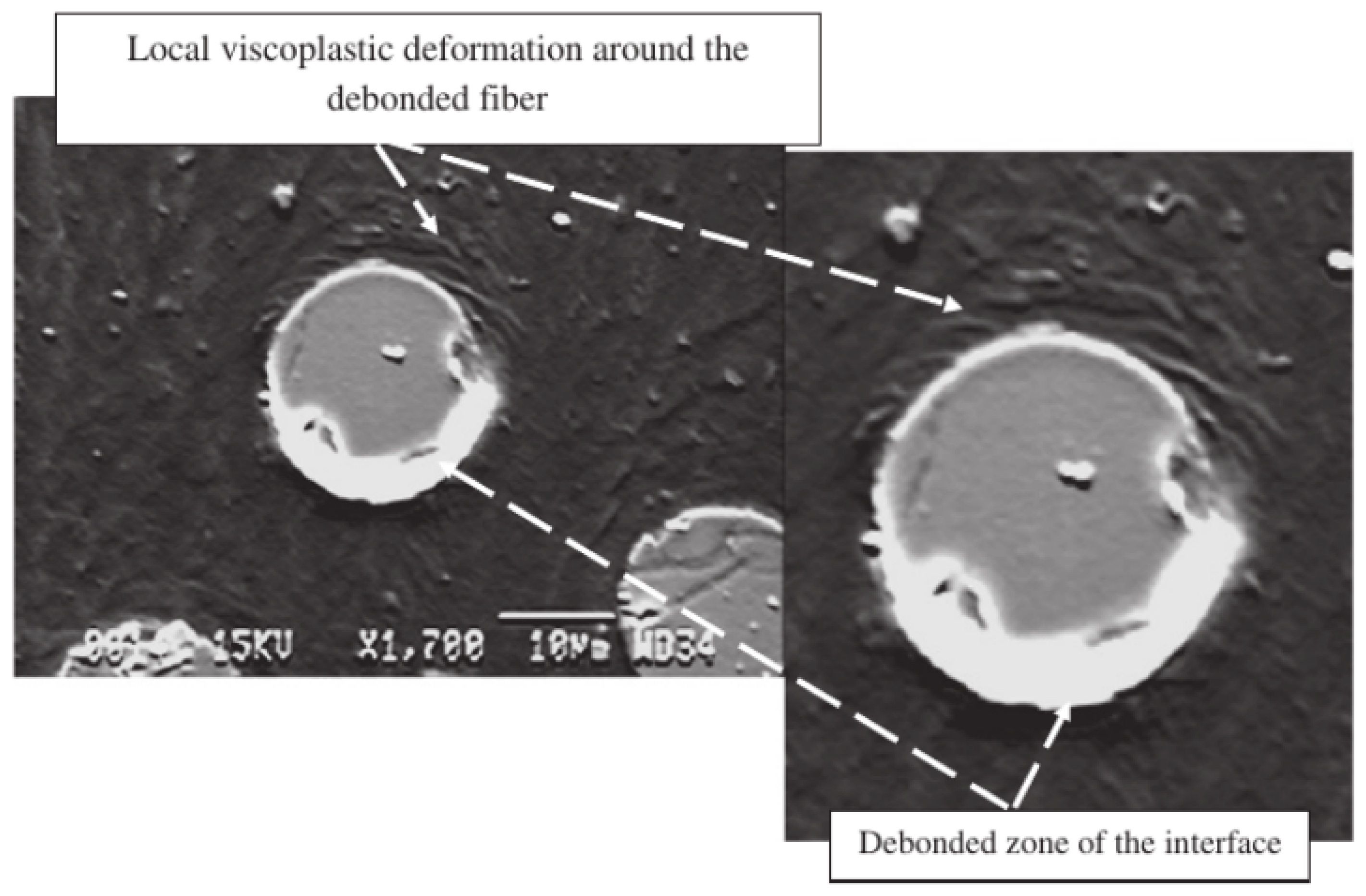
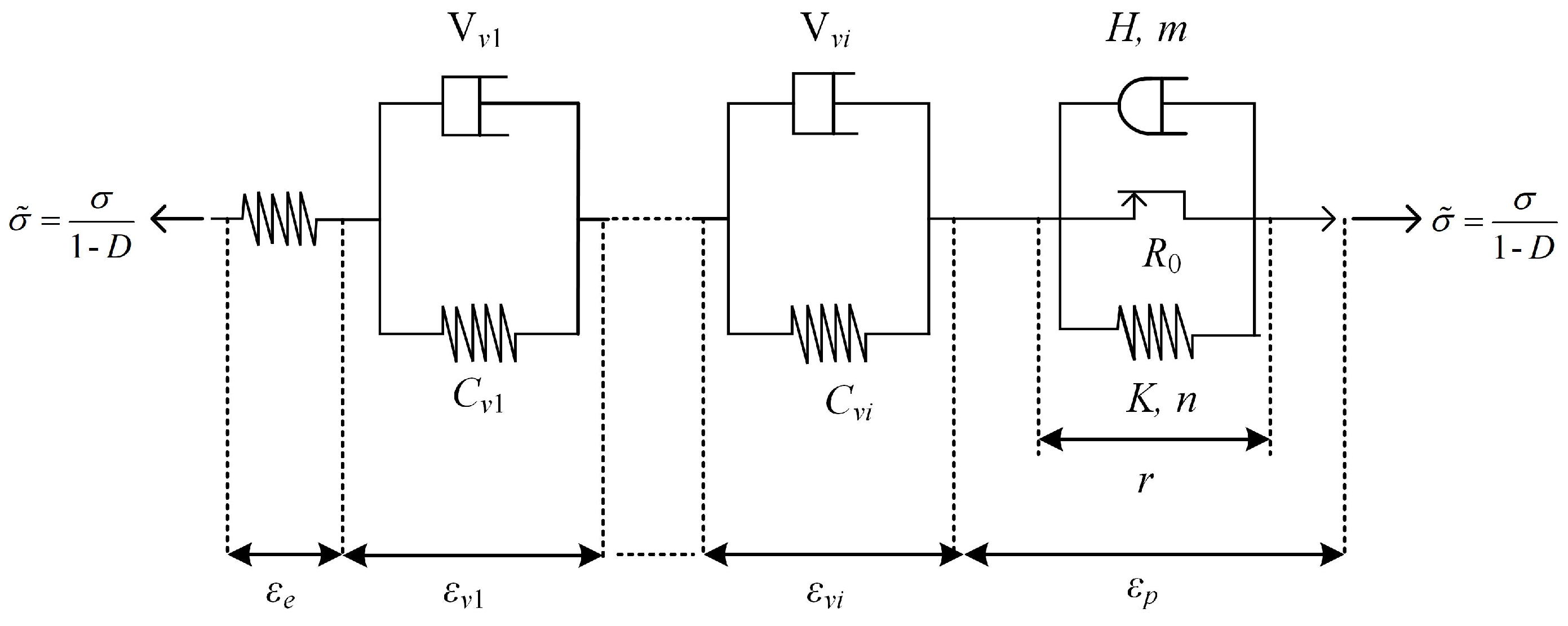
2.2. Viscous Composites
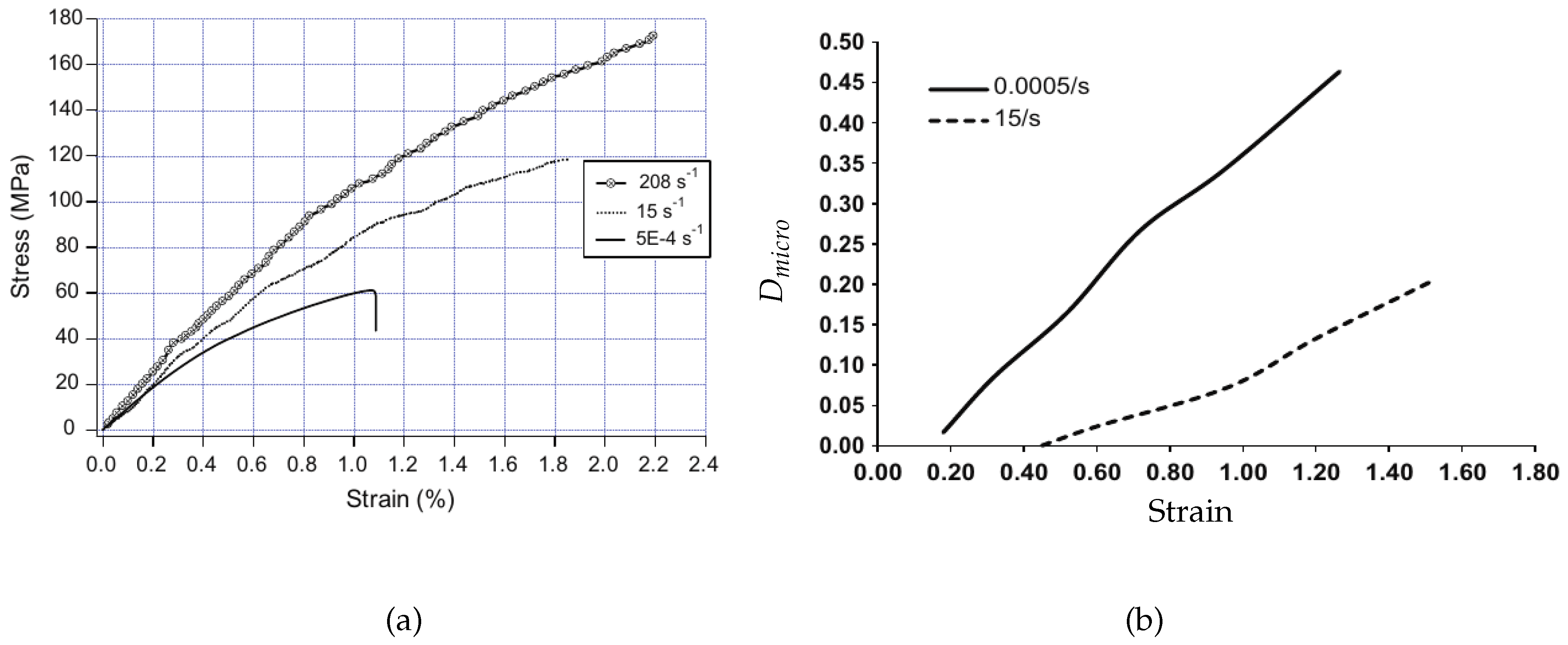
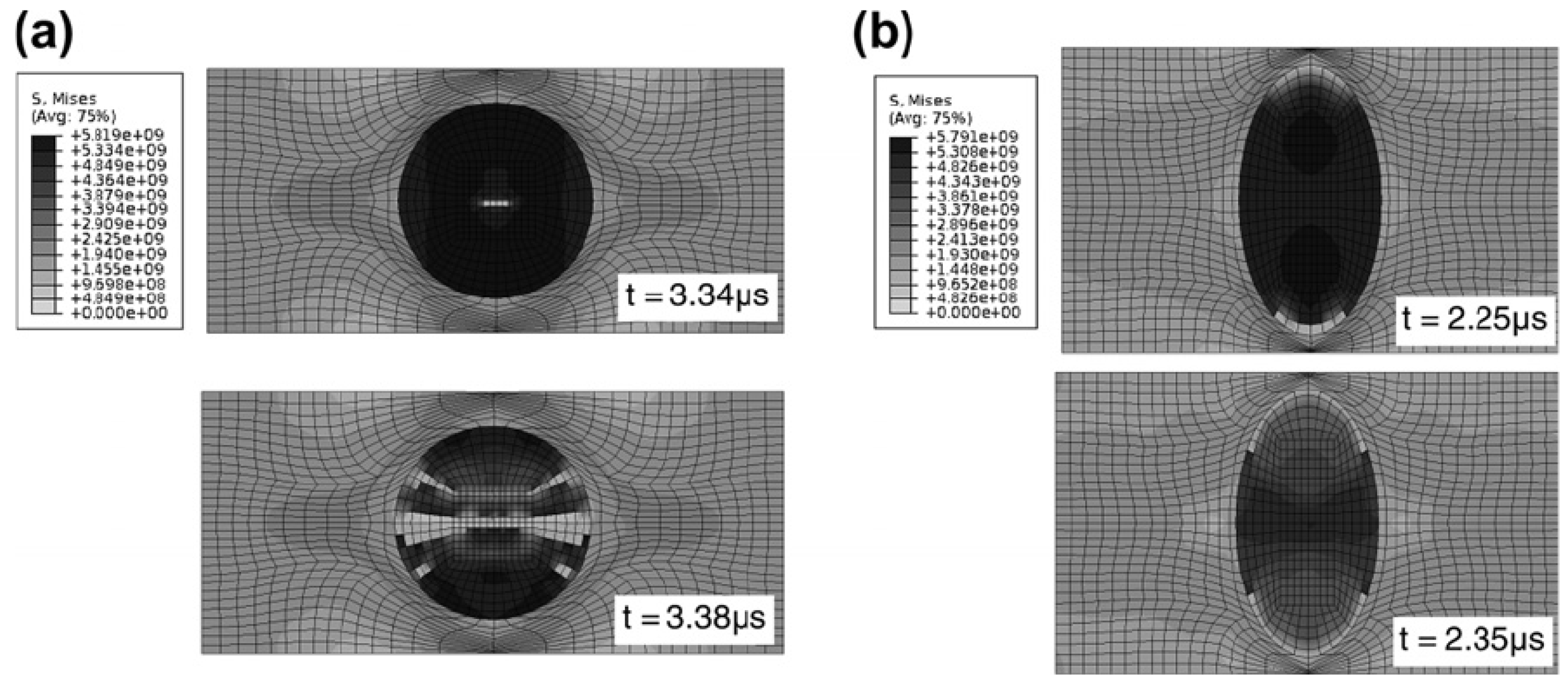
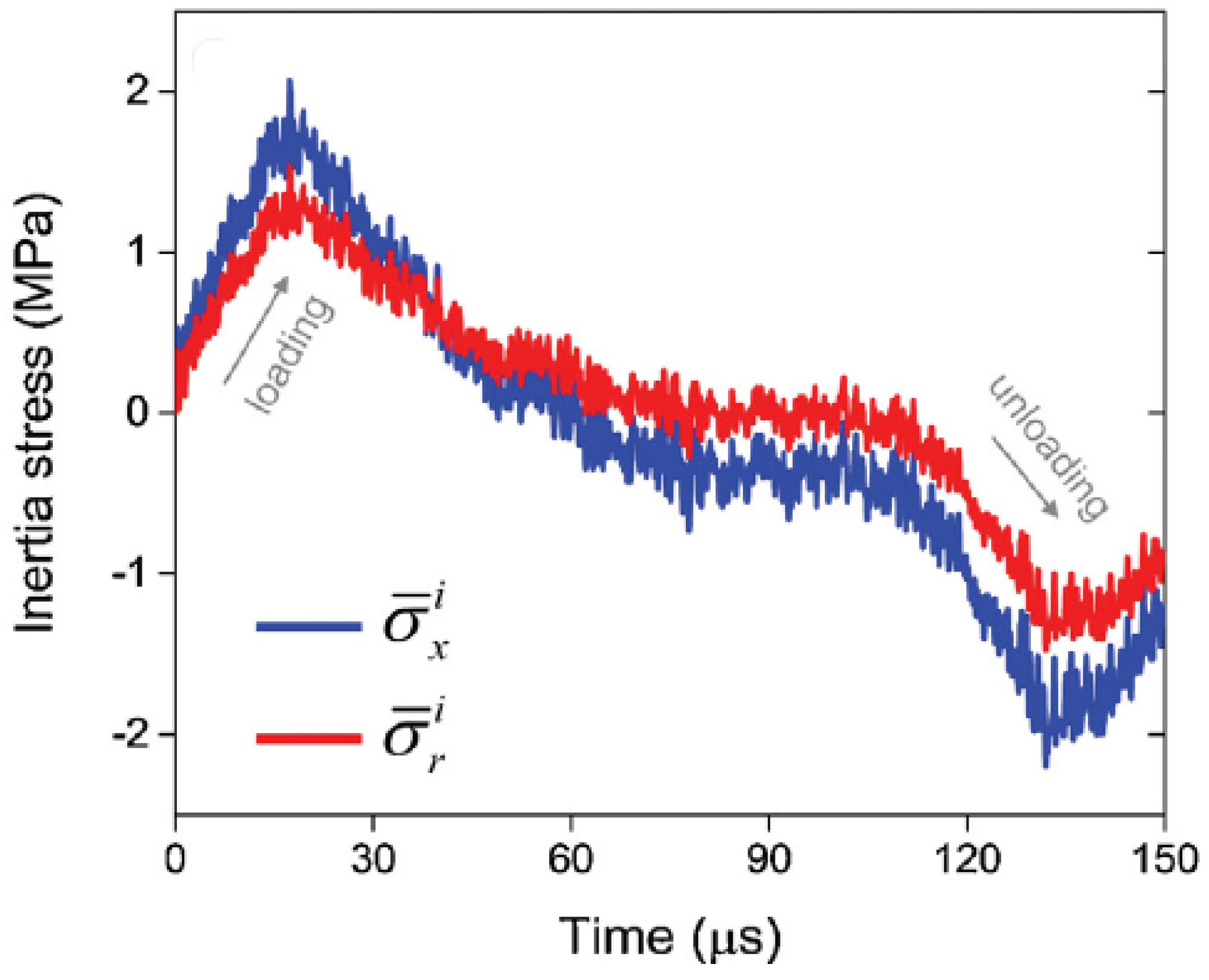
2.3. Inertia Effects
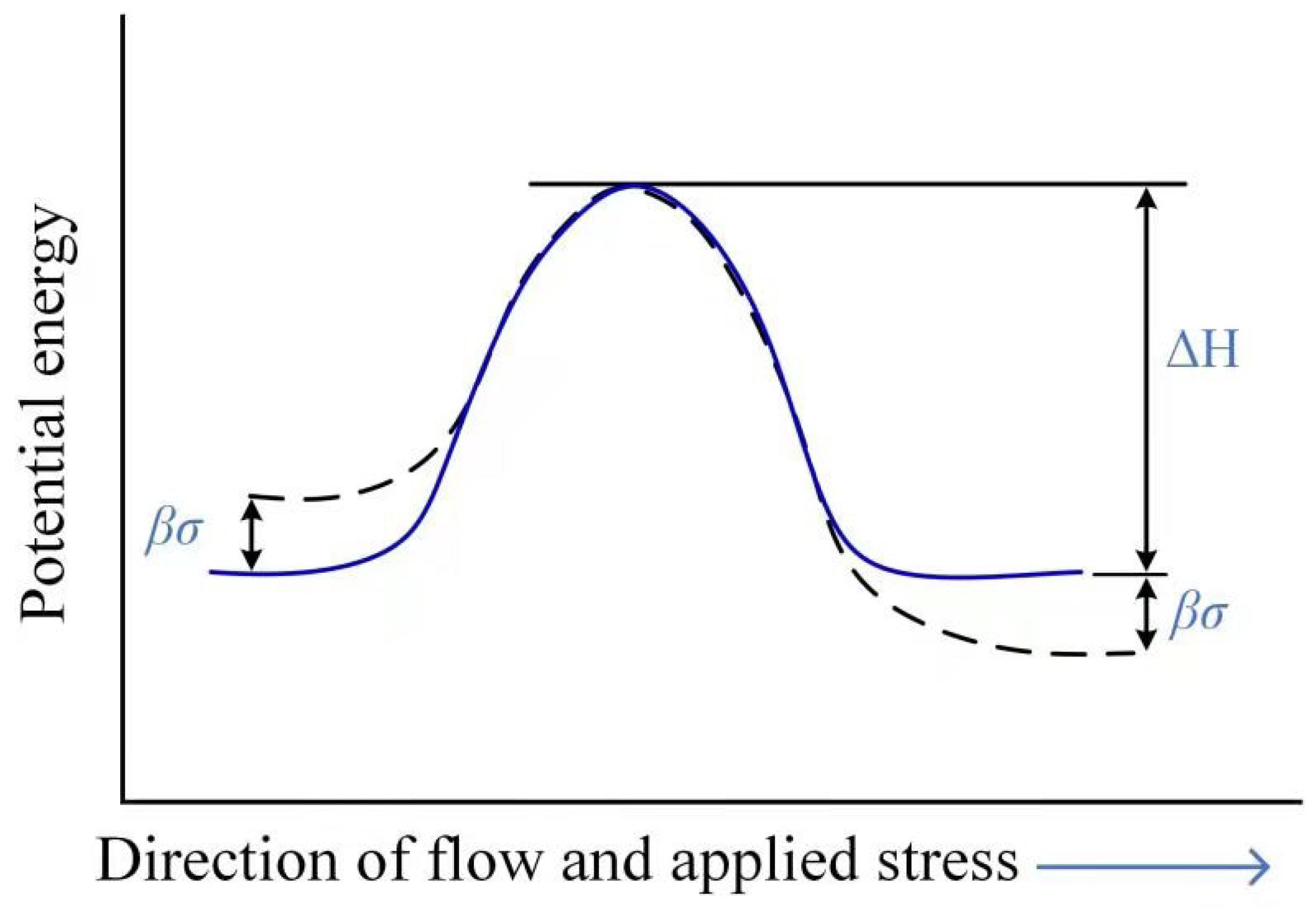
2.4. Thermomechanical Effects
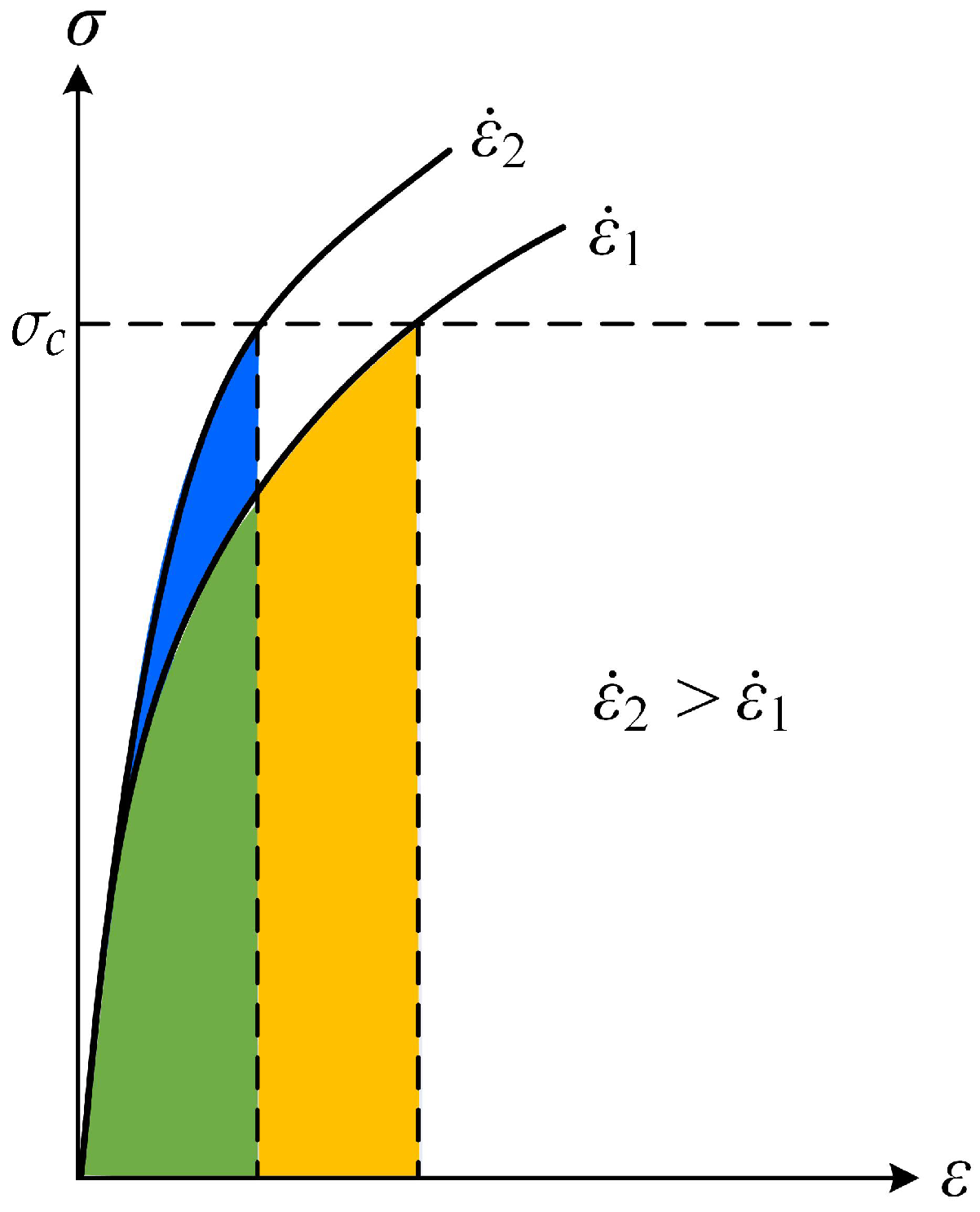
2.5. Characteristic Fracture Time
3. Numerical Models for Strain Rate Effects
3.1. Rate-Dependent Cohesive Law
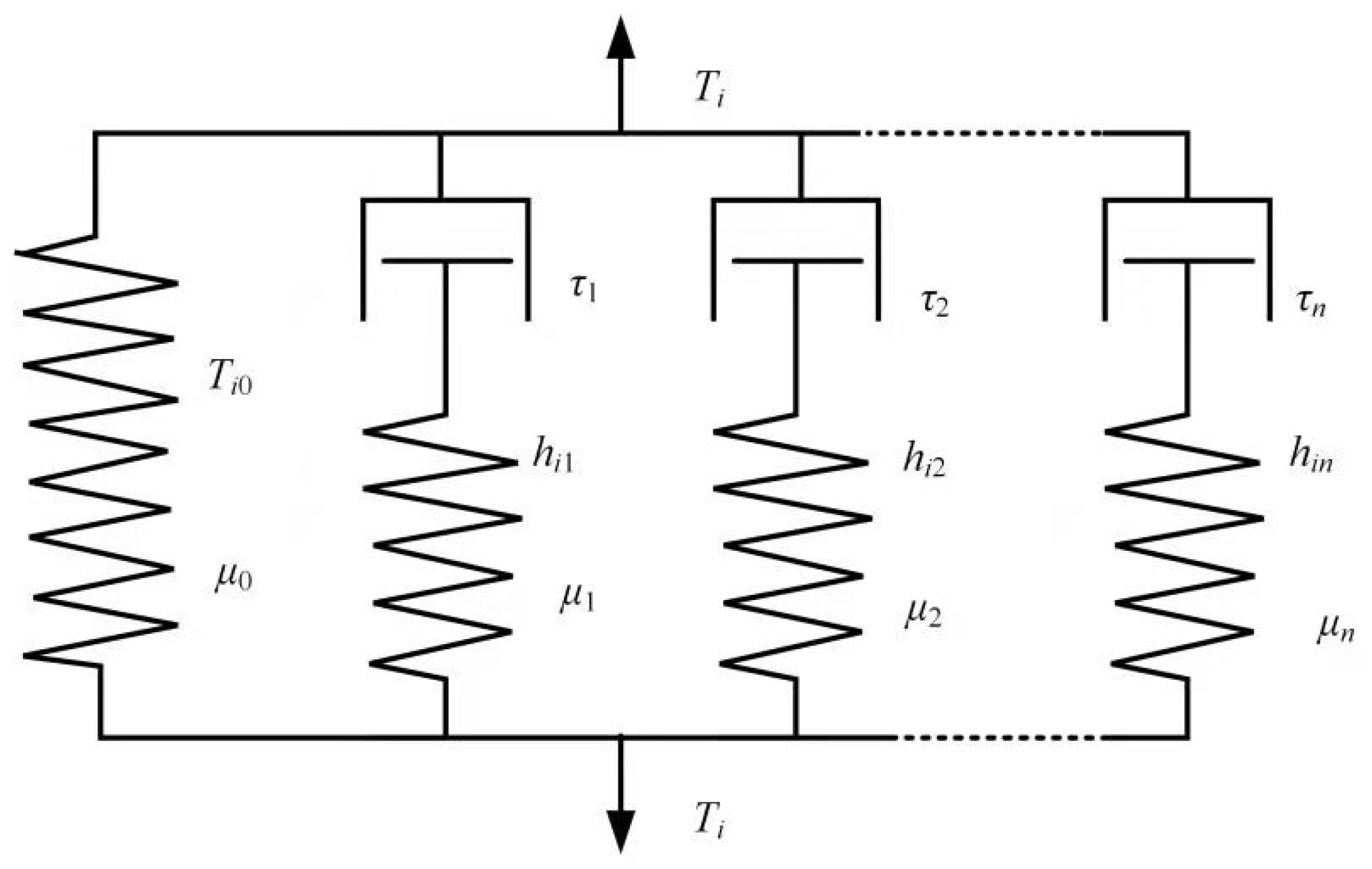
3.2. Modeling of Rate-Dependent Bulk
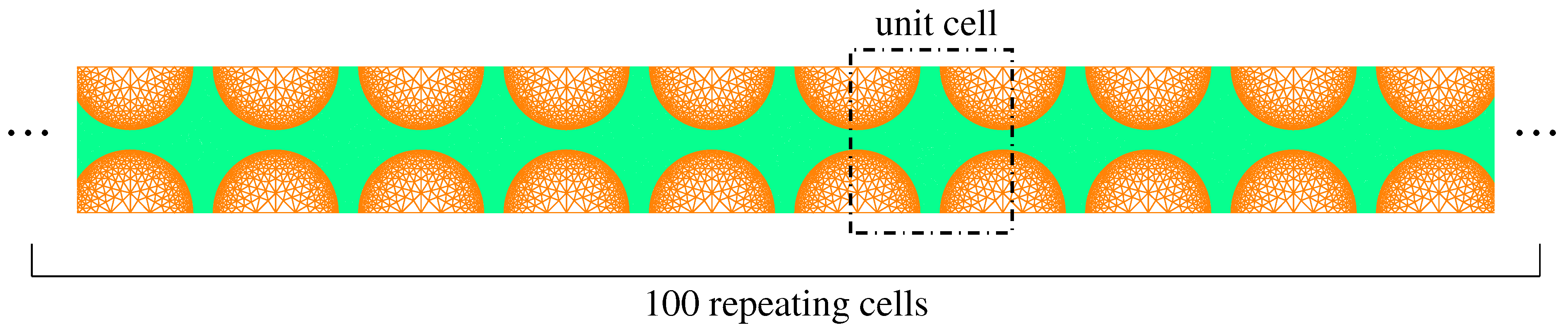
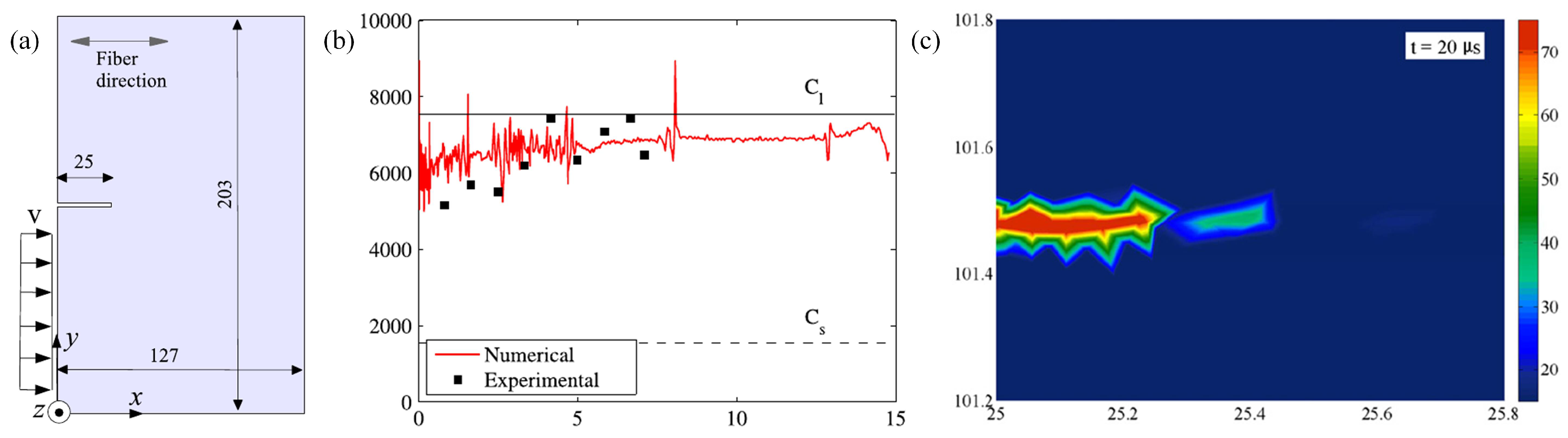
3.3. Mirco-Scale and Meso-Scale Inertia Effects
3.4. Thermo-Mechanical Model
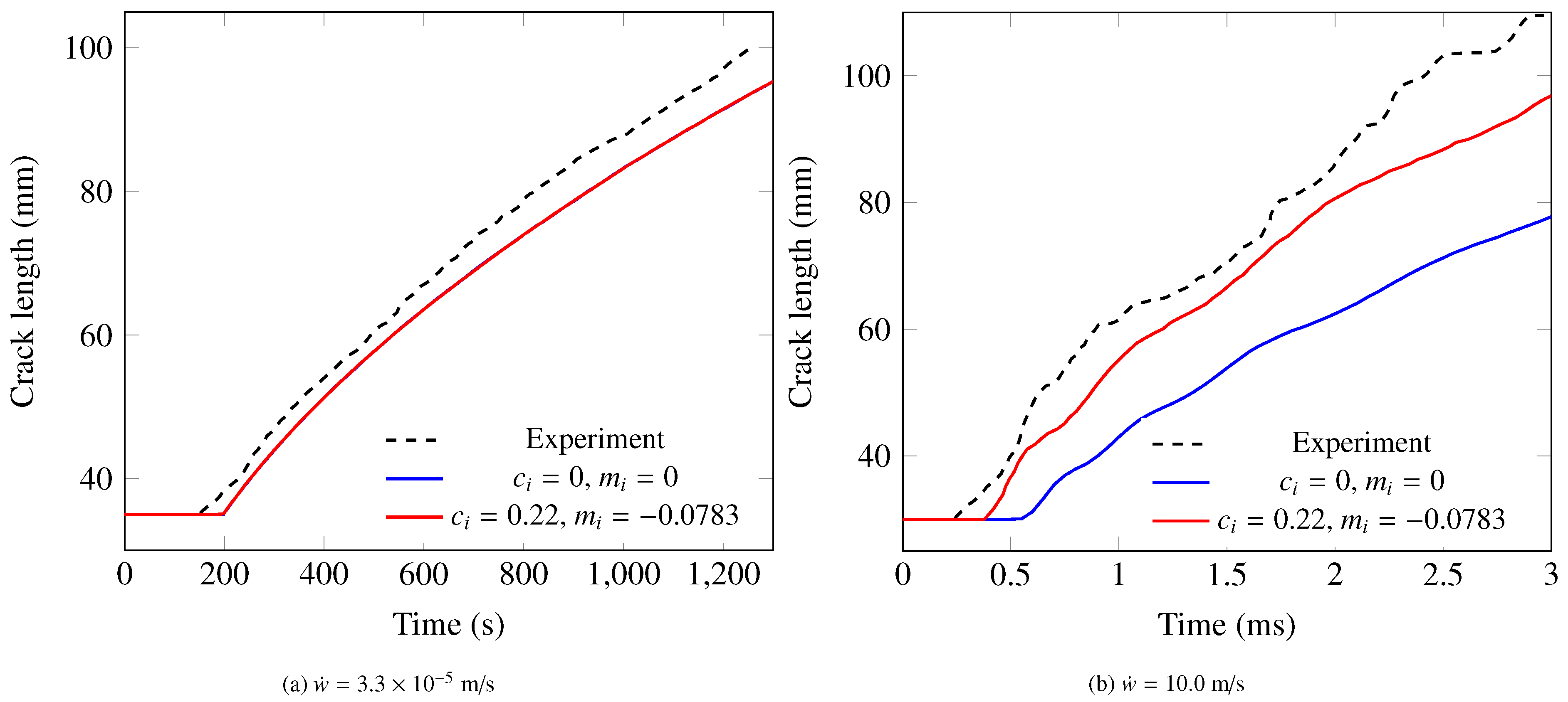
3.5. Characteristic Fracture Time
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mamidi, N.; Romo, I.L.; Barrera, E.V.; Elías-Zú niga, A. High throughput fabrication of curcumin embedded gelatin-polylactic acid forcespun fiber-aligned scaffolds for the controlled release of curcumin. MRS Commun. 2018, 8, 1395–1403. [Google Scholar] [CrossRef]
- Fan, J.; Wang, C. Dynamic compressive response of a developed polymer composite at different strain rates. Compos. Part Eng. 2018, 152, 96–101. [Google Scholar] [CrossRef]
- Wan, Y.; Sun, B.; Gu, B. Multi-scale structure modeling of damage behaviors of 3D orthogonal woven composite materials subject to quasi-static and high strain rate compressions. Mech. Mater. 2016, 94, 1–25. [Google Scholar] [CrossRef]
- Mamidi, N.; Gutiérrez, M.H.L.; Villela-Castrejón, J.; Isenhart, E.; Barrera, V.; Elías-Zú niga, A. Fabrication of gelatin-poly(epichlorohydrin-co-ethylene oxide) fiber scaffolds by Forcespinning® for tissue engineering and drug release. MRS Commun. 2017, 7, 913–921. [Google Scholar] [CrossRef]
- Zhu, L.; Chattopadhyay, A.; Goldberg, R.K. Failure Model for Rate-Dependent Polymer Matrix Composite Laminates under High-Velocity Impact. J. Aerosp. Eng. 2008, 21, 132–139. [Google Scholar] [CrossRef]
- Fan, J.; Weerheijm, J.; Sluys, L. Compressive response of a glass–polymer system at various strain rates. Mech. Mater. 2016, 95, 49–59. [Google Scholar] [CrossRef]
- Chen, D.; Luo, Q.; Meng, M.; Sun, G. Low velocity impact behavior of interlayer hybrid composite laminates with carbon/glass/basalt fibres. Compos. Part Eng. 2019, 176, 107191. [Google Scholar] [CrossRef]
- Sun, L.; Gibson, R.F.; Gordaninejad, F. Multiscale analysis of stiffness and fracture of nanoparticle-reinforced composites using micromechanics and global-local finite element models. Eng. Fract. Mech. 2011, 78, 2645–2662. [Google Scholar] [CrossRef]
- Mamidi, N.; Velasco Delgadillo, R.; Gonzáles Ortiz, A.; Barrera, E. Carbon Nano-Onions Reinforced Multilayered Thin Film System for Stimuli-Responsive Drug Release. Pharmaceutics 2020, 12, 1208. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, L.; Li, L.; Wei, J. Effects of strain rate and high temperature environment on the mechanical performance of carbon fiber reinforced thermoplastic composites fabricated by hot press molding. Compos. Part Appl. Sci. Manuf. 2020, 134, 105905. [Google Scholar] [CrossRef]
- Paknahad, A.; Goudarzi, M.; Kucko, N.W.; Leeuwenburgh, C.S.; Sluys, L.J. Calcium phosphate cement reinforced with poly (vinyl alcohol) fibers: An experimental and numerical failure analysis. Acta Biomater. 2021, 119, 458–471. [Google Scholar] [CrossRef] [PubMed]
- Mamidi, N.; Delgadillo, R.M.V.; González-Ortiz, A. Engineering of carbon nano-onion bioconjugates for biomedical applications. Mater. Sci. Eng. C 2021, 120, 111698. [Google Scholar] [CrossRef]
- Mamidi, N.; Zuníga, A.E.; Villela-Castrejón, J. Engineering and evaluation of forcespun functionalized carbon nano-onions reinforced poly (ϵ-caprolactone) composite nanofibers for pH-responsive drug release. Mater. Sci. Eng. C 2020, 112, 110928. [Google Scholar] [CrossRef]
- Okoli, O.I. The effects of strain rate and failure modes on the failure energy of fibre reinforced composites. Compos. Struct. 2001, 54, 299–303. [Google Scholar] [CrossRef]
- Schoßig, M.; Bierögel, C.; Grellmann, W.; Mecklenburg, T. Mechanical behavior of glass-fiber reinforced thermoplastic materials under high strain rates. Polym. Test. 2008, 27, 893–900. [Google Scholar] [CrossRef]
- Leite, L.F.M.; Leite, B.M.; Reis, V.L.; da Silveira, N.N.A.; Donadon, M.V. Donadon Strain rate effects on the intralaminar fracture toughness of composite laminates subjected to tensile load. Compos. Struct. 2018, 201, 455–467. [Google Scholar] [CrossRef]
- Field, J.; Walley, S.; Proud, W.; Goldrein, H.; Siviour, C. Review of experimental techniques for high rate deformation and shock studies. Int. J. Impact Eng. 2004, 30, 725–775. [Google Scholar] [CrossRef]
- Ramesh, K.T. High rates and impact experiments. In Springer Handbook of Experimental Solid Mechanics; Sharpe, W.N., Ed.; Springer: Boston, MA, USA, 2008; pp. 929–960. [Google Scholar]
- Gilat, A.; Goldberg, R.K.; Roberts, G.D. Experimental study of strain-rate-dependent behavior of carbon/epoxy composite. Compos. Technol. 2002, 62, 1469–1476. [Google Scholar] [CrossRef]
- Shirinbayan, M.; Fitoussi, J.; Meraghni, F.; Surowiec, B.; Bocquet, M.; Tcharkhtchi, A. High strain rate visco-damageable behavior of Advanced Sheet Molding Compound (A-SMC) under tension. Compos. Part B Eng. 2015, 82, 30–41. [Google Scholar] [CrossRef]
- Naik, N.; Yernamma, P.; Thoram, N.; Gadipatri, R.; Kavala, V. High strain rate tensile behavior of woven fabric e-glass/epoxy composite. Polym. Test. 2010, 29, 14–22. [Google Scholar] [CrossRef]
- Ochola, R.; Marcus, K.; Nurick, G.; Franz, T. Mechanical behaviour of glass and carbon fibre reinforced composites at varying strain rates. Compos. Struct. 2004, 63, 455–467. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Omidi, M.J. Compressive response of glass–fiber reinforced polymeric composites to increasing compressive strain rates. Compos. Struct. 2009, 89, 517–523. [Google Scholar] [CrossRef]
- Oguni, K.; Ravichandran, G. Dynamic compressive behavior of unidirectional E-glass/vinylester composites. J. Mater. Sci. 2001, 36, 831–838. [Google Scholar] [CrossRef]
- Hosur, M.; Alexander, J.; Vaidya, U.; Jeelani, S. High strain rate compression response of carbon/epoxy laminate composites. Compos. Struct. 2001, 52, 405–417. [Google Scholar] [CrossRef]
- Sun, B.; Niu, Z.; Zhu, L.; Gu, B. Mechanical behaviors of 2D and 3D basalt fiber woven composites under various strain rates. J. Compos. Mater. 2010, 44, 1779–1795. [Google Scholar]
- Chen, C.; Zhang, C.; Liu, C.; Miao, Y.; Wong, S.C.; Li, Y. Rate-dependent tensile failure behavior of short fiber reinforced PEEK. Compos. Part B Eng. 2018, 136, 187–196. [Google Scholar] [CrossRef]
- Schmack, T.; Filipe, T.; Deinzer, G.; Kassapoglou, C.; Walther, F. Experimental and numerical investigation of the strain rate-dependent compression behaviour of a carbon-epoxy structure. Compos. Struct. 2018, 189, 256–262. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Rodriguez-Millan, M.; Rusinek, A.; Arias, A. Investigation of mechanical impact behavior of short carbon-fiber-reinforced peek composites. Compos. Struct. 2015, 133, 1116–1126. [Google Scholar] [CrossRef]
- Ploeckl, M.; Kuhn, P.; Grosser, J.; Wolfahrt, M.; Koerber, H. A dynamic test methodology for analyzing the strain-rate effect on the longitudinal compressive behavior of fiber-reinforced composites. Compos. Struct. 2017, 180, 429–438. [Google Scholar] [CrossRef]
- Sierakowski, R.L. Strain Rate Effects in Composites. Appl. Mech. Rev. 1997, 50, 741–761. [Google Scholar] [CrossRef]
- Lifshitz, J.; Rotem, A. Time-dependent longitudinal strength of unidirectional fibrous composites. Fibre Sci. Technol. 1970, 3, 1–20. [Google Scholar] [CrossRef]
- Daniel, I.; Liber, T. Strain Rate Effects on Mechanical Properties of Fiber Composites. Part 3; Technical Report; Illinois Institute of Technology: Chicago, IL, USA, 1976. [Google Scholar]
- Harding, J.; Welsh, L.M. A tensile testing technique for fibre-reinforced composites at impact rates of strain. J. Mater. Sci. 1983, 18, 1810–1826. [Google Scholar] [CrossRef]
- Massaq, A.; Rusinek, A.; Klosak, M.; Bahi, S.; Arias, A. Strain rate effect on the mechanical behavior of polyamide composites under compression loading. Compos. Struct. 2019, 214, 114–122. [Google Scholar] [CrossRef]
- Smiley, A.; Pipes, R. Rate effects on mode i interlaminar fracture toughness in composite materials. J. Compos. Mater. 1987, 21, 670–687. [Google Scholar] [CrossRef]
- Kusaka, T.; Hojo, M.; Mai, Y.-W.; Kurokawa, T.; Nojima, T.; Ochiai, S. Rate dependence of mode i fracture behaviour in carbon-fibre/epoxy composite laminates. Compos. Sci. Technol. 1998, 58, 591–602. [Google Scholar] [CrossRef]
- Blackman, B.R.K.; Dear, J.P.; Kinloch, A.J.; Macgillivray, H.; Wang, Y.; Williams, J.G.; Yayla, P. The failure of fibre composites and adhesively bonded fibre composites under high rates of test. J. Mater. Sci. 1995, 30, 5885–5900. [Google Scholar] [CrossRef]
- Blackman, B.R.K.; Kinloch, A.J.; Wang, Y.; Williams, J.G. The failure of fibre composites and adhesively bonded fibre composites under high rates of test. J. Mater. Sci. 1996, 31, 4451–4466. [Google Scholar] [CrossRef]
- Zabala, H.; Aretxabaleta, L.; Castillo, G.; Aurrekoetxea, J. Loading rate dependency on mode I interlaminar fracture toughness of unidirectional and woven carbon fibre epoxy composites. Compos. Struct. 2015, 121, 75–82. [Google Scholar] [CrossRef]
- Liu, H.; Nie, H.; Zhang, C.; Li, Y. Loading rate dependency of Mode I interlaminar fracture toughness for unidirectional composite laminates. Compos. Sci. Technol. 2018, 167, 215–223. [Google Scholar] [CrossRef]
- Smiley, A.; Pipes, R. Rate sensitivity of mode ii interlaminar fracture toughness in graphite/epoxy and graphite/peek composite materials. Compos. Sci. Technol. 1987, 29, 1–15. [Google Scholar] [CrossRef]
- Guimard, J.-M.; Allix, O.; Pechnik, N.; Thévenet, P. Characterization and modeling of rate effects in the dynamic propagation of mode-ii delamination in composite laminates. Int. J. Fract. 2009, 160, 55–71. [Google Scholar] [CrossRef]
- Pennas, D.; Cantwell, W.J.; Compston, P. The influence of strain rate on the mode iii interlaminar fracture of composite materials. J. Compos. Mater. 2007, 41, 2595–2614. [Google Scholar] [CrossRef]
- Aliyu, A.; Daniel, I. Effects of strain rate on delamination fracture toughness of graphite/epoxy. In Delamination and Debonding of Materials; ASTM International: West Conshohocken, PA, USA, 1985. [Google Scholar]
- Cantwell, W.J.; Blyton, M. Influence of Loading Rate on the Interlaminar Fracture Properties of High Performance Composites—A Review. Appl. Mech. Rev. 1999, 52, 199–212. [Google Scholar] [CrossRef]
- May, M. Measuring the rate-dependent mode I fracture toughness of composites—A review. Compos. Part A Appl. Sci. Manuf. 2016, 81, 1–12. [Google Scholar] [CrossRef]
- Camacho, G.T.; Ortiz, M. Computational modelling of impact damage in brittle materials. Int. J. Solids Struct. 1996, 33, 2899–2938. [Google Scholar] [CrossRef]
- Corigliano, A.; Mariani, S.; Pandolfi, A. Numerical analysis of rate-dependent dynamic composite delamination. Compos. Sci. Technol. 2006, 66, 766–775. [Google Scholar] [CrossRef]
- Hauch, J.; Marder, M. Energy balance in dynamic fracture, investigated by a potential drop technique. Int. J. Fract. 1998, 90, 133–151. [Google Scholar] [CrossRef]
- Zhou, F.; Molinari, J.-F.; Shioya, T. A rate-dependent cohesive model for simulating dynamic crack propagation in brittle materials. Eng. Fract. Mech. 2005, 72, 1383–1410. [Google Scholar] [CrossRef]
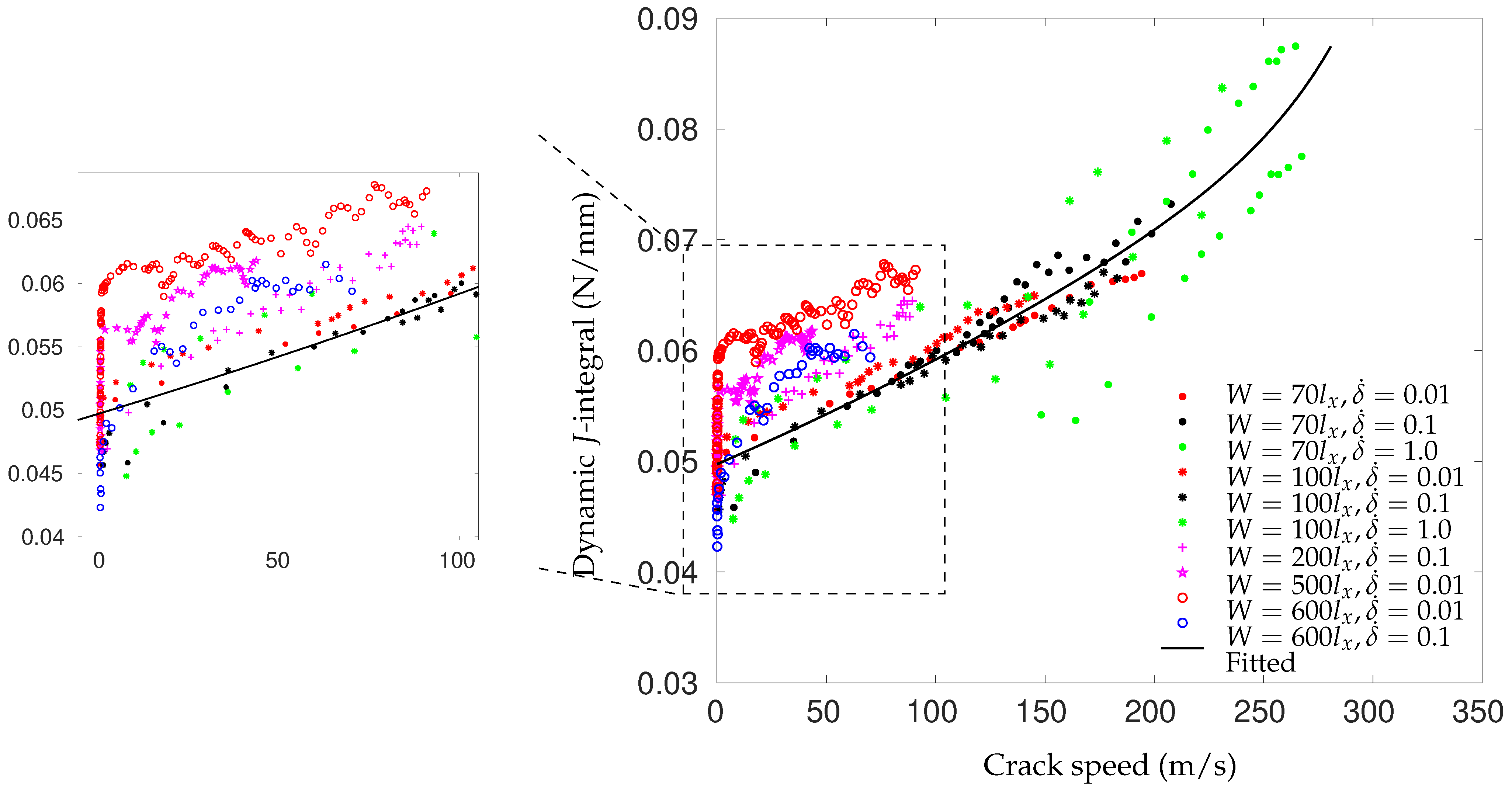
- Landis, C.M.; Pardoen, T.; Hutchinson, J.W. Crack velocity dependent toughness in rate dependent materials. Mech. Mater. 2000, 32, 663–678. [Google Scholar] [CrossRef]
- Fitoussi, J.; Bocquet, M.; Meraghni, F. Effect of the matrix behavior on the damage of ethylene–propylene glass fiber reinforced composite subjected to high strain rate tension. Compos. Part Eng. 2013, 45, 1181–1191. [Google Scholar] [CrossRef]
- Jendli, Z.; Meraghni, F.; Fitoussi, J.; Baptiste, D. Multi-scales modelling of dynamic behaviour for discontinuous fibre SMC composites. Compos. Sci. Technol. 2009, 69, 97–103. [Google Scholar] [CrossRef]
- Hoffmann, J.; Cui, H.; Petrinic, N. Determination of the strain-energy release rate of a composite laminate under high-rate tensile deformation in fibre direction. Compos. Sci. Technol. 2018, 164, 110–119. [Google Scholar] [CrossRef]
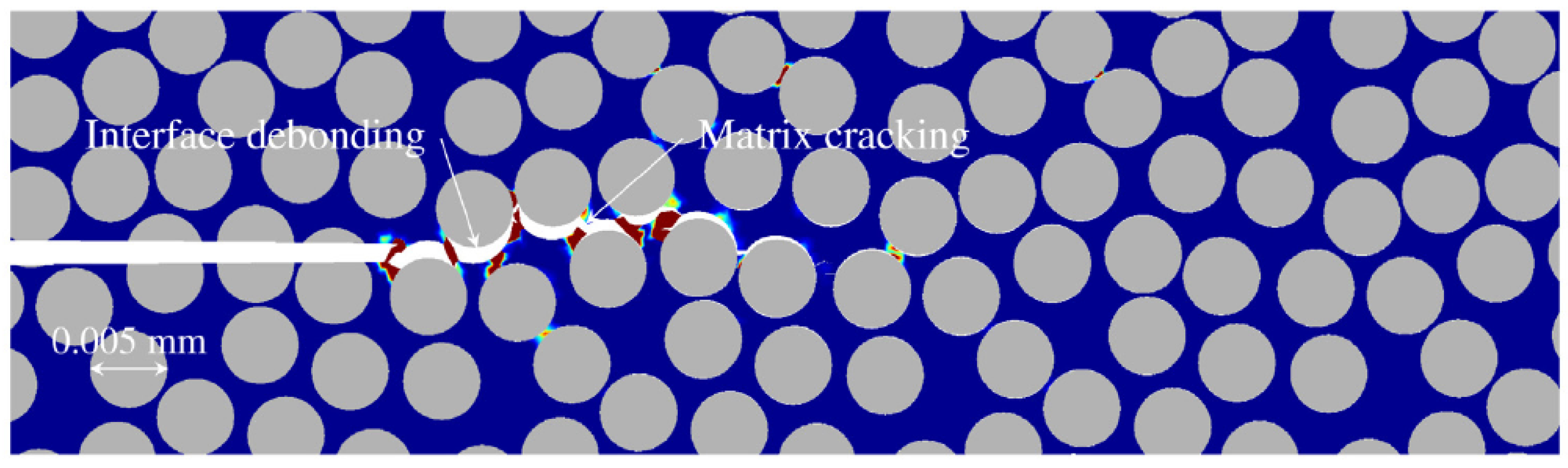
- Chen, Y.; Ghosh, S. Micromechanical analysis of strain rate-dependent deformation and failure in composite microstructures under dynamic loading conditions. Int. J. Plast. 2012, 32–33, 218–247. [Google Scholar] [CrossRef]
- Nishida, E.E. Distinguishing Inertia Effects from the Intrinsic Mechanical Behavior of Soft Materials at High Strain Rates by Kolsky Bar Experiments. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2010. [Google Scholar]
- Wang, Z.-P.; Sun, C.T. Modeling micro-inertia in heterogeneous materials under dynamic loading. Wave Motion 2002, 36, 473–485. [Google Scholar] [CrossRef]
- Hui, T.; Oskay, C. A high order homogenization model for transient dynamics of heterogeneous media including micro-inertia effects. Comput. Methods Appl. Mech. Eng. 2014, 273, 181–203. [Google Scholar] [CrossRef]
- Li, Z.; Lambros, J. Dynamic thermomechanical behavior of fiber reinforced composites. Compos. Part A Appl. Sci. Manuf. 2000, 31, 537–547. [Google Scholar] [CrossRef]
- Wang, J.; Wen, L.; Xiao, J.; Liang, T.; Hu, X.; Li, P. The mechanical properties and constitutive model of two woven composites including the influences of temperature, strain rate and damage growth. Compos. Part B Eng. 2019, 161, 502–513. [Google Scholar] [CrossRef]
- Kramer, E.J.; Berger, L.L. Fundamental processes of craze growth and fracture. In Crazing in Polymers; Springer: Berlin/Heidelberg, Germany, 1990; Volume 2, pp. 1–68. [Google Scholar]
- Knauss, W. Time dependent fracture of polymers. AFR 1989, 4, 2683–2711. [Google Scholar]
- Ward, I.M.; Hadley, D.W. An Introduction to the Mechanical Properties of Solid Polymers; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Argon, A.; Salama, M. The mechanism of fracture in glassy materials capable of some inelastic deformation. Mater. Sci. Eng. 1976, 23, 219–230. [Google Scholar] [CrossRef]
- Kramer, E.J. Craze fibril formation and breakdown. Polym. Eng. Sci. 1984, 24, 761–769. [Google Scholar] [CrossRef]
- Bucknall, C. New criterion for craze initiation. Polymer 2007, 48, 1030–1041. [Google Scholar] [CrossRef]
- Meyers, M.A. Dynamic Behavior of Materials; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Freund, L.B. Dynamic Fracture Mechanics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Liu, Y.; Meer, F.P.V.; Sluys, L.J. Cohesive zone and interfacial thick level set modeling of the dynamic double cantilever beam test of composite laminate. Theor. Appl. Fract. Mech. 2018, 96, 617–630. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, H.Y.; Mai, Y.W. Rate-dependent bridging law and its application to dynamic crack growth in brittle-matrix composite materials. Compos. Part A Appl. Sci. Manuf. 2003, 34, 1053–1063. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Shokrieh, M.M.; Camanho, P.P. Finite element modeling of mode I delamination growth in laminated DCB specimens with R-curve effects. Compos. Part Eng. 2013, 45, 897–903. [Google Scholar] [CrossRef]
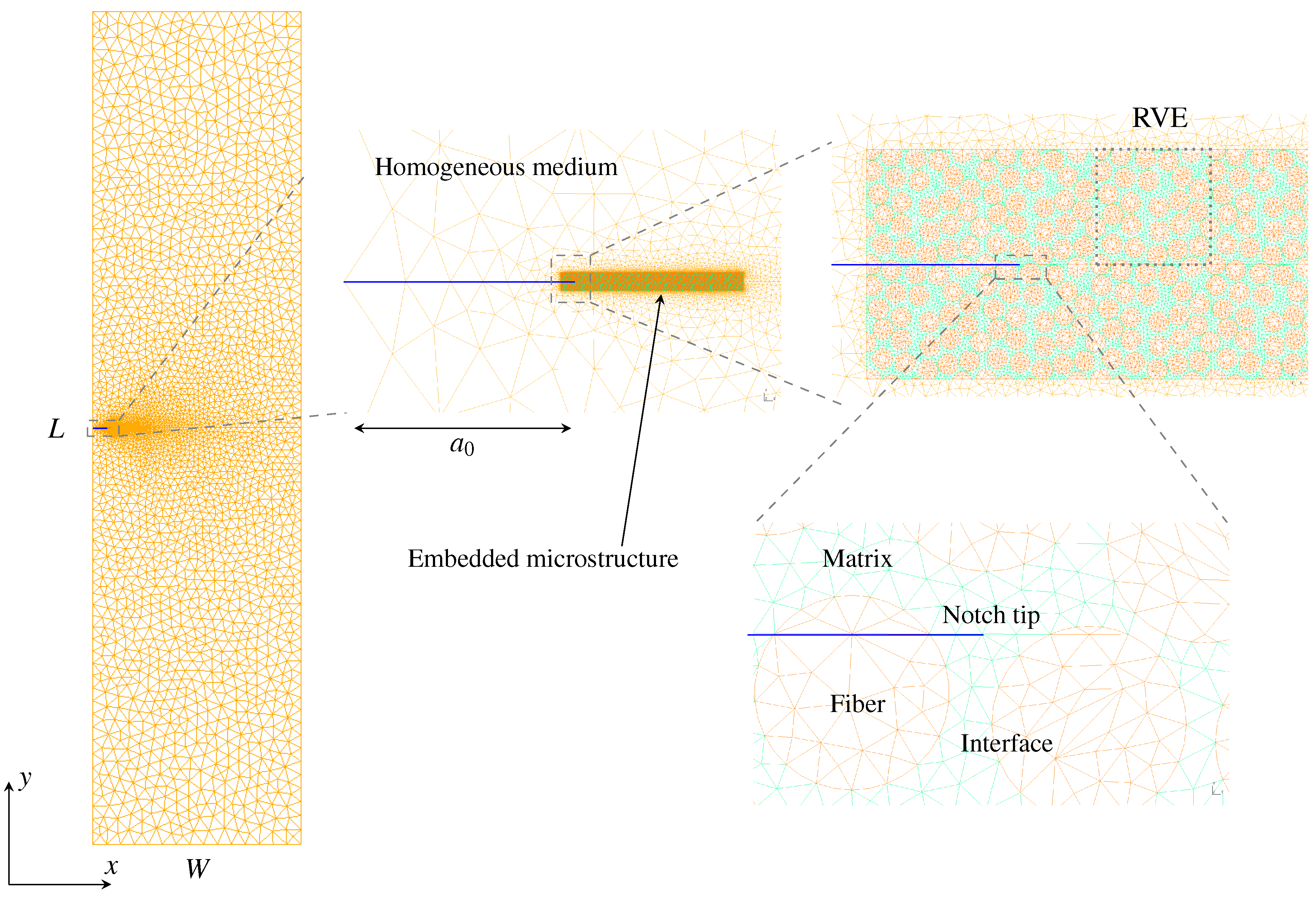
- Liu, Y.; Meer, F.P.V.; Sluys, L.J.; Ke, L. Modeling of dynamic mode I crack growth in glass fiber-reinforced polymer composites: Fracture energy and failure mechanism. Eng. Fract. Mech. 2021, 243, 107522. [Google Scholar] [CrossRef]
- Kinloch, A.J. Fracture Behaviour of Polymers; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Courtois, A.; Marcin, L.; Benavente, M.; Ruiz, E.; Lévesque, M. Numerical multiscale homogenization approach for linearly viscoelastic 3D interlock woven composites. Int. J. Solids Struct. 2019, 163, 61–74. [Google Scholar] [CrossRef]
- Van Der Sluis, O.; Schreurs, P.J.; Brekelmans, W.A.; Meijer, H.E. Overall behaviour of heterogeneous elastoviscoplastic materials: Effect of microstructural modelling. Mech. Mater. 2000, 32, 449–462. [Google Scholar] [CrossRef]
- Fish, J.; Filonova, V.; Kuznetsov, S. Micro-inertia effects in nonlinear heterogeneous media. Int. J. Numer. Methods Eng. 2012, 91, 1406–1426. [Google Scholar] [CrossRef]
- Liu, Y.; Meer, F.P.V.; Sluys, L.J. A dispersive homogenization model for composites and its RVE existence. Comput. Mech. 2020, 65, 79–98. [Google Scholar] [CrossRef]
- Koohbor, B.; Singh, N.K.; Kidane, A. Radial and axial inertia stresses in high strain rate deformation of polymer foams. Int. J. Mech. Sci. 2020, 181, 105679. [Google Scholar] [CrossRef]
- Mulliken, A.; Boyce, M. Mechanics of the rate-dependent elastic–plastic deformation of glassy polymers from low to high strain rates. Int. J. Solids Struct. 2006, 43, 1331–1356. [Google Scholar] [CrossRef]
- Yu, C.; Pandolfi, A.; Ortiz, M.; Coker, D.; Rosakis, A.J. Three-dimensional modeling of intersonic shear-crack growth in asymmetrically loaded unidirectional composite plates. Int. J. Solids Struct. 2002, 39, 6135–6157. [Google Scholar] [CrossRef]
- Bjerke, T.W.; Lambros, J. Theoretical development and experimental validation of a thermally dissipative cohesive zone model for dynamic fracture of amorphous polymers. J. Mech. Phys. Solids 2003, 51, 1147–1170. [Google Scholar] [CrossRef]
- Knauss, W.; Ravi-Chandar, K. Fundamental considerations in dynamic fracture. Eng. Fract. Mech. 1986, 23, 9–20. [Google Scholar] [CrossRef]
- Shockey, D.; Kalthoff, J.; Klemm, W.; Winkler, S. Simultaneous measurements of stress intensity and toughness for fast-running cracks in steel. Exp. Mech. 1983, 23, 140–145. [Google Scholar] [CrossRef]
- Shockey, D.; Erlich, D.; Kalthoff, J.; Homma, H. Short-pulse fracture mechanics. Eng. Fract. Mech. 1986, 23, 311–319. [Google Scholar] [CrossRef]
- Glennie, E. A strain-rate dependent crack model. J. Mech. Phys. Solids 1971, 19, 255–272. [Google Scholar] [CrossRef]
- Fager, L.O.; Bassani, J.L.; Hui, C.Y.; Xu, D.B. Aspects of cohesive zone models and crack growth in rate-dependent materials. Int. J. Fract. 1991, 52, 119–144. [Google Scholar]
- Langer, J.; Lobkovsky, A.E. Critical examination of cohesive-zone models in the theory of dynamic fracture. J. Mech. Phys. Solids 1998, 46, 1521–1556. [Google Scholar] [CrossRef]
- Kubair, D.V.; Geubelle, P.H.; Huang, Y.Y. Analysis of a rate-dependent cohesive model for dynamic crack propagation. Eng. Fract. Mech. 2002, 70, 685–704. [Google Scholar] [CrossRef]
- May, M. Numerical evaluation of cohesive zone models for modeling impact induced delamination in composite materials. Compos. Struct. 2015, 133, 16–21. [Google Scholar] [CrossRef]
- Morin, D.; Bourel, B.; Bennani, B.; Lauro, F.; Lesueur, D. A new cohesive element for structural bonding modelling under dynamic loading. Int. J. Impact Eng. 2013, 53, 94–105. [Google Scholar] [CrossRef]
- Corigliano, A.; Ricci, M. Rate-dependent interface models: Formulation and numerical applications. Int. J. Solids Struct. 2001, 38, 547–576. [Google Scholar] [CrossRef]
- Lu, Z.; Xu, Q. Cohesive zone modeling for viscoplastic behavior at finite deformations. Compos. Sci. Technol. 2013, 74, 173–178. [Google Scholar] [CrossRef]
- Moreo, P.; Garciaaznar, J.; Doblare, M. A coupled viscoplastic rate-dependent damage model for the simulation of fatigue failure of cement–bone interfaces. Int. J. Plast. 2007, 23, 2058–2084. [Google Scholar] [CrossRef]
- Giambanco, G.; Fileccia Scimemi, G. Mixed mode failure analysis of bonded joints with rate-dependent interface models. Int. J. Numer. Methods Eng. 2006, 67, 1160–1192. [Google Scholar] [CrossRef]
- Matzenmiller, A.; Gerlach, S.; Fiolka, M. A critical analysis of interface constitutive models for the simulation of delamination in composites and failure of adhesive bonds. J. Mech. Mater. Struct. 2010, 5, 185–211. [Google Scholar] [CrossRef][Green Version]
- Tvergaard, V.; Hutchinson, J.W. Toughness of an interface along a thin ductile layer joining elastic solids. Philos. Mag. 1994, 70, 641–656. [Google Scholar] [CrossRef]
- Johnson, G.R. A constitutive model and data for materials subjected to large strains, high strain rates, and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Allix, O.; Feissel, P.; Thévenet, P. A delay damage mesomodel of laminates under dynamic loading: Basic aspects and identification issues. Comput. Struct. 2003, 81, 1177–1191. [Google Scholar] [CrossRef]
- Musto, M.; Alfano, G. A novel rate-dependent cohesive-zone model combining damage and visco-elasticity. Comput. Struct. 2013, 118, 126–133. [Google Scholar] [CrossRef]
- Geißler, G.; Kaliske, M. Time-dependent cohesive zone modelling for discrete fracture simulation. Eng. Fract. Mech. 2010, 77, 153–169. [Google Scholar] [CrossRef]
- Xu, C.; Siegmund, T.; Ramani, K. Rate-dependent crack growth in adhesives: I. modeling approach. Int. J. Adhes. Adhes. 2003, 23, 9–13. [Google Scholar] [CrossRef]
- Xu, C.; Siegmund, T.; Ramani, K. Rate-dependent crack growth in adhesives II. experiments and analysis. Int. J. Adhes. Adhes. 2003, 23, 15–22. [Google Scholar] [CrossRef]
- Eyring, H. Viscosity, Plasticity, and Diffusion as Examples of Absolute Reaction Rates. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar] [CrossRef]
- Robertson, R.E. Theory for the plasticity of glassy polymers. J. Chem. Phys. 1966, 44, 3950–3956. [Google Scholar] [CrossRef]
- Argon, A.S. A theory for the low-temperature plastic deformation of glassy polymers. Philos. Mag. 1973, 28, 839–865. [Google Scholar] [CrossRef]
- Goldberg, R.K.; Roberts, G.D.; Gilat, A. Implementation of an Associative Flow Rule Including Hydrostatic Stress Effects into the High Strain Rate Deformation Analysis of Polymer Matrix Composites. J. Aerosp. Eng. 2005, 18, 18–27. [Google Scholar] [CrossRef]
- Praud, F.; Chatzigeorgiou, G.; Bikard, J.; Meraghni, F. Phenomenological multi-mechanisms constitutive modelling for thermoplastic polymers, implicit implementation and experimental validation. Mech. Mater. 2017, 114, 9–29. [Google Scholar] [CrossRef]
- Needleman, A. A Continuum Model for Void Nucleation by Inclusion Debonding. J. Appl. Mech. 1987, 54, 525–531. [Google Scholar] [CrossRef]
- Allen, D.H.; Jones, R.H.; Boyd, J.G. Micromechanical analysis of a continuous fiber metal matrix composite including the effects of matrix viscoplasticity and evolving damage. J. Mech. Phys. Solids 1994, 42, 505–529. [Google Scholar] [CrossRef]
- Matzenmiller, A.; Gerlach, S. Micromechanical modeling of viscoelastic composites with compliant fiber–matrix bonding. Comput. Mater. Sci. 2004, 29, 283–300. [Google Scholar] [CrossRef]
- Lissenden, C.J.; Herakovich, C.T. Numerical modelling of damage development and viscoplasticity in metal matrix composites. Comput. Methods Appl. Mech. Eng. 1995, 126, 289–303. [Google Scholar] [CrossRef]
- Miled, B.; Doghri, I.; Brassart, L.; Delannay, L. Micromechanical modeling of coupled viscoelastic-viscoplastic composites based on an incrementally affine formulation. Int. J. Solids Struct. 2013, 50, 1755–1769. [Google Scholar] [CrossRef]
- He, G.; Liu, Y.; Hammi, Y.; Bammann, D.J.; Horstemeyer, M.F. A combined viscoelasticity-viscoplasticity-anisotropic damage model with evolving internal state variables applied to fiber reinforced polymer composites. Mech. Adv. Mater. Struct. 2020, 6494, 1–22. [Google Scholar] [CrossRef]
- Yang, B.; Kim, B.; Lee, H. Predictions of viscoelastic strain rate dependent behavior of fiber-reinforced polymeric composites. Compos. Struct. 2012, 94, 1420–1429. [Google Scholar] [CrossRef]
- Liu, Y.; Van der Meer, F.P.; Sluys, L.J.; Fan, J.T. Used foA numerical homogenization scheme r derivation of a homogenized viscoelastic-viscoplastic model for the transverse response of fiber-reinforced polymer composites. Compos. Struct. 2020, 252, 112690. [Google Scholar] [CrossRef]
- Achenbach, J.D.; Sun, C.T.; Herrmann, G. On the vibrations of a laminated body. J. Appl. Mech. 1968, 35, 689–696. [Google Scholar] [CrossRef]
- Hegemier, G.; Gurtman, G.; Nayfeh, A.H. A continuum mixture theory of wave propagation in laminated and fiber reinforced composites. Int. J. Solids Struct. 1973, 9, 395–414. [Google Scholar] [CrossRef]
- Chen, W.; Fish, J. A Dispersive Model for Wave Propagation in Periodic Heterogeneous Media Based on Homogenization With Multiple Spatial and Temporal Scales. J. Appl. Mech. 2001, 68, 153–161. [Google Scholar] [CrossRef]
- Karamnejad, A.; Sluys, L.J. A dispersive multi-scale crack model for quasi-brittle heterogeneous materials under impact loading. Comput. Methods Appl. Mech. Eng. 2014, 278, 423–444. [Google Scholar] [CrossRef]
- Özdemir, I.; Brekelmans, W.A.M.; Geers, M.G.D. A Thermo-mechanical cohesive zone model. Comput. Mech. 2010, 46, 735–745. [Google Scholar] [CrossRef]
- Zreid, I.; Fleischhauer, R.; Kaliske, M. A thermomechanically coupled viscoelastic cohesive zone model at large deformation. Int. J. Solids Struct. 2013, 50, 4279–4291. [Google Scholar] [CrossRef]
- Ahmed, A.; Sluys, L.J. A phantom node formulation for modeling coupled adiabatic–isothermal cracking in FRP composites. Comput. Methods Appl. Mech. Eng. 2014, 278, 291–313. [Google Scholar] [CrossRef]
- Coker, D.; Rosakis, A.J. Experimental observations of intersonic crack growth in asymmetrically loaded unidirectional composite plates. Philos. Mag. A 2001, 81, 571–595. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Liu, F.; Liu, D.; Liu, Y. Review of Strain Rate Effects of Fiber-Reinforced Polymer Composites. Polymers 2021, 13, 2839. https://doi.org/10.3390/polym13172839
Ma L, Liu F, Liu D, Liu Y. Review of Strain Rate Effects of Fiber-Reinforced Polymer Composites. Polymers. 2021; 13(17):2839. https://doi.org/10.3390/polym13172839
Chicago/Turabian StyleMa, Lulu, Feng Liu, Dongyu Liu, and Yaolu Liu. 2021. "Review of Strain Rate Effects of Fiber-Reinforced Polymer Composites" Polymers 13, no. 17: 2839. https://doi.org/10.3390/polym13172839
APA StyleMa, L., Liu, F., Liu, D., & Liu, Y. (2021). Review of Strain Rate Effects of Fiber-Reinforced Polymer Composites. Polymers, 13(17), 2839. https://doi.org/10.3390/polym13172839





