Multiscale Simulation of Semi-Crystalline Polymers to Predict Mechanical Properties
Abstract
:1. Introduction
2. Nanoscale Structure Simulation
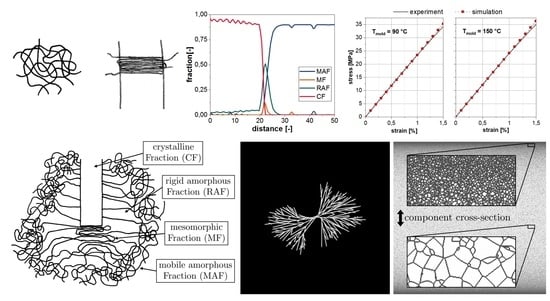
2.1. Four-Phase Model of Polymer Crystallization
2.2. Simulation
3. Microscale Structure Simulation
4. Predicting the Material Behavior under Consideration of the Micro- and Nanoscale
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AF | Amorphous Fraction |
| CF | Crystalline Fraction |
| DSC | Differential Scanning Calorimetry |
| FE | Finite Element |
| FEM | Finite Element Method |
| FSC | Fast Scanning Calorimetry |
| MAF | Mobile Amorphous Fraction |
| MF | Mesomorphic Fraction |
| PBT | Polybutylene Therephthalate |
| RAF | Rigid Amorphous Fraction |
| RVE | Representative Volume Element |
References
- Keller, A.; O’Connor, A. Large periods in polyethylene: The origin of low-angle X-ray scattering. Nature 1957, 180, 1289–1290. [Google Scholar] [CrossRef]
- Charbon, C.; Swaminarayan, S. A multiscale model for polymer crystallization. II: Solidification of a macroscopic part. Polym. Eng. Sci. 1998, 38, 644–656. [Google Scholar] [CrossRef]
- Raabe, D. Mesoscale simulation of spherulite growth during polymer crystallization by use of a cellular automaton. Acta Mater. 2004, 52, 2653–2664. [Google Scholar] [CrossRef]
- Raabe, D.; Godara, A. Mesoscale simulation of the kinetics and topology of spherulite growth during crystallization of isotactic polypropylene (iPP) by using a cellular automaton. Model. Simul. Mater. Sci. Eng. 2005, 13, 733. [Google Scholar] [CrossRef]
- Michaeli, W.; Hopmann, C.; Bobzin, K.; Arping, T.; Baranowski, T.; Heesel, B.; Laschet, G.; Schläfer, T.; Oete, M. Development of an integrative simulation method to predict the microstructural influence on the mechanical behaviour of semi-crystalline thermoplastic parts. Int. J. Mater. Res. 2012, 103, 120–130. [Google Scholar] [CrossRef]
- Spekowius, M.; Spina, R.; Hopmann, C. Mesoscale simulation of the solidification process in injection moulded parts. J. Polym. Eng. 2016, 36, 563–573. [Google Scholar] [CrossRef]
- Van Dommelen, J.V.; Parks, D.; Boyce, M.; Brekelmans, W.; Baaijens, F. Micromechanical modeling of the elasto-viscoplastic behavior of semi-crystalline polymers. J. Mech. Phys. Solids 2003, 51, 519–541. [Google Scholar] [CrossRef]
- Uchida, M.; Tokuda, T.; Tada, N. Finite element simulation of deformation behavior of semi-crystalline polymers with multi-spherulitic mesostructure. Int. J. Mech. Sci. 2010, 52, 158–167. [Google Scholar] [CrossRef]
- Uchida, M.; Tada, N. Micro-, meso-to macroscopic modeling of deformation behavior of semi-crystalline polymer. Int. J. Plast. 2013, 49, 164–184. [Google Scholar]
- Bédoui, F.; Diani, J.; Régnier, G.; Seiler, W. Micromechanical modeling of isotropic elastic behavior of semicrystalline polymers. Acta Mater. 2006, 54, 1513–1523. [Google Scholar] [CrossRef]
- Glüge, R.; Altenbach, H.; Kolesov, I.; Mahmood, N.; Beiner, M.; Androsch, R. On the effective elastic properties of isotactic polypropylene. Polymer 2019, 160, 291–302. [Google Scholar] [CrossRef]
- Laschet, G.; Spekowius, M.; Spina, R.; Hopmann, C. Multiscale simulation to predict microstructure dependent effective elastic properties of an injection molded polypropylene component. Mech. Mater. 2017, 105, 123–137. [Google Scholar] [CrossRef]
- Laschet, G.; Nokhostin, H.; Koch, S.; Meunier, M.; Hopmann, C. Prediction of effective elastic properties of a polypropylene component by an enhanced multiscale simulation of the injection molding process. Mech. Mater. 2020, 140, 103225. [Google Scholar] [CrossRef]
- Suzuki, H.; Grebowicz, J.; Wunderlich, B. Glass transition of poly (oxymethylene). Br. Polym. J. 1985, 17, 1–3. [Google Scholar] [CrossRef]
- Jabbari-Farouji, S.; Lame, O.; Perez, M.; Rottler, J.; Barrat, J.L. Role of the intercrystalline tie chains network in the mechanical response of semicrystalline polymers. Phys. Rev. Lett. 2017, 118, 217802. [Google Scholar] [CrossRef] [Green Version]
- Yeh, I.C.; Andzelm, J.W.; Rutledge, G.C. Mechanical and structural characterization of semicrystalline polyethylene under tensile deformation by molecular dynamics simulations. Macromolecules 2015, 48, 4228–4239. [Google Scholar] [CrossRef] [Green Version]
- Rastogi, R.; Vellinga, W.; Rastogi, S.; Schick, C.; Meijer, H. The three-phase structure and mechanical properties of poly (ethylene terephthalate). J. Polym. Sci. Part B Polym. Phys. 2004, 42, 2092–2106. [Google Scholar] [CrossRef]
- Strobl, G. The Physics of Polymers, Third Revised and Expanded Edition; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Strobl, G. A thermodynamic multiphase scheme treating polymer crystallization and melting. Eur. Phys. J. E 2005, 18, 295–309. [Google Scholar] [CrossRef]
- Di Lorenzo, M.L.; Righetti, M.C. Crystallization-induced formation of rigid amorphous fraction. Polym. Cryst. 2018, 1, e10023. [Google Scholar] [CrossRef]
- Horn, T.D.; Wulf, H.; Ihlemann, J. Crystallization of semi-crystalline polymers simulated with a cellular automaton. In Proceedings of the 8th GACM Colloquium on Computational Mechanics, Kassel, Germany, 28–30 August 2019; Volume 845, pp. 155–157. [Google Scholar]
- Mathot, V.; Pyda, M.; Pijpers, T.; Poel, G.V.; Van de Kerkhof, E.; Van Herwaarden, S.; Van Herwaarden, F.; Leenaers, A. The Flash DSC 1, a power compensation twin-type, chip-based fast scanning calorimeter (FSC): First findings on polymers. Thermochim. Acta 2011, 522, 36–45. [Google Scholar] [CrossRef]
- Ehrenstein, G.W. Polymer-Werkstoffe; Carl Hanser Verlag: Munich, Germany, 2011; Volume 2. [Google Scholar]
- Choe, C.R.; Lee, K.H. Nonisothermal crystallization kinetics of poly (etheretherketone)(PEEK). Polym. Eng. Sci. 1989, 29, 801–805. [Google Scholar] [CrossRef]
- Tobin, M.C. Theory of phase transition kinetics with growth site impingement. I. Homogeneous nucleation. J. Polym. Sci. Polym. Phys. Ed. 1974, 12, 399–406. [Google Scholar] [CrossRef]
- Mandelkern, L. Crystallization of Polymers: Volume 2, Kinetics and Mechanisms; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Cormia, R.; Price, F.; Turnbull, D. Kinetics of crystal nucleation in polyethylene. J. Chem. Phys. 1962, 37, 1333–1340. [Google Scholar] [CrossRef]
- Goldberg, N.; Donner, H.; Ihlemann, J. Evaluation of hyperelastic models for unidirectional short fibre reinforced materials using a representative volume element with refined boundary conditions. Tech. Mech. 2015, 35, 80–99. [Google Scholar]
- Bartelt, M.; Klöckner, O.; Dietzsch, J.; Groß, M. Higher order finite elements in space and time for anisotropic simulations with variational integrators. Application of an efficient GPU implementation. Math. Comput. Simul. 2020, 170, 164–204. [Google Scholar] [CrossRef]
- Horn, T.D.; Bartelt, M.; Wulf, H.; Ihlemann, J. Determination of the effective 2D material stiffness matrix using Abaqus. PAMM 2020, 20, e202000299. [Google Scholar]
- Kurita, T.; Fukuda, Y.; Takahashi, M.; Sasanuma, Y. Crystalline moduli of polymers, evaluated from density functional theory calculations under periodic boundary conditions. ACS Omega 2018, 3, 4824–4835. [Google Scholar] [CrossRef]
- Nakamae, K.; Kameyama, M.; Yoshikawa, M.; Matsumoto, T. Elastic modulus of the crystal regions in the direction perpendicular to the chain axis of poly (butylene terephthalate). Sen’i Gakkaishi 1980, 36, T33–T36. [Google Scholar] [CrossRef] [Green Version]
- Nakamae, K.; Kameyama, M.; Yoshikawa, M.; Matsumoto, T. Elastic modulus of crystalline regions of poly (butylene terephthalate) in the direction parallel to the chain axis. J. Polym. Sci. Polym. Phys. Ed. 1982, 20, 319–326. [Google Scholar] [CrossRef]













| G | K | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 337.47 MPa | 737.45 MPa | G | K | G | K |
| y | a [MPa] | b [MPa] | c [MPa] | d [MPa] |
|---|---|---|---|---|
| G | 8254 | 898 | 995 | |
| K | 1547 | 2071 | ||
| 4415 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horn, T.D.; Heidrich, D.; Wulf, H.; Gehde, M.; Ihlemann, J. Multiscale Simulation of Semi-Crystalline Polymers to Predict Mechanical Properties. Polymers 2021, 13, 3233. https://doi.org/10.3390/polym13193233
Horn TD, Heidrich D, Wulf H, Gehde M, Ihlemann J. Multiscale Simulation of Semi-Crystalline Polymers to Predict Mechanical Properties. Polymers. 2021; 13(19):3233. https://doi.org/10.3390/polym13193233
Chicago/Turabian StyleHorn, Tobias Daniel, Dario Heidrich, Hans Wulf, Michael Gehde, and Jörn Ihlemann. 2021. "Multiscale Simulation of Semi-Crystalline Polymers to Predict Mechanical Properties" Polymers 13, no. 19: 3233. https://doi.org/10.3390/polym13193233
APA StyleHorn, T. D., Heidrich, D., Wulf, H., Gehde, M., & Ihlemann, J. (2021). Multiscale Simulation of Semi-Crystalline Polymers to Predict Mechanical Properties. Polymers, 13(19), 3233. https://doi.org/10.3390/polym13193233