Axial and Radial Compression Behavior of Composite Rocket Launcher Developed by Robotized Filament Winding: Simulation and Experimental Validation
Abstract
:1. Introduction
- Finite element modeling of the cylindrical RPG by the computer-aided simulation using ANSYS software. The prediction of the axial and radial compression properties of the tubular composites.
- Preparation of the filament wound hybrid tubular composite structures by robotized filament winding machine using carbon and glass tows in different proportions.
- ○
- By changing the angle of wind of the helical layers keeping the stacking sequence constant.
- ○
- By changing the sequence of stacking of layers, i.e., hoop layers and helical layers at a constant angle of wind.
- Continuous impregnation of filaments with epoxy resin during the winding process.
- Comparison of the prepared tubular composite samples with respect to their axial and radial compression properties and the validation of FEM based prediction of compression properties with the experimental results.
2. Materials and Methods
2.1. Materials
- Carbon fiber: Torayca Grade T600B-12k-50B (Toray, Chuo City, Tokyo, Japan). This is a high-performance carbon fiber made from PAN (Polyacrylonitrile) precursor.
- The glass fiber is E-Glass grade T600-6k, (Hexcel, Les Avenieres, France). This fiber is also a high-performance fiber and compatible with a different range of resins.
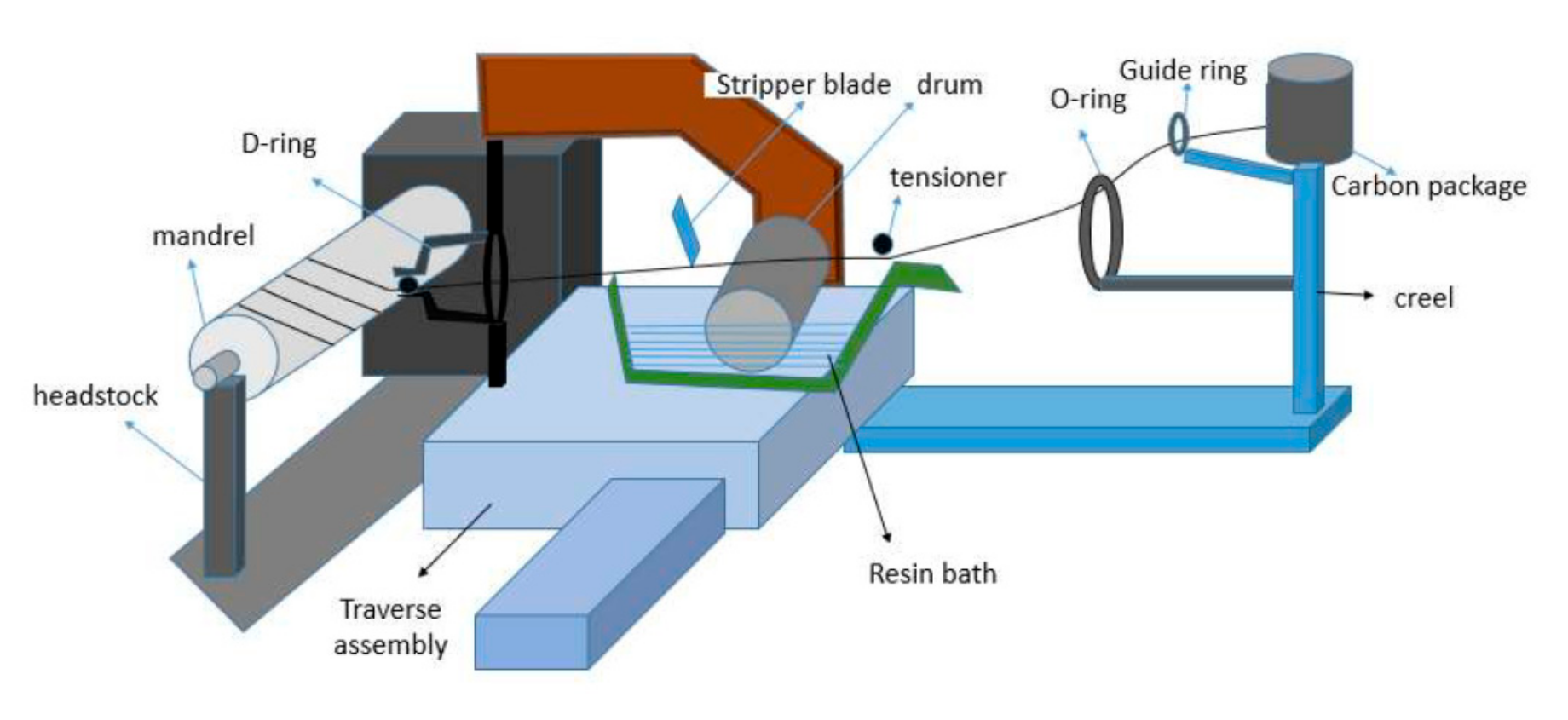
2.2. Winding Machine Description
2.3. Preparation of Tubular Composite Samples
2.4. Testing Standards & Testing Methods
2.4.1. Radial Compressional Behavior
2.4.2. Axial Compressional Behavior
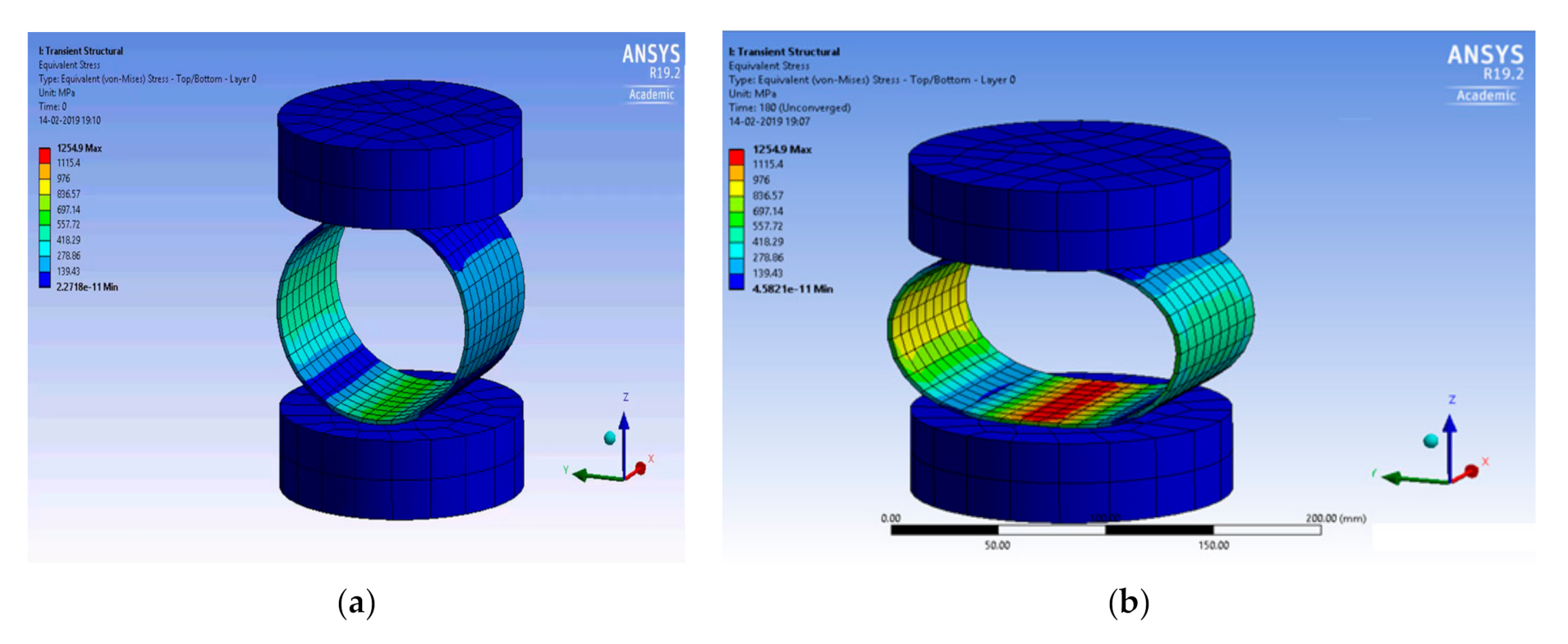
2.5. Modeling with ANSYS
3. Results and Discussion
3.1. Simulation of Radial and Axial Compression
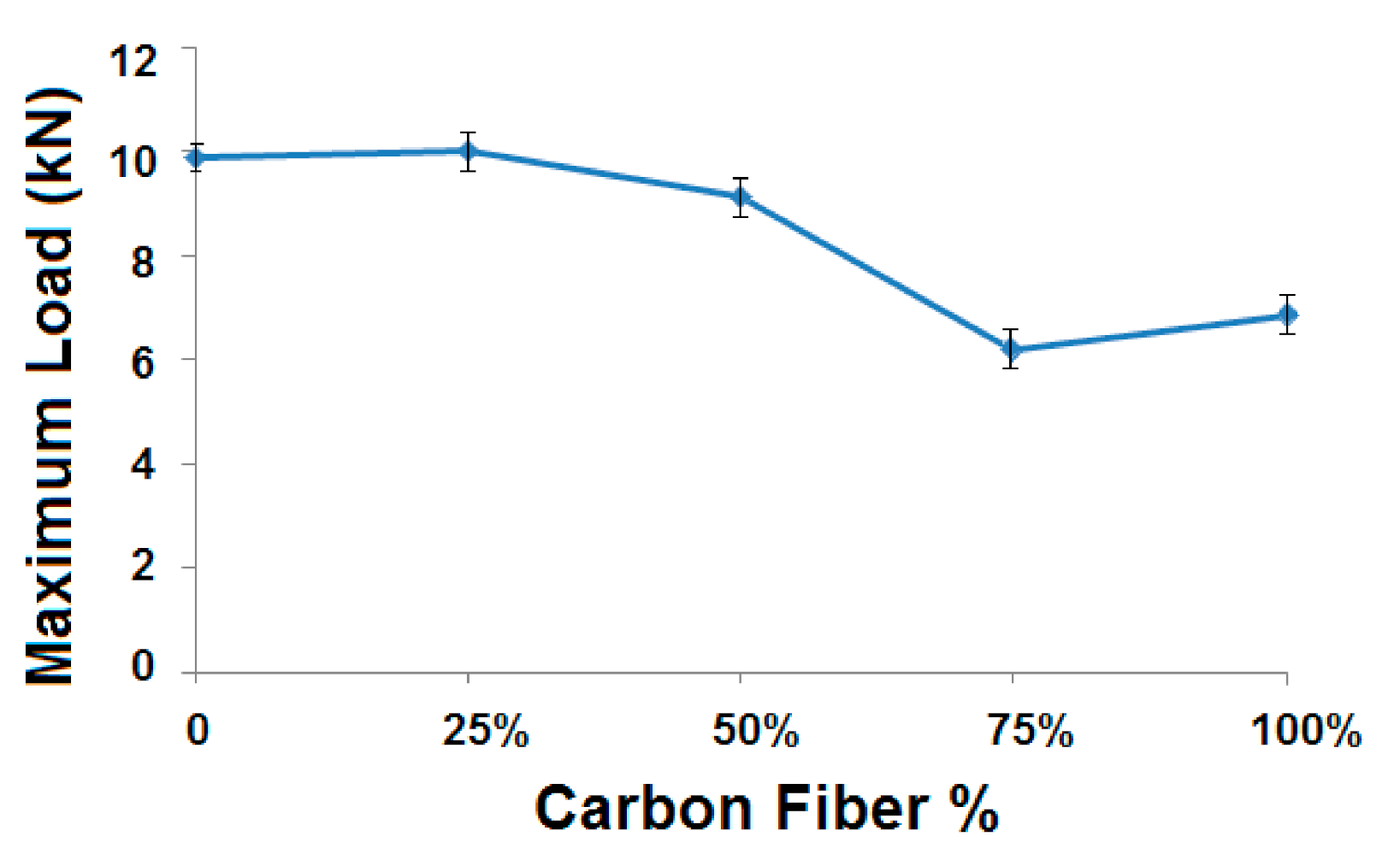
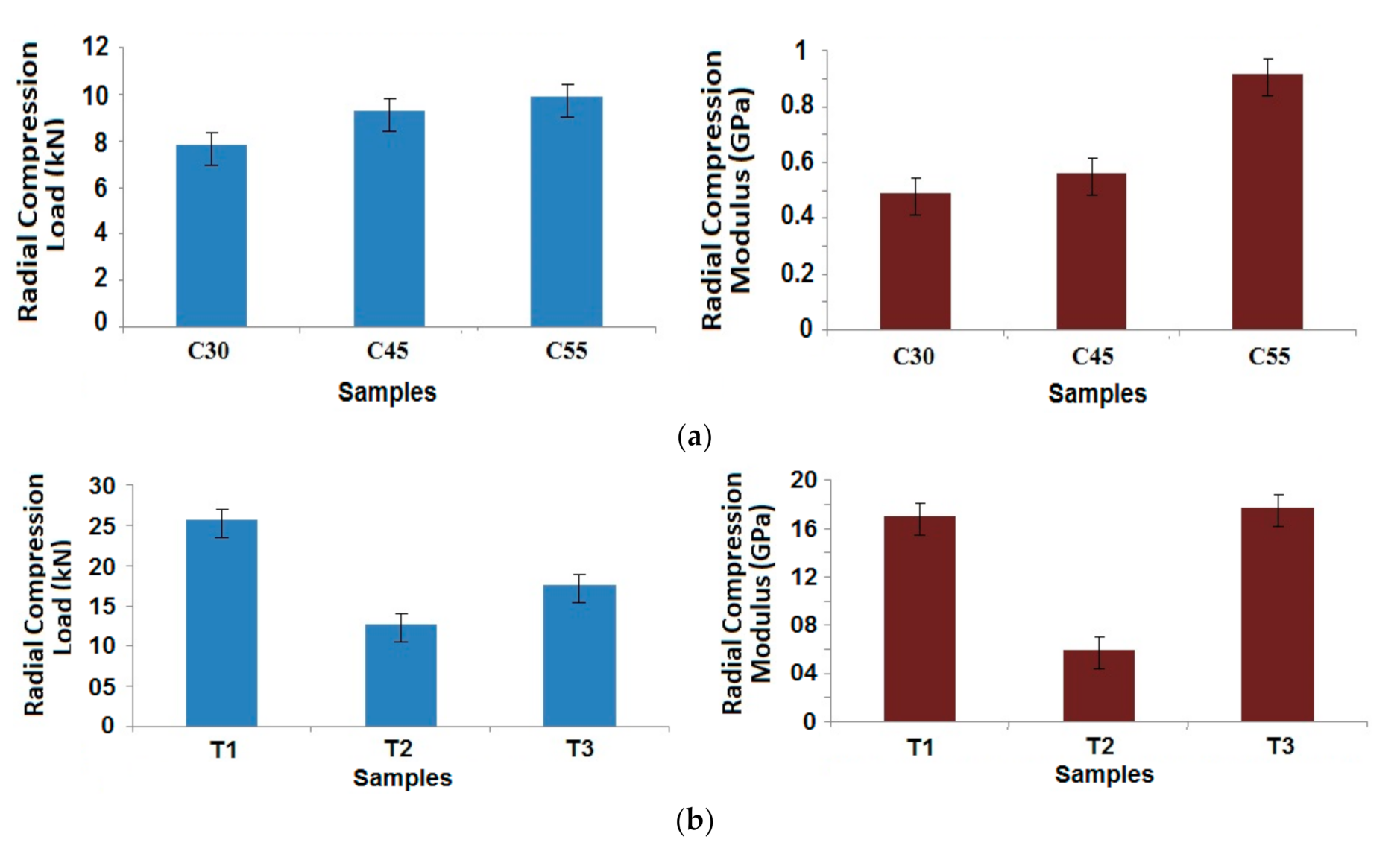
3.2. Experimental Validation of Radial and Axial Compression
3.2.1. Radial Compression Behavior
3.2.2. Axial Compression Behavior
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Minsch, N.; Herrmann, F.H.; Gereke, T.; Nocke, A.; Cherif, C. Analysis of filament winding processes and potential equipment technologies. Procedia CIRP 2017, 66, 125–130. [Google Scholar] [CrossRef]
- Harada, S.; Arai, Y.; Araki, W.; Iijima, T.; Kurosawa, A.; Ohbuchi, T.; Sasaki, N.A. A simplified method for predicting burst pressure of type III filament-wound CFRP composite vessels considering the inhomogeneity of fiber packing. Compos. Struct. 2018, 190, 79–90. [Google Scholar] [CrossRef]
- Koussios, S.; Bergsma, O.K.; Beukers, A. Filament winding. Part 1: Determination of the wound body related parameters. Compos. Part A Appl. Sci. Manuf. 2004, 35, 181–195. [Google Scholar] [CrossRef]
- Almeida, J.H.; Ribeiro, M.L.; Tita, V.; Amico, S.C. Damage and failure in carbon/epoxy filament wound composite tubes under external pressure: Experimental and numerical approaches. Mater. Des. 2016, 96, 431–438. [Google Scholar] [CrossRef]
- Martinec, T.; Mlýnek, J.; Petrů, M. Calculation of the robot trajectory for the optimum directional orientation of fiber placement in the manufacture of composite profile frames. Robot. Comput. Integr. Manuf. 2015, 35, 42–54. [Google Scholar] [CrossRef]
- Mlýnek, J.; Petru, M.; Martinec, T.; Koloor, S.S.R. Fabrication of high-quality polymer composite frame by a new method of fiber winding process. Polymers 2020, 12, 1037. [Google Scholar] [CrossRef]
- Rojas, E.V.; Chapelle, D.; Perreux, D.; Delobelle, B.; Thiebaud, F. Unified approach of filament winding applied to complex shape mandrels. Compos. Struct. 2014, 116, 805–813. [Google Scholar] [CrossRef] [Green Version]
- Humberto, S.A.; Maikson, L.P.; Ribeiro, M.L.; Tita, V.; Amico, S.C. Buckling and post-buckling of filament wound composite tubes under axial compression: Linear, nonlinear, damage and experimental analyses. Compos. Part B Eng. 2018, 149, 227–239. [Google Scholar] [CrossRef]
- Jia, X.; Chen, G.; Yu, Y.; Li, G.; Zhu, J.; Luo, X.; Duan, C.; Yang, X.; Hui, D. Effect of geometric factor, winding angle and pre-crack angle on quasi-static crushing behavior of filament wound CFRP cylinder. Compos. Part B Eng. 2013, 45, 1336–1343. [Google Scholar] [CrossRef]
- Quanjin, M.; Rejab, M.R.; Idris, M.S.; Bachtiar, B.; Siregar, J.P.; Harith, M.N. Design and optimize of 3-axis filament winding machine. IOP Conf. Ser. Mater. Sci. Eng. 2017, 257, 20–24. [Google Scholar] [CrossRef]
- Atiqah, A.; Maleque, M.A.; Jawaid, M.; Iqbal, M. Development of kenaf-glass reinforced unsaturated polyester hybrid composite for structural applications. Compos. Part B Eng. 2014, 56, 68–73. [Google Scholar] [CrossRef]
- Sahin, O.S.; Akdemir, A.; Avci, A.; Gemi, L. Fatigue crack growth behavior of filament wound composite pipes in corrosive environment. J. Reinf. Plast. Compos. 2008, 28, 2957–2969. [Google Scholar] [CrossRef]
- Thakur, V.K.; Thakur, M.K.; Gupta, R.K. Hybrid Polymer Composite Materials Processing; Woodhead Publishing: London, UK, 2017. [Google Scholar]
- Baker, E.; Voort, M.; Pope, M. NATO standards and practice for munitions safety and Insensitive munitions. In Proceedings of the XIIth International Armament Conference on Scientific Aspects of Armament and Safety Technology, Jachranka, Poland, 17–20 September 2018. [Google Scholar]
- AASTP-5. NATO Guidelines for the Storage, Maintenance and Transport of Ammunition on Deployed Mission or Operations, 1st ed.; Version 3; NATO: Brussels, Belgium, 2016. [Google Scholar]
- STANAG 4526. Edition 2—Shaped Charge Jet, Munitions Test Procedure, NATO AC326; NATO: Brussels, Belgium, 2004. [Google Scholar]
- Fuchs, B.; Baker, E.; Tomasello, K.; Becker, M. Review and update of STANAG 4526 shaped charge jet, munitions test procedure. In Proceedings of the International Explosives Safety Symposium & Exposition, San Diego, CA, USA, 6–9 August 2018. [Google Scholar]
- Baker, E.L.; Pham, J.; Madsen, T.; Poulos, W.; Fuchs, B.E. Shaped charge jet characterization and initiation test configuration for testing, The 12th hypervelocity impact symposium. Procedia. Eng. 2013, 58, 58–67. [Google Scholar] [CrossRef] [Green Version]
- Baker, E.L.; Daniels, A.; Fisher, S.; Al-Shehaba, N.; Ng, K.W.; Fuchs, B.E.; Cruz, F. Development of a small shaped charge insensitive munitions threat test, The 13th hypervelocity impact symposium. Procedia. Eng. 2015, 103, 27–34. [Google Scholar] [CrossRef] [Green Version]
- Behera, B.K.; Mishra, R.K. Artificial neural network-based prediction of aesthetic and functional properties of worsted suiting fabrics. Int. J. Cloth. Sci. Technol. 2007, 19, 259–276. [Google Scholar] [CrossRef]
- Zu, L. Stability of fiber trajectories for winding toroidal pressure vessels. Compos. Struct. 2012, 94, 1855–1860. [Google Scholar] [CrossRef]
- Behera, B.K.; Pattanayak, A.K.; Mishra, R. Prediction of fabric drape behavior using finite element method. J. Text. Eng. 2008, 54, 103–110. [Google Scholar] [CrossRef] [Green Version]
- Venkataraman, M.; Mishra, R.; Jasikova, D.; Kotresh, T.M. Thermodynamics of aerogel-treated nonwoven fabrics at subzero temperatures. J. Ind. Text. 2015, 45, 387–404. [Google Scholar] [CrossRef]
- Mishra, R.; Militky, J.; Gupta, N.; Pachauri, R.; Behera, B.K. Modelling and simulation of earthquake resistant 3D woven textile structural concrete composites. Compos. B Eng. 2015, 81, 91–97. [Google Scholar] [CrossRef]
- Panchagnula, K.K.; Panchagnula, J.S. Fabrication of hoop-wound glass fiber reinforced plastic cylindrical shells using filament winding machine. Mater. Today Proc. 2020, 27, 1315–1318. [Google Scholar] [CrossRef]
- Venkataraman, M.; Mishra, R.; Militky, J.; Hes, l. Aerogel based nanoporous fibrous materials for thermal insulation. Fibers Polym. 2014, 15, 1444–1449. [Google Scholar] [CrossRef]
- Hwang, T.K.; Park, J.B.; Kim, H.G. Evaluation of fiber material properties in filament-wound composite pressure vessels. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1467–1475. [Google Scholar] [CrossRef]
- Crina, B.; Blaga, M.; Luminita, V.; Mishra, R. Comfort properties of functional weft knitted spacer fabrics. Tekst Konfeksiyon. 2013, 23, 220–227. [Google Scholar]
- Zu, L.; Zhu, W.; Dong, H.; Ke, Y. Application of variable slippage coefficients to the design of filament wound toroidal pressure vessels. Compos. Struct. 2017, 172, 339–344. [Google Scholar] [CrossRef]
- Sorrentino, L.; Anamateros, E.; Bellini, C.; Carrino, L.; Corcione, G.; Leone, A.; Paris, G. Robotic filament winding: An innovative technology to manufacture complex shape structural parts. Compos. Struct. 2019, 220, 699–707. [Google Scholar] [CrossRef]
- Jamshaid, H.; Mishra, R.; Militky, J.; Pechociakova, M.; Noman, M.T. Mechanical, thermal and interfacial properties of green composites from basalt and hybrid woven fabrics. Fibers Polym. 2016, 17, 1675–1686. [Google Scholar] [CrossRef]
- Arumugam, V.; Mishra, R.; Militky, J.; Salacova, J. Investigation on thermo-physiological and compression characteristics of weft-knitted 3D spacer fabrics. J. Text. I. 2017, 108, 1095–1105. [Google Scholar] [CrossRef]
- Tucker, C.L.; Liang, E. Stiffness predictions for unidirectional short-fiber composites: Review and evaluation. Compos. Sci. Technol. 1999, 59, 655–671. [Google Scholar] [CrossRef]
- Halpin Affdl, J.C.; Kardos, J.L. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Budarapu, P.R.; Zhuang, X.; Rabczuk, T.; Bordas, S.P. Multiscale modeling of material failure: Theory and computational methods. Adv. Appl. Mech. 2019, 52, 1–103. [Google Scholar] [CrossRef]










| Properties | Glass | Carbon | Epoxy |
|---|---|---|---|
| Name | E-glass 6k | Torayca 12k | Araldyte LY556 |
| Tensile strength (GPa) | 3.44 | 3.53 | 0.345 |
| Modulus (GPa) | 73.5 | 230 | 25.5 |
| Elongation % | 4.8 | 1.5 | 1.2 |
| Density (g/cc) | 2.57 | 1.76 | 1.15 |
| Compressive strength (GPa) | 4.08 | 0.23 | - |
| Viscosity (mPa. s) | - | - | 10,000 |
| Filament tow fineness (Tex) | 600 | 600 | - |
| Sample Name | Type | Angle of Wind (degrees) | Winding and Hooping Pattern | Wall Thickness (mm) | Fiber Volume Fraction |
|---|---|---|---|---|---|
| C30 | Cylindrical | 30 | 30-h-30-h-30 | 3.1 | 0.48 |
| C45 | Cylindrical | 45 | 45-h-45-h-45 | 3.2 | 0.52 |
| C55 | Cylindrical | 55 | 55-h-55-h-55 | 2.8 | 0.51 |
| T 1 | Tapered | 45 | 45-h-45-h-45 | 2.7 | 0.51 |
| T 2 | Tapered | 45 | 45-h-h-h-45 | 2.8 | 0.52 |
| T 3 | Tapered | 45 | h-45-45-45-h | 3.1 | 0.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, R.; Behera, B.K.; Mukherjee, S.; Petru, M.; Muller, M. Axial and Radial Compression Behavior of Composite Rocket Launcher Developed by Robotized Filament Winding: Simulation and Experimental Validation. Polymers 2021, 13, 517. https://doi.org/10.3390/polym13040517
Mishra R, Behera BK, Mukherjee S, Petru M, Muller M. Axial and Radial Compression Behavior of Composite Rocket Launcher Developed by Robotized Filament Winding: Simulation and Experimental Validation. Polymers. 2021; 13(4):517. https://doi.org/10.3390/polym13040517
Chicago/Turabian StyleMishra, Rajesh, Bijoy Kumar Behera, Sayan Mukherjee, Michal Petru, and Miroslav Muller. 2021. "Axial and Radial Compression Behavior of Composite Rocket Launcher Developed by Robotized Filament Winding: Simulation and Experimental Validation" Polymers 13, no. 4: 517. https://doi.org/10.3390/polym13040517
APA StyleMishra, R., Behera, B. K., Mukherjee, S., Petru, M., & Muller, M. (2021). Axial and Radial Compression Behavior of Composite Rocket Launcher Developed by Robotized Filament Winding: Simulation and Experimental Validation. Polymers, 13(4), 517. https://doi.org/10.3390/polym13040517









