Water Vapor Sorption and Diffusivity in Bio-Based Poly(ethylene vanillate)—PEV
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Films Preparation
2.3. Differential Scanning Calorimetry (DSC) Analysis
2.4. Wide Angle X-ray Scattering (WAXS) Analysis
2.5. Dynamic Vapor Sorption/Desorption (DVS)
2.6. Modeling of Water Vapor Sorption Isotherm
2.7. Diffusion in a Homogeneous Plane Sheet of Material
2.8. Identification Parameter Procedure
3. Results and Discussion
3.1. Chemical Structure and Thermal Transitions
3.2. Film Crystallinity
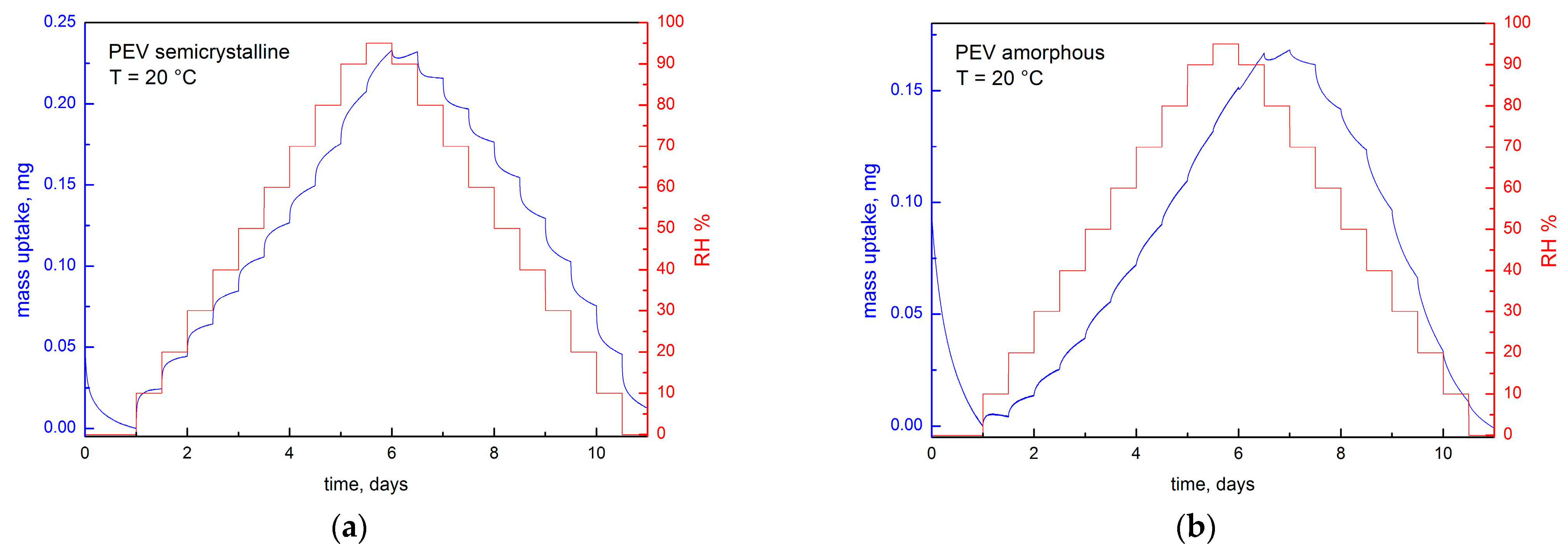
3.3. Sorption Measurements
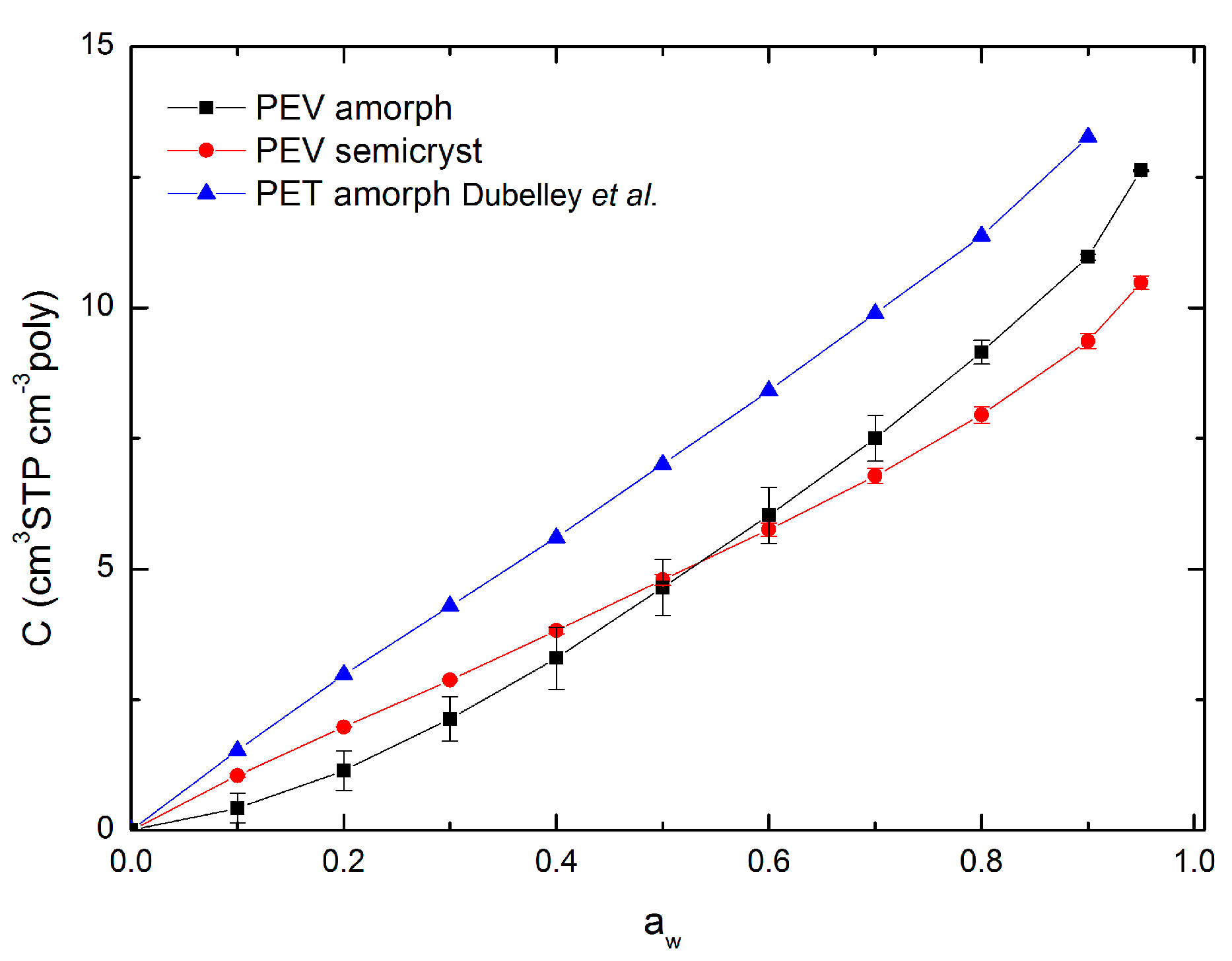
3.4. Sorption Isotherms
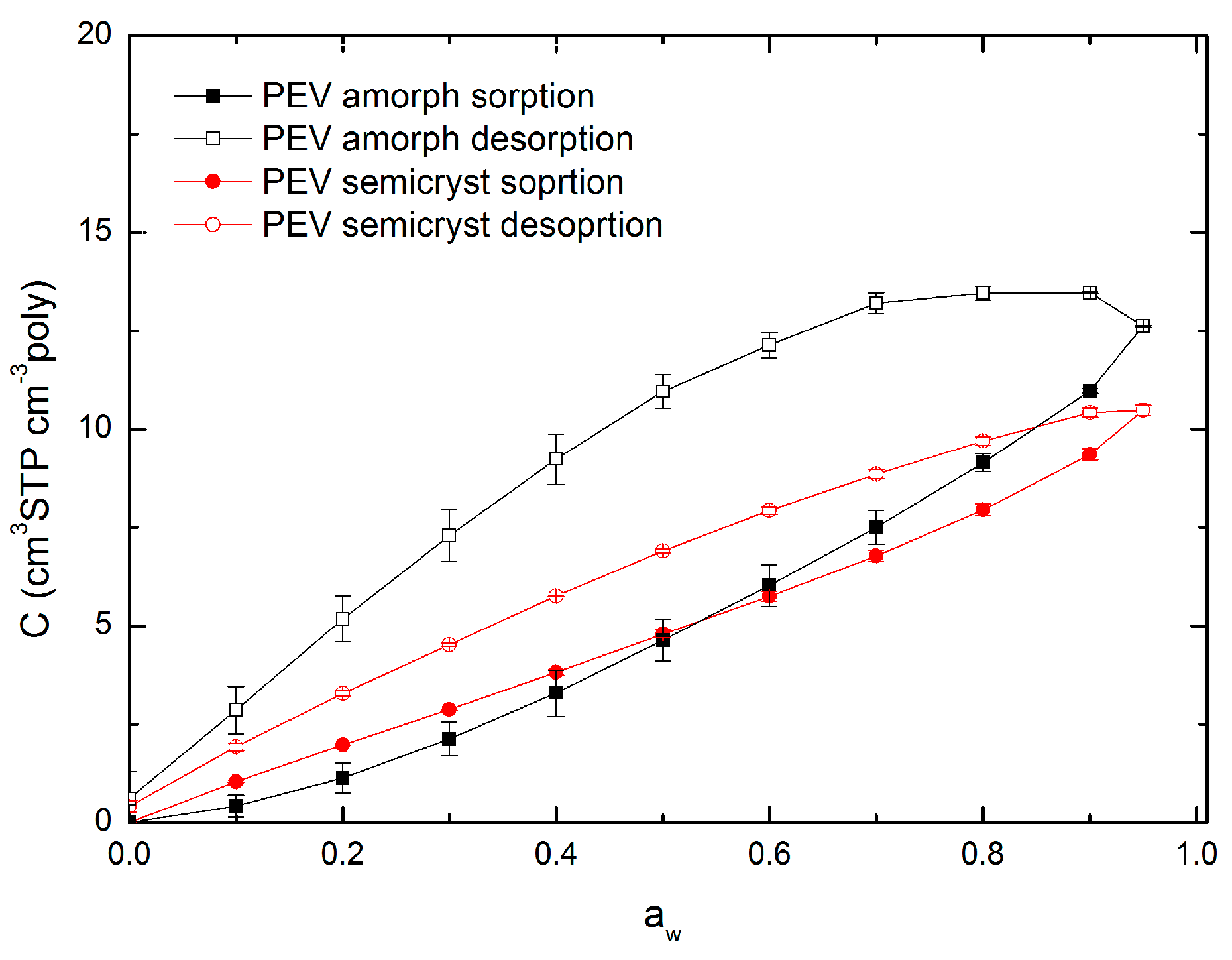
3.5. Hysteresis
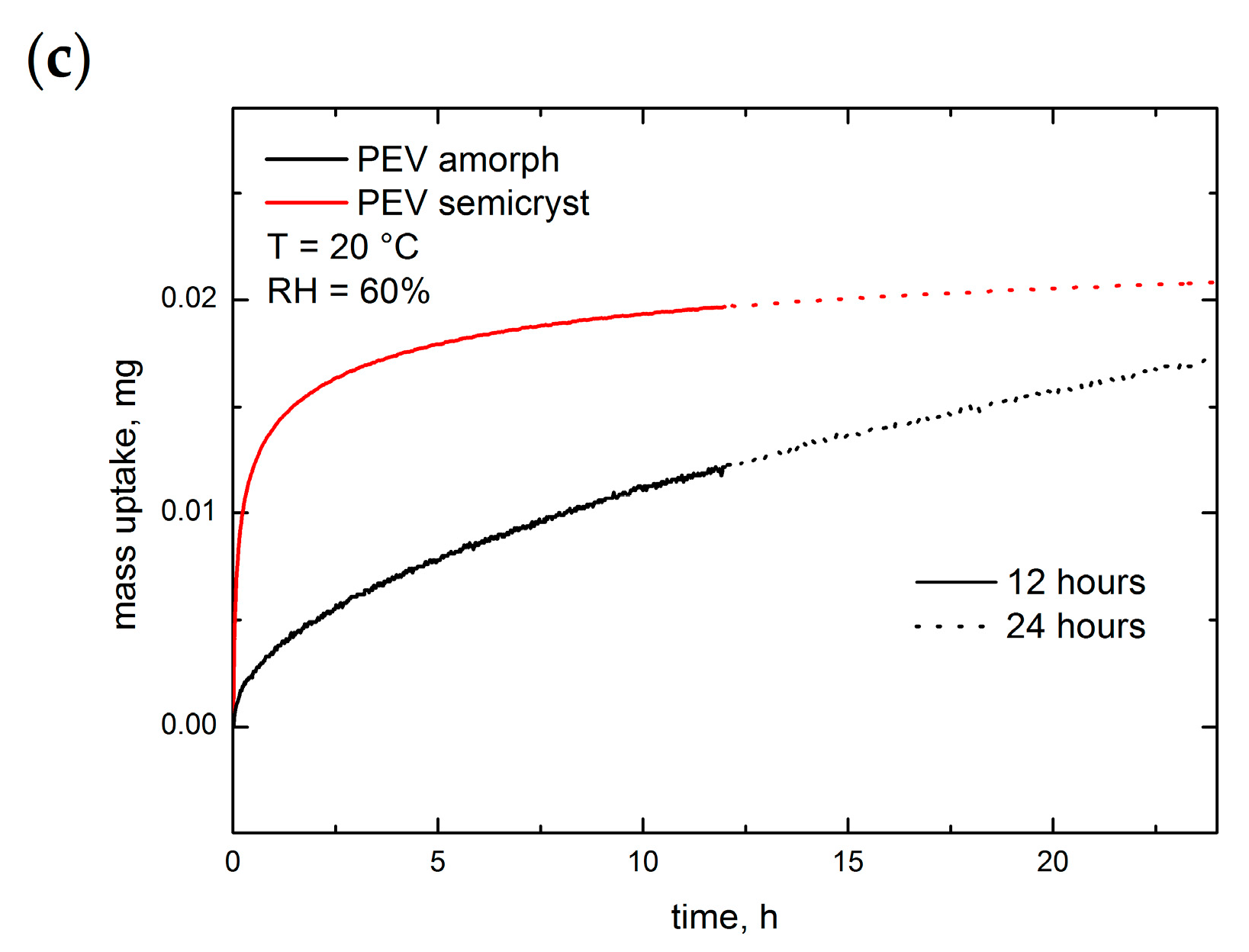
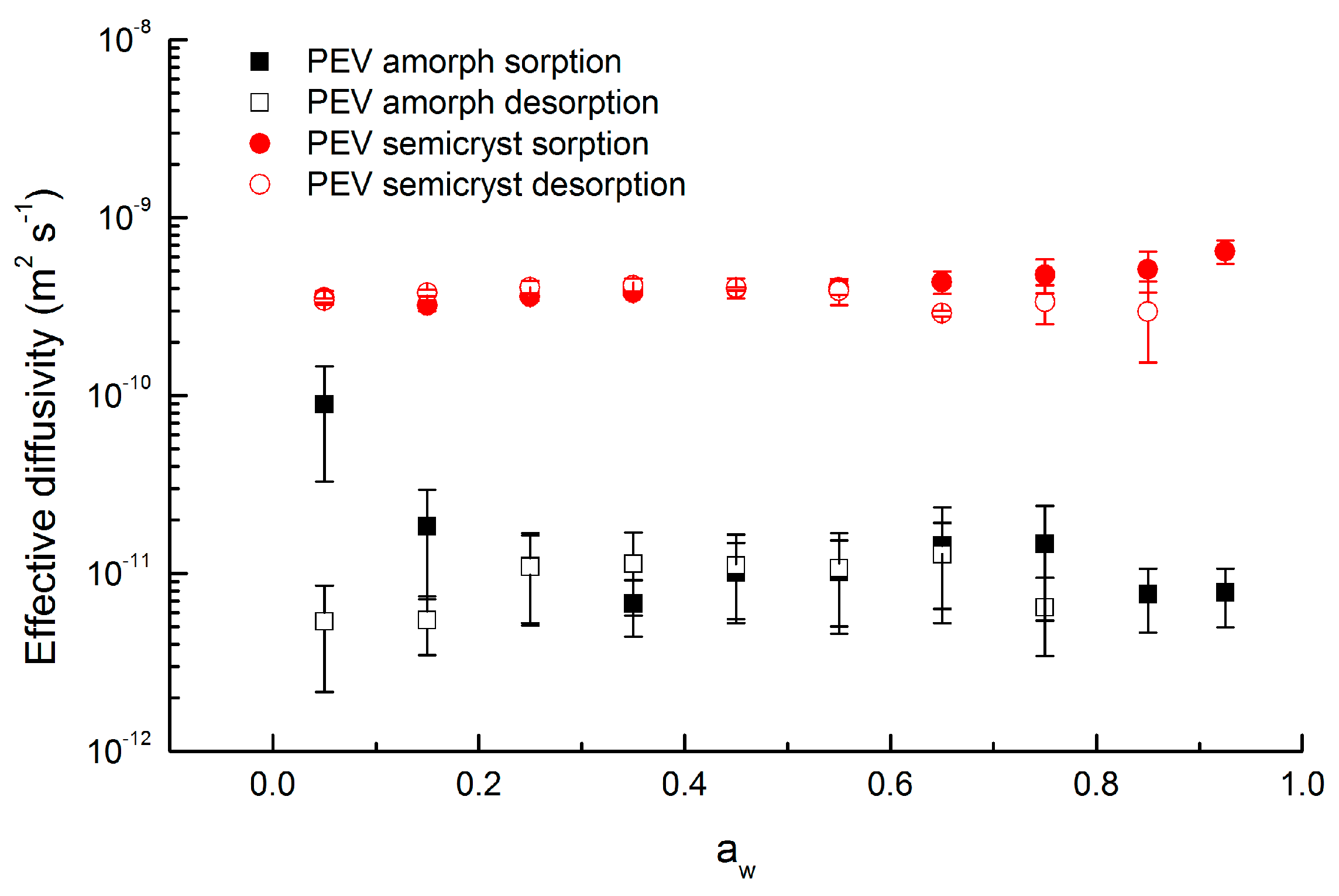
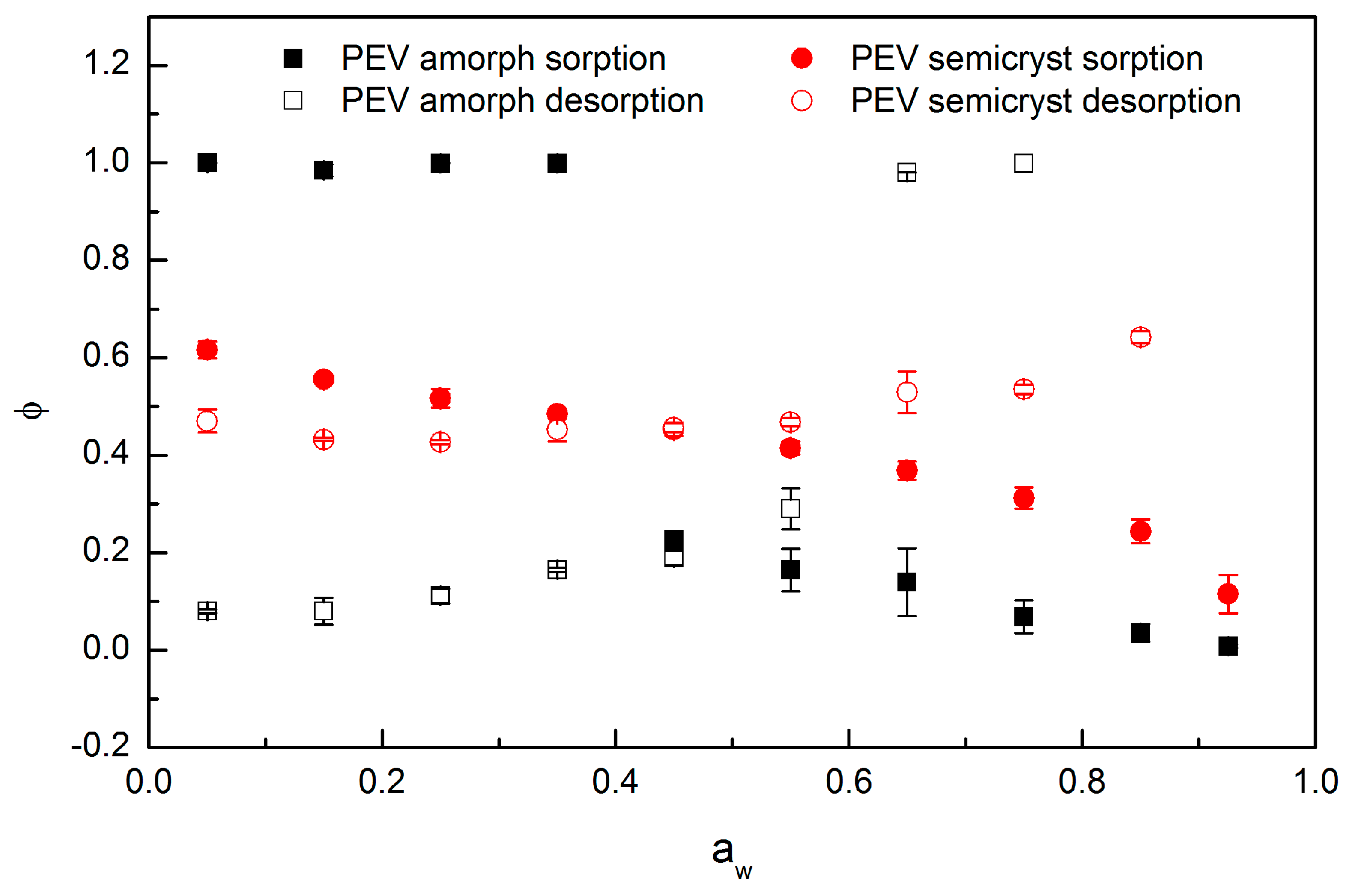
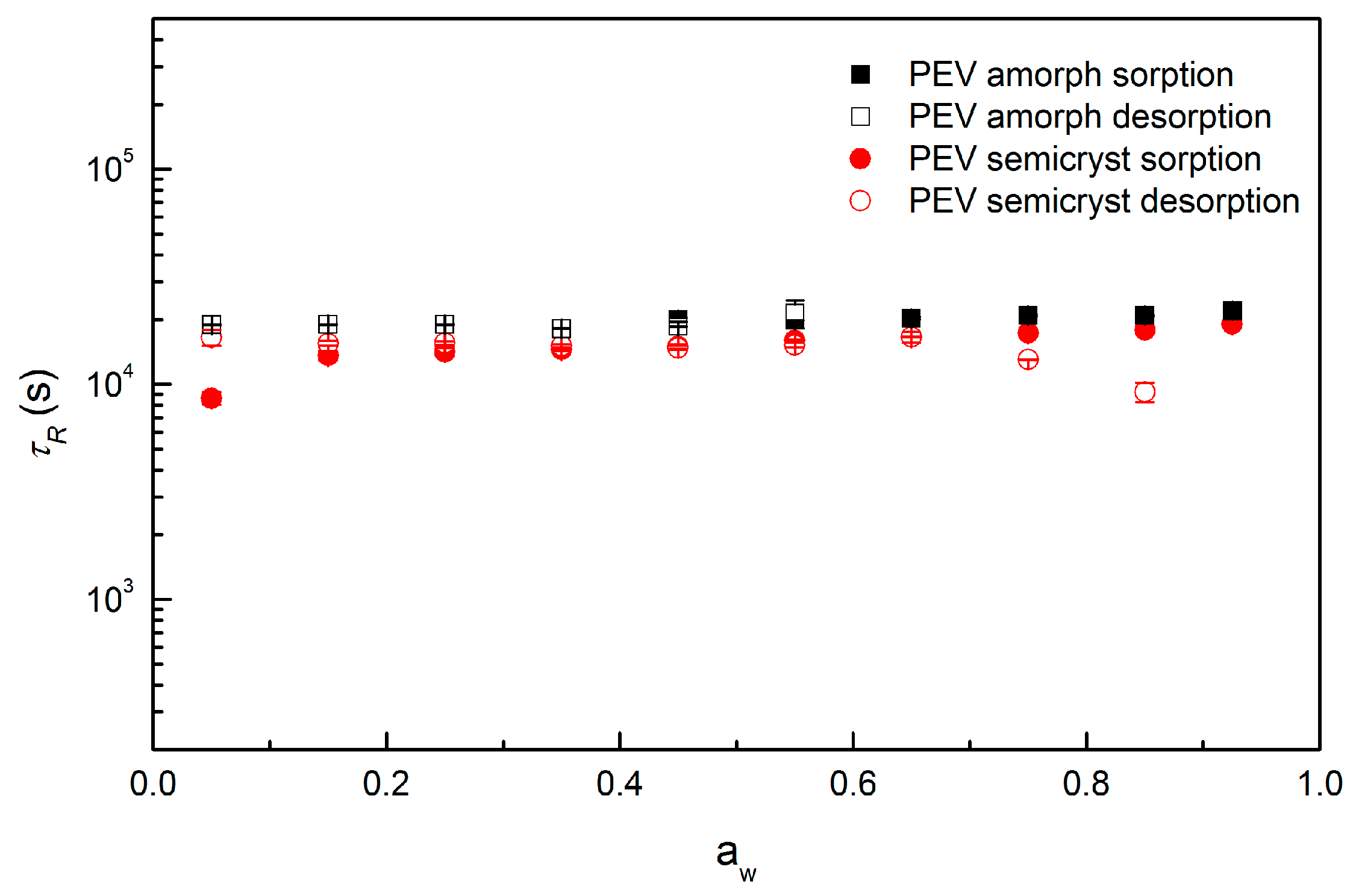
3.6. Diffusivity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Collins, M.N.; Nechifor, M.; Tanasă, F.; Zănoagă, M.; McLoughlin, A.; Stróżzk, M.A.; Culebras, M.; Teacă, C.-A. Valorization of lignin in polymer and composite systems for advanced engineering applications: A review. Int. J. Biol. Macromol. 2019, 131, 828–849. [Google Scholar] [CrossRef]
- Holladay, J.E.; White, J.F.; Bozell, J.J.; Johnson, D. Top Value-Added Chemicals from Biomass Volume II—Results of Screening for Potential Candidates from Biorefinery Lignin; U.S. Department of Energy: Washington, DC, USA, 2007.
- Gandini, A.; Lacerda, T.M. From monomers to polymers from renewable resources: Recent advances. Prog. Polym. Sci. 2015, 48, 1–39. [Google Scholar] [CrossRef]
- Gioia, C.; Banella, M.B.; Marchese, P.; Vannini, M.; Colonna, M.; Celli, A. Advances in the synthesis of bio-based aromatic polyesters: Novel copolymers derived from vanillic acid and ϵ-caprolactone. Polym. Chem. 2016, 7, 5396–5406. [Google Scholar] [CrossRef]
- Lotti, N.; Colonna, M.; Fiorini, M.; Finelli, L.; Berti, C. Poly(ethylene terephthalate), modified with bisphenol S units, with increased glass transition temperature. J. Appl. Polym. Sci. 2013, 128, 416–423. [Google Scholar] [CrossRef]
- Jabarin, S.A.; Lofgren, E.A. Effects of water absorption on physical properties and degree of molecular orientation of poly(ethylene terephthalate). Polym. Eng. Sci. 1986, 26, 620–625. [Google Scholar] [CrossRef]
- Bastioli, C.; Guanella, I.; Romano, G. Effects of water sorption on the physical properties of PET, PBT, and their long fibers composites. Polym. Compos. 1990, 11, 1–9. [Google Scholar] [CrossRef]
- Popineau, S.; Shanahan, M.E.R. Simple model to estimate adhesion of structural bonding during humid ageing. Int. J. Adhes. Adhes. 2006, 26, 363–370. [Google Scholar] [CrossRef]
- Immergut, E.H.; Mark, H.F. Principles of Plasticization. In Plasticization and Plasticizer Processes; Advances in Chemistry, American Chemical Society: Washington, DC, USA, 1965; pp. 1–26. [Google Scholar] [CrossRef] [Green Version]
- Dubelley, F.; Planes, E.; Bas, C.; Pons, E.; Yrieix, B.; Flandin, L. Water vapor sorption properties of polyethylene terephthalate over a wide range of humidity and temperature. J. Phys. Chem. B 2017, 121, 1953–1962. [Google Scholar] [CrossRef] [PubMed]
- Feng, H. Modeling of vapor sorption in glassy polymers using a new dual mode sorption model based on multilayer sorption theory. Polymer 2007, 48, 2988–3002. [Google Scholar] [CrossRef]
- Barens, A.R.; Hopfenberg, H.B. Diffusion and relaxation in glassy polymers powders: 2. Separation of diffusion and relaxation parameters. Polymer 1978, 19, 489–496. [Google Scholar] [CrossRef] [Green Version]
- Gioia, C.; Banella, M.B.; Totaro, G.; Vannini, M.; Marchese, P.; Colonna, M.; Sisti, L.; Celli, A. Biobased vanillic acid and ricinolein acid: Building blocks for fully renewable copolyesters. J. Renew. Mater. 2018, 6, 126–135. [Google Scholar] [CrossRef]
- Guillard, V.; Broyart, B.; Bonazzi, C.; Guilbert, S.; Gontard, N. Moisture diffusivity in sponge cake as related to porous structure evaluation and moisture content. J. Food Sci. 2003, 68, 555–562. [Google Scholar] [CrossRef]
- Thoury-Monbrun, V.; Gaucel, S.; Gontard, N.; Guillard, V.; Angellier-Coussy, H. Adapting gravimetric sorption analyzer to estimate water vapor diffusivity in micrometric size cellulose particles. Cellulose 2019, 26, 8575–8587. [Google Scholar] [CrossRef]
- Stannett, V.; Haider, M.; Koros, W.J.; Hopfenberg, H.B. Sorption and transport of water vapor in glassy poly(acrylonitrile). Polym. Eng. Sci. 1980, 20, 300–304. [Google Scholar] [CrossRef]
- Timmermann, E.O. A BET-like three sorption stage isotherm. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1989, 85, 1631–1645. [Google Scholar] [CrossRef]
- Timmermann, E.O. Multilayer sorption parameters: BET or GAB values? Colloids Surf. A Physicochem. Eng. Asp. 2003, 220, 235–260. [Google Scholar] [CrossRef] [Green Version]
- Jonquières, A.; Fane, A. Modified BET models for modeling water vapor sorption in hydrophilic glassy polymers and systems deviating strongly from ideality. J. Appl. Polym. Sci. 1998, 67, 1415–1430. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford Science Publications; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Burgess, S.K.; Mikkilineni, D.S.; Yu, D.B.; Kim, D.J.; Mubarak, C.R.; Kriegel, R.M.; Koros, W.J. Water sorption in poly(ethylene furanoate) compared to poly(ethylene terephthalate). Part 2: Kinetic sorption. Polymer 2014, 55, 6870–6882. [Google Scholar] [CrossRef]
- Torres, N.; Robin, J.J.; Boutevin, B. Study of thermal and mechanical properties of virgin and recycled poly(ethylene terephthalate) before and after injection molding. Eur. Polym. J. 2000, 36, 2075–2080. [Google Scholar] [CrossRef]
- Zamboulis, A.; Papadopoulus, L.; Terzopoulou, Z.; Bikiaris, D.N.; Patsiaoura, D.; Chrissafis, K.; Gazzano, M.; Lotti, N.; Papageorgiou, G.Z. Synthesis, thermal properties and decomposition mechanism of poly(ethylene vanillate) Polyester. Polymers 2019, 11, 1672. [Google Scholar] [CrossRef] [Green Version]
- Klung, H.P.; Alexander, L.E. X-ray Diffraction Procedures: For Polycrystalline and Amorphous Materials, 2nd ed.; J. Wiley and Sons: New York, NY, USA, 1974. [Google Scholar]
- Mo, Z.; Zhang, H. The degree of crystallinity in polymers by wide-angle X-ray diffraction (WAXD). J. Macromol. Sci. Part C 1995, 35, 555–580. [Google Scholar] [CrossRef]
- Semenova, S.I.; Ohya, H.; Smirnov, S.I. Physical transitions in polymers plasticized by interacting penetrant. J. Memb. Sci. 1997, 136, 1–11. [Google Scholar] [CrossRef]
- Kamiya, Y.; Mizoguchi, K.; Naito, Y. Plasticization of poly(ethyl methacrylate) by dissolved argon. J. Polym. Sci. Part B Polym. Phys. 1992, 30, 1183. [Google Scholar] [CrossRef]
- Koros, W.J.; Paul, D.R. CO₂ sorption in poly(ethylene terephthalate) above and below the glass transition. J. Polym. Sci. Polym. Phys. Ed. 1978, 16, 1947–1963. [Google Scholar] [CrossRef]
- Popineau, S.; Rondeau-Mouro, C.; Sulpice-Gaillet, C.; Shanahan, M.E.R. Free/bound water absorption in an epoxy adhesive. Polymer 2005, 46, 10733–10740. [Google Scholar] [CrossRef]
- Barbari, T.A.; Koros, W.J.; Paul, D.R. Gas sorption in polymers based on bisphenol-A. J. Polym. Sci. Part B Polym. Phys. 1988, 26, 729–744. [Google Scholar] [CrossRef]
- Koros, W.J.; Chan, A.H.; Paul, D.R. Sorption and transport of various gases in poly-carbonate. J. Memb. Sci. 1977, 2, 165–190. [Google Scholar] [CrossRef]
- Koros, W.J.; Paul, D.R.; Rocha, A.A. Carbon dioxide sorption and transport in polycarbonate. J. Polym. Sci. Part A-2 Polym. Phys. 1976, 14, 687–702. [Google Scholar] [CrossRef]
- Gouanvé, F.; Marais, S.; Bessadok, A.; Langevin, D.; Métayer, M. Kinetics of water sorption in flax and PET fibers. Eur. Polym. J. 2007, 43, 586–598. [Google Scholar] [CrossRef]
- Fukuda, M.; Kawai, H.; Yagi, N.; Kimura, O.; Ohta, T. FTIR study on the nature of water sorbed in poly(ethylene terphtalate) film. Polymer 1990, 31, 295–302. [Google Scholar] [CrossRef]
- Myers, A.V.; Meyer, J.A.; Rogers, C.E.; Stannett, V.; Szwarc, M. Studies in the gas and vapor permeability of plastic films and coated papers. The permeation of water paper. Tech. Assoc. Pulp Pap. Ind. 1961, 44, 58–67. [Google Scholar]
- Shigetomi, T.; Tsuzumi, H.; Toi, K.; Ito, T. Sorption and diffusion of water vapor in poly(ethylene terephthalate) film. J. Appl. Polym. Sci. 2000, 76, 67–74. [Google Scholar] [CrossRef]
- Lasoski, S.W.; Cobbs, W.H. Moisture permeability of polymers. I. Role of crystallinity and orientation. J. Polym. Sci. 1959, 36, 21–33. [Google Scholar] [CrossRef]
- Guo, J.; Barbari, T.A. Unified dual mode description of small molecule sorption and desorption kinetics in a glassy polymer. Macromolecules 2009, 42, 5700–5708. [Google Scholar] [CrossRef]
- Burgess, S.K.; Mikkilineni, D.S.; Yu, D.B.; Kim, D.J.; Mubarak, C.R.; Kriegel, R.M.; Koros, W.J. Water sorption in poly(ethylene furanoate) compared to poly(ethylene terephthalate). Part 1: Equilibrium sorption. Polymer 2014, 55, 6861–6869. [Google Scholar] [CrossRef]
- Righetti, M.C.; Laus, M.; Di Lorenzo, M.L. Temperature dependence of the rigid amorphous fraction in poly(ethylene terephthalate). Eur. Polym. J. 2014, 58, 60–68. [Google Scholar] [CrossRef]
- Lin, J.; Shenogin, S.; Nazarenko, S. Oxygen solubility and specific volume of rigid amorphous fraction in semicrystalline poly(ethylene terephthalate). Polymer 2002, 43, 4733–4743. [Google Scholar] [CrossRef]
- Barens, A.R. Effects of sample history, time, and temperature on the sorption of monomer vapor by PVC. J. Macromol. Sci. Part B Phys. 1977, 14, 483–498. [Google Scholar] [CrossRef]
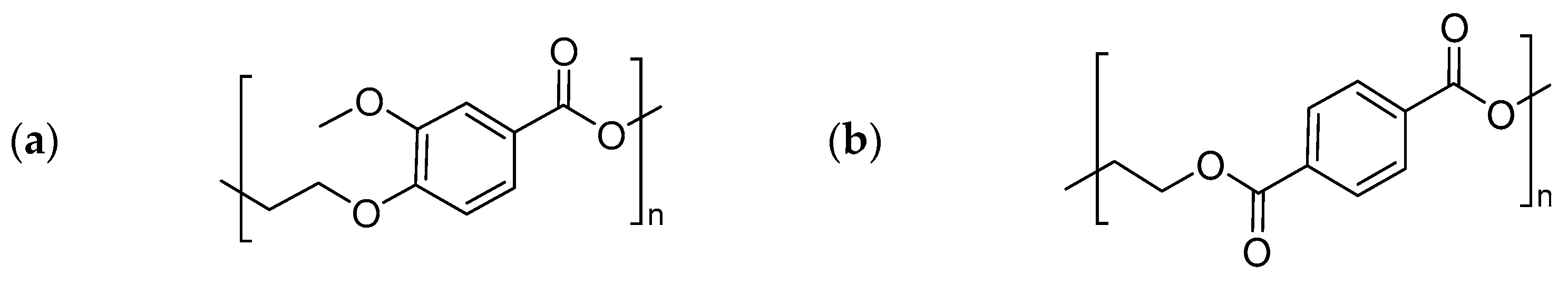
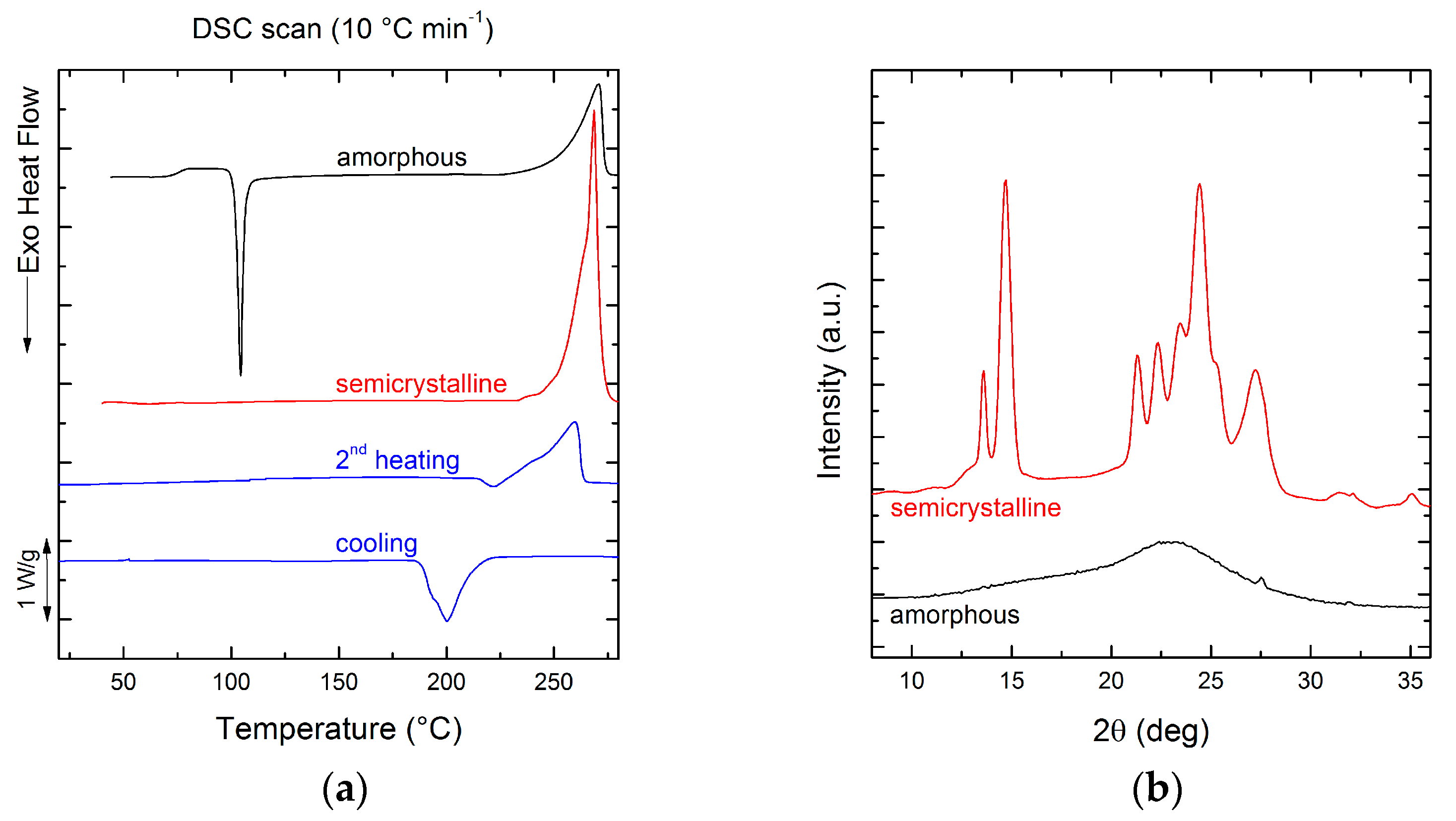


| Tc (°C) | ∆Hc (J g−1) | Tcc (°C) | ∆Hcc (J g−1) | Tm (°C) | ∆Hm (J g−1) | Tg (°C) | |
|---|---|---|---|---|---|---|---|
| 1st heating amorph 1 | - | - | 104 | 75.8 | 271 | 77.3 | 75 |
| 1st heating semicryst 2 | - | - | - | - | 269 | 108.3 | - |
| 2nd heating 3 | - | - | - | - | 260 | 74.2 | - |
| Cooling 3 | 200 | 72.8 | - | - | - | - | - |
| Sample | aw Range | Cp (cm3 STP cm−3 poly) | k′ | A′ | RMSE (cm3 STP cm−3 poly) |
|---|---|---|---|---|---|
| PEV amorph | 0–0.9 | 7.757 | 0.605 | 1.502 | 0.282 |
| PEV semicryst | 0–0.9 | 6.661 | 0.528 | 3.087 | 0.029 |
| PET amorph Dubelley | 0–0.9 | 10.161 | 0.496 | 3.217 | 0.049 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giacobazzi, G.; Gioia, C.; Vannini, M.; Marchese, P.; Guillard, V.; Angellier-Coussy, H.; Celli, A. Water Vapor Sorption and Diffusivity in Bio-Based Poly(ethylene vanillate)—PEV. Polymers 2021, 13, 524. https://doi.org/10.3390/polym13040524
Giacobazzi G, Gioia C, Vannini M, Marchese P, Guillard V, Angellier-Coussy H, Celli A. Water Vapor Sorption and Diffusivity in Bio-Based Poly(ethylene vanillate)—PEV. Polymers. 2021; 13(4):524. https://doi.org/10.3390/polym13040524
Chicago/Turabian StyleGiacobazzi, Greta, Claudio Gioia, Micaela Vannini, Paola Marchese, Valérie Guillard, Hélène Angellier-Coussy, and Annamaria Celli. 2021. "Water Vapor Sorption and Diffusivity in Bio-Based Poly(ethylene vanillate)—PEV" Polymers 13, no. 4: 524. https://doi.org/10.3390/polym13040524








