Thermodynamic Modeling and Validation of the Temperature Influence in Ternary Phase Polymer Systems
Abstract
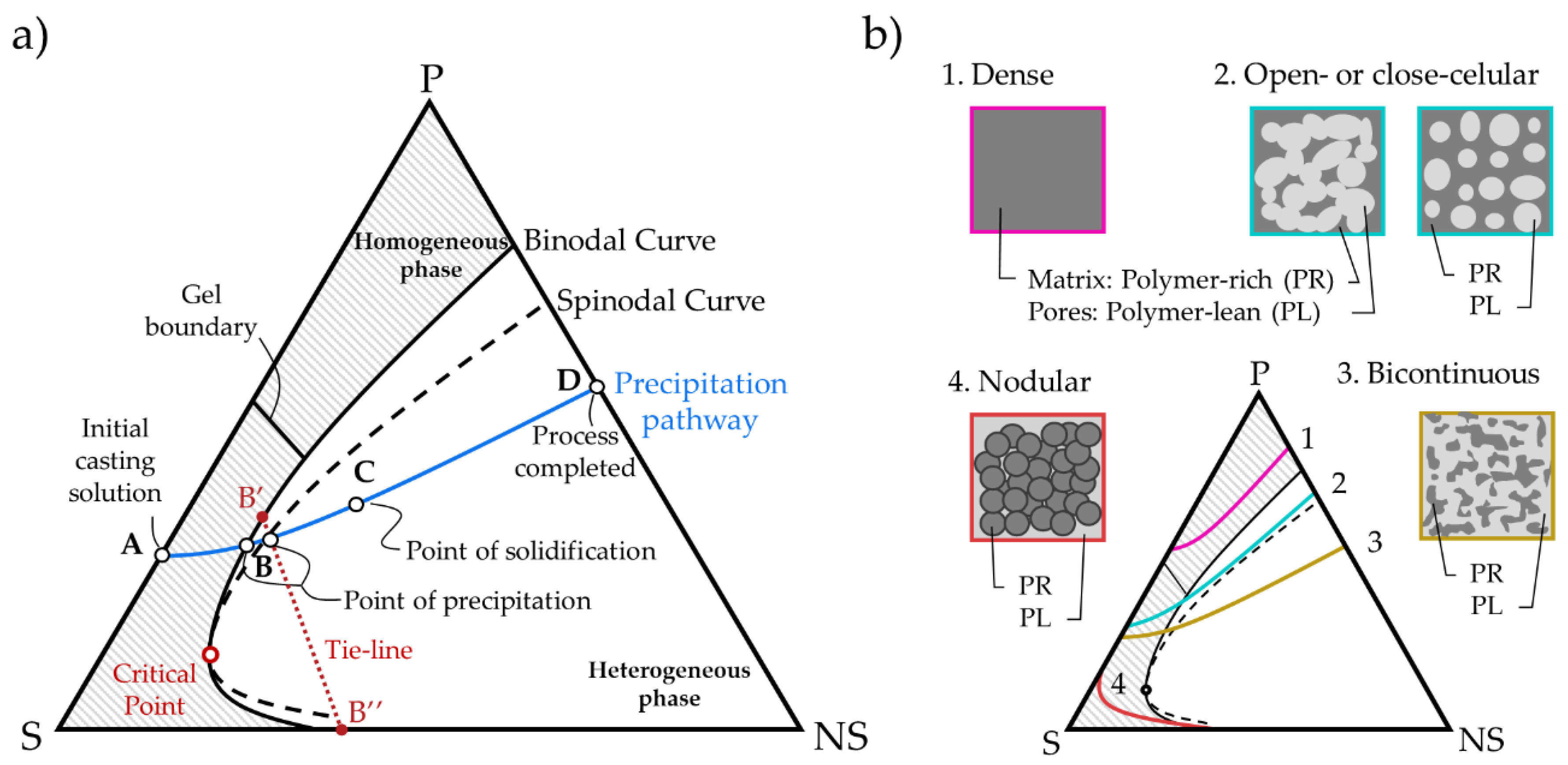
1. Introduction
2. Theoretical Section
2.1. Thermodynamic Model
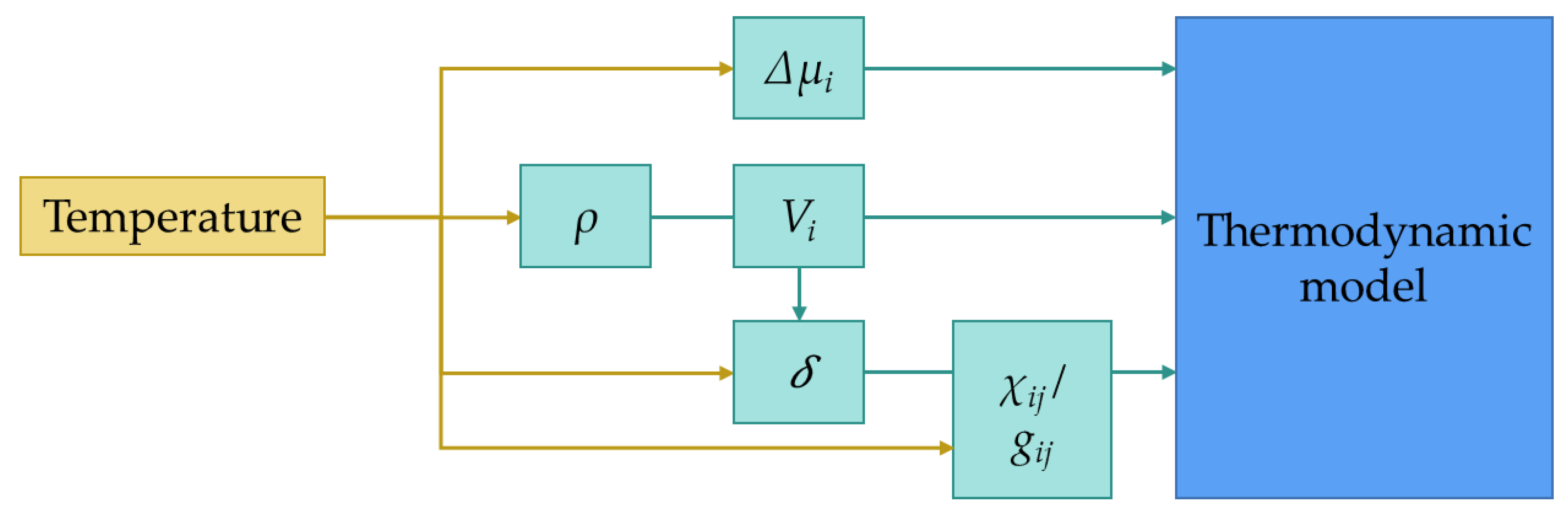
2.2. Influence of the Temperature in the Model
2.3. Calculation Procedure
3. Materials and Methods
3.1. Materials
3.2. Cloud Point
4. Results and Discussion
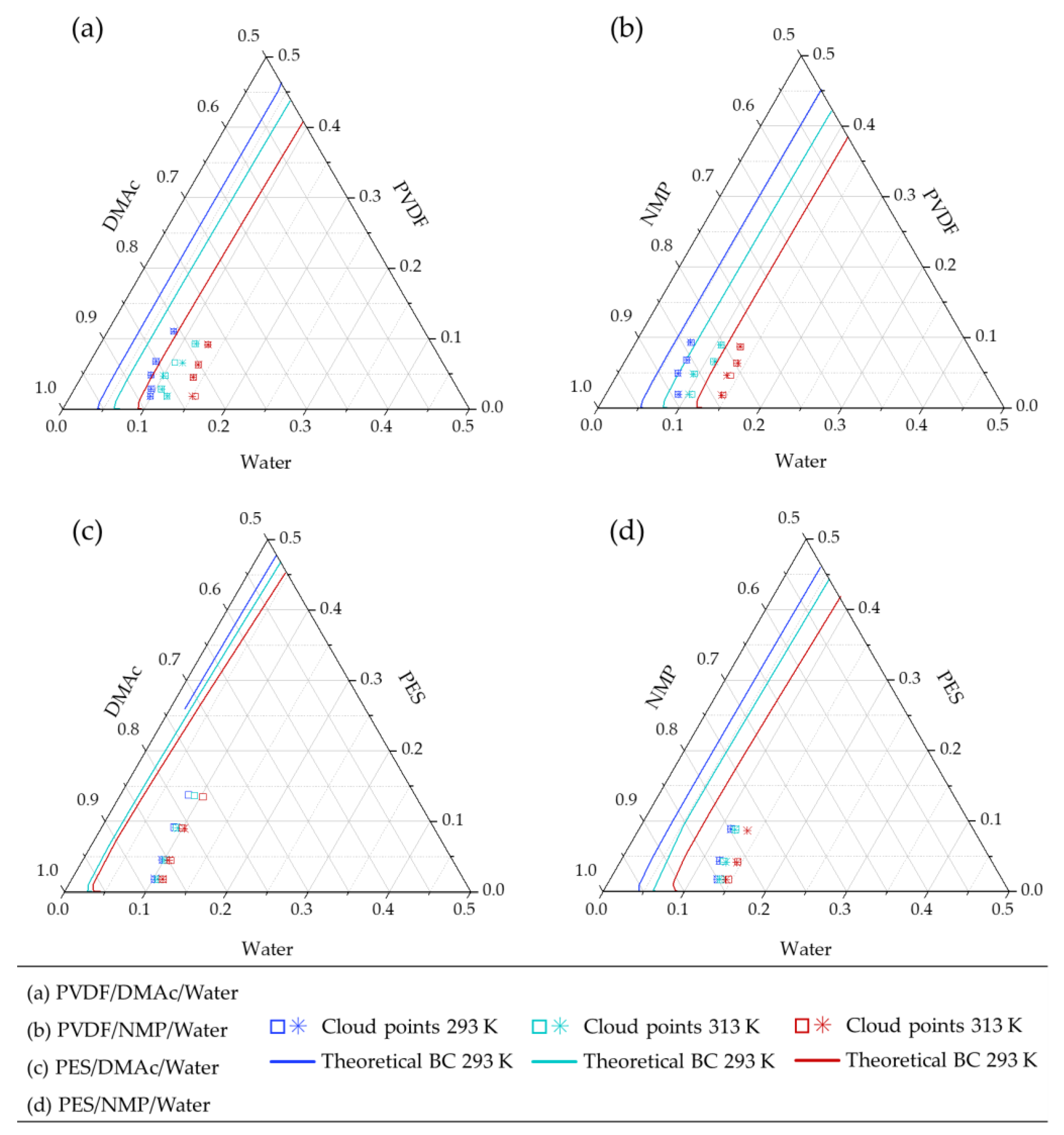
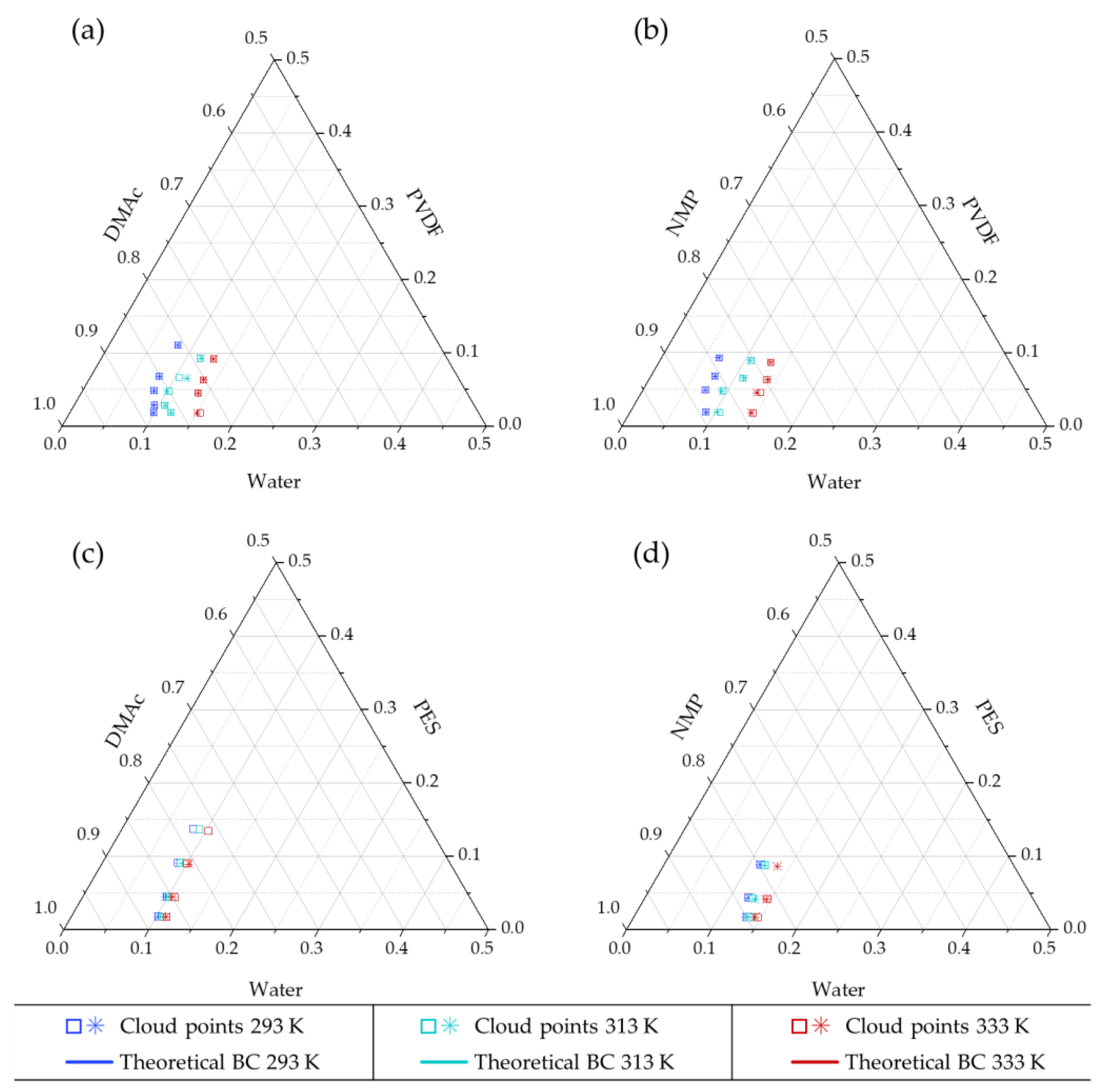
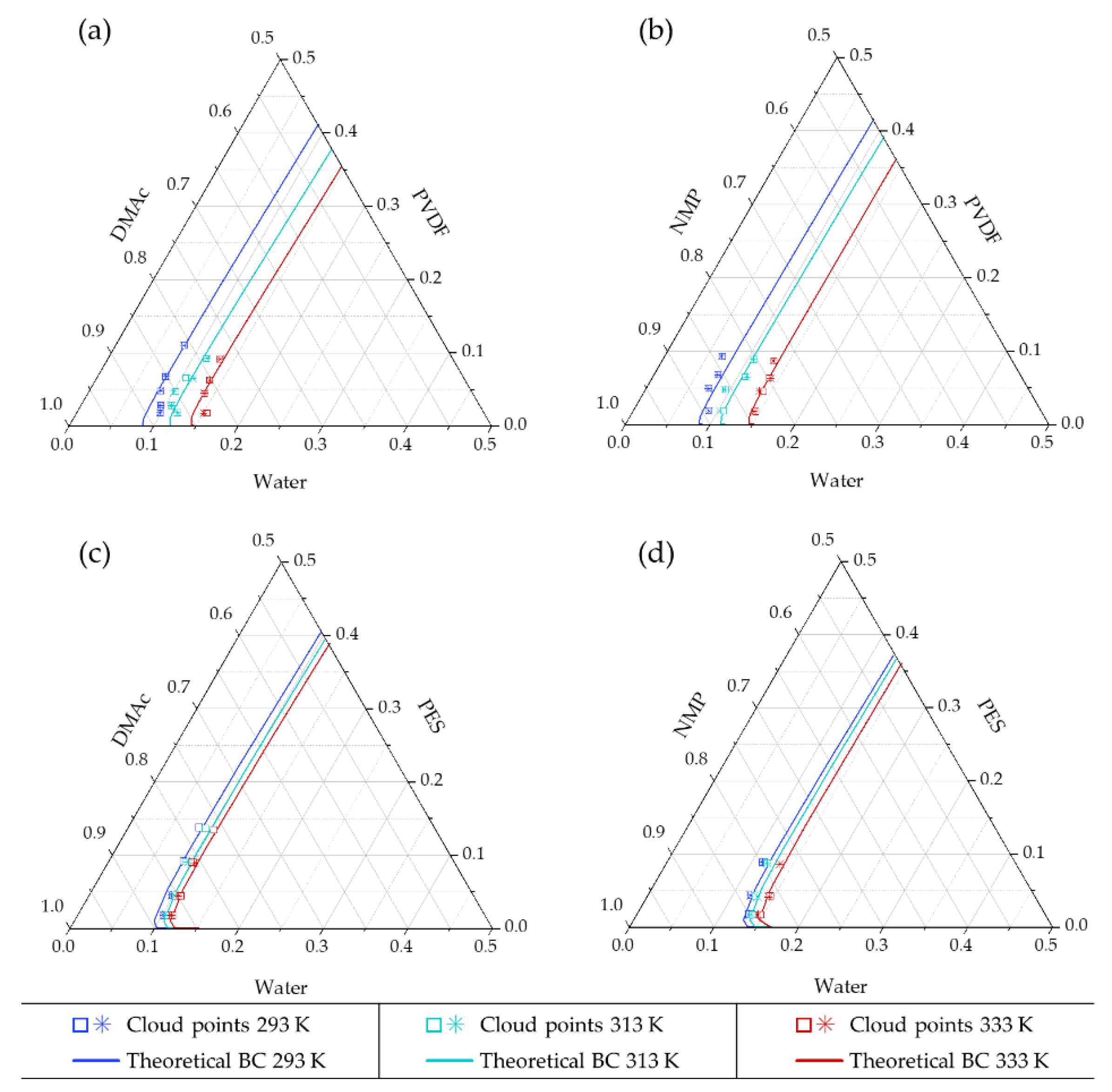
4.1. Experimental Cloud Point
4.2. Mathematical Modeling
4.2.1. Modeling Binodal Curves not Considering the Contribution of the Ternary Interaction Term
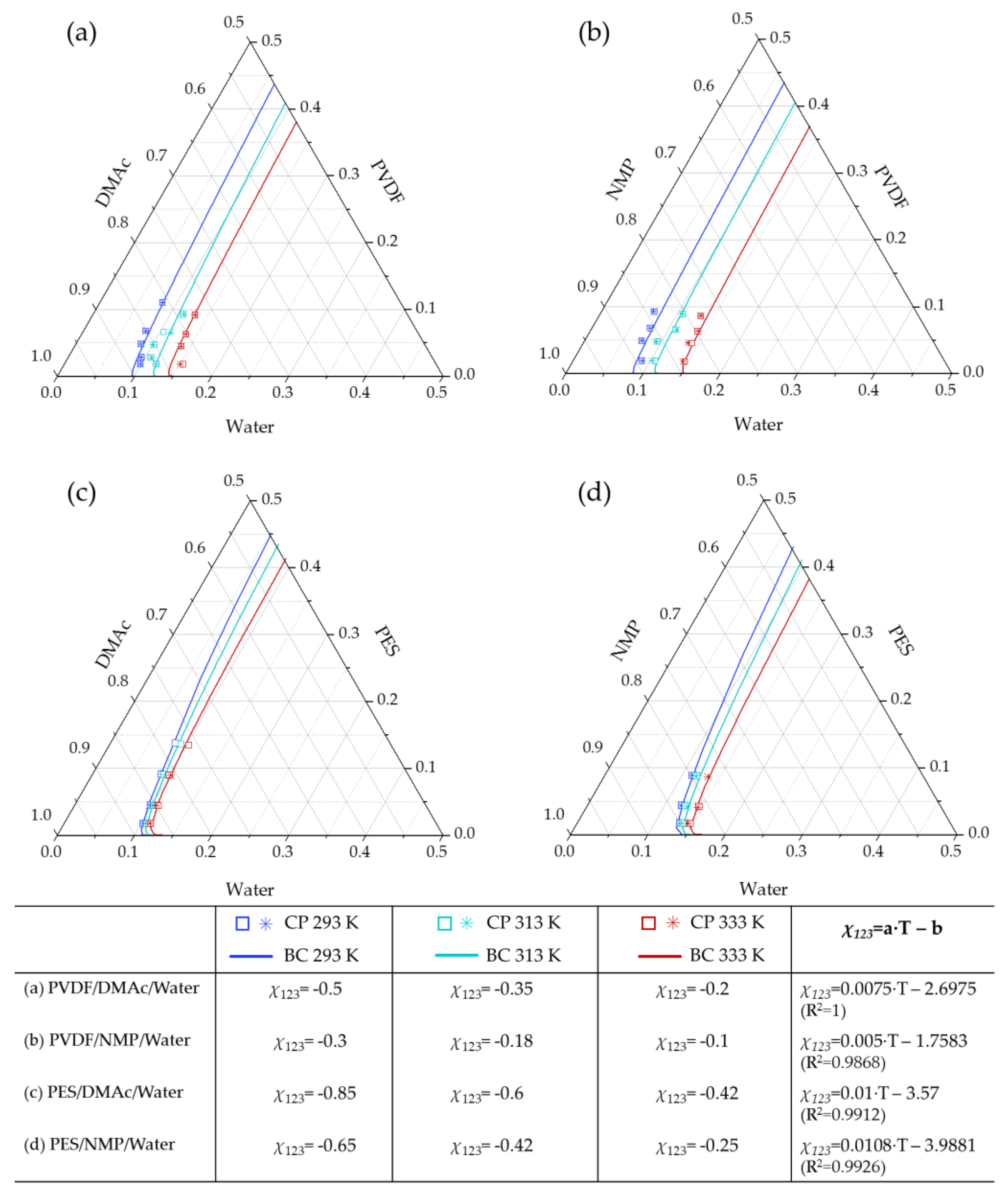
4.2.2. Modeling Binodal Curves Considering the Contribution of the Ternary Interaction Term
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| (A1) | ||
| Combinatorial | (A2) | |
| Residual : residual activity coefficient of group k in a reference solution containing molecules of type i | (A3) | |
| : group residual activity coefficient | (A4) | |
| Surface area/mole fraction ratio | (A5) | |
| Volume/mole fraction ratio | (A6) | |
| (A7) | ||
| Volume of the pure component (i) | (A8) | |
| Surface area of the pure component (i) | (A9) | |
| Area fraction of group (m) | (A10) | |
| Mole fraction of group m in the mixture | (A11) | |
| Group interaction parameter | (A12) |
| Compound | Formula | Structure | GROUP Assignment | Qk | Rk | |
|---|---|---|---|---|---|---|
| Group × Vik | Group-Sub Group No. | |||||
| DMAc | C4H9NO | 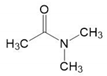 | CH3 × 1 | 1-1 | 1.0608 | 0.6325 |
| CON(CH3)2 × 1 | 48-101 | 1.9643 | 2.4748 | |||
| NMP | C5H9NO | 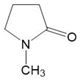 | cy-CH2 × 3 | 42-78 | 0.8635 | 0.7136 |
| cy-CON-CH3 × 1 | 46-86 | 3.2 | 3.981 | |||
| Water | H2O | 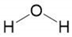 | H2O × 1 | 7 | 2.4561 | 1.7334 |
| n,m | anm,1 | anm,2 | anm,3 | amn,1 | amn,2 | amn,3 | |
|---|---|---|---|---|---|---|---|
| Water–DMAc | 1,7 | 1391.3 | −3.6156 | 0.001144 | −17.253 | 0.8389 | 0.000902 |
| 1,48 | 1529.52 | −6.2025 | 0.00975 | 82.6 | −0.615 | −0.00062 | |
| 7,48 | 64.43999 | −0.0094 | - | −439.58 | 0.3142 | - | |
| Water–NMP | 7,42 | 274.37 | −0.5861 | −0.0003 | 1632.9 | −2.8719 | 0.003455 |
| 7,46 | 659.22 | −1.8841 | - | −588.21 | 0.9707 | - | |
| 42,46 | 298.46 | −0.6823 | - | 499.59 | −0.8158 | - |
| ΦPVDF | ΦDMAc | ΦWater | |||||||
| 293 K | 0.0183 | ± | 2.00 × 105 | 0.8837 | ± | 5.90 × 104 | 0.0988 | ± | 1.95 × 104 |
| 0.0286 | ± | 1.00 × 105 | 0.8769 | ± | 2.15 × 104 | 0.0946 | ± | 2.25 × 104 | |
| 0.0482 | ± | 5.00 × 106 | 0.8673 | ± | 6.00 × 105 | 0.0845 | ± | 5.50 × 105 | |
| 0.0677 | ± | 2.00 × 105 | 0.8516 | ± | 8.50 × 105 | 0.0808 | ± | 1.05 × 104 | |
| 0.1103 | ± | 9.00 × 105 | 0.8084 | ± | 8.50 × 105 | 0.0813 | ± | 1.75 × 104 | |
| 313 K | 0.0184 | ± | 1.05 × 105 | 0.8626 | ± | 1.25 × 104 | 0.1190 | ± | 2.30 × 104 |
| 0.0282 | ± | 4.50 × 105 | 0.8645 | ± | 4.30 × 104 | 0.1073 | ± | 4.80 × 104 | |
| 0.0473 | ± | 6.50× 105 | 0.8512 | ± | 1.17 × 103 | 0.1016 | ± | 1.24 × 103 | |
| 0.0656 | ± | 3.45 × 104 | 0.8247 | ± | 4.55 × 103 | 0.1098 | ± | 4.89 × 103 | |
| 0.0926 | ± | 2.60 × 104 | 0.7904 | ± | 6.80 × 104 | 0.1169 | ± | 4.20 × 104 | |
| 333 K | 0.0180 | ± | 4.00 × 105 | 0.8297 | ± | 1.93× 103 | 0.1523 | ± | 1.97 × 103 |
| 0.0449 | ± | 0.00 × 100 | 0.8172 | ± | 0.00 × 100 | 0.1379 | ± | 0.00 × 100 | |
| 0.0630 | ± | 0.00 × 100 | 0.8017 | ± | 0.00 × 100 | 0.1354 | ± | 0.00 × 100 | |
| 0.0915 | ± | 0.00 × 100 | 0.7756 | ± | 0.00 × 100 | 0.1329 | ± | 0.00 × 100 | |
| ΦPVDF | ΦNMP | ΦWater | |||||||
| 293 K | 0.0192 | ± | 1.00 × 105 | 0.8917 | ± | 2.45 × 104 | 0.0892 | ± | 2.55 × 104 |
| 0.0491 | ± | 5.00 × 106 | 0.8771 | ± | 1.25 × 104 | 0.0738 | ± | 1.35 × 104 | |
| 0.0680 | ± | 3.00 × 105 | 0.8565 | ± | 1.80 × 104 | 0.0755 | ± | 2.05 × 104 | |
| 0.0929 | ± | 2.05 × 104 | 0.8392 | ± | 2.90 × 104 | 0.0679 | ± | 4.95 × 104 | |
| 313 K | 0.0189 | ± | 3.00 × 105 | 0.8767 | ± | 1.73 × 103 | 0.1044 | ± | 1.77 × 103 |
| 0.0480 | ± | 4.00 × 105 | 0.8576 | ± | 7.30 × 104 | 0.0944 | ± | 7.75 × 104 | |
| 0.0655 | ± | 7.00 × 105 | 0.8245 | ± | 7.30 × 104 | 0.1101 | ± | 8.05 × 104 | |
| 0.0890 | ± | 2.10 × 104 | 0.8039 | ± | 4.15 × 104 | 0.1071 | ± | 6.20 × 104 | |
| 333 K | 0.0180 | ± | 2.00 × 105 | 0.8378 | ± | 1.07 × 103 | 0.1442 | ± | 1.09 × 103 |
| 0.0457 | ± | 1.40 × 104 | 0.8161 | ± | 2.44 × 103 | 0.1382 | ± | 2.58 × 103 | |
| 0.0633 | ± | 8.00 × 105 | 0.7974 | ± | 8.55 × 104 | 0.1393 | ± | 9.30 × 104 | |
| 0.0865 | ± | 1.65 × 104 | 0.7816 | ± | 4.50 × 105 | 0.1318 | ± | 2.10 × 104 | |
| ΦPES | ΦDMAc | ΦWater | |||||||
| 293 K | 0.0179 | ± | 2.00 × 105 | 0.8798 | ± | 6.50 × 105 | 0.1023 | ± | 9.00 × 105 |
| 0.0450 | ± | 7.00 × 105 | 0.8566 | ± | 4.90 × 104 | 0.0984 | ± | 5.60 × 104 | |
| 0.0912 | ± | 3.65 × 104 | 0.8188 | ± | 7.50 × 104 | 0.0900 | ± | 1.11 × 103 | |
| 0.1375 | ± | 0.00 × 100 | 0.7787 | ± | 0.00 × 100 | 0.0838 | ± | 0.00 × 100 | |
| 313 K | 0.0178 | ± | 3.50 × 105 | 0.8759 | ± | 6.45 × 104 | 0.1063 | ± | 6.80 × 104 |
| 0.0448 | ± | 8.00 × 105 | 0.8533 | ± | 7.85 × 104 | 0.1018 | ± | 8.70 × 104 | |
| 0.0908 | ± | 3.80 × 104 | 0.8156 | ± | 9.20 × 104 | 0.0936 | ± | 1.30 × 103 | |
| 0.0684 | ± | 0.00 × 100 | 0.7751 | ± | 0.00 × 100 | 0.0881 | ± | 0.00 × 100 | |
| 333 K | 0.0177 | ± | 2.50 × 105 | 0.8703 | ± | 3.05 × 104 | 0.1120 | ± | 3.30 × 104 |
| 0.0446 | ± | 1.05 × 104 | 0.8483 | ± | 1.14 × 103 | 0.1071 | ± | 1.24 × 103 | |
| 0.0901 | ± | 3.55 × 104 | 0.8086 | ± | 7.50 × 10 | 0.1013 | ± | 1.11 × 103 | |
| ΦPES | ΦNMP | ΦWater | |||||||
| 293 K | 0.0174 | ± | 4.00 × 105 | 0.8511 | ± | 9.20 × 104 | 0.1315 | ± | 9.60 × 104 |
| 0.0429 | ± | 7.55 × 104 | 0.8341 | ± | 3.00 × 104 | 0.1230 | ± | 1.06 × 103 | |
| 0.0890 | ± | 5.25 × 104 | 0.8025 | ± | 3.68 × 103 | 0.1135 | ± | 8.25 × 104 | |
| 313 K | 0.0173 | ± | 4.00 × 105 | 0.8468 | ± | 8.75 × 104 | 0.1359 | ± | 9.10 × 104 |
| 0.0426 | ± | 7.75 × 104 | 0.8286 | ± | 6.90 × 104 | 0.1287 | ± | 1.46 × 103 | |
| 0.0881 | ± | 0.00 × 100 | 0.7926 | ± | 0.00 × 100 | 0.1194 | ± | 0.00 × 100 | |
| 333 K | 0.0171 | ± | 5.00 × 105 | 0.8382 | ± | 1.46 × 103 | 0.1447 | ± | 1.50 × 103 |
| 0.0419 | ± | 6.70 × 104 | 0.8138 | ± | 1.05 × 103 | 0.1444 | ± | 3.80 × 104 | |
| 0.0863 | ± | 0.00 × 100 | 0.7792 | ± | 0.00 × 100 | 0.1345 | ± | 0.00 × 100 | |
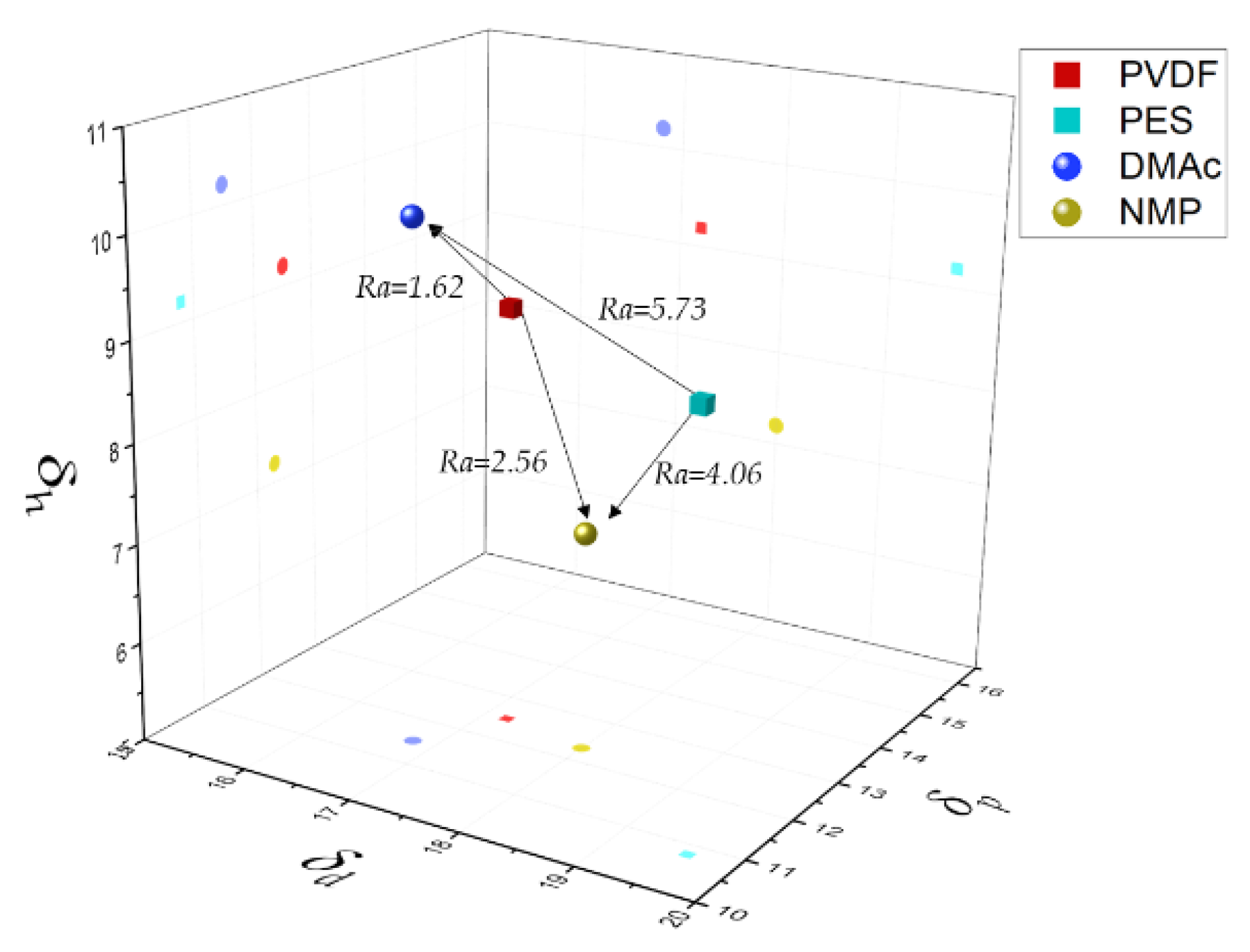
| T (K) | δd (MPa1/2) | δp (MPa1/2) | δh (MPa1/2) | δT (MPa1/2) |
|---|---|---|---|---|
| Polymer–PVDF | ||||
| 298 | 17.2 | 12.5 | 9.2 | 23.167 |
| 293 | 17.234 | 12.510 | 9.264 | 23.223 |
| 313 | 17.099 | 12.471 | 9.012 | 23.003 |
| 333 | 16.967 | 12.432 | 8.767 | 22.788 |
| Polymer–PES | ||||
| 298 | 19.6 | 10.8 | 9.2 | 24.196 |
| 293 | 19.632 | 10.807 | 9.262 | 24.249 |
| 313 | 19.503 | 10.779 | 9.015 | 24.038 |
| 333 | 19.376 | 10.750 | 8.775 | 23.833 |
| Solvent–DMAc | ||||
| 298 | 16.8 | 11.5 | 10.2 | 22.771 |
| 293 | 16.898 | 11.527 | 10.286 | 22.896 |
| 313 | 16.506 | 11.419 | 9.945 | 22.399 |
| 333 | 16.106 | 11.308 | 9.610 | 21.900 |
| Solvent–NMP | ||||
| 298 | 18 | 12.3 | 7.2 | 22.959 |
| 293 | 18.086 | 12.324 | 7.258 | 23.058 |
| 313 | 17.735 | 12.227 | 7.028 | 22.659 |
| 333 | 17.378 | 12.128 | 6.803 | 22.257 |
| Non-solvent–Water | ||||
| 298 | 15.5 | 16 | 42.3 | 47.807 |
| 293 | 15.538 | 16.015 | 42.600 | 48.090 |
| 313 | 15.388 | 15.954 | 41.413 | 46.972 |
| 333 | 15.211 | 15.880 | 40.228 | 45.846 |
References
- Wang, D.M.; Lai, J.Y. Recent advances in preparation and morphology control of polymeric membranes formed by nonsolvent induced phase separation. Curr. Opin. Chem. Eng. 2013, 2, 229–237. [Google Scholar] [CrossRef]
- Mulder, M. Basic Principles of Membrane Technology; Kluwer Academic Publishers: Enschede, The Netherlands, 1991; ISBN 0-7923-0978-2. [Google Scholar]
- Prézélus, F.; Tiruta-Barna, L.; Guigui, C.; Remigy, J.C. A generic process modelling—LCA approach for UF membrane fabrication: Application to cellulose acetate membranes. J. Memb. Sci. 2021, 618, 118594. [Google Scholar] [CrossRef]
- Romay, M.; Diban, N.; Rivero, M.J.; Urtiaga, A.; Ortiz, I. Critical Issues and Guidelines to Improve the Performance of Photocatalytic Polymeric Membranes. Catalysts 2020, 10, 570. [Google Scholar] [CrossRef]
- Baker, R.W. Membrane Technology and Applications, 3rd ed.; Wiley: West Sussex, UK, 2012; ISBN 9780470743720. [Google Scholar]
- Kahrs, C.; Gühlstorf, T.; Schwellenbach, J. Influences of different preparation variables on polymeric membrane formation via nonsolvent induced phase separation. J. Appl. Polym. Sci. 2020, 137, 48852. [Google Scholar] [CrossRef]
- Sadeghi, A.; Nazem, H.; Rezakazemi, M.; Shirazian, S. Predictive construction of phase diagram of ternary solutions containing polymer/solvent/nonsolvent using modified Flory-Huggins model. J. Mol. Liq. 2018, 263, 282–287. [Google Scholar] [CrossRef]
- Keshavarz, L.; Khansary, M.A.; Shirazian, S. Phase diagram of ternary polymeric solutions containing nonsolvent/ solvent/polymer: Theoretical calculation and experimental validation. Polymer 2015, 73, 1–8. [Google Scholar] [CrossRef]
- Ariono, D.; Aryanti, P.T.P.; Hakim, A.N.; Subagjo, S.; Wenten, I.G. Determination of thermodynamic properties of polysulfone/PEG membrane solutions based on Flory-Huggins model. AIP Conf. Proc. 2017, 1840, 090008. [Google Scholar]
- van Krevelen, D.W.; te Nijenhuis, K. Properties of Polymers, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009; ISBN 978-0-08-054819-7. [Google Scholar]
- Just, S.; Sievert, F.; Thommes, M.; Breitkreutz, J. Improved group contribution parameter set for the application of solubility parameters to melt extrusion. Eur. J. Pharm. Biopharm. 2013, 85, 1191–1199. [Google Scholar] [CrossRef] [PubMed]
- Stefanis, E.; Panayiotou, C. Prediction of Hansen Solubility Parameters with a New Group-Contribution Method. Int. J. Thermophys. 2008, 29, 568–585. [Google Scholar] [CrossRef]
- Kahrs, C.; Metze, M.; Fricke, C.; Schwellenbach, J. Thermodynamic analysis of polymer solutions for the production of polymeric membranes. J. Mol. Liq. 2019, 291. [Google Scholar] [CrossRef]
- Xu, L.; Qiu, F. Simultaneous determination of three Flory–Huggins interaction parameters in polymer/solvent/nonsolvent systems by viscosity and cloud point measurements. Polymer 2014, 55, 6795–6802. [Google Scholar] [CrossRef]
- Nivedita, S.; Ahamed, D.; Joseph, S. Thermodynamic analysis of phase diagram of H2O-DMF-PCL system: Investigation on the influence of inorganic additives TiO2/MMT. J. Mater. Sci. 2020, 55, 5431–5444. [Google Scholar] [CrossRef]
- Cohen, C.; Tanny, G.B.; Prager, S. Diffusion-Controlled Formation of Porous Structures in Ternary Polymer Systems. J. Polym. Sci. Polym. Phys. Ed. 1979, 17, 477–489. [Google Scholar] [CrossRef]
- Altena, F.W.; Smolders, C.A. Calculation of Liquid-Liquid Phase Separation in a Ternary System of a Polymer in a Mixture of a Solvent and a Nonsolvent. Org. Mol. Photophy. 1982, 15, 1558. [Google Scholar] [CrossRef]
- Yilmaz, L.; McHugh, A.J. Analysis of nonsolvent–solvent–polymer phase diagrams and their relevance to membrane formation modeling. J. Appl. Polym. Sci. 1986, 31, 997–1018. [Google Scholar] [CrossRef]
- Tan, X.M.; Rodrigue, D. A review on porous polymeric membrane preparation. Part I: Production Techniques with Polysulfone and Poly (Vinylidene Fluoride). Polymers 2019, 11, 1160. [Google Scholar] [CrossRef]
- Wittig, R.; Lohmann, J.; Gmehling, J. Vapor-Liquid Equilibria by UNIFAC Group Contribution. 6. Revision and Extension. Ind. Eng. Chem. Res. 2003, 42, 183–188. [Google Scholar] [CrossRef]
- Kurada, K.V.; De, S. Polyaniline doped ultrafiltration membranes: Mechanism of membrane formation and pH response characteristics. Polymer 2018, 153, 201–213. [Google Scholar] [CrossRef]
- Kurada, K.V.; Mukherjee, M.; De, S. Permeability hysteresis of polypyrrole-polysulfone blend ultrafiltration membranes: Study of phase separation thermodynamics and pH responsive membrane properties. Sep. Purif. Technol. 2019, 227, 115736. [Google Scholar] [CrossRef]
- Hansen, C.M. Hansen solubility parameters. A User’s Handbook, 2nd ed.; CRC Press Taylor & Francis Group: Oxfordshire, UK, 2007; Volume 118, ISBN 0-8493-7248-8. [Google Scholar]
- Zhang, J.; Zhang, Y.; Zhao, J. Thermodynamic study of non-solvent/dimethyl sulfoxide/polyacrylonitrile ternary systems: Effects of the non-solvent species. Polym. Bull. 2011, 67, 1073–1089. [Google Scholar] [CrossRef]
- Tang, Y.H.; Ledieu, E.; Cervellere, M.R.; Millett, P.C.; Ford, D.M.; Qian, X. Formation of polyethersulfone membranes via nonsolvent induced phase separation process from dissipative particle dynamics simulations. J. Memb. Sci. 2020, 599, 117826. [Google Scholar] [CrossRef]
- Kurada, K.V.; De, S. Modeling of solution thermodynamics: A method for tuning the properties of blend polymeric membranes. J. Memb. Sci. 2017, 540, 485–495. [Google Scholar] [CrossRef]
- Wei, Y.-M.; Xu, Z.-L.; Yang, X.-T.; Liu, H.-L. Mathematical calculation of binodal curves of a polymer/solvent/nonsolvent system in the phase inversion process. Desalination 2006, 192, 91–104. [Google Scholar] [CrossRef]
- Mohsenpour, S.; Safekordi, A.; Tavakolmoghadam, M.; Rekabdar, F.; Hemmati, M. Comparison of the membrane morphology based on the phase diagram using PVP as an organic additive and TiO2 as an inorganic additive. Polymer 2016, 97, 559–568. [Google Scholar] [CrossRef]
- Hamta, A.; Ashtiani, F.Z.; Karimi, M.; Safikhani, A. Manipulating of polyacrylonitrile membrane porosity via SiO2 and TiO2 nanoparticles: Thermodynamic and experimental point of view. Polym. Adv. Technol. 2021, 32, 872–885. [Google Scholar] [CrossRef]
- Sandler, S.I. Chemical and Engineering Thermodynamics, 3rd ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1940; ISBN 0-471-18210-9. [Google Scholar]
- Published Parameters UNIFAC(Do)—DDBST GmbH. Available online: http://www.ddbst.com/PublishedParametersUNIFACDO.html#ListOfMainGroups (accessed on 6 October 2020).
- Tompa, H. Phase relationships in polymer solutions. Trans. Faraday Soc. 1949, 45, 1142–1152. [Google Scholar] [CrossRef]
- Yeow, M.L.; Liu, Y.T.; Li, K. Isothermal Phase Diagrams and Phase-Inversion Behavior of Poly(vinylidene fluoride)/Solvents/Additives/Water Systems. J. Appl. Polym. Sci. 2003, 90, 2150–2155. [Google Scholar] [CrossRef]
- Fadaei, A.; Salimi, A.; Mirzataheri, M. Structural elucidation of morphology and performance of the PVDF/PEG membrane. J. Polym. Res. 2014, 21, 1–8. [Google Scholar] [CrossRef]
- Barzin, J.; Sadatnia, B. Theoretical phase diagram calculation and membrane morphology evaluation for water/solvent/polyethersulfone systems. Polymer 2007, 48, 1620–1631. [Google Scholar] [CrossRef]
- Lau, W.W.Y.; Guiver, M.D.; Matsuura, T. Phase separation in polysulfone/solvent/water and polyethersulfone/solvent/water systems. J. Memb. Sci. 1991, 59, 219–227. [Google Scholar] [CrossRef][Green Version]
- Zeman, L.; Tkacik, G. Thermodynamic analysis of a membrane-forming system water/N-methyl-2-pyrrolidone/polyethersulfone. J. Memb. Sci. 1988, 36, 119–140. [Google Scholar] [CrossRef]
- Sadrzadeh, M.; Bhattacharjee, S. Rational design of phase inversion membranes by tailoring thermodynamics and kinetics of casting solution using polymer additives. J. Memb. Sci. 2013, 441, 31–44. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Sun, D.; An, Q.; Chen, H. Formation mechanism and crystallization of poly(vinylidene fluoride) membrane via immersion precipitation method. Desalination 2009, 236, 170–178. [Google Scholar] [CrossRef]
- Sun, A.C.; Kosar, W.; Zhang, Y.; Feng, X. A study of thermodynamics and kinetics pertinent to formation of PVDF membranes by phase inversion. Desalination 2013, 309, 156–164. [Google Scholar] [CrossRef]
- Fashandi, H.; Yegane, A.; Abolhasani, M.M. Interplay of Liquid-liquid and Solid-liquid Phase Separation Mechanisms in Porosity and Polymorphism Evolution Within Poly(vinylidene fluoride) Nanofibers. Fibers Polym. 2015, 16, 326–344. [Google Scholar] [CrossRef]
- Sukitpaneenit, P.; Chung, T.S. Molecular elucidation of morphology and mechanical properties of PVDF hollow fiber membranes from aspects of phase inversion, crystallization and rheology. J. Memb. Sci. 2009, 340, 192–205. [Google Scholar] [CrossRef]
- Bottino, A.; Camera-Roda, G.; Capannelli, G.; Munari, S. The formation of microporous polyvinylidene difluoride membranes by phase separation. J. Memb. Sci. 1991, 57, 1–20. [Google Scholar] [CrossRef]
- Enayatzadeh, M.; Mohammadi, T. Morphology and performance of poly(vinylidene fluoride) flat sheet membranes: Thermodynamic and kinetic aspects. J. Appl. Polym. Sci. 2018, 135, 46419. [Google Scholar] [CrossRef]
- Zuo, D.; Li, H. Membrane formation mechanism for water-solvent-pvdf systems and membrane structure for ultrofiltration application. Adv. Mater. Res. 2012, 578, 129–132. [Google Scholar] [CrossRef]
- Mansourizadeh, A.; Mousavian, S. Structurally developed microporous polyvinylidene fluoride hollow-fiber membranes for CO2 absorption with diethanolamine solution. J. Polym. Res. 2013, 20, 1–12. [Google Scholar] [CrossRef]
- Mohsenpour, S.; Esmaeilzadeh, F.; Safekordi, A.; Tavakolmoghadam, M.; Rekabdar, F.; Hemmati, M. The role of thermodynamic parameter on membrane morphology based on phase diagram. J. Mol. Liq. 2016, 224, 776–785. [Google Scholar] [CrossRef]
- Chen, Q.P.; Xie, S.; Foudazi, R.; Lodge, T.P.; Siepmann, J.I. Understanding the Molecular Weight Dependence of χ and the Effect of Dispersity on Polymer Blend Phase Diagrams. Macromolecules 2018, 51, 3774–3787. [Google Scholar] [CrossRef]
- Lu, H.; Du, S. A phenomenological thermodynamic model for the chemo-responsive shape memory effect in polymers based on Flory-Huggins solution theory. Polym. Chem. 2014, 5, 1155–1162. [Google Scholar] [CrossRef]
- Lu, H.; Liu, Y.; Leng, J.; Du, S. Qualitative separation of the physical swelling effect on the recovery behavior of shape memory polymer. Eur. Polym. J. 2010, 46, 1908–1914. [Google Scholar] [CrossRef]
- Lindvig, T.; Michelsen, M.L.; Kontogeorgis, G.M. A Flory-Huggins model based on the Hansen solubility parameters. Fluid Phase Equilib. 2002, 203, 247–260. [Google Scholar] [CrossRef]
- Barth, C.; Wolf, B.A. Quick and reliable routes to phase diagrams for polyethersulfone and polysulfone membrane formation. Macromol. Chem. Phys. 2000, 201, 365–374. [Google Scholar] [CrossRef]
- Young, T.H.; Cheng, L.P.; Hsieh, C.C.; Chen, L.W. Phase behavior of EVAL polymers in water-2-propanol cosolvent. Macromolecules 1998, 31, 1229–1235. [Google Scholar] [CrossRef]
- Wolf, B.A.; Molinari, R.J. True cosolvency. Acetone/diethylether/polystyrene. Die Makromol. Chemie 1973, 173, 241–245. [Google Scholar] [CrossRef]
- Marino, T.; Galiano, F.; Simone, S.; Figoli, A. DMSO EVOLTM as novel non-toxic solvent for polyethersulfone membrane preparation. Environ. Sci. Pollut. Res. 2019, 26, 14774–14785. [Google Scholar] [CrossRef]
- Xie, W.; Tiraferri, A.; Liu, B.; Tang, P.; Wang, F.; Chen, S.; Figoli, A.; Chu, L.Y. First Exploration on a Poly(vinyl chloride) Ultrafiltration Membrane Prepared by Using the Sustainable Green Solvent PolarClean. ACS Sustain. Chem. Eng. 2020, 8, 91–101. [Google Scholar] [CrossRef]
- DDBST—DDBST GmbH. Available online: http://www.ddbst.com/ (accessed on 6 October 2020).

| Solvent | Formula | Structure | Mw (g/mol) | T (K) | ρ (g/cm3) | Vi (cm3/mol) |
|---|---|---|---|---|---|---|
| DMAc | C4H9NO |  | 87.12 | 298 | 0.9365 | 93.031 |
| 293 | 0.9408 | 92.599 | ||||
| 313 | 0.9233 | 94.355 | ||||
| 333 | 0.9054 | 96.224 | ||||
| NMP | C5H9NO | 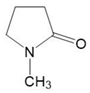 | 99.13 | 298 | 1.0262 | 96.600 |
| 293 | 1.0302 | 96.231 | ||||
| 313 | 1.0141 | 97.754 | ||||
| 333 | 0.9977 | 99.357 | ||||
| Water | H2O | 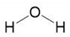 | 18.01 | 298 | 0.9945 | 18.114 |
| 293 | 0.9965 | 18.079 | ||||
| 313 | 0.9888 | 18.219 | ||||
| 333 | 0.9797 | 18.388 |
| δd (MPa)1/2 | δp (MPa)1/2 | δh (MPa)1/2 | δT (MPa)1/2 | |
|---|---|---|---|---|
| PVDF | 17.2 | 12.5 | 9.2 | 23.167 |
| PES | 19.6 | 10.8 | 9.2 | 24.196 |
| DMAc | 16.8 | 11.5 | 10.2 | 22.771 |
| NMP | 18 | 12.3 | 7.2 | 22.959 |
| Water | 15.5 | 16 | 42.3 | 47.807 |
| Polymer | Formula | Structure | ρ (g/cm3) | Mw* (g/mol) | Vw (cm3/mol) | T (K) | Vi* (cm3/mol) |
|---|---|---|---|---|---|---|---|
| PVDF | C2H2F2 | 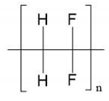 | 1.76 | 64.03 | 25.03 | 298 | 35.896 |
| 293 | 35.839 | ||||||
| 313 | 36.064 | ||||||
| 333 | 36.290 | ||||||
| PES | C12H8SO3 | 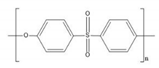 | 1.38 | 232.25 | 112.15 | 298 | 190.997 |
| 293 | 190.745 | ||||||
| 313 | 191.754 | ||||||
| 333 | 192.763 |
| Calculated Parameters | Fitted Parameters | ||
|---|---|---|---|
| χ13 | Equation (9) | α13 | Equation (9) |
| χ23 | Equation (9) | α23 | Equation (9) |
| g12 | Equation (19) | χ123 | Equations (4)–(6) |
| System | T (K) | a0 | a1 | a2 | a3 | a4 | a5 | a6 |
|---|---|---|---|---|---|---|---|---|
| DMAc/Water | 293 | 0.2265 | −0.0758 | 0.2781 | −1.1099 | 1.4731 | −0.815 | |
| 313 | 0.3396 | −0.0269 | 0.3184 | −1.1455 | 1.5387 | −0.8392 | ||
| 333 | 0.4223 | 0.0945 | −0.358 | 1.5048 | −3.2626 | 3.316 | −1.3648 | |
| NMP/Water | 293 | 0.3442 | 0.0751 | −0.0107 | 0.0549 | −0.0411 | ||
| 313 | 0.4617 | 0.1069 | −0.0234 | 0.0871 | −0.0693 | |||
| 333 | 0.5438 | 0.1373 | −0.0365 | 0.1273 | −0.1003 |
| Temperature (K) | 293 | 313 | 333 | |||
|---|---|---|---|---|---|---|
| Interaction Parameter | χ13 | χ23 | χ13 | χ23 | χ13 | χ23 |
| PVDF/DMAc/Water | 2.106 | 0.023 | 1.879 | 0.031 | 1.684 | 0.043 |
| PVDF/NMP/Water | 2.106 | 0.069 | 1.879 | 0.053 | 1.684 | 0.042 |
| PES/DMAc/Water | 2.237 | 0.299 | 2.003 | 0.337 | 1.802 | 0.380 |
| PES/NMP/Water | 2.237 | 0.157 | 2.003 | 0.174 | 1.802 | 0.195 |
| 293 K | 313 K | 333 K | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α13 | χ13 | α23 | χ23 | α13 | χ13 | α23 | χ23 | α13 | χ13 | α23 | χ23 | |
| PVDF/DMAc/Water | 0.7 | 1.474 | 1 | 0.0234 | 0.75 | 1.409 | 1 | 0.0307 | 0.83 | 1.397 | 1 | 0.0429 |
| PVDF/NMP/Water | 0.8 | 1.685 | 1 | 0.069 | 0.87 | 1.635 | 1 | 0.053 | 0.93 | 1.566 | 1 | 0.042 |
| PES/DMAc/Water | 0.64 | 1.432 | 0.1 | 0.030 | 0.75 | 1.502 | 0.1 | 0.034 | 0.85 | 1.531 | 0.2 | 0.076 |
| PES/NMP/Water | 0.64 | 1.432 | 0.5 | 0.078 | 0.75 | 1.502 | 0.5 | 0.087 | 0.85 | 1.531 | 0.5 | 0.098 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romay, M.; Diban, N.; Urtiaga, A. Thermodynamic Modeling and Validation of the Temperature Influence in Ternary Phase Polymer Systems. Polymers 2021, 13, 678. https://doi.org/10.3390/polym13050678
Romay M, Diban N, Urtiaga A. Thermodynamic Modeling and Validation of the Temperature Influence in Ternary Phase Polymer Systems. Polymers. 2021; 13(5):678. https://doi.org/10.3390/polym13050678
Chicago/Turabian StyleRomay, Marta, Nazely Diban, and Ane Urtiaga. 2021. "Thermodynamic Modeling and Validation of the Temperature Influence in Ternary Phase Polymer Systems" Polymers 13, no. 5: 678. https://doi.org/10.3390/polym13050678
APA StyleRomay, M., Diban, N., & Urtiaga, A. (2021). Thermodynamic Modeling and Validation of the Temperature Influence in Ternary Phase Polymer Systems. Polymers, 13(5), 678. https://doi.org/10.3390/polym13050678