Practical Prediction Models of Tensile Strength and Reinforcement-Concrete Bond Strength of Low-Calcium Fly Ash Geopolymer Concrete
Abstract
:1. Introduction
1.1. Background
1.2. Main Works
1.3. Research Significance
2. Materials and Methods
2.1. Strength Test
2.1.1. Materials
2.1.2. Mix Proportions
2.1.3. Preparation of Test Specimens
2.1.4. Splitting Tensile Strength Test
2.1.5. Bond Test
2.2. Database
2.3. Proposing Models and Corresponding 90% Prediction Intervals
- Different functions were adopted.
- Besides the bar diameter to development length ratio (d/l) and the minimum cover to bar diameter ratio (cmin/d), CEB-FIP also considered the bar diameter (1/d) and the maximum cover (cmax/cmin).
2.4. Validation of Models
3. Results
3.1. Database of Splitting Tensile Strength
3.2. Database of Bond Strength
4. Discussion
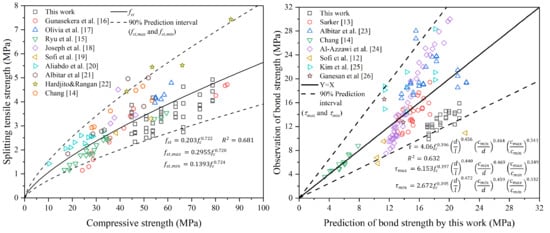
4.1. Splitting Tensile Strength Model
4.2. Validation of Splitting Tensile Strength Model
4.3. Bond Strength Model
4.4. Comparison of Bond Strength of Portland Cement Concrete (PCC) and Fly Ash Geopolymer Concrete (FAGC)
4.5. Validation of Bond Strength Model
4.6. Design Anchorage Length of Reinforced FAGC Beams
4.7. Prediction of Cracking Behaviors of Reinforced FAGC Beams
4.7.1. Cracking Moment
4.7.2. Crack Spacing and Width
5. Conclusions
- Compared with the previous strength models of FAGC, the tensile strength model in this study considers the effect of shape and size of tested specimens on strength, and the bond strength model in this study considers the cover to diameter ratio and the diameter to development length ratio. Therefore, the models in this study can be used as the design equations for estimating the tensile strength and reinforcement-concrete bond strength of FAGC.
- The strength models provide the corresponding 90% prediction intervals. The lower limit of the prediction intervals is the characteristic value of the strength.
- The splitting tensile strength of FAGC is slightly lower than that of PCC with the same compressive strength, while the scatter of the splitting tensile strength of FAGC is close to that of PCC.
- The scatter of the bond strength of FAGC is larger than that of PCC. This results in the fact that for the bond strength of FAGC, although the estimated mean value is higher than that of PCC in the same case, the characteristic value may be lower than that of PCC in the case of a small bar spacing.
- The strength prediction models of PCC cannot be used for FAGC.
- To ensure adequate anchorage and suitable design anchorage lengths of reinforced FAGC beams, the minimum bar spacing needs to be restricted in the design code for FAGC.
- Incorporating the models into the prediction models of the cracking behaviors for PCC gives good predictions on the cracking moment and crack spacing of reinforced FAGC beams.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Elahi, M.M.A.; Hossain, M.M.; Karim, M.R.; Zain, M.F.M.; Shearer, C. A review on alkali-activated binders: Materials composition and fresh properties of concrete. Constr. Build. Mater. 2020, 260, 119788. [Google Scholar] [CrossRef]
- Xie, T.; Visintin, P.; Zhao, X.; Gravina, R. Mix design and mechanical properties of geopolymer and alkali activated concrete: Review of the state-of-the-art and the development of a new unified approach. Constr. Build. Mater. 2020, 256, 119380. [Google Scholar] [CrossRef]
- Zhang, P.; Gao, Z.; Wang, J.; Guo, J.; Ling, Y. Properties of fresh and hardened fly ash/slag based geopolymer concrete: A review. J. Clean. Prod. 2020, 122389. [Google Scholar] [CrossRef]
- Fernández-Jiménez, A.M.; Palomo, A.; López-Hombrados, C. Engineering properties of alkali-activated fly ash concrete. Aci Mater. J. 2006, 103, 106–112. [Google Scholar]
- Bakharev, T. Durability of geopolymer materials in sodium and magnesium sulfate solutions. Cem. Concr. Res. 2005, 35, 1233–1246. [Google Scholar] [CrossRef]
- Song, X. Development and Performance of Class F Fly Ash Based Geopolymer Concretes against Sulphuric Acid Attack. Ph.D. Thesis, School of Civil and Environmental Engineering, The University of New South Wales, Kensington, Australia, 2007. [Google Scholar]
- Kong, D.L.Y.; Sanjayan, J.G.; Sagoe-Crentsil, K. Comparative performance of geopolymers made with metakaolin and fly ash after exposure to elevated temperatures. Cem. Concr. Res. 2007, 37, 1583–1589. [Google Scholar] [CrossRef]
- Adak, D.; Mandal, S. Strength and durability performance of fly ash–based process-modified geopolymer concrete. J. Mater. Civil Eng. 2019, 31, 04019174–1–04019174-8. [Google Scholar] [CrossRef]
- Mo, K.H.; Alengaram, U.J.; Jumaat, M.Z. Structural performance of reinforced geopolymer concrete members: A review. Constr. Build. Mater. 2016, 120, 251–264. [Google Scholar] [CrossRef]
- Hassan, A.; Arif, M.; Shariq, M. A review of properties and behavior of reinforced geopolymer concrete structural elements- A clean technology option for sustainable development. J. Clean. Prod. 2020, 245. [Google Scholar] [CrossRef]
- Sumajouw, D.M.J.; Hardjito, D.; Wallah, S.E.; Rangan, B.V. Fly ash-based geopolymer concrete: Study of slender reinforced columns. J. Mater. Sci. 2007, 42, 3124–3130. [Google Scholar] [CrossRef]
- Sofi, M.; van Deventer, J.S.J.; Mendis, P.A.; Lukey, G.C. Bond performance of reinforcing bars in inorganic polymer concrete (IPC). J. Mater. Sci. 2007, 42, 3107–3116. [Google Scholar] [CrossRef]
- Sarker, P.K. Bond strength of reinforcing steel embedded in fly ash-based geopolymer concrete. Mater. Struct. 2011, 44, 1021–1030. [Google Scholar] [CrossRef]
- Chang, E.H. Shear and Bond Behavior of Reinforced Fly Ash-Based Geopolymer Concrete Beams. Ph.D. Thesis, Curtin University of Technology, Perth, Australia, 2009. [Google Scholar]
- Ryu, G.S.; Lee, Y.B.; Koh, K.T.; Chung, Y.S. The mechanical properties of fly ash-based geopolymer concrete with alkaline activators. Constr. Build. Mater. 2013, 47, 409–418. [Google Scholar] [CrossRef]
- Gunasekera, C.; Setunge, S.; Law, D.W. Correlations between Mechanical Properties of Low-Calcium Fly Ash Geopolymer Concretes. J. Mater. Civil Eng. 2017, 29. [Google Scholar] [CrossRef]
- Olivia, M.; Nikraz, H. Properties of fly ash geopolymer concrete designed by Taguchi method. Mater. Des. 2012, 36, 191–198. [Google Scholar] [CrossRef] [Green Version]
- Joseph, B.; Mathew, G. Influence of aggregate content on the behavior of fly ash based geopolymer concrete. Sci. Iran. 2012, 19, 1188–1194. [Google Scholar] [CrossRef] [Green Version]
- Sofi, M.; van Deventer, J.S.J.; Mendis, P.A.; Lukey, G.C. Engineering properties of inorganic polymer concretes (IPCs). Cem. Concr. Res. 2007, 37, 251–257. [Google Scholar] [CrossRef]
- Aliabdo, A.A.; Abd Elmoaty, A.E.M.; Salem, H.A. Effect of cement addition, solution resting time and curing characteristics on fly ash based geopolymer concrete performance. Constr. Build. Mater. 2016, 123, 581–593. [Google Scholar] [CrossRef]
- Albitar, M.; Visintin, P.; Ali, M.S.M.; Drechsler, M. Assessing behavior of fresh and hardened geopolymer concrete mixed with class-F fly ash. KSCE J. Civ. Eng. 2015, 19, 1445–1455. [Google Scholar] [CrossRef]
- Hardjito, D.; Rangan, B.V. Development and Properties of Low-Calcium Fly Ash-Based Geopolymer Concrete; Research Report GC1; Faculty of Engineering, Curtin University of Technology: Perth, Australia, 2005; Available online: www.geopolymer.org/news/research-report-on-fly-ash-based-geopolymer-concrete/ (accessed on 5 March 2021).
- Albitar, M.; Visintin, P.; Ali, M.S.M.; Lavigne, O.; Gamboa, E. Bond Slip Models for Uncorroded and Corroded Steel Reinforcement in Class-F Fly Ash Geopolymer Concrete. J. Mater. Civ. Eng. 2017, 29. [Google Scholar] [CrossRef]
- Al-Azzawi, M.; Yu, T.; Hadi, M.N.S. Factors Affecting the Bond Strength Between the Fly Ash-based Geopolymer Concrete and Steel Reinforcement. Structures 2018, 14, 262–272. [Google Scholar] [CrossRef] [Green Version]
- Kim Jee, S.; Park, J. An Experimental Evaluation of Development Length of Reinforcements Embedded in Geopolymer Concrete. Appl. Mech. Mater. 2014, 578–579, 441–444. [Google Scholar] [CrossRef]
- Ganesan, N.; Indira, P.V.; Santhakumar, A. Bond behavior of reinforcing bars embedded in steel fibre reinforced geopolymer concrete. Mag. Concr. Res. 2015, 67, 9–16. [Google Scholar] [CrossRef]
- ACI 408R-03. Bond and Development of Straight Reinforcing Bars in Tension. Available online: www.concrete.org/store/productdetail.aspx?ItemID=40803&Format=DOWNLOAD&Language=English&Units=US_AND_METRIC (accessed on 5 March 2021).
- Luan, C.; Shi, X.; Zhang, K.; Utashev, N.; Yang, F.; Dai, J.; Wang, Q. A mix design method of fly ash geopolymer concrete based on factors analysis. Constr. Build. Mater. 2020. [Google Scholar] [CrossRef]
- Auyeung, Y.; Balaguru, P.; Chung, L. Bond behavior of corroded reinforcement bars. Aci Mater. J. 2000, 97, 214–220. [Google Scholar]
- Yazici, S.; Sezer, G.I. The effect of cylindrical specimen size on the compressive strength of concrete. Build. Environ. 2007, 42, 2417–2420. [Google Scholar] [CrossRef]
- Kadlecek, V.; Modry, S.; Kadlecek, V. Size effect of test specimens on tensile splitting strength of concrete: General relation. Mater. Struct. 2002, 35, 28–34. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, X. Reinforced Concrete Theory and Analyse; Tsinghua University Press: Beijing, China, 2003; p. 13. [Google Scholar]
- Rawlings, J.O.; Pantula, S.G.; Dickey, D.A. Applied Regression Analysis: A Research Tool, 2nd ed.; Springer: New York, NY, USA, 1998; pp. 1–93. [Google Scholar]
- ACI 318-19. Building Code Requirements for Structural Concrete. Available online: www.concrete.org/store/productdetail.aspx?ItemID=318U19&Language=English (accessed on 5 March 2021).
- CEB-FIP. Fib Model Code for Concrete Structures. 2010. Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9783433604090 (accessed on 5 March 2021).
- GB 50010—2010. Code for Deign of Concrete Structures. Available online: www.mohurd.gov.cn/wjfb/201511/t20151119_225665.html (accessed on 5 March 2021).
- Sumajouw, M.D.J.; Rangan, B.V. Low-Calcium Fly Ash-Based Geopolymer Concrete: Reinforced Beams and Columns; Research Report GC3; Faculty of Engineering, Curtin University of Technology: Perth, Australia, 2006. [Google Scholar]
- Rashid, K.; Li, X.; Xie, Y.; Deng, J.; Zhang, F. Cracking behavior of geopolymer concrete beams reinforced with steel and fiber reinforced polymer bars under flexural load. Compos. Part B Eng. 2020, 186, 107777. [Google Scholar] [CrossRef]
- Zhang, D.; Ueda, T.; Furuuchi, H. Average Crack Spacing of Overlay-Strengthened RC Beams. J. Mater. Civil Eng. 2011, 23, 1460–1472. [Google Scholar] [CrossRef] [Green Version]
- Thirugnanasambandam, S.; Kumaravel, S. Flexural Behaviour of Reinforced Low Calcium Fly Ash based Geopolymer Concrete Beam. Global Journal of Research in Engineering, [S.l.], dec. 2013. ISSN 2249-4596. Available online: https://www.engineeringresearch.org/index.php/GJRE/article/view/938 (accessed on 5 March 2021).
- Zhang, D.; Rashid, K.; Wang, B.; Ueda, T. Experimental and Analytical Investigation of Crack Spacing and Width for Overlaid RC Beams at Elevated Temperatures. ASCE J. Struct. Eng. 2017, 143, 04017168. [Google Scholar] [CrossRef] [Green Version]










| Composition | SiO2 | Al2O3 | Fe2O3 | CaO | P2O5 | Na2O | TiO2 | MgO |
|---|---|---|---|---|---|---|---|---|
| Mass% | 62.83 | 16.71 | 7.38 | 6.37 | 4.11 | 1.05 | 0.91 | 0.64 |
| Mix. | Coarse | Fine | Fly Ash | Alkaline Solution(kg/m3) | fc | ||
|---|---|---|---|---|---|---|---|
| Aggregate (kg/m3) | Aggregate (kg/m3) | (kg/m3) | Na2SiO3 | NaOH | Water | (MPa) | |
| 1 | 1173.00 | 527.00 | 500.00 | 142.86 | 18.00 | 39.14 | 58.51 |
| 2 | 1260.42 | 566.28 | 420.00 | 91.98 | 19.32 | 42.00 | 65.58 |
| 3 | 1250.28 | 561.72 | 420.00 | 112.00 | 19.64 | 36.36 | 75.90 |
| 4 | 1160.93 | 521.58 | 500.00 | 130.50 | 30.51 | 56.49 | 86.60 |
| 5 | 1240.14 | 557.16 | 420.00 | 130.50 | 19.98 | 32.22 | 69.87 |
| 6 | 1222.75 | 549.35 | 460.00 | 119.93 | 16.82 | 31.15 | 62.23 |
| 7 | 1211.64 | 544.36 | 460.00 | 110.40 | 28.17 | 45.43 | 92.86 |
| 8 | 1200.53 | 539.37 | 460.00 | 133.40 | 20.94 | 45.76 | 56.80 |
| 9 | 1185.08 | 532.43 | 500.00 | 121.67 | 23.28 | 37.55 | 79.83 |
| Strength Grade | 100 mm Cube | 150 mm Cube | 100 × 200 mm2 Cylinder | 150 × 300 mm2 Cylinder |
|---|---|---|---|---|
| C20-C40 | 0.762 | 0.8 | - | 1 |
| C50 | 0.790 | 0.83 | 1 | |
| C60 | 0.819 | 0.86 | 1 | |
| C70 | 0.833 | 0.875 | 1 | |
| C80 | 0.848 | 0.89 | 1 | |
| - | - | 0.971 | 1 |
| 100 mm Cube | 150 mm Cube | 75 × 150 mm2 Cylinder | 100 × 200 mm2 Cylinder | 150 × 300 mm2 Cylinder |
|---|---|---|---|---|
| 0.825 | 0.915 | 0.837 | 0.901 | 1 |
| Experiments | Specimens for fc | Specimens for fst | fc1 | fst1 | fc’1 | fst’1 |
|---|---|---|---|---|---|---|
| This work | 100 mm | 100 mm | 58.51 | 2.826 | 46.25 | 2.335 |
| cube | cube | 58.51 | 3.261 | 46.25 | 2.695 | |
| 58.51 | 3.306 | 46.25 | 2.732 | |||
| 58.51 | 3.288 | 46.25 | 2.718 | |||
| 58.51 | 3.722 | 46.25 | 3.076 | |||
| 65.58 | 3.391 | 53.72 | 2.803 | |||
| 65.58 | 3.137 | 53.72 | 2.592 | |||
| 65.58 | 3.756 | 53.72 | 3.104 | |||
| 65.58 | 3.363 | 53.72 | 2.78 | |||
| 65.58 | 5.048 | 53.72 | 4.172 | |||
| 75.9 | 4.057 | 63.25 | 3.353 | |||
| 75.9 | 4.585 | 63.25 | 3.789 | |||
| 75.9 | 4.075 | 63.25 | 3.368 | |||
| 75.9 | 4.256 | 63.25 | 3.517 | |||
| 75.9 | 4.76 | 63.25 | 3.934 | |||
| 86.6 | 4.066 | 73.41 | 3.36 | |||
| 86.6 | 4.691 | 73.41 | 3.877 | |||
| 86.6 | 4.669 | 73.41 | 3.859 | |||
| 86.6 | 4.46 | 73.41 | 3.686 | |||
| 86.6 | 5.2 | 73.41 | 4.297 | |||
| Gunasekera et al. | 100 × 200 mm2 | 150 × 300 mm2 | 82.5 | 4.26 | 80.1 | 4.26 |
| [16] | cylinder | cylinder | 36.9 | 2.49 | 35.83 | 2.49 |
| 29.6 | 1.6 | 28.74 | 1.6 | |||
| 24.9 | 1.15 | 24.17 | 1.15 | |||
| 86.5 | 4.67 | 83.98 | 4.67 | |||
| 45.6 | 3.41 | 44.27 | 3.41 | |||
| 36.5 | 2.32 | 35.44 | 2.32 | |||
| 27.7 | 1.3 | 26.89 | 1.3 | |||
| 87.4 | 4.72 | 84.85 | 4.72 | |||
| 47 | 3.71 | 45.63 | 3.71 | |||
| 42.8 | 2.9 | 41.55 | 2.9 | |||
| 28.7 | 1.86 | 27.86 | 1.86 | |||
| Olivia et al. | 100 × 200 mm2 | 150 × 300 mm2 | 56.49 | 4.13 | 54.84 | 4.13 |
| [17] | cylinder | cylinder | 56.24 | 3.96 | 54.6 | 3.96 |
| 60.2 | 4.29 | 58.45 | 4.29 | |||
| 56.51 | 4.18 | 54.86 | 4.18 | |||
| 58.85 | 4.1 | 57.14 | 4.1 | |||
| 63.29 | 4.79 | 61.45 | 4.79 | |||
| Ryu et al. | 100 × 200 mm2 | 100 × 200 mm2 | 17.17 | 1.3 | 16.67 | 1.171 |
| [15] | cylinder | cylinder | 19.32 | 1.3 | 18.76 | 1.171 |
| 19.46 | 1.53 | 18.89 | 1.378 | |||
| 21.94 | 1.59 | 21.3 | 1.432 | |||
| 24.14 | 1.97 | 23.44 | 1.775 | |||
| 26.51 | 1.97 | 25.74 | 1.775 | |||
| 26.67 | 2.18 | 25.89 | 1.964 | |||
| 28.02 | 2.03 | 27.2 | 1.829 | |||
| 29.35 | 2 | 28.5 | 1.802 | |||
| 26.92 | 2.4 | 26.14 | 2.162 | |||
| 30.01 | 2.22 | 29.14 | 2 | |||
| 31 | 2.44 | 30.1 | 2.198 | |||
| 33.98 | 2.68 | 32.99 | 2.414 | |||
| 34.94 | 2.82 | 33.92 | 2.541 | |||
| 35.27 | 2.73 | 34.24 | 2.459 | |||
| 36.18 | 2.68 | 35.13 | 2.414 | |||
| 56.02 | 3.65 | 54.39 | 3.288 | |||
| 58.91 | 3.68 | 57.19 | 3.315 | |||
| 61.19 | 3.93 | 59.41 | 3.541 | |||
| Benny Joseph | 150 mm | 150 × 300 mm2 | 45 | 3.1 | 36 | 3.1 |
| [18] | cube | cylinder | 47 | 3.34 | 37.6 | 3.34 |
| 56 | 3.45 | 46.48 | 3.45 | |||
| 49 | 4.51 | 39.2 | 4.51 | |||
| Sofi et al. | 150 × 300 mm2 | 150 × 300 mm2 | 38.3 | 2.7 | 38.3 | 2.7 |
| [19] | cylinder | cylinder | 52.8 | 3.3 | 52.8 | 3.3 |
| Aliabdo et al. | 100 mm | 75 × 150 mm2 | 22.5 | 2.45 | 17.14 | 2.059 |
| [20] | cube | cylinder | 27.5 | 2.75 | 20.95 | 2.311 |
| 36.5 | 3.05 | 27.81 | 2.563 | |||
| 35 | 3 | 26.67 | 2.521 | |||
| 43.5 | 3.3 | 33.14 | 2.773 | |||
| 13.5 | 1.7 | 10.29 | 1.429 | |||
| 37.5 | 3.05 | 28.57 | 2.563 | |||
| 33 | 2.7 | 25.14 | 2.269 | |||
| 25.3 | 2.5 | 19.28 | 2.101 | |||
| 31 | 3.1 | 23.62 | 2.605 | |||
| Albitar et al. | 100 × 200 mm2 | 100 × 200 mm2 | 18.66 | 2.04 | 18.12 | 1.838 |
| [21] | cylinder | cylinder | 33.17 | 3.08 | 32.2 | 2.775 |
| 34.41 | 3.14 | 33.41 | 2.829 | |||
| 29.45 | 2.96 | 28.59 | 2.667 | |||
| 51.42 | 4.23 | 49.92 | 3.811 | |||
| 53.42 | 5.55 | 51.86 | 5 | |||
| 44.58 | 5.51 | 43.28 | 4.964 | |||
| Hardjito | 100 × 200 mm2 | 150 × 300 mm2 | 89 | 7.43 | 86.41 | 7.43 |
| and Rangan | cylinder | cylinder | 68 | 5.52 | 66.02 | 5.52 |
| [22] | 55 | 5.45 | 53.4 | 5.45 | ||
| 44 | 4.43 | 42.72 | 4.43 | |||
| Chang | 100 × 200 mm2 | 150 × 300 mm2 | 37 | 3.62 | 35.92 | 3.62 |
| [14] | cylinder | cylinder | 30 | 2.96 | 29.13 | 2.96 |
| 55 | 4.06 | 53.4 | 4.06 | |||
| 48 | 4.48 | 46.6 | 4.48 | |||
| 29 | 2.93 | 28.16 | 2.93 | |||
| 51 | 4.65 | 49.51 | 4.65 |
| Experiments | τ (MPa) | fc (MPa) | Specimens for fc | fc’ (MPa) | l | d | cmin | cmax |
|---|---|---|---|---|---|---|---|---|
| Specimens for Bond Test | (mm) | |||||||
| This work | 11.34 | 65.58 | 100 mm | 53.716 | 80 | 16 | 67 | 67 |
| modified direct pull-out specimens | 13.43 | 65.58 | cube | 53.716 | 80 | 16 | 67 | 67 |
| 13.27 | 65.58 | 53.716 | 80 | 16 | 67 | 67 | ||
| 14.56 | 75.9 | 63.247 | 80 | 16 | 67 | 67 | ||
| 13.40 | 75.9 | 63.247 | 80 | 16 | 67 | 67 | ||
| 13.54 | 75.9 | 63.247 | 80 | 16 | 67 | 67 | ||
| 10.49 | 58.51 | 46.251 | 80 | 16 | 67 | 67 | ||
| 10.77 | 58.51 | 46.251 | 80 | 16 | 67 | 67 | ||
| 9.86 | 58.51 | 46.251 | 80 | 16 | 67 | 67 | ||
| 14.08 | 86.6 | 73.407 | 80 | 16 | 67 | 67 | ||
| 14.33 | 86.6 | 73.407 | 80 | 16 | 67 | 67 | ||
| 12.34 | 86.6 | 73.407 | 80 | 16 | 67 | 67 | ||
| P. K. Sarker. [13] | 10.61 | 25.5 | 100 × 200 mm2 | 24.757 | 100 | 24 | 42 | 113 |
| beam-end specimens | 13.02 | 25.5 | cylinder | 24.757 | 110 | 24 | 44 | 113 |
| 10.88 | 25.5 | 24.757 | 100 | 24 | 44 | 113 | ||
| 13.82 | 25.5 | 24.757 | 120 | 24 | 65 | 113 | ||
| 11.14 | 25.5 | 24.757 | 125 | 24 | 66 | 113 | ||
| 14.83 | 25.5 | 24.757 | 110 | 24 | 64 | 113 | ||
| 14.32 | 29.7 | 28.835 | 100 | 20 | 45 | 115 | ||
| 13.05 | 29.7 | 28.835 | 100 | 20 | 45 | 115 | ||
| 13.23 | 29.7 | 28.835 | 95 | 20 | 41 | 115 | ||
| 15.19 | 29.7 | 28.835 | 110 | 20 | 64 | 115 | ||
| 12.88 | 29.7 | 28.835 | 105 | 20 | 64 | 115 | ||
| 11.07 | 29.7 | 28.835 | 115 | 20 | 66 | 115 | ||
| 12.20 | 32.5 | 31.553 | 100 | 24 | 44 | 113 | ||
| 14.59 | 32.5 | 31.553 | 100 | 24 | 45 | 113 | ||
| 13.00 | 32.5 | 31.553 | 100 | 24 | 41 | 113 | ||
| 14.72 | 32.5 | 31.553 | 100 | 24 | 63 | 113 | ||
| 17.64 | 32.5 | 31.553 | 100 | 24 | 66 | 113 | ||
| 17.24 | 32.5 | 31.553 | 100 | 24 | 62 | 113 | ||
| 14.96 | 39.5 | 38.35 | 100 | 20 | 42 | 115 | ||
| 15.12 | 39.5 | 38.35 | 100 | 20 | 42 | 115 | ||
| 16.71 | 39.5 | 38.35 | 100 | 20 | 46 | 115 | ||
| 19.42 | 39.5 | 38.35 | 100 | 20 | 68 | 115 | ||
| 14.01 | 39.5 | 38.35 | 100 | 20 | 68 | 115 | ||
| 15.92 | 39.5 | 38.35 | 100 | 20 | 64 | 115 | ||
| M. Albitar et al. [23] | 17.68 | 33 | 100 × 200 mm2 | 32.039 | 60 | 12 | 24 | 69 |
| direct pull-out specimens | 17.25 | 33 | cylinder | 32.039 | 60 | 12 | 24 | 69 |
| 18.78 | 33 | 32.039 | 60 | 12 | 36 | 69 | ||
| 19.33 | 33 | 32.039 | 60 | 12 | 36 | 69 | ||
| 19.01 | 33 | 32.039 | 60 | 12 | 48 | 69 | ||
| 19.12 | 33 | 32.039 | 60 | 12 | 48 | 69 | ||
| 17.44 | 33 | 32.039 | 80 | 16 | 32 | 67 | ||
| 16.71 | 33 | 32.039 | 80 | 16 | 32 | 67 | ||
| 18.49 | 33 | 32.039 | 80 | 16 | 48 | 67 | ||
| 18.52 | 33 | 32.039 | 80 | 16 | 48 | 67 | ||
| 19.15 | 33 | 32.039 | 80 | 16 | 64 | 67 | ||
| 19.37 | 33 | 32.039 | 80 | 16 | 64 | 67 | ||
| 19.38 | 33 | 32.039 | 80 | 16 | 117 | 177 | ||
| 19.29 | 33 | 32.039 | 80 | 16 | 117 | 177 | ||
| 22.00 | 43 | 41.748 | 60 | 12 | 24 | 69 | ||
| 23.68 | 43 | 41.748 | 60 | 12 | 36 | 69 | ||
| 26.73 | 43 | 41.748 | 80 | 12 | 36 | 69 | ||
| 28.02 | 43 | 41.748 | 80 | 12 | 36 | 69 | ||
| 18.53 | 38 | 36.893 | 60 | 12 | 94 | 94 | ||
| 20.44 | 38 | 36.893 | 60 | 12 | 94 | 94 | ||
| 21.45 | 38 | 36.893 | 60 | 12 | 94 | 94 | ||
| 23.70 | 38 | 36.893 | 80 | 16 | 92 | 92 | ||
| 22.90 | 38 | 36.893 | 80 | 16 | 92 | 92 | ||
| 23.79 | 38 | 36.893 | 80 | 16 | 92 | 92 | ||
| Ee Hui Chang [14] | 4.94 | 37 | 100 × 200 mm2 | 35.922 | 355 | 24 | 20 | 32 |
| beam specimens | 6.03 | 37 | cylinder | 35.922 | 303 | 20 | 28 | 32 |
| 7.34 | 30 | 29.126 | 240 | 16 | 29 | 40 | ||
| 5.63 | 55 | 53.398 | 356 | 24 | 25 | 28 | ||
| 7.13 | 55 | 53.398 | 301 | 20 | 24 | 30 | ||
| 8.77 | 48 | 46.602 | 243 | 16 | 28 | 40 | ||
| 4.85 | 30 | 29.126 | 300 | 24 | 25 | 31 | ||
| 4.50 | 29 | 28.155 | 452 | 24 | 23 | 27 | ||
| 3.59 | 29 | 28.155 | 723 | 24 | 25 | 28 | ||
| 5.84 | 48 | 46.602 | 300 | 24 | 24 | 27 | ||
| 5.70 | 51 | 49.515 | 455 | 24 | 22 | 30 | ||
| 4.61 | 51 | 49.515 | 722 | 24 | 24 | 30 | ||
| Al-azzawi et al. [24] | 9.50 | 17 | 100 × 200 mm2 | 16.505 | 80 | 16 | 72 | 72 |
| direct pull-out specimens | 10.20 | 18 | cylinder | 17.476 | 80 | 16 | 72 | 72 |
| 10.40 | 21 | 20.388 | 80 | 16 | 72 | 72 | ||
| 10.00 | 19 | 18.447 | 80 | 16 | 72 | 72 | ||
| 12.00 | 20 | 19.417 | 80 | 16 | 72 | 72 | ||
| 14.00 | 22 | 21.359 | 80 | 16 | 72 | 72 | ||
| 10.40 | 22 | 21.359 | 80 | 16 | 72 | 72 | ||
| 12.00 | 25 | 24.272 | 80 | 16 | 72 | 72 | ||
| 14.00 | 26 | 25.243 | 80 | 16 | 72 | 72 | ||
| 8.60 | 19 | 18.447 | 80 | 16 | 72 | 72 | ||
| 10.00 | 20 | 19.417 | 80 | 16 | 72 | 72 | ||
| 11.70 | 20 | 19.417 | 80 | 16 | 72 | 72 | ||
| 9.20 | 20 | 19.417 | 80 | 16 | 72 | 72 | ||
| 10.60 | 21 | 20.388 | 80 | 16 | 72 | 72 | ||
| 12.60 | 22 | 21.359 | 80 | 16 | 72 | 72 | ||
| 13.70 | 21 | 20.388 | 80 | 16 | 72 | 72 | ||
| 14.00 | 25 | 24.272 | 80 | 16 | 72 | 72 | ||
| 15.00 | 26 | 25.243 | 80 | 16 | 72 | 72 | ||
| 7.50 | 16 | 15.534 | 80 | 16 | 72 | 72 | ||
| 8.30 | 18 | 17.476 | 80 | 16 | 72 | 72 | ||
| 9.80 | 19 | 18.447 | 80 | 16 | 72 | 72 | ||
| 9.50 | 18 | 17.476 | 80 | 16 | 72 | 72 | ||
| 10.50 | 19 | 18.447 | 80 | 16 | 72 | 72 | ||
| 11.20 | 20 | 19.417 | 80 | 16 | 72 | 72 | ||
| 10.50 | 21 | 20.388 | 80 | 16 | 72 | 72 | ||
| 11.80 | 21 | 20.388 | 80 | 16 | 72 | 72 | ||
| 13.00 | 23 | 22.33 | 80 | 16 | 72 | 72 | ||
| 24.00 | 45 | 43.689 | 80 | 16 | 72 | 72 | ||
| 22.00 | 39 | 37.864 | 80 | 16 | 72 | 72 | ||
| 20.00 | 34 | 33.01 | 80 | 16 | 72 | 72 | ||
| 26.00 | 58 | 56.311 | 80 | 16 | 72 | 72 | ||
| 25.00 | 47 | 45.631 | 80 | 16 | 72 | 72 | ||
| 24.00 | 42 | 40.777 | 80 | 16 | 72 | 72 | ||
| 30.00 | 64 | 62.136 | 80 | 16 | 72 | 72 | ||
| 29.60 | 62 | 60.194 | 80 | 16 | 72 | 72 | ||
| 27.90 | 53 | 51.456 | 80 | 16 | 72 | 72 | ||
| 17.00 | 30 | 29.126 | 80 | 16 | 72 | 72 | ||
| 16.00 | 28 | 27.184 | 80 | 16 | 72 | 72 | ||
| 14.00 | 27 | 26.214 | 80 | 16 | 72 | 72 | ||
| 21.00 | 35 | 33.981 | 80 | 16 | 72 | 72 | ||
| 19.60 | 30 | 29.126 | 80 | 16 | 72 | 72 | ||
| 18.30 | 28 | 27.184 | 80 | 16 | 72 | 72 | ||
| 25.80 | 49 | 47.573 | 80 | 16 | 72 | 72 | ||
| 25.10 | 41 | 39.806 | 80 | 16 | 72 | 72 | ||
| 22.70 | 36 | 34.951 | 80 | 16 | 72 | 72 | ||
| Sofi et al. [12] beam-end specimens | 9.50 | 30 | 150 × 300 mm2 | 30 | 168.8 | 12 | 36 | 106.5 |
| 6.80 | 30 | cylinder | 30 | 216.8 | 16 | 48 | 106.5 | |
| 5.80 | 30 | 30 | 234 | 20 | 70 | 106.5 | ||
| direct pull-out specimens | 10.90 | 59.8 | 59.8 | 60 | 12 | 69 | 69 | |
| Kim, Jee Sang [25] | 19.81 | 20 | 150 × 300 mm2 | 20 | 50 | 10 | 95 | 95 |
| direct pull-out specimens | 21.08 | 20 | cylinder | 20 | 50 | 10 | 95 | 95 |
| 28.35 | 20 | 20 | 50 | 10 | 95 | 95 | ||
| 18.58 | 20 | 20 | 80 | 16 | 92 | 92 | ||
| 14.48 | 20 | 20 | 80 | 16 | 92 | 92 | ||
| 21.14 | 20 | 20 | 80 | 16 | 92 | 92 | ||
| 18.76 | 20 | 20 | 125 | 25 | 87.5 | 87.5 | ||
| 14.93 | 20 | 20 | 125 | 25 | 87.5 | 87.5 | ||
| 18.09 | 20 | 20 | 125 | 25 | 87.5 | 87.5 | ||
| Ganesan et al. [26] | 12.73 | 41.23 | 150 mm | 32.984 | 100 | 12 | 69 | 69 |
| direct pull-out specimens | 16.57 | 41.23 | cube□ | 32.984 | 150 | 16 | 67 | 67 |
| Equations | Basic Equation | Model | t-Value | p Value | R2 |
|---|---|---|---|---|---|
| (20) | 13.693 | 0.000 | 0.681 | ||
| (21) | 41.364 | 0.000 | 0.584 | ||
| (22) | 11.989 | 0.000 | 0.620 | ||
| (23) | 43.155 | 0.000 | 0.616 |
| Specimens for fc | Specimens for fst | fc | fst | fc’ | fst’ |
|---|---|---|---|---|---|
| 100 mm | 100 mm | 69.87 | 4.086 | 57.23 | 3.371 |
| cube | cube | 69.87 | 3.848 | 57.23 | 3.175 |
| 69.87 | 4.503 | 57.23 | 3.715 | ||
| 69.87 | 4.330 | 57.23 | 3.572 | ||
| 69.87 | 4.243 | 57.23 | 3.500 | ||
| 62.23 | 4.128 | 50.97 | 3.406 | ||
| 62.23 | 3.520 | 50.97 | 2.904 | ||
| 62.23 | 3.333 | 50.97 | 2.750 | ||
| 62.23 | 3.034 | 50.97 | 2.503 | ||
| 62.23 | 3.966 | 50.97 | 3.272 | ||
| 92.86 | 4.928 | 78.74 | 4.065 | ||
| 92.86 | 4.889 | 78.74 | 4.033 | ||
| 92.86 | 5.678 | 78.74 | 4.684 | ||
| 92.86 | 5.967 | 78.74 | 4.923 | ||
| 92.86 | 5.371 | 78.74 | 4.431 | ||
| 56.80 | 4.073 | 44.87 | 3.360 | ||
| 56.80 | 4.327 | 44.87 | 3.569 | ||
| 56.80 | 3.226 | 44.87 | 2.662 | ||
| 56.80 | 4.684 | 44.87 | 3.865 | ||
| 56.80 | 4.284 | 44.87 | 3.534 | ||
| 79.83 | 3.322 | 66.50 | 2.741 | ||
| 79.83 | 3.563 | 66.50 | 2.939 | ||
| 79.83 | 4.086 | 66.50 | 3.371 | ||
| 79.83 | 5.609 | 66.50 | 4.628 | ||
| 79.83 | 4.765 | 66.50 | 3.931 |
| Experiment | τ (MPa) | fc (MPa) | Specimens for fc | fc’ (MPa) | l | d | cmin | cmax |
|---|---|---|---|---|---|---|---|---|
| Specimens for Bond Test | (mm) | |||||||
| This work | 13.98 | 69.87 | 100 mm | 57.23 | 80 | 16 | 67 | 67 |
| modified direct pull-out specimens | 12.29 | 69.87 | cube | 57.23 | 80 | 16 | 67 | 67 |
| 12.61 | 69.87 | 57.23 | 80 | 16 | 67 | 67 | ||
| 11.79 | 62.23 | 49.194 | 80 | 16 | 67 | 67 | ||
| 12.32 | 62.23 | 49.194 | 80 | 16 | 67 | 67 | ||
| 11.99 | 62.23 | 49.194 | 80 | 16 | 67 | 67 | ||
| 15.87 | 92.86 | 78.707 | 80 | 16 | 67 | 67 | ||
| 14.53 | 92.86 | 78.707 | 80 | 16 | 67 | 67 | ||
| 13.38 | 92.86 | 78.707 | 80 | 16 | 67 | 67 | ||
| 12.25 | 56.8 | 44.896 | 80 | 16 | 67 | 67 | ||
| 11.97 | 56.8 | 44.896 | 80 | 16 | 67 | 67 | ||
| 11.86 | 56.8 | 44.896 | 80 | 16 | 67 | 67 | ||
| 14.26 | 79.83 | 66.525 | 80 | 16 | 67 | 67 | ||
| 14.54 | 79.83 | 66.525 | 80 | 16 | 67 | 67 | ||
| 14.26 | 79.83 | 66.525 | 80 | 16 | 67 | 67 | ||
| Beam | fc | b | h | Mcr | Mcr Predicted by [37] | Mcr Predicted by Equation (38) | Test/Prediction |
|---|---|---|---|---|---|---|---|
| (MPa) | (mm) | (KN × m) | (KN × m) | (KN × m) | Ratio | ||
| GB1-1 | 37 | 200 | 300 | 13.40 | 10.39 | 12.68 | 1.06 |
| GB1-2 | 42 | 200 | 300 | 13.55 | 10.86 | 13.90 | 0.97 |
| GB1-3 | 42 | 200 | 300 | 13.50 | 10.61 | 13.90 | 0.97 |
| GB1-4 | 37 | 200 | 300 | 14.30 | 9.66 | 12.68 | 1.13 |
| GB2-1 | 46 | 200 | 300 | 15.00 | 11.65 | 14.84 | 1.01 |
| GB2-2 | 53 | 200 | 300 | 16.20 | 12.27 | 16.44 | 0.99 |
| GB2-3 | 53 | 200 | 300 | 16.65 | 12.02 | 16.44 | 1.01 |
| GB2-4 | 46 | 200 | 300 | 16.05 | 10.91 | 14.84 | 1.08 |
| GB3-1 | 76 | 200 | 300 | 19.00 | 15.13 | 21.33 | 0.89 |
| GB3-2 | 72 | 200 | 300 | 20.00 | 14.43 | 20.51 | 0.98 |
| GB3-3 | 72 | 200 | 300 | 21.00 | 14.18 | 20.51 | 1.02 |
| GB3-4 | 76 | 200 | 300 | 19.90 | 14.39 | 21.33 | 0.93 |
| Average | 1.00 | ||||||
| Standard Deviation | 0.06 | ||||||
| Experiment | Beam | Length of Pure Bending Zone | Number of Cracks | Scr | Predicted Scr | Test/Prediction Ratio |
|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | ||||
| Sumajouw | GB1-2 | 1000 | 14 | 76.92 | 68.17 | 1.13 |
| and Rangan [37] | GB1-3 | 1000 | 13 | 83.33 | 65.97 | 1.26 |
| GB3-1 | 1000 | 13 | 83.33 | 76.82 | 1.08 | |
| GB3-2 | 1000 | 12 | 90.91 | 72.70 | 1.25 | |
| Kumaravel and | GPC-1 | 1000 | 14 | 76.92 | 96.99 | 0.79 |
| Thirugnanasambandam | GPC-2 | 1000 | 10 | 111.11 | 96.99 | 1.15 |
| [40] | Average | 1.11 | ||||
| Standard Deviation | 0.17 | |||||
| Experiment | Beam | fc | d | cmax | cmin | At | |
|---|---|---|---|---|---|---|---|
| (MPa) | (mm) | (mm) | (mm) | (mm) | (mm2) | ||
| Sumajouw | GB1-2 | 42 | 16 | 25.5 | 25 | 150.72 | 129.52 |
| and Rangan [37] | GB1-3 | 42 | 20 | 25 | 22.5 | 188.4 | 155.65 |
| GB3-1 | 76 | 12 | 28.5 | 25 | 113.04 | 88.94 | |
| GB3-2 | 72 | 16 | 25.5 | 25 | 150.72 | 112.51 | |
| Kumaravel and | GPC-1 | 46.61 | 16 | 20 | 10.25 | 138.16 | 114.68 |
| Thirugnanasambandam [40] | GPC-2 | 46.61 | 16 | 20 | 10.25 | 138.16 | 114.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, C.; Wang, Q.; Yang, F.; Zhang, K.; Utashev, N.; Dai, J.; Shi, X. Practical Prediction Models of Tensile Strength and Reinforcement-Concrete Bond Strength of Low-Calcium Fly Ash Geopolymer Concrete. Polymers 2021, 13, 875. https://doi.org/10.3390/polym13060875
Luan C, Wang Q, Yang F, Zhang K, Utashev N, Dai J, Shi X. Practical Prediction Models of Tensile Strength and Reinforcement-Concrete Bond Strength of Low-Calcium Fly Ash Geopolymer Concrete. Polymers. 2021; 13(6):875. https://doi.org/10.3390/polym13060875
Chicago/Turabian StyleLuan, Chenchen, Qingyuan Wang, Fuhua Yang, Kuanyu Zhang, Nodir Utashev, Jinxin Dai, and Xiaoshuang Shi. 2021. "Practical Prediction Models of Tensile Strength and Reinforcement-Concrete Bond Strength of Low-Calcium Fly Ash Geopolymer Concrete" Polymers 13, no. 6: 875. https://doi.org/10.3390/polym13060875
APA StyleLuan, C., Wang, Q., Yang, F., Zhang, K., Utashev, N., Dai, J., & Shi, X. (2021). Practical Prediction Models of Tensile Strength and Reinforcement-Concrete Bond Strength of Low-Calcium Fly Ash Geopolymer Concrete. Polymers, 13(6), 875. https://doi.org/10.3390/polym13060875