Optical Encryption Based on Computer Generated Holograms in Photopolymer
Abstract
:1. Introduction
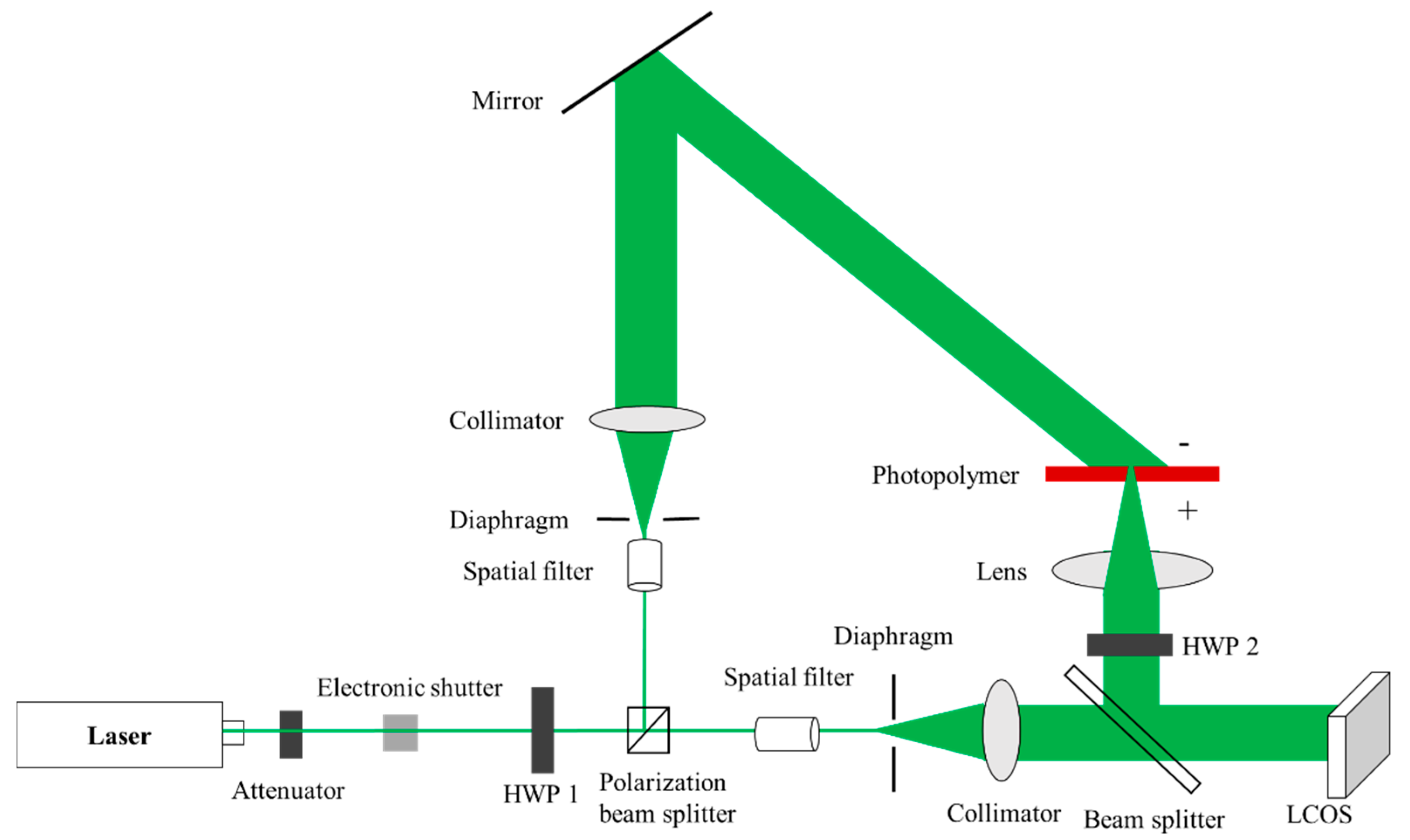
2. Design Theory and Method
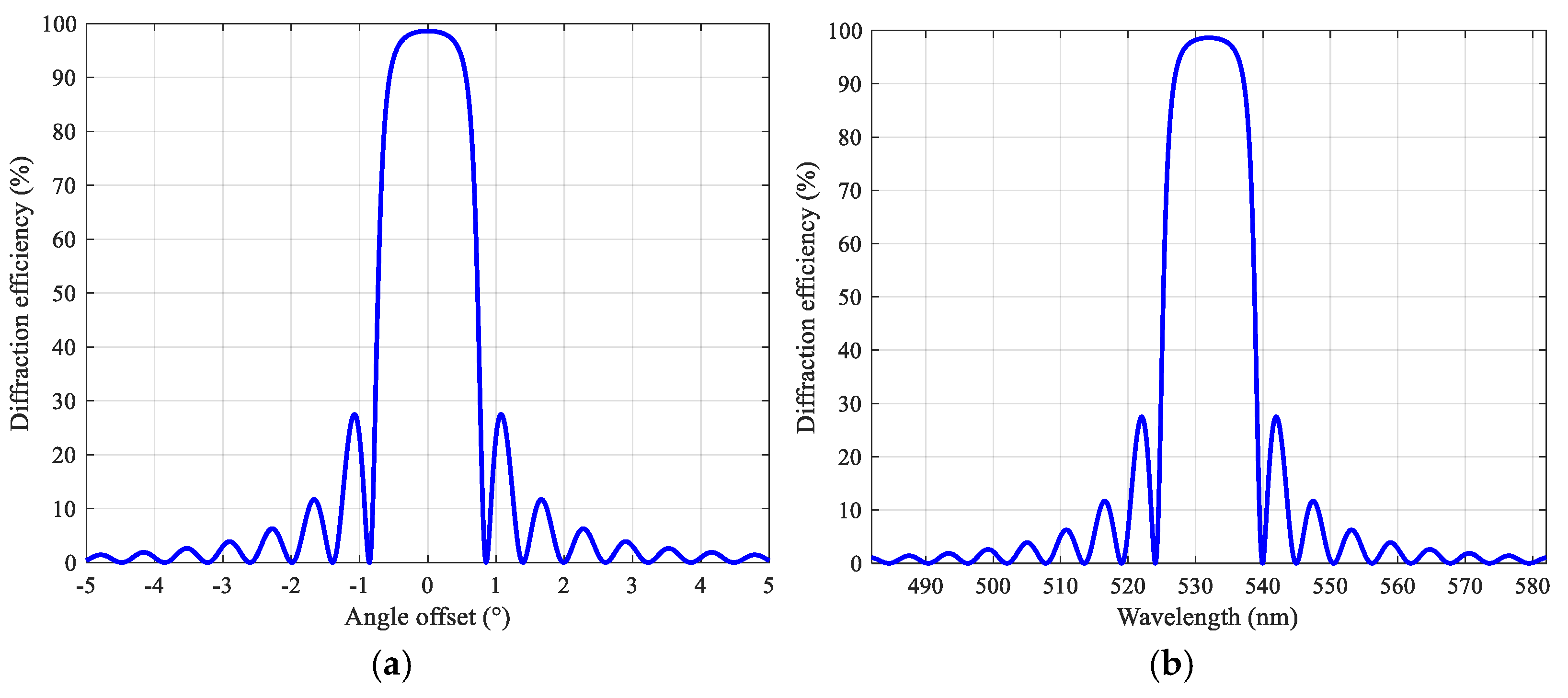
2.1. Coupled Wave Theory
2.2. The Gerchberg-Saxton Algorithm
2.3. The Angular-Spectrum Layer-Oriented Method
3. CGH Printing of Large Encrypted QR Code
3.1. Encrypted QR Code Generation
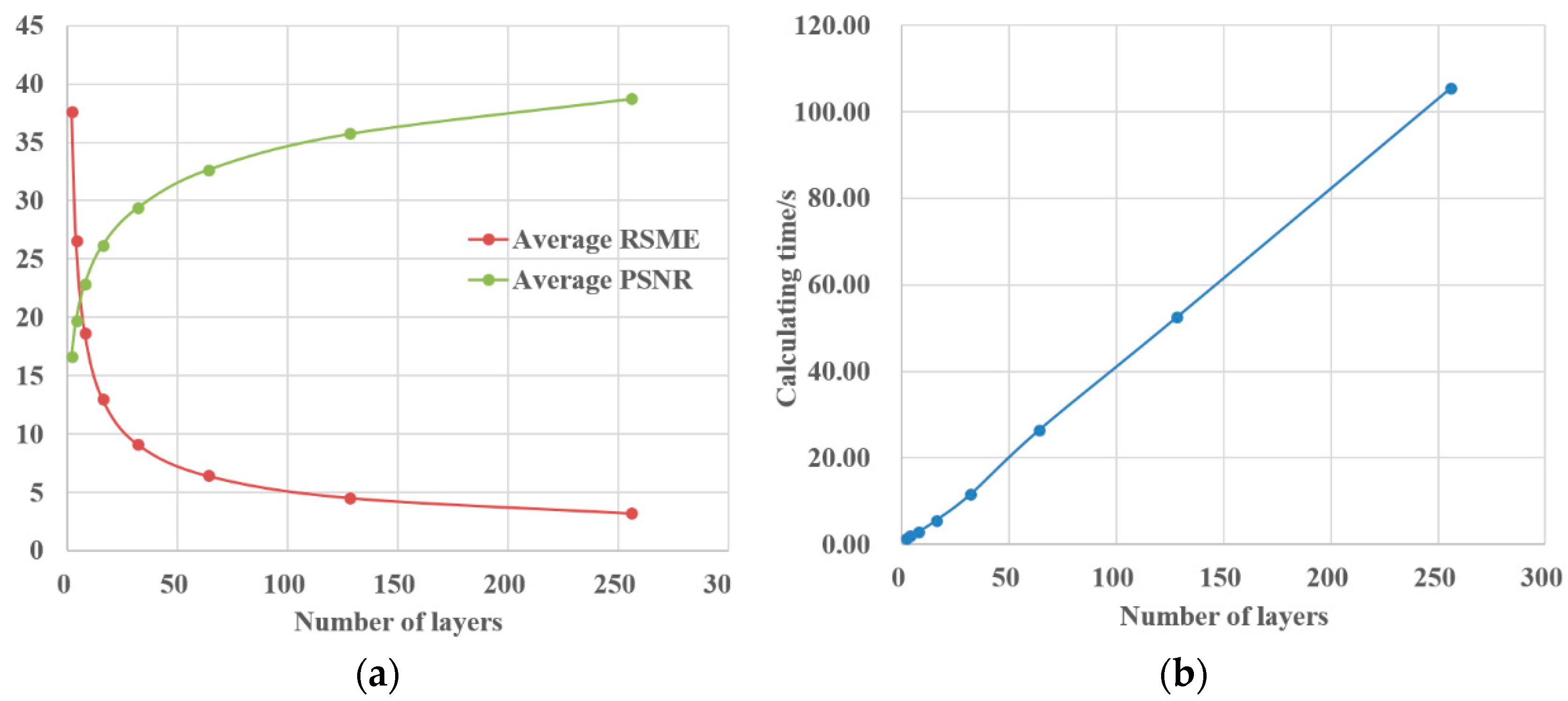
3.2. Reconstruction Quality Evaluation
4. CGH Printing of Miniature Keys
4.1. Miniature Key Generation
4.2. Miniature 3D Image Generation
4.3. Reconstruction Quality Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arief, B.; Adzmi, M.A.B.; Gross, T. Understanding cybercrime from its stakeholders’ perspectives: Part 1—Attackers. IEEE Secur. Priv. 2015, 13, 71–76. [Google Scholar] [CrossRef]
- Yan, A.; Lu, C.; Yu, J.; Tang, M.; Dong, J.; Hu, Z.; Zhang, H. Multiple-image encryption based on angular-multiplexing holography with quick response code and spiral phase keys. Appl. Opt. 2019, 58, G6–G10. [Google Scholar] [CrossRef] [PubMed]
- Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef]
- Guo, C.; Muniraj, I.; Sheridan, J.T. Phase-retrieval-based attacks on linear-canonical-transform-based DRPE systems. Appl. Opt. 2016, 55, 4720–4728. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.; Kumar, R.; Yadav, A.; Singh, K. Security analysis and modified attack algorithms for a nonlinear optical cryptosystem based on DRPE. Opt. Laser Eng. 2021, 139, 106501. [Google Scholar] [CrossRef]
- El-Bakary, E.M.; El-Rabaie, E.M.; Zahran, O.; Abd El-Samie, F.E. DRPE encryption with chaotic interleaving for video communication. Wirel. Pers. Commun. 2017, 97, 1373–1384. [Google Scholar] [CrossRef]
- Taheri, M.; Mozaffari, S. Phase mask generation for DRPE method using chaos theory and hash function. Optik 2013, 124, 2363–2367. [Google Scholar] [CrossRef]
- Elshamy, A.M.; Rashed, A.N.; Mohamed, A.E.A.; Faragalla, O.S.; Mu, Y.; Alshebeili, S.A.; Abd El-Samie, F. Optical image encryption based on chaotic baker map and double random phase encoding. J. Lightwave Technol. 2013, 31, 2533–2539. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Hu, Y.; Li, X.; Jiang, Y.; Wang, Y.; Dai, P.; Liu, Q.; Shu, Z.; Duan, H. Integrated metasurfaces with microprints and helicity-multiplexed holograms for real-time optical encryption. Adv. Opt. Mater. 2020, 8, 1902020. [Google Scholar] [CrossRef]
- Li, J.; Kamin, S.; Zheng, G.; Neubrech, F.; Zhang, S.; Liu, N. Addressable metasurfaces for dynamic holography and optical information encryption. Sci. Adv. 2018, 4, r6768. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Li, X.; Chen, X.; Li, J. An adaptive and secure holographic image watermarking scheme. Entropy 2019, 21, 460. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mehra, I.; Nishchal, N.K. Optical asymmetric watermarking using modified wavelet fusion and diffractive imaging. Opt. Laser Eng. 2015, 68, 74–82. [Google Scholar] [CrossRef]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 61802. [Google Scholar] [CrossRef]
- Pérez-Cabré, E.; Mohammed, E.; Millán, M.; Saadon, H. Photon-counting multifactor optical encryption and authentication. J. Opt. 2015, 17, 25706. [Google Scholar] [CrossRef]
- Larger, L.; Goedgebuer, J.; Delorme, F. Optical encryption system using hyperchaos generated by an optoelectronic wavelength oscillator. Phys. Rev. E 1998, 57, 6618. [Google Scholar] [CrossRef]
- Rajput, S.K.; Nishchal, N.K. Image encryption using polarized light encoding and amplitude and phase truncation in the Fresnel domain. Appl. Opt. 2013, 52, 4343–4352. [Google Scholar] [CrossRef] [PubMed]
- Rawat, N.; Kim, B.; Muniraj, I.; Situ, G.; Lee, B. Compressive sensing based robust multispectral double-image encryption. Appl. Opt. 2015, 54, 1782–1793. [Google Scholar] [CrossRef]
- Verma, G.; Liao, M.; Lu, D.; He, W.; Peng, X.; Sinha, A. An optical asymmetric encryption scheme with biometric keys. Opt. Laser Eng. 2019, 116, 32–40. [Google Scholar] [CrossRef]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high-security encryption. Nat. Photonics 2020, 14, 102–108. [Google Scholar] [CrossRef]
- Evtikhiev, N.N.; Krasnov, V.V.; Kuzmin, I.D.; Molodtsov, D.Y.; Rodin, V.G.; Starikov, R.S. Optical encryption of digital information in the scheme with spatially incoherent illumination based on micromirror light modulators. Procedia Comput. Sci. 2020, 169, 564–567. [Google Scholar] [CrossRef]
- Jeon, H.; Kim, B.; Jun, M.; Kim, H.; Hahn, J. High-resolution binary hologram printing methods. In Proceedings of the Practical Holography XXXIV: Displays, Materials, and Applications, San Francisco, CA, USA, 21 February 2020. [Google Scholar]
- Khaliq, H.S.; Akram, M.R.; Riaz, K.; Ansari, M.A.; Akbar, J.; Zhang, J.; Zhu, W.; Zhang, D.; Wang, X.; Zubair, M. Single-layered meta-reflectarray for polarization retention and spin-encrypted phase-encoding. Opt. Express 2021, 29, 3230–3242. [Google Scholar] [CrossRef] [PubMed]
- Vilardy, O.J.M.; Perez, R.A.; Torres, M.C.O. Optical image encryption using a nonlinear joint transform correlator and the collins diffraction transform. Photonics 2019, 6, 115. [Google Scholar] [CrossRef] [Green Version]
- Kogelnik, H. Coupled wave theory for thick hologram gratings. Bell Syst. Tech. J. 1969, 48, 2909–2947. [Google Scholar] [CrossRef]
- Gerchberg, R.W. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Zhao, Y.; Cao, L.; Zhang, H.; Kong, D.; Jin, G. Accurate calculation of computer-generated holograms using angular-spectrum layer-oriented method. Opt. Express 2015, 23, 25440–25449. [Google Scholar] [CrossRef]
- Mishra, A.; Mathuria, M. A review on QR code. Int. J. Comput. Appl. 2017, 164, 17–19. [Google Scholar] [CrossRef]
- Rijmen, V.; Daemen, J. Advanced encryption standard. In Proceedings of Federal Information Processing Standards Publications; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001; pp. 19–22. [Google Scholar]
- Anderson, R.; Biham, E.; Knudsen, L. Serpent: A proposal for the advanced encryption standard. NIST AES Proposal 1998, 174, 1–23. [Google Scholar]
- Bruder, F.; Fäcke, T.; Rölle, T. The chemistry and physics of Bayfol® HX film holographic photopolymer. Polymers 2017, 9, 472. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Wu, T.; Cui, Y.; Li, J.; Wang, J.; Su, P. Modified monomer diffusion model for volume holographic grating formation in photopolymers. Appl. Opt. 2020, 59, 3952–3958. [Google Scholar] [CrossRef]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.; Ma, J.; Wang, C.; Wang, H.; Cao, L.; Su, P. Optical Encryption Based on Computer Generated Holograms in Photopolymer. Polymers 2021, 13, 1358. https://doi.org/10.3390/polym13091358
Wu T, Ma J, Wang C, Wang H, Cao L, Su P. Optical Encryption Based on Computer Generated Holograms in Photopolymer. Polymers. 2021; 13(9):1358. https://doi.org/10.3390/polym13091358
Chicago/Turabian StyleWu, Taihui, Jianshe Ma, Chengchen Wang, Haibei Wang, Liangcai Cao, and Ping Su. 2021. "Optical Encryption Based on Computer Generated Holograms in Photopolymer" Polymers 13, no. 9: 1358. https://doi.org/10.3390/polym13091358







