Application of Taguchi Method to Optimize the Parameter of Fused Deposition Modeling (FDM) Using Oil Palm Fiber Reinforced Thermoplastic Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Design of Experiment (DOE)
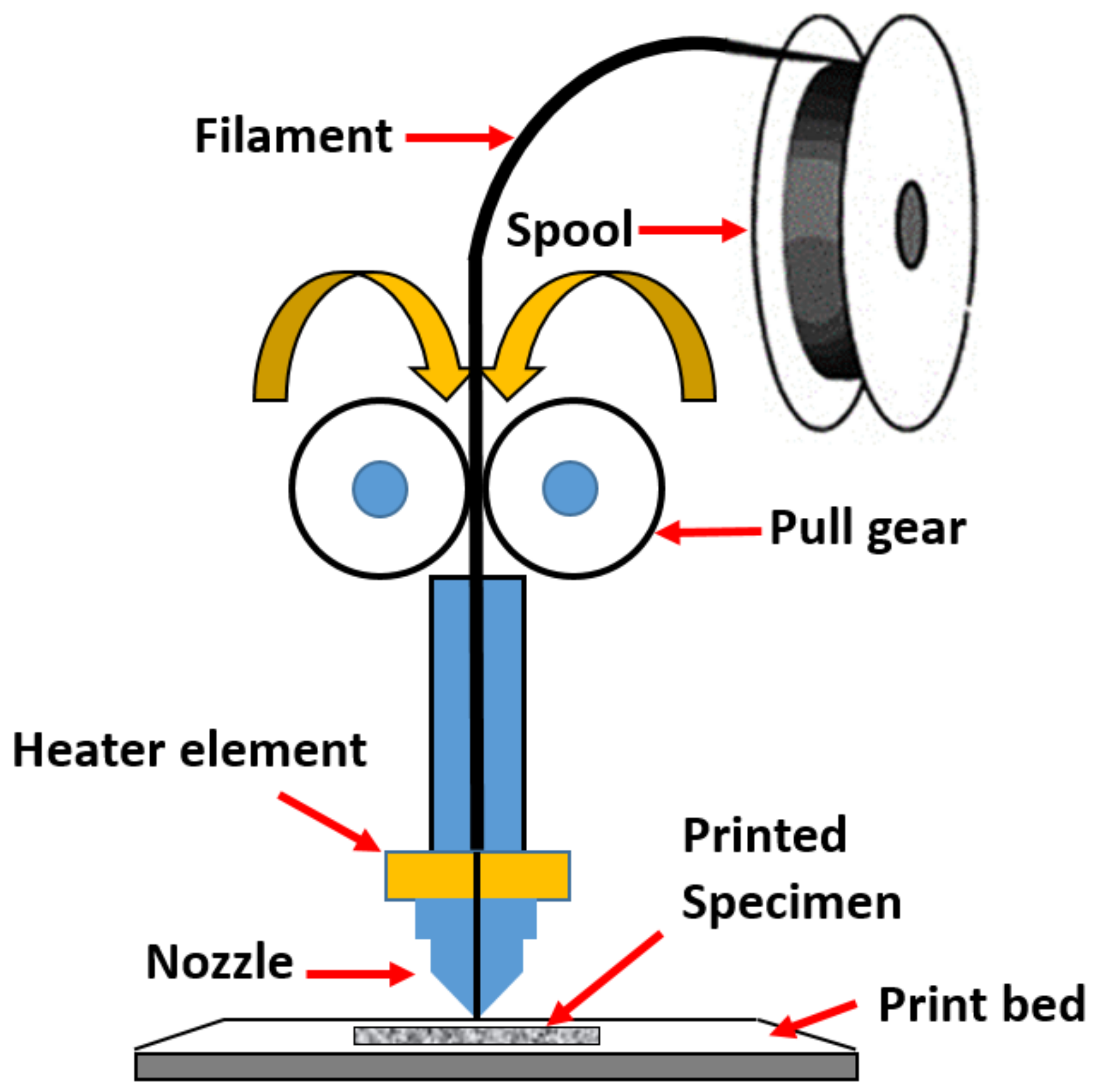
2.3. 3D Printing
2.4. Tensile Testing
2.5. Flexural Testing
2.6. Scanning Electron Microscope (SEM)
3. Results and Discussion
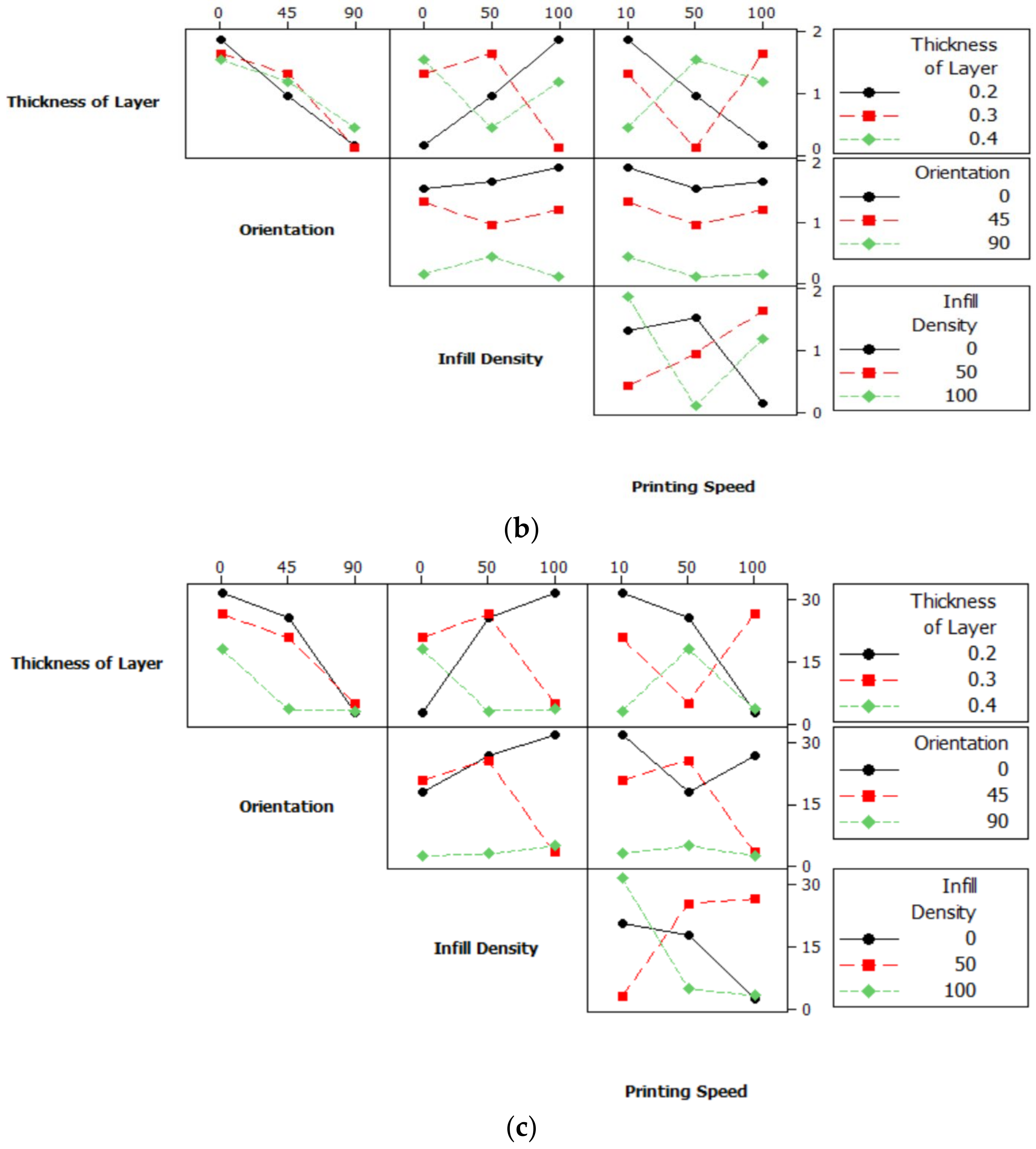
3.1. Interaction Plots, Probability Plots and ANOVA
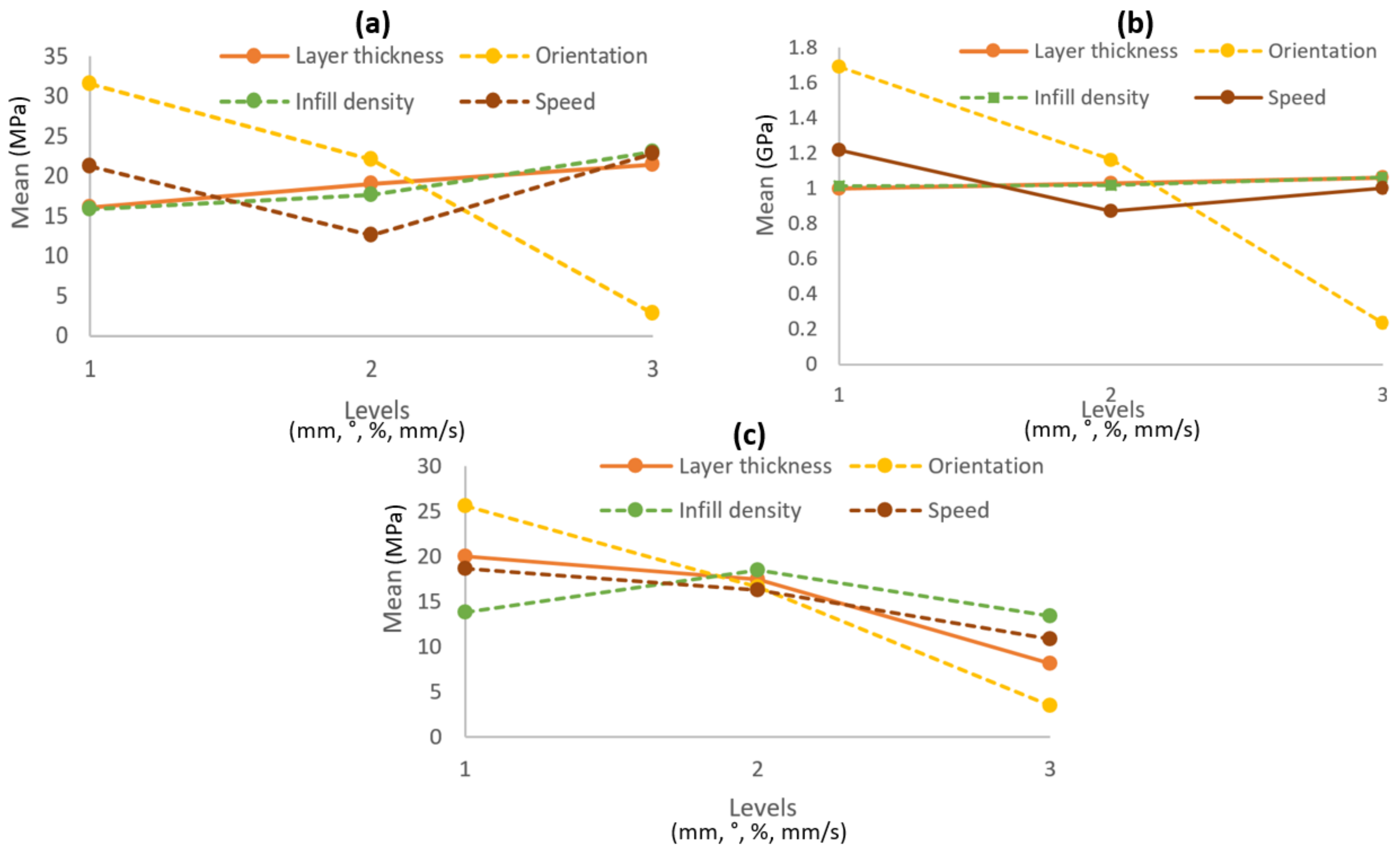
3.2. Main Effect Plots for Means
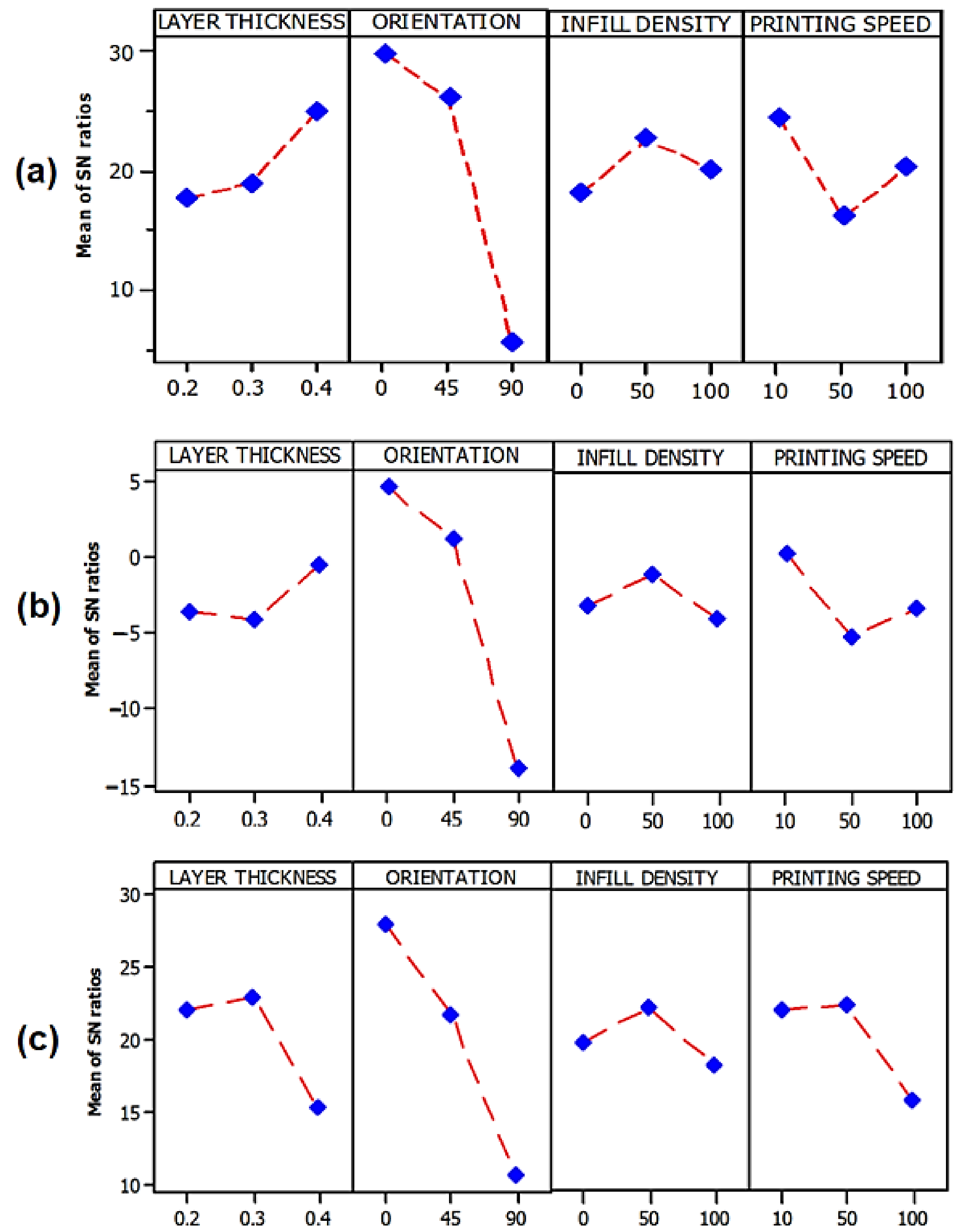
3.3. Taguchi Optimization by S/N Ratio
3.4. SEM Analysis of Fractured Surfaces
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive manufacturing of carbon fiber reinforced thermoplastic composites using fused deposition modeling. Compos. Part B Eng. 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Nath, S.D.; Nilufar, S. An overview of additive manufacturing of polymers and associated composites. Polymers 2020, 12, 2719. [Google Scholar] [CrossRef] [PubMed]
- Leite, M.; Varanda, A.; Ribeiro, A.R.; Silva, A.; Vaz, M.F. Mechanical properties and water absorption of surface modified ABS 3D printed by fused deposition modelling. Rapid Prototyp. J. 2018, 24, 195–203. [Google Scholar] [CrossRef]
- Ziemian, C.; Sharma, M.; Ziemi, S. Anisotropic mechanical properties of ABS parts fabricated by Fused Deposition Modelling. Mech. Eng. 2012, 23, 159–180. [Google Scholar]
- Abeykoon, C.; Sri-Amphorn, P.; Fernando, A. Optimization of fused deposition modeling parameters for improved PLA and ABS 3D printed structures. Int. J. Lightweight Mater. Manuf. 2020, 3, 284–297. [Google Scholar] [CrossRef]
- Camposeco-Negrete, C. Optimization of printing parameters in fused deposition modeling for improving part quality and process sustainability. Int. J. Adv. Manuf. Technol. 2020, 108, 2131–2147. [Google Scholar] [CrossRef]
- Dey, A.; Yodo, N. A systematic survey of FDM process parameter optimization and their influence on part characteristics. J. Manuf. Mater. Process. 2019, 3, 64. [Google Scholar] [CrossRef] [Green Version]
- Khan, I.; Kumar, N. Fused deposition modelling process parameters influence on the mechanical properties of ABS: A review. Mater. Today Proc. 2020, 21, 1659–1672. [Google Scholar] [CrossRef]
- Gkartzou, E.; Koumoulos, E.P.; Charitidis, C.A. Production and 3D printing processing of bio-based thermoplastic filament. Manuf. Rev. 2017, 4, 2016020. [Google Scholar] [CrossRef]
- Guo, R.; Ren, Z.; Bi, H.; Song, Y.; Xu, M. Effect of toughening agents on the properties of poplar wood flour/poly (lactic acid) composites fabricated with fused deposition modeling. Eur. Polym. J. 2018, 107, 34–45. [Google Scholar] [CrossRef]
- Gardan, J.; Roucoules, L. 3D printing device for numerical control machine and wood deposition. Julien Gardan Int. J. Eng. Res. App. 2014, 4, 123–131. [Google Scholar]
- Wimmer, R.; Steyrer, B.; Woess, J.; Koddenberg, T.; Mundigler, N. 3D Printing and wood. Pro Ligno 2015, 11, 144–149. [Google Scholar]
- Gardan, J.; Nguyen, D.C.; Roucoules, L.; Montay, G. Characterization of wood filament in additive deposition to study the mechanical behavior of reconstituted wood products. J. Eng. Fibers Fabr. 2016, 11, 56–63. [Google Scholar] [CrossRef]
- Rosenthal, M.; Henneberger, C.; Gutkes, A.; Bues, C.T. Liquid deposition modeling: A promising approach for 3D printing of wood. Eur. J. Wood Wood Prod. 2018, 76, 797–799. [Google Scholar] [CrossRef]
- Stoof, D.; Pickering, K. Sustainable composite fused deposition modelling filament using recycled pre-consumer polypropylene. Compos. Part B 2018, 135, 110–118. [Google Scholar] [CrossRef]
- Daver, F.; Lee, K.P.M.; Brandt, M.; Shanks, R. Cork–PLA composite filaments for fused deposition modelling. Compos. Sci. Technol. 2018, 168, 230–237. [Google Scholar] [CrossRef]
- Suteja, J.; Firmanto, H.; Soesanti, A.; Christian, C. Properties investigation of 3D printed continuous pineapple leaf fiber-reinforced PLA composite. J. Thermoplast. Compos. Mater. 2020. [Google Scholar] [CrossRef]
- Masood, S.H.; Song, W.Q. Development of new metal/polymer materials for rapid tooling using fused deposition modelling. Mater. Des. 2004, 25, 587–594. [Google Scholar] [CrossRef]
- Zhong, W.; Li, F.; Zhang, Z.; Song, L.; Li, Z. Short fiber reinforced composites for fused deposition modeling. Mater. Sci. Eng. A 2001, 301, 125–130. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, H.; Li, Z.; Li, P.; Shi, S.Q. Development and application of wood flour-filled polylactic acid composite filament for 3D printing. Materials 2017, 10, 339. [Google Scholar] [CrossRef] [Green Version]
- Subramaniyan, M.; Karuppan, S.; Eswaran, P.; Appusamy, A.; Shankar, A.N. State of art on fusion deposition modeling machines process parameter optimization on composite materials. Mater. Today Proc. 2021, 45, 820–827. [Google Scholar] [CrossRef]
- Sun, Q.; Rizvi, G.M.; Bellehumeur, C.T.; Gu, P. Effect of processing conditions on the bonding quality of FDM polymer filaments. Rapid Prototyp. J. 2008, 14, 72–80. [Google Scholar] [CrossRef]
- Tian, X.; Liu, T.; Yang, C.; Wang, Q.; Li, D. Interface and performance of 3D printed continuous carbon fiber reinforced PLA composites. Compos. A Appl. Sci. Manuf. 2016, 88, 198–205. [Google Scholar] [CrossRef]
- Garg, H.; Singh, R. Investigations for melt flow index of Nylon6-Fe composite based hybrid FDM filament. Rapid Prototyp. J. 2016, 22, 338–343. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Hu, Y.; Wang, H. Additive manufacturing of carbon fiber reinforced plastic composites using fused deposition modeling: Effects of process parameters on tensile properties. J. Compos. Mater. 2017, 51, 451–462. [Google Scholar] [CrossRef]
- Hill, N.; Haghi, M. Deposition direction-dependent failure criteria for fused deposition modeling polycarbonate. Rapid Prototyp. J. 2014, 20, 221–227. [Google Scholar] [CrossRef]
- Chockalingam, K.; Jawahar, N.; Praveen, J. Enhancement of anisotropic strength of fused deposited ABS parts by genetic algorithm. Mater. Manuf. Processes 2016, 31, 2001–2010. [Google Scholar] [CrossRef]
- Anitha, R.; Arunachalam, S.; Radhakrishnan, P. Critical parameters influencing the quality of prototypes in fused deposition modelling. J. Mater. Process. Technol. 2001, 118, 385–388. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. September. Experimental investigation of the influence of fabrication conditions on dynamic viscoelastic properties of PC-ABS processed parts by FDM process. IOP Conf. Ser. Mater. Sci. Eng. 2016, 149, 012122. [Google Scholar] [CrossRef]
- Huynh, H.N.; Nguyen, A.T.; Ha, N.L.; Ha Thai, T.T. Application of fuzzy Taguchi method to improve the dimensional accuracy of fused deposition modeling processed product. In Proceedings of the 2017 International Conference on System Science and Engineering, ICSSE 2017, Ho Chi Minh City, Vietnam, 21–23 July 2017. [Google Scholar]
- Raut, S.; Jatti, V.S.; Khedkar, N.K.; Singh, T.P. Investigation of the effect of built orientation on mechanical properties and total cost of FDM parts. Procedia Mater. Sci 2014, 6, 1625–1630. [Google Scholar] [CrossRef] [Green Version]
- El-Kassas, A.M.; Elsheikh, A.H. A new eco-friendly mechanical technique for production of rice straw fibers for medium density fiberboards manufacturing. Int. J. Environ. Sci. Technol. 2021, 18, 979–988. [Google Scholar] [CrossRef]
- Alafaghani, A.; Qattawi, A. Investigating the effect of fused deposition modeling processing parameters using Taguchi design of experiment method. J. Manuf. Process. 2018, 36, 164–174. [Google Scholar] [CrossRef]
- Hamza, I.; Abdellah, E.G.; Mohamed, O. Experimental optimization of fused deposition modeling process parameters: A Taguchi process approach for dimension and tolerance control. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Paris, France, 26–27 July 2018; pp. 2992–2993. [Google Scholar]
- Ahmad, M.N.; Ab Rahman, M.H.; Maidin, N.A.; Osman, M.H.; Wahid, M.K.; Mohamed Saiful Firdaus, H.; Abd Aziz, N.A. Optimization on Surface Roughness of Fused Deposition Modelling (FDM) 3D printed parts using taguchi approach. In Proceedings of the Symposium on Intelligent Manufacturing and Mechatronics, Melaka, Malaysia, 8 July 2019; Springer: Singapore, 2019; pp. 230–243. [Google Scholar]
- Uttarwar, P.B.; Raini, S.K.; Malwad, D.S. Optimization of process parameter on Surface Roughness (Ra) and Wall Thickness on SPIF Using Taguchi method. Int. Res. J. Eng. Technol. 2015, 2, 781–784. [Google Scholar]
- Naiju, C.D.; Anil, P.M. Influence of operating parameters on the reciprocating sliding wear of direct metal deposition (DMD) components using Taguchi method. Procedia Eng. 2017, 174, 1016–1027. [Google Scholar] [CrossRef]
- Lee, B.H.; Abdullah, J.; Khan, Z.A. Optimization of rapid prototyping parameters for production of flexible ABS object. J. Mater. Process. Technol. 2005, 169, 54–61. [Google Scholar] [CrossRef]
- Uddin, M.S.; Sidek, M.F.R.; Faizal, M.A.; Ghomashchi, R.; Pramanik, A. Evaluating mechanical properties and failure mechanisms of fused deposition modeling acrylonitrile butadiene styrene parts. J. Manuf. Sci. Eng. 2017, 139, 081018. [Google Scholar] [CrossRef]
- Onwubolu, G.C.; Rayegani, F. Characterization and optimization of mechanical properties of ABS parts manufactured by the fused deposition modelling process. Int. J. Manuf. Eng. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Kumar, S.; Kannan, V.N.; Sankaranarayanan, G. Parameter optimization of ABS-M30i parts produced by fused deposition modeling for minimum surface roughness. Int. J. Curr. Eng. Technol. 2014, 3, 93–97. [Google Scholar]
- Osman, M.H.; Ab Rahman, M.H.; Ahmad, M.N.; Wahid, M.K.; Maidin, N.A. Optimization of drilling parameters on diameter accuracy in dry drilling process of AISI D2 tool steel. Int. J. Appl. Eng. Res. 2017, 12, 9644–9652. [Google Scholar]
- Depuydt, D.; Balthazar, M.; Hendrickx, K.; Six, W.; Ferraris, E.; Desplentere, F.; Ivens, J.; van Vuure, A.W. Production and characterization of bamboo and flax fiber reinforced polylactic acid filaments for fused deposition modeling (FDM). Polym. Compos. 2019, 40, 1951–1963. [Google Scholar] [CrossRef]
- Filgueira, D.; Holmen, S.; Melbø, J.K.; Moldes, D.; Echtermeyer, A.T.; Chinga-Carrasco, G. Enzymatic-assisted modification of thermomechanical pulp fibers to improve the interfacial adhesion with poly-(lactic acid) for 3D printing. ACS Sustain. Chem. Eng. 2017, 5, 9338–9346. [Google Scholar] [CrossRef]
- Ahmad, M.N.; Ishak, M.R.; Taha, M.M.; Mustapha, F.; Leman, Z. Rheological and Morphological Properties of Oil Palm Fiber-Reinforced Thermoplastic Composites for Fused Deposition Modeling (FDM). Polymers 2021, 13, 3739. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.N.; Wahid, M.K.; Maidin, N.A.; Ab Rahman, M.H.; Osman, M.H. Mechanical characteristics of oil palm fiber reinforced thermoplastics as filament for fused deposition modeling (FDM). Adv. Manuf. 2020, 8, 72–81. [Google Scholar] [CrossRef]
- Irfan, M.S.; Umer, R.; Rao, S. Optimization of Compounding Parameters for Extrusion to Enhance Mechanical Performance of Kenaf-Polypropylene Composites. Fibers Polym. 2021, 22, 1378–1387. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Stephens, M.A. EDF statistics for goodness of fit and some comparisons. J. Am. Stat. Assoc. 1974, 69, 730–737. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Chacón, J.M.; Caminero, M.A.; García-Plaza, E.; Núnez, P.J. Additive manufacturing of PLA structures using fused deposition modelling: Effect of process parameters on mechanical properties and their optimal selection. Mater. Des. 2017, 124, 143–157. [Google Scholar] [CrossRef]
- Domingo-Espin, M.; Puigoriol-Forcada, J.M.; Garcia-Granada, A.A.; Llumà, J.; Borros, S.; Reyes, G. Mechanical property characterization and simulation of fused deposition modeling Polycarbonate parts. Mater. Des. 2015, 83, 670–677. [Google Scholar] [CrossRef]
- Tymrak, B.M.; Kreiger, M.; Pearce, J.M. Mechanical properties of components fabricated with open-source 3-D printers under realistic environmental conditions. Mater. Des. 2014, 58, 242–246. [Google Scholar] [CrossRef] [Green Version]
- Lanzotti, A.; Grasso, M.; Staiano, G.; Martorelli, M. The impact of process parameters on mechanical properties of parts fabricated in PLA with an open-source 3-D printer. Rapid Prototyp. J. 2015, 21, 604–617. [Google Scholar] [CrossRef] [Green Version]
- Sgriccia, N.; Hawley, M.; Misra, M. Characterization of natural fibre surfaces and natural fibre composites. Compos. Part A Appl. Sci. Manuf. 2008, 39, 514–522. [Google Scholar] [CrossRef]
- Taj, S.; Munawar, M.A.; Khan, S. Review: Natural fibre reinforced polymercomposites. Proc. Pak. Acad. Sci. 2007, 44, 129–144. [Google Scholar]
- Casavola, C.; Cazzato, A.; Moramarco, V.; Renna, G. Mechanical behaviour of ABS-Fused Filament Fabrication compounds under impact tensile loadings. Materials 2019, 12, 1295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Ozcan, S. Highly oriented carbon fiber–polymer composites via additive manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef] [Green Version]





| Factors | Levels | |||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
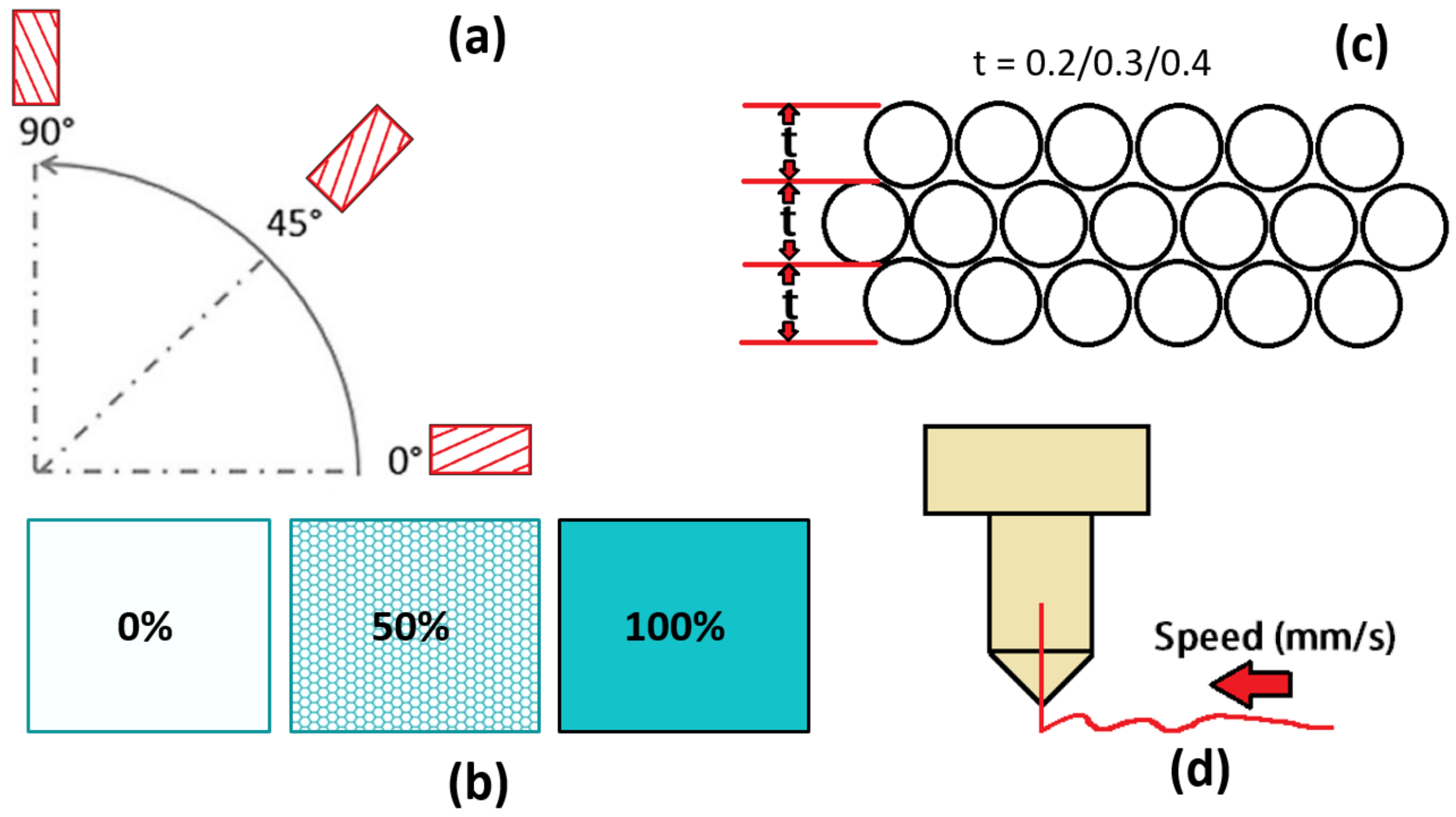
| A | Thickness of Layer (mm) | 0.2 | 0.3 | 0.4 |
| B | Orientation on Z-axis (°) | 0 | 45 | 90 |
| C | Infill Density (%) | 100 | 50 | 0 |
| D | Printing Speed (mm/s) | 10 | 50 | 100 |
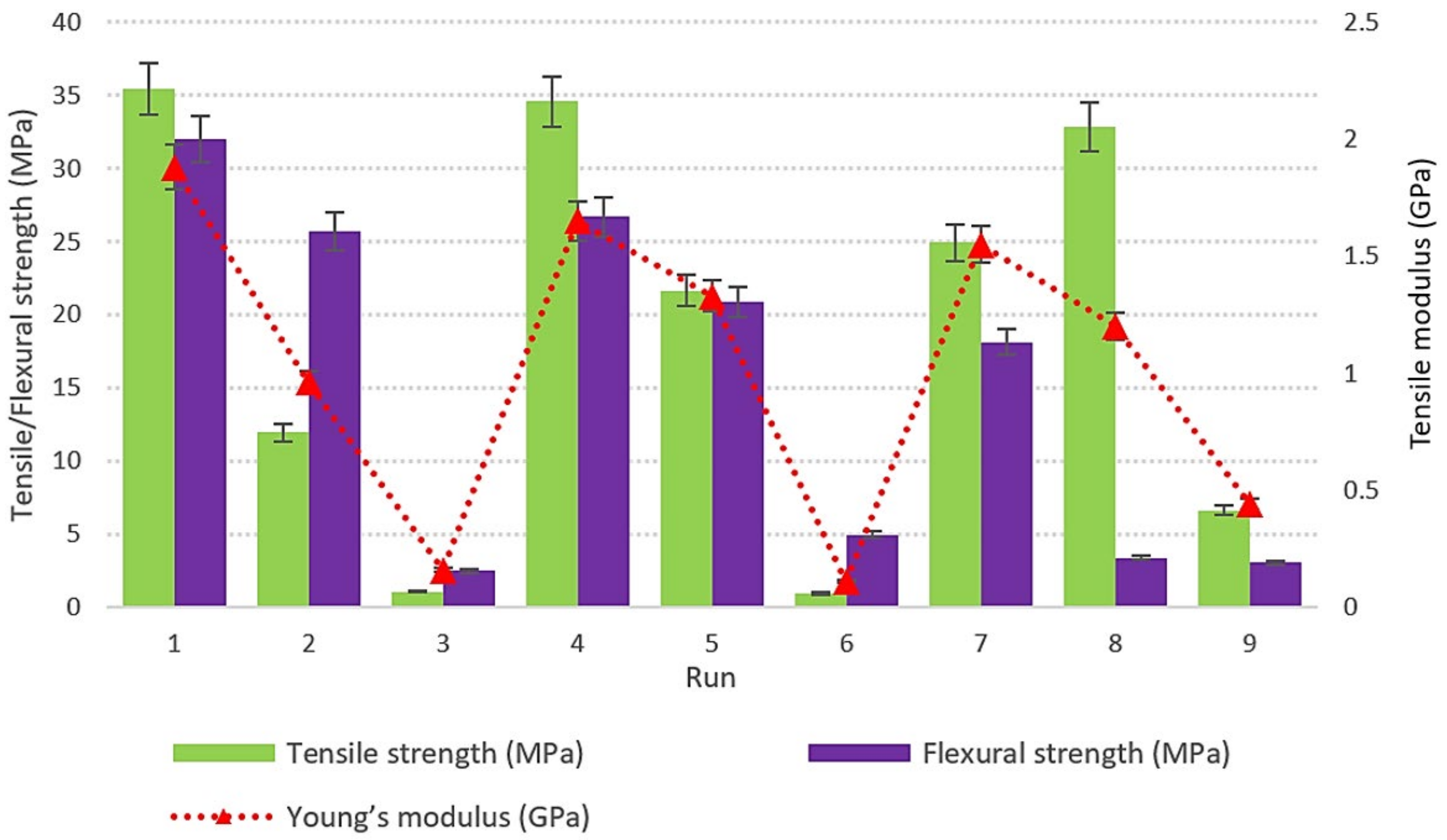
| Run | Layer Thickness (mm) | Orientation (°) | Infill Density (%) | Printing Speed (mm/s) | Responses | ||
|---|---|---|---|---|---|---|---|
| Tensile Strength (MPa) | Young’s Modulus (GPa) | Flexural Strength (MPa) | |||||
| 1 | 0.2 | 0 | 100 | 10 | 35.38 | 1.88 | 31.98 |
| 2 | 0.2 | 45 | 50 | 50 | 11.94 | 0.96 | 25.67 |
| 3 | 0.2 | 90 | 0 | 100 | 1.06 | 0.16 | 2.50 |
| 4 | 0.3 | 0 | 50 | 100 | 34.55 | 1.65 | 26.67 |
| 5 | 0.3 | 45 | 0 | 10 | 21.64 | 1.33 | 20.88 |
| 6 | 0.3 | 90 | 100 | 50 | 0.95 | 0.11 | 4.97 |
| 7 | 0.4 | 0 | 0 | 50 | 24.92 | 1.55 | 18.12 |
| 8 | 0.4 | 45 | 100 | 100 | 32.83 | 1.20 | 3.40 |
| 9 | 0.4 | 90 | 50 | 10 | 6.64 | 0.44 | 3.04 |
| Dimension (mm) | ASTM D638 | ASTM D790 |
|---|---|---|
| Overall length | 165 | 130 |
| Overall width | 19 | 13 |
| Distance between grips | 115 | - |
| Gage length | 50 | - |
| Length of narrow section | 57 | - |
| Thickness | 3.2 | 3 |
| Radius of fillet | 76 | - |
| Gage width | 13 | - |
| Response | Source | DoF | Adj SS | Adj MS | F-Value | p-Value | % Contribution | Remarks |
|---|---|---|---|---|---|---|---|---|
| Tensile strength | Layer thickness | 2 | 43.0 | 21.0 | 0.08 | 0.921 | 2.26 | Insignificant |
| Orientation | 2 | 1286.2 | 643.1 | 12.55 | 0.007 * | 67.67 | Significant | |
| Infill density | 2 | 83.0 | 42.0 | 0.17 | 0.851 | 4.37 | Insignificant | |
| Printing speed | 2 | 181.0 | 91.0 | 0.38 | 0.696 | 9.52 | Insignificant | |
| Error | 6 | 307.4 | 51.2 | 16.17 | ||||
| Total | 8 | 1900.6 | 100 | |||||
| Young’s modulus | Layer thickness | 2 | 0.006 | 0.003 | 0.01 | 0.995 | 0.09 | Insignificant |
| Orientation | 2 | 3.262 | 1.631 | 51.23 | 0.000 * | 48.51 | Significant | |
| Infill density | 2 | 0.005 | 0.002 | 0.00 | 0.996 | 0.07 | Insignificant | |
| Printing speed | 2 | 0.180 | 0.090 | 0.17 | 0.851 | 2.68 | Insignificant | |
| Error | 6 | 3.272 | 1.726 | 48.65 | ||||
| Total | 8 | 6.725 | 100 | |||||
| Flexural strength | Layer thickness | 2 | 234.0 | 117.0 | 0.80 | 0.494 | 15.68 | Insignificant |
| Orientation | 2 | 740.6 | 370.3 | 5.91 | 0.038 * | 49.62 | Significant | |
| Infill density | 2 | 47.0 | 23.0 | 0.13 | 0.880 | 3.15 | Insignificant | |
| Printing speed | 2 | 95.0 | 48.0 | 0.28 | 0.765 | 6.36 | Insignificant | |
| Error | 6 | 376.0 | 25.19 | |||||
| Total | 8 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, M.N.; Ishak, M.R.; Mohammad Taha, M.; Mustapha, F.; Leman, Z.; Anak Lukista, D.D.; Irianto; Ghazali, I. Application of Taguchi Method to Optimize the Parameter of Fused Deposition Modeling (FDM) Using Oil Palm Fiber Reinforced Thermoplastic Composites. Polymers 2022, 14, 2140. https://doi.org/10.3390/polym14112140
Ahmad MN, Ishak MR, Mohammad Taha M, Mustapha F, Leman Z, Anak Lukista DD, Irianto, Ghazali I. Application of Taguchi Method to Optimize the Parameter of Fused Deposition Modeling (FDM) Using Oil Palm Fiber Reinforced Thermoplastic Composites. Polymers. 2022; 14(11):2140. https://doi.org/10.3390/polym14112140
Chicago/Turabian StyleAhmad, Mohd Nazri, Mohamad Ridzwan Ishak, Mastura Mohammad Taha, Faizal Mustapha, Zulkiflle Leman, Debby Dyne Anak Lukista, Irianto, and Ihwan Ghazali. 2022. "Application of Taguchi Method to Optimize the Parameter of Fused Deposition Modeling (FDM) Using Oil Palm Fiber Reinforced Thermoplastic Composites" Polymers 14, no. 11: 2140. https://doi.org/10.3390/polym14112140
APA StyleAhmad, M. N., Ishak, M. R., Mohammad Taha, M., Mustapha, F., Leman, Z., Anak Lukista, D. D., Irianto, & Ghazali, I. (2022). Application of Taguchi Method to Optimize the Parameter of Fused Deposition Modeling (FDM) Using Oil Palm Fiber Reinforced Thermoplastic Composites. Polymers, 14(11), 2140. https://doi.org/10.3390/polym14112140









