Frequency Response of Thermo-Optic Phase Modulators Based on Fluorinated Polyimide Polymer Waveguide
Abstract
:1. Introduction
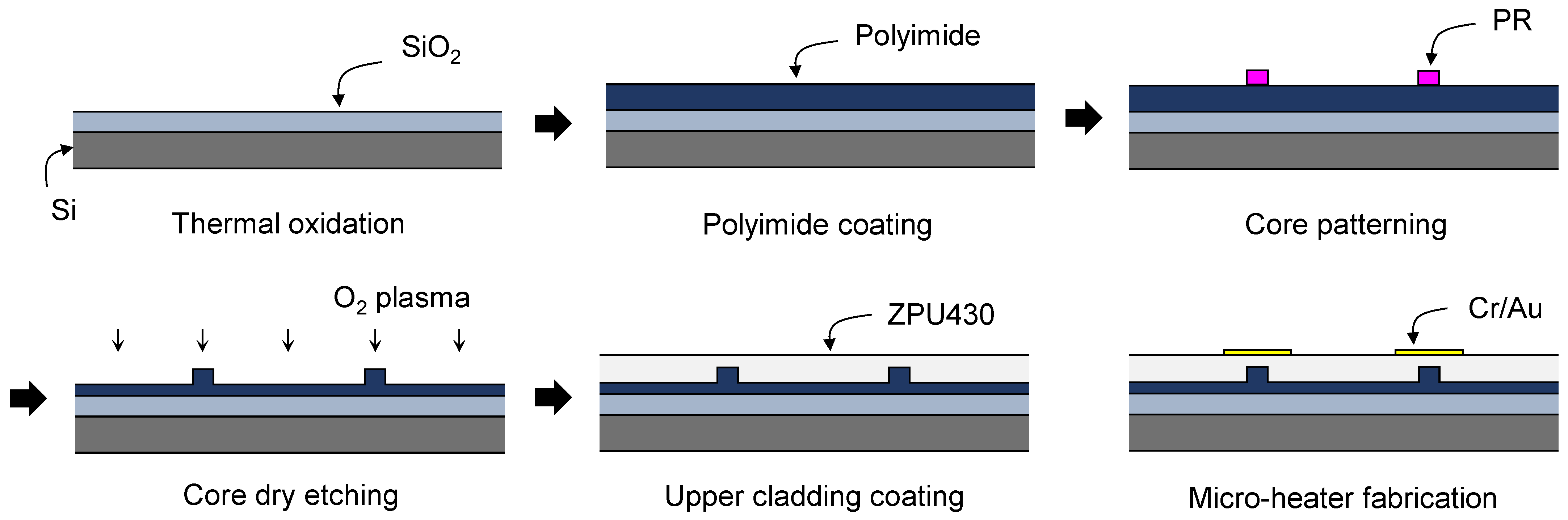
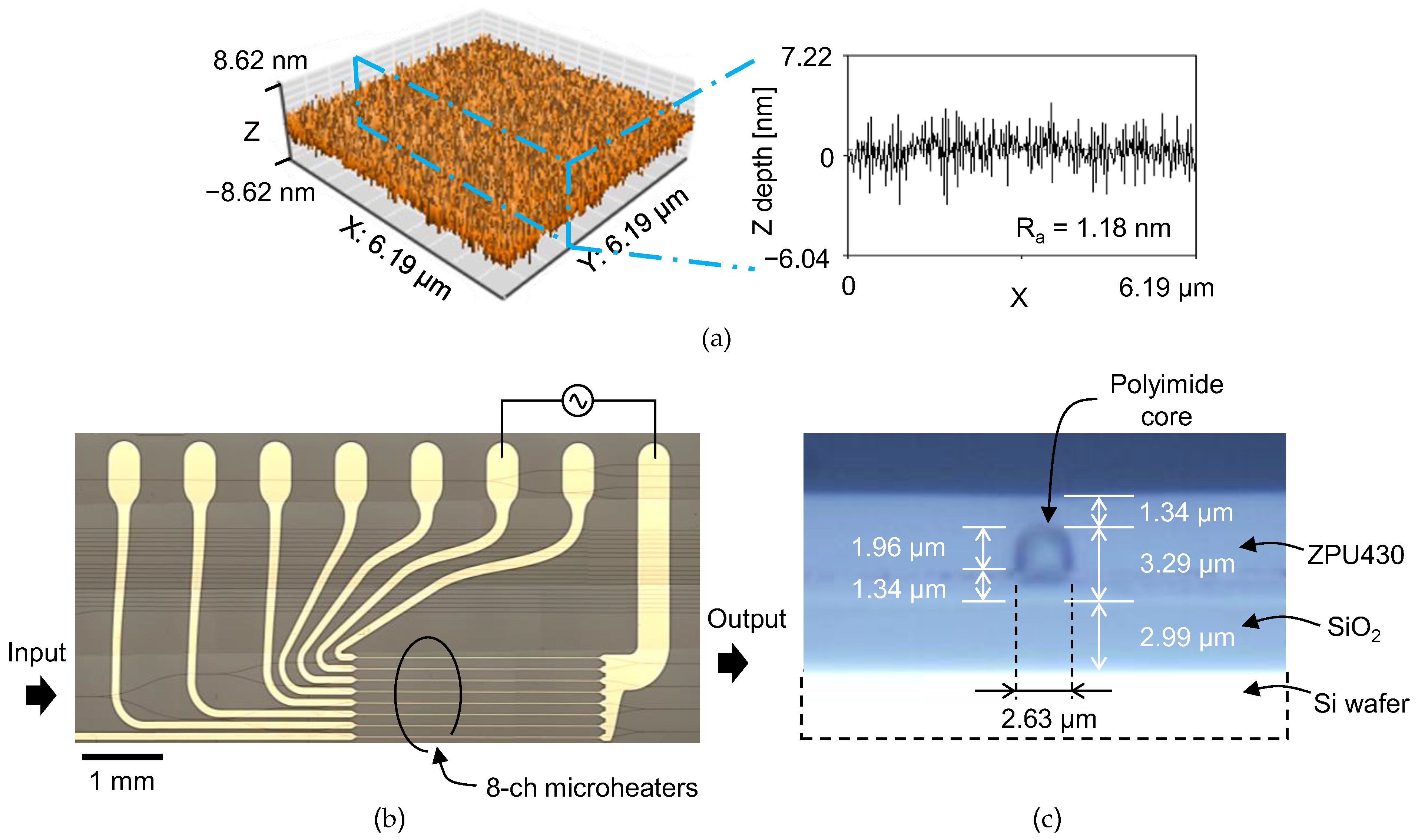
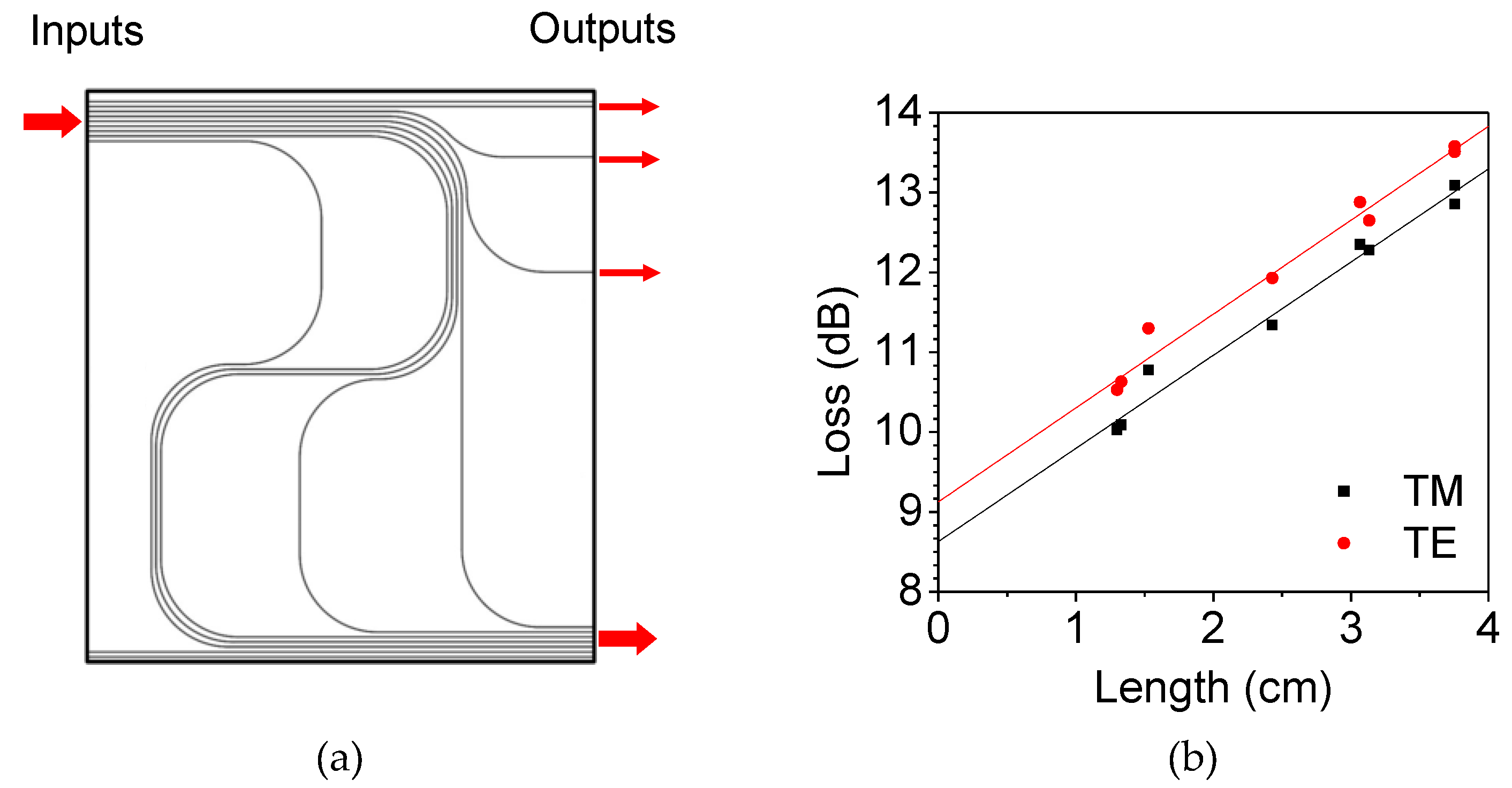
2. Design and Fabrication of Thermo-Optic Phase Modulators with Polymer Waveguides
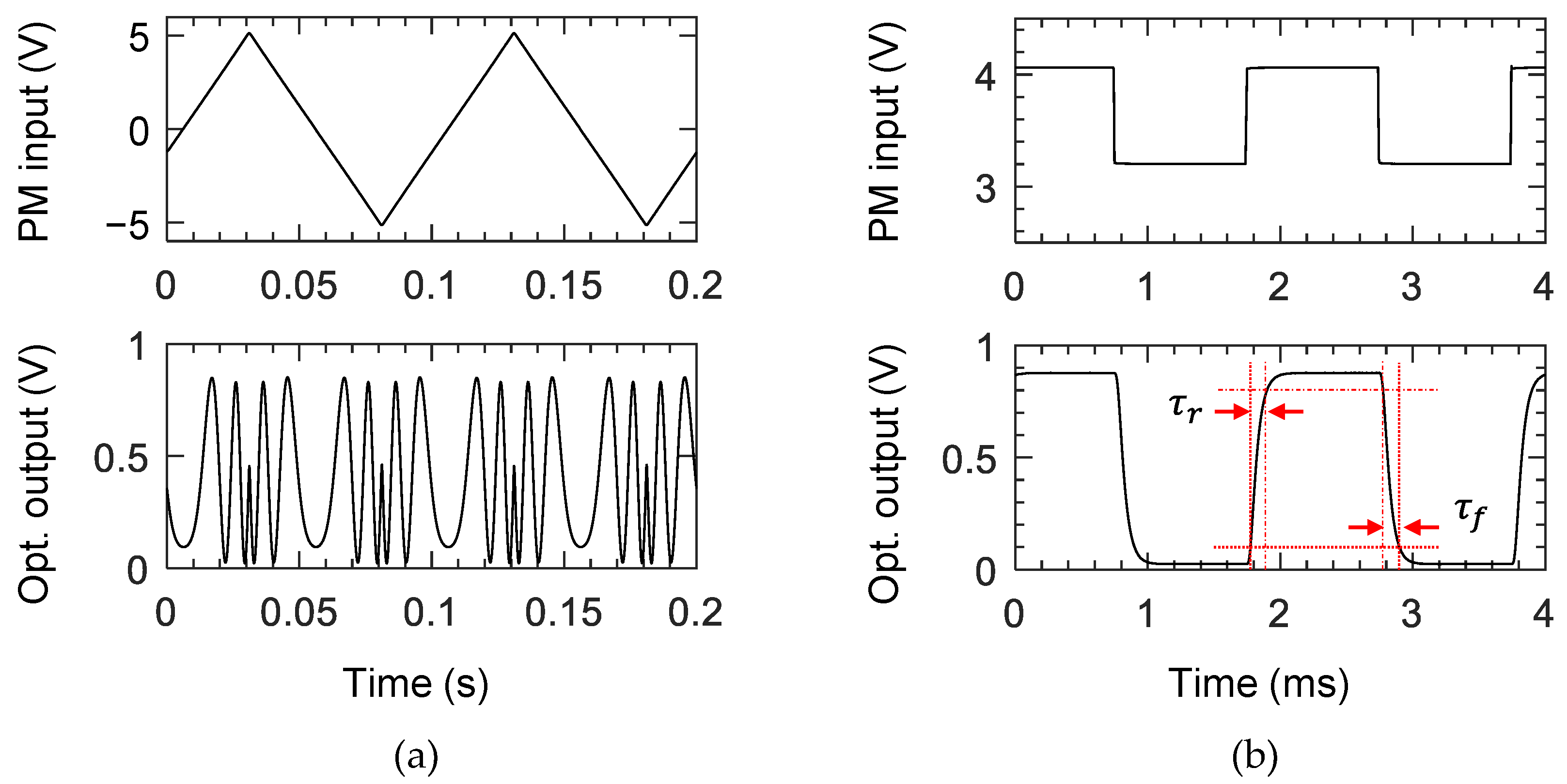
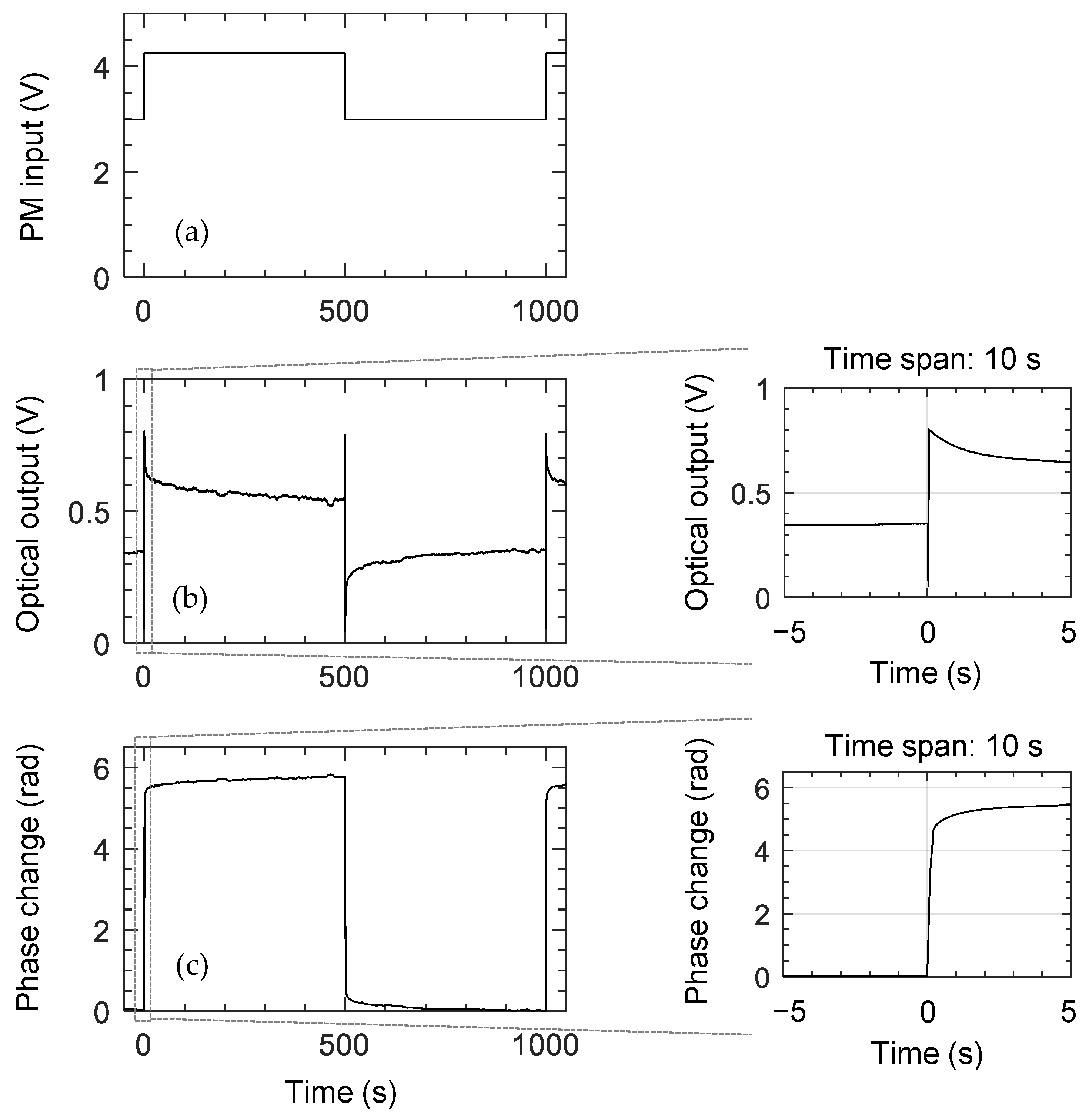
3. Temporal and Frequency Response of the Polyimide Phase Modulators
4. Verification of the Low Thermal Crosstalk between the Adjacent Polymer Modulators
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, S.-M.; Lee, E.-S.; Chun, K.-W.; Jin, J.; Oh, M.-C. Compact solid-state optical phased array beam scanners based on polymeric photonic integrated circuits. Sci. Rep. 2021, 11, 10576. [Google Scholar] [CrossRef] [PubMed]
- Park, T.-H.; Kim, S.-M.; Lee, E.-S.; Oh, M.-C. Polymer waveguide tunable transceiver for photonic front-end in the 5G wireless network. Photonics Res. 2021, 9, 181–186. [Google Scholar] [CrossRef]
- Kim, S.-M.; Park, T.-H.; Huang, G.; Oh, M.-C. Bias-free optical current sensors based on quadrature interferometric integrated optics. Opt. Express 2018, 26, 31599–31606. [Google Scholar] [CrossRef] [PubMed]
- Noh, Y.-O.; Lee, C.-H.; Kim, J.-M.; Hwang, W.-Y.; Won, Y.-H.; Lee, H.-J.; Han, S.-G.; Oh, M.-C. Polymer waveguide variable optical attenuator and its reliability. Opt. Commun. 2004, 242, 533–540. [Google Scholar] [CrossRef]
- De Felipe, D.; Kleinert, M.; Zawadzki, C.; Polatynski, A.; Irmscher, G.; Brinker, W.; Moehrle, M.; Bach, H.-G.; Keil, N.; Schell, M. Recent developments in polymer-based photonic components for disruptive capacity upgrade in data centers. J. Lightwave Technol. 2016, 35, 683–689. [Google Scholar] [CrossRef]
- Kim, S.-M.; Park, T.-H.; Huang, G.; Oh, M.-C. Optical waveguide tunable phase delay lines based on the superior thermo-optic effect of polymer. Polymers 2018, 10, 497. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.-M.; Park, T.-H.; Im, C.-S.; Lee, S.-S.; Kim, T.; Oh, M.-C. Temporal response of polymer waveguide beam scanner with thermo-optic phase-modulator array. Opt. Express 2020, 28, 3768–3778. [Google Scholar] [CrossRef]
- Im, C.-S.; Kim, S.-M.; Lee, K.-P.; Ju, S.-H.; Hong, J.-H.; Yoon, S.-W.; Kim, T.; Lee, E.-S.; Bhandari, B.; Zhou, C.; et al. Hybrid integrated silicon nitride polymer optical phased array for efficient light detection and ranging. J. Lightwave Technol. 2021, 39, 4402–4409. [Google Scholar] [CrossRef]
- Hicyilmaz, A.S.; Bedeloglu, A.C. Applications of polyimide coatings: A review. SN Appl. Sci. 2021, 3, 363. [Google Scholar] [CrossRef]
- Liaw, D.-J.; Wang, K.-L.; Huang, Y.-C.; Lee, K.-R.; Lai, J.-Y.; Ha, C.-S. Advanced polyimide materials: Syntheses, physical properties and applications. Prog. Polym. Sci. 2012, 37, 907–974. [Google Scholar] [CrossRef]
- Chen, J.; Liu, C.T. Technology advances in flexible displays and substrates. IEEE Access 2013, 1, 150–158. [Google Scholar] [CrossRef]
- Tao, L.; Yang, H.; Liu, J.; Fan, L.; Yang, S. Synthesis and characterization of highly optical transparent and low dielectric constant fluorinated polyimides. Polymer 2009, 50, 6009–6018. [Google Scholar] [CrossRef]
- Kowalczyk, T.C.; Kosc, T.; Singer, K.D.; Cahill, P.A.; Seager, C.H.; Meinhardt, M.B.; Beuhler, A.J.; Wargowski, D.A. Loss mechanisms in polyimide waveguides. J. Appl. Phys. 1994, 76, 2505–2508. [Google Scholar] [CrossRef]
- Prakash, D.P.; Scott, D.C.; Fetterman, H.R.; Matloubian, M.; Du, Q.; Wang, W. Integration of polyimide waveguides with traveling-wave phototransistors. IEEE Photonics Technol. Lett. 1997, 9, 800–802. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, Q.; Chen, R.T. Polyimide-waveguide-based thermal optical switch using total-internal-reflection effect. Appl. Phys. Lett. 2002, 81, 2947–2949. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, J.; Matsuura, T.; Sasaki, S.; Maruno, T. Single-mode optical waveguides fabricated from fluorinated polyimides. Appl. Opt. 1998, 37, 1032–1037. [Google Scholar] [CrossRef]
- Kobayashi, J.; Matsuura, T.; Hida, Y.; Sasaki, S.; Maruno, T. Fluorinated polyimide waveguides with low polarization-dependent loss and their applications to thermooptic switches. J. Lightwave Technol. 1998, 16, 1024–1029. [Google Scholar] [CrossRef]
- Ando, S. Optical properties of fluorinated polyimides and their applications to optical components and waveguide circuits. J. Photopolym. Sci. Technol. 2004, 17, 219–232. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.-W.; Kim, J.-J.; Kim, J.; Li, X.; Lee, M.-H. Low-loss and thermally stable TE-mode selective polymer waveguide using photosensitive fluorinated polyimide. IEEE Photonics Technol. Lett. 2002, 14, 1297–1299. [Google Scholar] [CrossRef]
- Cornic, C.; Lucas, B.; Moliton, A.; Colombeau, B.; Mercier, R. Elaboration and characterization of a 6FDA/MPDA polyimide-based optical waveguide. Synth. Met. 2002, 127, 299–302. [Google Scholar] [CrossRef]
- Gao, H.; Yan, C.; Guan, S.; Jiang, Z. Hyperbranched fluorinated polyimides with tunable refractive indices for optical waveguide applications. Polymer 2010, 51, 694–701. [Google Scholar] [CrossRef]
- Gupta, R.K.; Das, B.K. Performance analysis of metal-microheater integrated silicon waveguide phase-shifters. OSA Continuum 2018, 1, 703–714. [Google Scholar] [CrossRef]
- Della Corte, F.G.; Merenda, M.; Cocorullo, G.; Iodice, M.; Rendina, I.; Sarro, P.M. Modulation speed improvement in a Fabry-Perot thermo-optical modulator through a driving signal optimization technique. Opt. Eng. 2009, 48, 074601. [Google Scholar] [CrossRef] [Green Version]
- Jacques, M.; Samani, A.; El-Fiky, E.; Patel, D.; Xing, Z.; Plant, D.V. Optimization of thermo-optic phase-shifter design and mitigation of thermal crosstalk on the SOI platform. Opt. Express 2019, 27, 10456–10471. [Google Scholar] [CrossRef] [PubMed]
- Watts, M.R.; Sun, J.; DeRose, C.; Trotter, D.C.; Young, R.W.; Nielson, G.N. Adiabatic thermo-optic Mach-Zehnder switch. Opt. Lett. 2013, 38, 733–735. [Google Scholar] [CrossRef]
- Drineas, P.; Mahoney, M.W.; Muthukrishnan, S.; Sarlós, T. Faster least squares approximation. Numer. Math. 2011, 117, 219–249. [Google Scholar] [CrossRef] [Green Version]
- Paige, C.C.; Saunders, M.A. LSQR: An algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Softw. 1982, 8, 43–71. [Google Scholar] [CrossRef]
- Renaud, F.; Dion, J.L.; Chevallier, G.; Tawfiq, I.; Lemaire, R. A new identification method of viscoelastic behavior: Application to the generalized Maxwell model. Mech. Syst. Signal Process. 2011, 25, 991–1010. [Google Scholar] [CrossRef] [Green Version]
- Hida, Y.; Onose, K.; Imamura, S. Moisture-induced drift in thermo-optic phase shifters composed of deuterated and fluorinated methacrylate polymer waveguides. Appl. Opt. 1997, 36, 6828–6837. [Google Scholar] [CrossRef]
- Simon, P.P.; Ploehn, H.J. Molecular-level modeling of the viscoelasticity of crosslinked polymers: Effect of time and temperature. J. Rheol. 1997, 41, 641–670. [Google Scholar] [CrossRef] [Green Version]
- Stefani, A.; Andresen, S.; Yuan, W.; Bang, O. Dynamic characterization of polymer optical fibers. IEEE Sens. J. 2012, 12, 3047–3053. [Google Scholar] [CrossRef]



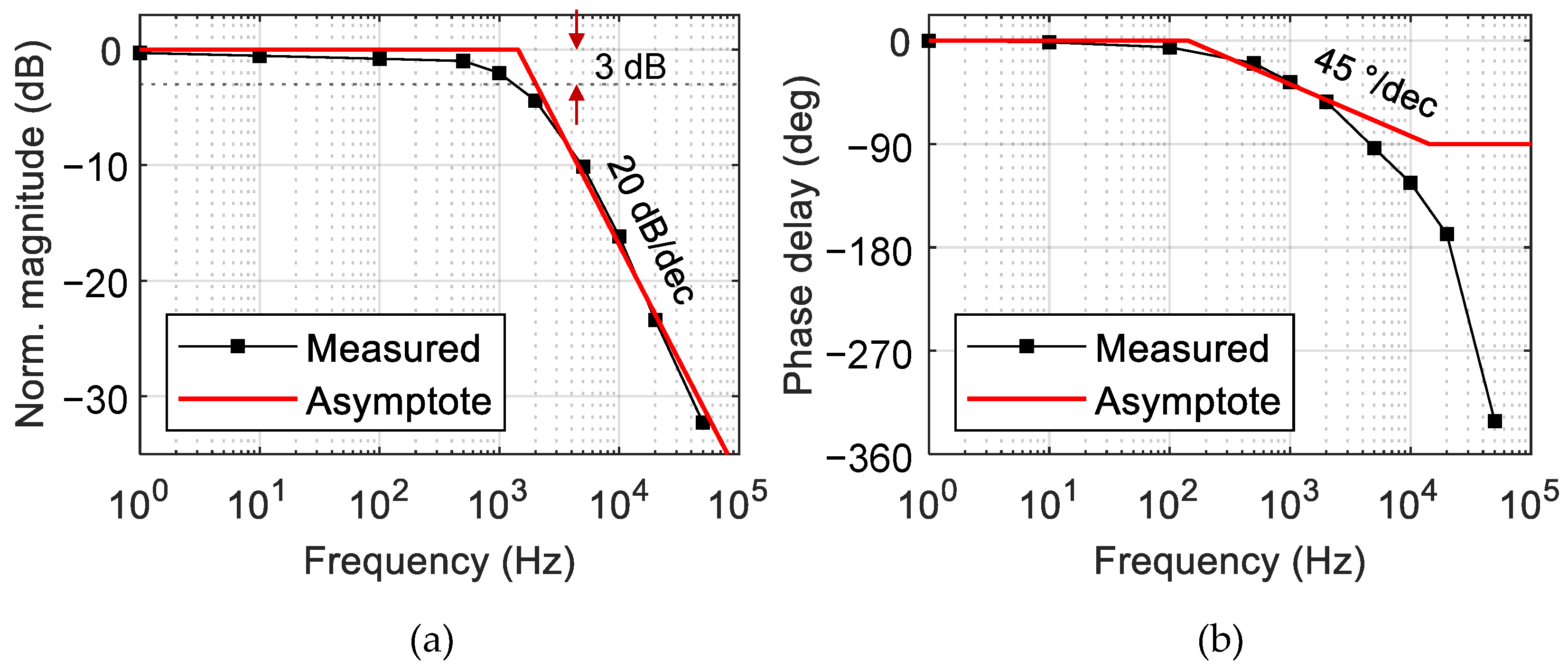
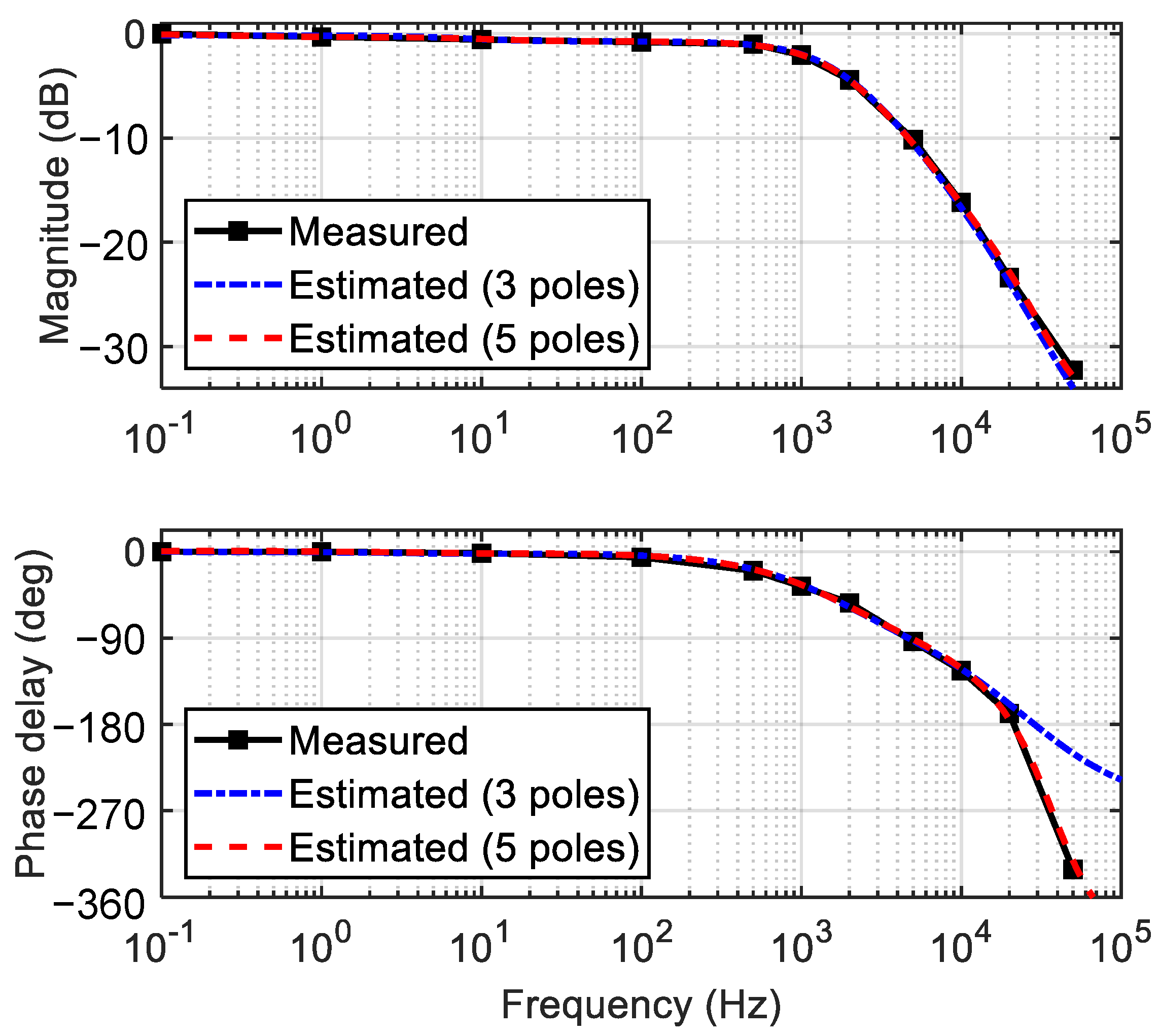


| Np | Transfer Function H(s) |
|---|---|
| 1 | |
| 3 | |
| 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, E.-S.; Chun, K.-W.; Jin, J.; Oh, M.-C. Frequency Response of Thermo-Optic Phase Modulators Based on Fluorinated Polyimide Polymer Waveguide. Polymers 2022, 14, 2186. https://doi.org/10.3390/polym14112186
Lee E-S, Chun K-W, Jin J, Oh M-C. Frequency Response of Thermo-Optic Phase Modulators Based on Fluorinated Polyimide Polymer Waveguide. Polymers. 2022; 14(11):2186. https://doi.org/10.3390/polym14112186
Chicago/Turabian StyleLee, Eun-Su, Kwon-Wook Chun, Jinung Jin, and Min-Cheol Oh. 2022. "Frequency Response of Thermo-Optic Phase Modulators Based on Fluorinated Polyimide Polymer Waveguide" Polymers 14, no. 11: 2186. https://doi.org/10.3390/polym14112186
APA StyleLee, E.-S., Chun, K.-W., Jin, J., & Oh, M.-C. (2022). Frequency Response of Thermo-Optic Phase Modulators Based on Fluorinated Polyimide Polymer Waveguide. Polymers, 14(11), 2186. https://doi.org/10.3390/polym14112186







