Effect of Four Groups of GO-CF/EP Composites with Ideal Infiltration Structure and Different Layering Ways on Damping Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Materials
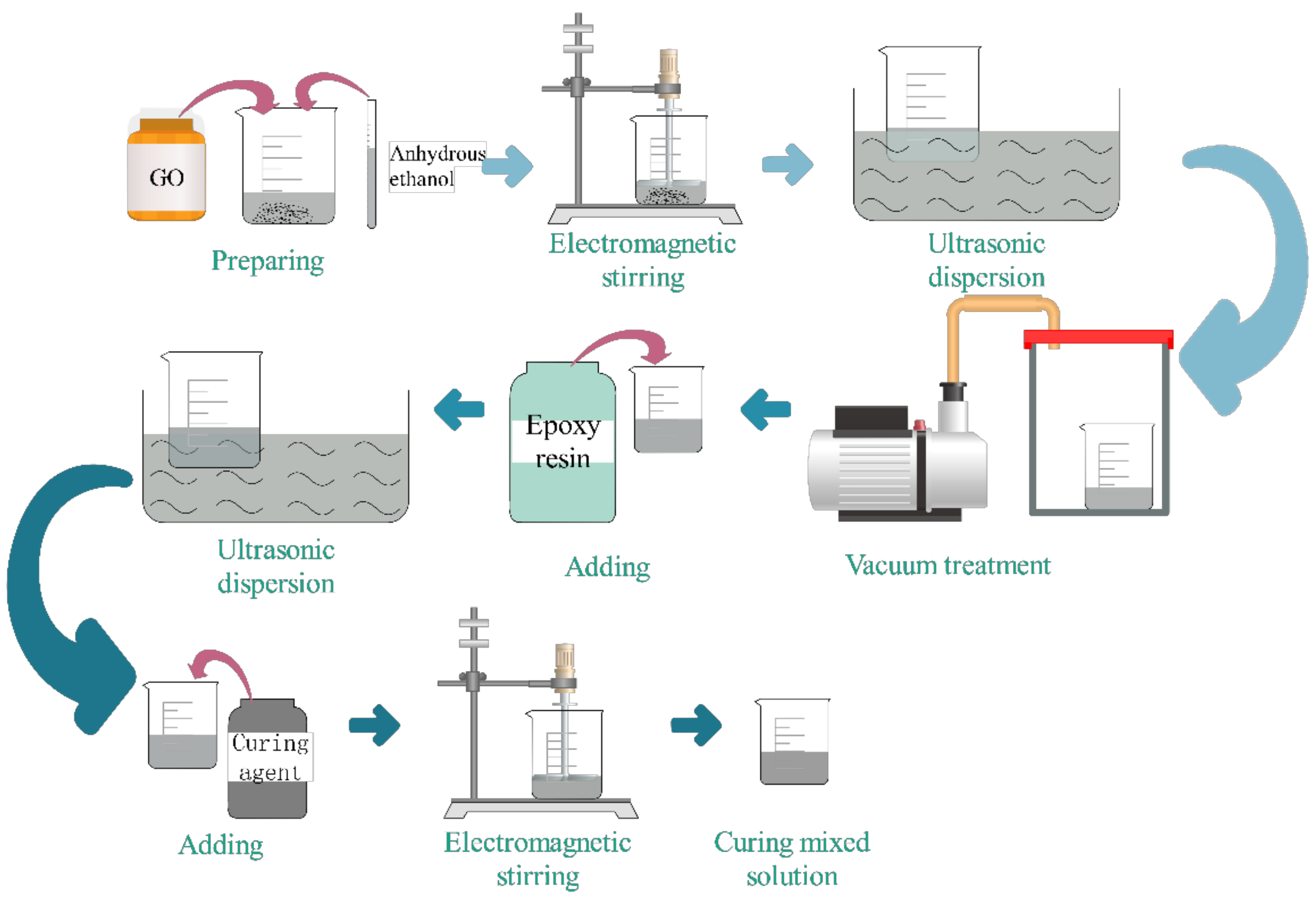
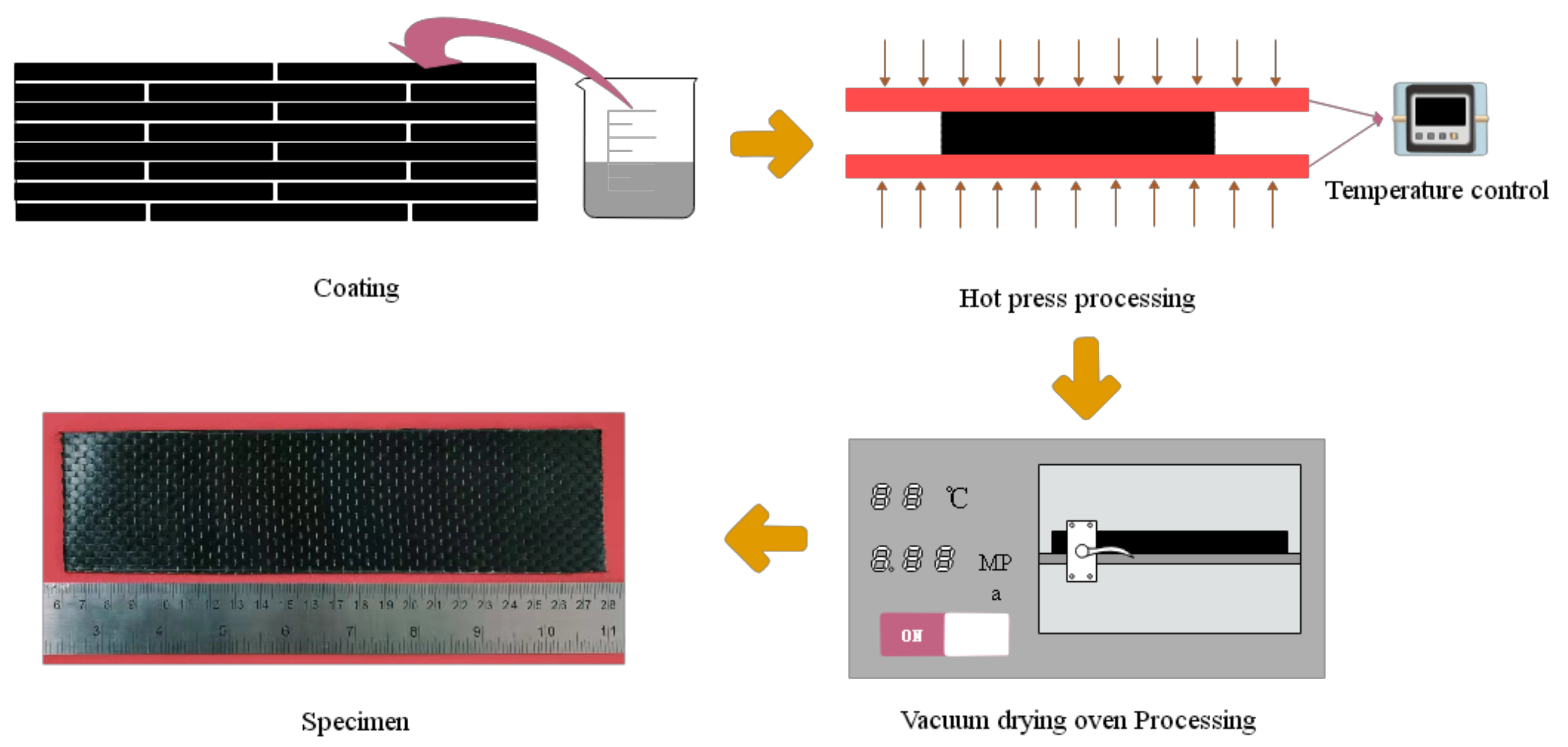
2.2. Preparation Process of Specimens
2.2.1. Preparation of Curing Mixed Solution Containing GO
2.2.2. Preparation of GO-CF/EP Composites
2.3. Test and Characterization Methods
3. Analysis of Test Results
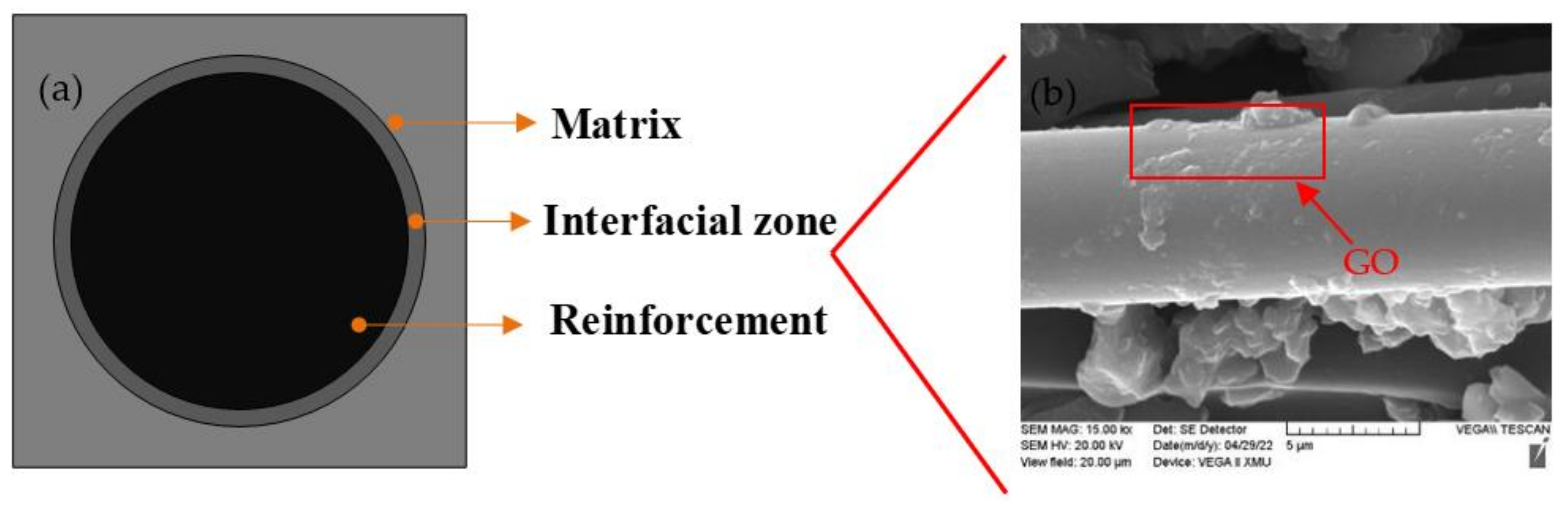
3.1. Microstructure
3.1.1. Microstructure of GO
3.1.2. Micromorphology of Infiltration Structure
3.2. Damping Performance
3.2.1. The Damping Ratio
3.2.2. Natural Frequency
4. Discussion
5. Conclusions
- (1)
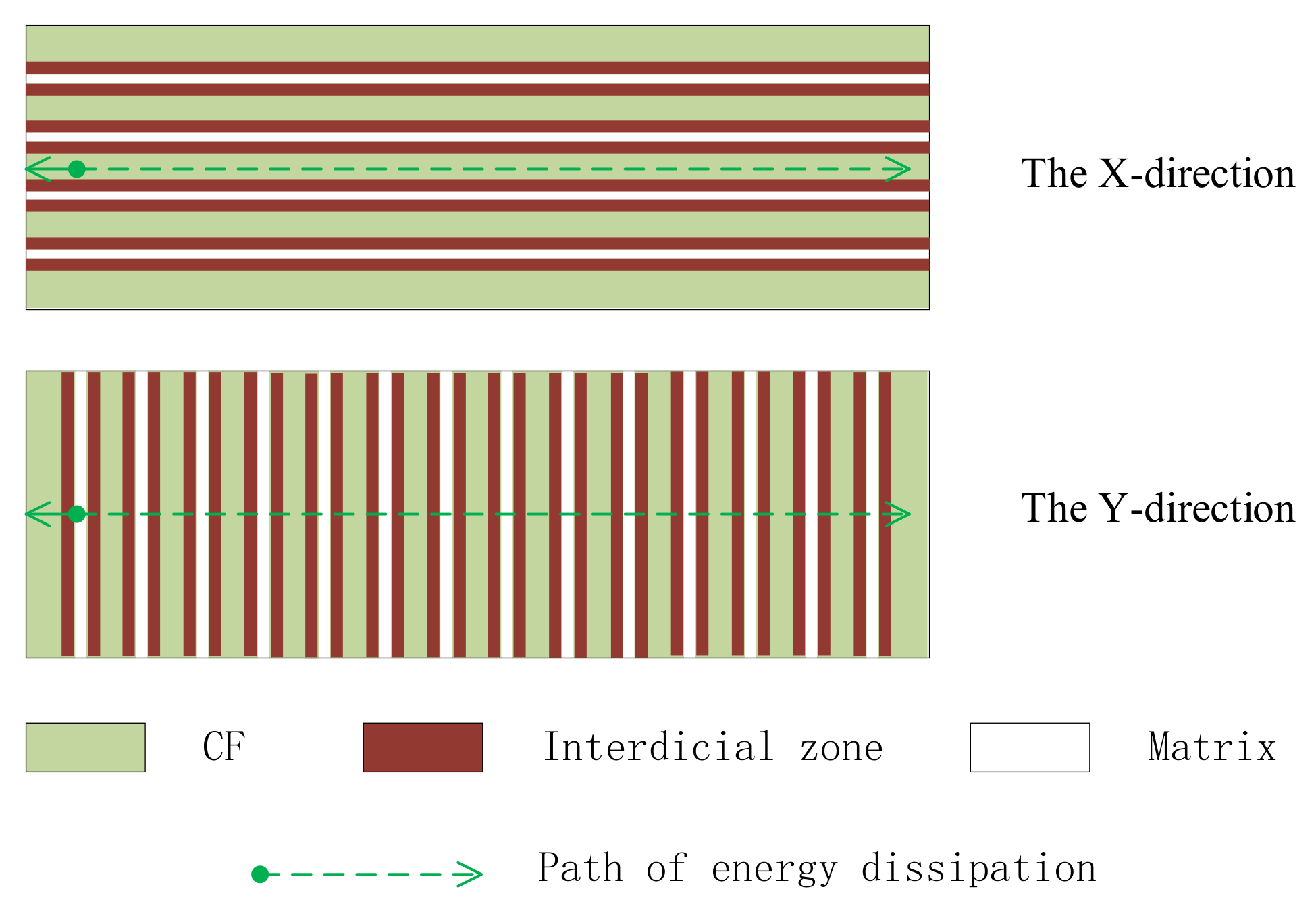
- The addition of nanoscale GO can significantly enhance the damping performance of CFRP composites. The main dissipation mechanism of GO-CF/EP composites is friction sliding. Compared with traditional reinforced materials, the addition of GO makes the friction area between GO and resin larger, so the dissipation mechanism is higher;
- (2)
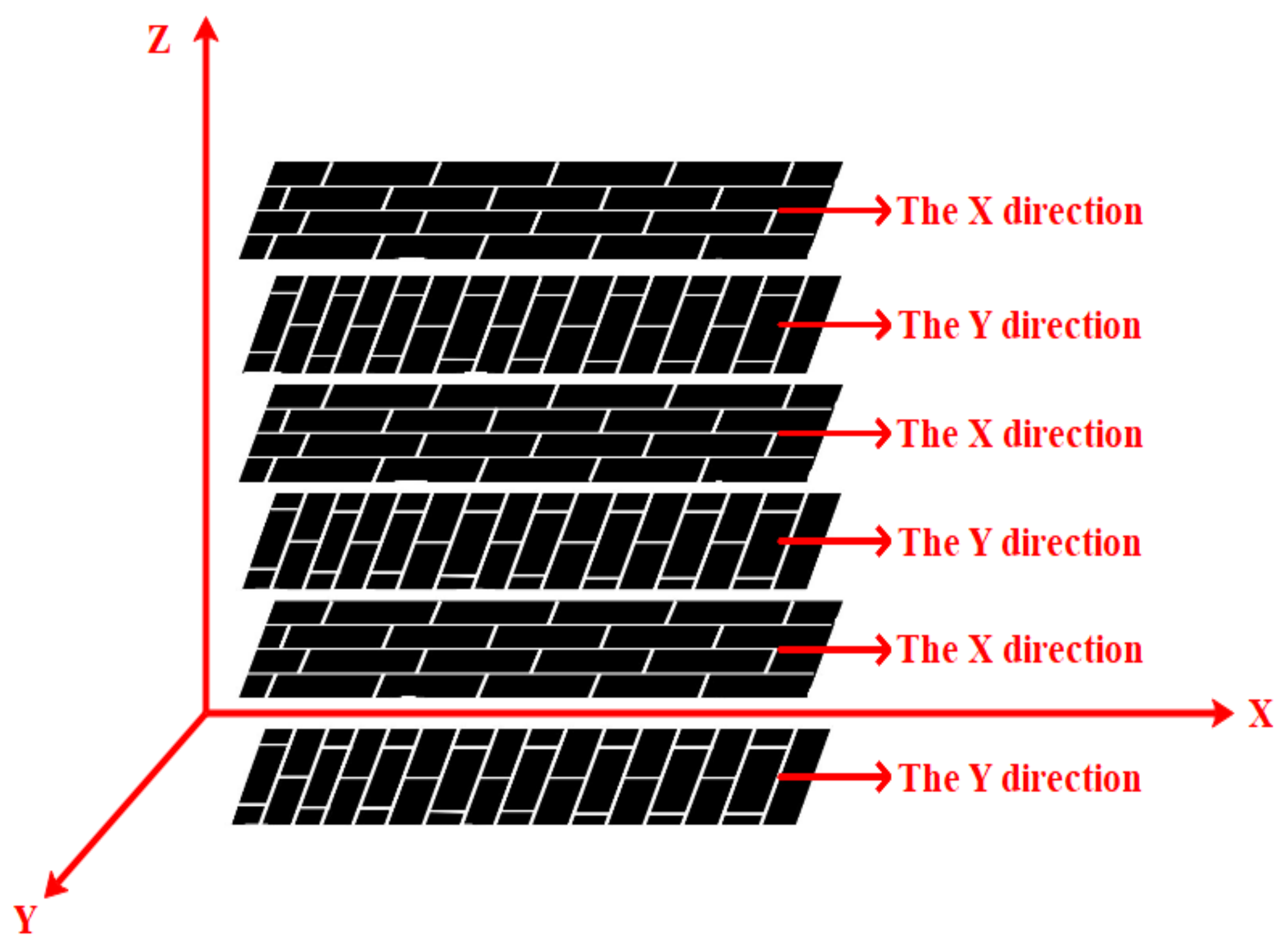
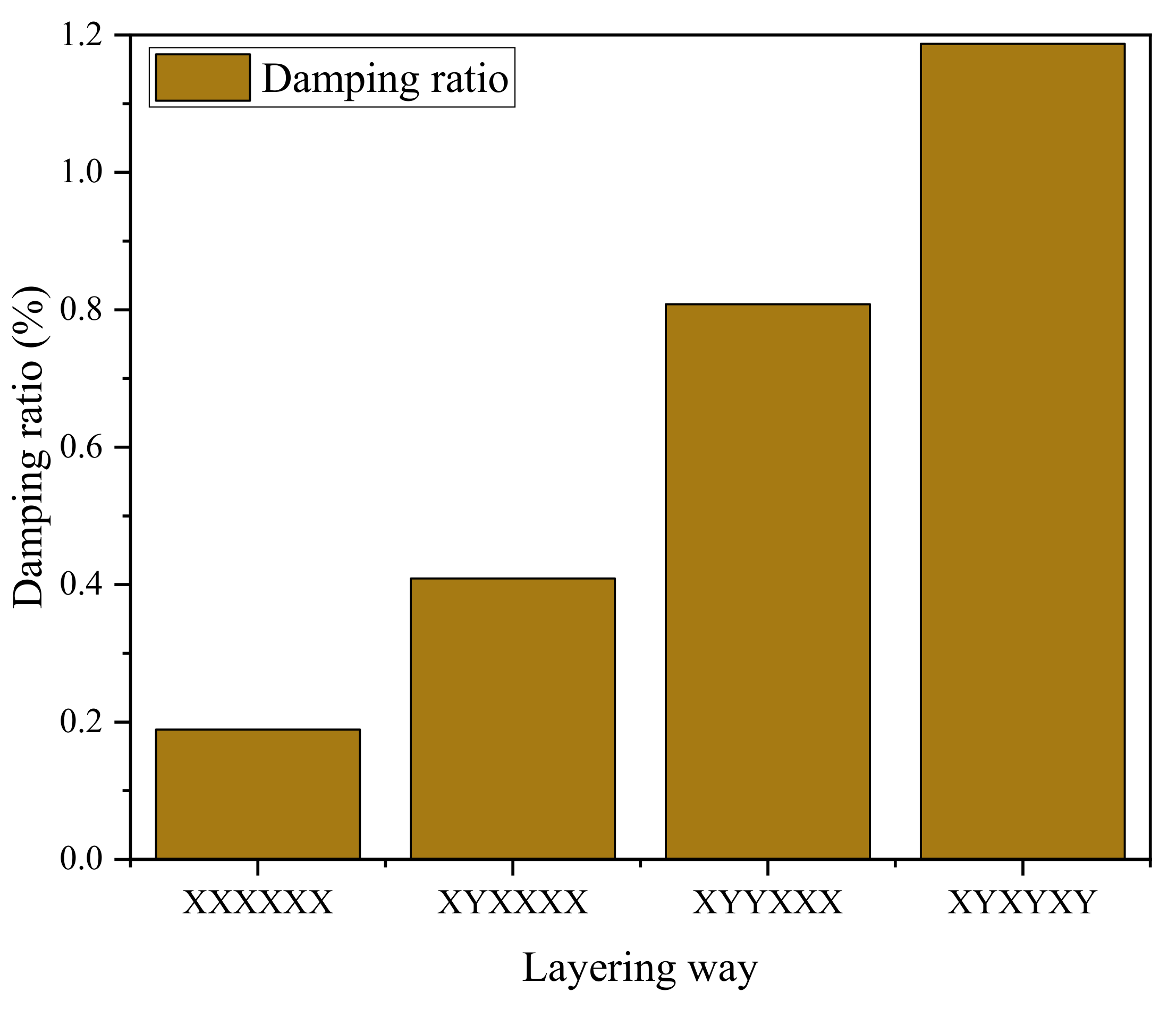
- Among the prepared specimens, the damping ratio of [XYXYXY]6 specimens is up to 1.189%, which is more than six times that of [XXXXXX]6 specimens. This is because, with the increase in the number of Y-direction layers, the participation of the matrix, which contributes greatly to the damping performance, gradually increases, thus improving the damping performance of GO-CF/EP composites;
- (3)
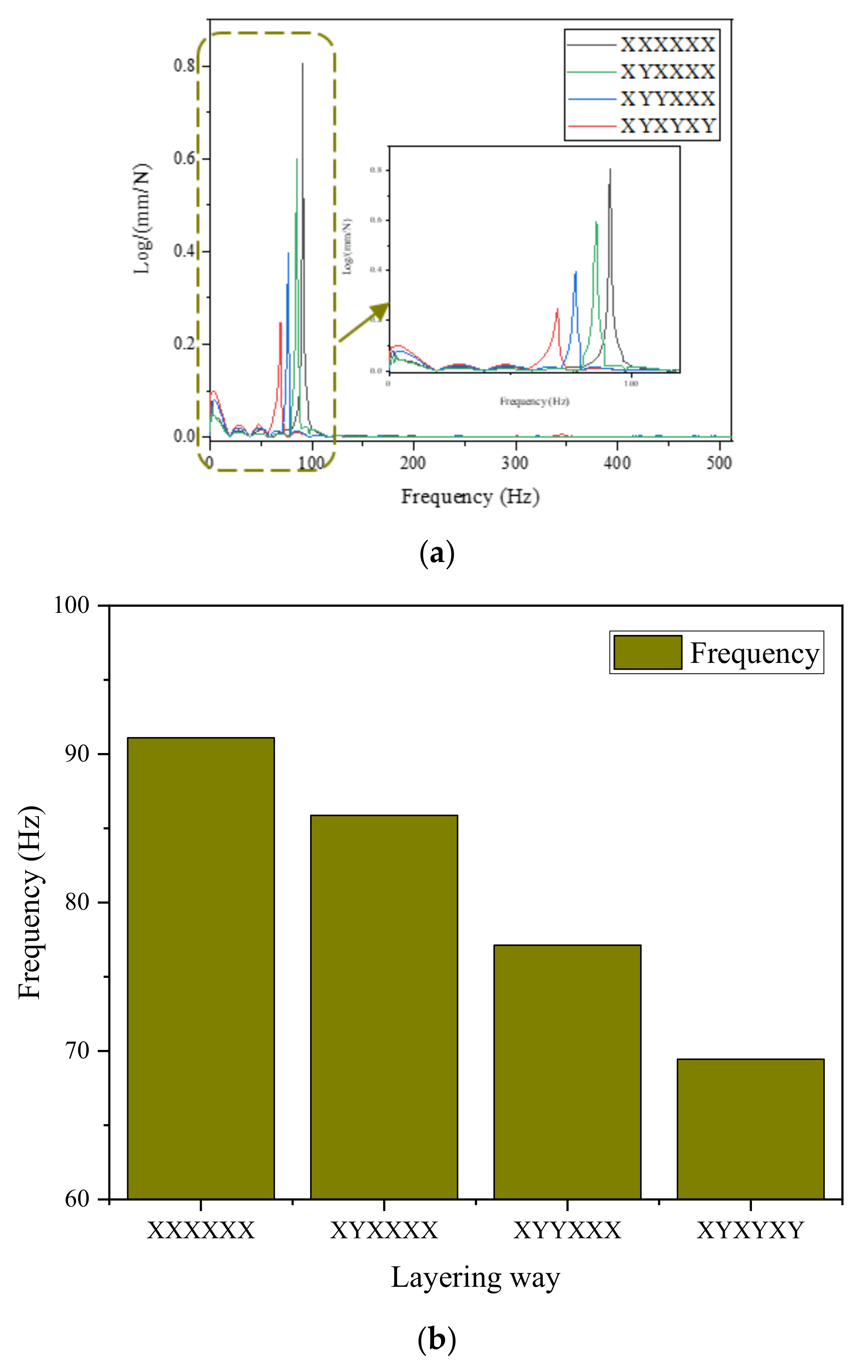
- The natural frequency of GO-CF/EP composites is greatly affected by the stiffness of the materials. The anisotropy of the stiffness of the specimen changes with different lamination modes, and so does the dynamic stiffness of the laminate. With the increase in the number of Y-direction layers, the dynamic stiffness decreases, and the natural frequency of the material decreases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, G.; Sun, Q.; Fenner, J.; Li, D.; Zeng, D.; Su, X.; Peng, Y. Crushing behaviors of unidirectional carbon fiber reinforced plastic composites under dynamic bending and axial crushing loading. Int. J. Impact Eng. 2020, 140, 103539. [Google Scholar] [CrossRef]
- Zhou, G.; Sun, Q.; Meng, Z.; Li, D.; Peng, Y.; Zeng, D.; Su, X. Experimental investigation on the effects of fabric architectures on mechanical and damage behaviors of carbon/epoxy woven composites. Compos. Struct. 2021, 257, 113366. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, D.; He, Z.; Yao, D.; Zheng, Y. Damping and mechanical properties of carbon nanotube solvent-free nanofluids-filled epoxy nanocomposites. Polym. Compos. 2021, 42, 3262–3271. [Google Scholar] [CrossRef]
- Lin, R.; Lu, C. Modeling of interfacial friction damping of carbon nanotube-based nanocomposites. Mech. Syst. Signal. Process. 2010, 24, 2996–3012. [Google Scholar] [CrossRef]
- Senthamaraikannan, C.; Ramesh, R. Evaluation of mechanical and vibration behavior of hybrid epoxy carbon composite beam carrying micron-sized CTBN rubber and nanosilica particles. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 233, 1738–1752. [Google Scholar] [CrossRef]
- Rahman, Z.; Jayaraman, K.; Mace, B.R. Vibration damping of flax fibre-reinforced polypropylene composites. Fibers Polym. 2017, 18, 2187–2195. [Google Scholar] [CrossRef]
- Florence, A.; Jaswin, M.A. Vibration and flexural characterization of hybrid honeycomb core sandwich panels filled with different energy absorbing materials. Mater. Res. Express 2019, 6, 075326. [Google Scholar] [CrossRef]
- Bhudolia, S.K.; Gohel, G.; Leong, K.F.; Joshi, S.C. Damping, impact and flexural performance of novel carbon/Elium® thermoplastic tubular composites. Compos. Part B Eng. 2020, 203, 108480. [Google Scholar] [CrossRef]
- Tsimouri, I.C.; Montibeller, S.; Kern, L.; Hine, P.J.; Spolenak, R.; Gusev, A.A.; Danzi, S. A simulation-driven design approach to the manufacturing of stiff composites with high viscoelastic damping. Compos. Sci. Technol. 2021, 208, 108744. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, J.; Zhao, Y.; Wei, X.; Ju, L.; Chen, Y. A New Vacuum Pressure Infiltration CFRP Method and Preparation Experimental Study of Composite. Polymers 2020, 12, 419. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Gibson, R.F.; Gordaninejad, F.; Suhr, J. Energy absorption capability of nanocomposites: A review. Compos. Sci. Technol. 2009, 69, 2392–2409. [Google Scholar] [CrossRef]
- Gong, L.; Zhang, F.; Peng, X.; Scarpa, F.; Huang, Z.; Tao, G.; Liu, H.Y.; Zhou, H.; Zhou, H. Improving the damping properties of carbon fiber reinforced polymer composites by interfacial sliding of oriented multilayer graphene oxide. Compos. Sci. Technol. 2022, 224, 109309. [Google Scholar] [CrossRef]
- Ghule, B.G.; Shinde, N.M.; Raut, S.D.; Gore, S.K.; Shaikh, S.F.; Ekar, S.U.; Ubaidullah, M.; Pak, J.J.; Mane, R.S. Self-assembled α-Fe2O3-GO nanocomposites: Studies on physical, magnetic and ammonia sensing properties. Mater. Chem. Phys. 2022, 278, 125617. [Google Scholar] [CrossRef]
- Sarikaya, S.; Henry, T.C.; Naraghi, M. Graphene Size and Morphology: Peculiar Effects on Damping Properties of Polymer Nanocomposites. Exp. Mech. 2020, 60, 753–762. [Google Scholar] [CrossRef]
- Lu, W.; Qin, F.; Wang, Y.; Luo, Y.; Wang, H.; Scarpa, F.; Li, J.; Sesana, R.; Cura, F.; Peng, H.-X. Engineering Graphene Wrinkles for Large Enhancement of Interlaminar Friction Enabled Damping Capability. ACS Appl. Mater. Interfaces 2019, 11, 30278–30289. [Google Scholar] [CrossRef]
- Lu, W.; Qin, F.; Zhang, Q.; Remillat, C.; Wang, H.; Scarpa, F.; Peng, H.-X. Engineering foam skeletons with multilayered graphene oxide coatings for enhanced energy dissipation. Compos. Part A Appl. Sci. Manuf. 2020, 137, 106035. [Google Scholar] [CrossRef]
- Matsubara, M.; Teramoto, S.; Nagatani, A.; Kawamura, S.; Tsujiuchi, N.; Ito, A.; Kobayashi, M.; Furuta, S. Effect of Fiber Orientation on Nonlinear Damping and Internal Microdeformation in Short-Fiber-Reinforced Natural Rubber. Exp. Tech. 2021, 45, 37–47. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Wang, D.-W.; Ma, L. Vibration and damping performance of carbon fiber-reinforced polymer 3D double-arrow-head auxetic metamaterials. J. Mater. Sci. 2021, 56, 1443–1460. [Google Scholar] [CrossRef]
- Rueppel, M.; Rion, J.; Dransfeld, C.; Fischer, C.; Masania, K. Damping of carbon fibre and flax fibre angle-ply composite laminates. Compos. Sci. Technol. 2017, 146, 1–9. [Google Scholar] [CrossRef]
- Assarar, M.; Zouari, W.; Sabhi, H.; Ayad, R.; Berthelot, J.-M. Evaluation of the damping of hybrid carbon–flax reinforced composites. Compos. Struct. 2015, 132, 148–154. [Google Scholar] [CrossRef]
- Wei, X.; Meng, Z.; Ruiz, L.; Xia, W.; Lee, C.; Kysar, J.W.; Hone, J.C.; Keten, S.; Espinosa, H.D. Recoverable Slippage Mechanism in Multilayer Graphene Leads to Repeatable Energy Dissipation. ACS Nano 2016, 10, 1820–1828. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Z.; Wu, H.; Nie, J. Research on damping performance and strength of the composite laminate. Sci. Rep. 2021, 11, 18281. [Google Scholar] [CrossRef]
- Al-Obaidi, A.J.; Ahmed, S.J.; Sukar, H.M. The effect of factors on the flexural of the composite leaf spring. Mater. Today Proc. 2020, 20, 566–571. [Google Scholar] [CrossRef]
- Varma, N.; Ahuja, R.; Vijayakumar, T.; Kannan, C. Design and analysis of composite mono leaf spring for passenger cars. Mater. Today Proc. 2021, 46, 7090–7098. [Google Scholar] [CrossRef]
- Bennet, C.; Rajini, N.; Jappes, J.W.; Siva, I.; Sreenivasan, V.; Amico, S. Effect of the stacking sequence on vibrational behavior of Sansevieria cylindrica/coconut sheath polyester hybrid composites. J. Reinf. Plast. Compos. 2015, 34, 293–306. [Google Scholar] [CrossRef]
- Gürgen, S.; Sofuoğlu, M.A. Experimental investigation on vibration characteristics of shear thickening fluid filled CFRP tubes. Compos. Struct. 2019, 226, 111236. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, K.K. Tribological behaviour of fibre-reinforced thermoset polymer composites: A review. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 1439–1449. [Google Scholar] [CrossRef]
- Birk, F.; Ali, F.; Weigold, M.; Abele, E.; Schützer, K. Lightweight hybrid CFRP design for machine tools with focus on simple manufacturing. Int. J. Adv. Manuf. Technol. 2020, 108, 3915–3924. [Google Scholar] [CrossRef]
- Chennamsetti, R.; Hood, A.; Guruprasad, S.; Roy, S.; Joshi, M. Damping ratios of pristine composite beam and constrained layer damped composite beam of equal stiffness. Int. J. Precis. Eng. Manuf. 2013, 14, 1655–1660. [Google Scholar] [CrossRef]
- Chandra, R.; Singh, S.P.; Gupta, K. Damping studies in fiber-reinforced composites—A review. Compos. Struct. 1999, 46, 41–51. [Google Scholar] [CrossRef]
- Zhang, W.L.; Choi, H.J. Graphene/graphene oxide: A new material for electrorheological and magnetorheological applications. J. Intell. Mater. Syst. Struct. 2015, 26, 1826–1835. [Google Scholar] [CrossRef]
- Khan, S.U.; Li, C.Y.; Siddiqui, N.A.; Kim, J.-K. Vibration damping characteristics of carbon fiber-reinforced composites containing multi-walled carbon nanotubes. Compos. Sci. Technol. 2011, 71, 1486–1494. [Google Scholar] [CrossRef]
- Song, M.; Yue, X.; Chang, C.; Cao, F.; Yu, G.; Wang, X. Investigation of the Compatibility and Damping Performance of Graphene Oxide Grafted Antioxidant/Nitrile-Butadiene Rubber Composite: Insights from Experiment and Molecular Simulation. Polymers 2022, 14, 736. [Google Scholar] [CrossRef] [PubMed]
- Ingle, R.; Ahuja, B. An experimental investigation on dynamic analysis of high speed carbon–epoxy shaft in aerostatic conical journal bearings. Compos. Sci. Technol. 2006, 66, 604–612. [Google Scholar] [CrossRef]
- Berthelot, J.-M.; Sefrani, Y. Damping analysis of unidirectional glass and Kevlar fibre composites. Compos. Sci. Technol. 2004, 64, 1261–1278. [Google Scholar] [CrossRef]
- Yim, J.H. A damping analysis of composite laminates using the closed form expression for the basic damping of Poisson’s ratio. Compos. Struct. 1999, 46, 405–411. [Google Scholar] [CrossRef]
- Adams, R.; Bacon, D. Effect of Fibre Orientation and Laminate Geometry on the Dynamic Properties of CFRP. J. Compos. Mater. 1973, 7, 402–428. [Google Scholar] [CrossRef]
- Berthelot, J.-M.; Sefrani, Y. Longitudinal and transverse damping of unidirectional fibre composites. Compos. Struct. 2007, 79, 423–431. [Google Scholar] [CrossRef]





| Author | Craft | Materials | Conclusion | Reference |
|---|---|---|---|---|
| Rahman | Vacuum bagging process | Flax fiber reinforced polypropylene composites | The loss factor increases with increasing frequency and decreases slightly with increasing fiber content. | [6] |
| Florence | Vacuum bag molding technique | Sandwich plates with a hybrid fiber of 70% CF and 30% of ‘E’ glass fiber | The polyurethane-filled sandwich plate had a higher damping performance than the Rohacell-filled panel and wheat husk-filled panel. | [7] |
| Bhudolia | B-RTM | Carbon–Elium composites | At different output positions in the tube, the structural damping of the carbon–Elium composite was improved by 21.7%. | [8] |
| Sarikaya | Solution mixing process | “single-layer graphene” and “GNP” | The addition of GNP will increase the damping properties of the nanocomposites by up to ~70%. | [14] |
| Wenjiang Lu | Modified dip-coating process | Open-cell PU foams containing multilayered GO | These engineered composite foams with extremely low GO content (−0.12 wt%) afford a significant increase in quasistatic energy dissipation (52%) and dynamic damping (76%) when compared with counterpart foams coated with the same number of pure PU dispersion layers. | [16] |
| Yun-Long Chen | Hot-press compression molding method and layer-by-layer assembly method | CFRP 3D DAH auxetic metamaterials | The natural frequency of CFRP 3D DAH attached metamaterials is mainly determined by the stiffness of the main vibration direction, and the loss factor is the highest when the angle of the layer is about 45°. | [18] |
| Rueppel | Autoclave manufacturing and compression resin transfer molding | CFRP and FFRP | The damping of the two materials increases with the increase in the angle. The matrix and interface seem to be primarily responsible for damping at lower frequencies. | [19] |
| Assarar | Platen press process | Flax–carbon twill epoxy composites | [C/F/C/C/F/C] laminates are 15% higher than non-hybrid carbon laminates without losing specific bending modulus. | [20] |
| Bao Zhang | Vacuum infusion molding process | Glass fiber reinforced composites | The 0° fiber layer is beneficial for improving the strength of the laminate. The 90° fiber layer is beneficial for the damping performance of the laminate. | [22] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, F.; Jo, S.-H.; Ma, Y.; Guo, H.; Xu, Y.; Xu, W.; Li, F. Effect of Four Groups of GO-CF/EP Composites with Ideal Infiltration Structure and Different Layering Ways on Damping Properties. Polymers 2022, 14, 2358. https://doi.org/10.3390/polym14122358
Cai F, Jo S-H, Ma Y, Guo H, Xu Y, Xu W, Li F. Effect of Four Groups of GO-CF/EP Composites with Ideal Infiltration Structure and Different Layering Ways on Damping Properties. Polymers. 2022; 14(12):2358. https://doi.org/10.3390/polym14122358
Chicago/Turabian StyleCai, Feichao, Soo-Ho Jo, Yuqin Ma, Haiyin Guo, Yi Xu, Wei Xu, and Fei Li. 2022. "Effect of Four Groups of GO-CF/EP Composites with Ideal Infiltration Structure and Different Layering Ways on Damping Properties" Polymers 14, no. 12: 2358. https://doi.org/10.3390/polym14122358
APA StyleCai, F., Jo, S.-H., Ma, Y., Guo, H., Xu, Y., Xu, W., & Li, F. (2022). Effect of Four Groups of GO-CF/EP Composites with Ideal Infiltration Structure and Different Layering Ways on Damping Properties. Polymers, 14(12), 2358. https://doi.org/10.3390/polym14122358






