A Mechanics Analysis of Carbon Fiber Plain-Woven Thermoset Prepreg during Forming Process Considering Temperature Effect
Abstract
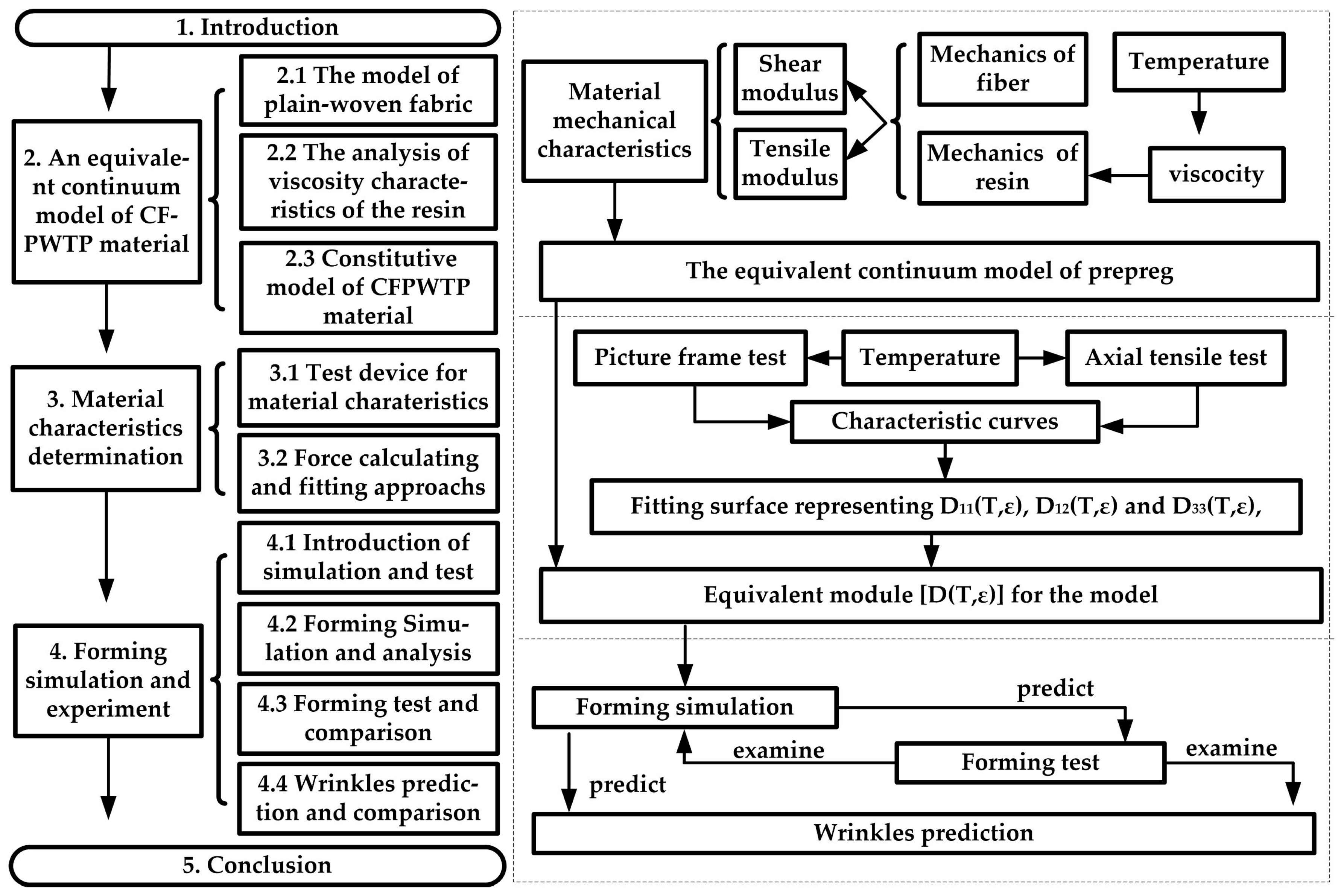
:1. Introduction
2. An Equivalent Continuum Model of CFPWTP Material
2.1. The Model of Plain-Woven Fabric
2.1.1. The Material Mechanic Analysis
2.1.2. The Orthogonal Coordinate Transforming
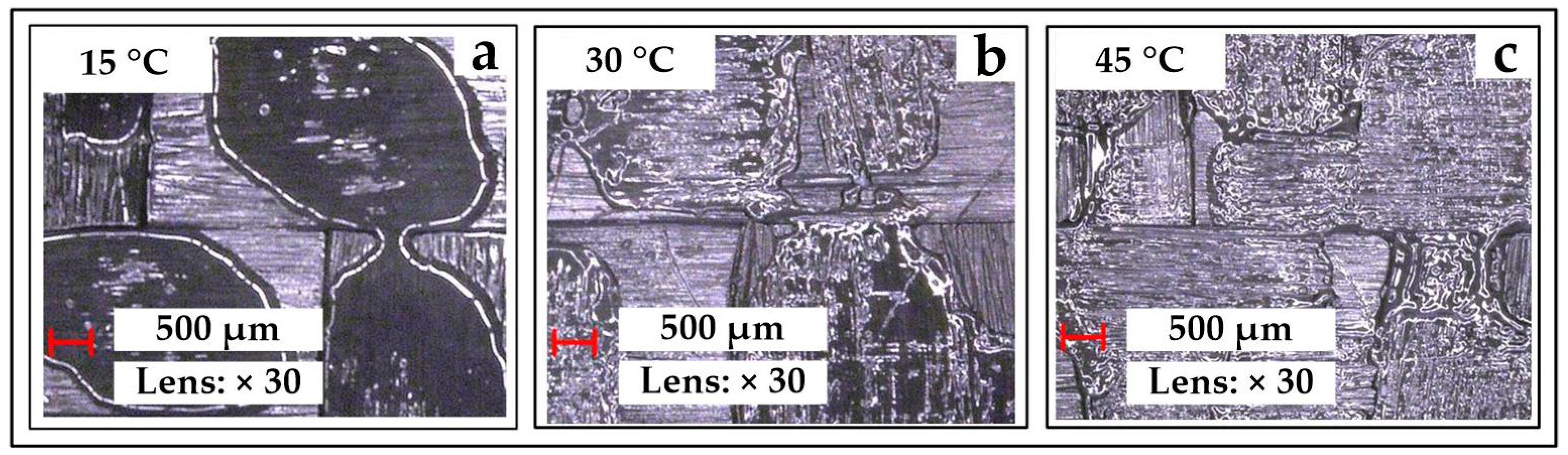
2.2. The Analysis of Viscosity Characteristics of the Resin
2.3. Constitutive Model of CFPWTP Material
- (a)
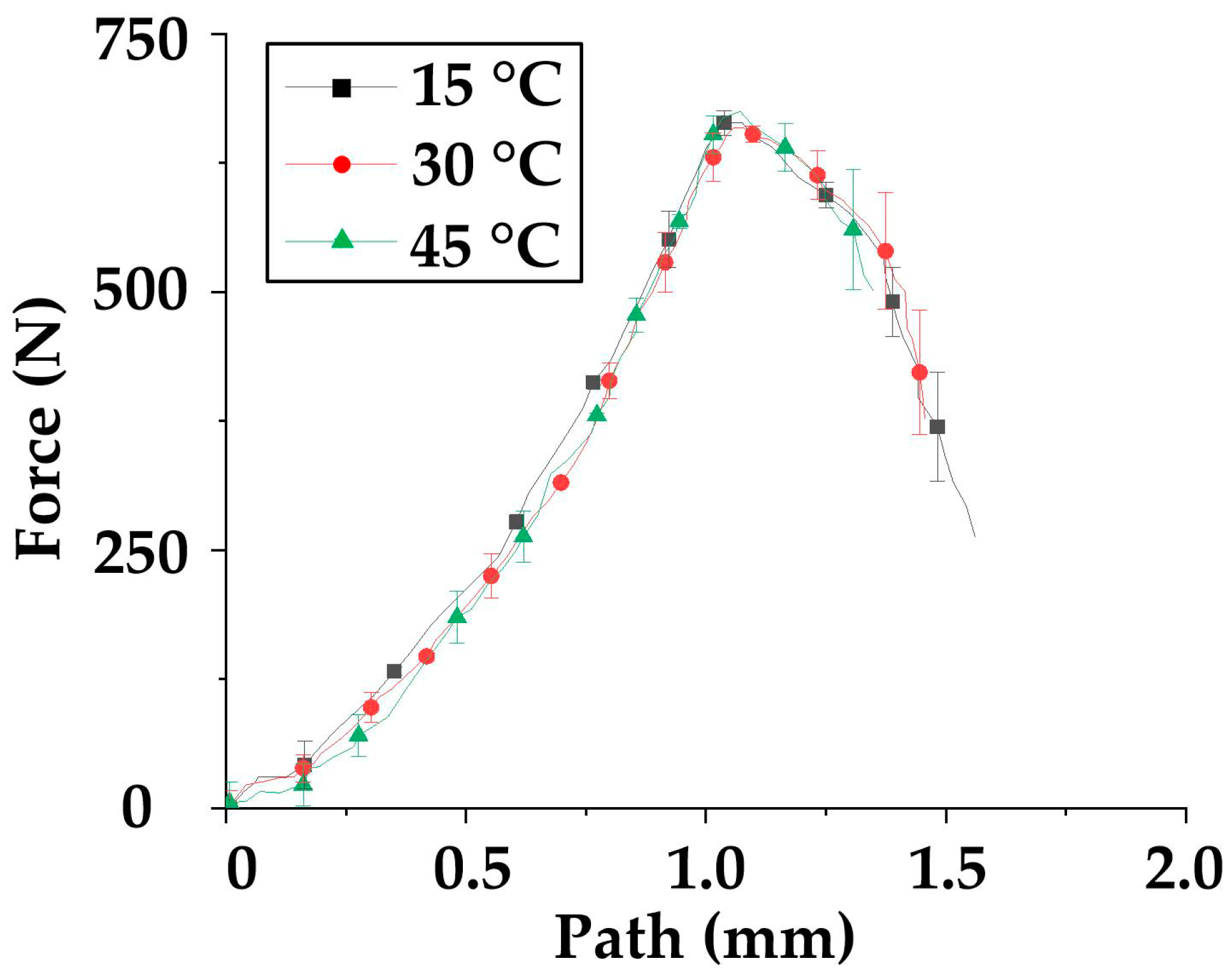
- Obtain the force-displacement characteristic curve CF-P through the test at a specific temperature, T.
- (b)
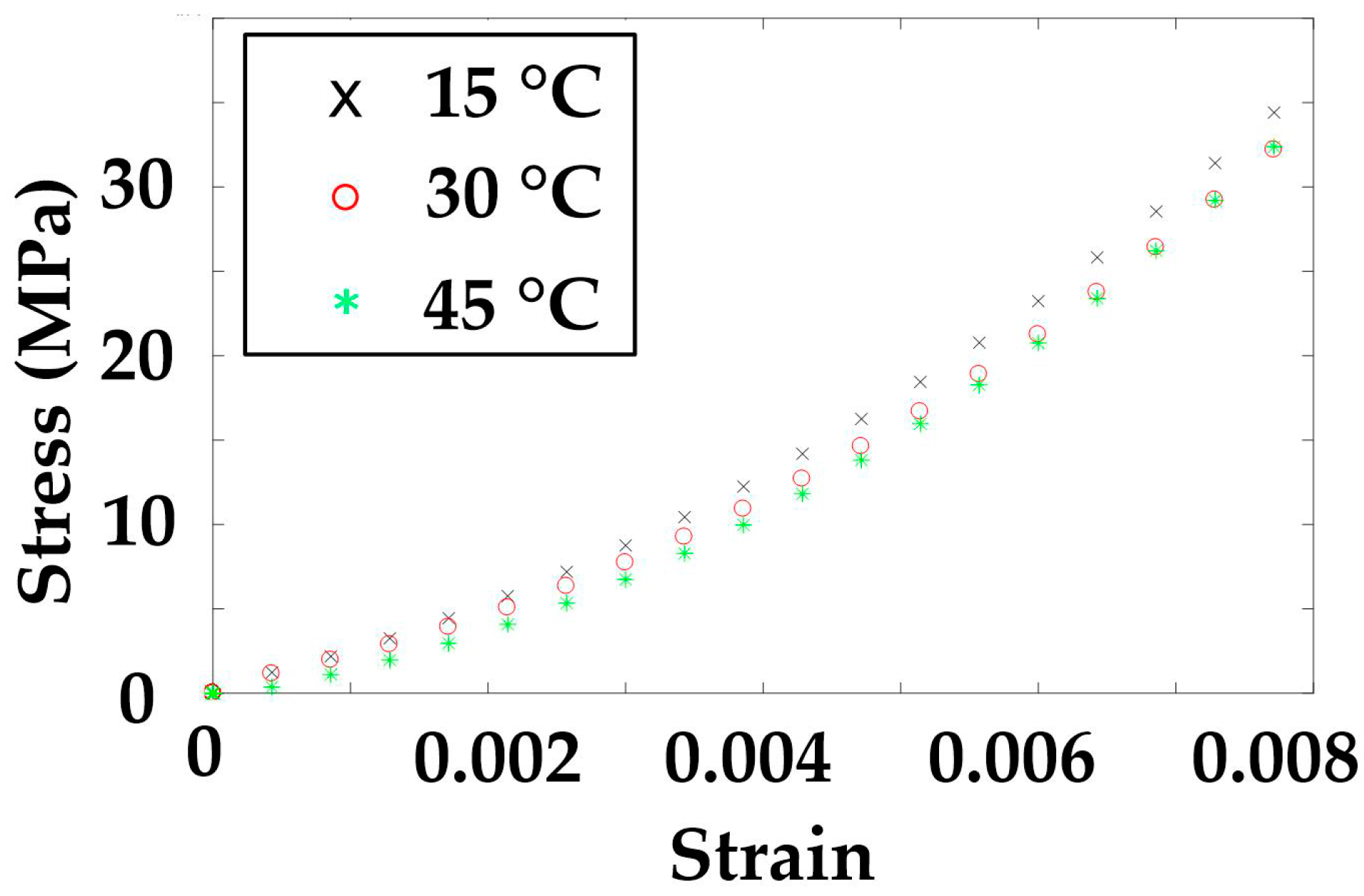
- Combined with Equations (6)–(9), the characteristic curve CF-P is transformed into the stress-strain curve Cδ-ε of the temperature T.
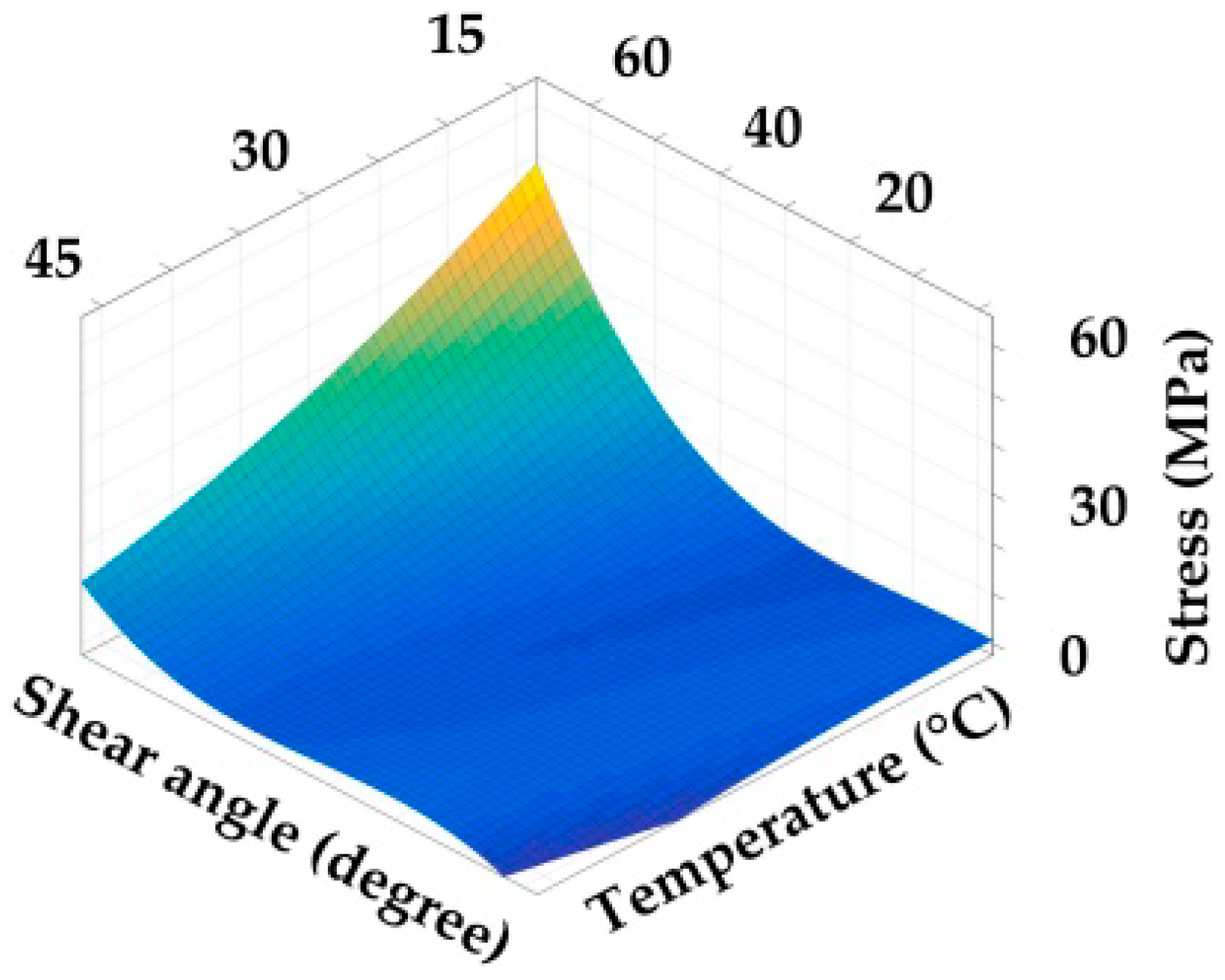
- (c)
- Using characteristic curve set {Cδ-ε(T1), Cδ-ε(T2), Cδ-ε(T3), Cδ-ε(T4)⋯} to construct the surface Sδ-ε-T equation, which characterizes the relationship between temperature T, stress δ and strain ε.
- (d)
- Based on Equation (15), calculating the fitting surface equation with the nonlinear regression, where i, j = 1, 2, 3.
3. Material Characteristic Determination
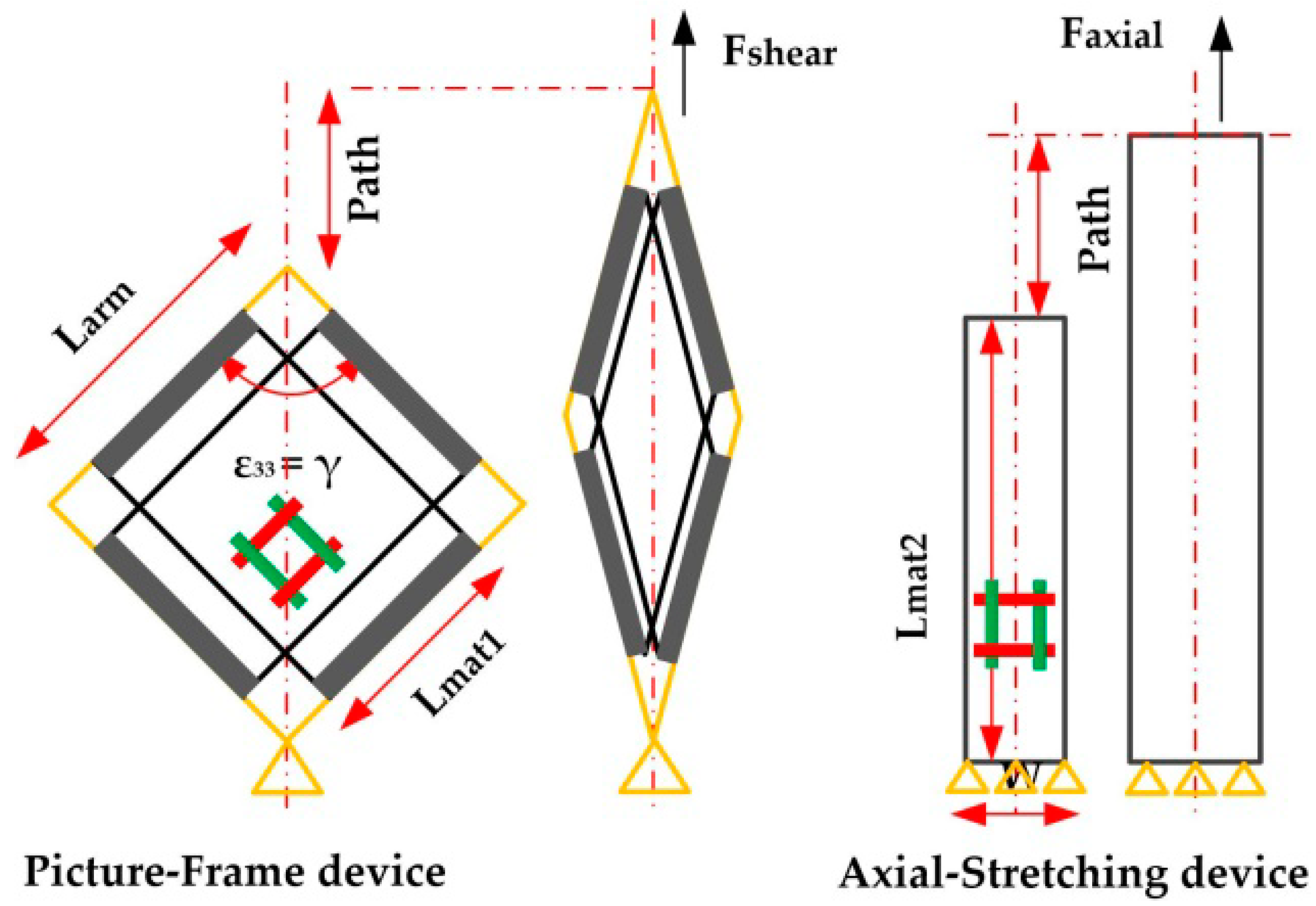
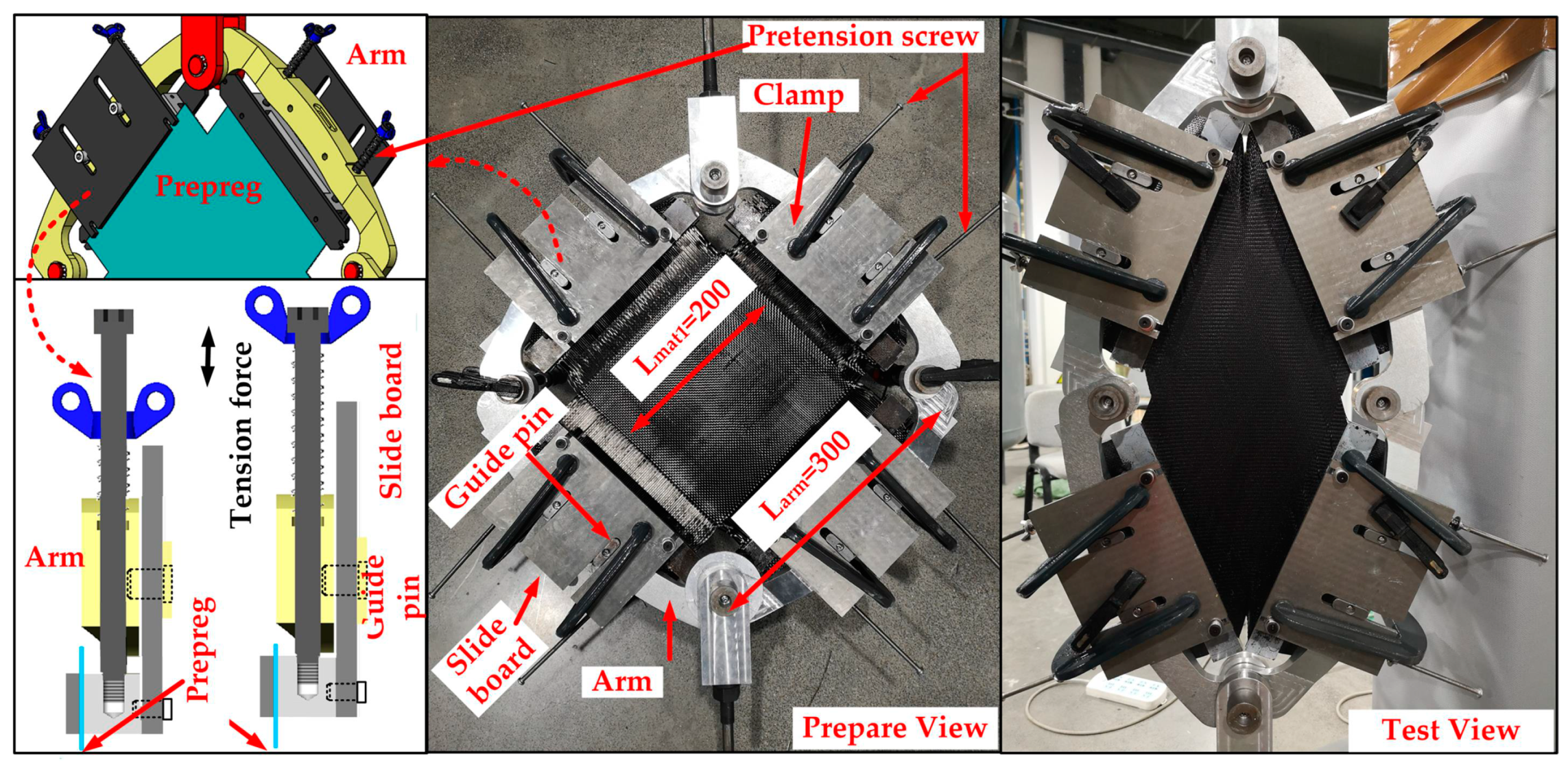
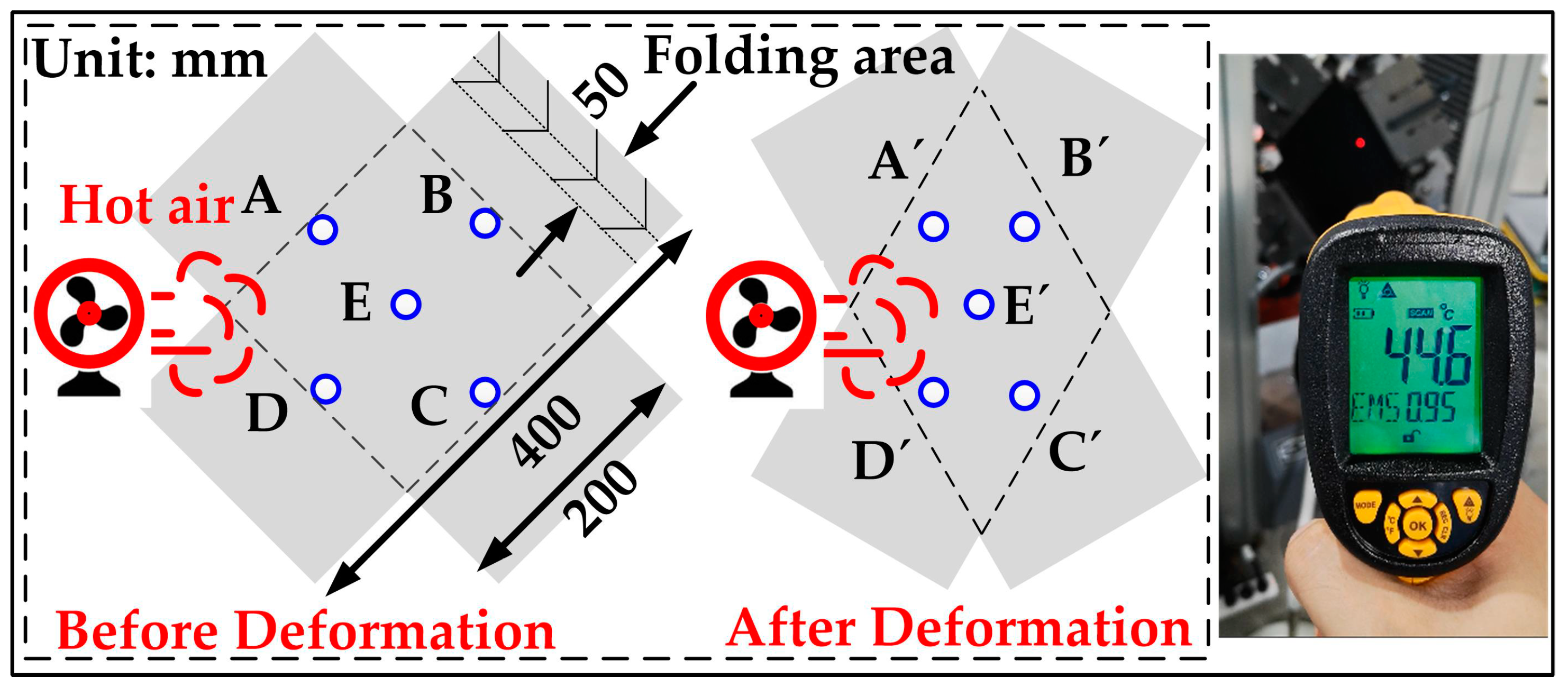
3.1. Test Device for Material Characteristics
3.2. Parameters Calculation and Fitting Approaches
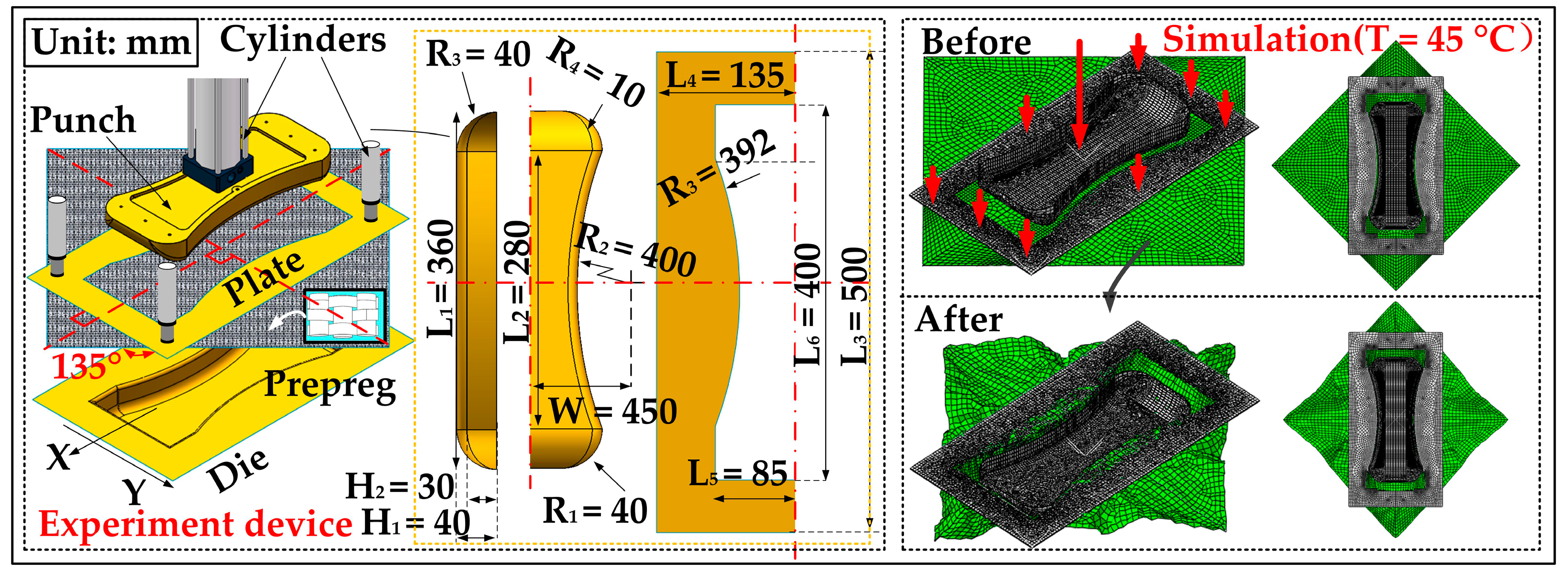
4. Forming Simulation and Experiment
4.1. Introduction of Simulation and Test
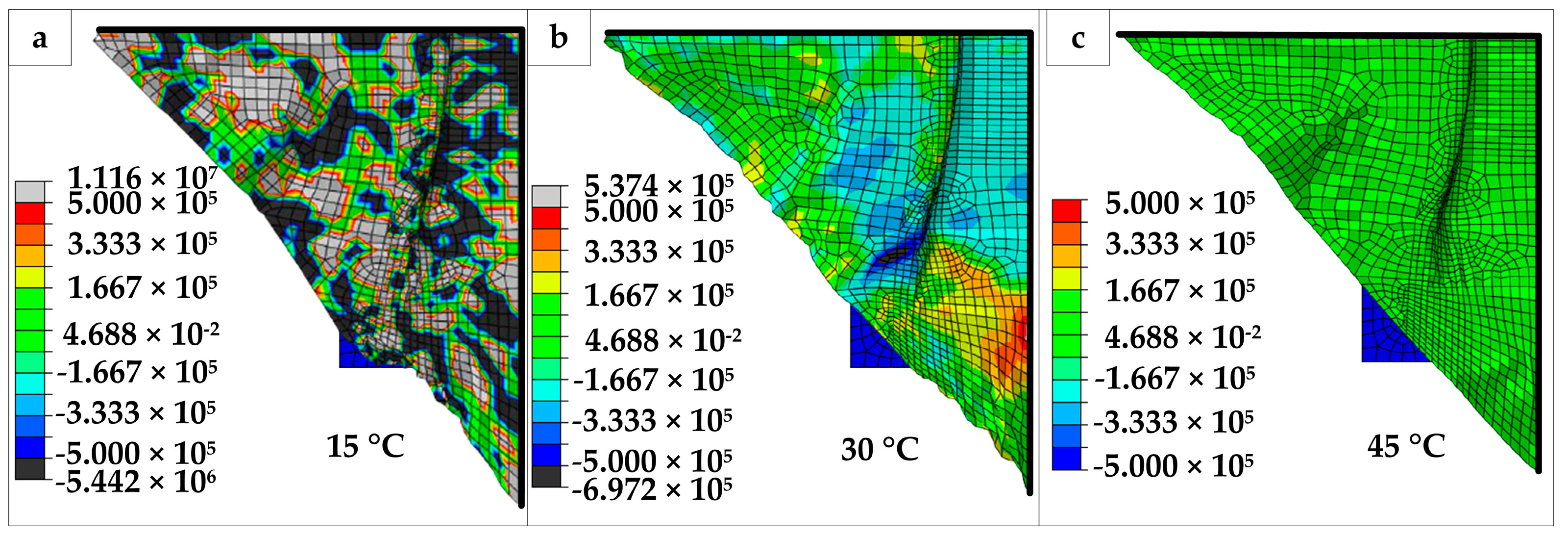
4.2. Forming Simulation and Test
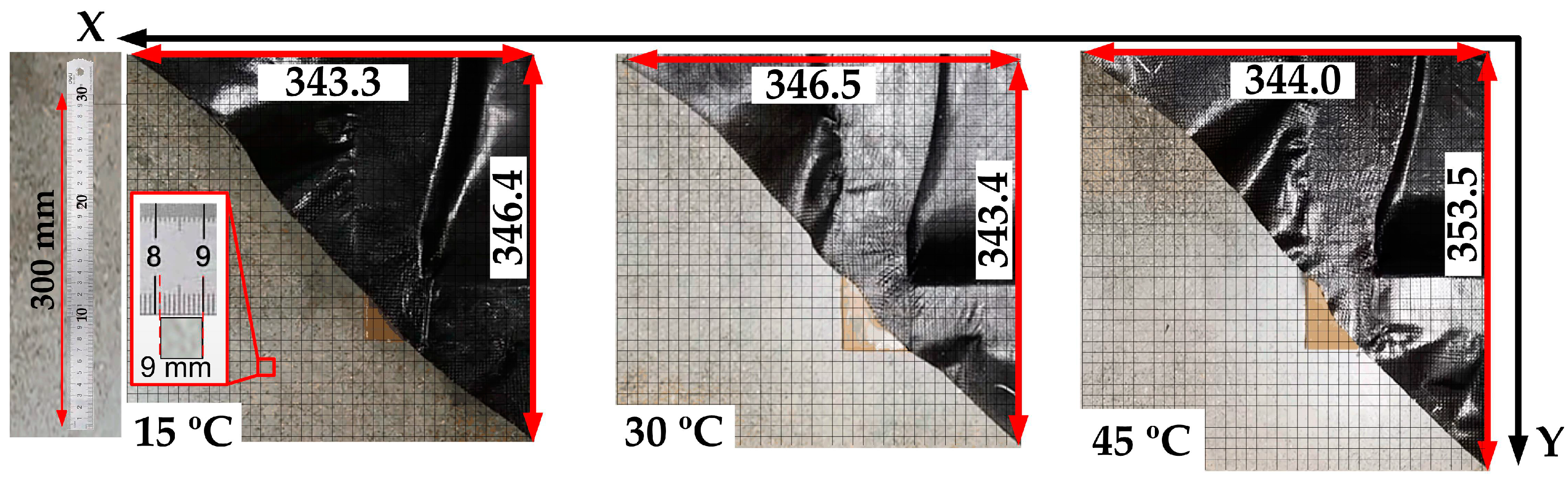
4.3. Forming Test and Comparison
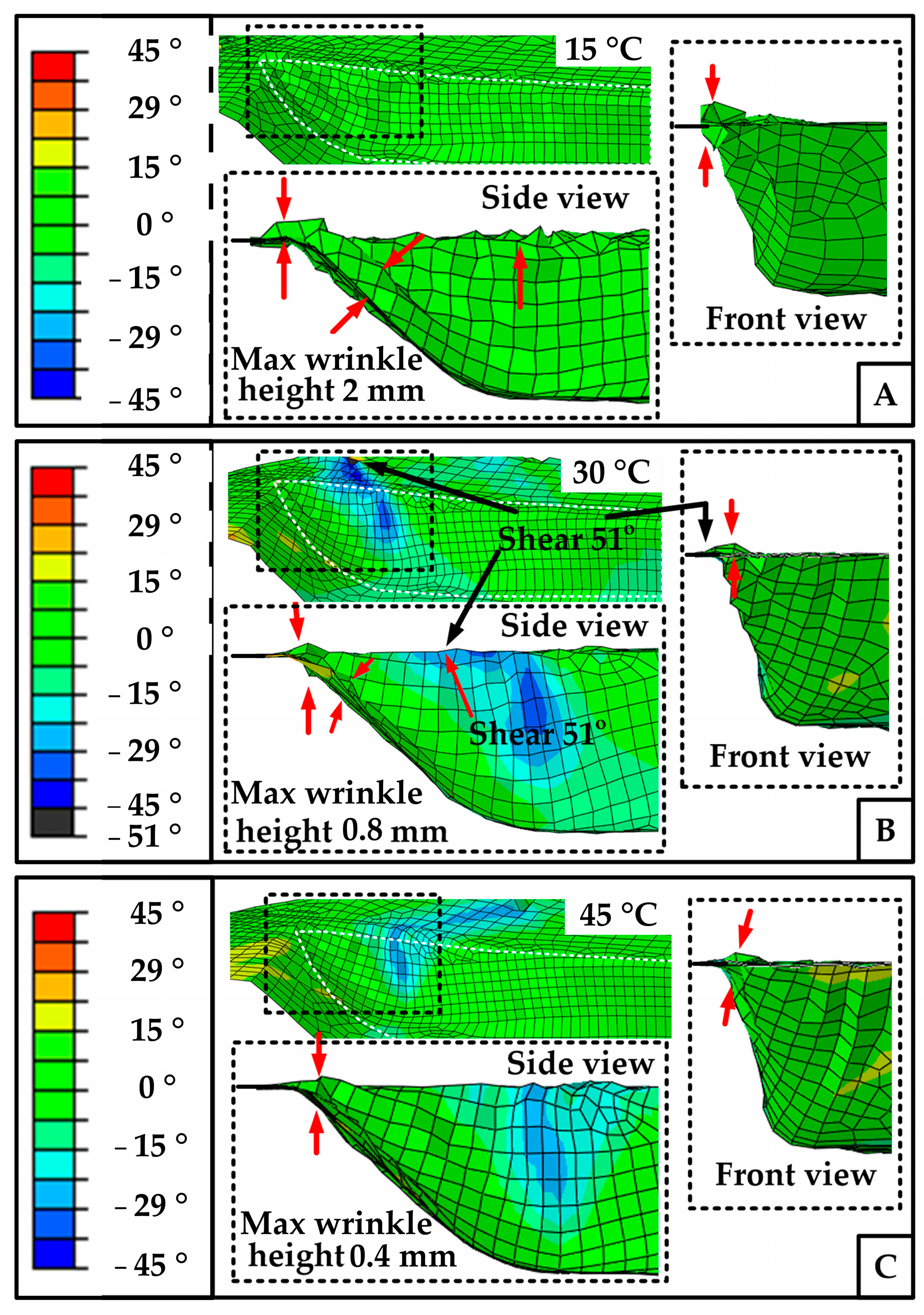
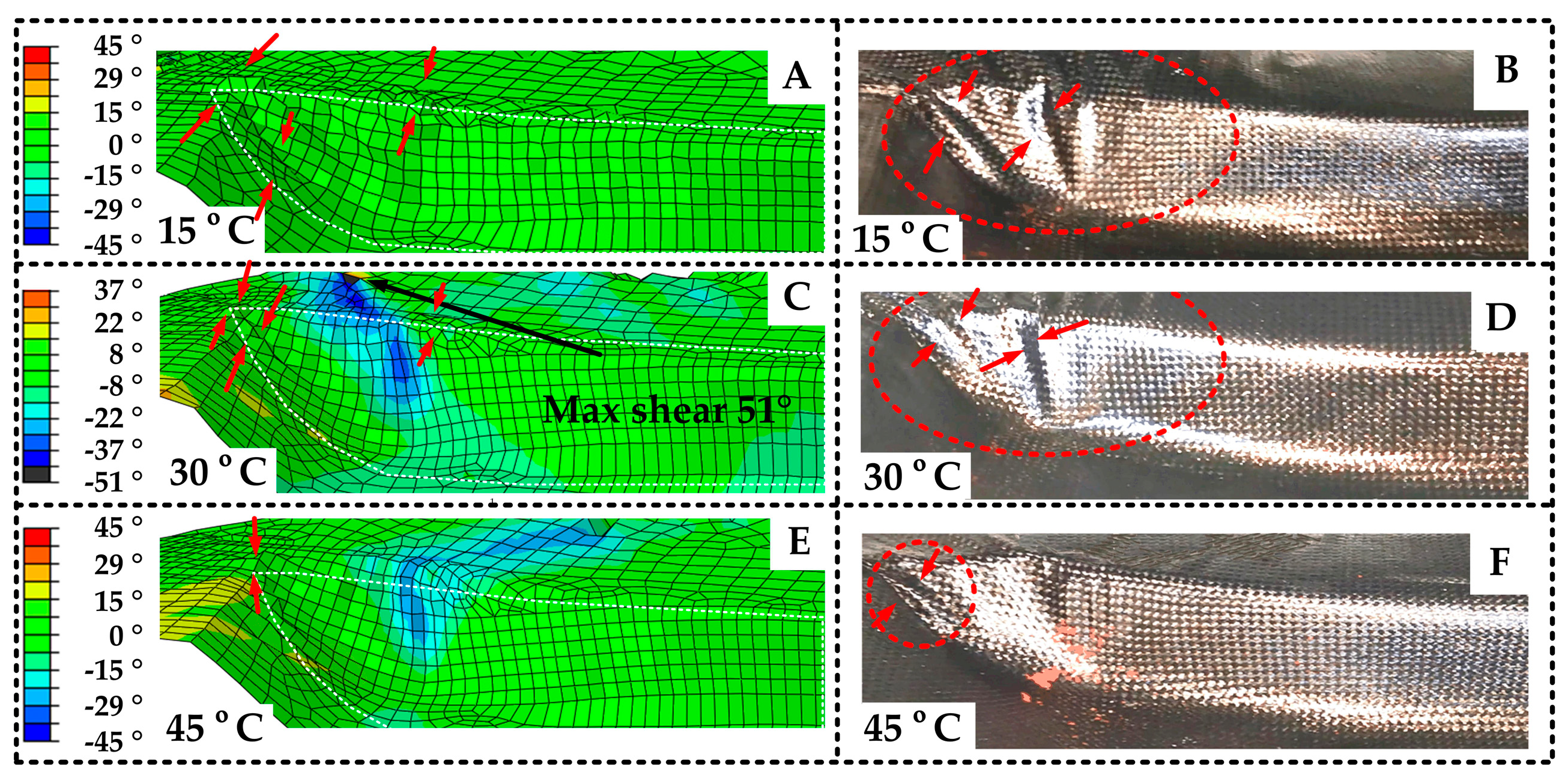
4.4. Wrinkles Prediction and Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chai, X.; Mi, H.; Zhu, C.; He, C.; Xu, J.; Zhou, X.; Liu, J. Low-temperature thermal stabilization of polyacrylontrile-based precursor fibers towards efficient preparation of carbon fibers with improved mechanical properties. Polymer 2015, 76, 131–139. [Google Scholar] [CrossRef]
- Stein, O.; Grinspun, E.; Crane, K. Developability of triangle meshes. ACM Trans. Graph. 2018, 37, 1–14. [Google Scholar] [CrossRef]
- Moezzi, M.; Haji-Badali, A.; Barez, F. Analysis of the wrinkle geometry of the woven fabrics during uniaxial bias extension test using Ricker wavelet algorithm. Compos. Part A Appl. Sci. Manuf. 2021, 141, 106230. [Google Scholar] [CrossRef]
- Aridhi, A.; Arfaoui, M.; Mabrouki, T.; Naouar, N.; Denis, Y.; Zarroug, M.; Boisse, P. Textile composite structural analysis taking into account the forming process. Compos. Part B Eng. 2019, 166, 773–784. [Google Scholar] [CrossRef] [Green Version]
- Elkington, M.; Bloom, D.; Ward, C.; Chatzimichali, A.; Potter, K. Hand layup understanding the manual process. Adv. Manuf. Polym. Compos. Sci. 2015, 1, 138–151. [Google Scholar]
- Qu, W.; He, R.; Cheng, L.; Yang, D.; Gao, J.; Wang, H.; Yang, Q.; Ke, Y. Placement suitability analysis of automated fiber placement on curved surfaces considering the influence of prepreg tow, roller and AFP machine. Compos. Struct. 2021, 262, 113608. [Google Scholar] [CrossRef]
- Rajan, S.; Sutton, M.A.; Sockalingam, S.; McMakin, W.; Gurdal, Z.; Kidane, A. Simulations and experiments for automated fiber placement of prepreg slit tape: Wrinkle formation and fundamental observations. Compos. Part B Eng. 2020, 201, 108287. [Google Scholar] [CrossRef]
- Christian, P.; Dominik, D.; Frank, H.; Luise, K. Experimental and numerical investigation of the shear behaviour of infiltrated woven fabrics. Compos. Part A Appl. Sci. Manuf. 2018, 114, 327–337. [Google Scholar]
- Šimáček, P.; Advani, S.G. A continuum approach for consolidation modeling in composites processing. Compos. Sci. Technol. 2020, 186, 107892. [Google Scholar] [CrossRef]
- Rashidi, A.; Montazerian, H.; Yesilcimen, K.; Milani, A.S. Experimental characterization of the inter-ply shear behavior of dry and prepreg woven fabrics: Significance of mixed lubrication mode during thermoset composites processing. Compos. Part A Appl. Sci. Manuf. 2020, 129, 105725. [Google Scholar] [CrossRef]
- Boisse, P.; Hamila, N.; Guzman-Maldonado, E.; Madeo, A.; Hivet, G.; Dell Isola, F. The bias-extension test for the analysis of in-plane shear properties of textile composite reinforcements and prepregs: A review. Int. J. Mater. Form. 2017, 10, 473–492. [Google Scholar] [CrossRef]
- Chen, Q.; Boisse, P.; Park, C.H.; Saouab, A.; Bréard, J. Intra/inter-ply shear behaviors of continuous fiber reinforced thermoplastic composites in thermoforming processes—Sciencedirect. Compos. Struct. 2011, 93, 1692–1703. [Google Scholar] [CrossRef]
- Cao, J.; Akkerman, R.; Boisse, P.; Chen, J.; Cheng, H.S.; de Graaf, E.F.; Gorczyca, J.L.; Harrison, P.; Hivet, G.; Launay, J.; et al. Characterization of mechanical behavior of woven fabrics: Experimental methods and benchmark results. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1037–1053. [Google Scholar] [CrossRef] [Green Version]
- Bilisik, K. Properties of yarn pull-out in para-aramid fabric structure and analysis by statistical model. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1930–1942. [Google Scholar] [CrossRef]
- Nosrat-Nezami, F.; Gereke, T.; Eberdt, C.; Cherif, C. Characterisation of the shear–tension coupling of carbon-fibre fabric under controlled membrane tensions for precise simulative predictions of industrial preforming processes. Compos. Part A Appl. Sci. Manuf. 2014, 67, 131–139. [Google Scholar] [CrossRef]
- Naito, Y.; Nishikawa, M.; Mobuchon, C.; Poursartip, A.; Matsuda, N.; Hojo, M. Effect of rheological transitions in matrix resin on flow mechanism of carbon Fiber/Epoxy prepreg. Compos. Part A Appl. Sci. Manuf. 2021, 151, 106612. [Google Scholar] [CrossRef]
- Wang, L.; Xu, P.; Peng, X.; Zhao, K.; Wei, R. Characterization of inter-ply slipping behaviors in hot diaphragm preforming: Experiments and modelling. Compos. Part A Appl. Sci. Manuf. 2019, 121, 28–35. [Google Scholar] [CrossRef]
- Gereke, T.; Cherif, C. A review of numerical models for 3D woven composite reinforcements. Compos. Struct. 2019, 209, 60–66. [Google Scholar] [CrossRef]
- Boisse, P.; Colmars, J.; Hamila, N.; Naouar, N.; Steer, Q. Bending and wrinkling of composite fiber preforms and prepregs. A review and new developments in the draping simulations. Compos. Part B Eng. 2018, 141, 234–249. [Google Scholar] [CrossRef]
- Peng, X.Q.; Cao, J. A continuum mechanics-based non-orthogonal constitutive model for woven composite fabrics. Compos. Part A Appl. Sci. Manuf. 2005, 36, 859–874. [Google Scholar] [CrossRef]
- Peng, X.Q.; Cao, J.; Chen, J.; Xue, P.; Lussier, D.S.; Liu, L. Experimental and numerical analysis on normalization of picture frame tests for composite materials. Compos. Sci. Technol. 2004, 64, 11–21. [Google Scholar] [CrossRef]
- Charmetant, A.; Vidal-Sallé, E.; Boisse, P. Hyperelastic modelling for mesoscopic analyses of composite reinforcements. Compos. Sci. Technol. 2011, 71, 1623–1631. [Google Scholar] [CrossRef]
- Boisse, P.; Gasser, A.; Hivet, G. Analyses of fabric tensile behaviour: Determination of the biaxial tension–strain surfaces and their use in forming simulations. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1395–1414. [Google Scholar] [CrossRef]
- Badel, P.; Vidal-Sallé, E.; Boisse, P. Computational determination of in plane shear mechanical behaviour of textile composite reinforcements. Comp. Mater. Sci. 2007, 40, 439–448. [Google Scholar] [CrossRef]
- Liang, B.; Boisse, P. A review of numerical analyses and experimental characterization methods for forming of textile reinforcements. Chin. J. Aeronaut.. 2021, 34, 143–163. [Google Scholar] [CrossRef]
- Haghi Kashani, M. A Coupled Non-Orthogonal Hypoelastic Constitutive Model for Simulation of Woven Fabrics. Ph.D. Thesis, The University of British, Okanagan, BC, Canada, 2017. [Google Scholar]
- Chen, S. Fabric Forming Simulation and Process Optimisation for Composites. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2016. [Google Scholar]
- Komeili, M. Multi-Scale Characterization and Modeling of Shear-Tension Interaction in Woven Fabrics for Composite Forming and Structural Applications. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 2014. [Google Scholar]
- Aono, M.; Breen, D.E.; Wozny, M.J. Modeling methods for the design of 3D broadcloth composite parts. Comput. Aided Des. 2001, 33, 989–1007. [Google Scholar] [CrossRef]
- Iwata, A.; Inoue, T.; Naouar, N.; Boisse, P.; Stepan, V.L. Coupled meso-macro simulation of woven fabric local deformation during draping. Compos. Part A 2019, 118, 267–280. [Google Scholar] [CrossRef]
- Nishi, M.; Wang, S.; Dougherty, S. Forming Simulation for Fiber Reinforced Thermoplastic with Introduction to J-Composites. In Proceedings of the 15th International LS-DYNA Users Conference, Dearborn, MI, USA, 10–12 June 2018. [Google Scholar]
- Basit, M.M.; Luo, S.; Mitra, A. A simplified constitutive and finite element model of plain weave fabric reinforcements for the biaxial loading. Multiscale Multidiscip. Modeling Exp. Des. 2019, 2, 249–258. [Google Scholar] [CrossRef]
- Alshahrani, H.; Hojjati, M. Experimental and numerical investigations on formability of out-of-autoclave thermoset prepreg using a double diaphragm process. Compos. Part A Appl. Sci. Manuf. 2017, 101, 199–214. [Google Scholar] [CrossRef]
- Guzman-Maldonado, E.; Wang, P.; Hamila, N.; Boisse, P. Experimental and numerical analysis of wrinkling during forming of multi-layered textile composites. Compos. Struct. 2019, 208, 213–223. [Google Scholar] [CrossRef]
- Rashidi, A.; Milani, A.S. A multi-step biaxial bias extension test for wrinkling/de-wrinkling characterization of woven fabrics: Towards optimum forming design guidelines. Mater. Des. 2018, 146, 273–285. [Google Scholar] [CrossRef]
- Alshahrani, H.; Mohan, R.; Mehdi, H. Experimental Investigation of In-Plane Shear Deformation of Out-of-Autoclave Prepreg. Int. J. Compos. Mater. 2015, 5, 81–87. [Google Scholar]
- Kärger, L.; Galkin, S.; Zimmerling, C.; Dörr, D.; Linden, J.; Oeckerath, A.; Wolf, K. Forming optimisation embedded in a CAE chain to assess and enhance the structural performance of composite components. Compos. Struct. 2018, 192, 143–152. [Google Scholar] [CrossRef]
- Hosseini, A.; Kashani, M.H.; Sassani, F.; Milani, A.S.; Ko, F.K. Identifying the distinct shear wrinkling behavior of woven composite preforms under bias extension and picture frame tests. Compos. Struct. 2018, 185, 764–773. [Google Scholar] [CrossRef]
- Shanwan, A.; Allaoui, S. Different experimental ways to minimize the preforming defects of multi-layered interlock dry fabric. Int. J. Mater. Form. 2019, 12, 69–78. [Google Scholar] [CrossRef] [Green Version]
- Boisse, P.; Hamila, N.; Vidal-Sallé, E.; Dumont, F. Simulation of wrinkling during textile composite reinforcement forming. Influence of tensile, in-plane shear and bending stiffnesses. Compos. Sci. Technol. 2011, 71, 683–692. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Xu, P.; Peng, X.; Wei, R.; Yao, Y.; Zhao, K. A lamination model for forming simulation of woven fabric reinforced thermoplastic prepregs. Compos. Struct. 2018, 196, 89–95. [Google Scholar] [CrossRef]
- Poppe, C.; Rosenkranz, T.; Dörr, D.; Kärger, L. Comparative experimental and numerical analysis of bending behaviour of dry and low viscous infiltrated woven fabrics. Compos. Part A Appl. Sci. Manuf. 2019, 124, 105466. [Google Scholar] [CrossRef]
- Wang, J.; Peng, X.; Huang, Z.; Zhou, H. A temperature -dependent 3D anisotropic visco-hyperelastic constitutive model for jute woven fabric reinforced poly (butylene succinate) biocomposite in thermoforming. Compos. Part B Eng. 2021, 208, 108584. [Google Scholar] [CrossRef]
- Jeong, E.; Kim, Y.; Hong, S.; Yoon, K.; Lee, S. Innovative Injection Molding Process for the Fabrication of Woven Fabric Reinforced Thermoplastic Composites. Polymers 2022, 14, 1577. [Google Scholar] [CrossRef]
- Toray Composite Materials America, Inc. T1100G Technical Data Sheet. Available online: https://www.toraycma.com/wp-content/uploads/T1100G-Technical-Data-Sheet-1.pdf.pdf (accessed on 17 January 2018).
- Boisse, P.; Naouar, N.; Charmetant, A. Finite element analysis of composite forming at macroscopic and mesoscopic scale. In Advances in Composites Manufacturing and Process Design; Boisse, P., Ed.; Woodhead Publishing: Sawston, UK, 2015; pp. 297–315. [Google Scholar]
- Peng, X.; Cao, J. A dual homogenization and finite element approach for material characterization of textile composites. Compos. Part B Eng. 2002, 33, 45–56. [Google Scholar] [CrossRef]
- Ding, F.; Peng, X. Validation of a non-orthogonal constitutive model for woven composite fabrics via hemispherical stamping simulation. Acta Mater. Compos. Sin. 2011, 42, 400–407. [Google Scholar]
- Weihai Guangwei Composite Company. Weihai GW Compos. Data Sheet. Available online: https://book.yunzhan365.com/xech/oses/mobile/index.html (accessed on 1 June 2022).
- Toray Composite Materials America, Inc. G-94M Prepreg System. Available online: https://www.toraycma.com/wp-content/uploads/G-94M-PREPREG-SYSTEM.pdf (accessed on 26 October 2021).







| Name | Type | Tensile Modulus | Shear Modulus | Thickness | |
|---|---|---|---|---|---|
| filament | T1100G | 324 GPa | Φ = 5 μm | ||
| preprep | Plain Weave (3960 Resin/12K) | 0° Tensile Modulus | 88.79 GPa | In Plain Shear 3.7 GPa | 0.2 mm |
| 90° Tensile Modulus | 88.74 GPa | ||||
| Name | Type | Filament Tensile Modulus | Matrix | Thickness |
|---|---|---|---|---|
| wp-3011 | plain weave (TZ300/3K) | 230 GPa | epoxy resin | 0.2 mm |
| Set-Value (°C) | Real-Temperature at Point | Max-Diff | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | |||
| 15 | Before | 15.0 | 15.1 | 15.1 | 15.1 | 15.0 | 0.1 |
| After | 15.0 | 15.0 | 15.0 | 15.0 | 14.9 | 0.1 | |
| 30 | Before | 30.1 | 30.1 | 30.1 | 30.0 | 30.0 | 0.1 |
| After | 30.1 | 29.9 | 29.9 | 30.0 | 30.0 | 0.2 | |
| 45 | Before | 45.1 | 45.1 | 45.2 | 45.1 | 45.0 | 0.2 |
| After | 45.0 | 44.6 | 45.0 | 45.0 | 44.8 | 0.4 | |
| Title | Shearing Test | Axial Tensile Test | ||||||
|---|---|---|---|---|---|---|---|---|
| Curve | 15 °C | 30 °C | 45 °C | 15 °C | 30 °C | 45 °C | ||
| R² | 0.998 | 0.993 | 0.995 | 0.980 | 0.999 | 0.999 | 0.997 | 0.997 |
| Size Error (mm) | 15 °C | 30 °C | 45 °C |
|---|---|---|---|
| Xsim | 342.5 | 343.3 | 340.7 |
| Xexp | 343.3 | 346.5 | 344.0 |
| Xerr = (Xexp − Xsim)/Xexp | 0.2% | 0.9% | 0.9% |
| Ysim | 353.5 | 353.2 | 336.2 |
| Yexp | 346.4 | 343.4 | 353.5 |
| Yerr = (Yexp − Xsim)/Yexp | 2.0% | 2.7% | 5.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, J.; Li, L.; Wang, Y.; Gao, H. A Mechanics Analysis of Carbon Fiber Plain-Woven Thermoset Prepreg during Forming Process Considering Temperature Effect. Polymers 2022, 14, 2618. https://doi.org/10.3390/polym14132618
Qi J, Li L, Wang Y, Gao H. A Mechanics Analysis of Carbon Fiber Plain-Woven Thermoset Prepreg during Forming Process Considering Temperature Effect. Polymers. 2022; 14(13):2618. https://doi.org/10.3390/polym14132618
Chicago/Turabian StyleQi, Jialiang, Lun Li, Yiqi Wang, and Hang Gao. 2022. "A Mechanics Analysis of Carbon Fiber Plain-Woven Thermoset Prepreg during Forming Process Considering Temperature Effect" Polymers 14, no. 13: 2618. https://doi.org/10.3390/polym14132618
APA StyleQi, J., Li, L., Wang, Y., & Gao, H. (2022). A Mechanics Analysis of Carbon Fiber Plain-Woven Thermoset Prepreg during Forming Process Considering Temperature Effect. Polymers, 14(13), 2618. https://doi.org/10.3390/polym14132618







