Thermal Modification of Spruce and Maple Wood for Special Wood Products
Abstract
:1. Introduction
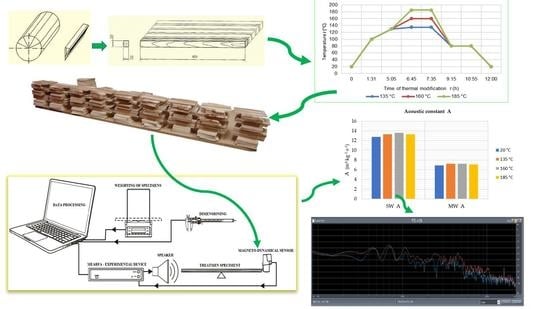
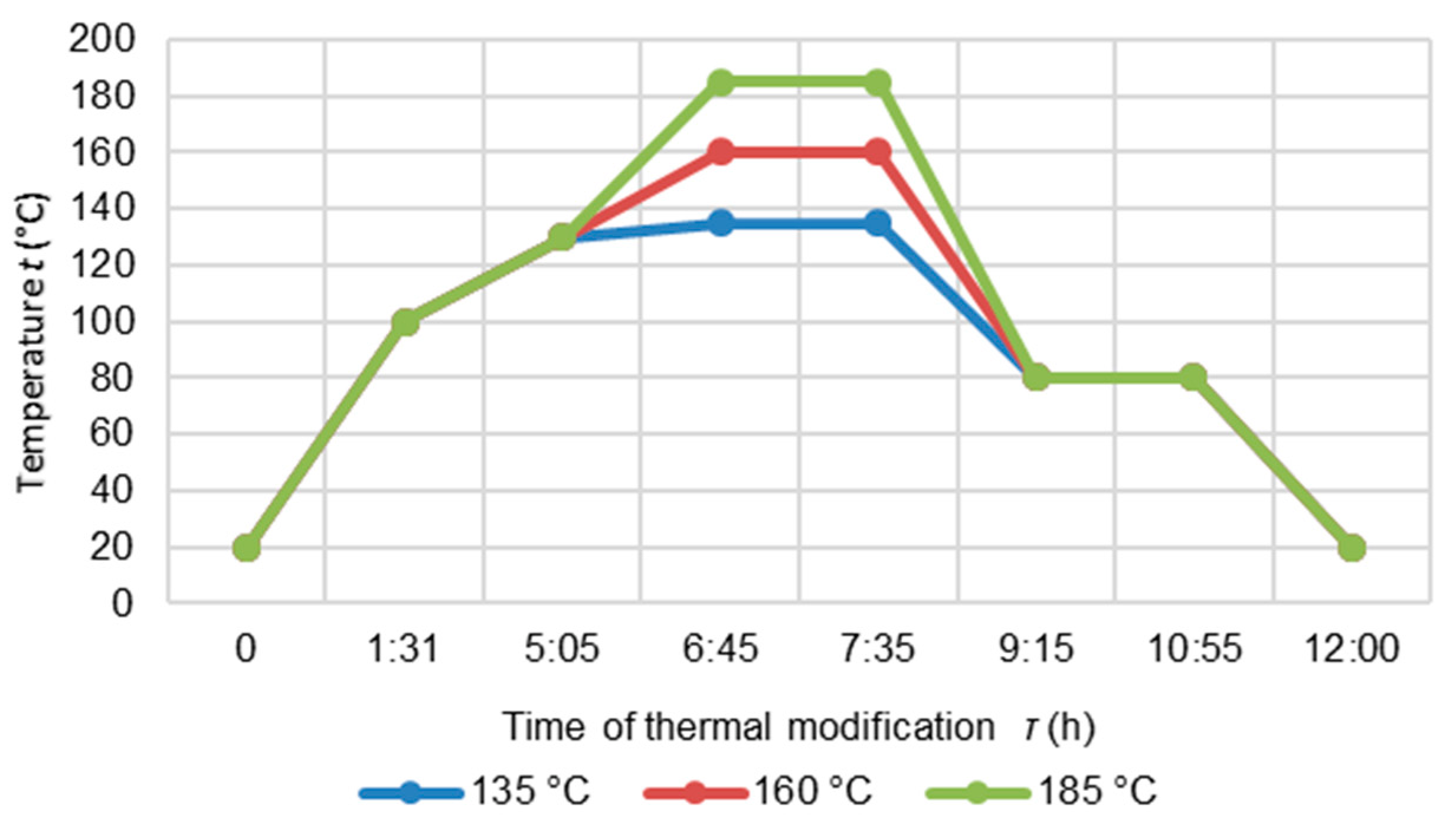
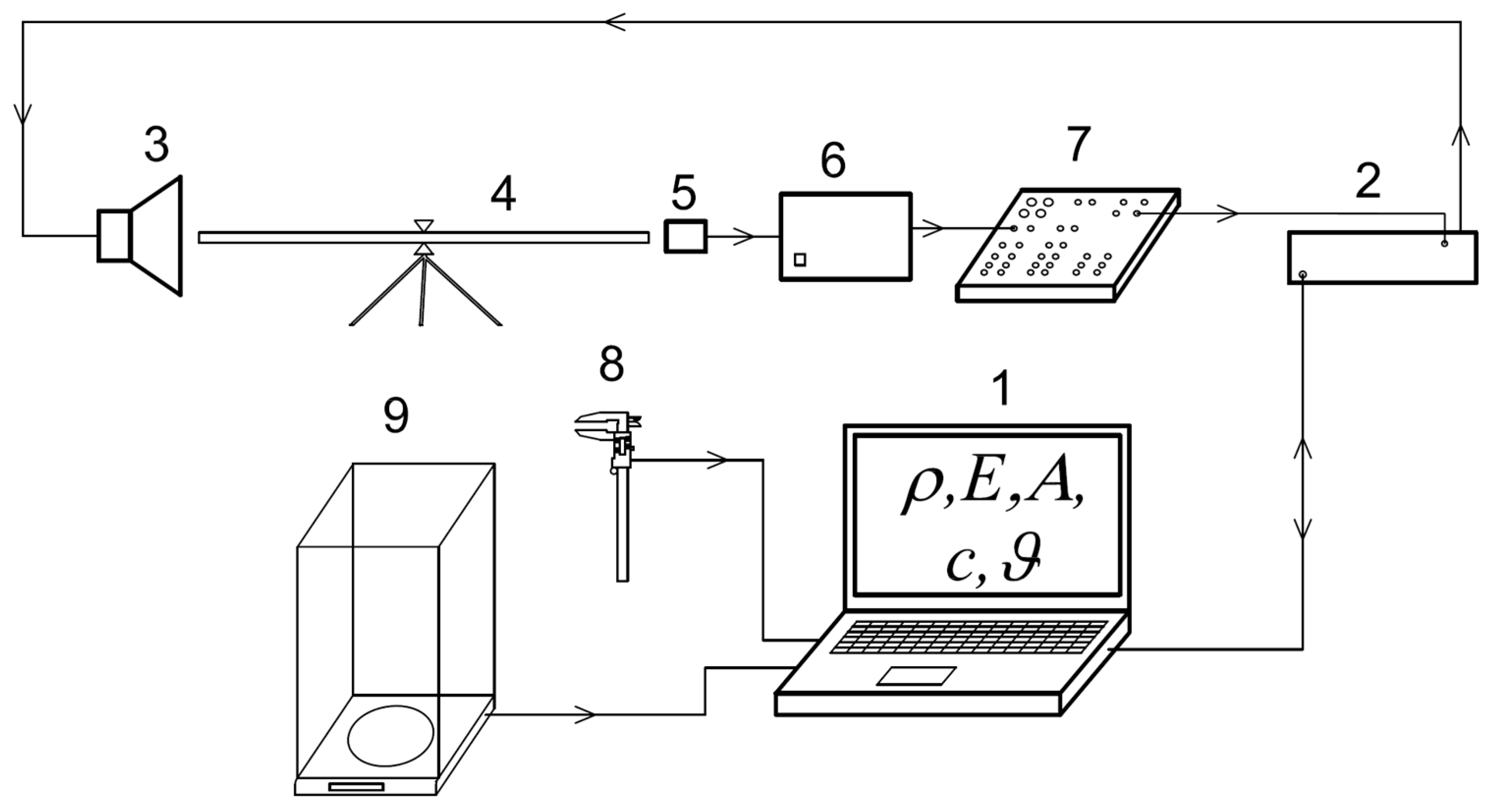
2. Material and Methods
3. Results and Discussion
3.1. Effect of Thermal Modification on Density
3.2. Effect of Thermal Modification on Modulus of Elasticity
3.3. Effect of Thermal Modification on Acoustic Constant
3.4. Effect of Thermal Modification on Speed of Sound
3.5. Effect of Thermal Modification on Specific Modulus of Elasticity
3.6. Effect of Thermal Modification on Logarithmic Damping Decrement
3.7. Effect of Thermal Modification on Loss Coefficient and Characteristic Acoustic Impedance
3.8. Effect of Thermal Modification on Acoustic Conversion Efficiency (ACE) and on Sound Quality Factor Q
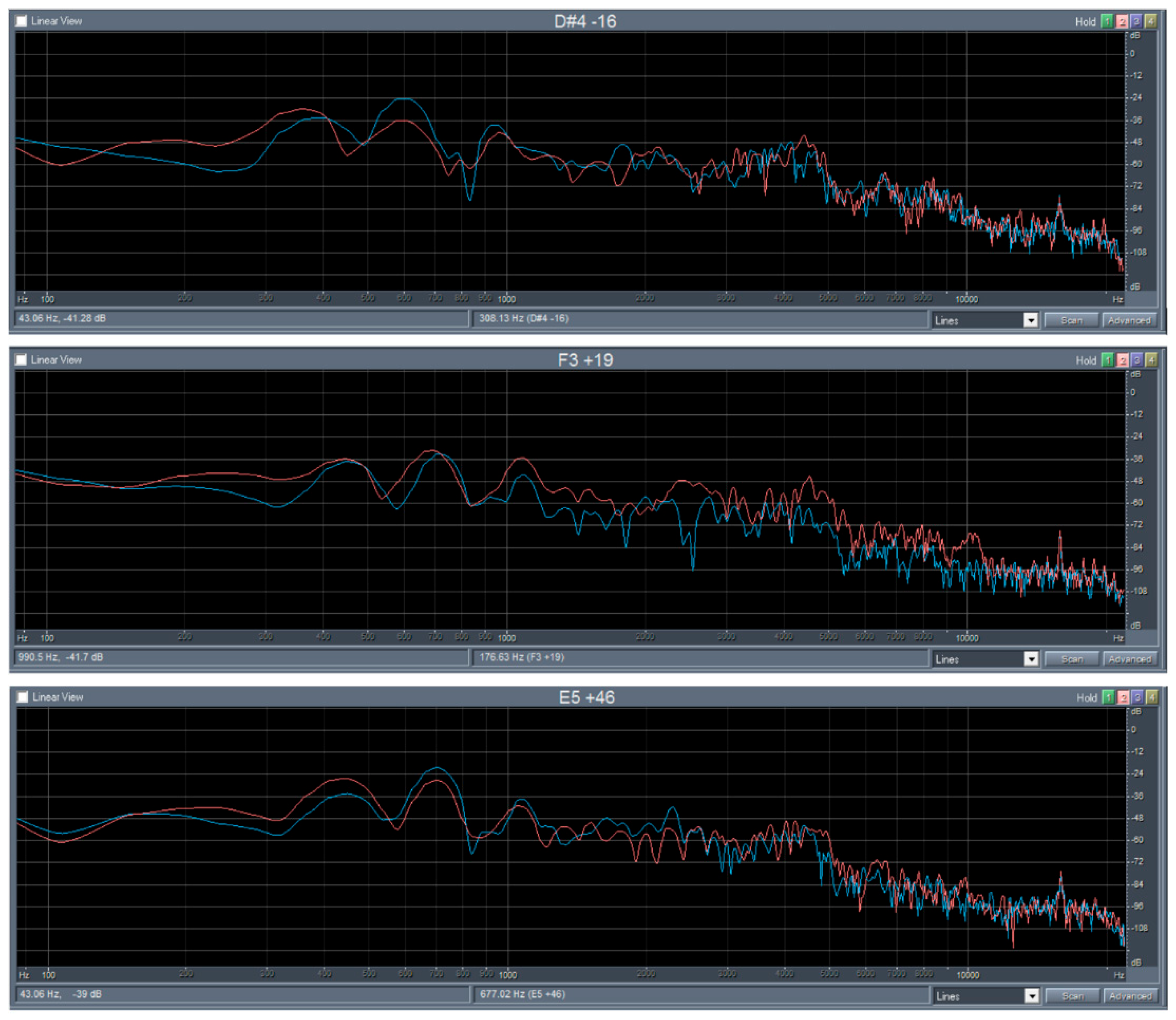
3.9. Effect of Thermal Modification on Timber of Sound
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Froidevaux, J.; Parviz, N. Aging law of spruce wood. Wood Mater. Sci. Eng. 2013, 8, 46–52. [Google Scholar] [CrossRef]
- Kránitz, K.; Sonderegger, W.; Bues, C.T. Effects of aging on wood: A literature review. Wood Sci. Technol. 2016, 50, 7–22. [Google Scholar] [CrossRef]
- Borgin, K.; Faix, O.; Schweers, W. The effect of aging on lignins of wood. Wood Sci. Technol. 1975, 9, 207–211. [Google Scholar] [CrossRef]
- Bucur, V. Ageing of wood. In Handbook of Materials for String Musical Instruments; Springer: Cham, Switzerland, 2016; Volume 1, pp. 283–323. [Google Scholar]
- Obataya, E. Effects of natural and artificial ageing on the physical and acoustic properties of wood in musical instruments. J. Cult. Herit. 2017, 27, S63–S69. [Google Scholar] [CrossRef] [Green Version]
- Danihelová, A.; Čulík, M.; Nĕmec, M.; Gejdoš, M.; Danihelová, Z. Modified wood of black locust—Alternative to Honduran rosewood in the production of xylophones. Acta Phys. Pol. A 2015, 127, 106–109. [Google Scholar] [CrossRef]
- Puszyński, J.; Warda, M. Possibilities of using the thermally modified wood in the electric string instruments. For. Wood Technol. 2014, 85, 200–204. [Google Scholar]
- Pfriem, A. Thermally Modified Wood for Use in Musical Instruments. Drv. Ind. 2015, 66, 251–253. [Google Scholar] [CrossRef] [Green Version]
- Mania, P.; Gąsiorek, M. Acoustic Properties of Resonant Spruce Wood Modified Using Oil-Heat Treatment (OHT). Materials 2020, 13, 1962. [Google Scholar] [CrossRef]
- Mania, P.; Moliński, W.; Roszyk, E.; Górska, M. Optimization of Spruce (Picea abies L.) Wood Thermal Treatment Temperature to Improve Its Acoustic Properties. Bioresources 2019, 15, 505–516. [Google Scholar] [CrossRef]
- Rapp, A.O.; Sailer, M. Oil-heat-treatment of wood—Process and properties. Drv. Ind. 2001, 52, 63–70. [Google Scholar]
- Zatloukal, P.; Suchomelová, P.; Dömény, J.; Doskočil, T.; Manzo, G.; Tippner, J. Possibilities of Decreasing Hygroscopicity of ResonanceWood Used in Piano Soundboards Using Thermal Treatment. Appl. Sci. 2021, 11, 475. [Google Scholar] [CrossRef]
- Danihelová, A.; Spišiak, D.; Reinprecht, L.; Gergeľ, T.; Vidholdová, Z.; Ondrejka, V. Acoustic Properties of Norway Spruce Wood Modified with Staining Fungus (Sydowia polyspora). BioResources 2019, 18, 3432–3444. [Google Scholar] [CrossRef]
- Schwarze, F.W.M.R.; Spycher, M.; Fink, S. Superior wood for violins–wood decay fungi as a substitute for cold climate. New Phytol. 2008, 179, 1095–1104. [Google Scholar] [CrossRef]
- Spycher, M. The Application of Wood Decay Fungi to Improve the Acoustic Properties of Resonance Wood for Violins. Ph.D. Thesis, Albert-Ludwigs-Universität, Freiburg im Breisgau, Germany, 2008. Available online: https://d-nb.info/98820701X/34 (accessed on 20 June 2022).
- Hill, C. Wood Modification: Chemical, Thermal and Other Processes; John Wiley & Sons, Ldt.: West Sussex, UK, 2006; p. 264. [Google Scholar]
- Candelier, K.; Thevenon, M.F.; Petrissans, A. Control of wood thermal treatment and its effects on decay resistance. Ann. For. Sci. 2016, 73, 571–583. [Google Scholar] [CrossRef] [Green Version]
- Korkut, S.; Budakci, M. The effects of high temperature heat—Treatment on physical properties and surface roughness of rowan (Sorbus Aucuparia, L.) wood. Wood Res. 2010, 55, 67–78. [Google Scholar] [CrossRef]
- Mitsui, K.; Inagaki, T.; Tsuchikawa, S. Monitoring of hydroxyl groups in wood during heat treatment using NIR spectroscopy. Biomacromolecules 2008, 9, 286–288. [Google Scholar] [CrossRef]
- Čermák, P.; Rautkari, L.; Horáček, P.; Saake, B.; Rademacher, P.; Sablík, P. Analysis of Dimensional Stability of Thermally Modified Wood Affected by Re-Wetting Cycles. BioResources 2015, 10, 3242–3253. [Google Scholar] [CrossRef] [Green Version]
- Reinprecht, L. Wood Deterioration, Protection and Maintenance; Wiley-Blackwell: Hoboken, NJ, USA, 2016; p. 376. [Google Scholar]
- Tjeerdsma, B.; Stevens, M.; Militz, H. Durability aspects of (hydro) thermal treated wood. In Proceedings of the International Research Group on Wood Preservation, Kona, Hawaii, 14–19 May 2000; IRG-WP: Stockholm, Sweden, 2000. [Google Scholar]
- Bekhta, P.; Niemz, P. Effect of High Temperature on the Change in Color, Dimensional Stability and Mechanical Properties of Spruce Wood. Holzforschung 2003, 57, 539–546. [Google Scholar] [CrossRef]
- Nieminen, P.; Nieminen, R. Thermally Aged Tonewood; MES—The Finnish Music Foundation: Helsinki, Finland, 2020; p. 35. [Google Scholar]
- Huss and Dalton TD R 20th Anniversary Thermo-Cured Red Spruce and Bubinga. Available online: https://reverb.com/item/2834248-huss-and-dalton-td-r-20th-anniversary-guitar-thermo-cured-red-spruce-and-bubinga-pre-owned-2015 (accessed on 8 November 2021).
- Wagenführ, A.; Pfriem, A.; Grothe, T.; Eichelberger, K. Untersuchungen zur vergleichenden Charakterisierung von thermisch modifi zierter Fichte für Resonanzdecken von Gitarren. Holz als Roh- Und Werkstoff 2006, 64, 313–316. [Google Scholar] [CrossRef]
- Rajčan, E. Application of acoustic to some problems of material science related to the making of musical instruments. Acustica 1998, 84, 122–128. [Google Scholar]
- Obataya, E.; Ono, T.; Norimoto, M. Vibrational properties of wood along the grain. J. Mater. Sci. 2000, 35, 2993–3001. [Google Scholar] [CrossRef]
- Wegst, U.G.K. Wood for Sound. Am. J. Bot. 2006, 93, 1439–1448. [Google Scholar] [CrossRef] [PubMed]
- Čulík, M.; Danihelová, A.; Danihelová, Z. Wood for musical instruments. Akustika 2016, 25, 66–72. [Google Scholar]
- Gejdoš, M.; Suchomel, J. Potential of wood for musical instruments in Slovakia. Akustika 2013, 20, 16–23. [Google Scholar]
- Čulík, M. Drevo a Jeho Využitie vo Výrobe Hudobných Nástrojov [Wood and Its Use in the Manufacture of Musical Instruments]; TU in Zvolen: Zvolen, Slovakia, 2013; p. 93. [Google Scholar]
- Tetri, T. ThermoWood® Handbook; International ThermoWood Association: Helsinki, Finland, 2003; p. 56. [Google Scholar]
- Korošec, R.C.; Lavrič, B.; Pohleven, F.; Bukovec, P. Thermogravimetry as a possible tool for determining modification degree of thermally treated Norway spruce wood. J. Therm. Anal. Calorim. 2009, 98, 189–195. [Google Scholar] [CrossRef]
- Reinprecht, L.; Vidholdová, Z. Termodrevo—Príprava, Vlastnosti a Aplikácie [Thermowood—Its Preparation, Properties and Application]; Technical University in Zvolen: Zvolen, Slovakia, 2009; p. 89. [Google Scholar]
- Danihelová, A.; Čulík, M.; Danihelová, Z. The most popular wood for making Slovak folk flutes with open ends. Akustika 2012, 17, 6–9. [Google Scholar]
- Obataya, E.F.; Tanaka, M.; Norimoto, B.T. Hygroscopicity of heat-treated wood 1. Effects of after-treatments on the hygroscopicity of heat-treated wood. J. Jpn. Wood Res. Soc. 2000, 46, 77–87. [Google Scholar]
- Abdolahian Sohi, A.M.; Khademi-Eslam, H.; Hemmasi, A.H.; Roohnia, M.; Talaiepour, M. Nondestructive detection of the effect of drilling on acoustic performance of wood. BioResources 2011, 6, 2632–2646. [Google Scholar] [CrossRef]
- Bismarck, G. Sharpness as an Attribute of the Timbre of Steady Sounds. Acta Acust. United Acust. 1974, 30, 159–172. [Google Scholar]
- Alén, R.; Kotilainen, R.; Zaman, A. Thermochemical behavior of Norway spruce (Picea abies) at 180–225 °C. Wood Sci. Technol. 2002, 36, 163–171. [Google Scholar] [CrossRef]
- Esteves, B.; Marques, A.V.; Domongos, I.; Pereira, H. Influence of steam heating on the properties of pine (Pinus pinaster) and eucalypt (Eucalyptus globulus) wood. Wood Sci. Technol. 2007, 41, 193–207. [Google Scholar] [CrossRef]
- Esteves, B.M.; Domingos, I.J.; Pereira, H.M. Pine wood modification by heat treatment in air. Bioresources 2008, 3, 142–154. [Google Scholar] [CrossRef]
- Stamm, A.J. Thermal degradation of wood and cellulose. Ind. Eng. Chem. 1956, 48, 413–417. [Google Scholar] [CrossRef]
- Fung, D.P.C.; Stevenson, J.A.; Shields, J.K. The effect of heat and NH4H2PO4 on the dimensional and anatomical properties of Douglas-fir. Wood Sci. 1974, 7, 13–20. [Google Scholar]
- Zauer, M.; Kowalewski, A.; Sproßmann, R.; Stonjek, H.; Wagenführ, A. Thermal modification of European beech at relatively mild temperatures for the use in electric bass guitars. Eur. J. Wood Wood Prod. 2016, 74, 43–48. [Google Scholar] [CrossRef]
- Čabalová, I.; Výbohová, E.; Igaz, R.; Kristak, L.; Kačík, F.; Antov, P.; Papadopoulos, A.N. Effect of oxidizing thermal modification on the chemical properties and thermal conductivity of Norway spruce (Picea abies L.) wood. Wood Mater. Sci. Eng. 2021. [Google Scholar] [CrossRef]
- Alén, R.; Oesch, P.; Kuoppala, E. Py-GC/AED studies on thermochemical behavior of softwood. J. Anal. Appl. Pyrolysis 1995, 35, 259–265. [Google Scholar] [CrossRef]
- Millett, M.A.; Gerhards, G.C. Accelerated aging: Residual weight and flexural properties of wood heated in air at 115 °C to 175 °C. Wood Sci. Technol. 1972, 4, 193–201. [Google Scholar]
- Navickas, P.; Karpavičiūtė, S.; Albrektas, D. Effect of heat treatment on wettability and MOE of pine and spruce wood. Mater. Sci. 2015, 21, 400–404. [Google Scholar] [CrossRef]
- Kubojima, Y.; Okano, T.; Ohta, M. Bending strength and toughness of heat-treated wood. J. Wood Sci. 2000, 46, 8–15. [Google Scholar] [CrossRef]
- Rusche, H. Thermal degradation of wood at temperatures up to 200 deg C. I. Strength properties of wood after heat treatment. Holz Als Roh-Und Werkst. 1973, 31, 273–281. [Google Scholar] [CrossRef]
- Wegst, U.G.K. Bamboo and Wood in Musical Instruments. Ann. Rev. Mater. Res. 2008, 38, 323–349. [Google Scholar] [CrossRef]
- Bucur, V. Acoustics of Wood, 2nd ed.; Timell, T.E., Wimmer, R., Eds.; Birkhäuser: Berlin, Germany, 2006; p. 403. [Google Scholar]
- Esteves, B.; Pereira, H. Wood modification by heat treatment: A review. BioResources 2008, 4, 370–404. [Google Scholar] [CrossRef]
- Brémaud, I. Acoustical properties of wood in string instruments soundboards and tuned idiophones: Biological and cultural diversity. J. Acoust. Soc. Am. 2012, 131, 807–818. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Wu, X.; Yang, F.; Zhang, H.; Feng, X.; Zhang, J. Effect of Thermal Modification on the Nano-Mechanical Properties of the Wood Cell Wall and Waterborne Polyacrylic Coating. Forests 2020, 11, 1247. [Google Scholar] [CrossRef]
- Zhang, X.; Li, L.; Xu, F. Chemical Characteristics of Wood Cell Wall with an Emphasis on Ultrastructure: A Mini-Review. Forests 2022, 13, 439. [Google Scholar] [CrossRef]
- Roohnia, M.; Kohantorabi, M.; Tajdini, A. Maple wood extraction for a better acoustical performance. Eur. J. Wood Wood Prod. 2015, 73, 139–142. [Google Scholar] [CrossRef]
- Karlinasari, L.; Baihaqi, H.; Maddu, A.; Mardikanto, T.R. The Acoustical Properties of Indonesian Hardwood Species. Makara J. Sci. 2012, 16, 110–114. [Google Scholar] [CrossRef]
- Brémaud, I.; El Kaïm, Y.; Guibal, D.; Minato, K.; Thibaut, B.; Gril, J. Characterisation and categorisation of the diversity in viscoelastic vibrational properties between 98 wood types. Ann. For. Sci. 2012, 69, 373–386. [Google Scholar] [CrossRef]
- Alkadri, A.; Carlier, C.; Wahyudi, I.; Gril, J.; Langbour, P.; Brémaud, I. Relationships between anatomical and vibrational properties of wavy sycamore maple. IAWA J. 2018, 39, 63–86. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Liu, Y.; Liu, Z. Effect of high-temperature heat treatment on the acoustic-vibration performance of picea jezoensis. BioResources 2016, 11, 4921–4934. [Google Scholar] [CrossRef]
- Hilde, C.; Woodward, R.; Avramidis, S.; Hartley, I.D. The Acoustic Properties of Water Submerged Lodgepole Pine (Pinus contorta) and Spruce (Picea spp.) Wood and Their Suitability for Use as Musical Instruments. Materials 2014, 7, 5688–5699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barlow, C.Y. Materials selection for musical instruments. Proc. Inst. Acoust. 1997, 19, 69–78. [Google Scholar]
- Ilmoniemi, M.; Välimäki, V.; Huotilainen, M. Subjective evaluation of musical instrument timbre modifications. In Proceedings of the Joint Baltic-Nordic Acoustics Meeting, Mariehamn, Aland Islands, 8–10 June 2004. [Google Scholar]


| PACH | Norway Spruce | Sycamore Maple | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Unmod. | 135 °C | 160 °C | 185 °C | Unmod. | 135 °C | 160 °C | 185 °C | ||
| ρ (kg∙m−3) | MV | 425 | 420 | 413 | 415 | 609 | 601 | 603 | 604 |
| SD | 32.8 | 21.6 | 13.8 | 17.9 | 38.6 | 24.2 | 19.6 | 20.5 | |
| y = 0.0671x + 426.64 R2 = 0.8274 | y = −0.037x + 608.87 R2 = 0.628 | ||||||||
| EL (GPa) | MV | 12.48 | 13.12 | 12.99 | 12.63 | 10.70 | 11.35 | 11.43 | 11.02 |
| SD | 0.025 | 0.018 | 0.020 | 0.017 | 0.034 | 0.021 | 0.028 | 0.0361 | |
| y = 0.0021x + 12.544 R2 = 0.257 | y = 0.0032x + 10.723 R2 = 0.4911 | ||||||||
| Esp (106∙m2∙s−2) | MV | 29.36 | 31.24 | 31.45 | 30.43 | 17.57 | 18.88 | 18.95 | 18.24 |
| SD | 0.031 | 0.023 | 0.019 | 0.13 | 0.33 | 0.24 | 0.25 | 0.28 | |
| y = 0.0098x + 29.396 R2 = 0.5668 | y = 0.0064x + 17.614 R2 = 0.519 | ||||||||
| cL (m·s−1) | MV | 5419 | 5589 | 5608 | 5517 | 4192 | 4346 | 4353 | 4271 |
| SD | 390 | 228 | 263 | 281 | 285 | 223 | 231 | 197 | |
| y = 0.089x + 5422 R2 = 0.5739 | y = 0.747x + 4197 R2 = 0.5215 | ||||||||
| A (m4∙kg−1·s−1) | MV | 12.75 | 13.31 | 13.58 | 13.29 | 6.88 | 7.23 | 7.22 | 7.07 |
| SD | 1.15 | 0.88 | 0.96 | 0.86 | 0.82 | 0.63 | 0.68 | 0.65 | |
| y = 0.0042x + 12.707 R2 = 0.7767 | y = 0.0017x + 6.89 R2 = 0.5587 | ||||||||
| fr (Hz) | MV | 6025 | 6211 | 6238 | 6192 | 5240 | 5410 | 5382 | 5328 |
| SD | 527 | 462 | 428 | 483 | 535 | 436 | 323 | 341 | |
| y = 0.0042x + 12.105 R2 = 0.8241 | y = 0.0042x + 12.105 R2 = 0.8241 | ||||||||
(-) | MV | 0.036 | 0.030 | 0.031 | 0.033 | 0.055 | 0.052 | 0.053 | 0.051 |
| SD | 0.00369 | 0.00312 | 0.00279 | 0.00264 | 0.00427 | 0.00381 | 0.00363 | 0.00356 | |
| y = −3∙10−5 x+ 0.0358 R2 = 0.5142 | y = −2∙10−5 + 0.0554 R2 = 0.8283 | ||||||||
| η (-) | MV | 0.0115 | 0.0095 | 0.0099 | 0.0105 | 0.0175 | 0.0165 | 0.0168 | 0.0162 |
| SD | 0.0018 | 0.0009 | 0.0011 | 0.0012 | 0.0021 | 0.0019 | 0.0017 | 0.0019 | |
| y = −9∙10−6x + 0.0114 R2 = 0.5108 | y = −7∙10−6x + 0.0176 R2 = 0.8532 | ||||||||
| z (MPa∙s∙m−1) | MV | 2303 | 2347 | 2316 | 2290 | 2553 | 2612 | 2625 | 2580 |
| SD | 12.84 | 4.79 | 3.63 | 5.03 | 11.01 | 5.35 | 4.53 | 4.39 | |
| y = 0.0072x + 2313 R2 = 0.0005 | y = 0.2966x + 2555 R2 = 0.4449 | ||||||||
| Q | MV | 86.96 | 105.26 | 101.01 | 95.23 | 56.82 | 60.61 | 59.52 | 61.73 |
| SD | 5.8 | 4.1 | 3.7 | 3.9 | 5.2 | 4.6 | 4.2 | 3.8 | |
| y = 0.0734x + 87.938 R2 = 0.4568 | y = 0.0268x + 56.324 R2 = 0.8613 | ||||||||
| ACE (m4∙kg−1·s−1) | MV | 1109 | 1401 | 1372 | 1266 | 393.1 | 438.2 | 429.8 | 436.4 |
| SD | 183 | 165 | 162 | 157 | 108 | 98 | 96 | 93 | |
| y = 1.3508x + 1118 R2 = 0.556 | y = 0.2714x + 390.45 R2 = 0.8767 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danihelová, A.; Vidholdová, Z.; Gergeľ, T.; Spišiaková Kružlicová, L.; Pástor, M. Thermal Modification of Spruce and Maple Wood for Special Wood Products. Polymers 2022, 14, 2813. https://doi.org/10.3390/polym14142813
Danihelová A, Vidholdová Z, Gergeľ T, Spišiaková Kružlicová L, Pástor M. Thermal Modification of Spruce and Maple Wood for Special Wood Products. Polymers. 2022; 14(14):2813. https://doi.org/10.3390/polym14142813
Chicago/Turabian StyleDanihelová, Anna, Zuzana Vidholdová, Tomáš Gergeľ, Lucia Spišiaková Kružlicová, and Michal Pástor. 2022. "Thermal Modification of Spruce and Maple Wood for Special Wood Products" Polymers 14, no. 14: 2813. https://doi.org/10.3390/polym14142813
APA StyleDanihelová, A., Vidholdová, Z., Gergeľ, T., Spišiaková Kružlicová, L., & Pástor, M. (2022). Thermal Modification of Spruce and Maple Wood for Special Wood Products. Polymers, 14(14), 2813. https://doi.org/10.3390/polym14142813