Effects of Mechanical Stress on Insulation Structure and Performance of HV Cable
Abstract
:1. Introduction
2. Materials and Methods
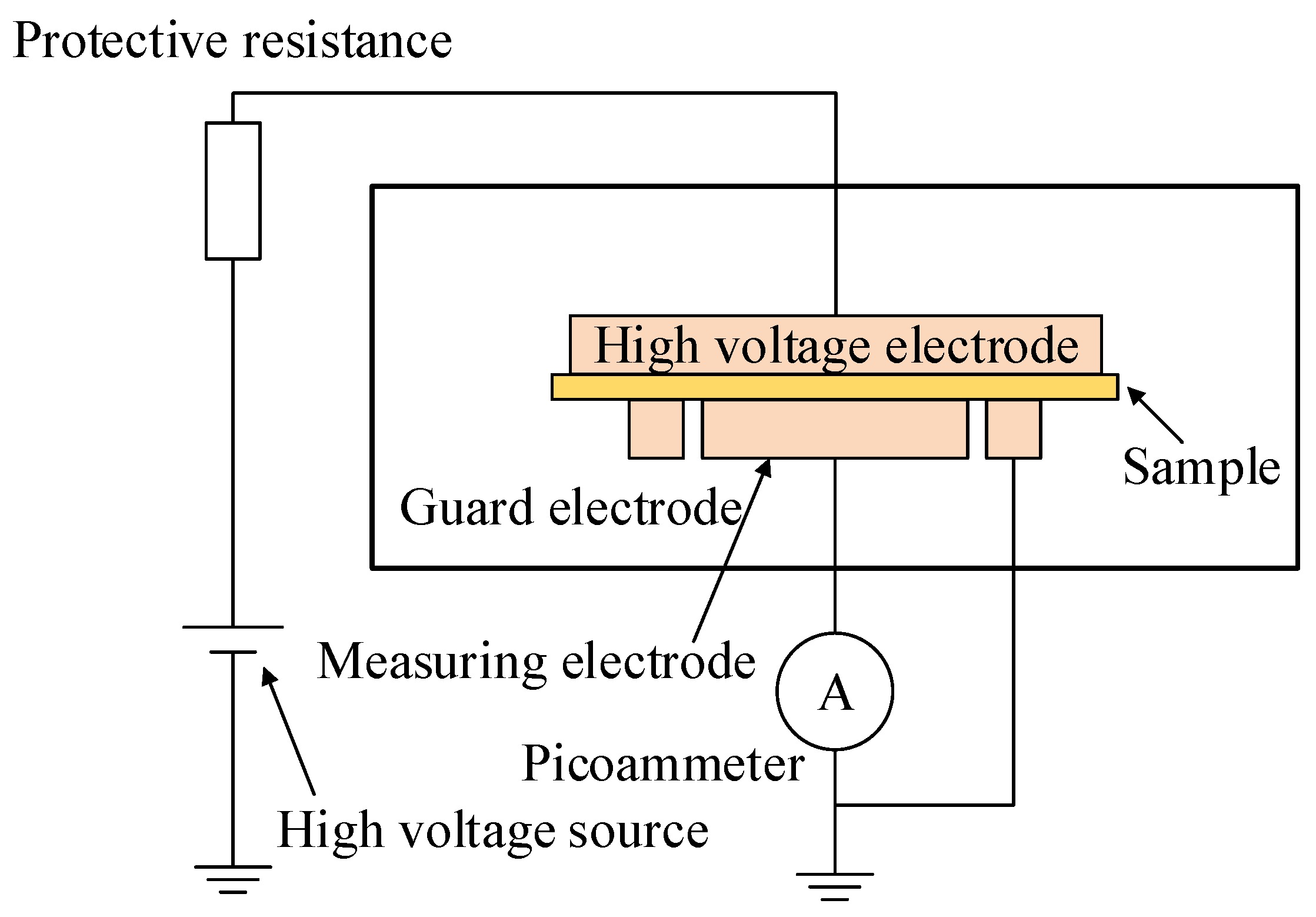
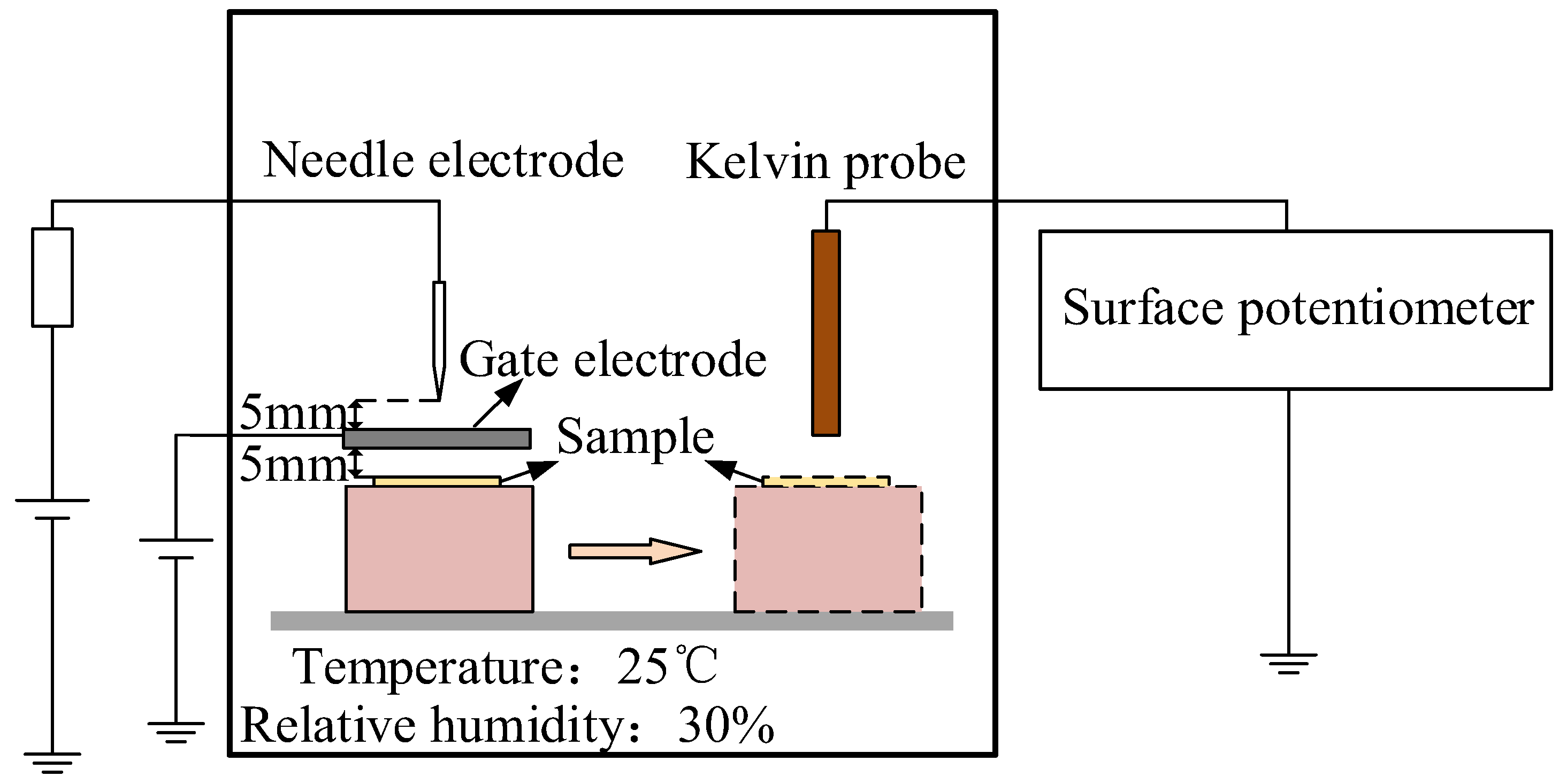
2.1. Specimen Preparation and Test Set-Up
2.2. Simulation Model Construction
3. Results and Discussions
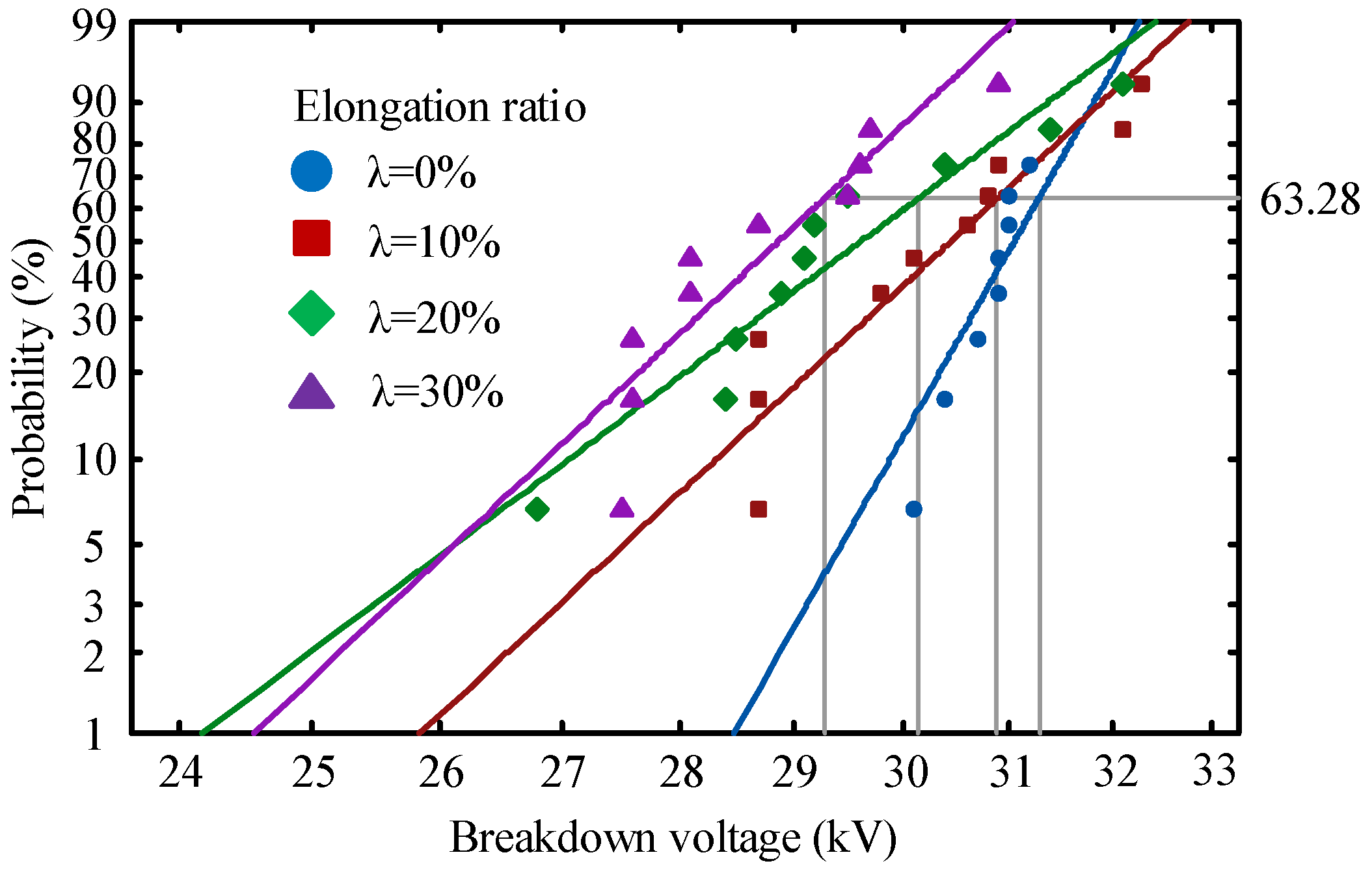
3.1. Effect of Stress on the Insulation Properties of Polyethylene
3.2. Effect of Stress on the Microstructure of Polyethylene
4. Conclusions
- The crystallinity and microcrystalline size of polyethylene decreased at a stretching ratio of 30% compared to unstretched. It is due to the increase of tensile stress which makes the grain breakage and leads to the obstruction of the orientation movement of molecular chains.
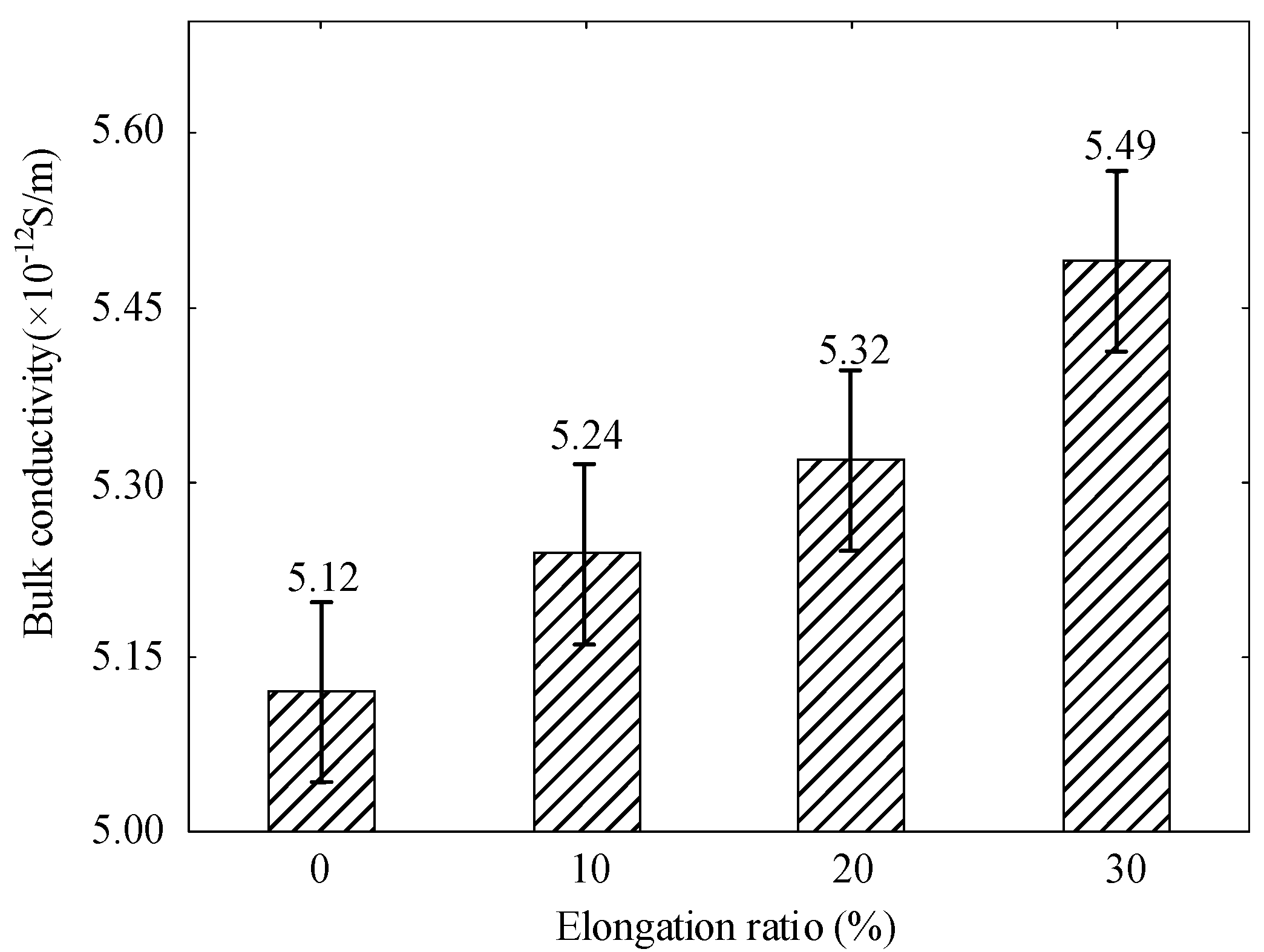
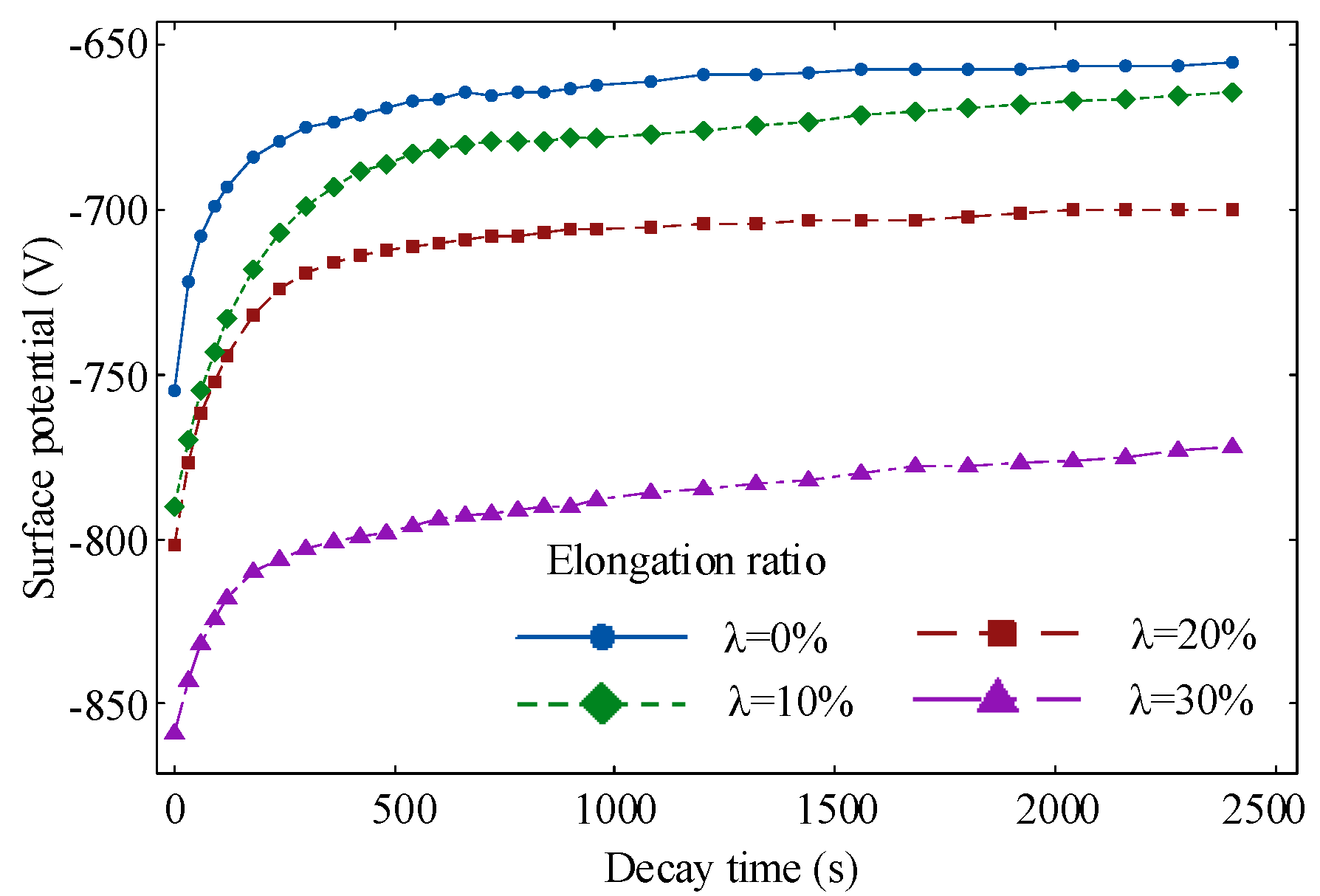
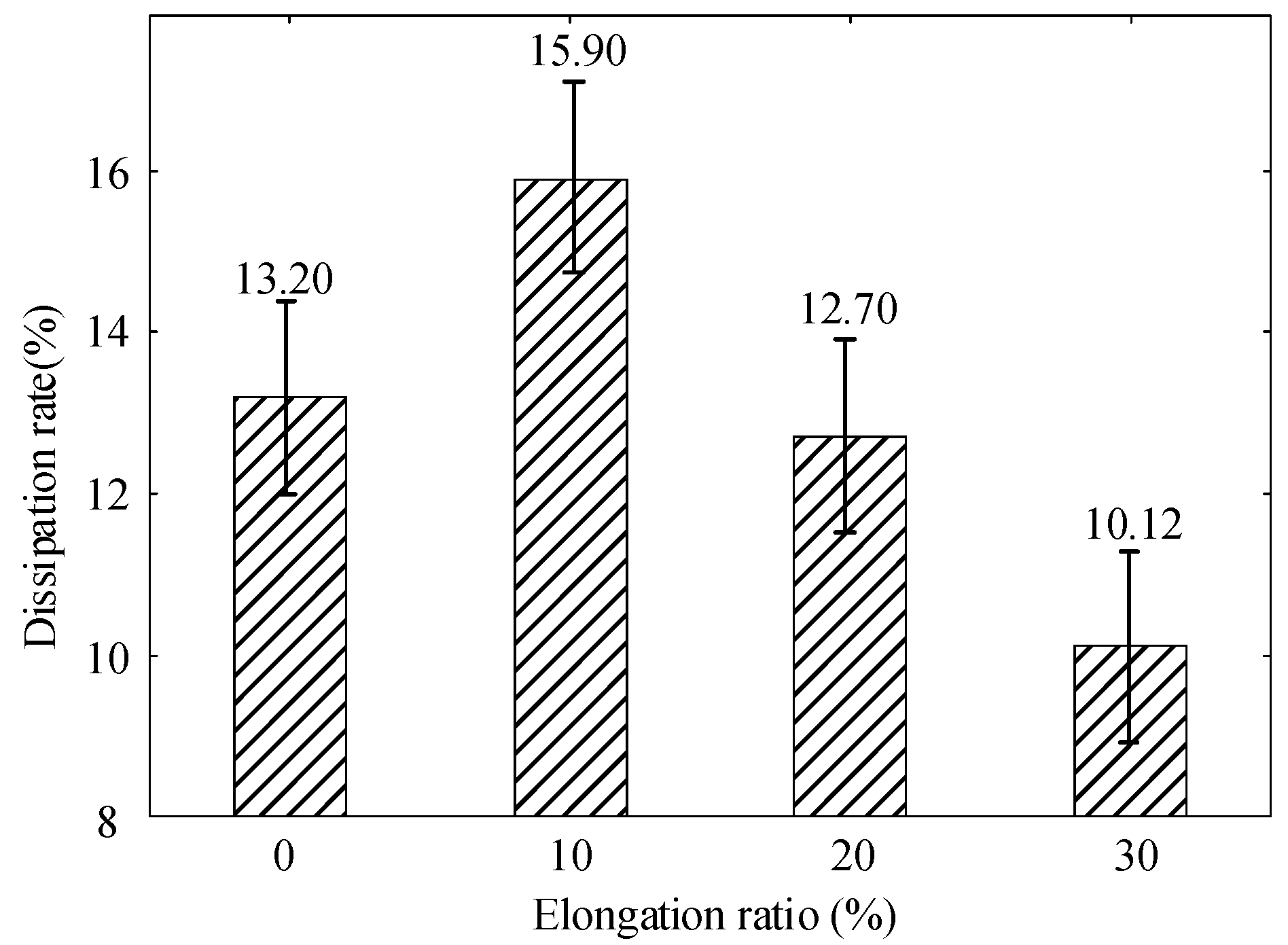
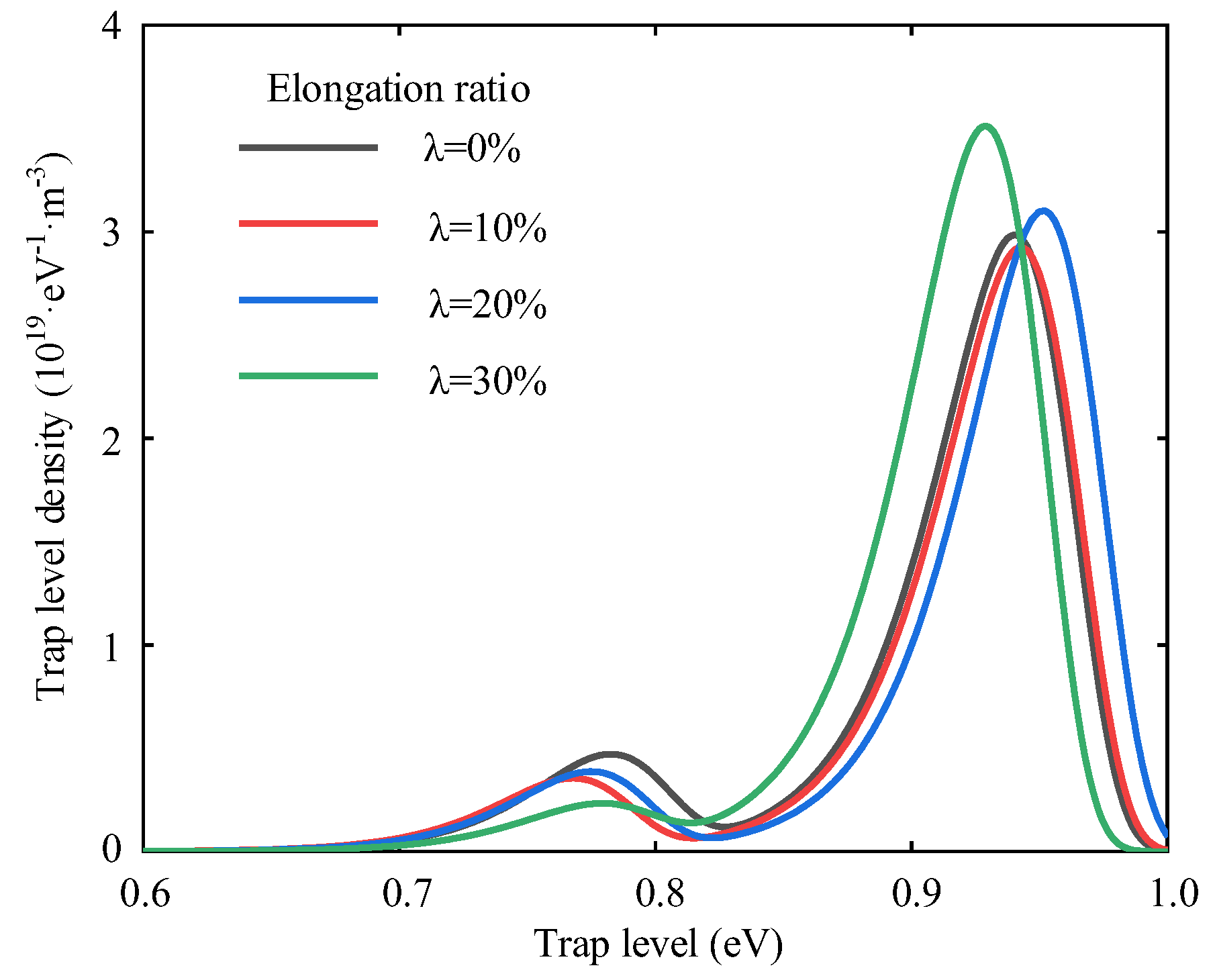
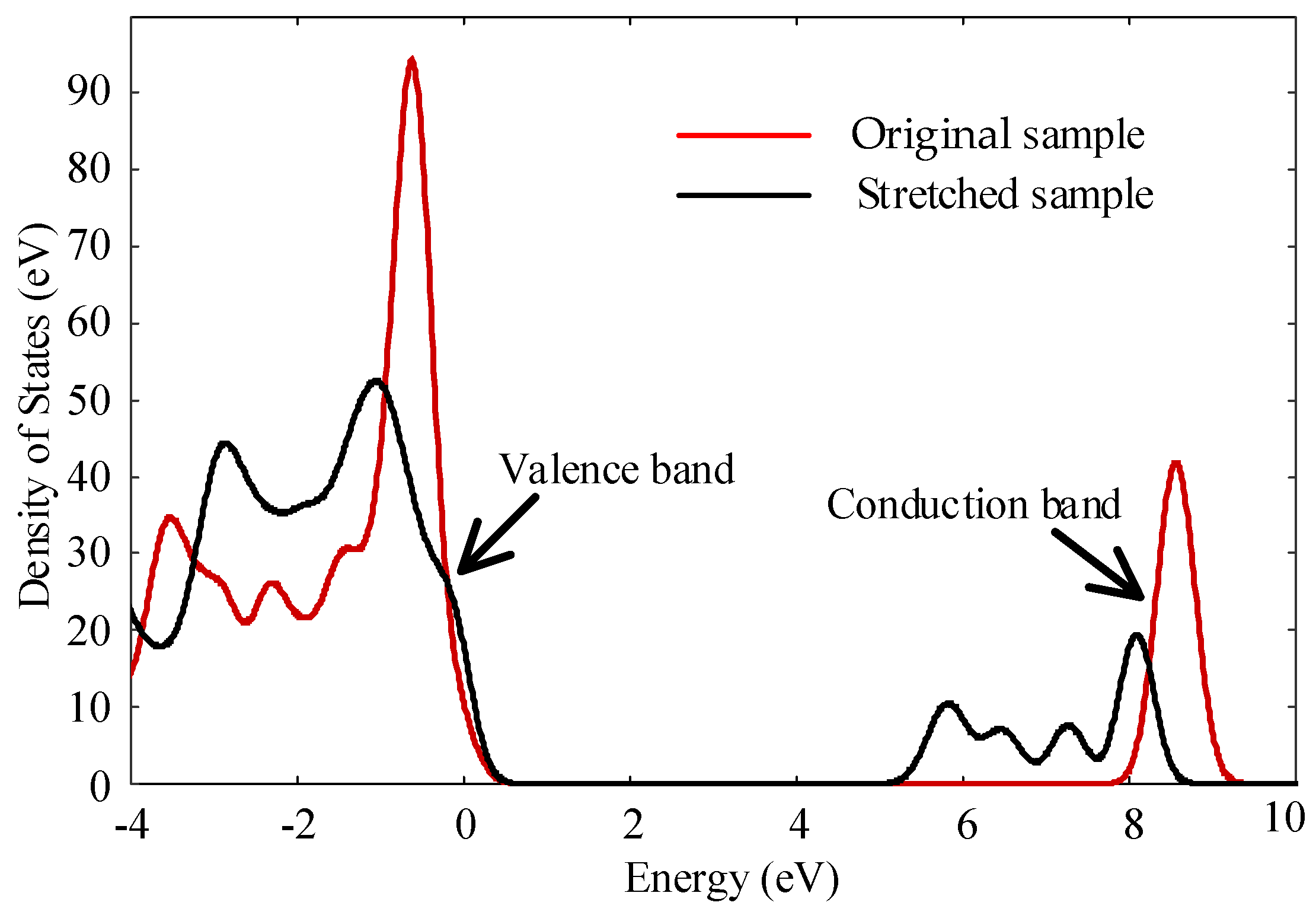
- With the increase of tensile stress, the breakdown field strength of polyethylene decreases continuously. At the same time, conductivity increases with the increase of stretching. When the elongation ratio is 10%, the distance between the molecular chains becomes larger, which is conducive to the migration of ions and electrons, and the decay rate of surface potential increases. As the stretching increases further, more defects are created within the sample, the trap depth becomes deeper, which reduces the rate of decay of the surface potential, resulting in a large amount of charge accumulation in the sample and reduces the insulation performance of the material.
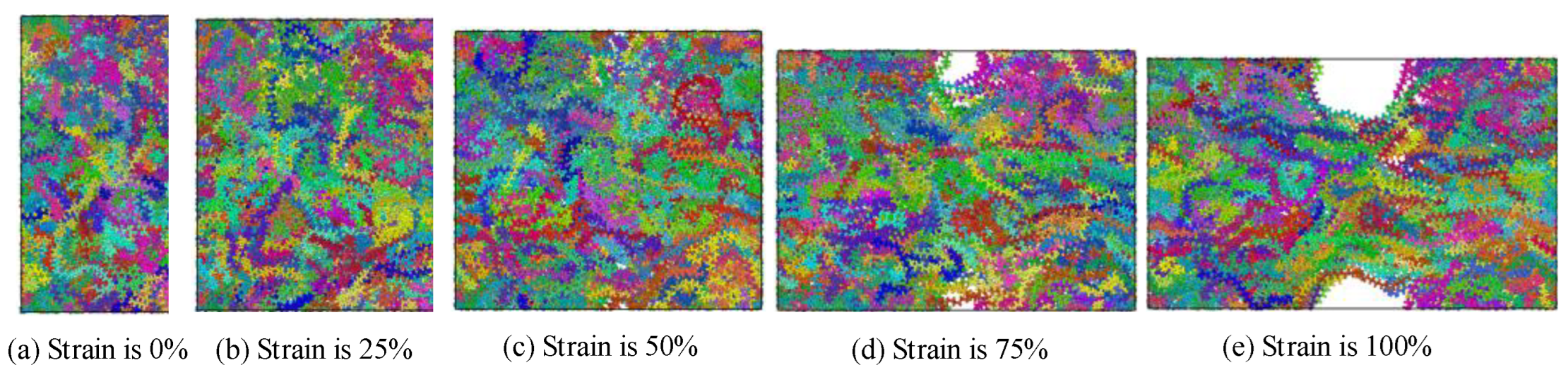
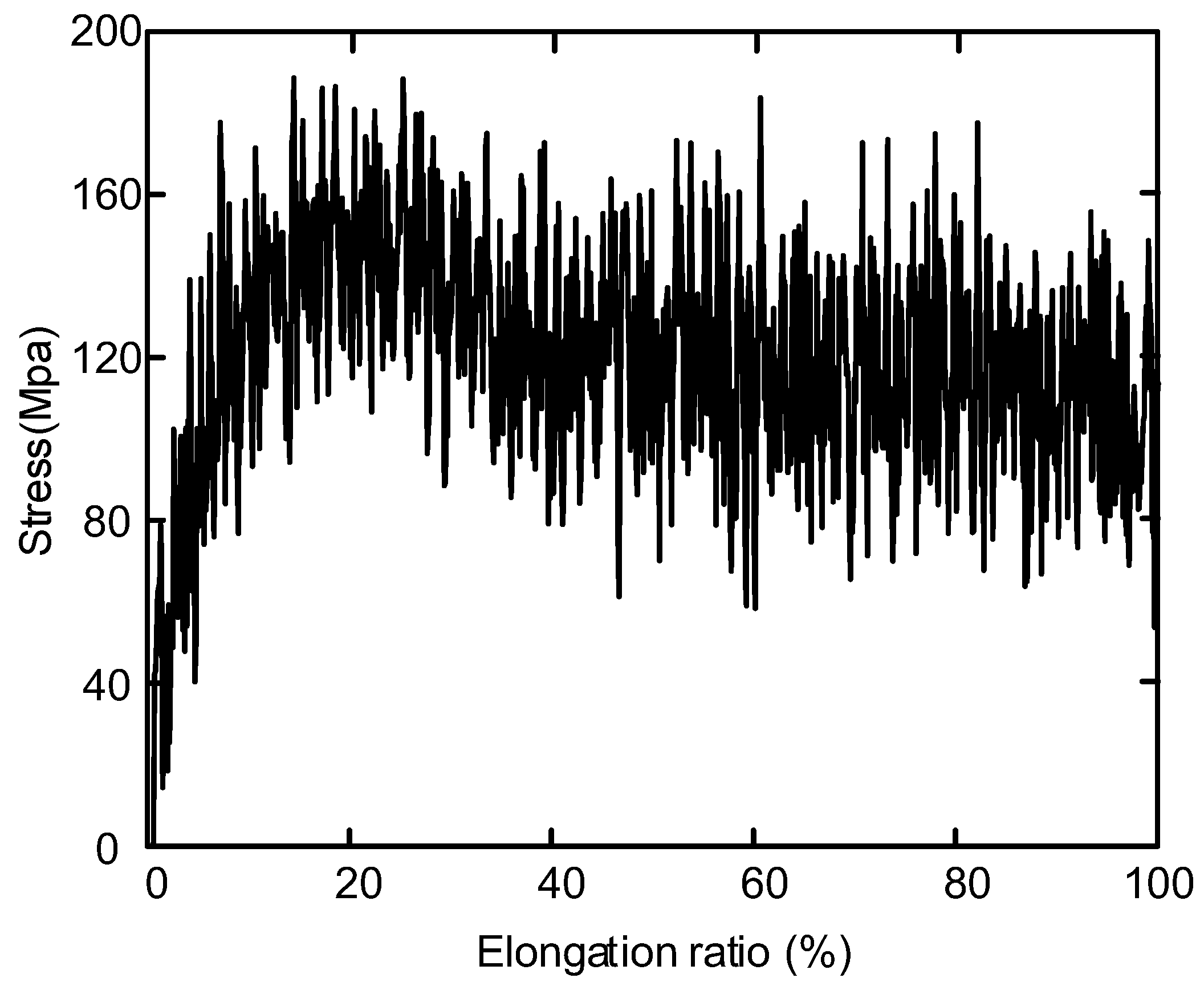
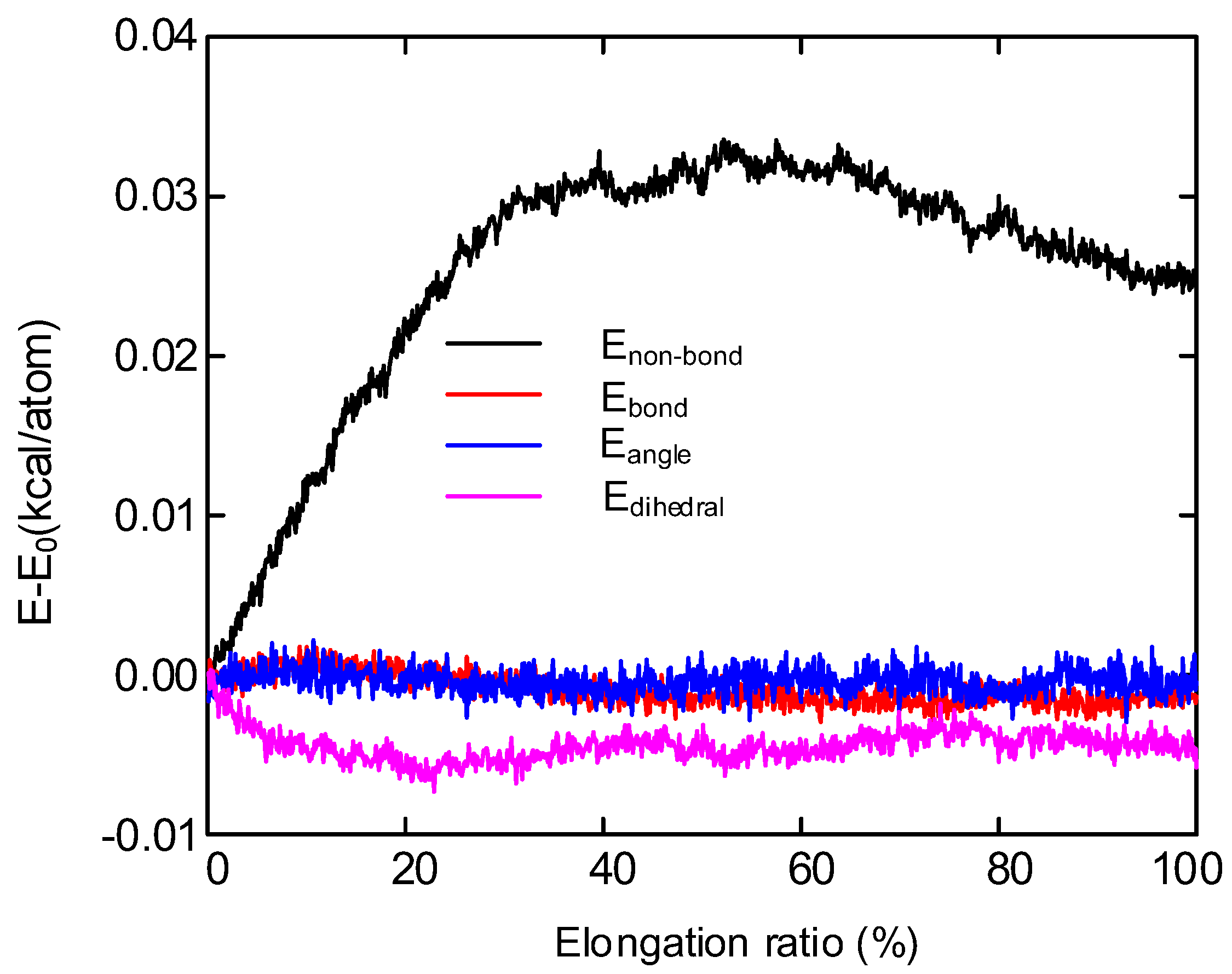
- The main structural changes of semi crystalline polyethylene during stretching are the orientation and unwrapping movement of molecular chain, the sliding of crystal region and the transformation of part of crystal region to amorphous region. The simulated stress-strain curve includes four parts: elastic deformation, yield, strain softening and strain strengthening. Non-bonding energy play an important role in the potential energy change during stretching. The changes in the microstructure of polyethylene during the experimental process are verified by simulating the motion states of the molecules observed during the stretching process. The changes in the electrical properties of polyethylene during the stretching process are explained from a microscopic point of view.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, S.; Zhang, J. Research and analysis on defect detection of semi-conductive layer of high voltage cable. E3S Web Conf. 2020, 185, 01057. [Google Scholar] [CrossRef]
- Teyssedre, G.; Laurent, C. From LDPE to XLPE: Investigating the change of electrical properties. Part II. luminescence. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 447–454. [Google Scholar] [CrossRef]
- Yao, Z.; Peng, S. Polymeric insulation materials for HVDC cables: Development, challenges and future perspective. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1308–1318. [Google Scholar]
- Amyot, N.; David, E. Influence of post-manufacturing residual mechanical stress and crosslinking by-products on dielectric strength of HV extruded cables. IEEE Trans. Dielectr. Electr. Insul. 2002, 9, 458–466. [Google Scholar] [CrossRef]
- Leguenza, E.L.; Robert, R.; Moura, W.A.; Giacometti, J.A. Dielectric behavior of XLPE aged under multi-stressing conditions. In Proceedings of the International Symposium on Electrets, Salvador, Brazil, 11–14 September 2005. [Google Scholar]
- Wang, X.; He, H.Q. Dielectric properties and crystalline morphology of low-density polyethylene blended with metallocene catalyzed polyethylene. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 319–326. [Google Scholar] [CrossRef]
- Yahagi, K. Dielectric properties and morphology in polyethylene. IEEE Trans. Electr. Insul. 1980, 15, 241–250. [Google Scholar] [CrossRef]
- David, E.; Parpal, J.L.; Crine, J.P. Influence of mechanical strain and stress on the electrical performance of XLPE cable insulation. In Proceedings of the Conference Record of the IEEE International Symposium on Electrical Insulation, Pittsburgh, PA, USA; 1994; pp. 170–173. [Google Scholar]
- Mohamed, A.I.; Saari, M.M.; Ozaki, R.; Kadowaki, K. Influence of mechanical pressure on space charge penetration behavior in low-density polyethylene (LDPE) sheet. In Proceedings of the 2017 International Symposium on Electrical Insulating Materials (ISEIM), Toyohashi, Japan, 11–14 September 2017; pp. 184–187. [Google Scholar]
- Xu, H.; Du, B. Space charge behaviors and trap distributions of polypropylene/polyolefin elastomer blend under different elongation ratios. High. Volt. Eng. 2017, 43, 453–459. [Google Scholar]
- Makke, A.; Perez, M. Mechanical testing of glassy and rubbery polymers in numerical simulations: Role of boundary conditions in tensile stress experiments. J. Chem. Phys. 2009, 131, 014904. [Google Scholar] [CrossRef]
- Sheng, H.C.; Qiang, L. Molecular dynamics simulations of graphene/polyethylene and its tensile properties. Acta Polym. Sin. 2017, 4, 716–726. [Google Scholar]
- Lavine, M.S.; Waheed, N.; Rutledge, G.C. Molecular dynamics simulation of orientation and crystallization of polyethylene during uniaxial extension. Polymer 2003, 44, 1771–1779. [Google Scholar] [CrossRef]
- Uchida, M.; Tada, N. Micro-, meso- to macroscopic modeling of deformation behavior of semi-crystalline polymer. Int. J. Plast. 2013, 49, 164–184. [Google Scholar] [CrossRef]
- Hong, K.; Rastogi, A.; Strobl, G.A. Model treating tensile deformation of semicrystalline polymers: Quasi-static stress-strain Relationship and viscous stress determined for a sample of polyethylene. Macromolecules 2004, 37, 10165–10173. [Google Scholar] [CrossRef]
- Hong, K.; Rastogi, A.; Strobl, G.A. Model treatment of tensile deformation of semicrystalline polymers: Static elastic moduli and creep parameters derived for a sample of polyethylene. Macromolecules 2004, 37, 116–127. [Google Scholar] [CrossRef]
- Jabbari-Farouji, S.; Rottler, J.; Lame, O.; Makke, A.; Perez, M.; Barrat, J.L. Plastic deformation mechanisms of semicrystalline and amorphous polymers. ACS Macro Lett. 2015, 4, 147–150. [Google Scholar] [CrossRef] [PubMed]
- Queyroy, S.; Monasse, B. Effect of the molecular structure of semicrystalline polyethylene on mechanical properties studied by molecular dynamics. J. Appl. Polym. Sci. 2012, 125, 4358–4367. [Google Scholar] [CrossRef]
- Yeh, I.C.; Andzelm, J.W.; Rutledge, G.C. Mechanical and structural characterization of semicrystalline polyethylene under tensile deformation by molecular dynamics simulations. Macromolecules 2015, 48, 4228–4239. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.J.; Wang, Z.Y. Improved dielectric breakdown strength of polyimide by incorporating polydopamine-coated graphitic carbon nitride. Polymers 2022, 14, 385. [Google Scholar]
- He, S.; Hu, J. Performance improvement in nano-alumina filled silicone rubber composites by using vinyl tri-methoxy silane. Polym. Test. 2018, 67, 295–301. [Google Scholar] [CrossRef]
- Gao, M.; Yang, J.; Zhao, H.; He, H.; Hu, M.; Xie, S. Preparation methods of polypropylene/nano-silica/styrene-ethylene-butylene-styrene composite and its effect on electrical properties. Polymers 2019, 11, 797. [Google Scholar] [CrossRef] [Green Version]
- Dong, W.; Wang, X. Acetylated SEBS enhanced DC insulation performances of polyethylene. Polymers 2019, 11, 1033. [Google Scholar] [CrossRef] [Green Version]
- Lebedev, O.V.; Goncharuk, G.P. Changes in electrical conductance of polymer composites melts due to carbon nanofiller particles migration. Polymers 2021, 13, 1030. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Zhong, L. Electric field distribution based on radial nonuniform conductivity in HVDC XLPE cable insulation. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 121–127. [Google Scholar] [CrossRef]
- Zhuang, Y.; Hao, M.; Chen, G. Effect of ground electrode on charge injection and surface potential of corona charged polyethylene film. J. Electrostat. 2017, 90, 139–146. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.; Zha, L. Polymer semicrystalline texture made by interplay of crystal growth. Polymer 2009, 50, 5871–5875. [Google Scholar] [CrossRef]
- Hossain, D.; Tschopp, M.A. Molecular dynamics simulations of deformation mechanisms of amorphous polyethylene. Polymer 2010, 51, 6071–6083. [Google Scholar] [CrossRef]
- Sami, A.; David, E.; Fréchette, M. Procedure for evaluating the crystallinity from X-ray diffraction scans of high and low density polyethylene/SiO2 composites. In Proceedings of the 2010 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, West Lafayette, IN, USA, 17–20 October 2010; pp. 1–4. [Google Scholar]
- Poletto, M.; Zattera, A.J.; Forte, M.M.C.; Santana, R.M.C. Thermal decomposition of wood: Influence of wood components and cellulose crystallite size. Bioresour. Technol. 2012, 109, 148–153. [Google Scholar] [CrossRef]
- Cai, S.R.; Gao, Z.W. Simulation of carrier transport and energy accumulation modulated DC breakdown Weibull distribution in polypropylene. J. Electr. Eng. 2021, 16, 50–59. [Google Scholar]
- Zheng, J.; Shen, Y.; Li, J.; Xing, Y. Electrical tree characteristics of epoxy resin/AlN nanocomposites in LN2 with repetitive nanosecond pulse voltage. IEEE Trans. Appl. Supercond. 2021, 99, 1–5. [Google Scholar] [CrossRef]
- Artbauer, J. Electric strength of polymers. J. Phys. D Appl. Phys. 1999, 29, 446. [Google Scholar] [CrossRef]
- Sato, M.; Kumada, A.; Hidaka, K.; Hirano, T.; Sato, F. Multi-scale computational evaluation of hole mobility in amorphous polyethylene. In Proceedings of the 2016 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Toronto, ON, Canada, 16–19 October 2016; pp. 74–77. [Google Scholar]
- Wang, W.; Min, D.; Li, S. Understanding the conduction and breakdown properties of polyethylene nanodielectrics: Effect of deep traps. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 564–572. [Google Scholar] [CrossRef]
- Simmons, J.G.; Tam, M.C. Theory of isothermal currents and the direct determination of trap parameters in semiconductors and insulators containing arbitrary trap distributions. Phys. Rev. B 1973, 7, 3706–3713. [Google Scholar] [CrossRef]
- Lewis, J.T. Interfaces are the dominant feature of dielectrics at the nanometric level. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 739–753. [Google Scholar] [CrossRef]
- Lewis, T.J. The physico-chemical origins and nature of space charge in insulating solids under electrical stress. In Proceedings of the IEEE International Conference on Solid Dielectrics, Eindhoven, The Netherlands, 25–29 June 2001; pp. 223–227. [Google Scholar]
- Kim, J.M.; Locker, R. Plastic Deformation of semicrystalline polyethylene under extension, compression and shear using molecular dynamics simulation. Macromolecules 2014, 47, 2515–2528. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Yang, X. Fracture mecha5nism of amorphous polymers at strain fields. Phys. Chem. Chem. Phys. 2014, 16, 24892–24898. [Google Scholar] [CrossRef] [PubMed]
- Fangli, D.; Yikuang, J. Microstructure evolution during tension deformation of semi-crystalline polymer. Chin. J. Theor. Appl. Mech. 2016, 48, 369–377. [Google Scholar]
- Bao, Q.; Yang, Z. Molecular dynamics simulation of amorphous polyethylene (PE) under cyclic tensile-compressive loading below the glass transition temperature. Polymer 2020, 186, 121968. [Google Scholar] [CrossRef]
- Huzayyin, A.; Boggs, S. Quantum mechanical studies of carbonyl impurities in dielectric polyethylene. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 920–925. [Google Scholar] [CrossRef]
- Guo, N. Composite micro-nanoarchitectonics of MMT-SiO2: Space charge characteristics under tensile state. Polymers 2021, 13, 4354. [Google Scholar]


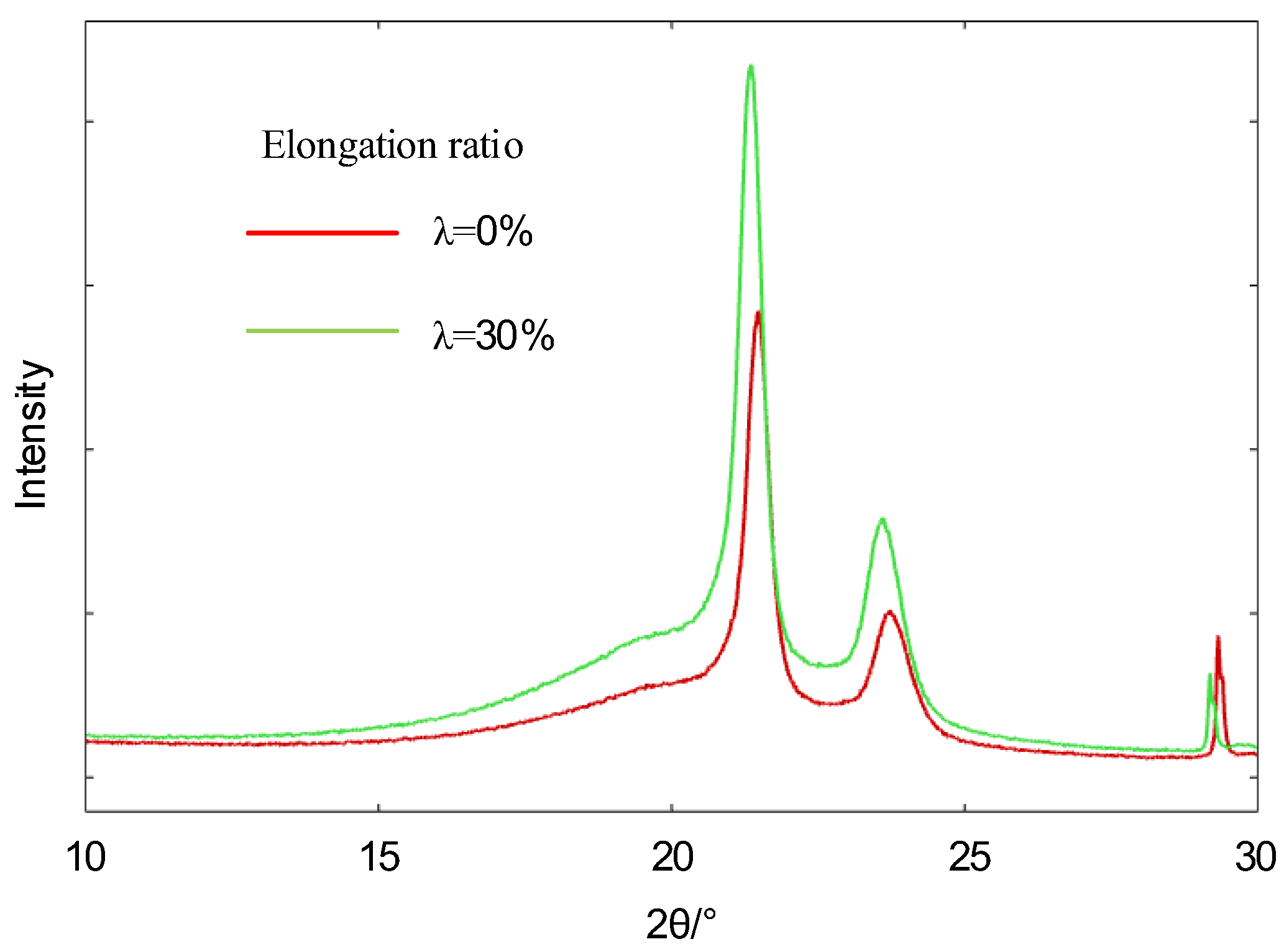

| Elongation Ratio | L(110)/nm | L(200)/nm | W/% |
|---|---|---|---|
| 0% | 9.1 | 9.9 | 58.1% |
| 30% | 8.2 | 9.6 | 46.13% |
| Elongation Ratio | Scale Parameters/kV | Shape Parameters | Standard Deviations |
|---|---|---|---|
| 0% | 31.25 | 46.29 | 0.56 |
| 10% | 30.59 | 28.04 | 1.26 |
| 20% | 30.22 | 20.56 | 1.45 |
| 30% | 29.18 | 24.60 | 1.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Wei, L.; Zheng, J.; Liu, J.; Zhang, P.; Pang, X.; Xing, Y. Effects of Mechanical Stress on Insulation Structure and Performance of HV Cable. Polymers 2022, 14, 2927. https://doi.org/10.3390/polym14142927
Su J, Wei L, Zheng J, Liu J, Zhang P, Pang X, Xing Y. Effects of Mechanical Stress on Insulation Structure and Performance of HV Cable. Polymers. 2022; 14(14):2927. https://doi.org/10.3390/polym14142927
Chicago/Turabian StyleSu, Jingang, Liqiang Wei, Jingquan Zheng, Jiahao Liu, Peng Zhang, Xianhai Pang, and Yunqi Xing. 2022. "Effects of Mechanical Stress on Insulation Structure and Performance of HV Cable" Polymers 14, no. 14: 2927. https://doi.org/10.3390/polym14142927







