3. Experimental Investigations, Results, Analysis and Discussion
Following the conditions described in the chapters above, uniaxial tensile tests on strip specimens made of ETFE foils from three different material producers were performed in the machine direction (MD) at four different temperatures (T0 = 0 °C, T23 = 23 °C, T40 = 40 °C and T50 = 50 °C), five different test speeds ( = 10 mm/min, = 50 mm/min, = 100 mm/min, = 200 mm/min and = 500 mm/min) and two foil thicknesses (100 µm and 250 µm). For each parameter combination (temperature-test speed-foil thickness), five tests were carried out, apart from the tests at testing temperature T0 for the ETFE foil from producer III with only three tests per test combination. In total, 580 uniaxial tensile tests were carried out. Considering measurement uncertainty, all results were rounded to one digit.
All resulting experimental uniaxial stress-strain curves showed the already mentioned three basic parts as expected: the viscoelastic, viscoelastic-plastic and viscoplastic material behaviour with hardening effects in the viscoplastic material stage after yielding. Hereby, the strength point fve marks the end of the viscoelastic stage and simultaneously the beginning of the second linear part in the viscoelastic-plastic stage. The yield point fy, as described in EN ISO 527-1, marks the end of the viscoelastic-plastic stage and simultaneously the beginning of the viscoplastic material stage.
At first, the achieved stress-strain curves at T
23 = 23 °C and
were compared for both foil thicknesses of all three producers, see
Figure 3.
The stress-strain curves for each test series show a consistent behaviour with only very small deviations. The resulting coefficients of variation (COV) determined at the previously mentioned specific strains are listed in
Table 3. Here, the elastic capabilities are described by the stress f
1 at 1% strain. The second material stage—the viscoelastic-plastic part—is described by f
10. The foil producers typically evaluate and issue the stresses at 10% strain as mean values in their data sheets and—if available—in their inspection certificates 3.1 acc. to EN 10204 [
26]. Additionally, f
y and further stresses were evaluated, the latter ones at specific strains ranging from 50% to 200% strain to characterise the viscoplastic material stage.
In all test series listed in
Table 3, the highest COV values occur at the breaking stress, ranging from 3.5% to 7.2%. The main reason for these high deviations is that the breaking stress is not reached at equal strains, but at different strains for each test. This behaviour is explained by the fact that various parameters influence the breaking stress and breaking strain. These parameters are the specimen preparation and the clamping, as well as the clamp itself. On the other side, it becomes obvious that the stress-strain curves for each parameter combination show a very similar behaviour up to 200% strain, and even above. Stresses at 200% strain will not be reached in building structures due to the applied deformation limits in the serviceability limit state. Typically, strains of up to 8% (stress ratio MD:TD = 1:1) to 10% (2:1) at room temperature can be expected in executed ETFE structures when they are designed using the method based on biaxial hysteresis tests offered by prCEN/TS 19102, Annex E (with MD: machine direction and TD: transverse direction). At 200% strain, the highest achieved COV values equal only 1.7% for 100 µm foils and only 0.6% for 250 µm foils. The stresses at the distinct strain values exhibit a very low scatter with COV values up to 1.7%, apart from the scatter at 1% strain. Due to the relatively small stresses at 1% strain of e.g., 10.2 MPa (producer III, 250 µm) with a COV of 6.5%, the standard deviation s yields to 0.7 MPa. However, the measured stress-strain curves in
Figure 3 emphasize the overall small scatter, even at 1% strain. In everyday engineering of ETFE foils, the elastic limit represents an important design value, if plastic strains are prohibited in the structure, so that the knowledge of the material behaviour of ETFE foils in the elastic and viscoelastic region is of great interest.
Apart from the overall comparable stress-strain curves for the 250 µm foils, which are given in
Figure 3, the mechanical behaviour deviates in the first and second material stages. Here, an influence of the different producers can be observed. Tests carried out at 250 µm foils of producers I and III result in a similar stress-strain behaviour in the elastic up to the end of the viscoelastic region, represented by f
1 and f
ip, respectively, the viscoelastic-plastic stage, characterised by f
10 as well as the yield point f
y, and the stress at 200% strain f
200, which describes the viscoplastic stage. In contrast, the material of producer II exhibits considerable smaller stresses at above mentioned strains compared to those materials of the other producers. This behaviour can be observed for both foil thicknesses. For example, the mean f
1-values for the 250 µm foils are 10.8 MPa and 10.2 MPa for producers I and III, and 9.2 MPa for producer II. However, the 100 µm foils show different behaviours in all three material stages and for all three producers. Here, the stresses at 1% strain equal 12.6 MPa, 11.3 MPa and 10.0 MPa for material producers I, III, and II, respectively. Even though the absolute deviations at 1% strain across the investigated foils of the three producers seem quite small with values of Δ
250µm,I–II = 1.6 MPa for the 250 µm foils and Δ
100µm,I–II = 2.6 MPa for the 100 µm foils, the percentile increase from producer II to I equals 15.7% and 26.0%, respectively. This results in considerably different design limits for the serviceability limit state design (SLS) used in prCEN/TS 19102 which should not be neglected for economic reasons. Currently, in the SLS design, the characteristic elastic stress limit at room temperature f
el23 can be taken as 15 MPa according to prCEN/TS 19102. f
el23 can be compared to f
ip. The experimental results show that the characteristic elastic stress limit f
el23 complies with the proposed value of 15 MPa and that significantly higher design limits depending on the used material can be achieved. For both foil thicknesses, the material producer II displays overall lower stresses at specific strains than the material of the other two producers. Additionally, it becomes obvious that 100 µm foils achieve generally higher stress levels at specific strains compared to 250 µm foils.
To illustrate the temperature- and strain rate-dependent material behaviour of the 250 µm foils, the mean value stress-strain curves of the uniaxial tensile tests are displayed in
Figure 4. With a decrease in temperature, the material’s strength increases. An equivalent material response occurs with an increase in the strain rate. A contradictory material behaviour is present if the temperature increases and/or the strain rate decreases as the ETFE foil gets softer and weaker. The stress-strain curves show that the test temperature has a significantly higher influence on the material behaviour than the strain rate. For instance, the 10%-strain stress can vary by a factor of roughly 1.6 for producers I and III and 1.7 for producer II in the tested temperature range. In the tested range of strain rates, it varies only by a factor of about 1.15 for all three producers. Furthermore, with a decrease in temperature, the elongation capability of the material is reduced. Simultaneously, the achievable breaking stresses increase. Equivalent material behaviour is also described in, e.g., [
7,
8,
9,
10,
12,
13,
14,
15,
16,
17].
The temperature and strain rate also influence the yielding capability of ETFE foils. The lower the test temperature and the higher the strain rate, the smaller the elongation capability. Using the definition of the yield point of EN ISO 527-1, it can be observed that the yield point f
y for material of producer II is not clearly delineated in tests performed with low strain rates. This behaviour changes with an increase of the strain rate. Under comparatively high strain rates, distinct yield points become visible. The materials of producers I and III, on the other hand, exhibit clearly determinable yield points with upper and lower bounds, even at high temperatures and low strain rates. Here, after reaching the yield point f
y, a decrease of the stress is measurable even though the strain increases (see
Figure 4). These findings illustrate that the presence of a clear yield point is not a characteristic of ETFE in general but depends on the recipe or the manufacturing conditions. Additionally, it emphasises that ETFE behaves differently depending on the producer. Despite the fact that a clearly determinable yield point is not present for every test combination, the material stiffness for every foil product (I, II or III) drastically changes with reaching the third material stage. In uniaxial tensile tests, yielding—beginning of material stage three—occurs between 12% and 20% strain depending on the test combination of temperature, strain rate, and material.
Evaluating the illustrated uniaxial tensile tests and following the determination process described in chapter 2.2 regarding the stress parameters f*, as well as the stiffness parameters E
0 and E
ve, allows for insight into the material behaviour and its characterisation process. To design foil structures, knowledge about the elastic stage, as well as the corresponding stiffness E
0, is required. Here, the proportional limit is described by f
1.
Figure 5 contains the derived mean stresses f* for 250 µm foils at specific strains, 1%, 10%, 50% and 200%. Additionally, values are given for the first inflexion point f
ip, the strength characteristic f
ve, the yield stress f
y and the ultimate tensile strength f
u. The standard deviations s are illustrated using whiskers.
All derived stresses emphasise the temperature- and strain rate-dependent material behaviour in all three material stages (viscoelastic, viscoelastic-plastic, viscoplastic). The influence of the temperature and strain rate increases with an increase of the applied stresses. Exemplary, focusing on the stresses at 1% strain shows the relatively low impact of the test speed. Here, at T23, an increase of the test speed from 10 mm/min to 500 mm/min (factor 50) leads to an increase of the stresses of ΔI,f1,v500–v10 = 0 MPa (0%), ΔII,f1,v500–v10 = 0.1 MPa (1.5%) and ΔIII,f1,v500–v10 = 0.1 MPa (1.2%), for producers I, II, and III, respectively, with their low COVs ranging from 1.3% to 4.7% at the investigated test combinations. This means that influence of the test speed and thus the strain rate is rather small in the proportional region. Determining the impact of the test speed at f10, the same increase of the test speed from 10 mm/min to 500 mm/min yields to increases in the stresses of ΔI,f10,v500–v10 = 2.6 MPa (11.5%), ΔII,f10,v500–v10 = 2.8 MPa (14.2%) and ΔIII,f10,v500–v10 = 3.7 MPa (17.0%), respectively. At f10 and at these investigated test combinations, the COVs range from only 0.4% to 2.4%, which suggests a constant mechanical behaviour independent of the test combination. Apparently, the impact of increasing strain rates is linked to the first inflexion point fip. Here, the same increase of the test speed leads to increases of the stress of ΔI,fip,v500–v10 = 3.0 MPa (17.3%), ΔII,fip,v500–v10 = 3.1 MPa (22.1%) and ΔIII,fip,v500–v10 = 3.9 MPa (26.0%), respectively. In contrast, the effects of different test temperatures are comparatively high. An increase of the test temperature from 0 °C to 50 °C (± 2 K) at a test speed of results in deviations of the stresses at 1% strain of ΔI,f1,T50–T0 = −3.0 MPa (–24.9%), ΔII,f1,T50–T0 = −2.5 MPa (−27.3%) and ΔIII,f1,T50–T0 = −2.8 MPa (−29.5%), respectively. This influence even increases at f10 to deviations of ΔI,f10,T50–T0 = −11.3 MPa (−35.7%), ΔII,f10,T50–T0 = −11.9 MPa (−42.1%) and ΔIII,f10,T50–T0 = −12.2 MPa (−38.9%), respectively. At f1 the COVs range from 2.0% to 14.5% and at f10 from only 0.6% to 1.9%. The relatively high scatter of 14.5% equals a standard deviation of 1.4 MPa and occurs at T0 for producer III. However, the small COVs at 10% strain emphasize the constant material behaviour.
These results illustrate the nonlinear degressive temperature and progressive strain rate dependencies on the strength of ETFE foils. Shortly after reaching 10% strain, the yield point fy occurs. Again, the mechanical responses of the materials of producers I and III are similar. Here, at T23 and , yielding occurs at comparable stresses of 24.5 MPa and 23.5 MPa for materials of producers I and III with very low COVs of 1.6% and 0.9%, respectively. The material of producer II exhibits smaller stresses at comparable strains (e.g., yielding occurs at 21.3 MPa under same temperature and test speed conditions but with also a very low COV of 0.9%). By comparing the stresses at fy and f50, it becomes clear that in buildings structures yielding of the ETFE foils has to be for sure avoided. By reaching higher stresses than fy, a structural displacement control is not ensured anymore. Under high strains occurring after yielding (e.g., due to water ponding), events or failure due to contact with other components may occur.
Additional information can be achieved by evaluating the standard deviation of each test combination, illustrated by the whiskers in the diagrams. Here, independent of the different materials investigated, different test temperatures and test speeds do not show any influence on the achieved standard deviations for all test series. Herewith, it can be seen, that ETFE foils demonstrate a constant mechanical behaviour in short-term uniaxial tensile tests. However, the derived standard deviations at fu exhibit a relatively high scatter in the stresses, ranging from COV = 1.0% to 17.6%. In addition to the comparatively high scatter of the breaking stresses, different breaking strains occur as well. This makes a comparison of different breaking stresses difficult. As mentioned above and to characterise the viscoplastic stage, f200 has been introduced in the presented study. Even at 200% strain, the materials of producers I and III show higher strengths than the material of producer II, e.g., with 30.1 MPa, 27.4 MPa, and 28.0 MPa for producers I, II, and III at T23 and , respectively. Their COVs are very low, ranging from 2.2% (producer I) to 0.9% (producer II).
The relative high influence of the test temperature and comparatively low influence of the strain rate can also be observed when looking at the material stiffnesses. An increase in the strain rate does not increase the stiffness significantly compared to the impact of a reduction in test temperature. With a decrease of the test temperature, the stiffness increases. However, irregularities in the stress at 1% strain and in the Young’s modulus can be observed, both, in the influence of test temperatures and strain rates. The derived initial material stiffnesses E
0 are illustrated in
Figure 6. It can be observed that material of producer I shows a distinctly stiffer material behaviour than material supplied by producers II and III, independent of the test condition. Comparing the material response of the material of producers II and III, similarities are recognized. This follows the observations already made for f
1. By reaching the viscoelastic-plastic material stage after the first inflexion point, the material stiffness drastically decreases independent of the test combination or material. The material of producer III indicates the stiffest material response after the first inflexion point.
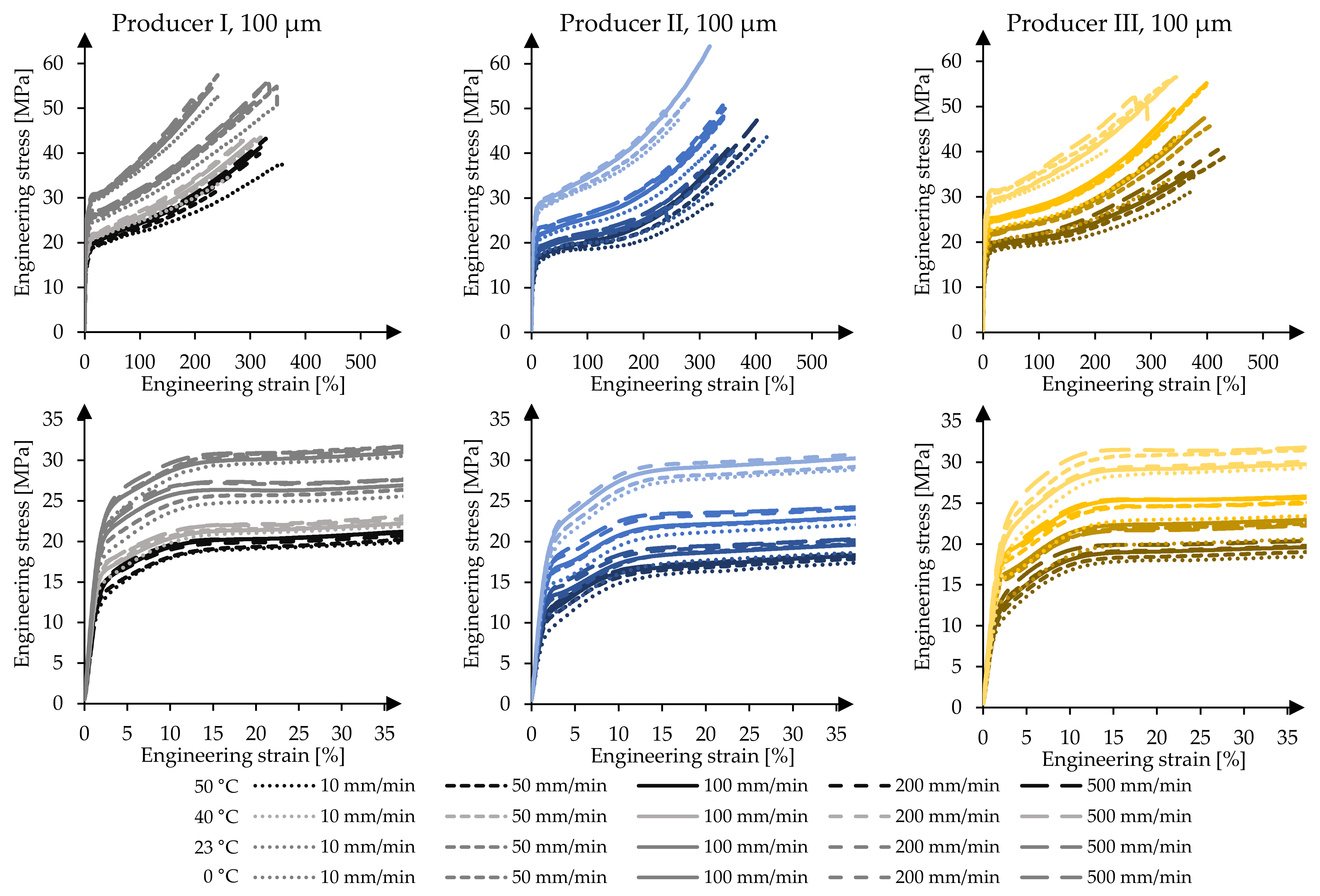
Figure 7 illustrates the material responses of the 100 µm foils. As for the 250 µm foils, the 100 µm foils show a similar temperature and strain rate dependent mechanical behaviour. With a decrease of the temperature and an increase of the strain rate, the material’s strength increases independent of the producer. Regarding the breaking strains, the 100 µm foils show a smaller elongation capability than the 250 µm foils. This complies with a smaller yield plateau achieved by the 100 µm foils compared to that achieved by the 250 µm foils. A distinct and long yield plateau cannot be identified due to the fact that the stress and strain constantly increase. Additionally, the material of producer II shows again smaller stresses at specific strains compared to the foils of the other two material producers. A remarkable influence caused by the material thickness can be observed in material stage three after yielding. Shortly after reaching f
y, the hardening characteristics can again be identified.
Figure 8 illustrates the mean stresses at specific strains for the 100 µm and 250 µm foils under the influence of varying test temperatures and test speeds. As in the case of the 250 µm foils, with decreasing temperatures and increasing strain rates, the stresses of the 100 µm foils at comparable strains increase. Again, the response caused by increasing the strain rates at constant test temperature is less significant compared to the impact of changing test temperatures and keeping the strain rate constant. This can be shown using the derived f
1-values at T
23 for test speeds
and
. Increasing the test speed by a factor of 50 leads to an increase of the stress at 1% strain of Δ
I,f1,v500–v10 = 0.2 MPa (1.6%), Δ
II,f1,v500–v10 = 0.6 MPa (5.9%) and Δ
III,f1,v500–v10 = 0.1 MPa (0.6%), for materials of producers I, II and III, respectively. Here, the COVs range from low 1.2% to moderate 5.9%. Analysing the stresses at 10% strain f
10 shows that the same increase of the test speed—10 mm/min to 500 mm/min—leads to increased stresses of Δ
I,f10,v500–v10 = 3.0 MPa (12.5%), Δ
II,f10,v500–v10 = 3.0 MPa (15.6%) and Δ
III,f10,v500–v10 = 3.1 MPa (14.4%) with COVs ranging from only 0.7% to 1.5%. The material thickness affects the stress levels in general. For 100 µm foils, the overall measured stresses at comparable strains are higher than those achieved for 250 µm foils. For example, at 1% strain, the 100 µm foils of producer I exhibit 12.6 MPa at T
23 and
with a COV of 1.1% and the 250 µm foils exhibit 10.8 MPa with a COV of 1.6%. This indicates higher stiffnesses for 100 µm foils as well.
The derived material stiffnesses for the first and second material stages are illustrated in
Figure 9. As for 250 µm foils, the material stiffness of the 100 µm foils increases significantly with decreasing test temperatures. The impact of the strain rate, however, is again far less significant.
Comparing the stiffnesses of the 250 µm foils with the derived stiffnesses of the 100 µm foils underlines the achieved slightly higher stresses at f1 of 100 µm. For example, the stiffnesses E0 at T23 and are E0,I,250µm = 1161 MPa, E0,II,250µm = 940 MPa and E0,III,250µm = 1067 MPa with COVs of 2.2%, 0.6% and 9.1% for materials of producers I, II and III, respectively. In contrast, the stiffnesses for 100 µm foils at T23 and become E0,I,100µm = 1315 MPa, E0,II,100µm = 1054 MPa and E0,II,100µm = 1207 MPa with COVs of 1.9%, 3.2% and 2.4%, respectively. Herewith, a decrease of the foil thickness of 40% leads to an increase of the stiffness of about 13.3%, 12.1%, and 13.1% for this specific test combination, respectively.
Nevertheless, comparing the first stage and the second stage of the measured stress-strain curves for the 100 µm foils and 250 µm foils, the materials show similar responses, so that an analytical model can be developed to describe the stress-strain behaviour of ETFE foils under consideration of temperature and strain rate effects. To cover the ETFE foil market for both foil thicknesses, 5% fractile curves were derived independently of the material producer but depending on the foil thickness.