Homogenisation of the Local Thermal Conductivity in Injection-Moulded Short Fibre Reinforced Composites
Abstract
:1. Introduction
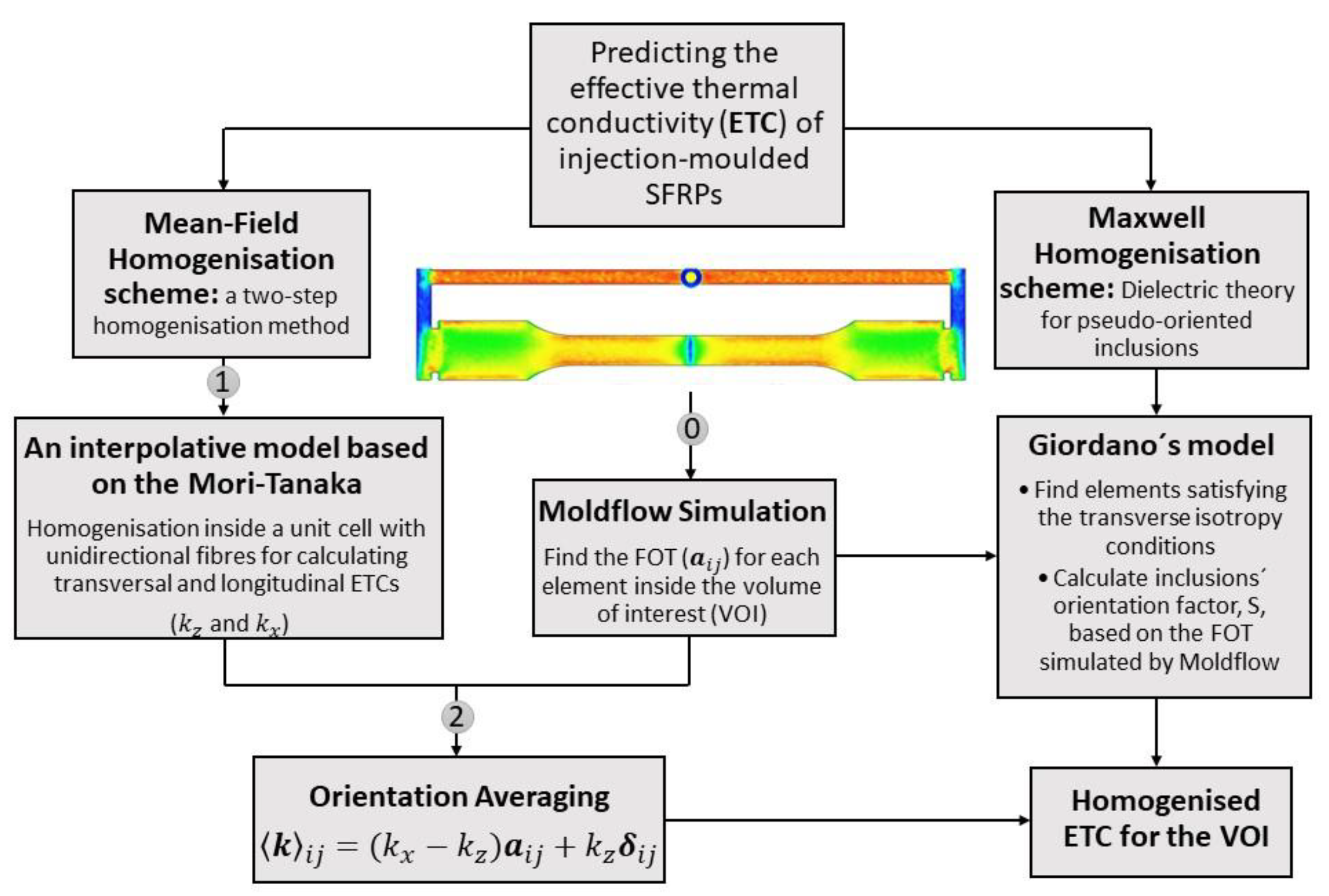
2. Methodologies
2.1. Homogenisation Models
2.1.1. Dielectric Theory for Pseudo-Oriented Inclusions: Giordano’s Model
2.1.2. The Mori–Tanaka (MT) Model and Lielens Interpolation
2.1.3. FEM Analysis: Unidirectional Fibre Alignment
2.1.4. Orientation Averaging
2.2. Autodesk Moldflow Simulation
2.3. Cases to Evaluate the Models
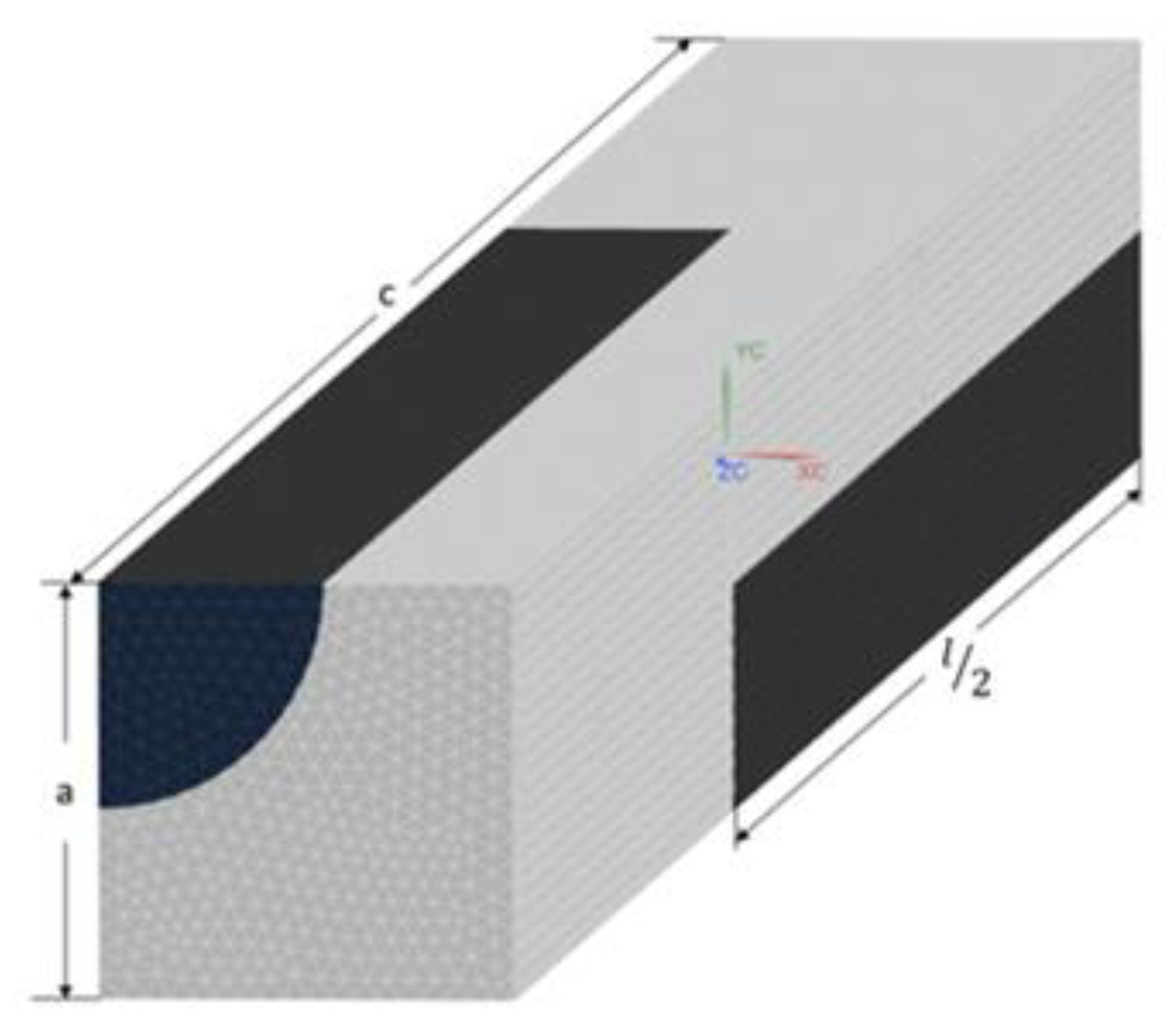
2.3.1. Case study 1: Uniform Distribution of Fibres
2.3.2. Case Study 2: Fibre Orientation of Injection-Moulded SFRPs
2.4. Micro-Computed X-ray Tomography
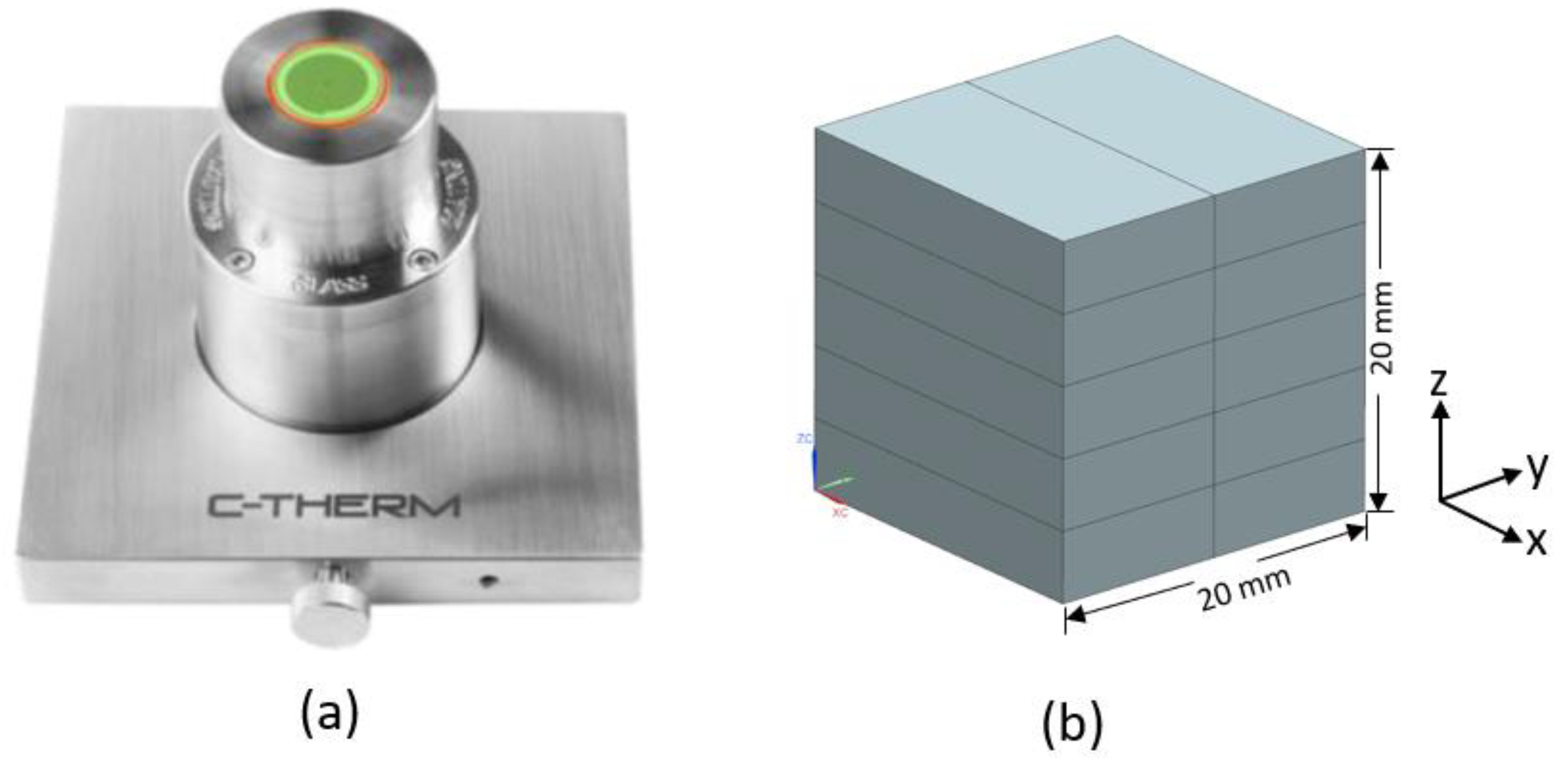
2.5. Experimental Measurement of the ETC
3. Results and Discussions
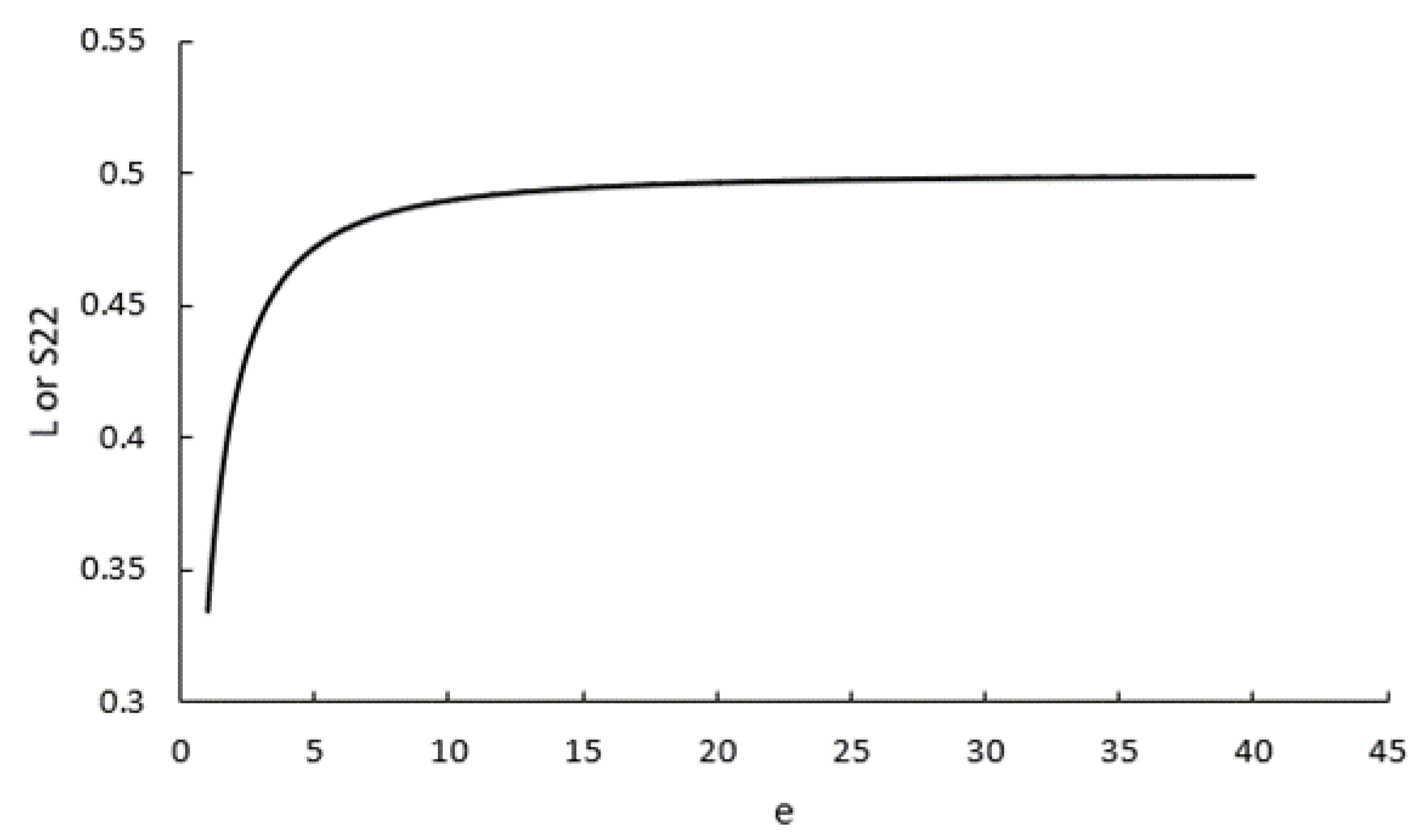
3.1. Calculation of the Depolarisation Factor and Eshelby Tensor for the Cases Studies
3.2. ETC Prediction for Unidirectional Fibre Alignment
3.3. ETC Prediction for the Uniform Distribution of Fibres: Case Study 1
3.4. ETC Prediction for Misaligned Fibres in Injection-Moulded SFRPs: Case Study 2
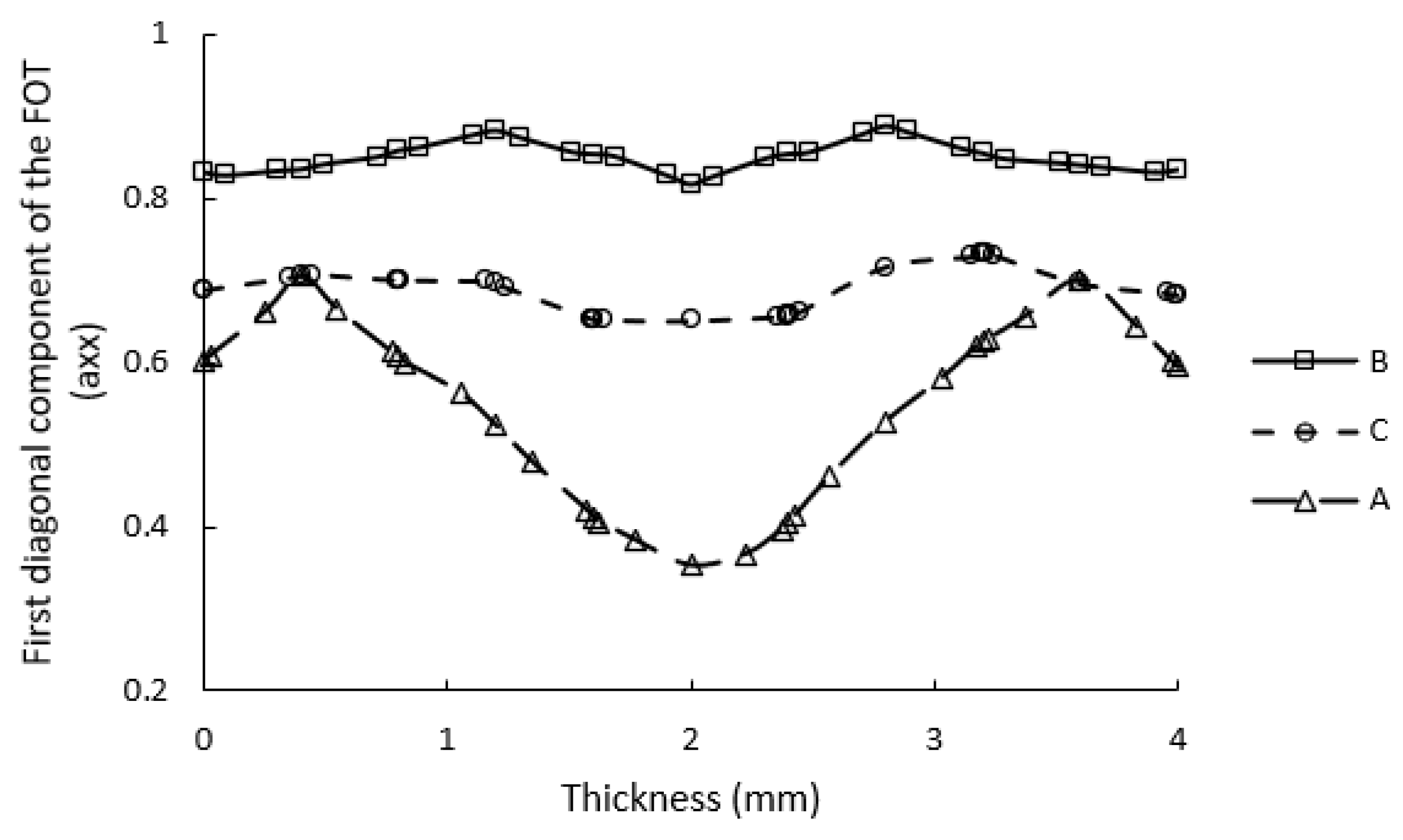
3.4.1. Simulated FOT Predictions and Validation
3.4.2. Homogenisation of Thermal Conductivity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amjadi, M.; Fatemi, A. A Fatigue Damage Model for Life Prediction of Injection-Molded Short Glass Fiber-Reinforced Thermoplastic Composites. Polymers 2021, 13, 2250. [Google Scholar] [CrossRef]
- Huang, C.-T.; Chen, X.-W.; Fu, W.-W. Investigation on the Fiber Orientation Distributions and Their Influence on the Mechanical Property of the Co-Injection Molding Products. Polymers 2019, 12, 24. [Google Scholar] [CrossRef] [PubMed]
- Naili, C.; Doghri, I.; Kanit, T.; Sukiman, M.S.; Aissa-Berraies, A.; Imad, A. Short Fiber Reinforced Composites: Unbiased Full-Field Evaluation of Various Homogenization Methods in Elasticity. Compos. Sci. Technol. 2020, 187, 107942. [Google Scholar] [CrossRef]
- Wieme, T.; Duan, L.; Mys, N.; Cardon, L.; D’hooge, D.R. Effect of Matrix and Graphite Filler on Thermal Conductivity of Industrially Feasible Injection Molded Thermoplastic Composites. Polymers 2019, 11, 87. [Google Scholar] [CrossRef] [PubMed]
- Zhai, S.; Zhang, P.; Xian, Y.; Zeng, J.; Shi, B. Effective Thermal Conductivity of Polymer Composites: Theoretical Models and Simulation Models. Int. J. Heat Mass Transf. 2018, 117, 358–374. [Google Scholar] [CrossRef]
- Tian, W.; Qi, L.; Zhou, J.; Liang, J.; Ma, Y. Representative Volume Element for Composites Reinforced by Spatially Randomly Distributed Discontinuous Fibers and Its Applications. Compos. Struct. 2015, 131, 366–373. [Google Scholar] [CrossRef]
- Sliseris, J.; Yan, L.; Kasal, B. Numerical Modelling of Flax Short Fibre Reinforced and Flax Fibre Fabric Reinforced Polymer Composites. Compos. Part B Eng. 2016, 89, 143–154. [Google Scholar] [CrossRef]
- Zhang, N.; Gao, S.; Song, M.; Chen, Y.; Zhao, X.; Liang, J.; Feng, J. A Multiscale Study of CFRP Based on Asymptotic Homogenization with Application to Mechanical Analysis of Composite Pressure Vessels. Polymers 2022, 14, 2817. [Google Scholar] [CrossRef] [PubMed]
- Mirkhalaf, S.M.; Eggels, E.; Anantharanga, A.T.; Larsson, F.; Fagerström, M. Short Fiber Composites: Computational Homogenization vs Orientation Averaging. ICCM22 2019, 2019, 3000. [Google Scholar]
- Duan, H.L.; Karihaloo, B.L. Effective Thermal Conductivities of Heterogeneous Media Containing Multiple Imperfectly Bonded Inclusions. Phys. Rev. B 2007, 75, 064206. [Google Scholar] [CrossRef]
- Kushch, V.I.; Sevostianov, I. Maxwell Homogenization Scheme as a Rigorous Method of Micromechanics: Application to Effective Conductivity of a Composite with Spheroidal Particles. Int. J. Eng. Sci. 2016, 98, 36–50. [Google Scholar] [CrossRef]
- Duan, H.L.; Karihaloo, B.L.; Wang, J.; Yi, X. Effective Conductivities of Heterogeneous Media Containing Multiple Inclusions with Various Spatial Distributions. Phys. Rev. B 2006, 73, 174203. [Google Scholar] [CrossRef]
- Ordóñez-Miranda, J.; Alvarado-Gil, J.J.; Medina-Ezquivel, R. Generalized Bruggeman Formula for the Effective Thermal Conductivity of Particulate Composites with an Interface Layer. Int. J. Thermophys. 2010, 31, 975–986. [Google Scholar] [CrossRef]
- Giordano, S. Effective Medium Theory for Dispersions of Dielectric Ellipsoids. J. Electrostat. 2003, 58, 59–76. [Google Scholar] [CrossRef]
- Giordano, S. Order and Disorder in Heterogeneous Material Microstructure: Electric and Elastic Characterisation of Dispersions of Pseudo-Oriented Spheroids. Int. J. Eng. Sci. 2005, 43, 1033–1058. [Google Scholar] [CrossRef]
- Pierard, O.; Friebel, C.; Doghri, I. Mean-Field Homogenization of Multi-Phase Thermo-Elastic Composites: A General Framework and Its Validation. Compos. Sci. Technol. 2004, 64, 1587–1603. [Google Scholar] [CrossRef]
- Tian, W.; Qi, L.; Su, C.; Zhou, J.; Jing, Z. Numerical Simulation on Elastic Properties of Short-Fiber-Reinforced Metal Matrix Composites: Effect of Fiber Orientation. Compos. Struct. 2016, 152, 408–417. [Google Scholar] [CrossRef]
- Tian, W.; Fu, M.W.; Qi, L.; Ruan, H. Micro-Mechanical Model for the Effective Thermal Conductivity of the Multi-Oriented Inclusions Reinforced Composites with Imperfect Interfaces. Int. J. Heat Mass Transf. 2020, 148, 119167. [Google Scholar] [CrossRef]
- Camacho, C.W.; Tucker, C.L., III; Yalvaç, S.; McGee, R.L. Stiffness and Thermal Expansion Predictions for Hybrid Short Fiber Composites. Polym. Compos. 1990, 11, 229–239. [Google Scholar] [CrossRef]
- Breuer, K.; Stommel, M.; Korte, W. Analysis and Evaluation of Fiber Orientation Reconstruction Methods. J. Compos. Sci. 2019, 3, 67. [Google Scholar] [CrossRef]
- Tian, W.; Qi, L.; Su, C.; Liang, J.; Zhou, J. Numerical Evaluation on Mechanical Properties of Short-Fiber-Reinforced Metal Matrix Composites: Two-Step Mean-Field Homogenization Procedure. Compos. Struct. 2016, 139, 96–103. [Google Scholar] [CrossRef]
- Modniks, J.; Andersons, J. Modeling Elastic Properties of Short Flax Fiber-Reinforced Composites by Orientation Averaging. Comput. Mater. Sci. 2010, 50, 595–599. [Google Scholar] [CrossRef]
- Mirkhalaf, S.M.; Eggels, E.H.; van Beurden, T.J.H.; Larsson, F.; Fagerström, M. A Finite Element Based Orientation Averaging Method for Predicting Elastic Properties of Short Fiber Reinforced Composites. Compos. Part B Eng. 2020, 202, 108388. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L., III. The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Caton-Rose, P.; Hine, P.; Bernasconi, A.; Conrado, E. Experimental and Numerical Analysis of Fibre Orientation in Injection Moulded Short Glass Fibre Reinforced Polyamide 6 Notched Specimens. In Proceedings of the 16th European Conference on Composite Materials, Seville, Spain, 22–26 June 2014; pp. 22–26. [Google Scholar]
- Foss, P.H.; Tseng, H.; Snawerdt, J.; Chang, Y.; Yang, W.; Hsu, C. Prediction of Fiber Orientation Distribution in Injection Molded Parts Using Moldex3D Simulation. Polym. Compos. 2014, 35, 671–680. [Google Scholar] [CrossRef]
- Tucker, C.L., III; Liang, E. Stiffness Predictions for Unidirectional Short-Fiber Composites: Review and Evaluation. Compos. Sci. Technol. 1999, 59, 655–671. [Google Scholar] [CrossRef]
- Hiroshi, H.; Minoru, T. Equivalent Inclusion Method for Steady State Heat Conduction in Composites. Int. J. Eng. Sci. 1986, 24, 1159–1172. [Google Scholar] [CrossRef]
- Lielens, G.; Pirotte, P.; Couniot, A.; Dupret, F.; Keunings, R. Prediction of Thermo-Mechanical Properties for Compression Moulded Composites. Compos. Part A Appl. Sci. Manuf. 1998, 29, 63–70. [Google Scholar] [CrossRef]
- Whiteside, B.R.; Coates, P.D.; Hine, P.J.; Duckett, R.A. Glass Fibre Orientation within Injection Moulded Automotive Pedal: Simulation and Experimental Studies. Plast. Rubber Compos. 2000, 29, 38–45. [Google Scholar] [CrossRef]
- Fu, S.; Mai, Y. Thermal Conductivity of Misaligned Short-fiber-reinforced Polymer Composites. J. Appl. Polym. Sci. 2003, 88, 1497–1505. [Google Scholar] [CrossRef]
- Sinchuk, Y.; Department of Materials, Textiles and Chemical Engineering, Faculty of Engineering and Architecture, Ghent University, Ghent, Belgium; Finazzi, D.; Department of Materials, Textiles and Chemical Engineering, Faculty of Engineering and Architecture, Ghent University, Ghent, Belgium; Sevenois, R.; Department of Materials, Textiles and Chemical Engineering, Faculty of Engineering and Architecture, Ghent University, Ghent, Belgium; Van Paepegem, W.; Department of Materials, Textiles and Chemical Engineering, Faculty of Engineering and Architecture, Ghent University, Ghent, Belgium. Automatic instance segmentation of individual fibres in a short fibre glass/PA-6 composite. In UGent Internal Report for FWO-SBO Project “Moccha-CT”, Unpublished work. 2022.
- Karamov, R.; Martulli, L.M.; Kerschbaum, M.; Sergeichev, I.; Swolfs, Y.; Lomov, S.V. Micro-CT Based Structure Tensor Analysis of Fibre Orientation in Random Fibre Composites versus High-Fidelity Fibre Identification Methods. Compos. Struct. 2020, 235, 111818. [Google Scholar] [CrossRef]
- Straumit, I.; Lomov, S.V.; Wevers, M. Quantification of the Internal Structure and Automatic Generation of Voxel Models of Textile Composites from X-ray Computed Tomography Data. Compos. Part A Appl. Sci. Manuf. 2015, 69, 150–158. [Google Scholar] [CrossRef]
- Stratton, J.A. Electromagnetic Theory; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 33, ISBN 0470131535. [Google Scholar]



| Model | Case Study 1: Random Orientation of the Fibres | Case Study 2: An Injection-Moulded SFRP | ||
|---|---|---|---|---|
| Giordano | 67.96 | 66.67 | 0.498 | 0.384 |
| Mori–Tanaka | 67.96 | 66.70 | 0.498 | 0.378 |
| Lielens | 67.96 | 66.67 | 0.498 | 0.386 |
| FEM | 67.69 | 66.52 | 0.505 | 0.390 |
| FOT | Moldflow Simulation | Micro-CT Scans Processed in VoxTex |
|---|---|---|
| 0.85 | 0.87 | |
| 0.09 | 0.09 | |
| 0.06 | 0.04 |
| Region | Avg. | Avg. | Avg. | Two-Step Hom. | Giordano | Experiments | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % Ele. | ||||||||||||
| A | 0.63 | 0.35 | 0.02 | 0.457 | 0.425 | 0.388 | 0 | - | - | 0.452 ± 0.008 | 0.446 ± 0.007 | 0.409 ± 0.002 |
| B | 0.84 | 0.09 | 0.07 | 0.480 | 0.396 | 0.394 | 67% | 0.487 | 0.394 | 0.472 ± 0.004 | 0.419 ± 0.005 | 0.418 ± 0.001 |
| C | 0.49 | 0.31 | 0.20 | 0.441 | 0.421 | 0.408 | 10% | 0.463 | 0.409 | 0.441 ± 0.009 | 0.431 ± 0.004 | 0.424 ± 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mokarizadehhaghighishirazi, M.; Buffel, B.; Lomov, S.V.; Desplentere, F. Homogenisation of the Local Thermal Conductivity in Injection-Moulded Short Fibre Reinforced Composites. Polymers 2022, 14, 3360. https://doi.org/10.3390/polym14163360
Mokarizadehhaghighishirazi M, Buffel B, Lomov SV, Desplentere F. Homogenisation of the Local Thermal Conductivity in Injection-Moulded Short Fibre Reinforced Composites. Polymers. 2022; 14(16):3360. https://doi.org/10.3390/polym14163360
Chicago/Turabian StyleMokarizadehhaghighishirazi, Majid, Bart Buffel, Stepan V. Lomov, and Frederik Desplentere. 2022. "Homogenisation of the Local Thermal Conductivity in Injection-Moulded Short Fibre Reinforced Composites" Polymers 14, no. 16: 3360. https://doi.org/10.3390/polym14163360






