1. Introduction
Additive manufacturing (AM) technologies create an object from a 3D CAD model by adding material layer to layer from information provided by a slicing software, thus, allowing for the manufacture of high complexity parts with minor or no further postprocessing [
1]. Additionally, AM materials range continues to grow, from polymers to metals and ceramics [
2,
3]. Due to their low fusion temperature, one of the first AM materials segments was polymers, particularly thermoplastics. Some of the thermoplastic AM processes are fused filament fabrication (FFF), laminated object manufacturing (LOM), and stereolithography (SLA). Nonetheless, they have the disadvantage of producing not functional or stiff parts, mainly for prototyping but not for structural applications. A solution for this issue are fiber-reinforced additive manufacturing (FRAM) composites, which can improve the material properties of polymeric AM by increasing the stiffness and strength [
4]. Nowadays, FRAM applications are in manufacturing fixture tooling, mold equipment, biomedicine, and functional prototyping [
5]. Fundamentally, FRAM parts can be of two types: short fiber-reinforced AM composites or long fiber-reinforced, also called continuous-fiber composites. Short fibers are usually shorter than 200 μm. For example, commercially available nylon reinforced with chopped carbon fiber can be printed in consumer desktop 3D printers, such as Prusa i3. In contrast, the continuous fiber-reinforced fiber length goes from 30 mm to even meters, depending on the layer configuration, and requires more specialized and costly equipment [
6].
Early research works were focused on determining static mechanical properties of FRAM, such as the stiffness, strength, and failure behavior of different structures subjected to different load types, such as impact, flexural, tension, compression, and interlayer strength [
7,
8,
9]. FRAM significantly improves the stiffness and strength of the raw polymer material, sometimes by a factor of three [
10], depending on the fiber type and its configuration. As with traditional composite manufacturing, the load type affects the failure mechanisms [
11]. For example, the tension in fiber longitudinal direction is characterized by fiber rupture, while tension in and out-of-plane direction usually causes interlayer debonding. León B. et al. [
12] perform a state-of-the-art review of damage and failure mechanisms for continuous fiber-reinforced AM. Diaz-Rodriguez et al. [
13] critically review the mechanical properties of FRAM in which the high range of mechanical properties and process parameters are analyzed, revealing that the scattering of the mechanical properties is inherent to manufacturing process parameters, constituent material properties, and environmental conditions. Justo et al. [
14] have shown that stiffness and strength depend on the process parameters, such as print direction, type of fiber, layer thickness, and volumetric fiber fraction. The process parameters can be tuned to satisfy or optimize a given mechanical property, as Ahmed et al. [
15] show for the optimal variable to enhance the interfacial bond strength.
Given the significant number of possible variations and the unmanageable number of experiments it will take to characterize them fully, researchers are looking for models that accurately predict the mechanical properties and failure behavior of FRAM. We can find models considering a physical interpretation of the stress state [
16], numerical experiments [
17,
18], or raw experimental data for data-driven models [
19]. In addition, some researchers are interested in knowing the physical and micromechanical composition of continuous-FRAM for a better physical description of the 3D printed material. One of the critical microstructural descriptors is the volumetric fiber fraction of as-received filament, which is obtained through different methods. Thermogravimetric analysis (TGA) gives the volumetric fiber fraction and thermal behavior of the composite by increasing the temperature, leaving only the fibers, due to the lower fusion and evaporation point of thermoplastics matrices. Moreover, calcination uses the same principle of separating phases using temperature. Other methods involve using chemical acids for dissolving the thermoplastic [
20]. The characterization of the matrix chemical nature can be determined using differential scanning calorimetry (DSC). The methods for characterizing the single fiber separate it from the matrix using chemical solvents, and then subject it to mechanical traction. Other authors acknowledge the effects of process parameters and environment on the FRAM properties, for instance, Chabaud et al. [
20] investigate the effect of environmental conditions on the stiffness and strength of the FRAM parts by performing thermogravimetric and image processing analysis, showing that the carbon fiber filament has a volumetric fraction of 35% and the fiberglass filament has 39%. The humidity plays an important role, showing variations of 18% in stiffness or 25% in strength for the longitudinal direction, while other directional properties are more affected than in the fiber direction. At the same time, microscopic and image analysis can be used to determine the void fraction [
21]. They can also help determine the fiber size, resin-rich or resin-poor matrix regions, and other defects, which can reach values of 15.1% for continuous carbon fiber polyamide cCF/PA parts and 12.3% for cGF/PA parts.
As more physic and microstructural based models appear, a complete description of the behavior of the FRAM for the full characterization of an orthotropic composite 3D printed lamina is needed for engineering calculations and designs. From a composite materials design perspective, nine elastic constants should be given, implying numerous experiments. A helpful approach requiring fewer experiments is obtaining the individual matrix and fiber’s mechanical properties, and then obtaining the overall properties of the composite lamina. For that task, micromechanics deals with the determination of all of the composite properties based on the properties of the constituents. Research has been done in the microstructural characterization of FRAM and micromechanical analysis. Some authors present the transverse area of the FRAM, employing imaging for measuring the volumetric fiber fraction [
21]. Moreover, in the work of Pascual-González et al. [
22], an extensive experimental micromechanics characterization of AM manufacturing was performed for the single fiber properties, the fiber distribution and content, and the polymer nature. Micromechanics is also valuable for failure behavior, and failure prediction of additive manufacturing composites is the subject of recent investigations. Dutra et al. [
23] developed an expanded Puck and Schürmann (ExPan) interfiber fracture criterion, which considers the semi-brittle nature of the thermoplastic matrix. Moreover, they present the failure envelops of 3D-printed composites.
As the number of parameters on which the FRAM mechanical behavior and failure mechanisms depend grows, the experimental work and even the employment of in silico models, such as finite elements, are not feasible. One tool to resolve the problem is using artificial intelligence and data-driven models to predict the properties or design the FRAM architecture. Although machine learning is becoming a powerful tool to tackle challenging problems, a lot of data are required to train a predictive model. Some authors use deep learning to predict the strength of AM parts, while this approach can be used for FRAM parts. Zhang et al. [
24] perform a tensile strength prediction of FFF PLA thermoplastic, considering the temporal aspect of the manufacturing process and the time process variations characterized by inter-layer interactions. The model is constructed using the layerwise process signals (vibration and temperature) as inputs of a long short-term memory LSTM network, a recurrent neural network (RNN). Later, Zhang et al. [
25] performed the strength prediction for a composite AM sample. This time, they develop an ensemble of different types of machine learning algorithms, such as least absolute shrinkage and selection operator (lasso), K-nearest neighbors, and support vector machines. The input parameters are process-related parameters, such as fiber layers, polymer layers, fiber rings, and infill patterns. Other deep learning applications optimize fiber paths and reverse engineering AM parts [
26]. Artificial neural networks (ANN) are also employed as an optimization algorithm that can enhance the mechanical strength of FFF polymers by selecting the optimum process parameters. A deep-learning algorithm proves highly competitive with other optimization algorithms [
27].
For connecting the microstructural characteristics with stiffness, strength, and failure mechanisms, Young et al. [
28] perform fractographical analysis in additive manufacturing thermoplastic composites, where microstructural differences are found between ABS and CF-ABS, presenting lower porosity values in the former, probably due to the thermal conductivity enhancement of the carbon fiber. Chadha et al. [
29] present fractographical evidence of different breaking fracture modes for different infill patterns, such as brittle fracture in a grid structure and ductile fracture in a honeycomb. Other authors could identify fiber slippage, fiber waviness [
30], fiber pull out, and interfacial debonding [
31]. Furthermore, a counter-intuitive behavior was evident in the work of Seifans et al. [
32], where the strength of the 45° reinforced tensile sample was less than 90° angle. Fractographic analysis tools clarify that as the printer deposits a continuous strand of fiber, there are areas in the turns with fiber at 0°, thus elevating the strength.
Given the numerous works in the mechanical characterization of FRAM and the incremental research interest in modeling mechanical properties and failure, there is a need to evaluate micromechanical and data-driven models on continuous FRAM data for predicting the strength. Therefore, this work aims to fill this knowledge gap and elucidate the best possible path by evaluating their accuracy and ease of implementation. First, the micromechanical models are described based solely on constituent properties for the stiffness calculation and in-situ experimental data and back-calculated parameters for the strength prediction. Then, in the second approach, a deep-learning algorithm describes a series of models to perform the stiffness and strength characterization. After establishing the two methods, we introduce the data obtention and curation methodology and the available data set. Finally, comparison and discussion of the results are made.
3. Machine-Learning Architectures
In this work, our interest is in predicting the mechanical properties of AM composites. Therefore, it is a regression problem, a kind of supervised learning. Numerous regression models include simple linear regression models, regression trees, support vector machines, Gaussian process regression (GPR) models, and neural networks [
37]. The models were tested in the regression learner app from the machine learning and statistics toolbox of MATLAB software 2021. The data set is partitioned into five cross-validations folds and estimates the accuracy on each fold to avoid overfitting.
The denotes the design matrix, also called the training matrix, data matrix, or input matrix, and contains the complete input dataset. The columns correspond to each point in the feature space (training sample) and the rows to each factor. Therefore, it is, in a general way, a non-square matrix. The number of explanatory variables or factors p, is the number of rows of , while the number of points m is the number of columns. The variable is the output, response, or predictor value. It is a column vector in which each row is associated with the corresponding column or feature vector in the data matrix . {} are the coefficients of the variables in the model, they are also called weights. represents the error associated with the model, and is called bias, a constant value.
3.1. Decision Trees
Regression trees predict responses to data by following a series of decisions in the tree, from the root (beginning) node down to a leaf. The leaf node contains the response [
38].
3.2. Linear Regression
Linear regression models describe the relationship between the explanatory variables and the
p number of factors or features. The matrix
of observations is an
m by
p matrix, with
m the total number of data points. The response variable is called
as each point has an associated output value. In general, a linear regression model can be a model of the form represented in Equation (18).
where
is a scalar-valued function of the independent variables
. The functions
might be in any form, including nonlinear functions and polynomials. The coefficients
are linear. That is, the response variable,
y, is a linear function of the coefficients
[
37].
3.3. Support Vector Machines
Support vector machines (SVM) is a nonparametric technique relying on kernel functions. Matlab regressor app implements linear
-insensitive SVM (
-SVM) regression. The goal is to find a function
that deviates from
by a value smaller than
for each training point
, and at the same time, it is as flat as possible. So the path to follow is to find a linear function:
Find
with the minimal norm value
formulating a convex optimization problem that has to be minimized:
Subject to the residuals being less than
, that is:
where
is the predicted output.
3.4. Gaussian Process Regression
The available data set is in the form
, where
∈ ℝ
d and
∈ ℝ are drawn from an unknown distribution. A Gaussian process regression (GPR) model predicts the value of a response variable, given the new input vector and the training data. A linear Gaussian regression model is of the form
where
. The error variance
and the coefficients
are estimated from the data. A GPR model explains the response by introducing latent variables,
from a Gaussian process (GP), and explicit basis functions
h. A GP is a set of random variables, such that any finite number of them have a joint Gaussian distribution. If
is a GP, then given
n observations
, the joint distribution of the random variables
is Gaussian.
3.5. Neural Networks
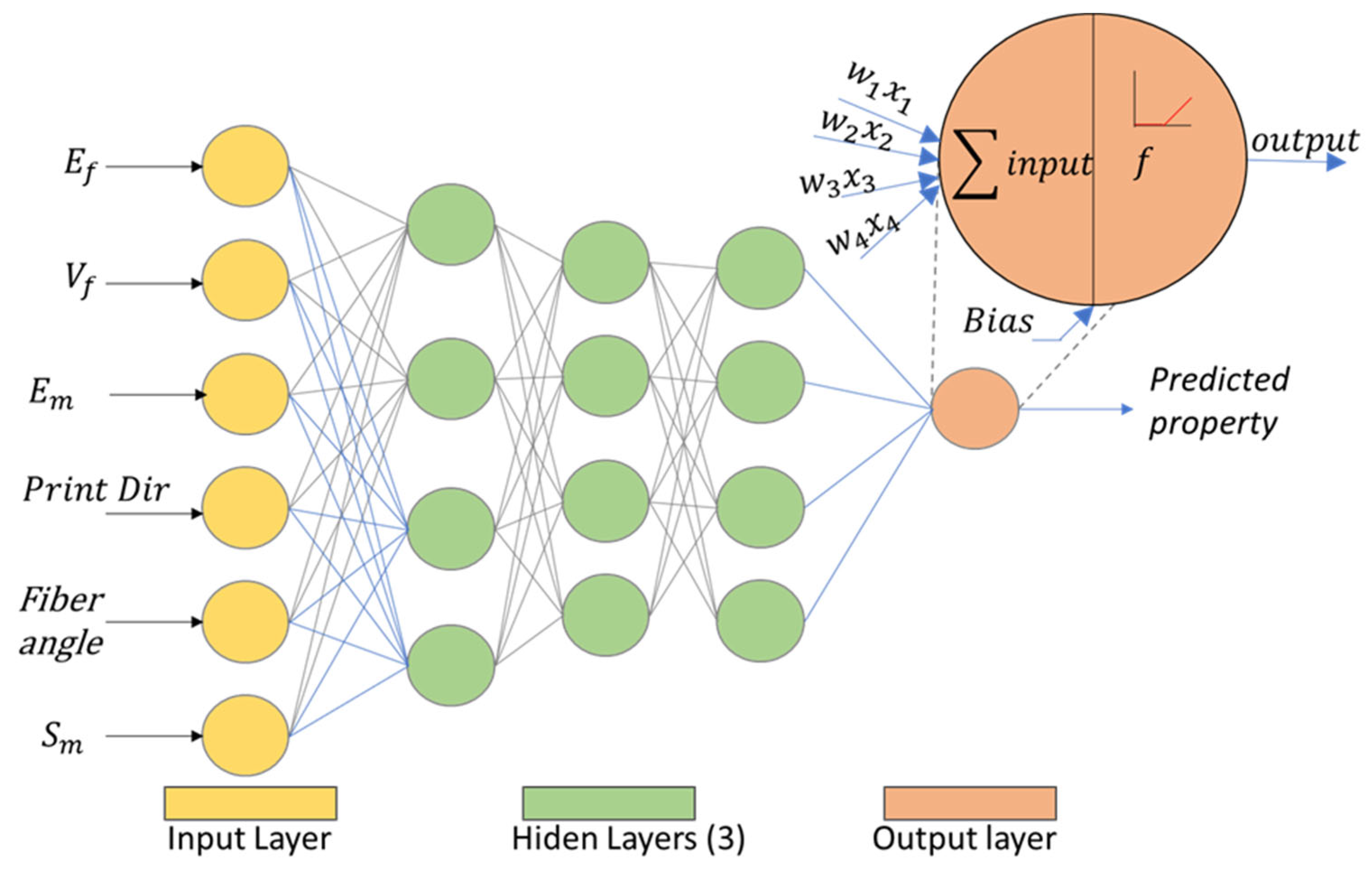
Artificial neural networks (ANN) get their name by the resemblance to a neuron, a biological cell, in which usually more than one stimulus enters the neuron, and the response output connects to other neurons in the network. Raw data can be used to train and test an artificial neural network. In this case, the input layer consists of a vector of a set of parameters with dimension
n = 9, namely: {fiber stiffness, fiber angle, fiber strength, fiber Poissons ratio, matrix stiffness, matrix strength, matrix Poissons ratio, print direction, number of fiber layers}. The output is the stiffness or the tensile strength of such AM parts (
Figure 1). The proposed neural network has various hidden layers and a varying number of neurons in each layer, using ReLu for the activation function.
The data set is grouped in two matrices, in which
is the input matrix of dimensions
and
is the output matrix of dimension
. They have the form
The error function employed to evaluate the ANN is the one employed in the gradient descent formulation:
While the cost function, which is the parameter to minimize, is given by
4. Materials and Methods
Data were gathered from experiments for determining the tensile behavior performed following ASTM D3039, as well as from datasets available in the literature. The raw experimental data are available in
Table A1 in
Appendix A. The experimental design is presented in
Table 1. The experiment design was proposed with three factors, as shown in the columns in
Table 1, with various levels at each factor. Although a standardized design of the experiment was not suitable due to the uneven distribution of levels in each factor from manufacturing constraints, at least four specimens per point were tested, accounting for 52 samples.
MarkTwo desktop printer fabricates the specimens of dimensions 150 mm × 15 mm × 2 mm with a Nylon White matrix and a continuous carbon fiber reinforcement in an aligned arrangement (called “isotropic” in the slicer software Eiger v1.1, Markforged Inc., (Watertown, MA, USA)); Markforged
® supplied all the above materials. The total number of layers is 16 in the flat direction and 110 in the on-edge direction, see
Figure 2. Each layer has 1.25 mm in thickness. The fiber fraction levels are divided into levels corresponding to 2, 4 and 6 reinforced layers in the flat printing direction; and 28, 42, 55, and 70 reinforced layers in the on-edge printing direction.
Samples were visually inspected before testing, and some specimens had minor defects, such as lack of adhesion in local points. However, no general or great-extent defects such as warping, missing layers, or voids were found. Samples are then tested in an MTS Bionix 370.02 with a mechanical MTS 634.12F axial extensometer to accurately determine the elastic response (
Figure 3), and the extensometer length is calibrated at 25 mm. The chosen gripping method was cloth, as Pyl et al. [
39] show the low variance of the results. The testing test speed was 2 mm/min.
6. Conclusions
The effect of the volumetric fiber fraction and printing direction on the mechanical response and failure mechanisms of additive manufacturing composites was assessed. This work tested different models to evaluate stiffness and strength prediction capabilities. Micromechanical models outperformed machine learning with an RMSE of 7.66 GPa in stiffness and 70.05 MPa in strength. In addition, they have the advantage of being physics-based. However, the performance of the ML algorithms was not very good in part due to a lack of consistent data, with a widespread range of materials, methods, and machines for the production of continuous FRAM. Poor data amount derives from the difficulty in obtaining data, and the lack of a standard for reporting the printing process and parameters. For instance, the articles did not report most of the assumed flat printing direction. Moreover, volumetric fiber fraction is not always reported. Among the ANNs, the trilayered NN performed the best.
Considerable strength variations were observed, and there are many reasons for this significant difference. First, is a lack of consistent definition of strength: the maximum stress or the linear elastic stress, also known as yield. Moreover, intrinsic variability and the effect of the manufacturing process means the provided materials could have a microporous difference in the reinforcing fibers. The manufacturing process feed rate, humidity, and the adhesion of the part into the building plate are variables that modify the strength [
58,
59]. Moreover, poor test methods impact the results and, although this effect was minimized with careful manipulation of the specimens, it was not possible to ensure the same conditions in other experimental work. Such conditions include the use and type of grip tabs. The results of stiffness and strength were independent of the stack-up order (this holds for longitudinal testing, such as tension and compression). However, a flexural model will give inaccurate results. One could then express the individual compliance matrices of the laminate.
Failure mechanisms, macroscopic damage appearance, and microstructural differences in specimens were observed. In specimens where fibers were aligned to zero degrees, there is a tendency to fail in a translaminar manner. At the same time, the other tested angles exhibited extensive intralaminar damage and plastic drawn out of the matrix.
The generalization capabilities of machine learning algorithms are good, giving reasonable estimates of the longitudinal and transverse modulus and strength of AM composites. However, the lack of an estimate of the other directions’ properties makes its generalization relatively poor. A possible way to overcome this issue would be to perform a data augmentation based on micromechanical formulations, preferably more accurate ones. Thus, the two models will cooperate instead of competing.
The model assumes a perfect bonding between layers, which in AM components is difficult to obtain. In addition, defects, such as bed level issues, thermal management of the extruder, warping of the piece, and hygroscopic characteristics of the nylon, can affect the interlayer bonding. Although, in reality, we have a composite sandwich in which forces are applied to a laminate, thus, this work aimed at comparing a basic model in which the mesoscale is not entirely depicted and instead gives an estimate of the mechanical properties.