Experimental and Numerical Investigation of 3D Printing PLA Origami Tubes under Quasi-Static Uniaxial Compression
Abstract
:1. Introduction
2. Materials and Methods
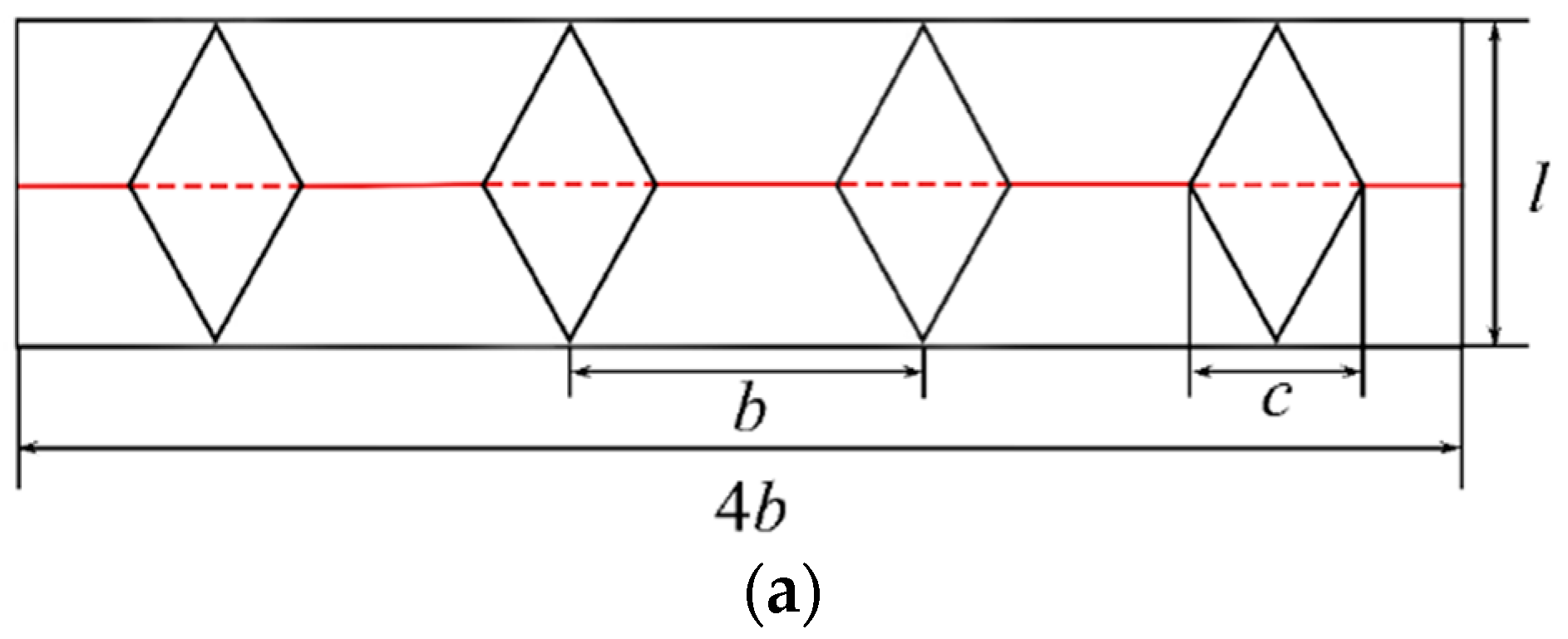
2.1. Geometry
2.2. Materials
2.3. Mechanical Test
2.3.1. Tensile Test
2.3.2. Quasi-Static Uniaxial Compression Test
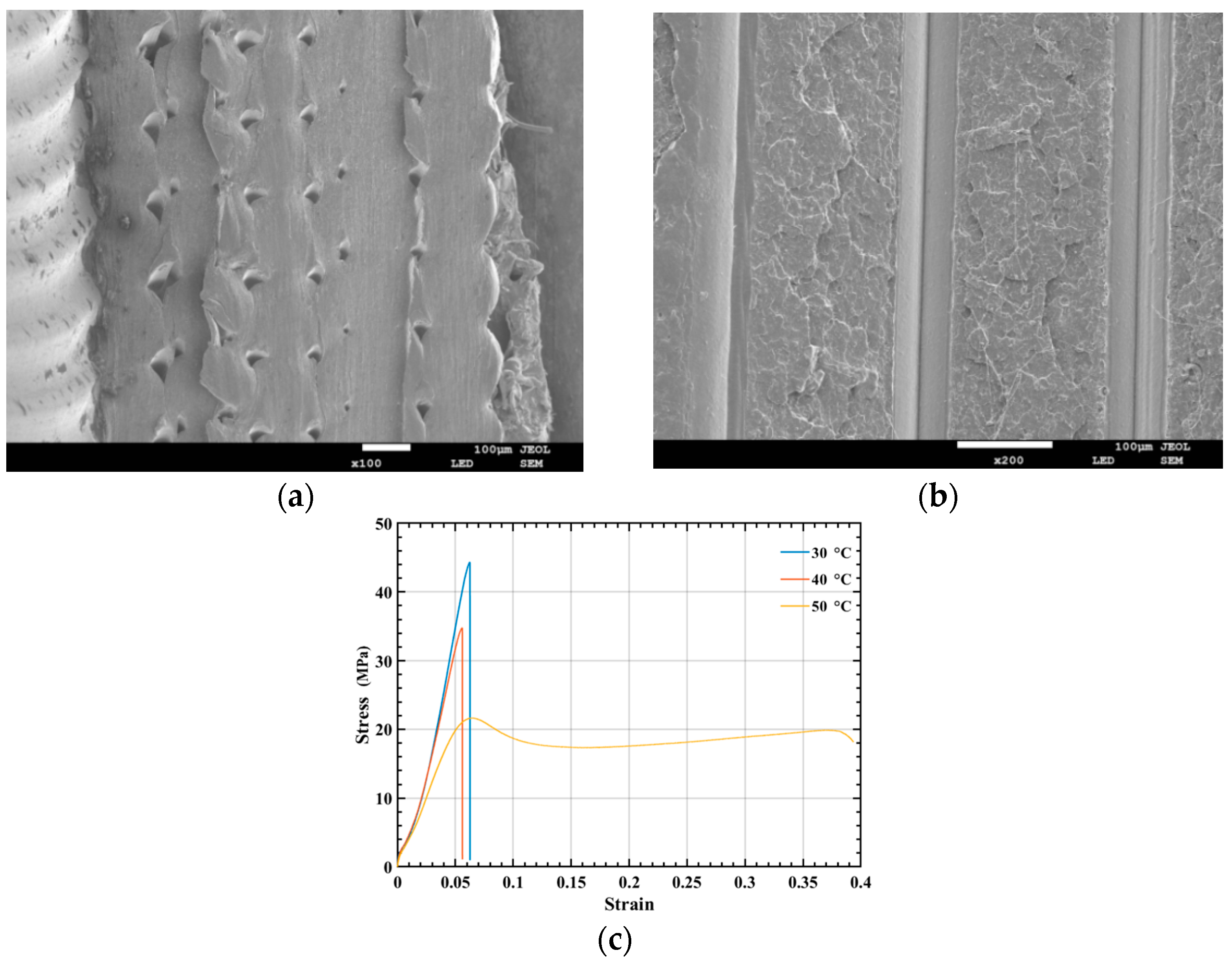
2.3.3. SEM
2.4. Numerical Simulation Method
2.4.1. The Damage Models
2.4.2. The Realization Process of VUMAT Subroutine
2.4.3. Verification of VUMAT Subroutine
2.4.4. Finite Element Modeling (FEM)
3. Result and Discussion
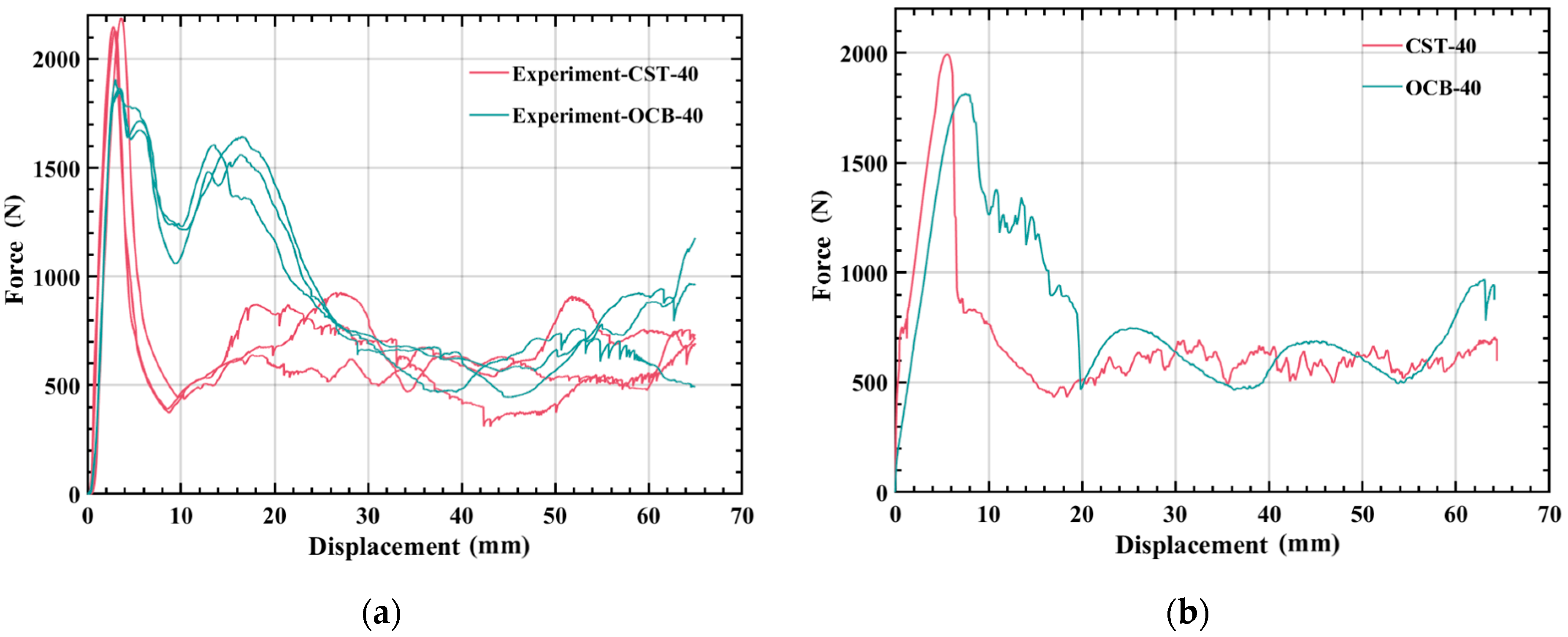
3.1. Experimental and Simulation Analysis
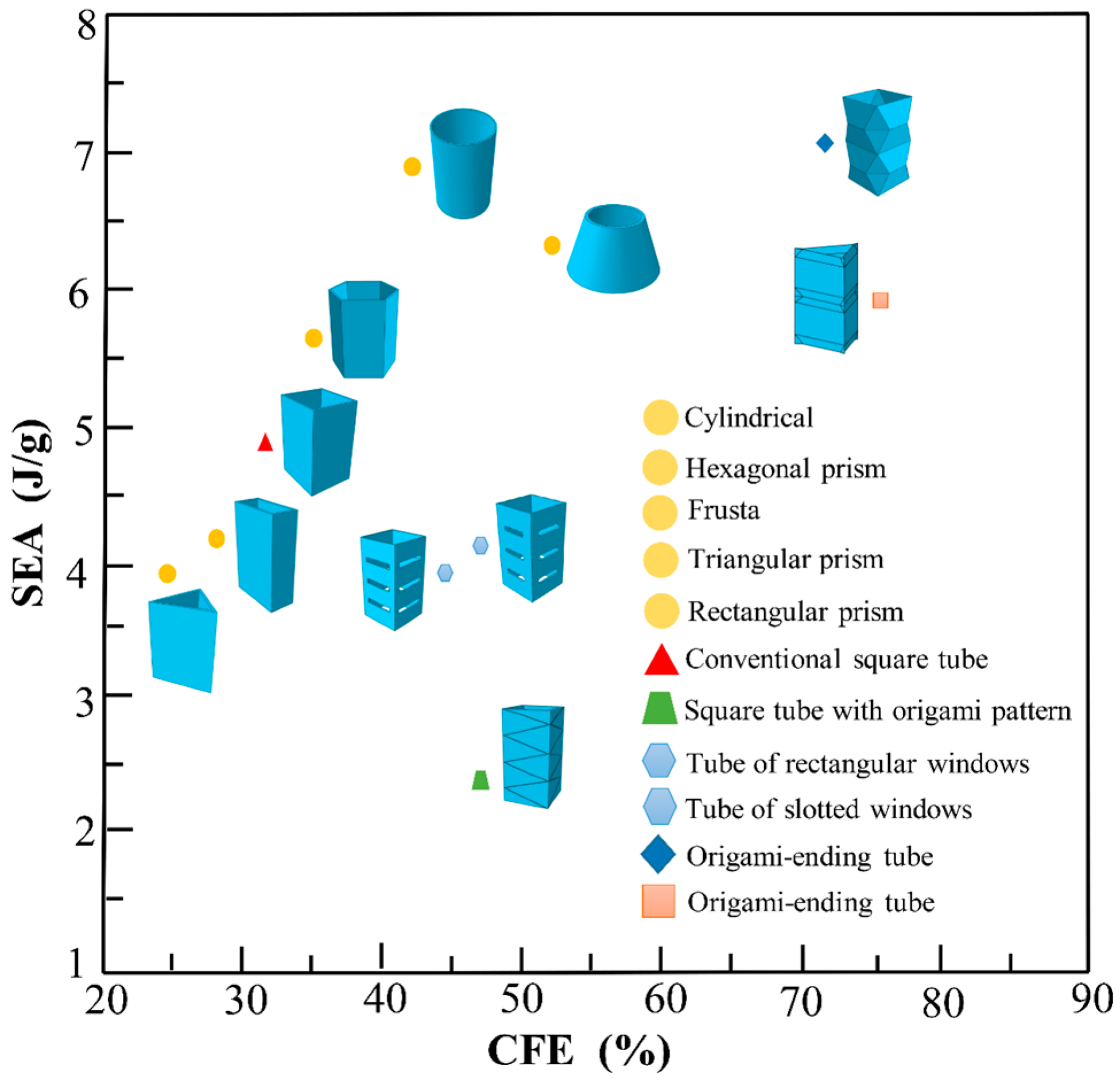
3.2. Comparison between Different Types of Tubes
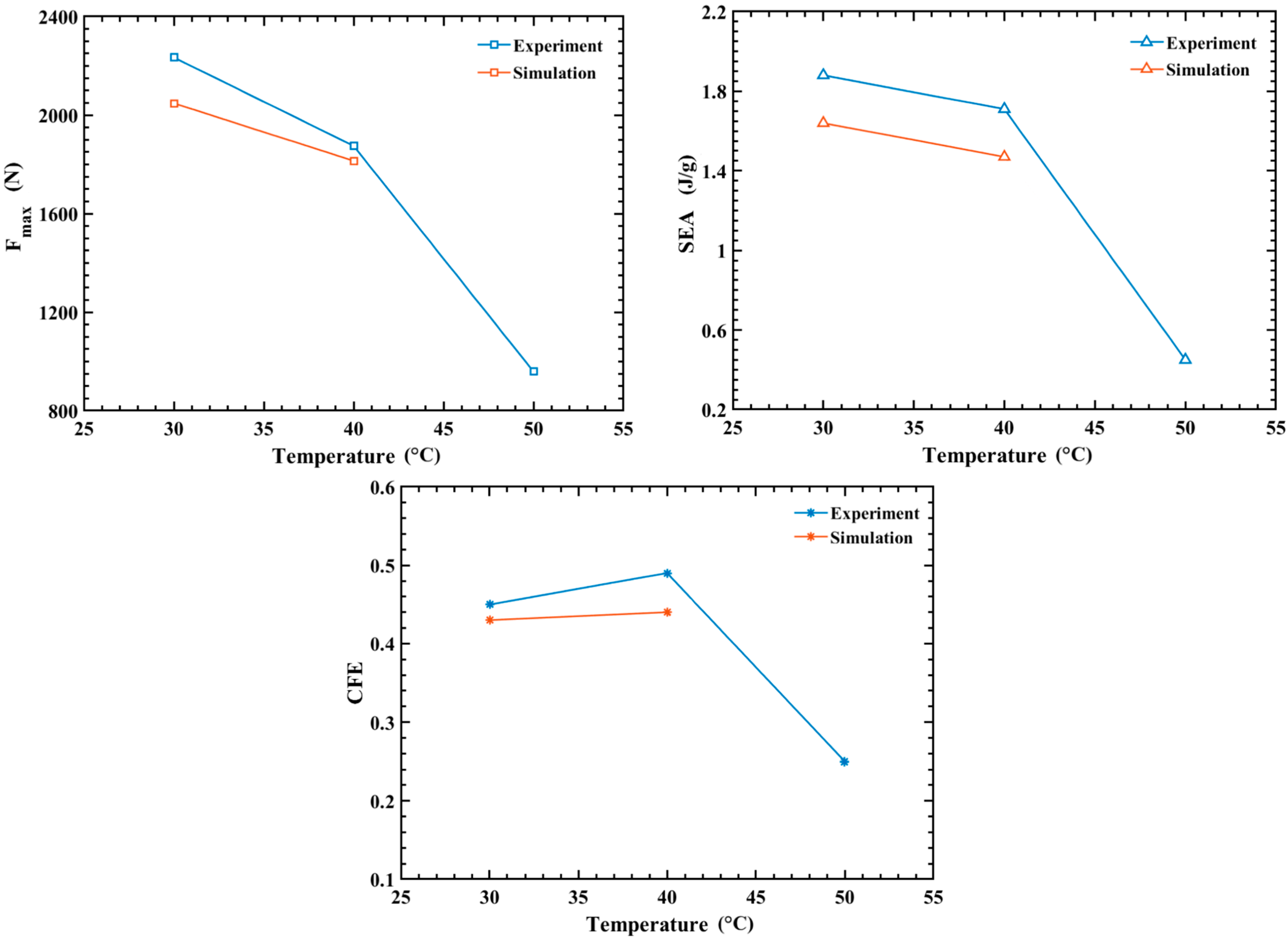
3.3. The Effect of Temperature on OCB
3.4. Theoretical Solution of OCB at 50 °C
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
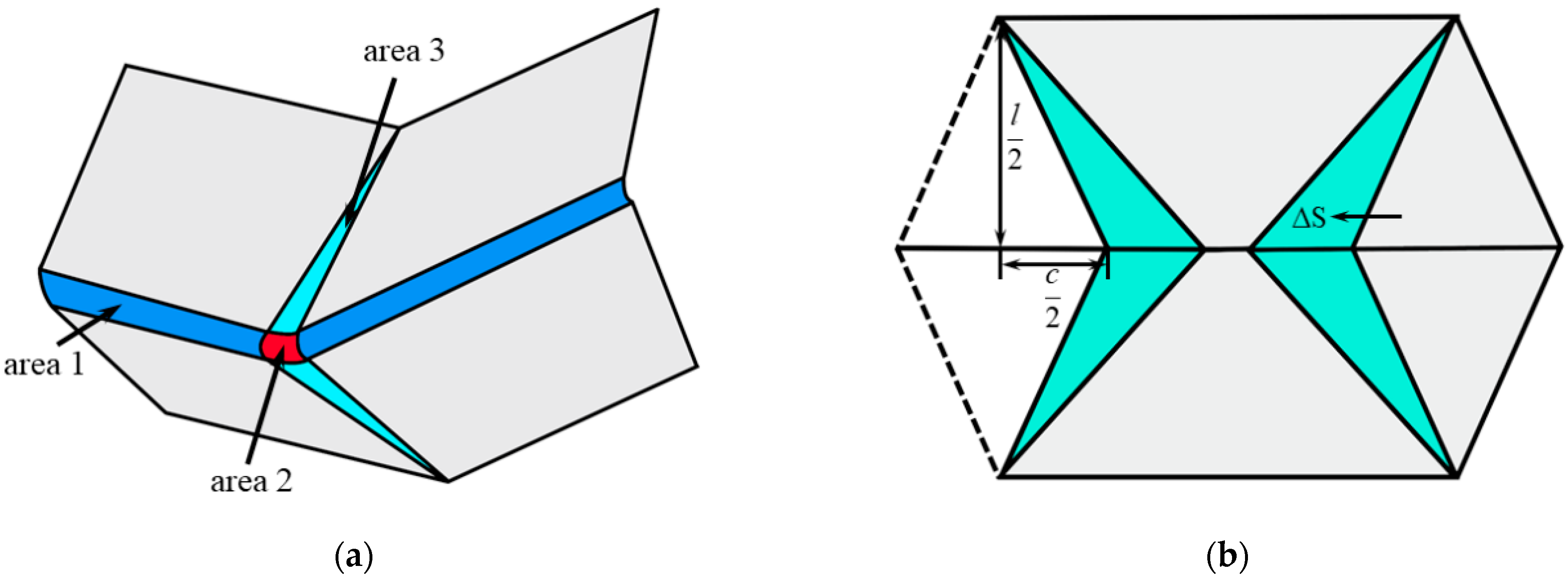
Appendix A. Theoretical Derivation



References
- Jacob, G.C.; Fellers, J.F.; Starbuck, J.M.; Simunovic, S. Crashworthiness of automotive composite material systems. J. Appl. Polym. Sci. 2004, 92, 3218–3255. [Google Scholar] [CrossRef]
- Jacob, G.C.; Starbuck, J.M.; Fellers, J.F.; Simunovic, S.; Boeman, R.G. Crashworthiness of various random chopped carbon fiber reinforced epoxy composite materials and their strain rate dependence. J. Appl. Polym. Sci. 2006, 101, 1477–1486. [Google Scholar] [CrossRef]
- Deng, X.; Liu, W. Experimental and numerical investigation of a novel sandwich sinusoidal lateral corrugated tubular structure under axial compression. Int. J. Mech. Sci. 2019, 151, 274–287. [Google Scholar] [CrossRef]
- Liu, S.; Lv, W.; Chen, Y.; Lu, G. Deployable Prismatic Structures With Rigid Origami Patterns. J. Mech. Robot. 2016, 8, 031002. [Google Scholar] [CrossRef]
- Nia, A.A.; Rahpeima, R.; Chahardoli, S.; Nateghi, I. Evaluation of the effect of inner and outer transverse and longitudinal grooves on energy absorption characteristics of cylindrical thin-walled tubes under quasi-static axial load. Int. J. Crashworth. 2017, 24, 1–12. [Google Scholar]
- Deng, X.; Liu, W.; Lin, Z. Experimental and theoretical study on crashworthiness of star-shaped tubes under axial compression. Thin-Walled Struct. 2018, 130, 321–331. [Google Scholar] [CrossRef]
- Hong, H.; Hu, M.; Dai, L. Dynamic Mechanical Behavior of Hierarchical Resin Honeycomb by 3D Printing. Polymers 2021, 13, 19. [Google Scholar] [CrossRef]
- Niutta, C.B.; Ciardiello, R.; Tridello, A. Experimental and Numerical Investigation of a Lattice Structure for Energy Absorption: Application to the Design of an Automotive Crash Absorber. Polymers 2022, 14, 1116. [Google Scholar] [CrossRef]
- Nojima, T. Modelling of Folding Patterns in Flat Membranes and Cylinders by Origami. JSME. Int. J. C Mech. Syst. 2002, 45, 364–370. [Google Scholar] [CrossRef] [Green Version]
- Nia, A.A.; Hamedani, J.H. Comparative analysis of energy absorption and deformations of thin walled tubes with various section geometries. Thin-Walled Struct. 2010, 48, 946–954. [Google Scholar]
- Ma, J.; Hou, D.; Chen, Y.; You, Z. Quasi-static axial crushing of thin-walled tubes with a kite-shape rigid origami pattern: Numerical simulation. Thin-Walled Struct. 2016, 100, 38–47. [Google Scholar] [CrossRef]
- Albert, P.C.; Ghani, A.R.A.; Othman, M.Z.; Zaidi, A.M.A. Axial Crushing Behavior of Aluminum Square Tube with Origami Pattern. Mod. Appl. Sci. 2016, 10, 90–108. [Google Scholar] [CrossRef]
- Zhou, C.; Ming, S.; Xia, C.; Wang, B.; Bi, X.; Hao, P.; Ren, M. The energy absorption of rectangular and slotted windowed tubes under axial crushing. Int. J. Mech. Sci. 2018, 141, 89–100. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, C. The imperfection-sensitivity of origami crash boxes. Int. J. Mech. Sci. 2017, 121, 58–66. [Google Scholar] [CrossRef]
- Ming, S.; Song, Z.; Li, T.; Du, K.; Zhou, C.; Wang, B. The energy absorption of thin-walled tubes designed by origami approach applied to the ends. Mater. Des. 2020, 192, 108725. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Abramowicz, W. On the Crushing Mechanics of Thin-Walled Structures. J. Appl. Mech. 1983, 50, 727–734. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, D.; Jin, Y.; Wang, M.; You, Z.; Yu, G. Study of collapsed deformation and energy absorption of polymeric origami-based tubes with viscoelasticity. Thin-Walled Struct. 2019, 144, 106246. [Google Scholar] [CrossRef]
- Lin, Y.; Min, J.; Li, Y.; Lin, J. A thin-walled structure with tailored properties for axial crushing. Int. J. Mech. Sci. 2019, 157–158, 119–135. [Google Scholar] [CrossRef]
- Ye, H.; Ma, J.; Zhou, X.; Wang, H.; You, Z. Energy absorption behaviors of pre-folded composite tubes with the full-diamond origami patterns. Compos. Struct. 2019, 221, 110904. [Google Scholar] [CrossRef]
- Sun, G.; Li, S.; Li, G.; Li, Q. On crashing behaviors of aluminium/CFRP tubes subjected to axial and oblique loading: An experimental study. Compos. Part B Eng. 2018, 145, 47–56. [Google Scholar] [CrossRef]
- Hanefi, E.H. Axial resistance and energy absorption of externally reinforced metal tubes. Compos. B 1996, 27, 387–394. [Google Scholar] [CrossRef]
- Chen, W.; Wierzbicki, T. Relative merits of single-cell, multi-cell and foam-filled thin-walled structures in energy absorption. Thin-Walled Struct. 2001, 39, 287–306. [Google Scholar] [CrossRef]
- Ma, J.; You, Z. Energy Absorption of Thin-Walled Square Tubes With a Prefolded Origami Pattern—Part I: Geometry and Numerical Simulation. J. Appl. Mech. 2014, 81, 011003. [Google Scholar] [CrossRef] [Green Version]
- Xiang, X.M.; Lu, G.; You, Z. Energy absorption of origami inspired structures and materials. Thin-Walled Struct. 2020, 157, 107130. [Google Scholar] [CrossRef]
- Zhou, C.; Li, T.; Ming, S.; Song, Z.; Wang, B. Effects of welding on energy absorption of kirigami cruciform under axial crushing. Thin-Walled Struct. 2019, 142, 297–310. [Google Scholar] [CrossRef]
- Zhou, C.; Zhou, Y.; Wang, B. Crashworthiness design for trapezoid origami crash boxes. Thin-Walled Struct. 2017, 117, 257–267. [Google Scholar] [CrossRef]
- Zhou, C.H.; Wang, B.; Luo, H.Z.; Chen, Y.W.; Zeng, Q.H.; Zhu, S.Y. Quasi-Static Axial Compression of Origami Crash Boxes. Int. J. Appl. Mech. 2017, 09, 1750066. [Google Scholar] [CrossRef]
- Harris, J.A.; McShane, G.J. Metallic stacked origami cellular materials: Additive manufacturing, properties, and modelling. Int. J. Solids Struct. 2020, 185–186, 448–466. [Google Scholar] [CrossRef]
- Raquez, J.-M.; Habibi, Y.; Murariu, M.; Dubois, P. Polylactide (PLA)-based nanocomposites. Prog. Polym. Sci. 2013, 38, 1504–1542. [Google Scholar] [CrossRef]
- Notta-Cuvier, D.; Odent, J.; Delille, R.; Murariu, M.; Lauro, F.; Raquez, J.M.; Bennani, B.; Dubois, P. Tailoring polylactide (PLA) properties for automotive applications: Effect of addition of designed additives on main mechanical properties. Polym. Test. 2014, 36, 1–9. [Google Scholar] [CrossRef]
- Spoerk, M.; Arbeiter, F.; Cajner, H.; Sapkota, J.; Holzer, C. Parametric optimization of intra- and inter-layer strengths in parts produced by extrusion-based additive manufacturing of poly(lactic acid). J. Appl. Polym. Sci. 2017, 134, 45401. [Google Scholar] [CrossRef]
- Yao, T.; Ye, J.; Deng, Z.; Zhang, K.; Ma, Y.; Ouyang, H. Tensile failure strength and separation angle of FFF 3D printing PLA material: Experimental and theoretical analyses. Compos. B Eng. 2020, 188, 107894. [Google Scholar] [CrossRef]
- Qu, P.; Sun, X.; Ping, L.; Zhang, D.; Jia, Y. A new numerical model for the analysis on low-velocity impact damage evolution of carbon fiber reinforced resin composites. J. Appl. Polym. Sci. 2017, 134, 44374. [Google Scholar] [CrossRef]
- Verbeek, C.J.R.; Yapa, P.M. Influence of morphology on the dynamic and quasi-static energy absorption of polylactic acid-based lattice structures. J. Appl. Polym. Sci. 2022, 139, 52343. [Google Scholar] [CrossRef]
- Zhou, C.; Jiang, L.; Tian, K.; Bi, X.; Wang, B. Origami Crash Boxes Subjected to Dynamic Oblique Loading. J. Appl. Mech. 2017, 84, 091006. [Google Scholar] [CrossRef]
- Dezaki, M.L.; Ariffin, M.K.A.M. The Effects of Combined Infill Patterns on Mechanical Properties in FFF Process. Polymers 2020, 12, 2792. [Google Scholar] [CrossRef]
- Sallier, L.; Forquin, P. On the use of Hillerborg regularization method to model the softening behaviour of concrete subjected to dynamic tensile loading. Eur. Phys. J. Spec. Top. 2012, 206, 97–105. [Google Scholar] [CrossRef]
- Zhou, X.; Li, J.; Qu, C.; Bu, W.; Liu, Z.; Fan, Y.; Bao, G. Bending behavior of hybrid sandwich composite structures containing 3D printed PLA lattice cores and magnesium alloy face sheets. J. Adhesion. 2021, 98, 1713–1731. [Google Scholar] [CrossRef]
- Zhou, J.; Mu, Y.; Wang, B. A damage-coupled unified viscoplastic constitutive model for prediction of forming limits of 22MnB5 at high temperatures. Int. J. Mech. Sci. 2017, 133, 457–468. [Google Scholar] [CrossRef]
- Lee, S.W.; Pourboghrat, F. Finite element simulation of the punchless piercing process with Lemaitre damage model. Int. J. Mech. Sci. 2005, 47, 1756–1768. [Google Scholar] [CrossRef]
- Yu, H.; Guo, Y.; Zhang, K.; Lai, X. Constitutive model on the description of plastic behavior of DP600 steel at strain rate from 10−4 to 103 s−1. Comput. Mater. Sci. 2009, 46, 36–41. [Google Scholar] [CrossRef]
- Yu, H.; Guo, Y.; Lai, X. Rate-dependent behavior and constitutive model of DP600 steel at strain rate from 10−4 to 103 s−1. Mater. Des. 2009, 30, 2501–2505. [Google Scholar] [CrossRef]
- Li, Y.; Wierzbicki, T. Prediction of plane strain fracture of AHSS sheets with post-initiation softening. Int. J. Solids. Struct. 2010, 47, 2316–2327. [Google Scholar] [CrossRef] [Green Version]
- Khelifa, M.; Celzard, A. Numerical analysis of flexural strengthening of timber beams reinforced with CFRP strips. Compos. Struct. 2014, 111, 393–400. [Google Scholar] [CrossRef]
- Gao, W.; Chen, X.; Hu, C.; Zhou, C.; Cui, S. New damage evolution model of rock material. Appl. Math. Model. 2020, 86, 207–224. [Google Scholar] [CrossRef]
- François, H.; Gilbert, H.; Damien, H.; Mikaël, G.; Thomas, B. CDM approach applied to fatigue crack propagation on airframe structural alloys. Proced. Eng. 2010, 2, 1403–1412. [Google Scholar] [CrossRef] [Green Version]
- Lv, L.; Bohong, G. Transverse Impact Damage and Energy Absorption of Three-Dimensional Orthogonal Hybrid Woven Composite: Experimental and FEM Simulation. J. Compos. Mater. 2008, 42, 1763–1786. [Google Scholar] [CrossRef]
- Platek, P.; Rajkowski, K.; Cieplak, K.; Sarzynski, M.; Malachowski, J.; Wozniak, R.; Janiszewski, J. Deformation Process of 3D Printed Structures Made from Flexible Material with Different Values of Relative Density. Polymers 2020, 12, 2120. [Google Scholar] [CrossRef]
- Yu, T.X.; Xiang, Y.F.; Wang, M.; Yang, L.M. Key Performance Indicators of Tubes Used as Energy Absorbers. Key. Eng. Mater. 2014, 626, 155–161. [Google Scholar] [CrossRef]
- Xiang, Y.; Yu, T.; Yang, L. Comparative analysis of energy absorption capacity of polygonal tubes, multi-cell tubes and honeycombs by utilizing key performance indicators. Mater. Des. 2016, 89, 689–696. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, L.; Yang, P.; Fang, J.; Li, W. Energy absorption of additively manufactured functionally bi-graded thickness honeycombs subjected to axial loads. Thin-Walled Struct. 2021, 164, 107810. [Google Scholar] [CrossRef]
- Meng, Q.; Al-Hassani, S.T.S.; Soden, P.D. Axial crushing of square tubes. Int. J. Mech. Sci. 1983, 25, 747–773. [Google Scholar] [CrossRef]
- Singace, A.A.; El-Sobky, H. Behaviour of axially crushed corrugated tubes. Int. J. Mech. Sci. 1997, 39, 249–268. [Google Scholar] [CrossRef]
- Santosa, S.P.; Wierzbicki, T.; Hanssen, A.G.; Langseth, M. Experimental and numerical studies of foam-filled sections. Int. J. Impact. Eng. 2000, 24, 509–534. [Google Scholar] [CrossRef]







| Temperature | Density | Elastic Modulus (MPa) | Poisson’s Ratio | |||
|---|---|---|---|---|---|---|
| 30 °C | 1250 kg/m3 | 2341 | 0.36 | 0.19 | −8.21 | 1.38 |
| 40 °C | 1250 kg/m3 | 1650 | 0.36 | 0.26 | −7.65 | 0.68 |
| Temperature | Specimen | SEA (J/g) | (%) | (%) | (%) | |||
|---|---|---|---|---|---|---|---|---|
| 40 °C | Experiment-CST-1 | 2131.63 | 43.48 | 668.92 | 1.26 | - | - | - |
| Experiment-CST-2 | 2188.70 | 40.46 | 622.46 | 1.17 | - | - | - | |
| Experiment-CST-3 | 2148.93 | 44.80 | 689.23 | 1.29 | - | - | - | |
| CST-EA | 2156.42 | 42.91 | 660.15 | 1.24 | - | - | - | |
| CST-40 | 1992.64 | 43.79 | 673.69 | 1.27 | 7.59 | 2.01 | 2.36 |
| Temperature | Specimen | b (mm) | c (mm) | H (mm) | (N) | (N) | SEA (J/g) | (%) | (%) |
|---|---|---|---|---|---|---|---|---|---|
| 40 °C | CST-EA | 60.00 | - | 120.00 | 2156.42 | 660.15 | 1.24 | - | - |
| OCB-EA | 60.00 | 30.00 | 120.00 | 1874.91 | 915.88 | 1.71 | 15.01 | 27.49 | |
| CST-40 | 60.00 | - | 120.00 | 1992.64 | 673.69 | 1.27 | - | - | |
| OCB-40 | 60.00 | 30.00 | 120.00 | 1814.40 | 789.85 | 1.47 | 8.94 | 13.61 |
| Temperature | Specimen | SEA (J/g) | CFE | |||
|---|---|---|---|---|---|---|
| 30 °C | Experiment-1 | 2296.98 | 71.58 | 1101.20 | 2.05 | 0.48 |
| Experiment-2 | 2223.29 | 63.17 | 971.87 | 1.81 | 0.44 | |
| Experiment-3 | 2182.16 | 61.82 | 951.14 | 1.77 | 0.44 | |
| EA | 2234.14 | 65.52 | 1008.07 | 1.88 | 0.45 | |
| 40 °C | Experiment-1 | 1864.73 | 60.15 | 925.41 | 1.73 | 0.50 |
| Experiment-2 | 1906.43 | 57.19 | 879.77 | 1.64 | 0.46 | |
| Experiment-3 | 1853.57 | 61.30 | 942.46 | 1.76 | 0.51 | |
| EA | 1874.91 | 59.53 | 915.88 | 1.71 | 0.49 |
| Temperature | Specimen | SEA (J/g) | CFE | |||
|---|---|---|---|---|---|---|
| 30 °C | OCB-EA-30 | 2234.14 | 65.52 | 1008.07 | 1.88 | 0.45 |
| 40 °C | OCB-EA-40 | 1874.91 | 59.53 | 915.88 | 1.71 | 0.49 |
| 50 °C | OCB-EA-50 | 958.80 | 15.79 | 242.92 | 0.45 | 0.25 |
| Specimen | SEA (J/g) | CFE | (%) | (%) | (%) | |||
|---|---|---|---|---|---|---|---|---|
| Experiment-EA-30 | 2234.14 | 65.52 | 1008.07 | 1.88 | 0.45 | - | - | - |
| Experiment-EA-40 | 1874.91 | 59.53 | 915.88 | 1.71 | 0.49 | 16.08 | 9.04 | −8.89 |
| OCB-30 | 2047.99 | 57.12 | 878.77 | 1.64 | 0.43 | |||
| OCB-40 | 1814.40 | 51.34 | 789.85 | 1.47 | 0.44 | 11.41 | 10.37 | −2.33 |
| Temperature | Specimen | SEA (J/g) | CFE | (%) | (%) | |||
|---|---|---|---|---|---|---|---|---|
| 50 °C | Experiment-1 | 974.42 | 15.59 | 239.85 | 0.45 | 0.25 | - | - |
| Experiment-2 | 950.02 | 14.86 | 228.62 | 0.43 | 0.24 | - | - | |
| Experiment-3 | 951.97 | 16.91 | 260.15 | 0.49 | 0.27 | - | - | |
| EA | 958.80 | 15.79 | 242.92 | 0.45 | 0.25 | - | - | |
| OCB-TS-50 | - | 18.52 | 284.92 | 0.53 | - | 14.74 | 15.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Guo, C.; Zuo, X.; Zhao, J.; Peng, Y.; Wang, Y. Experimental and Numerical Investigation of 3D Printing PLA Origami Tubes under Quasi-Static Uniaxial Compression. Polymers 2022, 14, 4135. https://doi.org/10.3390/polym14194135
Chen W, Guo C, Zuo X, Zhao J, Peng Y, Wang Y. Experimental and Numerical Investigation of 3D Printing PLA Origami Tubes under Quasi-Static Uniaxial Compression. Polymers. 2022; 14(19):4135. https://doi.org/10.3390/polym14194135
Chicago/Turabian StyleChen, Weidong, Chengjie Guo, Xiubin Zuo, Jian Zhao, Yang Peng, and Yixiao Wang. 2022. "Experimental and Numerical Investigation of 3D Printing PLA Origami Tubes under Quasi-Static Uniaxial Compression" Polymers 14, no. 19: 4135. https://doi.org/10.3390/polym14194135
APA StyleChen, W., Guo, C., Zuo, X., Zhao, J., Peng, Y., & Wang, Y. (2022). Experimental and Numerical Investigation of 3D Printing PLA Origami Tubes under Quasi-Static Uniaxial Compression. Polymers, 14(19), 4135. https://doi.org/10.3390/polym14194135






