A Service Life Prediction Method of Stranded Carbon Fiber Composite Core Conductor for Overhead Transmission Lines
Abstract
:1. Introduction
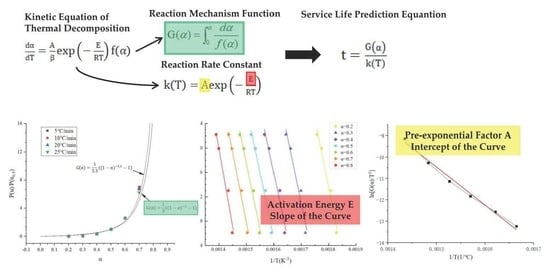
2. Pyrolysis Kinetics Model
3. Pyrolysis Kinetic State Parameters
3.1. TGA Test
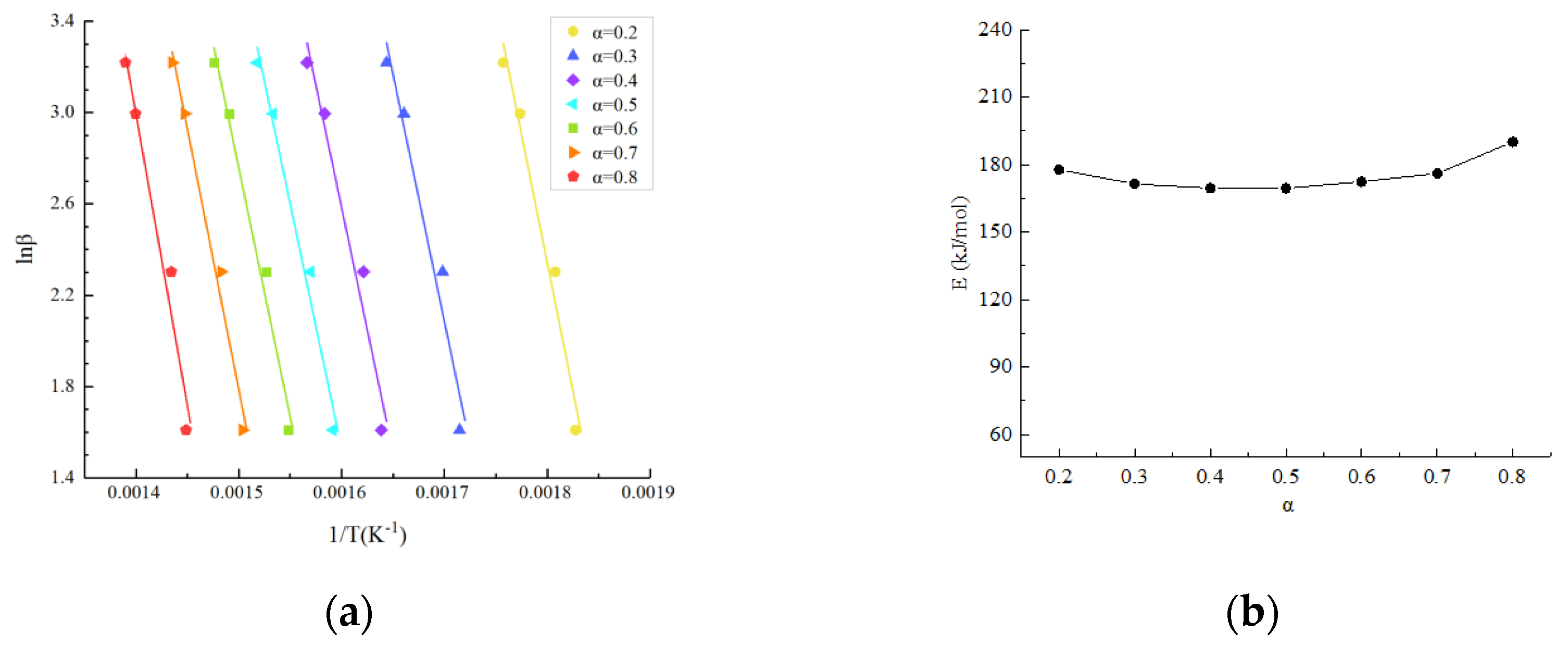
3.2. Activation Energy
3.3. Reaction Mechanism Function
3.4. Pre-Exponential Factor
3.5. Service Life Prediction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, X.; Wang, Q.; Zhou, Z.; Li, R.; Liao, Y.; He, J.; Gong, B.; Zheng, D.; Chen, W.; Fan, L.; et al. Technical and Economic Analysis of Aluminum Conductor with Multi-stranded Composite Core and Its Application. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Asia, Chengdu, China, 21–24 May 2019. [Google Scholar]
- Wu, X.; Chuang, C.; Chen, C.; Chen, Z.; Xing, B.; Huang, W.; Wang, Q.M. Research of characteristic and construction technology of hinged type carbon fiber core Line. China Electr. Power 2014, 4, 58–61. [Google Scholar]
- Middleton, J.; Burks, B.; Wells, T.; Setters, A.M.; Jasiuk, I.; Kumosa, M. The effect of ozone and high temperature on polymer degradation in polymer core composite conductors. Polym. Degrad. Stab. 2013, 98, 2282–2290. [Google Scholar] [CrossRef]
- Middleton, J.; Hoffman, J.; Burks, B.; Predecki, P.; Kumosa, M. Aging of a polymer core composite conductor: Mechanical properties and residual stresses. Compos. Part A Appl. Sci. Manuf. 2015, 69, 159–167. [Google Scholar] [CrossRef]
- Alawar, A.; Bosze, E.; Nutt, S. A Composite Core Conductor for Low Sag at High Temperatures. IEEE Trans. Power Deliv. 2005, 20, 2193–2199. [Google Scholar] [CrossRef]
- Rashmi; Shivashankar, G.; Poornima. Overview of different overhead transmission line conductors. Mater. Today Proc. 2017, 4, 11318–11324. [Google Scholar] [CrossRef]
- Bosze, E.; Alawar, A.; Bertschger, O.; Tsai, Y.-I.; Nutt, S. High-temperature strength and storage modulus in unidirectional hybrid composites. Compos. Sci. Technol. 2006, 66, 1963–1969. [Google Scholar] [CrossRef]
- Ju, Y.; Che, L.; Meng, Y. Comparative research on aluminum conductor composite core and traditional conductor. East China Electr. Power 2011, 39, 1191–1194. [Google Scholar]
- Minzheng, M.; Chunping, P. Application research on aluminium conductor multi-Strand carbon-fiber core cable in new power transmission lines. South. Energy Constr. 2017, 4, 82–87. [Google Scholar]
- Burks, B.; Armentrout, D.; Baldwin, M.; Buckley, J.; Kumosa, M. Hybrid composite rods subjected to excessive bending loads. Compos. Sci. Technol. 2009, 69, 2625–2632. [Google Scholar] [CrossRef]
- Kavanagh, T.; Armstrong, O. An Evaluation of High Temperature Low Sag conductor for the 220 kV Transmission Network in Ireland. In Proceedings of the 45th International Universities Power Engineering Conference (UPEC2010), Cardiff, Wales, UK, 31 August–3 September 2010. [Google Scholar]
- IEC 60826-2017; Overhead Transmission Lines-Design Criteria. International Electrotechnical Commission: Geneva, Switzerland, 2017.
- GB 50545-2010; Code for Design of 110 kV~750 kV Overhead Transmission line. Ministry of Housing and Urban Rural Integration of the People’s Republic of China: Beijing, China, 2010.
- Xin, L.; Peng, Z.; Li, S.; Jian, L.; Dai, P.; Zhu, J. Study on calculation method of carbon emission in utilization of ACCC conductor in new or modified power lines. In Proceedings of the 2016 China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016. [Google Scholar]
- Cunliffe, A.M.; Jones, N.; Williams, P.T. Recycling of fibre-reinforced polymeric waste by pyrolysis: Thermo-gravimetric and bench-scale investigations. J. Anal. Appl. Pyrolysis 2003, 70, 315–338. [Google Scholar] [CrossRef]
- Régnier, N.; Fontaine, S. Determination of the Thermal Degradation Kinetic Parameters of Carbon Fibre Reinforced Epoxy Using TG. J. Therm. Anal. 2001, 64, 789–799. [Google Scholar] [CrossRef]
- Li, R.; Liao, Y.; Gong, B.; Shen, C.; He, J.; Wang, Q.; Qiu, Z.; Ni, W. Effect of Alkali on Aging Properties of Carbon Fiber Composite Core. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020. [Google Scholar]
- Kotikalapudi, S.T.; Akula, R.; Singh, R.P. Degradation mechanisms in carbon fiber–epoxy laminates subjected to constant low-density direct current. Compos. Part B Eng. 2022, 233, 109516. [Google Scholar] [CrossRef]
- Woo, E.M.; Chen, J.S.; Carter, C.S. Mechanisms of degradation of polymer composites by galvanic reactions between metals and carbon fiber. Polym. Compos. 1993, 14, 395–401. [Google Scholar] [CrossRef]
- Meng, X.; Mei, H.; Zhu, B.; Yin, F.; Wang, L. Influence of pollution on surface streamer discharge. Electr. Power Syst. Res. 2022, 212, 108638. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, L.; Liao, R.; Liu, Y.; Wang, X.; Wang, T.; Fu, J. Process Improvement to Restrain Emergency Heating Defect of Composite Insulator. IEEE Trans. Dielectr. Electr. Insul. 2022, 29, 446–453. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, Y.; Chen, R.; Zhang, S.; Liao, R.; Yang, L.; Wang, T. Method for Predicting the Water Absorption of External Insulating Silicone Rubber. IEEE Trans. Dielectr. Electr. Insul. 2022, 29, 1242–1250. [Google Scholar] [CrossRef]
- Wu, X.; Sun, J.; Wang, J.; Jiang, Y.; Li, J. Investigation on galvanic corrosion behaviors of CFRPs and aluminum alloys systems for automotive applications. Mater. Corros. 2018, 70, 1036–1043. [Google Scholar] [CrossRef]
- Ofoegbu, S.U.; Ferreira, M.G.; Zheludkevich, M.L. Galvanically Stimulated Degradation of Carbon-Fiber Reinforced Polymer Composites: A Critical Review. Materials 2019, 12, 651. [Google Scholar] [CrossRef] [Green Version]
- Santos, T.F.D.A.; Vasconcelos, G.; de Souza, W.; Costa, M.; Botelho, E. Suitability of carbon fiber-reinforced polymers as power cable cores: Galvanic corrosion and thermal stability evaluation. Mater. Des. 2014, 65, 780–788. [Google Scholar] [CrossRef]
- Kondo, Y. High corrosion resistance of ACFR conductor. In Proceedings of the CIGRE-IEC 2019 Conference on EHV and UHV (AC & DC), Hakodate, Japan, 23–26 April 2019. [Google Scholar]
- Chi, Q. A Study of Natural Storing and Accelerated Hydrothermal Aging of S2/TDE85 Composites. Fiber Compos. 2002, 3, 32–34. [Google Scholar]
- Mao, N.; Chen, Z.; Bian, R.; Chen, K.; Wang, Z.; Zhang, Y. Properties of Fiber Reinforced Resin Matrix Composite Cores Simulating Wet and Hot Aging. Eng. Plast. Appl. 2021, 49, 114–119. [Google Scholar]
- Lan, F.; Chen, X.; Yang, Q.; Yang, C. Experimental Study on the Creep Performance of Carbon Fiber Reinforced Composite Core Used in Transmission Lines. Synth. Mater. Aging Appl. 2015, 44, 5–10. [Google Scholar]
- Dakin, T.W. Electrical Insulation Deterioration Treated as a Chemical Rate Phenomenon. Cond. Affect. Success Main Line Electrif. 1948, 67, 113–122. [Google Scholar] [CrossRef]
- Liu, G.; Liu, S.; Jin, S. Comprehensive evaluation of remaining life of 110kV XLPE insulated cable based on physical, chemical and electrical properties. Trans. China Electrotech. Soc. 2016, 31, 72–79, 107. [Google Scholar]
- Ren, P.; Li, Q.; Peng, P.; Zhang, W.; Cong, H.; Jin, H.; Li, R. Residual Lifetime Expectancy Prediction of the GIS Basin-type Insulators Based on Thermal Dynamics Analysis. Proc. CSEE 2019, 39, 6774–6782. [Google Scholar]
- Dixon, R.R. Thermal aging predictions from an Arrhenius plot with only one data point. IEEE Trans. Electr. Insul. 1980, 4, 33–37. [Google Scholar]
- Wise, J.; Gillen, K.; Clough, R. An ultrasensitive technique for testing the Arrhenius extrapolation assumption for thermally aged elastomers. Polym. Degrad. Stab. 1995, 49, 403–418. [Google Scholar] [CrossRef]
- Barral, L.; Díez, F.; García-Garabal, S.; López, J.; Montero, B.; Montes, R.; Ramírez, C.; Rico, M. Thermodegradation kinetics of a hybrid inorganic–organic epoxy system. Eur. Polym. J. 2005, 41, 1662–1666. [Google Scholar] [CrossRef]
- Li, S.; Jiang, Z.; Yuan, K.; Yu, S.; Chow, W.K. Studies on the thermal behavior of polyurethanes. Polym. Plast. Technol. Eng. 2006, 45, 95–108. [Google Scholar]
- ISO 11358-2:2021; Plastics—Thermogravimetry (TG) of Polymers—Part 2: Determination of Activation Energy. International Organization for Standardization: Geneva, Switzerland, 2021.
- Fu, H. Carbon Fiber and Its Application Technology; Chemical Industry Press: Beijing, China, 2004. [Google Scholar]
- Ozawa, T. A New Method of Analyzing Thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction Kinetics in Differential Thermal Analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Tanaka, H.; Koga, N. Kinetics of the thermal dehydration of potassium copper(II) chloride dihydrate. Appl. Mech. Mater. 2012, 170–173, 1634–1637. [Google Scholar] [CrossRef]
- Tang, W.; Liu, Y.; Xi, Y.; Wang, C. Kinetic studies of the calcination of ammonium metavanadate by thermal methods. Ind. Eng. Chem. Res. 2004, 43, 2054–2059. [Google Scholar]
- Coats, A.W.; Redfern, J.P. Kinetic Parameters from Thermogravimetric Data. Nature 1964, 201, 68–69. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, G.; Ren, P.; Wang, J. Thermodegradation kinetics of epoxy/DDS/POSS system. Polym. Compos. 2010, 28, 755–761. [Google Scholar] [CrossRef]

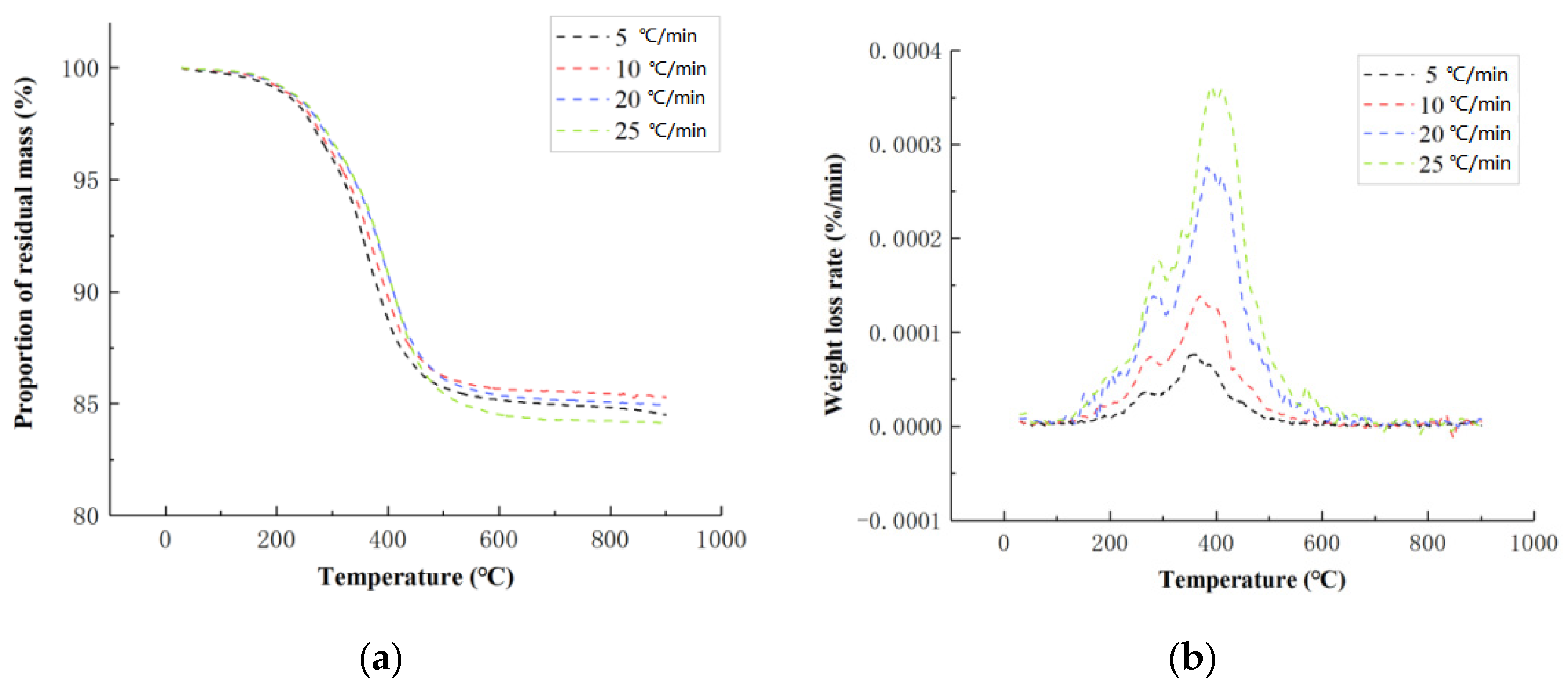
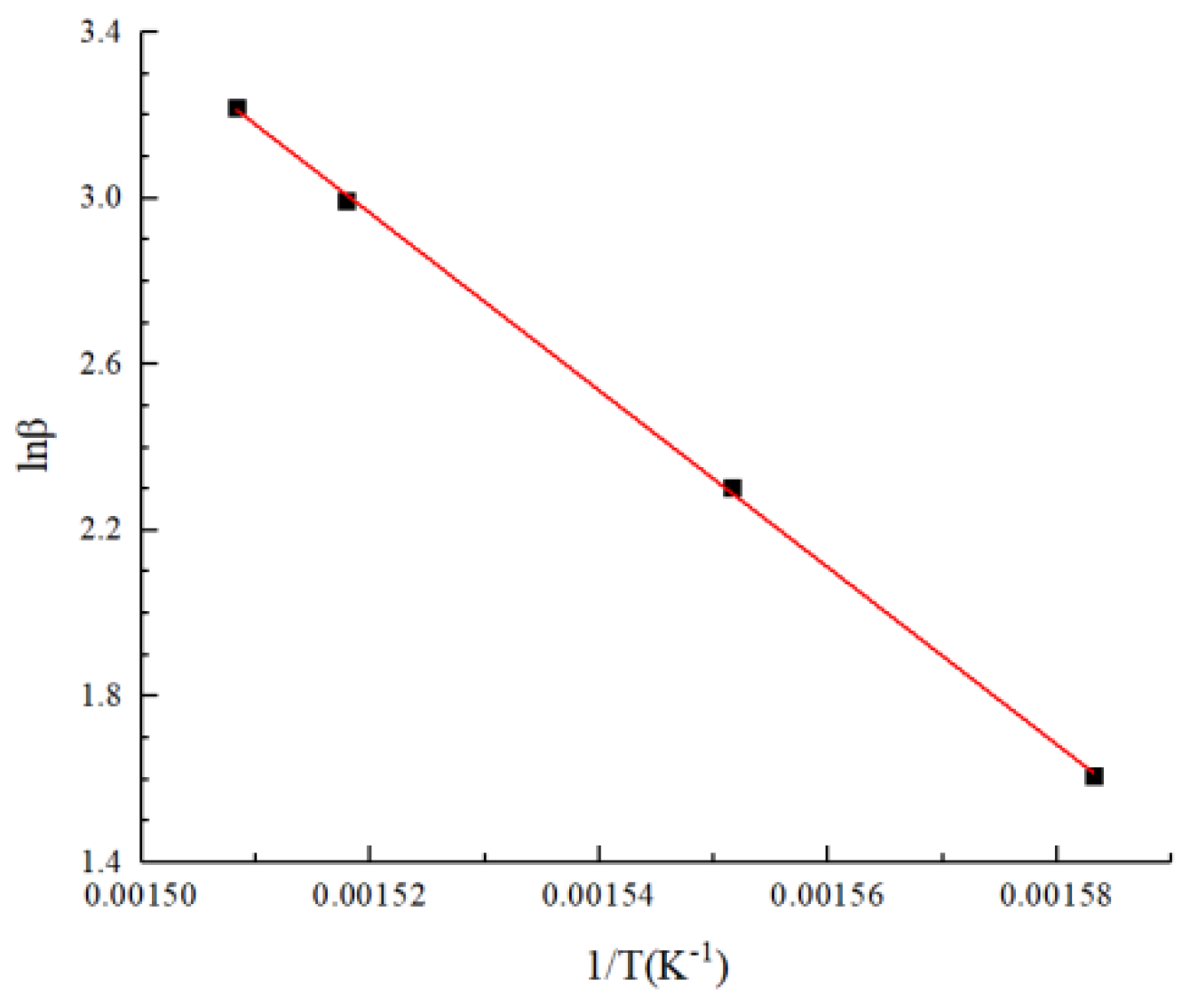
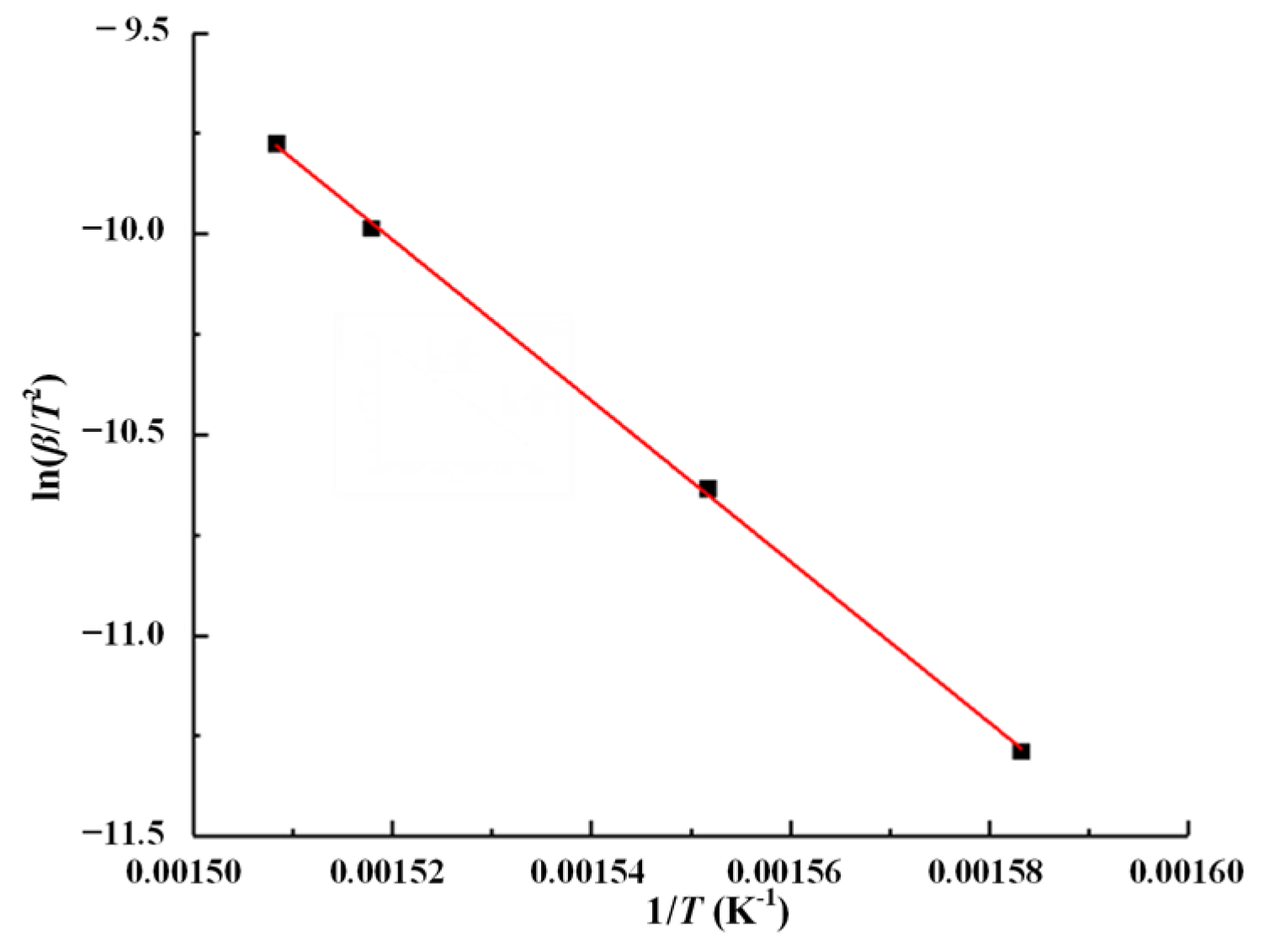
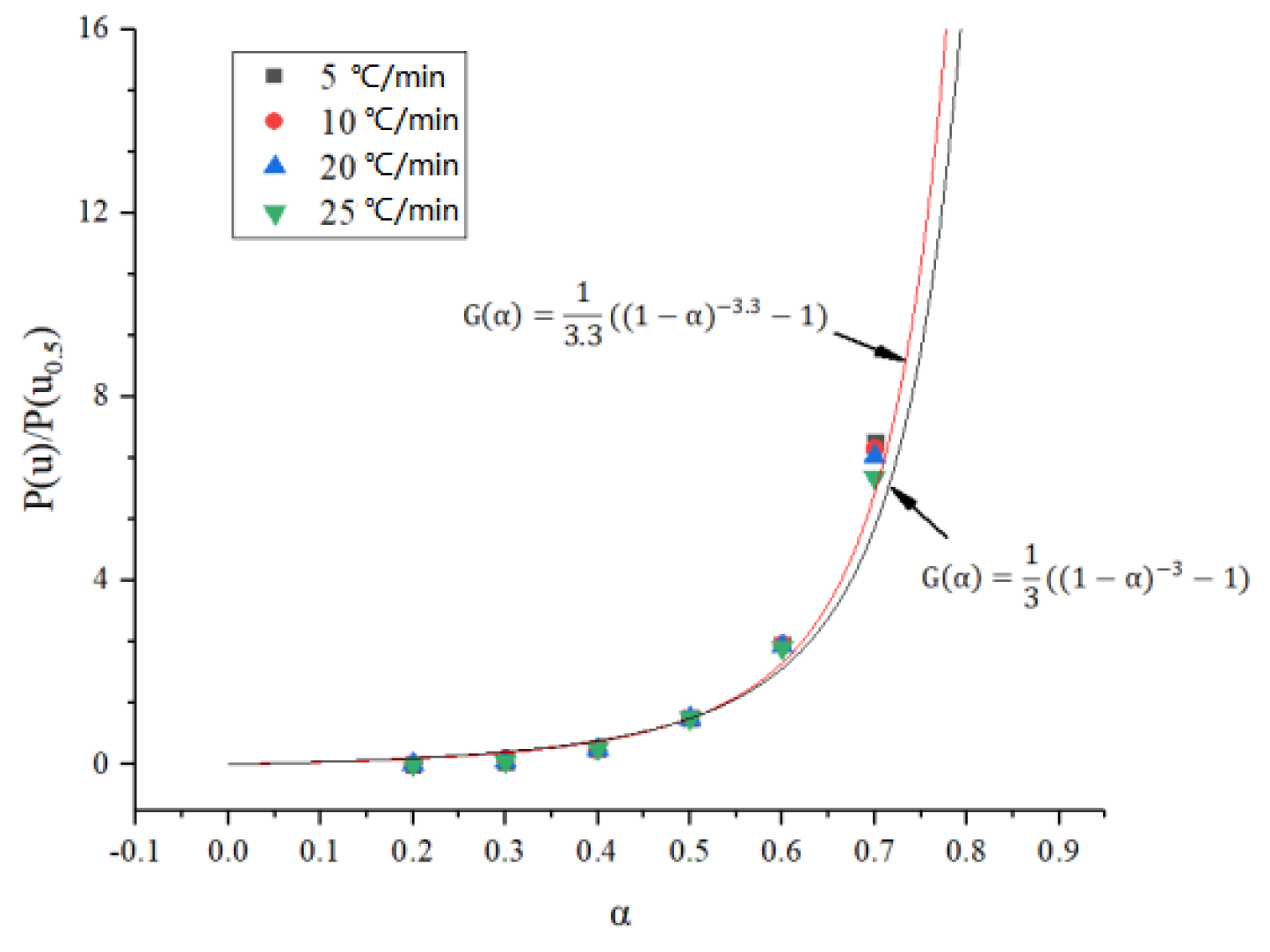
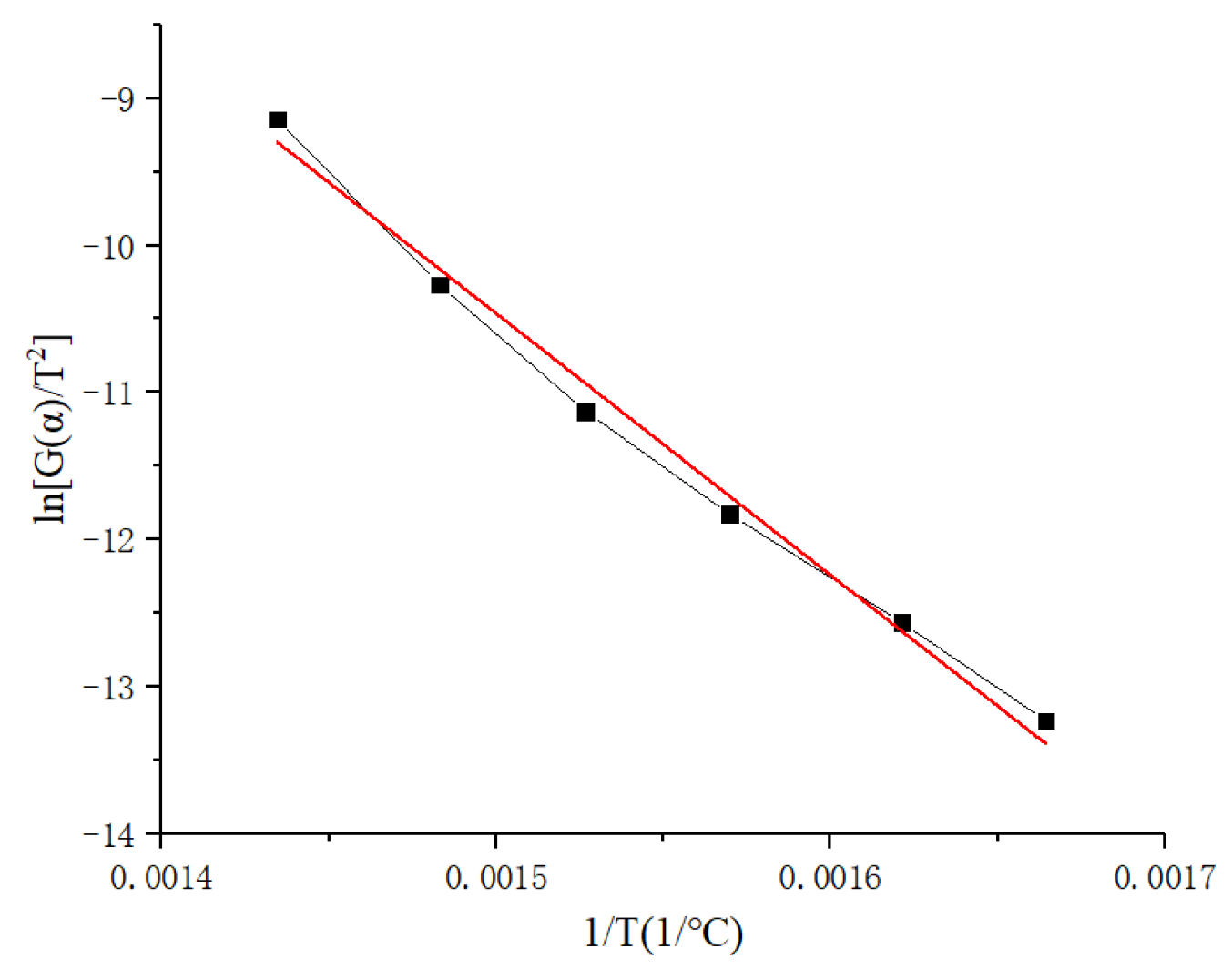
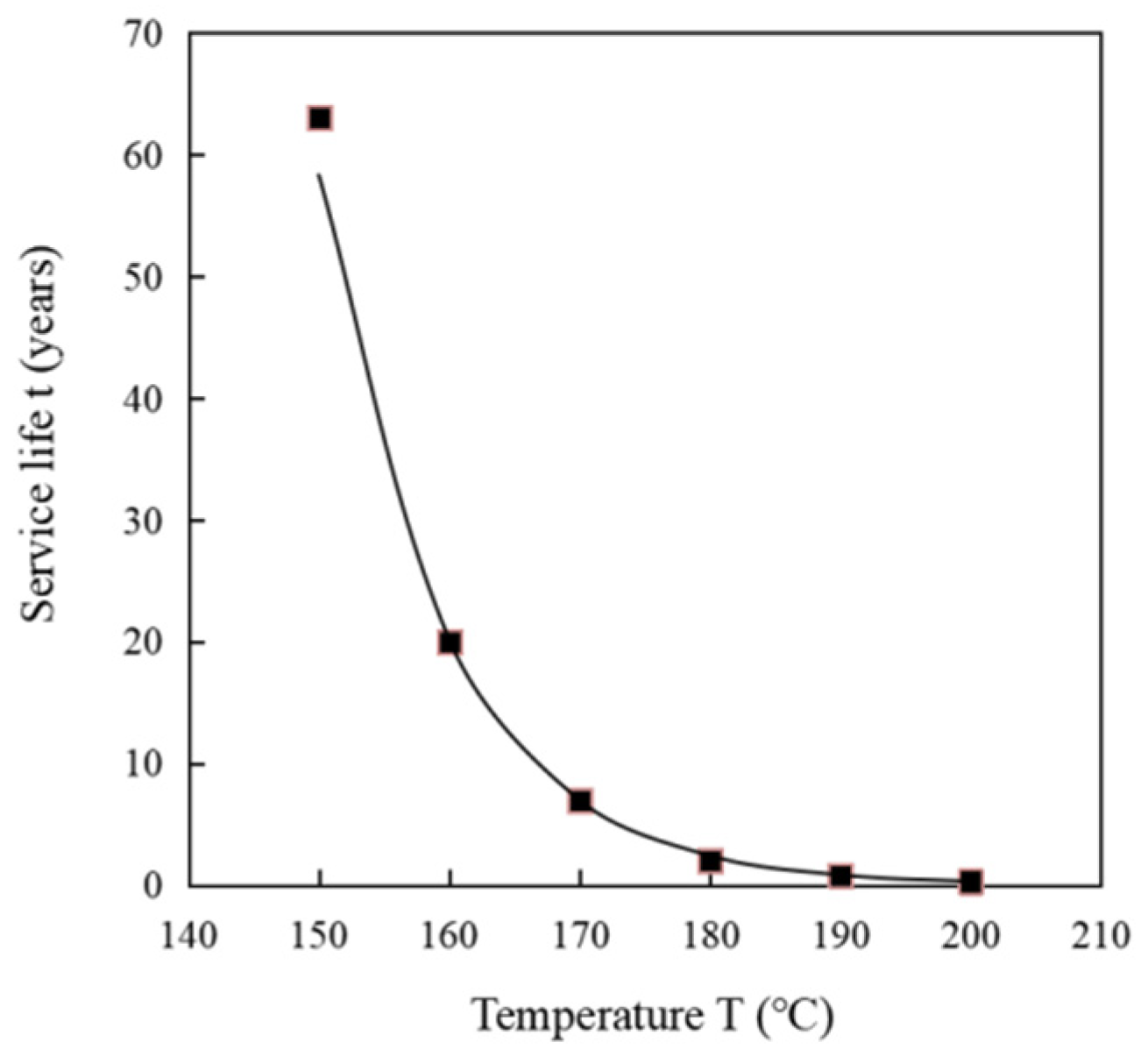
| Heating Rate β (°C/min) | Peak Temperature Tpi (°C) | Peak Temperature Tpi (K) |
|---|---|---|
| 5 | 359.500 | 631.650 |
| 10 | 372.333 | 644.483 |
| 20 | 386.667 | 658.817 |
| 25 | 390.833 | 662.983 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.; Li, R.; Shen, C.; Gong, B.; Yin, F.; Wang, L. A Service Life Prediction Method of Stranded Carbon Fiber Composite Core Conductor for Overhead Transmission Lines. Polymers 2022, 14, 4431. https://doi.org/10.3390/polym14204431
Liao Y, Li R, Shen C, Gong B, Yin F, Wang L. A Service Life Prediction Method of Stranded Carbon Fiber Composite Core Conductor for Overhead Transmission Lines. Polymers. 2022; 14(20):4431. https://doi.org/10.3390/polym14204431
Chicago/Turabian StyleLiao, Yongli, Ruihai Li, Chuying Shen, Bo Gong, Fanghui Yin, and Liming Wang. 2022. "A Service Life Prediction Method of Stranded Carbon Fiber Composite Core Conductor for Overhead Transmission Lines" Polymers 14, no. 20: 4431. https://doi.org/10.3390/polym14204431
APA StyleLiao, Y., Li, R., Shen, C., Gong, B., Yin, F., & Wang, L. (2022). A Service Life Prediction Method of Stranded Carbon Fiber Composite Core Conductor for Overhead Transmission Lines. Polymers, 14(20), 4431. https://doi.org/10.3390/polym14204431