Locating Method for Electrical Tree Degradation in XLPE Cable Insulation Based on Broadband Impedance Spectrum
Abstract
:1. Introduction
2. Experimental Setup
2.1. Cable Parameters
2.2. Electrical Tree Experiment and Capacitance Measurement
2.3. BIS Measurement
3. Transmission Line Model and Improved Location Algorithm
3.1. Transmission Line Model
3.2. Improved Location Algorithm
3.3. Simulation of Location Algorithm
4. Results and Discussion
4.1. Electrical Trees
4.2. Capacitance Results
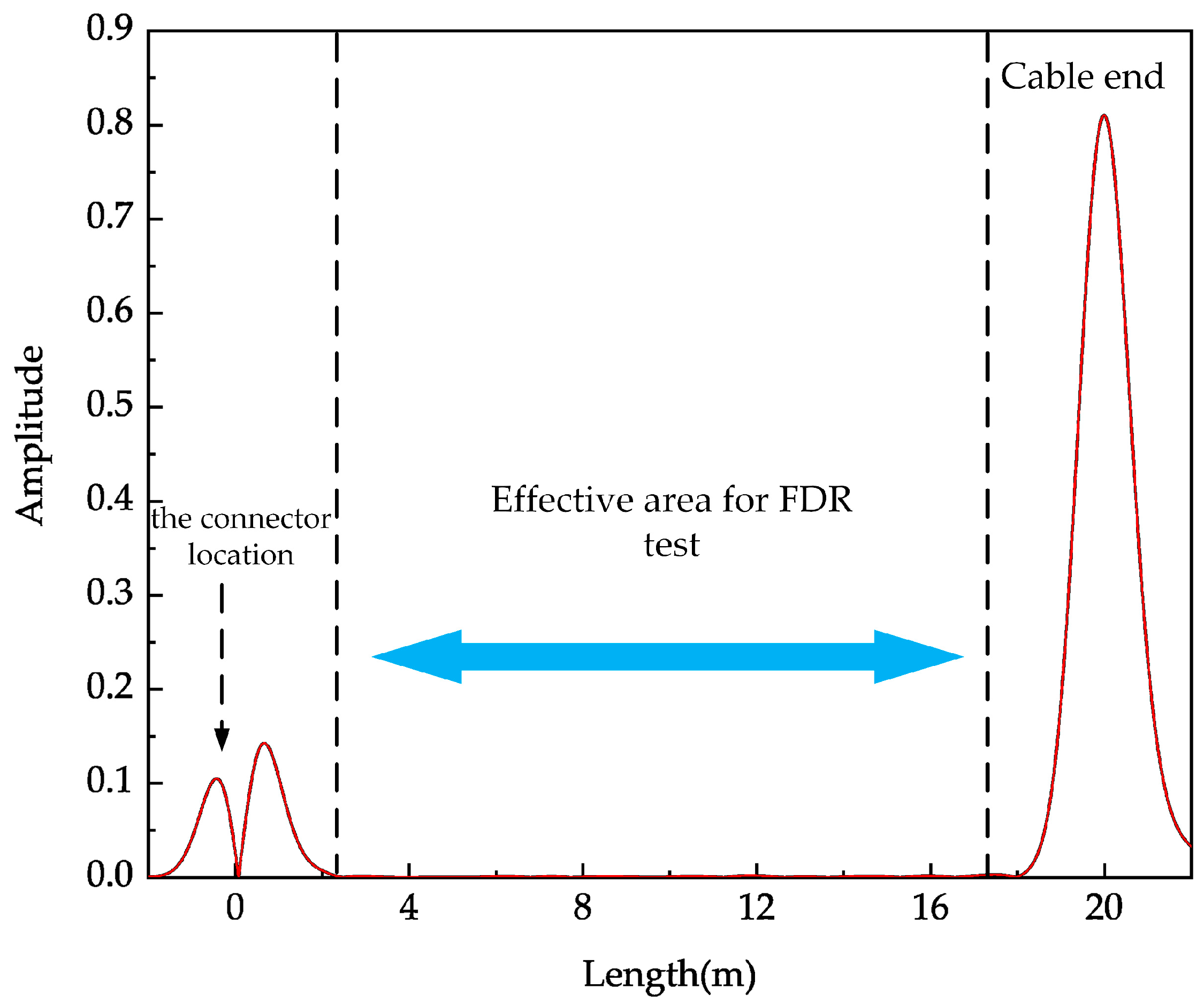
4.3. Location Results
4.4. Analysis of Location Error
5. Conclusions
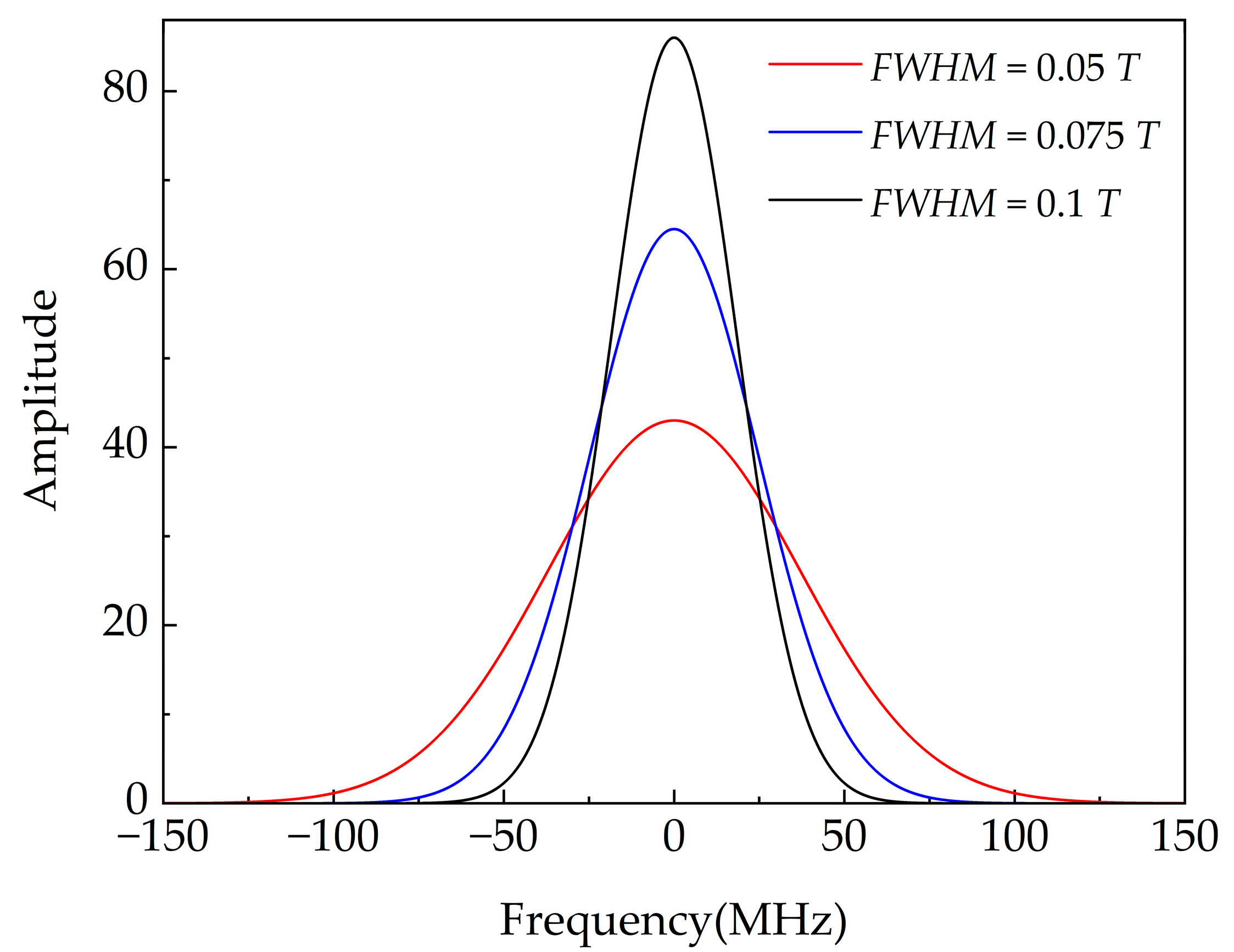
- A Gaussian pulse with FWHM of 0.075 T was selected as the simulated incident signal. The location spectrum obtained by multiplying the reflection coefficient and the incident signal shows an improved locating accuracy and reduced spectral leakage.
- The location spectrum shows double peaks at changed capacitance and a single peak at changed conductance. The midpoint between two peaks is used to locate capacitance change, and the location of the maximum reflected peak is used to locate conductance change.
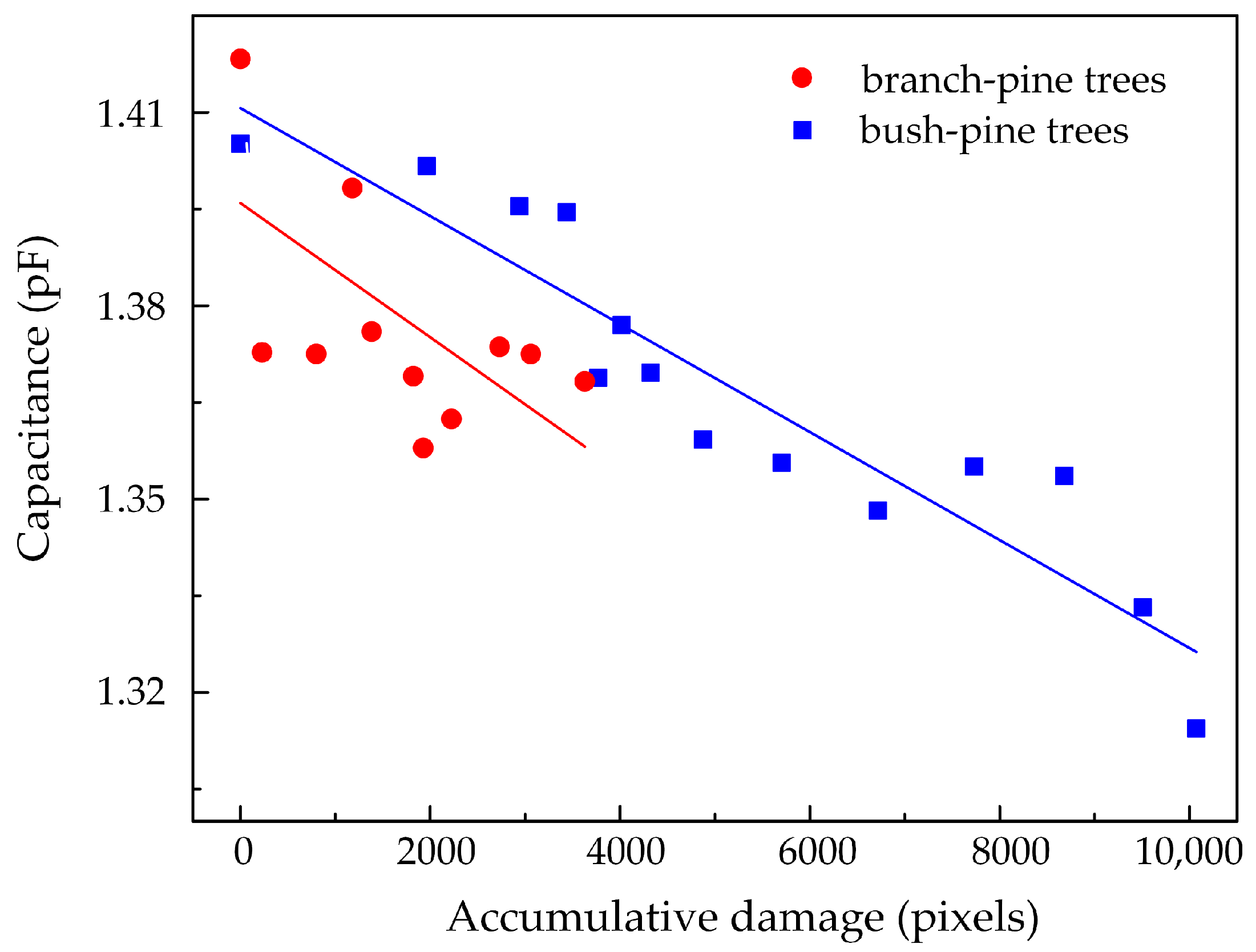
- The capacitance will decrease with the growth of electrical trees. The influence of the bush-pine tree on capacitance was greater than that of the branch-pine tree. The location spectrum shows double reflected peaks when bush-pine trees grow and shows one single peak when branch-pine trees grow.
- By improving the BIS algorithm, the location error of the branch-pine tree was less than 3% and the location error of the bush-pine tree was less than 1%.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Chen, X.; Zhang, H.; Liu, J.; Zhang, C.; Jiao, J. Analysis on the temperature field and the ampacity of XLPE submarine HV cable based on electro-thermal-flow multiphysics coupling simulation. Polymers 2020, 12, 952. [Google Scholar] [CrossRef] [PubMed]
- Zou, Z.; Yao, J. Fault Protection of Urban Distribution Network Using a Superconducting Cable Joint. IEEE Trans. Appl. Supercond. 2021, 31, 4805105. [Google Scholar] [CrossRef]
- Drissi-Habti, M.; Raj-Jiyoti, D.; Vijayaraghavan, S.; Fouad, E.C. Numerical simulation for void coalescence (water treeing) in XLPE insulation of submarine composite power cables. Energies 2020, 13, 5472. [Google Scholar] [CrossRef]
- Monssef, D.H.; Sriharsha, M.; Abhijit, N.; Valter, C.; Pierre-Jean, B. Numerical Simulation of Aging by Water-Trees of XPLE Insulator Used in a Single Hi-Voltage Phase of Smart Composite Power Cables for Offshore Farms. Energies 2022, 15, 1844. [Google Scholar] [CrossRef]
- Lungulescu, E.M.; Setnescu, R.; Ilie, S.; Taborelli, M. On the Use of Oxidation Induction Time as a Kinetic Parameter for Condition Monitoring and Lifetime Evaluation under Ionizing Radiation Environments. Polymers 2022, 14, 2357. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Xu, Y.; Cao, X.; Gubanski, S.M. Electrical treeing behavior at high temperature in XLPE cable insulation samples. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2841–2851. [Google Scholar] [CrossRef]
- Su, J.; Du, B.; Li, J.; Li, Z. Electrical tree degradation in high-voltage cable insulation, progress and challenges. High Volt. 2020, 5, 353–364. [Google Scholar] [CrossRef]
- Arachchige, T.G.; Zhong, X.; Ekanayake, C.; Ma, H.; Saha, T. Electrical Tree Driven Breakdown of XLPE Under Step Stress Breakdown Test at Multiple Frequencies. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 2065–2073. [Google Scholar] [CrossRef]
- Fard, M.A.; Farrag, M.E.; McMeekin, S.; Reid, A. Electrical treeing in cable insulation under different HVDC operational conditions. Energies 2018, 11, 2406. [Google Scholar] [CrossRef]
- He, J.; He, K.; Cui, L. Charge-simulation-based electric field analysis and electrical tree propagation model with defects in 10 kV XLPE cable joint. Energies 2019, 12, 4519. [Google Scholar] [CrossRef] [Green Version]
- Juan, Y.J.; Birlasekaran, S. Diagnosis of Electrical Treeing Phenomenon in XLPE Insulation. In Proceedings of the Electrical Insulation Conference and Electrical Manufacturing Expo, Indianapolis, IN, USA, 23–26 October 2005; pp. 20–25. [Google Scholar]
- Wang, W.; Chen, S.; Yang, K.; He, D.; Yu, Y. The relationship between electric tree aging degree and the equivalent time-frequency characteristic of PD pulses in high voltage cable. In Proceedings of the 2012 IEEE International Symposium on Electrical Insulation, San Juan, PR, USA, 10–13 June 2012; pp. 18–21. [Google Scholar]
- Donoso, P.; Schurch, R.; Ardila, J.; Orellana, L. Analysis of partial discharges in electrical tree growth under very low frequency (VLF) excitation through pulse sequence and nonlinear time series analysis. IEEE Access 2020, 8, 163673–163684. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, L.; Liao, R.; George, C. Study on Propagation Characteristics and Analysis of Partial Discharges for Electrical Treeing in XLPE Power Cables. In Proceedings of the 2010 10th IEEE International Conference on Solid Dielectrics, Potsdam, Germany, 4–9 July 2010; pp. 1–4. [Google Scholar]
- Nyanteh, Y.; Graber, L.; Srivastava, S.; Edrington, C.; Cartes, D. A novel approach towards the determination of the time to breakdown of electrical machine insulating materials. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 232–240. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Gao, J.; Guo, N.; Han, G. Pattern Recognition of Growth Characteristics Based on UHF PD Signals of Electrical Tree. IEEE Access 2022, 10, 49853–49861. [Google Scholar] [CrossRef]
- Cataldo, A.; De Benedetto, E.; Masciullo, A.; Cannazza, G. A new measurement algorithm for TDR-based localization of large dielectric permittivity variations in long-distance cable systems. Measurement 2021, 174, 109066. [Google Scholar] [CrossRef]
- Cheng, B.; Hua, L.; Zhu, W.; Zhang, Q.; Lei, J.; Xiao, H. Distributed temperature sensing with unmodified coaxial cable based on random reflections in TDR signal. Meas. Sci. Technol. 2018, 30, 015105. [Google Scholar] [CrossRef]
- Yu, Y.; Di, Y.; Lv, Q.; Zhang, L.; Xu, P.; Gao, Y. Study on Impedance Characteristics of Moisture Ingress in Cable Joint and Its Detection Method. In Proceedings of the 2021 11th International Conference on Power and Energy Systems (ICPES), Shanghai, China, 18–20 December 2021; pp. 95–100. [Google Scholar]
- Kim, H.J.; Park, J.; Mun, J.; Kim, D.-H.; Hwangbo, S.; Yi, D.-Y.; Byun, J.-K. Sensitivity analysis of water tree and input pulse parameters for time-domain reflectometry of power cables using taguchi method. J. Electr. Eng. Technol. 2021, 16, 633–642. [Google Scholar] [CrossRef]
- Ohki, Y.; Hirai, N. Location feasibility of degradation in cable through Fourier transform analysis of broadband impedance spectrum. Electr. Eng. Jpn. 2013, 183, 1–8. [Google Scholar] [CrossRef]
- Ohki, Y.; Hirai, N. Comparison of Location Abilities of Degradation in a Polymer-Insulated Cable between Frequency Domain Reflectometry and Line Resonance Analysis. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chengdu, China, 19–22 September 2016; pp. 1–4. [Google Scholar]
- Yamada, T.; Hirai, N.; Ohki, Y. Improvement in Sensitivity of Broadband Impedance Spectroscopy for Locating Degradation in Cable Insulation by Ascending the Measurement Frequency. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 23–27 September 2012; pp. 677–680. [Google Scholar]
- Hirai, N.; Ohki, Y. Location Attempt of Multiple Heated Spots in a Polymer-Insulated Coaxial Cable by Frequency Domain Reflectometry. In Proceedings of the 2018 Condition Monitoring and Diagnosis (CMD), Bentley, WA, Australia, 23–26 September 2018; pp. 1–4. [Google Scholar]
- Zhang, H.; Mu, H.; Lu, X.; Tian, J.; Zou, X.; Zhang, G. A method for locating and diagnosing cable abrasion based on broadband impedance spectroscopy. Energy Rep. 2022, 8, 1492–1499. [Google Scholar] [CrossRef]
- Li, Y.; Du, B.; Li, J.; Li, Z.; Han, T.; Ran, Z. Electrical Tree Characteristics in Graphene/SiR Nanocomposites under Temperature Gradient. In Proceedings of the 2021 International Conference on Electrical Materials and Power Equipment (ICEMPE), Chongqing, China, 11–15 April 2021; pp. 1–4. [Google Scholar]
- Lv, Z.; Rowland, S.M.; Chen, S.; Zheng, H. Modelling and simulation of PD characteristics in non-conductive electrical trees. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 2250–2258. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, X. Electrical tree growth characteristics in XLPE cable insulation under DC voltage conditions. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3676–3684. [Google Scholar] [CrossRef]
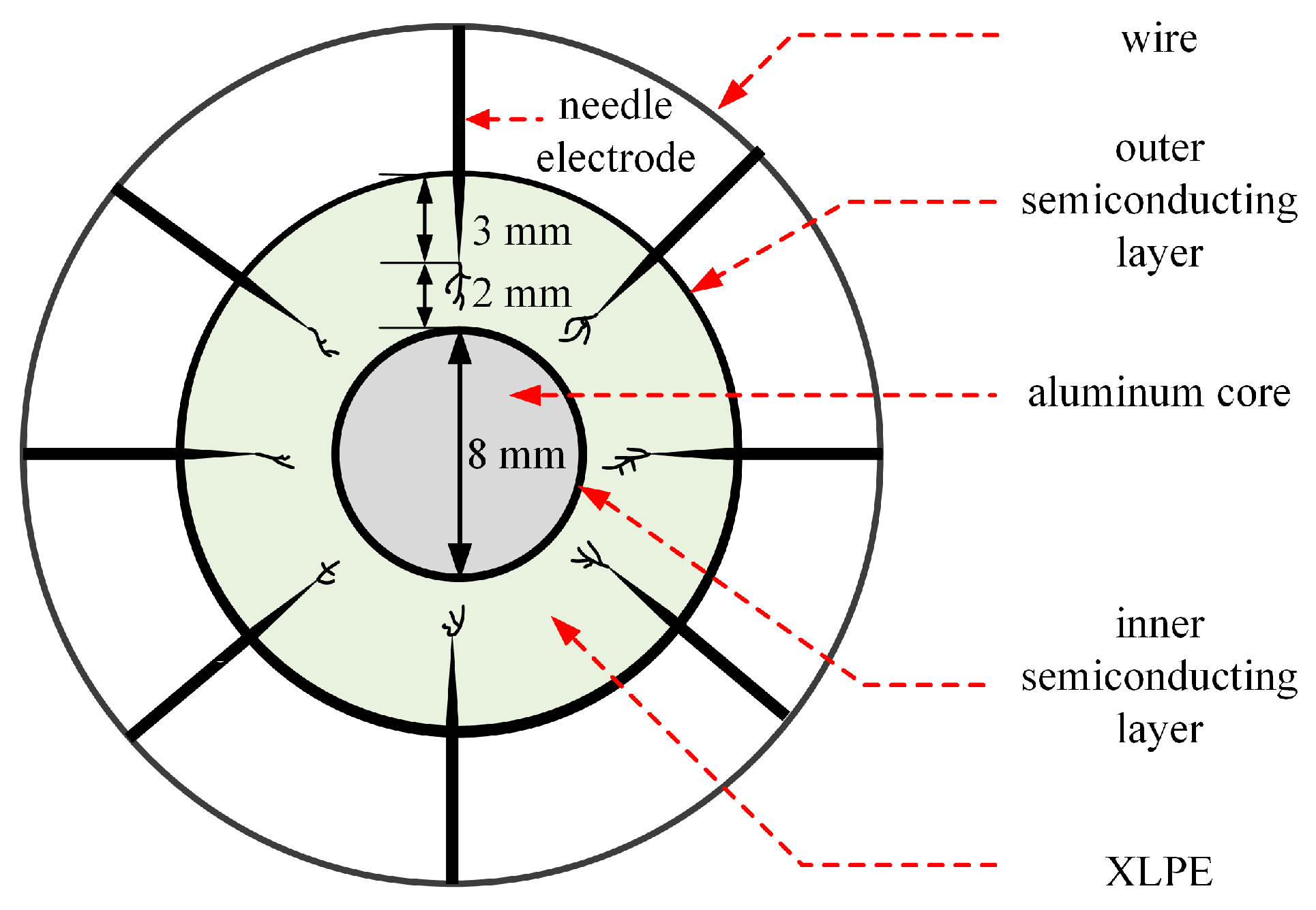
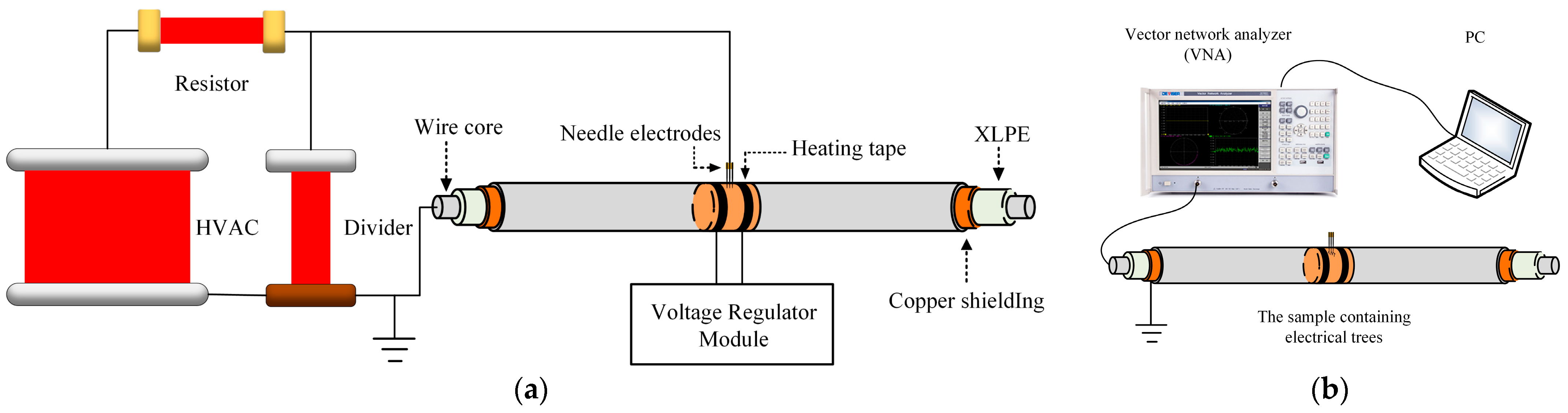
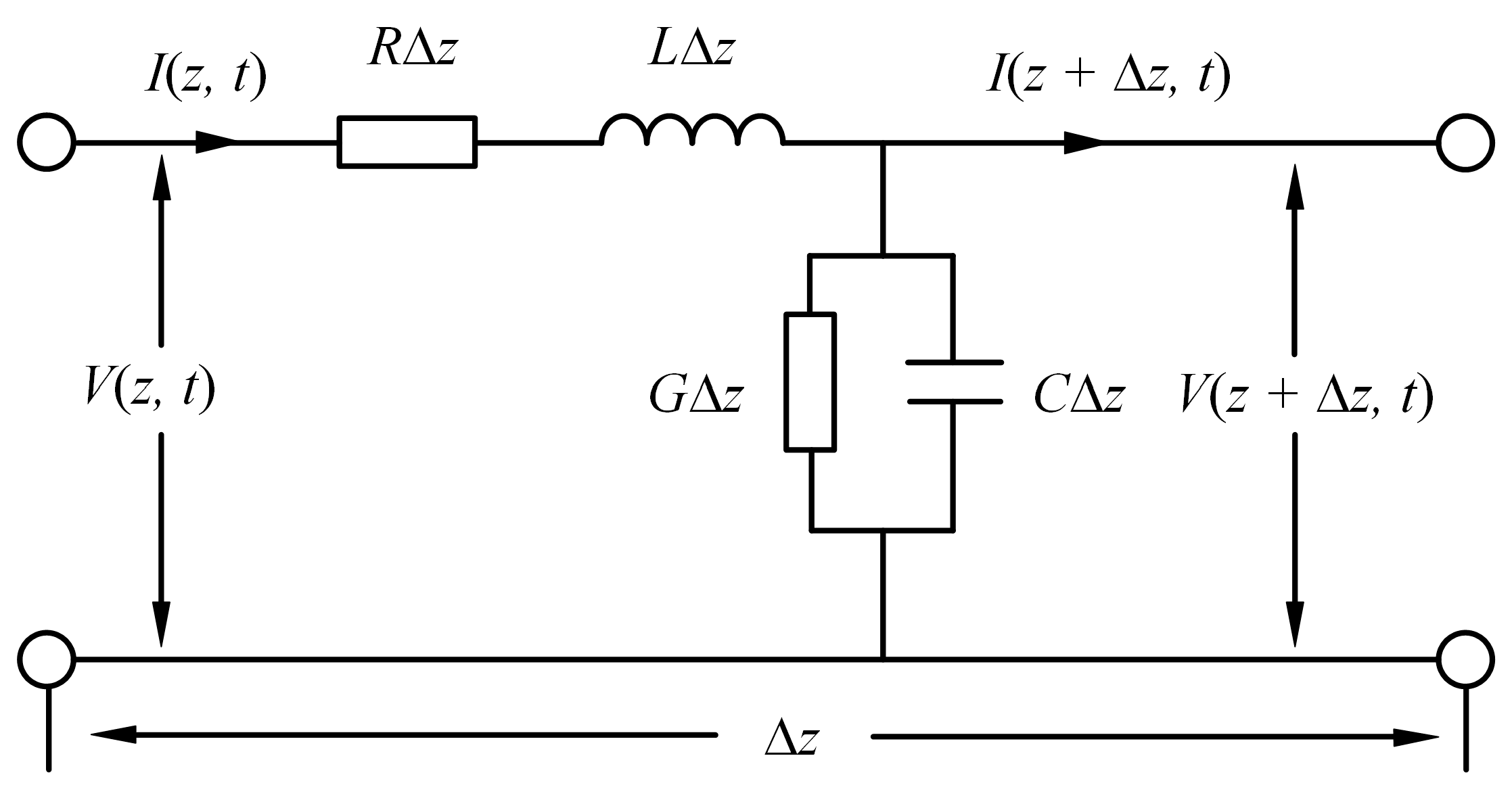
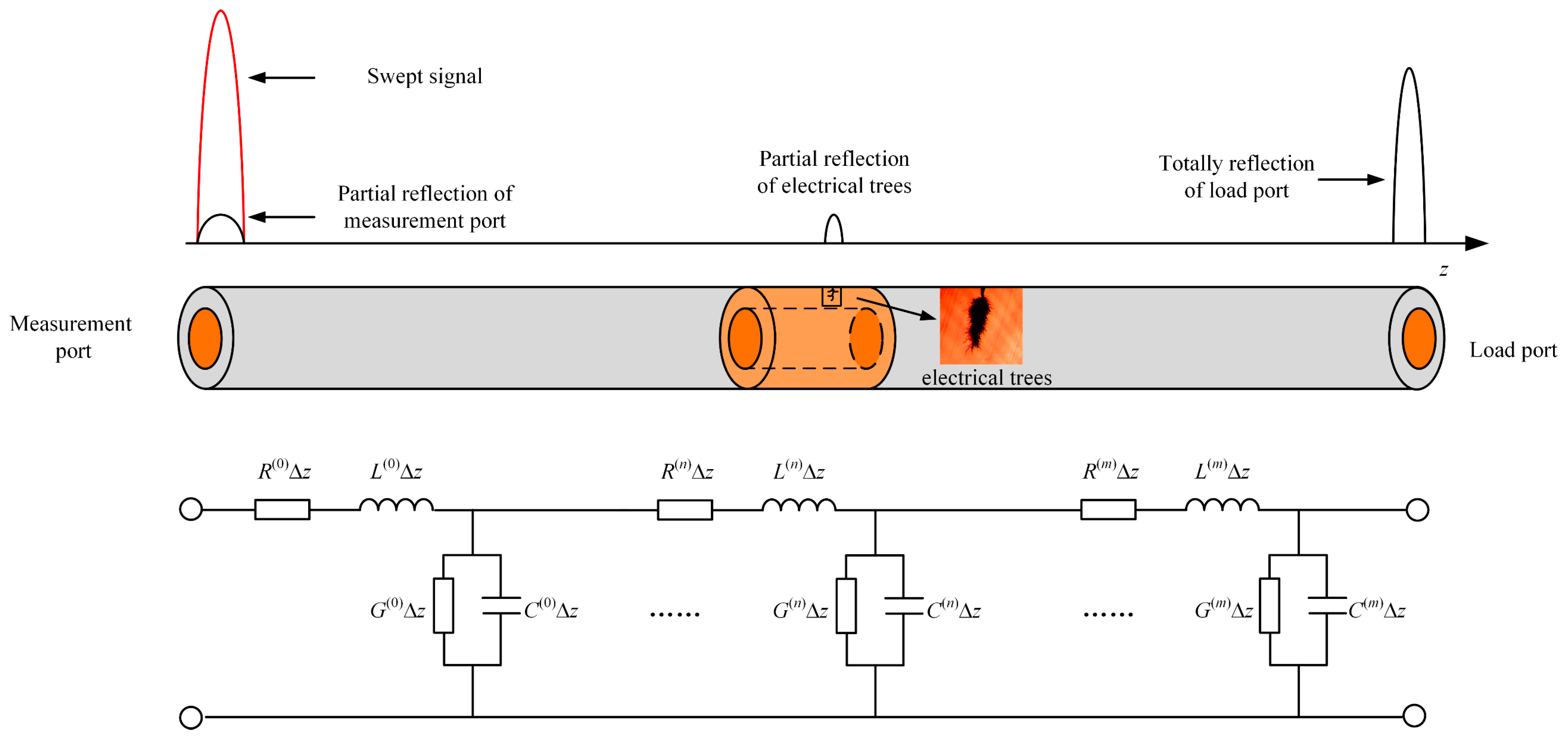






| The Parameters of the Cable | Values |
|---|---|
| The radius of aluminum wire core rc (mm) | 4 |
| The radius of copper shielding rs (mm) | 9 |
| The relative dielectric constant of XLPE εr | 2.3 |
| The conductivity of wire core γc (S/m) | 3.538 × 107 |
| The conductivity of XLPE γr (S/m) | 1 × 10−17 |
| The conductivity of copper shielding γs (S/m) | 5.714 × 107 |
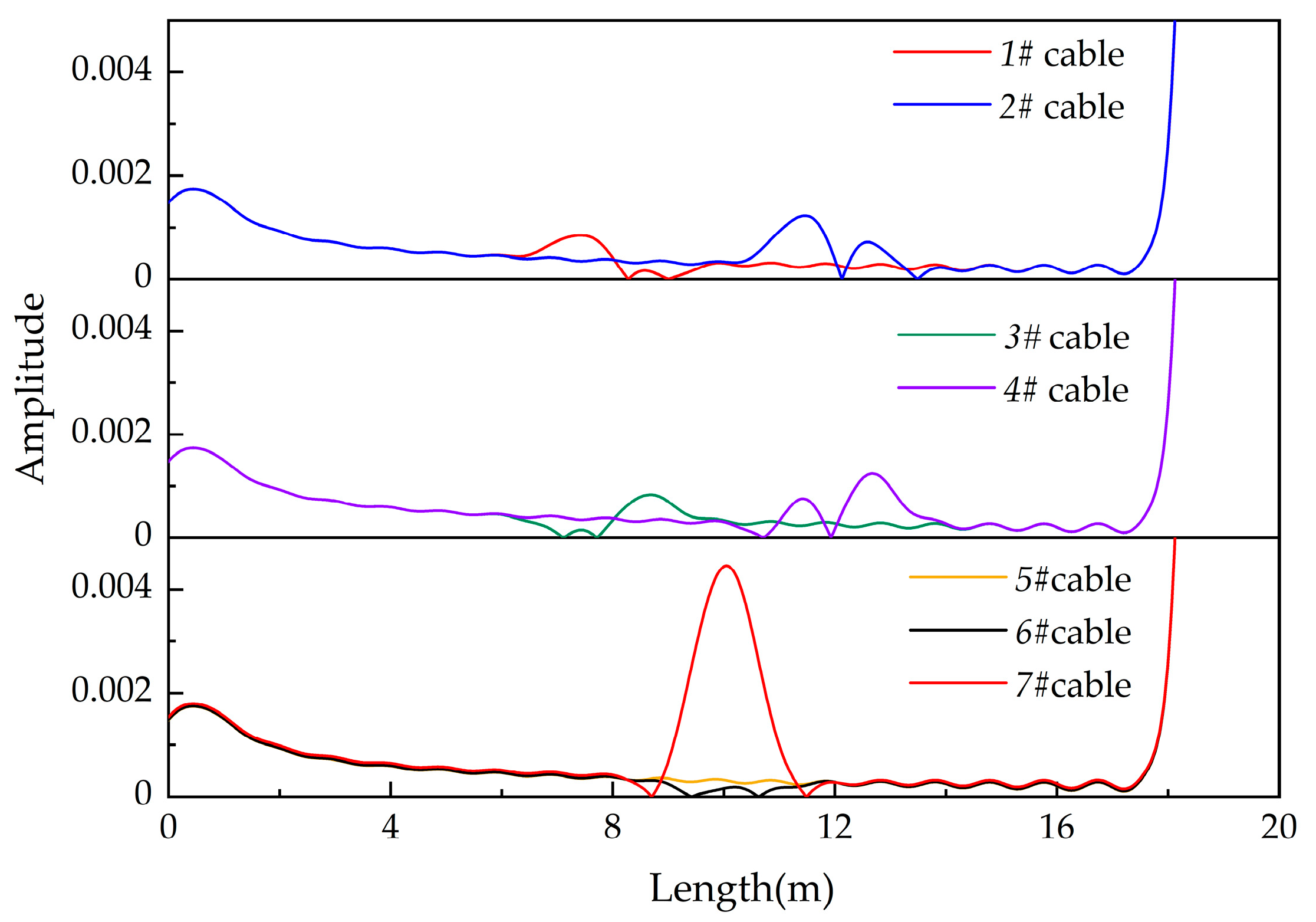
| Number | Degradation Location (m) | Conductance (S/m) | Capacitance (F/m) |
|---|---|---|---|
| 1# | 7.98~8.02 | G0 | 0.95 C0 |
| 2# | 11.98~12.02 | G0 | 0.90 C0 |
| 3# | 7.98~8.02 | G0 | 1.05 C0 |
| 4# | 11.98~12.02 | G0 | 1.10 C0 |
| 5# | 9.98~10.02 | 1 × 1012 G0 | C0 |
| 6# | 9.98~10.02 | 1 × 1013 G0 | C0 |
| 7# | 9.98~10.02 | 1 × 1014 G0 | C0 |
| Number | Location of the Largest Peak (m) | Midpoint between Peaks (m) | Degradation Location (m) |
|---|---|---|---|
| 1# | 7.425 | 7.994 | 7.98~8.02 |
| 2# | 11.484 | 12.041 | 11.98~12.02 |
| 3# | 8.687 | 8.044 | 7.98~8.02 |
| 4# | 12.647 | 12.041 | 11.98~12.02 |
| 5# | — | — | 9.98~10.02 |
| 6# | 10.197 | — | 9.98~10.02 |
| 7# | 10.073 | — | 9.98~10.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, T.; Yao, Y.; Li, Q.; Huang, Y.; Zheng, Z.; Gao, Y. Locating Method for Electrical Tree Degradation in XLPE Cable Insulation Based on Broadband Impedance Spectrum. Polymers 2022, 14, 3785. https://doi.org/10.3390/polym14183785
Han T, Yao Y, Li Q, Huang Y, Zheng Z, Gao Y. Locating Method for Electrical Tree Degradation in XLPE Cable Insulation Based on Broadband Impedance Spectrum. Polymers. 2022; 14(18):3785. https://doi.org/10.3390/polym14183785
Chicago/Turabian StyleHan, Tao, Yufei Yao, Qiang Li, Youcong Huang, Zhongnan Zheng, and Yu Gao. 2022. "Locating Method for Electrical Tree Degradation in XLPE Cable Insulation Based on Broadband Impedance Spectrum" Polymers 14, no. 18: 3785. https://doi.org/10.3390/polym14183785
APA StyleHan, T., Yao, Y., Li, Q., Huang, Y., Zheng, Z., & Gao, Y. (2022). Locating Method for Electrical Tree Degradation in XLPE Cable Insulation Based on Broadband Impedance Spectrum. Polymers, 14(18), 3785. https://doi.org/10.3390/polym14183785







