Unexpected Slow Kinetics of Poly(Methacrylic Acid) Phase Separation in the Semi-Dilute Regime
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
2.2. Methods
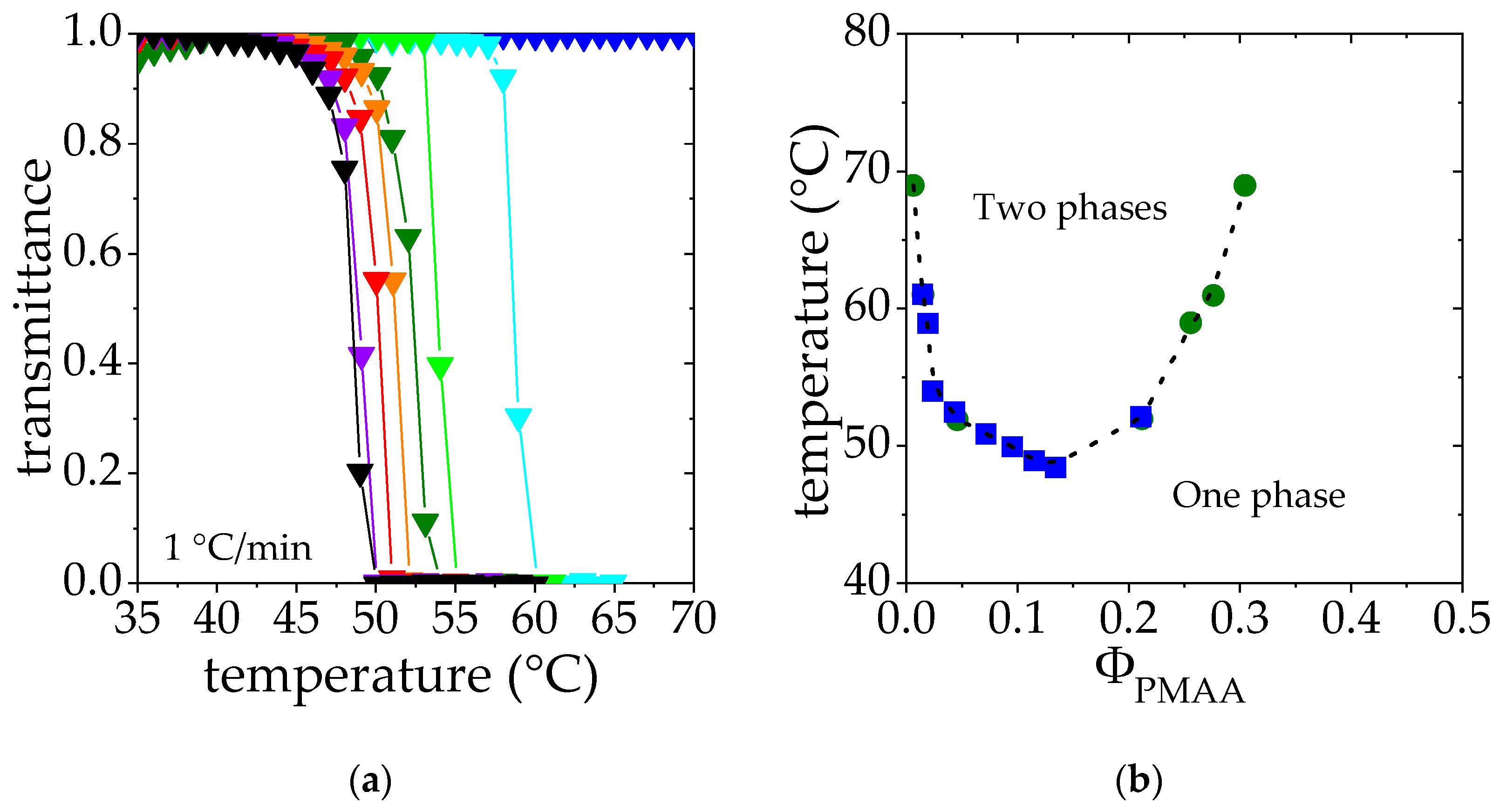
2.2.1. Cloud Point Measurements
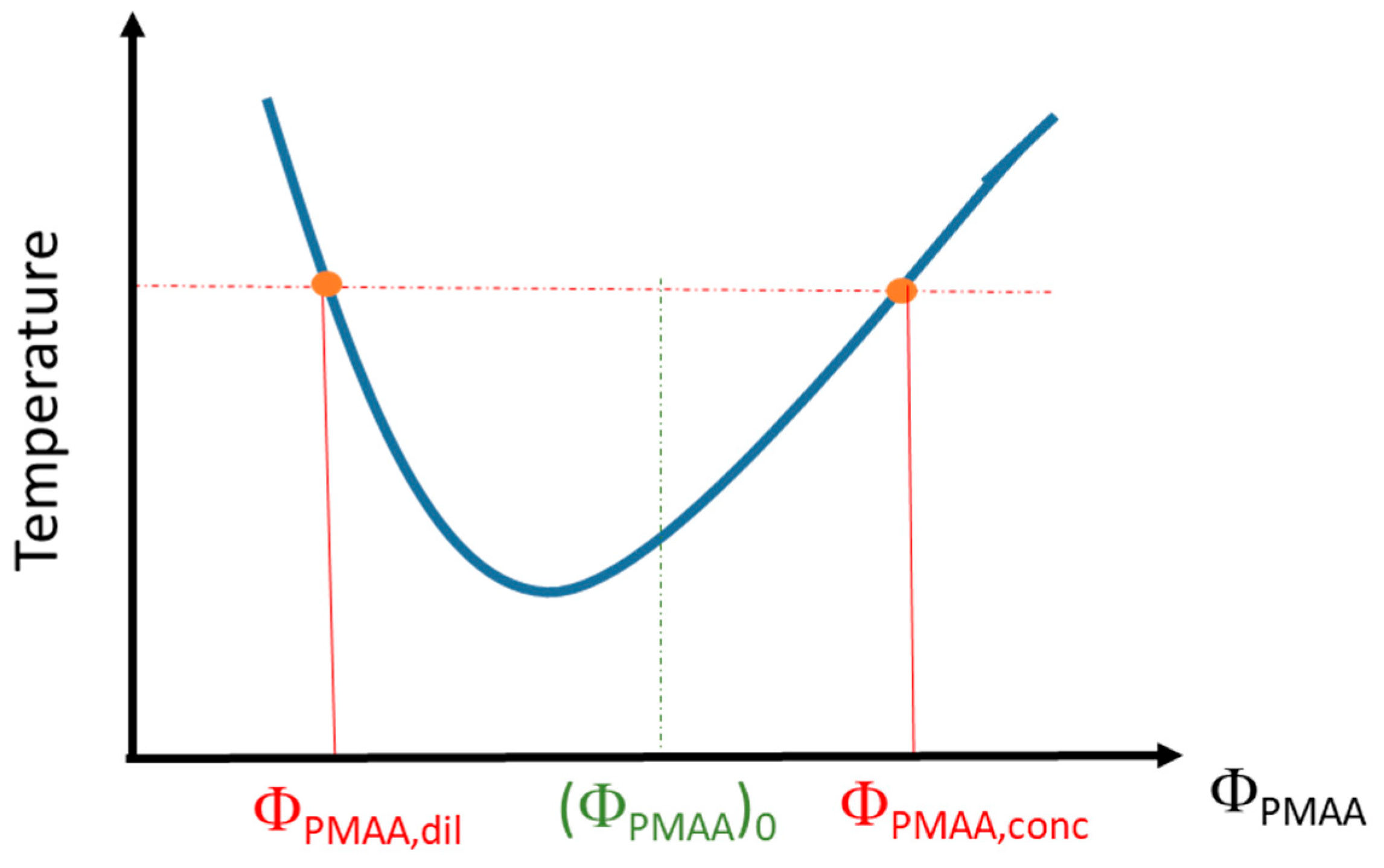
2.2.2. Determination of the Phase Diagrams from Phase Separation
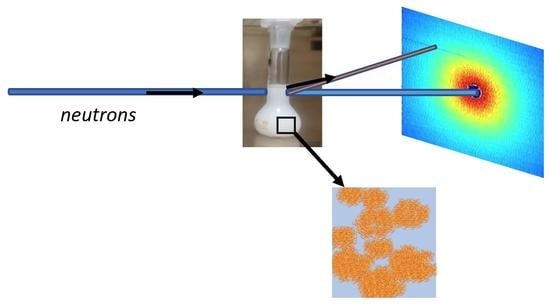
2.2.3. Small-Angle Neutron Scattering (SANS)
3. Results and Discussion
3.1. Phase Diagram Construction
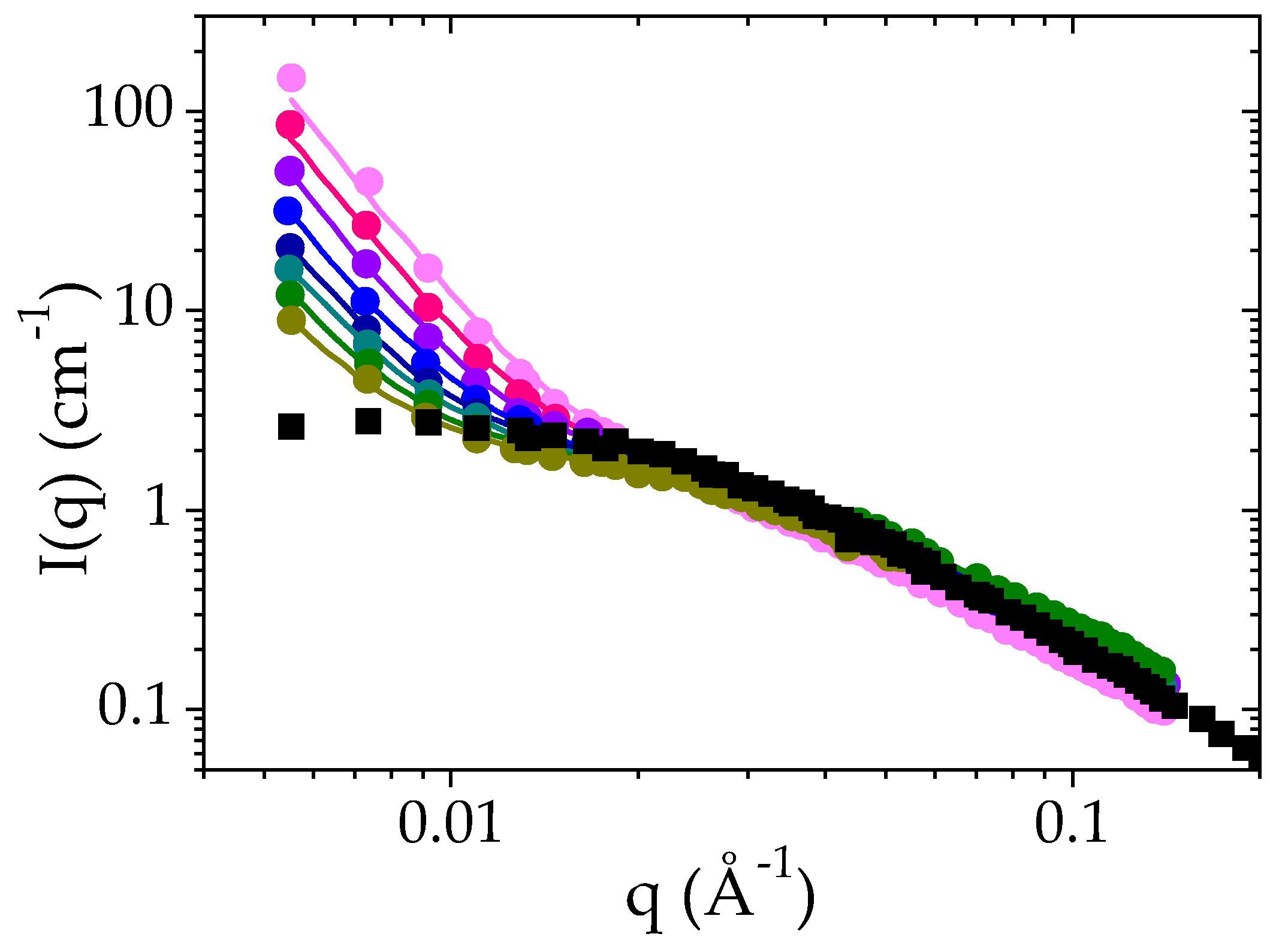
3.2. Structure of the PMAA Solutions below the LCST
3.3. Kinetics of the Phase Separation
3.3.1. Structures of a Semi-Dilute Solution of PMAA in D2O +1 °C above Cloud Point (52 °C)
3.3.2. Structures of a Semi-Dilute Solution of PMAA in D2O + 10 °C above Cloud Point (61 °C)
3.3.3. Effect of the PMAA Concentration
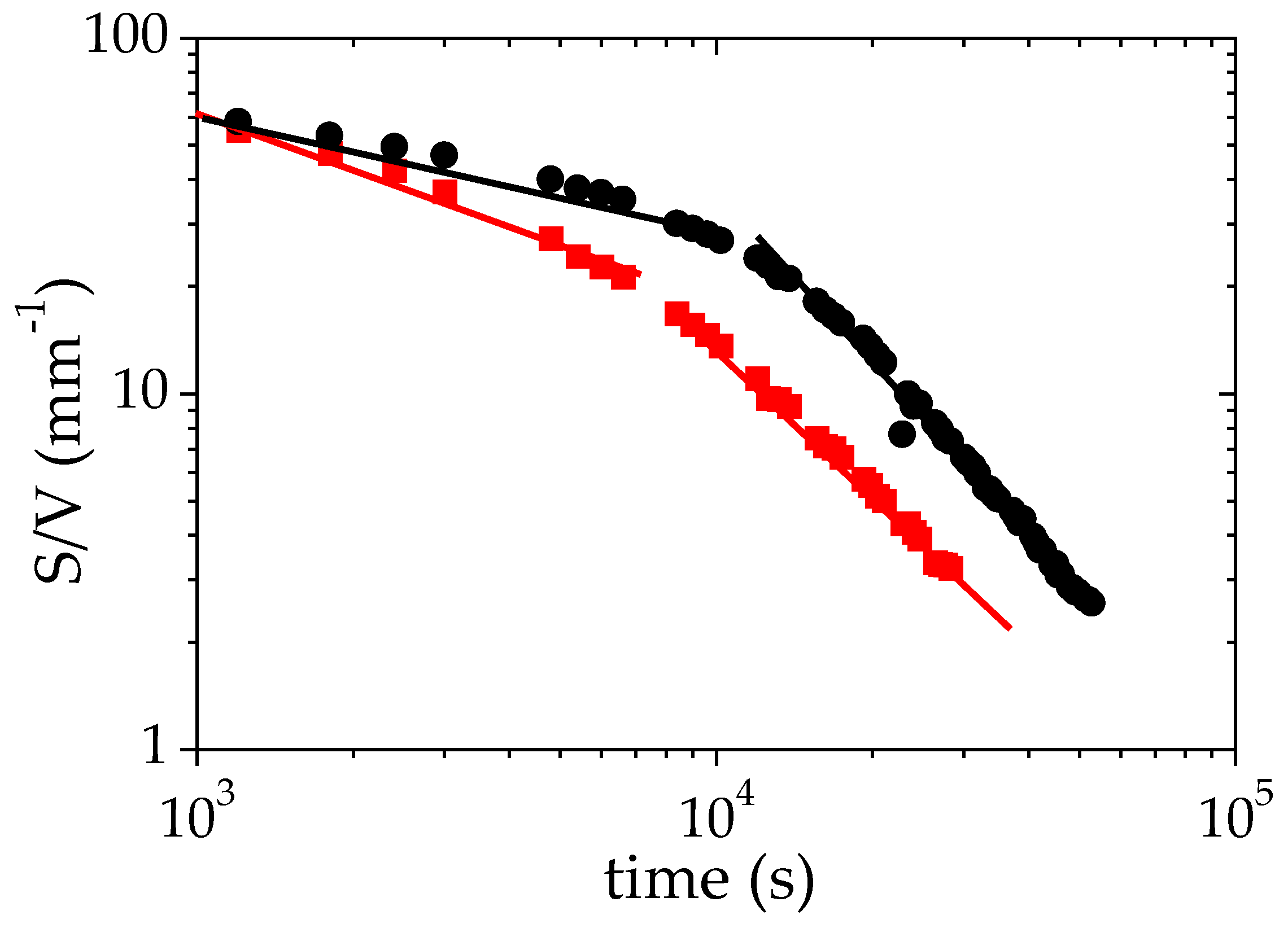
3.4. Discussion of the Time Decays of S/V
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pasparakis, G.; Tsitsilianis, C. LCST Polymers: Thermoresponsive Nanostructured Assemblies towards Bioapplications. Polymer 2020, 211, 123146. [Google Scholar] [CrossRef]
- Qiao, S.; Wang, H. Temperature-Responsive Polymers: Synthesis, Properties, and Biomedical Applications. Nano Res. 2018, 11, 5400–5423. [Google Scholar] [CrossRef]
- Sponchioni, M.; Capasso Palmiero, U.; Moscatelli, D. Thermo-Responsive Polymers: Applications of Smart Materials in Drug Delivery and Tissue Engineering. Mater. Sci. Eng. C 2019, 102, 589–605. [Google Scholar] [CrossRef] [PubMed]
- Klouda, L.; Mikos, A.G. Thermoresponsive Hydrogels in Biomedical Applications. Eur. J. Pharm. Biopharm. 2008, 68, 34–45. [Google Scholar] [CrossRef] [Green Version]
- Schmaljohann, D. Thermo- and PH-Responsive Polymers in Drug Delivery. Adv. Drug Deliv. Rev. 2006, 58, 1655–1670. [Google Scholar] [CrossRef]
- Kozlovskaya, V.; Kharlampieva, E. Self-Assemblies of Thermoresponsive Poly(N-Vinylcaprolactam) Polymers for Applications in Biomedical Field. ACS Appl. Polym. Mater. 2020, 2, 26–39. [Google Scholar] [CrossRef] [Green Version]
- Abuwatfa, W.H.; Awad, N.S.; Pitt, W.G.; Husseini, G.A. Thermosensitive Polymers and Thermo-Responsive Liposomal Drug Delivery Systems. Polymers 2022, 14, 925. [Google Scholar] [CrossRef]
- Nagase, K.; Yamato, M.; Kanazawa, H.; Okano, T. Poly(N-Isopropylacrylamide)-Based Thermoresponsive Surfaces Provide New Types of Biomedical Applications. Biomaterials 2018, 153, 27–48. [Google Scholar] [CrossRef]
- Sun, X.; Tyagi, P.; Agate, S.; McCord, M.G.; Lucia, L.A.; Pal, L. Highly Tunable Bioadhesion and Optics of 3D Printable PNIPAm/Cellulose Nanofibrils Hydrogels. Carbohydr. Polym. 2020, 234, 115898. [Google Scholar] [CrossRef]
- Ksendzov, E.A.; Nikishau, P.A.; Zurina, I.M.; Presniakova, V.S.; Timashev, P.; Rochev, Y.A.; Kotova, S.; Kostjuk, S.V. Graft Copolymers of N-Isopropylacrylamide with Poly(d,l-Lactide) or Poly(ε-Caprolactone) Macromonomers: A Promising Class of Thermoresponsive Polymers with a Tunable LCST. ACS Appl. Polym. Mater. 2022, 4, 1344–1357. [Google Scholar] [CrossRef]
- Dompé, M.; Vahdati, M.; van Ligten, F.; Cedano-Serrano, F.J.; Hourdet, D.; Creton, C.; Zanetti, M.; Bracco, P.; van der Gucht, J.; Kodger, T.; et al. Enhancement of the Adhesive Properties by Optimizing the Water Content in PNIPAM-Functionalized Complex Coacervates. ACS Appl. Polym. Mater. 2020, 2, 1722–1730. [Google Scholar] [CrossRef] [Green Version]
- Wong, Y.L.; Pandey, M.; Choudhury, H.; Lim, W.M.; Bhattamisra, S.K.; Gorain, B. Development of In-Situ Spray for Local Delivery of Antibacterial Drug for Hidradenitis Suppurativa: Investigation of Alternative Formulation. Polymers 2021, 13, 2770. [Google Scholar] [CrossRef] [PubMed]
- Tekin, H.; Sanchez, J.G.; Tsinman, T.; Langer, R.; Khademhosseini, A. Thermoresponsive Platforms for Tissue Engineering and Regenerative Medicine. AIChE J. 2011, 57, 3249–3258. [Google Scholar] [CrossRef] [PubMed]
- Majstorović, N.; Agarwal, S. Strong, Stretchable, Dual-Responsive PNIPAM Nanogel Cross-Linked UCST-Type Macrogels for Biomedical Applications. ACS Appl. Polym. Mater. 2022, 4, 5996–6005. [Google Scholar] [CrossRef]
- Pelton, R. Poly(N-Isopropylacrylamide) (PNIPAM) Is Never Hydrophobic. J. Colloid Interface Sci. 2010, 348, 673–674. [Google Scholar] [CrossRef]
- Lang, X.; Lenart, W.R.; Sun, J.E.P.; Hammouda, B.; Hore, M.J.A. Interaction and Conformation of Aqueous Poly(N-Isopropylacrylamide) (PNIPAM) Star Polymers below the LCST. Macromolecules 2017, 50, 2145–2154. [Google Scholar] [CrossRef]
- de Oliveira, T.E.; Mukherji, D.; Kremer, K.; Netz, P.A. Effects of Stereochemistry and Copolymerization on the LCST of PNIPAm. J. Chem. Phys. 2017, 146, 034904. [Google Scholar] [CrossRef]
- Zhang, Y.; Furyk, S.; Sagle, L.B.; Cho, Y.; Bergbreiter, D.E.; Cremer, P.S. Effects of Hofmeister Anions on the LCST of PNIPAM as a Function of Molecular Weight. J. Phys. Chem. C 2007, 111, 8916–8924. [Google Scholar] [CrossRef] [Green Version]
- Plunkett, K.N.; Zhu, X.; Moore, J.S.; Leckband, D.E. PNIPAM Chain Collapse Depends on the Molecular Weight and Grafting Density. Langmuir 2006, 22, 4259–4266. [Google Scholar] [CrossRef]
- Haq, M.A.; Su, Y.; Wang, D. Mechanical Properties of PNIPAM Based Hydrogels: A Review. Mater. Sci. Eng. C 2017, 70, 842–855. [Google Scholar] [CrossRef]
- Halperin, A.; Kröger, M.; Winnik, F.M. Poly(N-Isopropylacrylamide) Phase Diagrams: Fifty Years of Research. Angew. Chem. Int. Ed. 2015, 54, 15342–15367. [Google Scholar] [CrossRef] [PubMed]
- Guan, Y.; Zhang, Y. PNIPAM Microgels for Biomedical Applications: From Dispersed Particles to 3D Assemblies. Soft Matter 2011, 7, 6375–6384. [Google Scholar] [CrossRef]
- Xu, X.; Liu, Y.; Fu, W.; Yao, M.; Ding, Z.; Xuan, J.; Li, D.; Wang, S.; Xia, Y.; Cao, M. Poly(N-Isopropylacrylamide)-Based Thermoresponsive Composite Hydrogels for Biomedical Applications. Polymers 2020, 12, 580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Denmark, D.J.; Hyde, R.H.; Gladney, C.; Phan, M.-H.; Bisht, K.S.; Srikanth, H.; Mukherjee, P.; Witanachchi, S. Photopolymerization-Based Synthesis of Iron Oxide Nanoparticle Embedded PNIPAM Nanogels for Biomedical Applications. Drug Deliv. 2017, 24, 1317–1324. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Xia, Y.; Zhang, D.; Sun, X.; Chen, X.; Oliver, S.; Shi, S.; Lei, L. Hydrogen-Bonding Reinforced Injectable Hydrogels: Application As a Thermo-Triggered Drug Controlled-Release System. ACS Appl. Polym. Mater. 2020, 2, 1587–1596. [Google Scholar] [CrossRef]
- Gürdap, S.; Bayram, N.N.; İşoğlu, İ.A.; Dinçer İşoğlu, S. Sulfobetaine-Based Homo- and Copolymers by RAFT: Cross-Linked Micelles and Aqueous Solution Properties. ACS Appl. Polym. Mater. 2022, 4, 6303–6311. [Google Scholar] [CrossRef]
- Eliassaf, J.; Silberberg, A. The Gelation of Aqueous Solutions of Polymethacrylic Acid. Polymer 1962, 3, 555–564. [Google Scholar] [CrossRef]
- Buscall, R.; Corner, T. The Phase-Separation Behaviour of Aqueous Solutions of Polyacrylic Acid and Its Partial Sodium Salts in the Presence of Sodium Chloride. Eur. Polym. J. 1982, 18, 967–974. [Google Scholar] [CrossRef]
- Aoki, T.; Kawashima, M.; Katono, H.; Sanui, K.; Ogata, N.; Okano, T.; Sakurai, Y. Temperature-Responsive Interpenetrating Polymer Networks Constructed with Poly(Acrylic Acid) and Poly(N,N-Dimethylacrylamide). Macromolecules 1994, 27, 947–952. [Google Scholar] [CrossRef]
- Zhao, C.; Dolmans, L.; Zhu, X.X. Thermoresponsive Behavior of Poly(Acrylic Acid-Co-Acrylonitrile) with a UCST. Macromolecules 2019, 52, 4441–4446. [Google Scholar] [CrossRef]
- Sinek, A.; Kupczak, M.; Mielańczyk, A.; Lemanowicz, M.; Yusa, S.; Neugebauer, D.; Gierczycki, A. Temperature and PH-Dependent Response of Poly(Acrylic Acid) and Poly(Acrylic Acid-Co-Methyl Acrylate) in Highly Concentrated Potassium Chloride Aqueous Solutions. Polymers 2020, 12, 486. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morawetz, H. Revisiting Some Phenomena in Polyelectrolyte Solutions. J. Polym. Sci. Part B Polym. Phys. 2002, 40, 1080–1086. [Google Scholar] [CrossRef]
- Ruiz-Pérez, L.; Pryke, A.; Sommer, M.; Battaglia, G.; Soutar, I.; Swanson, L.; Geoghegan, M. Conformation of Poly(Methacrylic Acid) Chains in Dilute Aqueous Solution. Macromolecules 2008, 41, 2203–2211. [Google Scholar] [CrossRef]
- Kogej, K. Thermodynamic Analysis of the Conformational Transition in Aqueous Solutions of Isotactic and Atactic Poly(Methacrylic Acid) and the Hydrophobic Effect. Polymers 2016, 8, 168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandel, M.; Leyte, J.; Stadhouder, M. The Conformational Transition of Poly(Methacrylic Acid) in Solution. J. Phys. Chem. 1967, 71, 603–612. [Google Scholar] [CrossRef]
- Moussaid, A.; Schosseler, F.; Munch, J.P.; Candau, S.J. Structure of Polyacrylic Acid and Polymethacrylic Acid Solutions: A Small Angle Neutron Scattering Study. J. Phys. II France 1993, 3, 573–594. [Google Scholar] [CrossRef]
- Pleštil, J.; Ostanevich, Y.M.; Bezzabotnov, V.Y.; Hlavatá, D. Small-Angle Scattering by Polyelectrolyte Solutions. Hydration and Conformation of Poly(Methacrylic Acid). Polymer 1986, 27, 1241–1246. [Google Scholar] [CrossRef]
- Heitz, C.; Rawiso, M.; François, J. X-Ray Scattering Study of a Poly(Methacrylic Acid) Sample as a Function of Its Neutralization Degree. Polymer 1999, 40, 1637–1650. [Google Scholar] [CrossRef]
- Sedlák, M. Poly(Alkylacrylic Acid)s: Solution Behavior and Self-Assembly. Colloid Polym. Sci. 2017, 295, 1281–1292. [Google Scholar] [CrossRef]
- Horský, J.; Morawetz, H. Kinetics of the Conformational Transition of Poly(Methacrylic Acid) after a PH Jump, 2. Studies of Nonradiative Energy Transfer. Die Makromol. Chem. 1988, 189, 2475–2483. [Google Scholar] [CrossRef]
- Soutar, I.; Swanson, L. Luminescence Studies of Polyelectrolyte Behavior in Solution. 3. Time-Resolved Fluorescence Anisotropy Measurements of the Conformational Behavior of Poly(Methacrylic Acid) in Dilute Aqueous Solutions. Macromolecules 1994, 27, 4304–4311. [Google Scholar] [CrossRef]
- Kanevskaya, Y.A.; Zubov, P.I.; Ivanova, L.V.; Lipatov, Y.S. The Temperature Dependence of the Light Scattering and Viscosity of Solutions of Poly(Methacrylic Acid). Polym. Sci. U.S.S.R. 1964, 6, 1080–1087. [Google Scholar] [CrossRef]
- Pleštil, J.; Ostanevich, Y.M.; Bezzabotonov, V.Y.; Hlavatá, D.; Labský, J. Small-Angle Scattering from Polyelectrolyte Solutions: Dimensions of Poly(Methacrylic Acid) Chains in Salt-Free Solutions. Polymer 1986, 27, 839–842. [Google Scholar] [CrossRef]
- Cazares-Cortes, E.; Baker, B.C.; Nishimori, K.; Ouchi, M.; Tournilhac, F. Polymethacrylic Acid Shows Thermoresponsivity in an Organic Solvent. Macromolecules 2019, 52, 5995–6004. [Google Scholar] [CrossRef] [Green Version]
- Balu, C.; Delsanti, M.; Guenoun, P.; Monti, F.; Cloitre, M. Colloidal Phase Separation of Concentrated PNIPAm Solutions. Langmuir 2007, 23, 2404–2407. [Google Scholar] [CrossRef]
- M’barki, O.; Hanafia, A.; Bouyer, D.; Faur, C.; Sescousse, R.; Delabre, U.; Blot, C.; Guenoun, P.; Deratani, A.; Quemener, D.; et al. Greener Method to Prepare Porous Polymer Membranes by Combining Thermally Induced Phase Separation and Crosslinking of Poly(Vinyl Alcohol) in Water. J. Membr. Sci. 2014, 458, 225–235. [Google Scholar] [CrossRef]
- Couvreur, L.; Lefay, C.; Belleney, J.; Charleux, B.; Guerret, O.; Magnet, S. First Nitroxide-Mediated Controlled Free-Radical Polymerization of Acrylic Acid. Macromolecules 2003, 36, 8260–8267. [Google Scholar] [CrossRef]
- Robin, C.; Lorthioir, C.; Amiel, C.; Fall, A.; Ovarlez, G.; Le Cœur, C. Unexpected Rheological Behavior of Concentrated Poly(Methacrylic Acid) Aqueous Solutions. Macromolecules 2017, 50, 700–710. [Google Scholar] [CrossRef]
- Polymer Phase Diagrams: A Textbook; Oxford University Press: Oxford, NY, USA, 2001.
- Schäfer-Soenen, H.; Moerkerke, R.; Berghmans, H.; Koningsveld, R.; Dušek, K.; Šolc, K. Zero and Off-Zero Critical Concentrations in Systems Containing Polydisperse Polymers with Very High Molar Masses. 2. The System Water−Poly(Vinyl Methyl Ether). Macromolecules 1997, 30, 410–416. [Google Scholar] [CrossRef]
- Baulin, V.A.; Halperin, A. Concentration Dependence of the Flory χ Parameter within Two-State Models. Macromolecules 2002, 35, 6432–6438. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: New York, NY, USA, 2003; Volume 23. [Google Scholar]
- Dobrynin, A.V.; Rubinstein, M. Theory of Polyelectrolytes in Solutions and at Surfaces. Prog. Polym. Sci. 2005, 30, 1049–1118. [Google Scholar] [CrossRef]
- Katchalsky, A.; Eisenberg, H. Molecular Weight of Polyacrylic and Polymethacrylic Acid. J. Polym. Sci. 1951, 6, 145–154. [Google Scholar] [CrossRef]
- Meier-Koll, A.; Pipich, V.; Busch, P.; Papadakis, C.M.; Müller-Buschbaum, P. Phase Separation in Semidilute Aqueous Poly(N-Isopropylacrylamide) Solutions. Langmuir 2012, 28, 8791–8798. [Google Scholar] [CrossRef] [PubMed]
- Sinha, S.K.; Sirota, E.B.; Garoff, S.; Stanley, H.B. X-Ray and Neutron Scattering from Rough Surfaces. Phys. Rev. B 1988, 38, 2297–2311. [Google Scholar] [CrossRef]
- Van Durme, K.; Van Assche, G.; Van Mele, B. Kinetics of Demixing and Remixing in Poly(N-Isopropylacrylamide)/Water Studied by Modulated Temperature DSC. Macromolecules 2004, 37, 9596–9605. [Google Scholar] [CrossRef]
- Zheng, X.; Tong, Z.; Xie, X.; Zeng, F. Phase Separation in Poly(N -Isopropyl Acrylamide)/Water Solutions I. Cloud Point Curves and Microgelation. Polym. J. 1998, 30, 284–288. [Google Scholar] [CrossRef] [Green Version]
- Tong, Z.; Zeng, F.; Zheng, X.; Sato, T. Inverse Molecular Weight Dependence of Cloud Points for Aqueous Poly(N-Isopropylacrylamide) Solutions. Macromolecules 1999, 32, 4488–4490. [Google Scholar] [CrossRef]
- Zhou, X.; Li, J.; Wu, C.; Zheng, B. Constructing the Phase Diagram of an Aqueous Solution of Poly(N-Isopropyl Acrylamide) by Controlled Microevaporation in a Nanoliter Microchamber. Macromol. Rapid Commun. 2008, 29, 1363–1367. [Google Scholar] [CrossRef]
- Kabalnov, A. Ostwald Ripening and Related Phenomena. J. Dispers. Sci. Technol. 2001, 22, 1–12. [Google Scholar] [CrossRef]
- Ostwald, W. Über die vermeintliche Isomerie des roten und gelben Quecksilberoxyds und die Oberflächenspannung fester Körper. Zeitschrift für Physikalische Chemie 1900, 34U, 495–503. [Google Scholar] [CrossRef]
- Gunton, J.; Droz, M. Introduction to the Theory of Metastable and Unstable States; Springer: Berlin/Heidelberg, Germany, 1983; Volume 183. [Google Scholar] [CrossRef]
- Garate, H.; Li, K.-W.; Bouyer, D.; Guenoun, P. Optical Tracking of Relaxation Dynamics in Semi-Dilute Hydroxypropylcellulose Solutions as a Precise Phase Transition Probe. Soft Matter 2017, 13, 7161–7171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, S.-W.; Torkelson, J.M. Coarsening Effects on the Formation of Microporous Membranes Produced via Thermally Induced Phase Separation of Polystyrene-Cyclohexanol Solutions. J. Membr. Sci. 1995, 98, 209–222. [Google Scholar] [CrossRef]
- Villetti, M.A.; Soldi, V.; Rochas, C.; Borsali, R. Phase-Separation Kinetics and Mechanism in a Methylcellulose/Salt Aqueous Solution Studied by Time-Resolved Small-Angle Light Scattering (SALS). Macromol. Chem. Phys. 2011, 212, 1063–1071. [Google Scholar] [CrossRef]
- Weitz, D.A.; Huang, J.S.; Lin, M.Y.; Sung, J. Dynamics of Diffusion-Limited Kinetic Aggregation. Phys. Rev. Lett. 1984, 53, 1657–1660. [Google Scholar] [CrossRef]
- Shibayama, M.; Tanaka, T.; Han, C.C. Small Angle Neutron Scattering Study on Poly(N-isopropyl Acrylamide) Gels near Their Volume-phase Transition Temperature. J. Chem. Phys. 1998, 97, 6829. [Google Scholar] [CrossRef]
- Powell, M.J. Site Percolation in Randomly Packed Spheres. Phys. Rev. B 1979, 20, 4194–4198. [Google Scholar] [CrossRef]




| Mw (g.mol−1) | Mn (g.mol−1) | PDI | Rg (Å) | c* (g/L) |
|---|---|---|---|---|
| 391,000 | 313,000 | 1.25 | 190 | 23 |
| (ΦPMAA)0 | 0.017 | 0.065 | 0.065 | 0.104 |
|---|---|---|---|---|
| Temperature T | 69 °C | 52 °C | 61 °C | 59 °C |
| Temperature above cloud point | +10 °C | +1 °C | +10 °C | +10 °C |
| ΦPMAA,dil | 0.0038 | 0.040 | 0.013 | 0.015 |
| ΦPMAA,conc | 0.265 | 0.200 | 0.260 | 0.230 |
| (xconc)extrapolated | 0.051 | 0.156 | 0.21 | 0.42 |
| (xconc)measured | 0.05 | 0.16 | 0.21 | 0.43 |
| × 10−6 Å−2 | 5.26 | 5.53 | 5.30 | 5.42 |
| × 10−6 Å−2 | 6.31 | 6.17 | 6.28 | 6.27 |
| (ΦPMAA)0 | 0.017 | 0.065 | 0.104 | |
|---|---|---|---|---|
| T-TCP | ||||
| β (short-time regime) | 1 10 | - 0.65 | 0.30 0.58 | - 0.63 |
| β (long-time regime) | 1 10 | - 1.40 | 1.60 1.44 | - 1.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robin, C.; Lorthioir, C.; Fall, A.; Ovarlez, G.; Amiel, C.; Le Coeur, C. Unexpected Slow Kinetics of Poly(Methacrylic Acid) Phase Separation in the Semi-Dilute Regime. Polymers 2022, 14, 4708. https://doi.org/10.3390/polym14214708
Robin C, Lorthioir C, Fall A, Ovarlez G, Amiel C, Le Coeur C. Unexpected Slow Kinetics of Poly(Methacrylic Acid) Phase Separation in the Semi-Dilute Regime. Polymers. 2022; 14(21):4708. https://doi.org/10.3390/polym14214708
Chicago/Turabian StyleRobin, Clément, Cédric Lorthioir, Abdoulaye Fall, Guillaume Ovarlez, Catherine Amiel, and Clémence Le Coeur. 2022. "Unexpected Slow Kinetics of Poly(Methacrylic Acid) Phase Separation in the Semi-Dilute Regime" Polymers 14, no. 21: 4708. https://doi.org/10.3390/polym14214708
APA StyleRobin, C., Lorthioir, C., Fall, A., Ovarlez, G., Amiel, C., & Le Coeur, C. (2022). Unexpected Slow Kinetics of Poly(Methacrylic Acid) Phase Separation in the Semi-Dilute Regime. Polymers, 14(21), 4708. https://doi.org/10.3390/polym14214708