Height-to-Diameter Ratio and Porosity Strongly Influence Bulk Compressive Mechanical Properties of 3D-Printed Polymer Scaffolds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material and 3D Printing of Scaffold Test Specimens
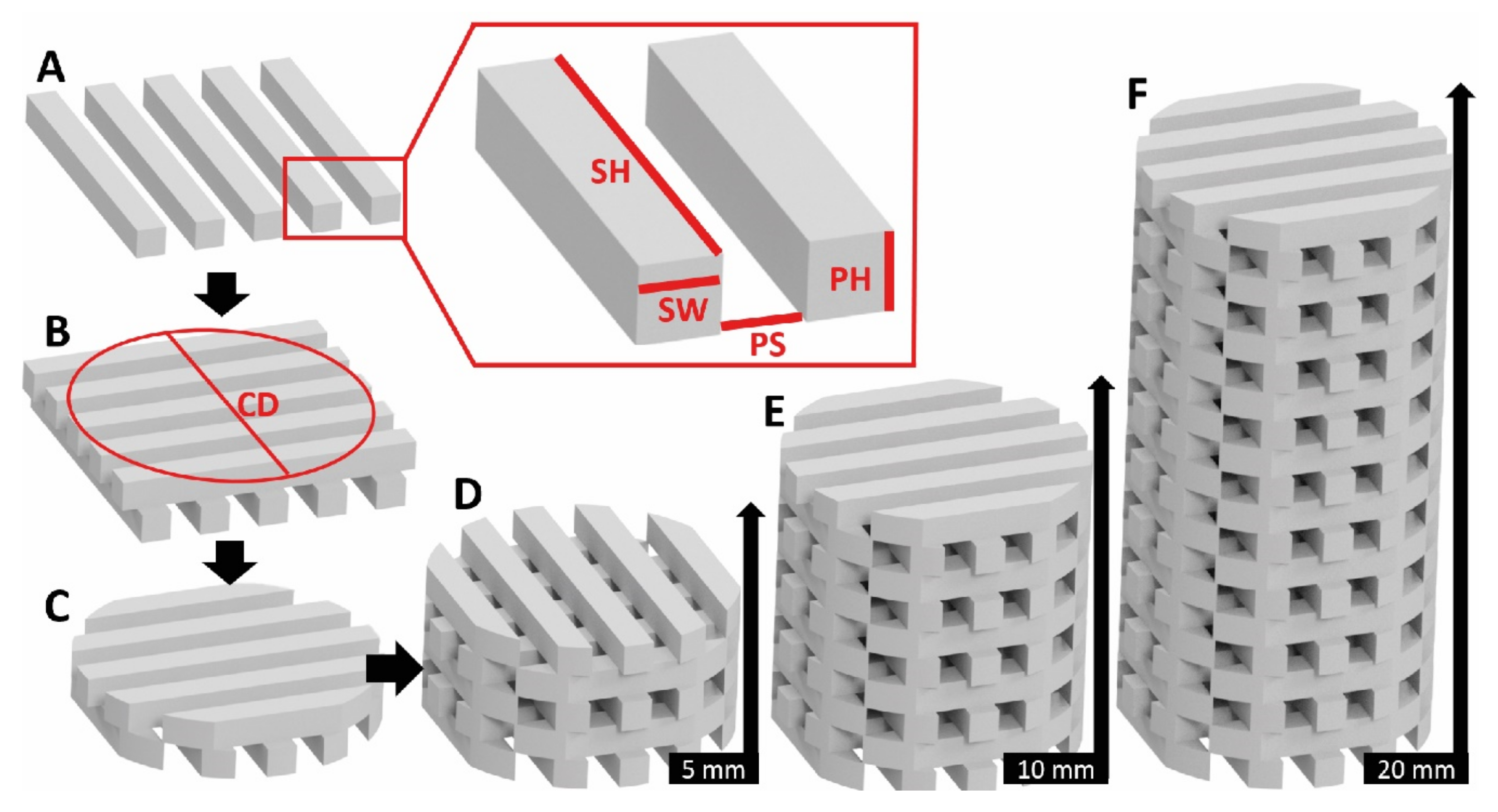
2.2. Scaffold Test Specimen Design and Fabrication Process
- Height, H: A “low” height value of 5 mm represented a 1/2 H/D ratio (D = 10 mm) and is commonly used in biological assessment. End-effects, as defined by St. Venant’s principle, tend to be significant in these geometries. To minimize influence of end-effects, ASTM D695 defines an H/D ratio of 2/1. Accordingly, a ”high” height value of 20 mm was defined in this study. To effectively compare the mechanical behavior and the influence of the end effects, a “medium” height value of 10 mm was additionally defined representing an H/D ratio of 1/1. Thus, the respective H/D ratios were 0.5, 1.0 and 2.0.
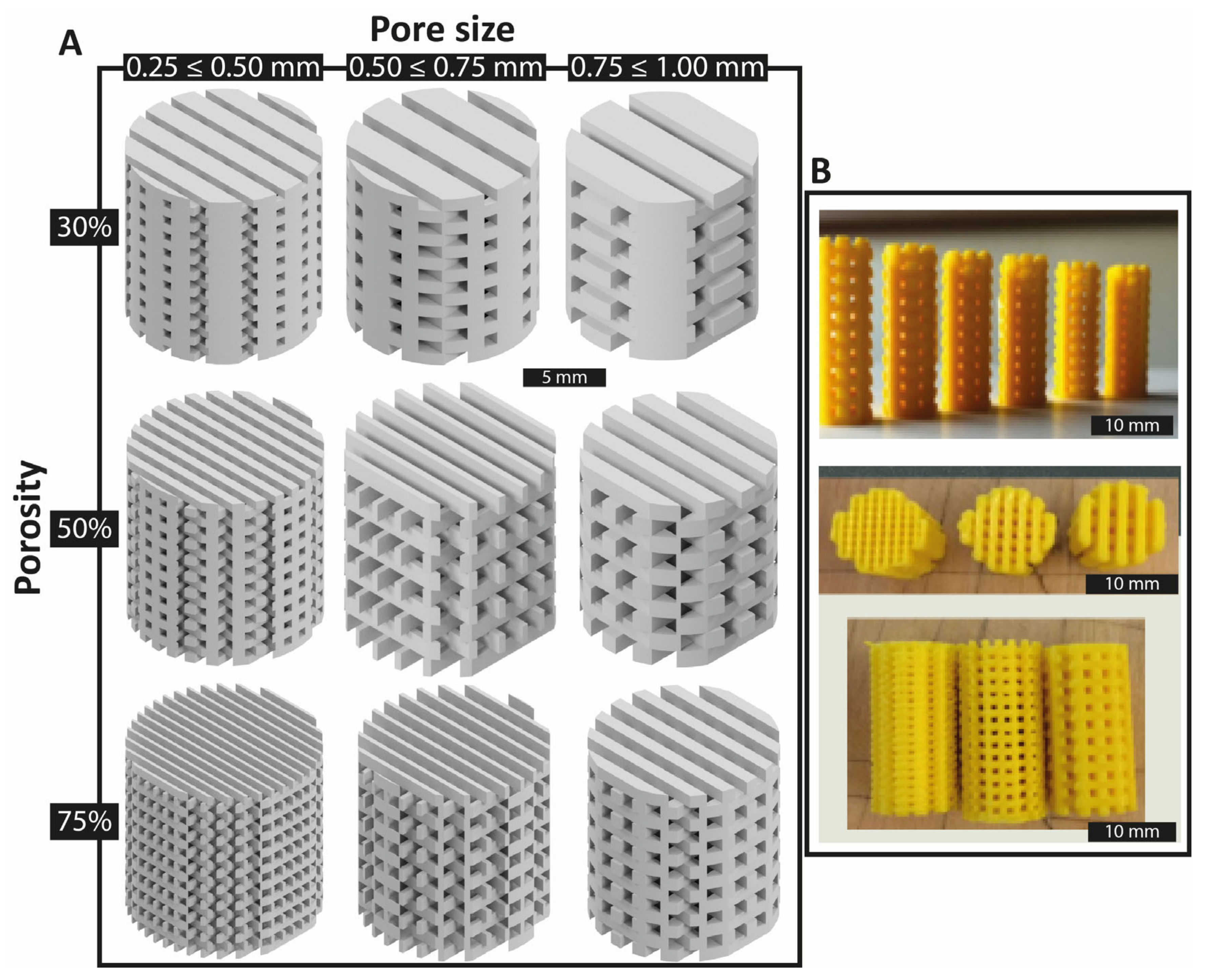
- Porosity: Scaffold designs generally mimic the porosity of bone tissue. Low porosity structures such as cortical bone range between 5–30% porosity, while cancellous bone porosity is mostly in the range of 75–95% [36]. In this study, a “low” porosity level close to 30% and a “high” level near 75% were defined. The “medium” porosity was 50%.
- Pore size: In the current study, pore sizes from 0.25 to 0.5 mm were defined as the “low” level. Pores from 0.5 mm until 0.75 mm were “medium” level and pore sizes from 0.75 to 1.00 mm were the “high” level.
2.3. Morphology Characterization
2.4. Scaffold Test Specimen Mechanical Property Characterization
2.5. Data Analysis
3. Results
3.1. Scaffold Test Specimen Morphology Characterization
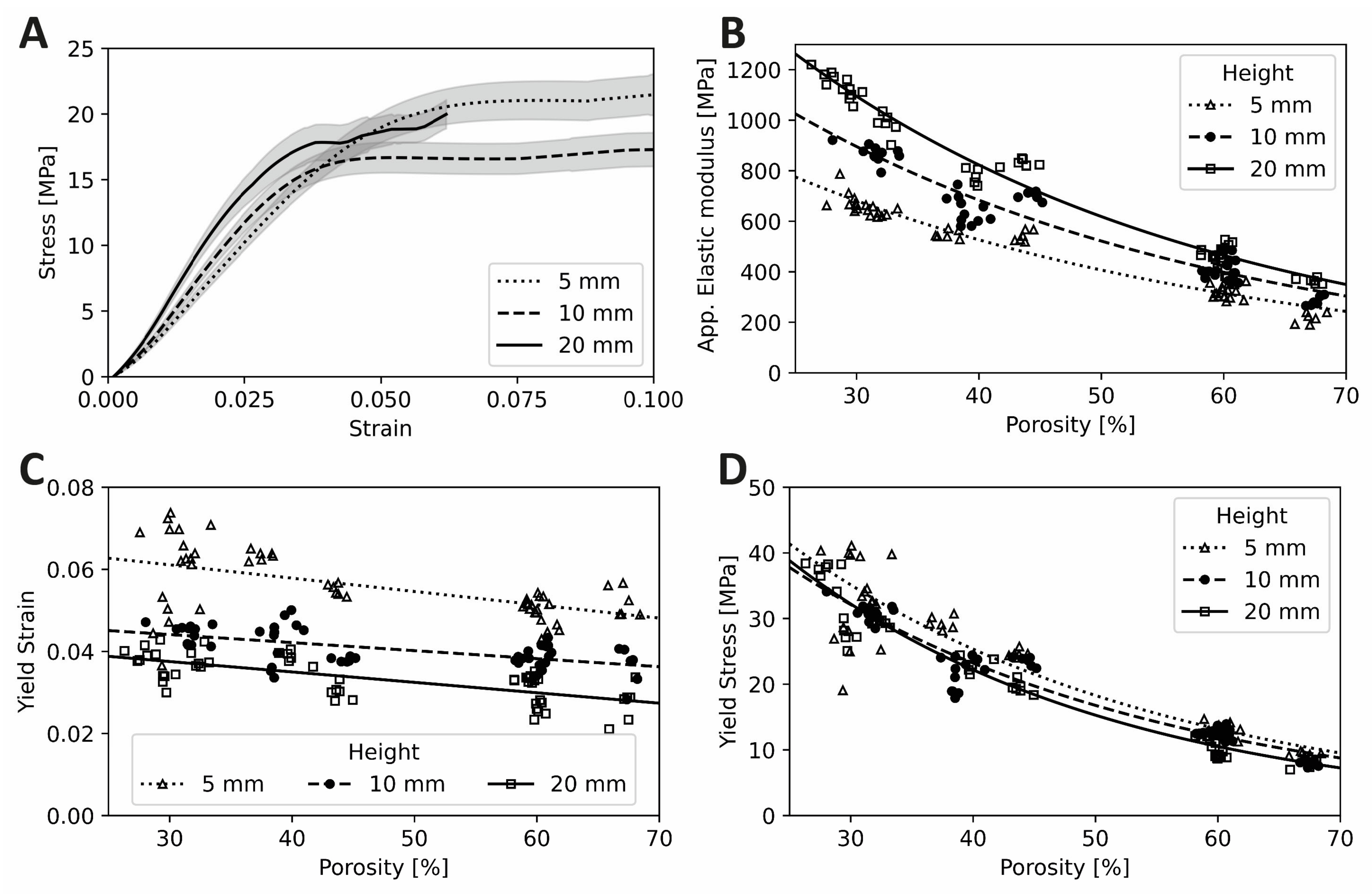
3.2. Scaffold Test Specimen Mechanical Property Characterization
3.3. Multiple Linear Regression Analysis
4. Discussion
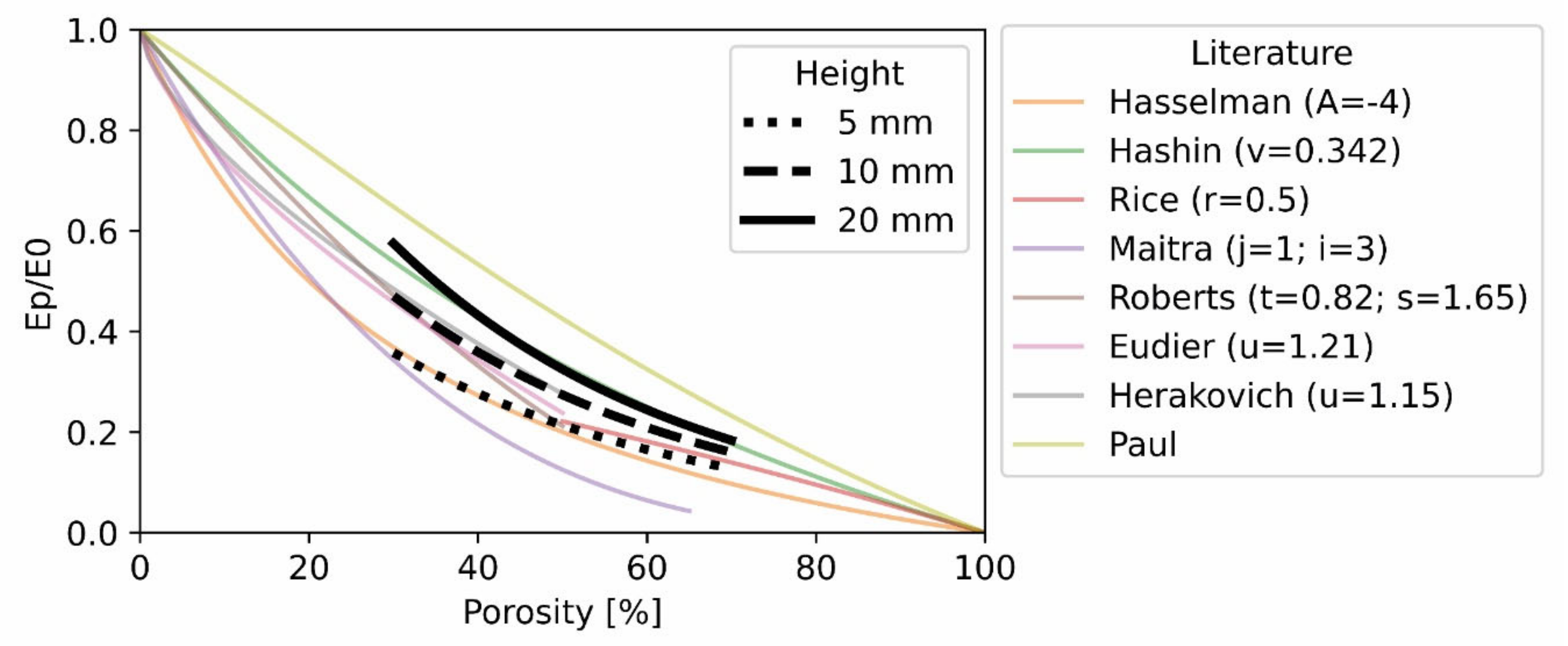
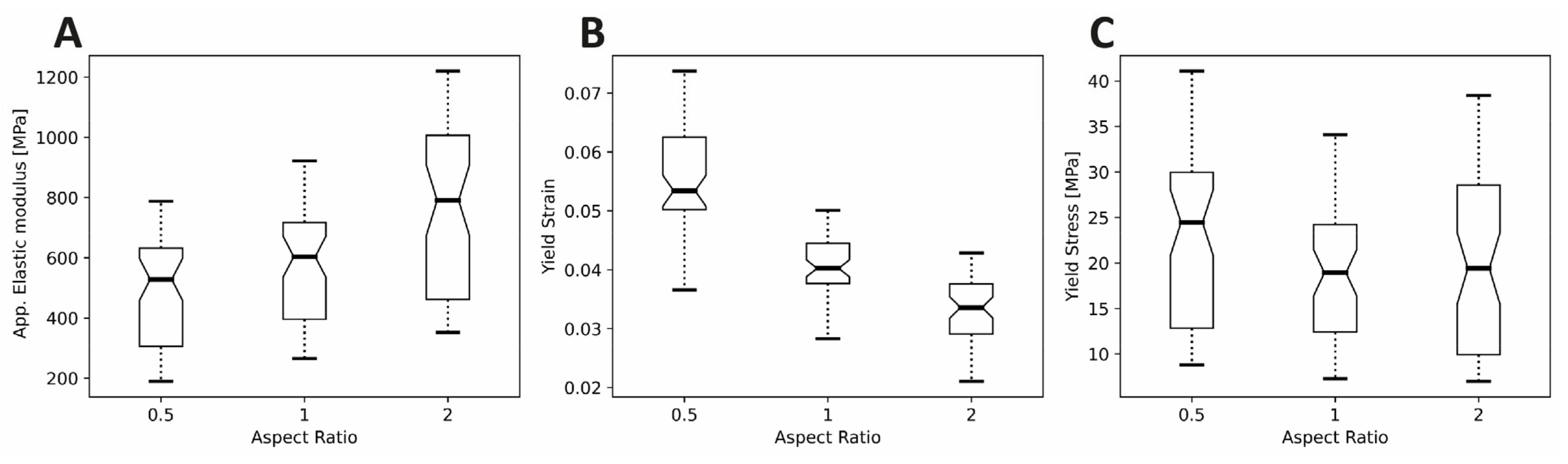
4.1. Elastic Modulus
4.2. Yield Strain
4.3. Yield Stress
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kasten, P.; Beyen, I.; Niemeyer, P.; Luginbühl, R.; Bohner, M.; Richter, W. Porosity and pore size of β-tricalcium phosphate scaffold can influence protein production and osteogenic differentiation of human mesenchymal stem cells: An in vitro and in vivo study. Acta Biomater. 2008, 4, 1904–1915. [Google Scholar] [CrossRef] [PubMed]
- Khatiwala, C.B.; Peyton, S.; Putnam, A. Intrinsic mechanical properties of the extracellular matrix affect the behavior of pre-osteoblastic MC3T3-E1 cells. Am. J. Physiol. Cell Physiol. 2006, 290, 1640–1650. [Google Scholar] [CrossRef] [PubMed]
- Mygind, T.; Stiehler, M.; Baatrup, A.; Li, H.; Zou, X.; Flyvbjerg, A.; Kassem, M.; Bünger, C. Mesenchymal stem cell ingrowth and differentiation on coralline hydroxyapatite scaffolds. Biomaterials 2007, 28, 1036–1047. [Google Scholar] [CrossRef] [PubMed]
- Vivanco, J.; Aiyangar, A.; Araneda, A.; Ploeg, H.-L. Mechanical characterization of injection-molded macro porous bioceramic bone scaffolds. J. Mech. Behav. Biomed. Mater. 2012, 9, 137–152. [Google Scholar] [CrossRef] [PubMed]
- Hutmacher, D.W. Scaffolds in tissue engineering bone and cartilage. In The Biomaterials: Silver Jubilee Compendium; Williams, D.F., Ed.; Elsevier Science: Oxford, UK, 2000; pp. 175–189. [Google Scholar] [CrossRef]
- Van Bael, S.; Chai, Y.C.; Truscello, S.; Moesen, M.; Kerckhofs, G.; Van Oosterwyck, H.; Kruth, J.-P.; Schrooten, J. The effect of pore geometry on the in vitro biological behavior of human periosteum-derived cells seeded on selective laser-melted Ti6Al4V bone scaffolds. Acta Biomater. 2012, 8, 2824–2834. [Google Scholar] [CrossRef] [PubMed]
- Karageorgiou, V.; Kaplan, D. Porosity of 3D biomaterial scaffolds and osteogenesis. Biomaterials 2005, 26, 5474–5491. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, N.; Hamlet, S.; Love, R.M.; Nguyen, N.-T. Porous scaffolds for bone regeneration. J. Sci. Adv. Mater. Devices 2020, 5, 1–9. [Google Scholar] [CrossRef]
- Flautre, B.; Descamps, M.; Delecourt, C.; Blary, M.C.; Hardouin, P. Porous HA ceramic for bone replacement: Role of the pores and interconnections—Experimental study in the rabbit. J. Mater. Sci. Mater. Med. 2001, 12, 679–682. [Google Scholar] [CrossRef]
- Galois, L.; Mainard, D. Bone ingrowth into two porous ceramics with different pore sizes: An experimental study. Acta Orthop. Belg. 2004, 70, 598–603. [Google Scholar] [PubMed]
- Gauthier, O.; Bouler, J.-M.; Aguado, E.; Pilet, P.; Daculsi, G. Macroporous biphasic calcium phosphate ceramics: Influence of macropore diameter and macroporosity percentage on bone ingrowth. Biomaterials 1998, 19, 133–139. [Google Scholar] [CrossRef]
- Cheung, H.Y.; Lau, K.T.; Lu, T.P.; Hui, D. A critical review on polymer-based bio-engineered materials for scaffold development. Compos. Part B Eng. 2007, 38, 291–300. [Google Scholar] [CrossRef]
- Eggli, P.S.; Muller, W.; Schenk, R.K. Porous hydroxyapatite and tricalcium phosphate cylinders with two different pore size ranges implanted in the cancellous bone of rabbits. A comparative histomorphometric and histologic study of bone ingrowth and implant substitution. Clin. Orthop. Relat. Res. 1988, 232, 127–138. [Google Scholar] [CrossRef]
- Schek, R.M.; Wilke, E.N.; Hollister, S.J.; Krebsbach, P.H. Combined use of designed scaffolds and adenoviral gene therapy for skeletal tissue engineering. Biomaterials 2006, 27, 1160–1166. [Google Scholar] [CrossRef] [PubMed]
- Hollister, S.; Lin, C.; Saito, E.; Schek, R.; Taboas, J.; Williams, J.; Partee, B.; Flanagan, C.; Diggs, A.; Wilke, E.; et al. Engineering craniofacial scaffolds. Orthod. Craniofacial Res. 2005, 8, 162–173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buckley, C.T.; O’Kelly, K.U. Fabrication and characterization of a porous multidomain hydroxyapatite scaffold for bone tissue engineering investigations. J. Biomed. Mater. Res. Part B Appl. Biomater. 2010, 93, 459–467. [Google Scholar] [CrossRef]
- Moradi, M.; Aminzadeh, A.; Rahmatabadi, D.; Hakimi, A. Experimental investigation on mechanical characterization of 3D printed PLA produced by fused deposition modeling (FDM). Mater. Res. Express 2021, 8, 035304. [Google Scholar] [CrossRef]
- Bobbert, F.; Lietaert, K.; Eftekhari, A.; Pouran, B.; Ahmadi, S.; Weinans, H.; Zadpoor, A. Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties. Acta Biomater. 2017, 53, 572–584. [Google Scholar] [CrossRef] [Green Version]
- Kelly, C.N.; Miller, A.T.; Hollister, S.; Guldberg, R.E.; Gall, K. Design and Structure–Function Characterization of 3D Printed Synthetic Porous Biomaterials for Tissue Engineering. Adv. Healthc. Mater. 2018, 7, e201701095. [Google Scholar] [CrossRef] [PubMed]
- Baier, R.V.; Raggio, J.I.C.; Arancibia, C.T.; Bustamante, M.; Pérez, L.; Burda, I.; Aiyangar, A.; Vivanco, J.F. Structure-function assessment of 3D-printed porous scaffolds by a low-cost/open source fused filament fabrication printer. Mater. Sci. Eng. C 2021, 123, 111945. [Google Scholar] [CrossRef] [PubMed]
- Vivanco, J.F.; Slane, J.; Aiyangar, A. Multiscale Biomechanical Characterization of Bioceramic Bone Scaffolds. In Experimental Methods in Orthopaedic Biomechanics; Academic Press: Cambridge, MA, USA, 2017; pp. 201–216. [Google Scholar] [CrossRef]
- Pioletti, D.P. Biomechanics in bone tissue engineering. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 837–846. [Google Scholar] [CrossRef] [Green Version]
- Zadpoor, A.A.; Malda, J. Additive Manufacturing of Biomaterials, Tissues, and Organs. Ann. Biomed. Eng. 2017, 45, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Keaveny, T.M.; Pinilla, T.P.; Crawford, R.P.; Kopperdahl, D.L.; Lou, A. Systematic and random errors in compression testing of trabecular bone. J. Orthop. Res. 1997, 15, 101–110. [Google Scholar] [CrossRef]
- Aiyangar, A.K.; Vivanco, J.; Au, A.G.; Anderson, P.A.; Smith, E.L.; Ploeg, H.L. Dependence of anisotropy of human lumbar vertebral trabecular bone on quantitative computed tomography-based apparent density. J. Biomech. Eng. 2014, 136, 091003. [Google Scholar] [CrossRef] [PubMed]
- Abidin, Z.; Fadhlurrahman, I.G.; Akbar, I.; Putra, R.U.; Prakoso, A.T.; Kadir, M.Z.; Astuti, A.; Syahrom, A.; Ammarullah, M.I.; Jamari, J.; et al. Numerical Investigation of the Mechanical Properties of 3D Printed PLA Scaffold 2022. In Proceedings of the 5th FIRST T1 T2 2021 International Conference (FIRST-T1-T2 2021), Palembang, Indonesia, 20–21 October 2021. [Google Scholar] [CrossRef]
- Pagano, C.; Rebaioli, L.; Baldi, F.; Fassi, I. Relationships between size and mechanical properties of scaffold-like structures. Mech. Adv. Mater. Struct. 2020, 28, 1812–1817. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, R.; Singh, M. On compressive and morphological features of 3D printed almond skin powder reinforced PLA matrix. Mater. Res. Express 2020, 7, 025311. [Google Scholar] [CrossRef]
- ASTM D695; Standard Test Method for Compressive Properties of Rigid Plastics 1 Standard Test Method for Compressive Properties of Rigid Plastics. ASTM International: West Conshohocken, PA, USA, 2015.
- Gregor, A.; Filová, E.; Novák, M.; Kronek, J.; Chlup, H.; Buzgo, M.; Blahnová, V.; Lukášová, V.; Bartoš, M.; Nečas, A.; et al. Designing of PLA scaffolds for bone tissue replacement fabricated by ordinary commercial 3D printer. J. Biol. Eng. 2017, 11, 31. [Google Scholar] [CrossRef] [Green Version]
- Tamaddon, M.; Blunn, G.; Tan, R.; Yang, P.; Sun, X.; Chen, S.-M.; Luo, J.; Liu, Z.; Wang, L.; Li, D.; et al. In vivo evaluation of additively manufactured multi-layered scaffold for the repair of large osteochondral defects. Bio-Design Manuf. 2022, 5, 481–496. [Google Scholar] [CrossRef] [PubMed]
- Al-Barqawi, M.O.; Church, B.; Thevamaran, M.; Thoma, D.J.; Rahman, A. Design and Validation of Additively Manufactured Metallic Cellular Scaffold Structures for Bone Tissue Engineering. Materials 2022, 15, 3310. [Google Scholar] [CrossRef] [PubMed]
- Soleyman, E.; Rahmatabadi, D.; Soltanmohammadi, K.; Aberoumand, M.; Ghasemi, I.; Abrinia, K.; Baniassadi, M.; Wang, K.; Baghani, M. Shape memory performance of PETG 4D printed parts under compression in cold, warm, and hot programming. Smart Mater. Struct. 2022, 31, 085002. [Google Scholar] [CrossRef]
- Kilian, D.; von Witzleben, M.; Lanaro, M.; Wong, C.S.; Vater, C.; Lode, A.; Allenby, M.C.; Woodruff, M.A.; Gelinsky, M. 3D Plotting of Calcium Phosphate Cement and Melt Electrowriting of Polycaprolactone Microfibers in One Scaffold: A Hybrid Additive Manufacturing Process. J. Funct. Biomater. 2022, 13, 75. [Google Scholar] [CrossRef]
- Baier, R.V.; Raggio, J.I.C.; Giovanetti, C.M.; Palza, H.; Burda, I.; Terrasi, G.; Weisse, B.; De Freitas, G.S.; Nyström, G.; Vivanco, J.F.; et al. Shape fidelity, mechanical and biological performance of 3D printed polycaprolactone-bioactive glass composite scaffolds. Mater. Sci. Eng. C 2021, 134, 112540. [Google Scholar] [CrossRef] [PubMed]
- Hajiali, F.; Tajbakhsh, S.; Shojaei, A. Fabrication and Properties of Polycaprolactone Composites Containing Calcium Phosphate-Based Ceramics and Bioactive Glasses in Bone Tissue Engineering: A Review. Polym. Rev. 2018, 58, 164–207. [Google Scholar] [CrossRef]
- Ziemian, C.; Sharma, M.; Ziemi, S. Anisotropic Mechanical Properties of ABS Parts Fabricated by Fused Deposition Modelling. In Mechanical Engineering; InTech: London, UK, 2012. [Google Scholar] [CrossRef] [Green Version]
- Ho, S.T.; Hutmacher, D.W. A comparison of micro CT with other techniques used in the characterization of scaffolds. Biomaterials 2006, 27, 1362–1376. [Google Scholar] [CrossRef] [PubMed]
- Raheem, Z. Designation: D695–15 Standard Test Method for Compressive Properties of Rigid Plastics 1 Standard Test Method for Compressive Properties of Rigid Plastics 1 2019; ASTM International: West Conshohocken, PA, USA, 2019. [Google Scholar] [CrossRef]
- Ashby, M.; Shercliff, H.; Cebon, D. Materials: Engineering, science, processing and design. Mater. Today 2010, 13, 67. [Google Scholar] [CrossRef]
- Liviano, D.; Pujol, M. Análisis Cuantitativo con R: Matemáticas, Estadística y Econometría; UOC: Barcelona, Spain, 2017. [Google Scholar]
- Pirie, W. Spearman Rank Correlation Coefficient. In Encyclopedia of Statistical Sciences; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Zhang, Z. Variable selection with stepwise and best subset approaches. Ann. Transl. Med. 2016, 4, 136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cayuela, L. Modelos Lineales: Regresión, ANOVA y ANCOVA. 2014. Available online: https://tauniversity.org/sites/default/files/modelos_lineales_regresion_anova_y_ancova.pdf (accessed on 16 November 2022).
- Choren, J.A.; Heinrich, S.M.; Silver-Thorn, M.B. Young’s modulus and volume porosity relationships for additive manufacturing applications. J. Mater. Sci. 2013, 48, 5103–5112. [Google Scholar] [CrossRef]
- Hashin, Z. The elastic moduli of heterogeneous materials. J. Appl. Mech. Trans. ASME 1960, 29, 143–150. [Google Scholar] [CrossRef]
- Hasselman, D.P.H. On the Porosity Dependence of the Elastic Moduli of Polycrystalline Refractory Materials. J. Am. Ceram. Soc. 1962, 45, 452–453. [Google Scholar] [CrossRef]
- Herakovich, C.T.; Baxter, S.C. Influence of pore geometry on the effective response of porous media. J. Mater. Sci. 1999, 34, 1595–1609. [Google Scholar] [CrossRef]
- Maitra, A.K.; Phani, K.K. Ultrasonic evaluation of elastic parameters of sintered powder compacts. J. Mater. Sci. 1994, 29, 4415–4419. [Google Scholar] [CrossRef]
- Rice, R.W. Evaluation and extension of physical property-porosity models based on minimum solid area. J. Mater. Sci. 1996, 31, 102–118. [Google Scholar] [CrossRef]
- Spriggs, R.M. Expression for Effect of Porosity on Elastic Modulus of Polycrystalline Refractory Materials, Particularly Aluminum Oxide. J. Am. Ceram. Soc. 1961, 44, 628–629. [Google Scholar] [CrossRef]
- Ledbetter, H.M.; Lei, M.; Datta, S.K. Elastic Properties of Porous Ceramics. MRS Proc. 1988, 142, 3041–3048. [Google Scholar] [CrossRef]
- Torres-Sanchez, C.; Al Mushref, F.R.A.; Norrito, M.; Yendall, K.; Liu, Y.; Conway, P.P. The effect of pore size and porosity on mechanical properties and biological response of porous titanium scaffolds. Mater. Sci. Eng. C 2017, 77, 219–228. [Google Scholar] [CrossRef] [PubMed]
- Torres-Sanchez, C.; McLaughlin, J.; Fotticchia, A. Porosity and pore size effect on the properties of sintered Ti35Nb4Sn alloy scaffolds and their suitability for tissue engineering applications. J. Alloys Compd. 2018, 731, 189–199. [Google Scholar] [CrossRef] [Green Version]
- Guarino, V.; Causa, F.; Ambrosio, L. Porosity and mechanical properties relationship in PCL porous scaffolds. J. Appl. Biomater. Biomech. 2007, 5, 149–157. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Li, L.; Ding, S.; Liu, C.; Ai, J. Effect of porous structure and pore size on mechanical strength of 3D-printed comby scaffolds. Mater. Lett. 2018, 223, 21–24. [Google Scholar] [CrossRef]
- Alaboodi, A.S.; Sivasankaran, S. Experimental design and investigation on the mechanical behavior of novel 3D printed biocompatibility polycarbonate scaffolds for medical applications. J. Manuf. Process. 2018, 35, 479–491. [Google Scholar] [CrossRef]
- Guo, T.; Holzberg, T.R.; Lim, C.G.; Gao, F.; Gargava, A.; Trachtenberg, J.E.; Mikos, A.G.; Fisher, J.P. 3D printing PLGA: A quantitative examination of the effects of polymer composition and printing parameters on print resolution. Biofabrication 2017, 9, 024101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, H.; Han, Q.; Wang, C.; Liu, Y.; Chen, B.; Wang, J. Porous Scaffold Design for Additive Manufacturing in Orthopedics: A Review. Front. Bioeng. Biotechnol. 2020, 8, 609. [Google Scholar] [CrossRef] [PubMed]
- McGill, R.; Tukey, J.W.; Larsen, W.A. Variations of box plots. Am. Stat. 1978, 32, 12–16. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]


| Extrusion temperature (°C) | 210 |
| Bed temperature (°C) | 24 |
| Nozzle diameter (mm) | 0.4 |
| Layer thickness (mm) | 0.15 |
| Extrusion speed (mm/s) | 60 |
| Travel speed (mm/s) | 90 |
| Printing direction (°) | 0 and 90 |
| Parameters | Levels: | Low | Medium | High |
|---|---|---|---|---|
| Porosity (%) | ~30 | ~50 | ~70 | |
| Height (mm) | 5 | 10 | 20 | |
| Pore size (mm) | 0.25–0.50 | 0.50–0.75 | 0.75–1.00 | |
| H/D ratio | 0.5 | 1.0 | 2.0 | |
| Design Parameters | Measured Morphology and Mechanical Properties (n = 6) | |||||
|---|---|---|---|---|---|---|
| Height | Porosity | Pore size | Porosity (%) | Eapp (MPa) | σy (MPa) | εy (%) |
| 5 | 30 | L–M–H | 30.57 ± 1.40 | 659.77 ± 39.25 | 32.93 ± 6.25 | 6.03 ± 1.08 |
| 50 | L–M–H | 54.69 ± 7.84 | 393.48 ± 106.94 | 16.74 ± 5.62 | 5.10 ± 0.41 | |
| 75 | L–M–H | 54.82 ± 12.6 | 361.03 ± 139.91 | 17.35 ± 8.66 | 5.57 ± 0.60 | |
| 10 | 30 | L–M–H | 33.80 ± 3.38 | 802.87 ± 99.06 | 27.39 ± 5.40 | 4.26 ± 0.41 |
| 50 | L–M–H | 54.53 ± 7.22 | 515.64 ± 134.45 | 16.33 ± 5.09 | 3.76 ± 0.14 | |
| 75 | L–M–H | 55.97 ± 11.9 | 423.73 ± 143.24 | 14.31 ± 6.48 | 4.15 ± 0.52 | |
| 20 | 30 | L–M–H | 29.94 ± 2.04 | 1086.85 ± 85.69 | 31.95 ± 4.49 | 3.74 ± 0.35 |
| 50 | L–M–H | 54.31 ± 7.43 | 586.79 ± 159.47 | 13.19 ± 4.30 | 2.96 ± 0.34 | |
| 75 | L–M–H | 55.67 ± 11.5 | 522.31 ± 187.85 | 13.79 ± 6.60 | 3.29 ± 0.56 | |
| Independent Variables | Response Variables | |||||
|---|---|---|---|---|---|---|
| Height | Porosity | Pore Size | Eapp | Yield Stress | Yield Strain | |
| Height | 1 | −0.113 | 0.009 | 0.501 | −0.043 | −0.761 |
| Porosity | - | 1 | 0.255 | −0.859 | −0.912 | −0.269 |
| Pore size | - | - | 1 | −0.178 | −0.204 | −0.135 |
| Eapp | - | - | - | 1 | 0.784 | −0.112 |
| Yield Stress | - | - | - | - | 1 | 0.481 |
| Yield Strain | - | - | - | - | - | 1 |
| Y | X | p-Value | |||
|---|---|---|---|---|---|
| Eapp (MPa) | Intercept | 817.31 | <0.0001 | **** | |
| Height | 0.19 | 43.36 | <0.0001 | **** | |
| Porosity | 0.73 | −8.92 | <0.0001 | **** | |
| Pore size | NA | NA | NA | ||
| Height:Porosity | 0.04 | −8.92 | <0.0001 | **** | |
| Porosity:Pore size | NA | NA | NA | ||
| Final Model: | Eapp = (Height) × β1 + (Porosity) × β2 + (Height:Porosity) × β4 + Intercept | ||||
| Yield Stress (MPa) | Intercept | 52.93 | <0.0001 | **** | |
| Height | 0.02 | −0.19 | <0.0001 | **** | |
| Porosity | 0.94 | −0.67 | <0.0001 | **** | |
| Pore size | 0.003 | 2.49 | 0.002 | ** | |
| Height:Porosity | NA | NA | NA | ||
| Porosity:Pore size | NA | NA | NA | ||
| Final Model: | Yield stress = (Height) × β1 + (Porosity) × β2 + (Pore size) × β3 + Intercept | ||||
| Yield Strain | Intercept | 0.07 | <0.0001 | **** | |
| Height | 0.60 | −1.40 × 10−3 | <0.0001 | **** | |
| Porosity | 0.12 | −2.76 × 10−4 | <0.0001 | **** | |
| Pore size | NA | NA | NA | ||
| Height:Porosity | NA | NA | NA | ||
| Porosity:Pore size | NA | NA | NA | ||
| Final Model: | Yield strain = (Height) × β1 + (Porosity) × β2 + Intercept | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contreras Raggio, J.I.; Arancibia, C.T.; Millán, C.; Ploeg, H.-L.; Aiyangar, A.; Vivanco, J.F. Height-to-Diameter Ratio and Porosity Strongly Influence Bulk Compressive Mechanical Properties of 3D-Printed Polymer Scaffolds. Polymers 2022, 14, 5017. https://doi.org/10.3390/polym14225017
Contreras Raggio JI, Arancibia CT, Millán C, Ploeg H-L, Aiyangar A, Vivanco JF. Height-to-Diameter Ratio and Porosity Strongly Influence Bulk Compressive Mechanical Properties of 3D-Printed Polymer Scaffolds. Polymers. 2022; 14(22):5017. https://doi.org/10.3390/polym14225017
Chicago/Turabian StyleContreras Raggio, José I., Carlos Toro Arancibia, Carola Millán, Heidi-Lynn Ploeg, Ameet Aiyangar, and Juan F. Vivanco. 2022. "Height-to-Diameter Ratio and Porosity Strongly Influence Bulk Compressive Mechanical Properties of 3D-Printed Polymer Scaffolds" Polymers 14, no. 22: 5017. https://doi.org/10.3390/polym14225017
APA StyleContreras Raggio, J. I., Arancibia, C. T., Millán, C., Ploeg, H.-L., Aiyangar, A., & Vivanco, J. F. (2022). Height-to-Diameter Ratio and Porosity Strongly Influence Bulk Compressive Mechanical Properties of 3D-Printed Polymer Scaffolds. Polymers, 14(22), 5017. https://doi.org/10.3390/polym14225017







