Enthalpic Interactions and Solution Behaviors of Solvent-Free Polymer Brushes
Abstract
:1. Introduction
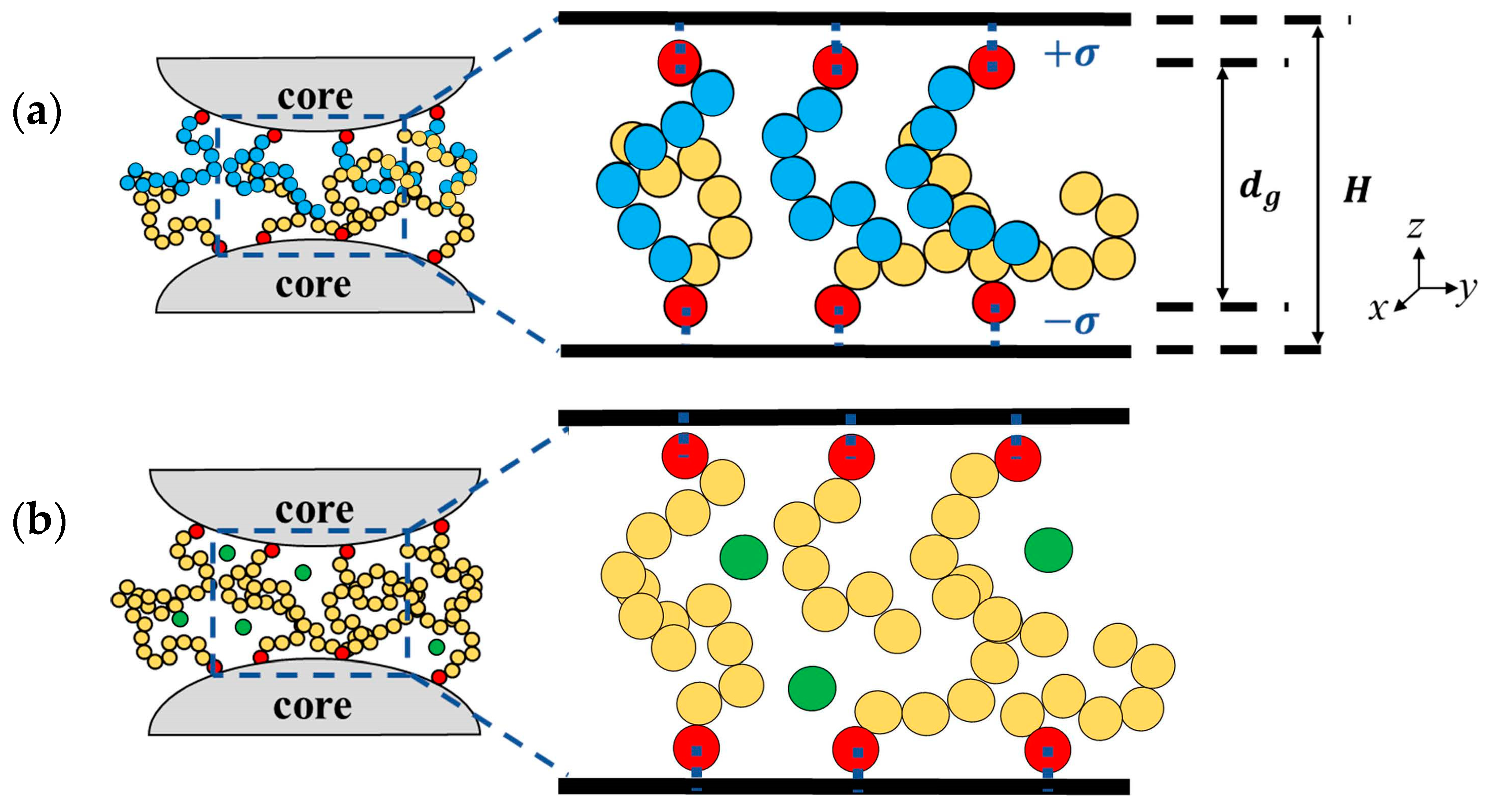
2. Models and Simulation Methods
3. Results And Discussion
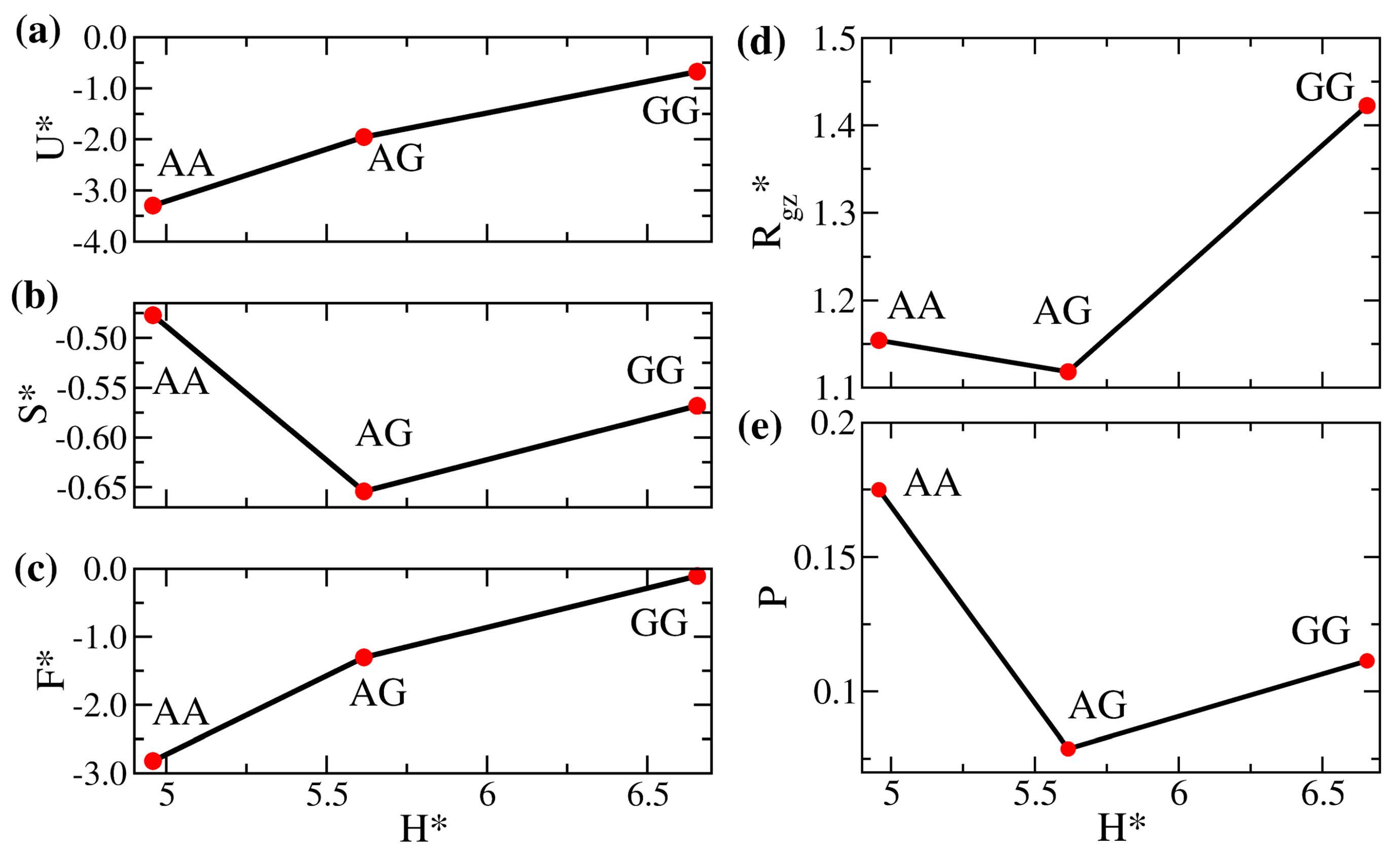
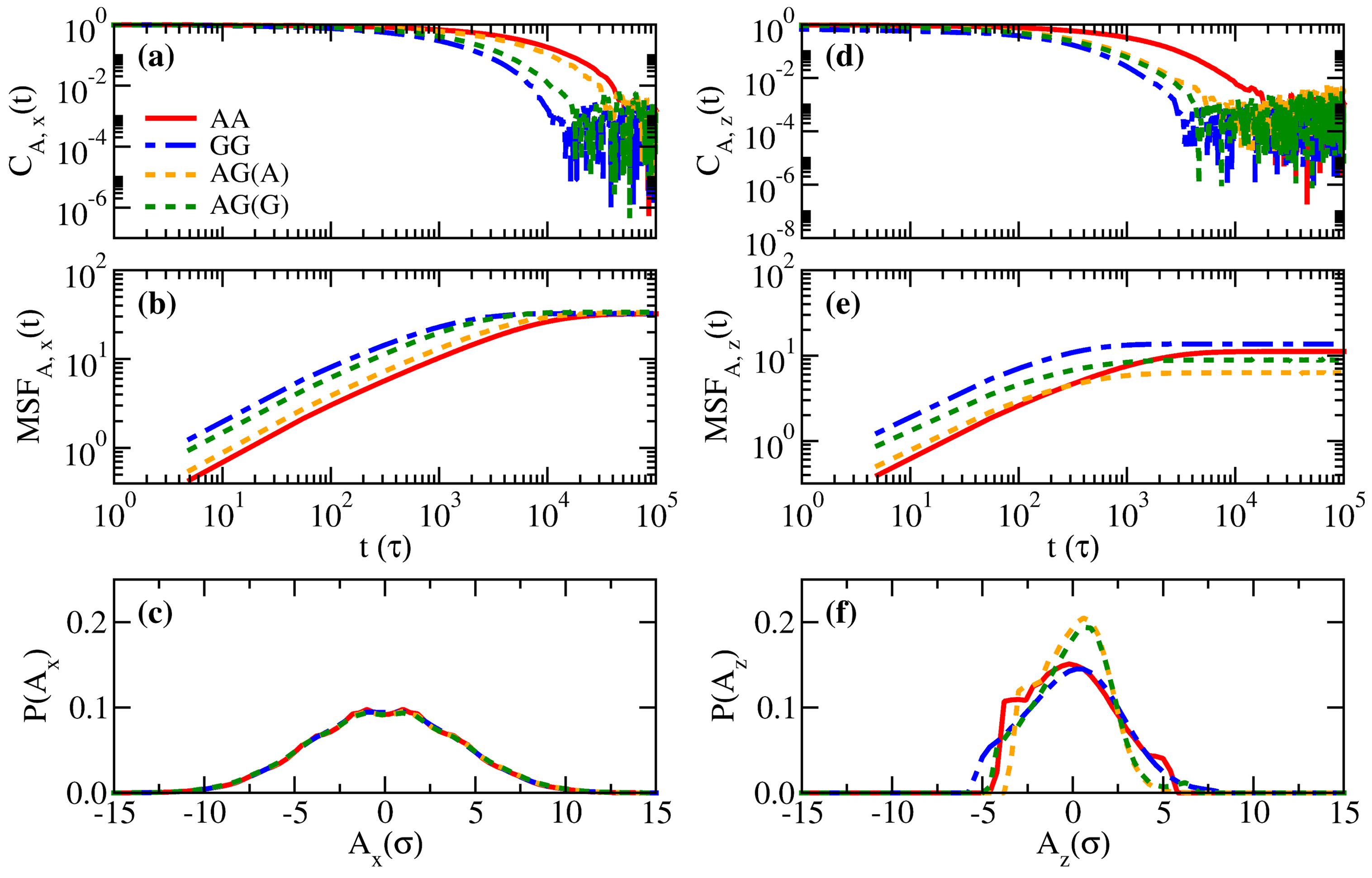
3.1. Properties of Solvent-Free Binary Polymer Brushes
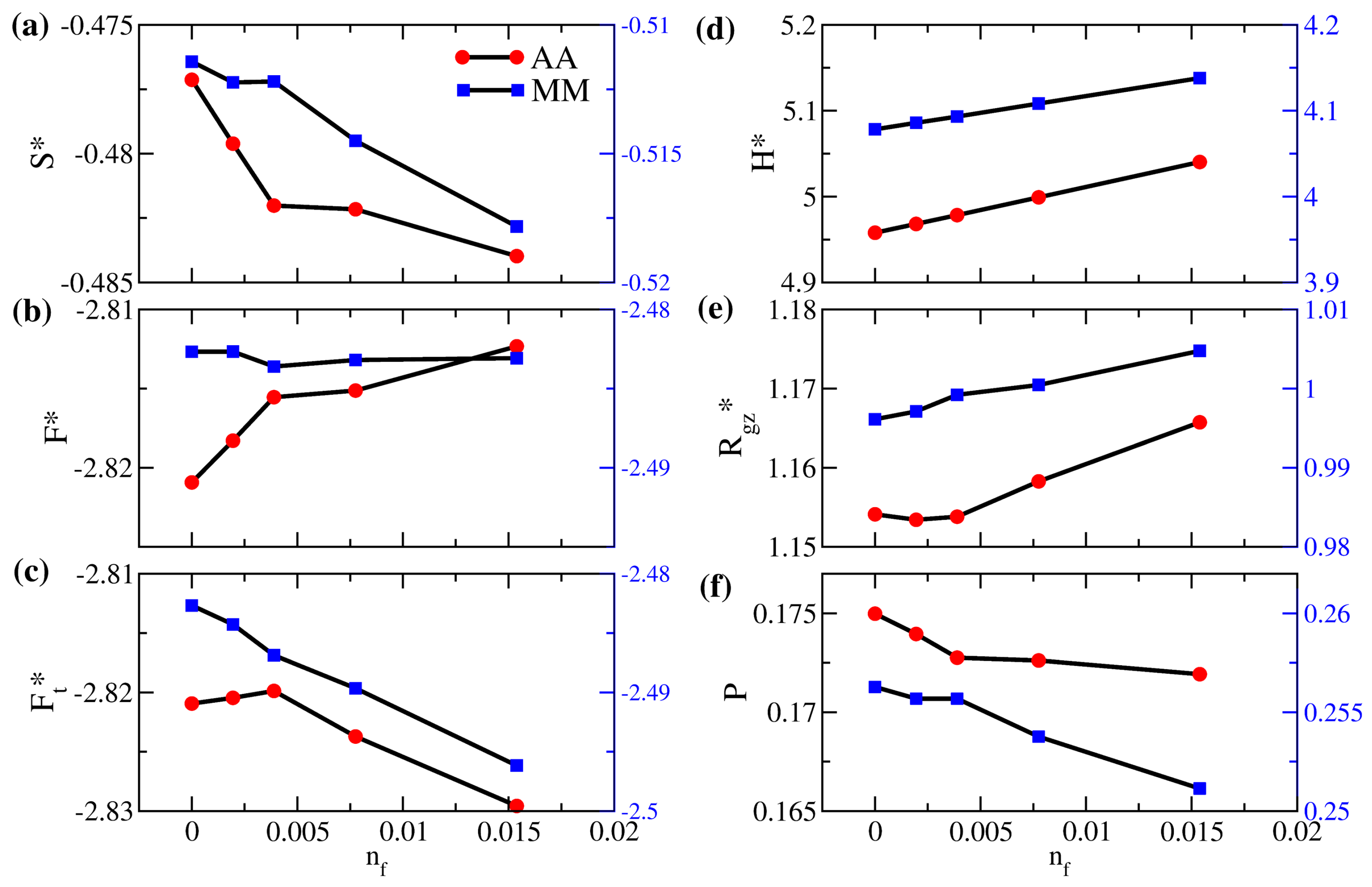
3.2. Solution Behaviors of Polymer Brushes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bourlinos, A.; Chowdhury, S.R.; Herrera, R.; Jiang, D.; Zhang, Q.; Archer, L.; Giannelis, E. Functionalized Nanostructures with Liquid-Like Behavior: Expanding the Gallery of Available Nanostructures. Adv. Funct. Mater. 2005, 15, 1285–1290. [Google Scholar] [CrossRef]
- Rodriguez, R.; Herrera, R.; Archer, L.A.; Giannelis, E.P. Nanoscale Ionic Materials. Adv. Mater. 2008, 20, 4353–4358. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, R.; Herrera, R.; Bourlinos, A.B.; Li, R.; Amassian, A.; Archer, L.A.; Giannelis, E.P. The Synthesis and Properties of Nanoscale Ionic Mterials. Appl. Organomet. Chem. 2010, 24, 581–589. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, S.; Choudhury, S.; Agrawal, A.; Archer, L.A. Self-Suspended Polymer Grafted Nanoparticles. Curr. Opin. Chem. Eng. 2017, 16, 92–101. [Google Scholar] [CrossRef]
- Liu, X.; Abel, B.A.; Zhao, Q.; Li, S.; Choudhury, S.; Zheng, J.; Archer, L.A. Microscopic Origins of Caging and Equilibration of Self-Suspended Hairy Nanoparticles. Macromolecules 2019, 52, 8187–8196. [Google Scholar] [CrossRef]
- Yu, H.Y.; Koch, D.L. Structure of Solvent-Free Nanoparticle-Organic Hybrid Materials. Langmuir 2010, 26, 16801–16811. [Google Scholar] [CrossRef]
- Tai, C.H.; Pan, G.T.; Yu, H.Y. Entropic Effects in Solvent-Free Bidisperse Polymer Brushes Investigated Using Density Functional Theories. Langmuir 2019, 35, 16835–16849. [Google Scholar] [CrossRef]
- Nugent, J.L.; Moganty, S.S.; Archer, L.A. Nanoscale Organic Hybrid Electrolytes. Adv. Mater. 2010, 22, 3677–3680. [Google Scholar] [CrossRef] [Green Version]
- Moganty, S.S.; Jayaprakash, N.; Nugent, J.L.; Shen, J.; Archer, L.A. Ionic-Liquid-Tethered Nanoparticles: Hybrid Electrolytes. Angew. Chem. 2010, 122, 9344–9347. [Google Scholar] [CrossRef]
- Agrawal, A.; Choudhury, S.; Archer, L.A. A Highly Conductive, Non-Flammable Polymer–Nanoparticle Hybrid Electrolyte. RSC Adv. 2015, 5, 20800–20809. [Google Scholar] [CrossRef]
- Choudhury, S.; Agrawal, A.; Wei, S.; Jeng, E.; Archer, L.A. Hybrid Hairy Nanoparticle Electrolytes Stabilizing Lithium Metal Batteries. Chem. Mater. 2016, 28, 2147–2157. [Google Scholar] [CrossRef]
- Feric, T.G.; Hamilton, S.T.; Haque, M.A.; Jeddi, J.; Sangoro, J.; Dadmun, M.D.; Park, A.H.A. Impacts of Bond Type and Grafting Density on the Thermal, Structural, and Transport Behaviors of Nanoparticle Organic Hybrid Materials-Based Electrolytes. Adv. Funct. Mater. 2022, 32, 2203947. [Google Scholar] [CrossRef]
- Kim, D.; Archer, L.A. Nanoscale Organic-Inorganic Hybrid Lubricants. Langmuir 2011, 27, 3083–3094. [Google Scholar] [CrossRef] [PubMed]
- Ye, M.; Cai, T.; Shang, W.; Zhao, L.; Zhang, Y.; Liu, D.; Liu, S. Friction-induced transfer of carbon quantum dots on the interface: Microscopic and spectroscopic studies on the role of inorganic–organic hybrid nanoparticles as multifunctional additive for enhanced lubrication. Tribol. Int. 2018, 127, 557–567. [Google Scholar] [CrossRef]
- Lin, K.Y.A.; Park, A.H.A. Effects of Bonding Types and Functional Groups on CO2 Capture using Novel Multiphase Systems of Liquid-like Nanoparticle Organic Hybrid Materials. Environ. Sci. Technol. 2011, 45, 6633–6639. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Decatur, J.; Lin, K.Y.A.; Park, A.H.A. Investigation of CO2 capture mechanisms of liquid-like nanoparticle organic hybrid materials via structural characterization. Phys. Chem. Chem. Phys. 2011, 13, 18115–18122. [Google Scholar] [CrossRef] [Green Version]
- Lin, K.Y.A.; Petit, C.; Park, A.H.A. Effect of SO2 on CO2 Capture Using Liquid-like Nanoparticle Organic Hybrid Materials. Energy Fuels 2013, 27, 4167–4174. [Google Scholar] [CrossRef]
- Wang, J.; Fang, W.; Luo, J.; Gao, M.; Wan, Y.; Zhang, S.; Zhang, X.; Park, A.H.A. Selective separation of CO2 using novel mixed matrix membranes based on Pebax and liquid-like nanoparticle organic hybrid materials. J. Membr. Sci. 2019, 584, 79–88. [Google Scholar] [CrossRef]
- Wang, D.; Song, S.; Zhang, W.; He, Z.; Wang, Y.; Zheng, Y.; Yao, D.; Pan, Y.; Yang, Z.; Meng, Z.; et al. CO2 selective separation of Pebax-based mixed matrix membranes (MMMs) accelerated by silica nanoparticle organic hybrid materials (NOHMs). Sep. Purif. Technol. 2020, 241, 116708. [Google Scholar] [CrossRef]
- Qiu, H.Y.; Liu, H.J.; Liu, X.L.; Yao, H. Synthesis of novel Al2O3 nanoparticle organic hybrid materials for enhancing the CO2-separation performance of prepared Al2O3-NOHMs/Pebax mixed matrix membrane. Mater. Lett. 2022, 325, 132854. [Google Scholar] [CrossRef]
- Agrawal, A.; Wenning, B.M.; Choudhury, S.; Archer, L.A. Interactions, structure, and dynamics of polymer-tethered nanoparticle blends. Langmuir 2016, 32, 8698–8708. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Moon, S.; Park, Y. Spectroscopic Investigation of Entropic Canopy–Canopy Interactions of Nanoparticle Organic Hybrid Materials. Langmuir 2020, 36, 9626–9633. [Google Scholar] [CrossRef] [PubMed]
- Haque, M.A.; Feric, T.G.; Hamilton, S.T.; Park, A.H.A.; Dadmun, M.D. Structure and Dispersion of Free and Grafted Polymer in Nanoparticle Organic Hybrid Materials-Based Solutions by Small-Angle Neutron Scattering. J. Phys. Chem. C 2021, 125, 5327–5334. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G.S. Structure of a grafted polymer brush—A molecular-dynamics simulation. Macromolecules 1989, 22, 4054–4059. [Google Scholar] [CrossRef]
- Dimitrov, D.I.; Milchev, A.; Binder, K. Polymer brushes in solvents of variable quality: Molecular dynamics simulations using explicit solvent. J. Chem. Phys. 2007, 127, 9. [Google Scholar] [CrossRef]
- Elliott, I.G.; Kuhl, T.L.; Faller, R. Compression of High Grafting Density Opposing Polymer Brushes Using Molecular Dynamics Simulations in Explicit Solvent. J. Phys. Chem. B 2013, 117, 4134–4141. [Google Scholar] [CrossRef]
- Desai, P.R.; Sinha, S.; Das, S. Compression of polymer brushes in the weak interpenetration regime: Scaling theory and molecular dynamics simulations. Soft Matter 2017, 13, 4159–4166. [Google Scholar] [CrossRef]
- Chang, Y.Y.; Yu, H.Y. Structural and Dynamical Coupling in Solvent-Free Polymer Brushes Elucidated by Molecular Dynamics Simulations. Langmuir 2021, 37, 3331–3345. [Google Scholar] [CrossRef]
- Adhikari, S.; Nikoubashman, A.; Leibler, L.; Rubinstein, M.; Midya, J.; Kumar, S.K. Gas Transport in Interacting Planar Brushes. ACS Polym. Au 2021, 1, 39–46. [Google Scholar] [CrossRef]
- Lai, P.Y.; Binder, K. Structure and dynamics of grafted polymer layers—A Monte-Carlo simulation. J. Chem. Phys. 1991, 95, 9288–9299. [Google Scholar] [CrossRef]
- Pepin, M.P.; Whitmore, M.D. Monte Carlo and numerical self-consistent field study of end-tethered polymers in good solvent. J. Chem. Phys. 1999, 111, 10381–10388. [Google Scholar] [CrossRef]
- Ohno, K.; Sakamoto, T.; Minagawa, T.; Okabe, Y. Entropy of polymer brushes in good solvents: A Monte Carlo study. Macromolecules 2007, 40, 723–730. [Google Scholar] [CrossRef]
- Halagan, K.; Banaszak, M.; Jung, J.; Polanowski, P.; Sikorski, A. Polymerization and Structure of Opposing Polymer Brushes Studied by Computer Simulations. Polymers 2021, 13, 4294. [Google Scholar] [CrossRef]
- Cheng, J.; Vishnyakov, A.; Neimark, A.V. Morphological Transformations in Polymer Brushes in Binary Mixtures: DPD Study. Langmuir 2014, 30, 12932–12940. [Google Scholar] [CrossRef] [PubMed]
- Doyle, P.S.; Shaqfeh, E.S.G.; Gast, A.P. Rheology of polymer brushes: A Brownian dynamics study. Macromolecules 1998, 31, 5474–5486. [Google Scholar] [CrossRef] [Green Version]
- Lo Verso, F.; Egorov, S.A.; Milchev, A.; Binder, K. Spherical polymer brushes under good solvent conditions: Molecular dynamics results compared to density functional theory. J. Chem. Phys. 2010, 133, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chremos, A.; Panagiotopoulos, A.Z.; Yu, H.Y.; Koch, D.L. Structure of solvent-free grafted nanoparticles: Molecular dynamics and density-functional theory. J. Chem. Phys. 2011, 135, 114901. [Google Scholar] [CrossRef]
- Xi, S.; Liu, J.; Valiya Parambathu, A.; Zhang, Y.; Chapman, W.G. An Efficient Algorithm for Molecular Density Functional Theory in Cylindrical Geometry: Application to Interfacial Statistical Associating Fluid Theory (iSAFT). Ind. Eng. Chem. Res. 2020, 59, 6716–6728. [Google Scholar] [CrossRef]
- Egorov, S.A. Interactions between Sterically Stabilized Nanoparticles: The Effects of Brush Bidispersity and Chain Stiffness. Polymers 2021, 13, 2296. [Google Scholar] [CrossRef]
- Wu, D.T.; Fredrickson, G.H.; Carton, J.P.; Ajdari, A.; Leibler, L. Distribution of chain ends at the surface of a polymer melt: Compensation effects and surface tension. J. Polym. Sci. Part B Polym. Phys. 1995, 33, 2373–2389. [Google Scholar] [CrossRef]
- Wu, D.T.; Fredrickson, G.H.; Carton, J. Surface segregation in conformationally asymmetric polymer blends: Incompressibility and boundary conditions. J. Chem. Phys. 1996, 104, 6387–6397. [Google Scholar] [CrossRef]
- Minnikanti, V.S.; Archer, L.A. Entropic Attraction of Polymers toward Surfaces and Its Relationship to Surface Tension. Macromolecules 2006, 39, 7718–7728. [Google Scholar] [CrossRef]
- Stein, G.E.; Laws, T.S.; Verduzco, R. Tailoring the Attraction of Polymers toward Surfaces. Macromolecules 2019, 52, 4787–4802. [Google Scholar] [CrossRef] [Green Version]
- Park, Y.; Shin, D.; Jang, Y.N.; Park, A.H.A. CO2 Capture Capacity and Swelling Measurements of Liquid-like Nanoparticle Organic Hybrid Materials via Attenuated Total Reflectance Fourier Transform Infrared Spectroscopy. J. Chem. Eng. Data 2012, 57, 40–45. [Google Scholar] [CrossRef]
- Smook, L.A.; Ritsema van Eck, G.C.; de Beer, S. Vapor sorption in binary polymer brushes: The effect of the polymer-polymer interface. J. Chem. Phys. 2021, 155, 10. [Google Scholar] [CrossRef]
- van Eck, G.C.R.; Veldscholte, L.B.; Nijkamp, J.; de Beer, S. Sorption Characteristics of Polymer Brushes in Equilibrium with Solvent Vapors. Macromolecules 2020, 53, 8428–8437. [Google Scholar] [CrossRef]
- Smook, L.A.; van Eck, G.C.R.; de Beer, S. Concentrating Vapor Traces with Binary Brushes of Immiscible Polymers. ACS Appl. Polym. Mater. 2021, 3, 2336–2340. [Google Scholar] [CrossRef]
- Smook, L.A.; van Eck, G.C.R.; de Beer, S. Friends, Foes, and Favorites: Relative Interactions Determine How Polymer Brushes Absorb Vapors of Binary Solvents. Macromolecules 2020, 53, 10898–10906. [Google Scholar] [CrossRef]
- Desai, P.R.; Das, S. Lubrication in polymer-brush bilayers in the weak interpenetration regime: Molecular dynamics simulations and scaling theories. Phys. Rev. E 2018, 98, 7. [Google Scholar] [CrossRef] [Green Version]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Chremos, A.; Panagiotopoulos, A.Z.; Koch, D.L. Dynamics of solvent-free grafted nanoparticles. J. Chem. Phys. 2012, 136, 044902. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Hong, B.B.; Chremos, A.; Panagiotopoulos, A.Z. Simulations of the structure and dynamics of nanoparticle-based ionic liquids. Faraday Discuss. 2012, 154, 29–40. [Google Scholar] [CrossRef]
- Chang, T.M.; Dang, L.X. Transfer of chloroform across the water-carbon tetrachloride liquid-liquid interface. J. Chem. Phys. 1998, 108, 818–819. [Google Scholar] [CrossRef]
- Smith, D.E.; Dang, L.X. Computer-simulations of NACL association in polarizable water. J. Chem. Phys. 1994, 100, 3757–3766. [Google Scholar] [CrossRef]
- Chang, T.M.; Dang, L.X.; Peterson, K.A. Computer simulation of chloroform with a polarizable potential model. J. Phys. Chem. B 1997, 101, 3413–3419. [Google Scholar] [CrossRef]
- Mattice, W.L.; Helfer, C.A.; Sokolov, A.P. On the Relationship between the Characteristic Ratio of a Finite Chain, Cn, and the Asymptotic Limit, C∞. Macromolecules 2003, 36, 9924–9928. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: New York, NY, USA, 2003; Volume 23. [Google Scholar]
- Grest, G.S.; Lacasse, M.D.; Kremer, K.; Gupta, A.M. Efficient continuum model for simulating polymer blends and copolymers. J. Chem. Phys. 1996, 105, 10583–10594. [Google Scholar] [CrossRef]
- Hill, T. An Introduction to Statistical Thermodynamics; Addison-Wesley Series in Chemistry; Dover Publications: Mineola, NY, USA, 1986. [Google Scholar]
- Yu, H.Y. Density-Functional Theories for Solvent-Free Nanoparticle-Organic Hybrid Materials. Ph.D Thesis, Cornell University, Ithaca, NY, USA, 2012. [Google Scholar]



| Brush ID | N | |
|---|---|---|
| A | 32 | 1.0 |
| B | 32 | 0.9 |
| C | 32 | 0.8 |
| D | 32 | 0.75 |
| E | 32 | 0.7 |
| F | 32 | 0.6 |
| G | 32 | 0.5 |
| H | 32 | 0.4 |
| I | 32 | 0.3 |
| J | 32 | 0.2 |
| M | 16 | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-J.; Yu, H.-Y. Enthalpic Interactions and Solution Behaviors of Solvent-Free Polymer Brushes. Polymers 2022, 14, 5237. https://doi.org/10.3390/polym14235237
Chen Y-J, Yu H-Y. Enthalpic Interactions and Solution Behaviors of Solvent-Free Polymer Brushes. Polymers. 2022; 14(23):5237. https://doi.org/10.3390/polym14235237
Chicago/Turabian StyleChen, Yi-Ju, and Hsiu-Yu Yu. 2022. "Enthalpic Interactions and Solution Behaviors of Solvent-Free Polymer Brushes" Polymers 14, no. 23: 5237. https://doi.org/10.3390/polym14235237
APA StyleChen, Y.-J., & Yu, H.-Y. (2022). Enthalpic Interactions and Solution Behaviors of Solvent-Free Polymer Brushes. Polymers, 14(23), 5237. https://doi.org/10.3390/polym14235237







