Numerical and Experimental Studies on the Improvement of Gas Chamber Structure during Gas-Assisted Extrusion
Abstract
:1. Introduction
2. Numerical Modelling and Methods
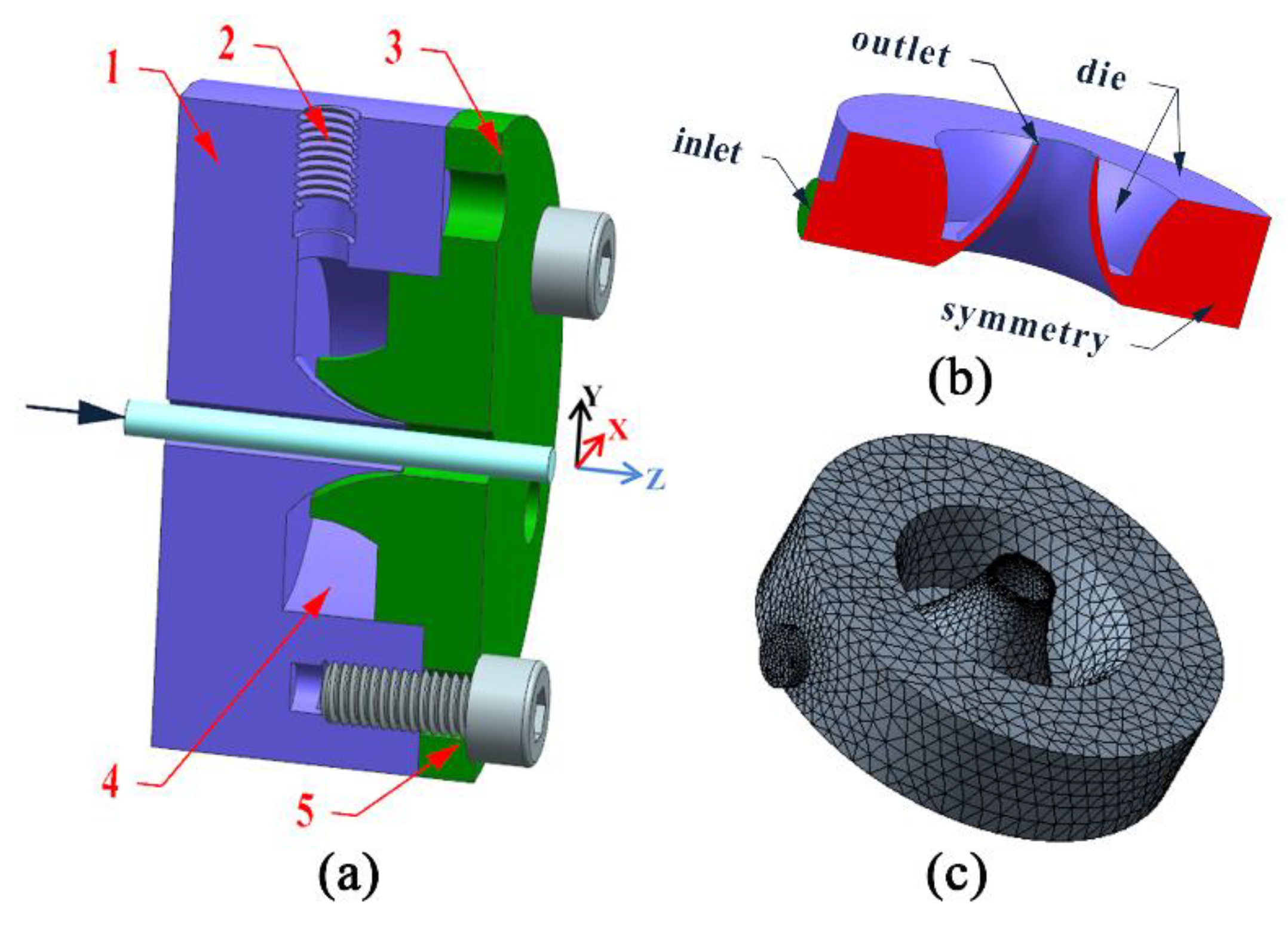
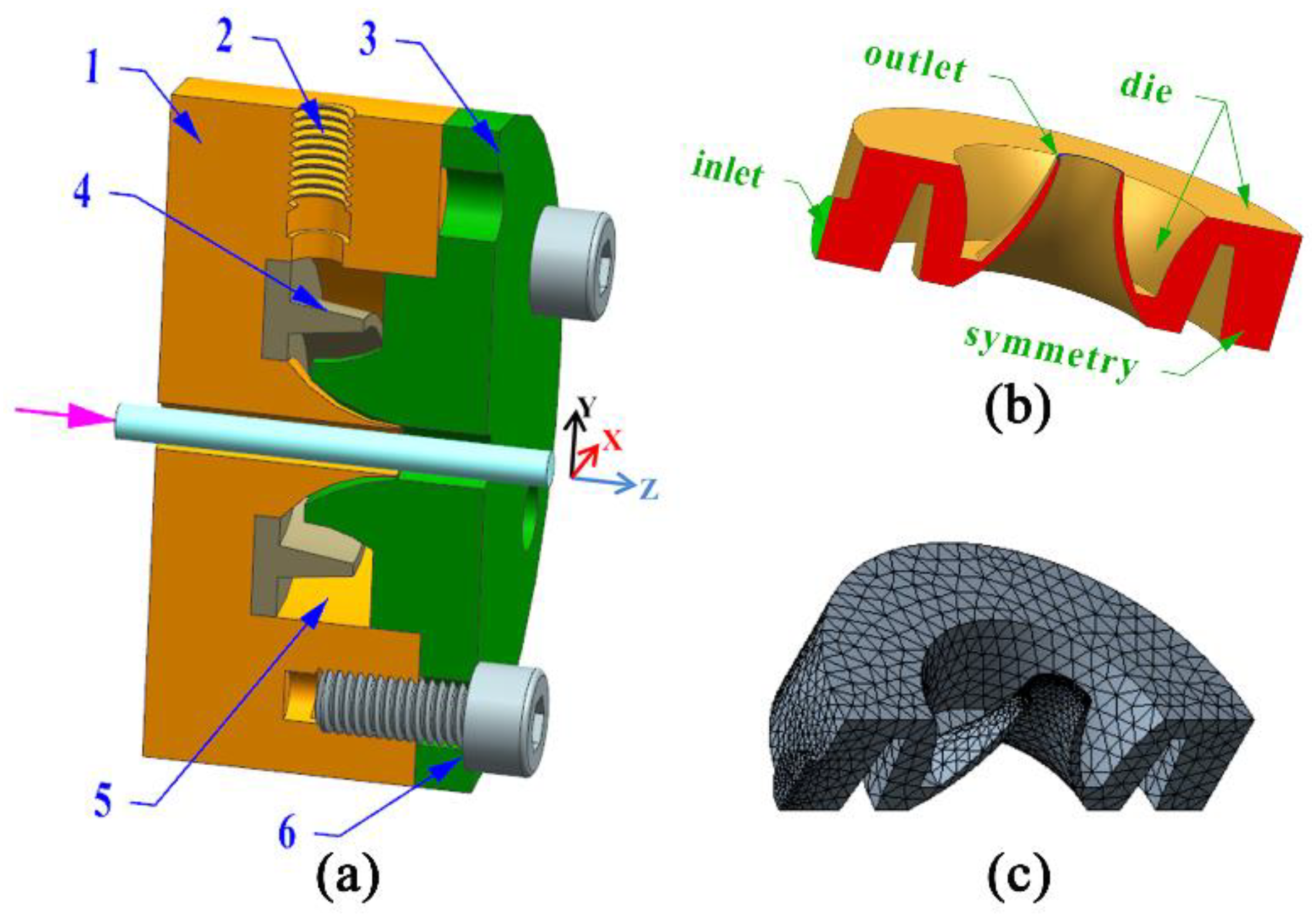
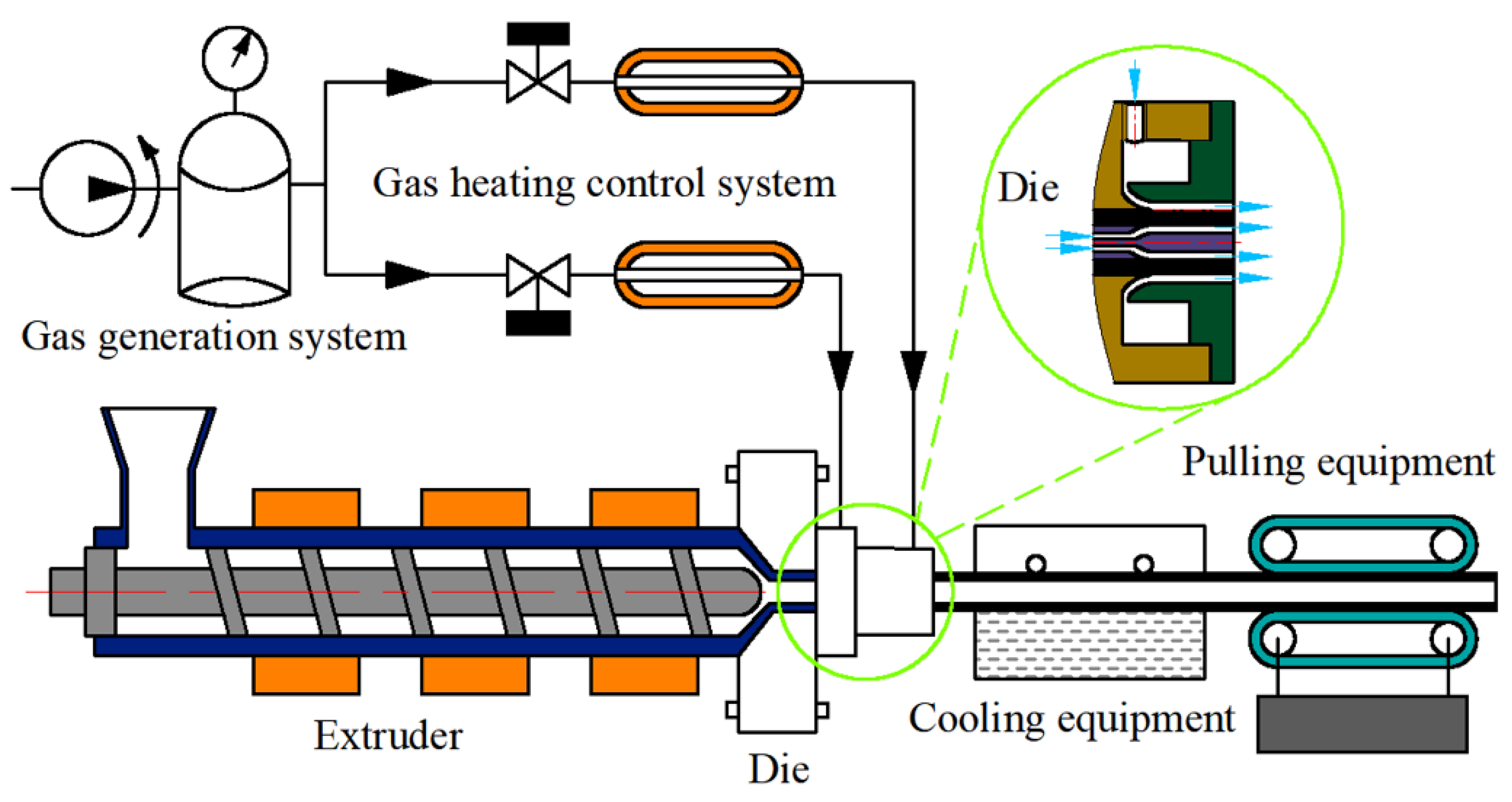
2.1. Geometric and Finite Element Models
2.2. Control Equations
2.3. Boundary Conditions
- (1)
- Gas inlet boundary: the inlet boundary is set as the velocity inlet boundary. The gas inlet velocities are set to 2, 4, 6 and 8 m/s, respectively. The temperature at the inlet boundary is set to 210 °C.
- (2)
- Wall boundary: the wall boundary is regarded as a non-slip, rigid, and static interface. The temperature is set to 210 °C.
- (3)
- Gas outlet boundary: During the gas-assisted extrusion process, the gas is distributed around the melt in a ring shape after flowing out of the gas outlet boundary, which forms a stable gas cushion layer. Therefore, the gas outlet boundary is set as the outflow boundary.
2.4. Numerical Methods
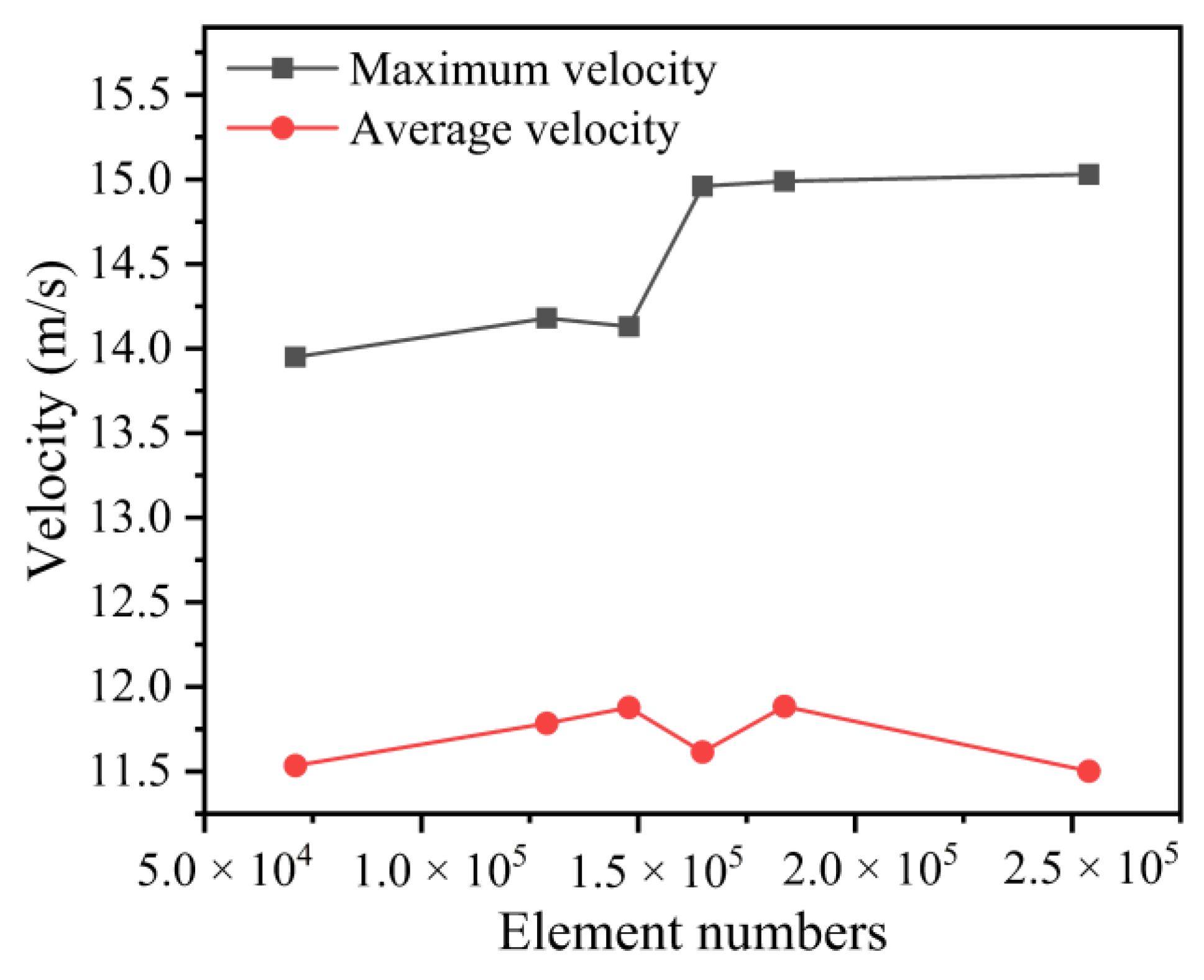
2.5. Evaluation Indicators
3. Simulation Results and Discussion
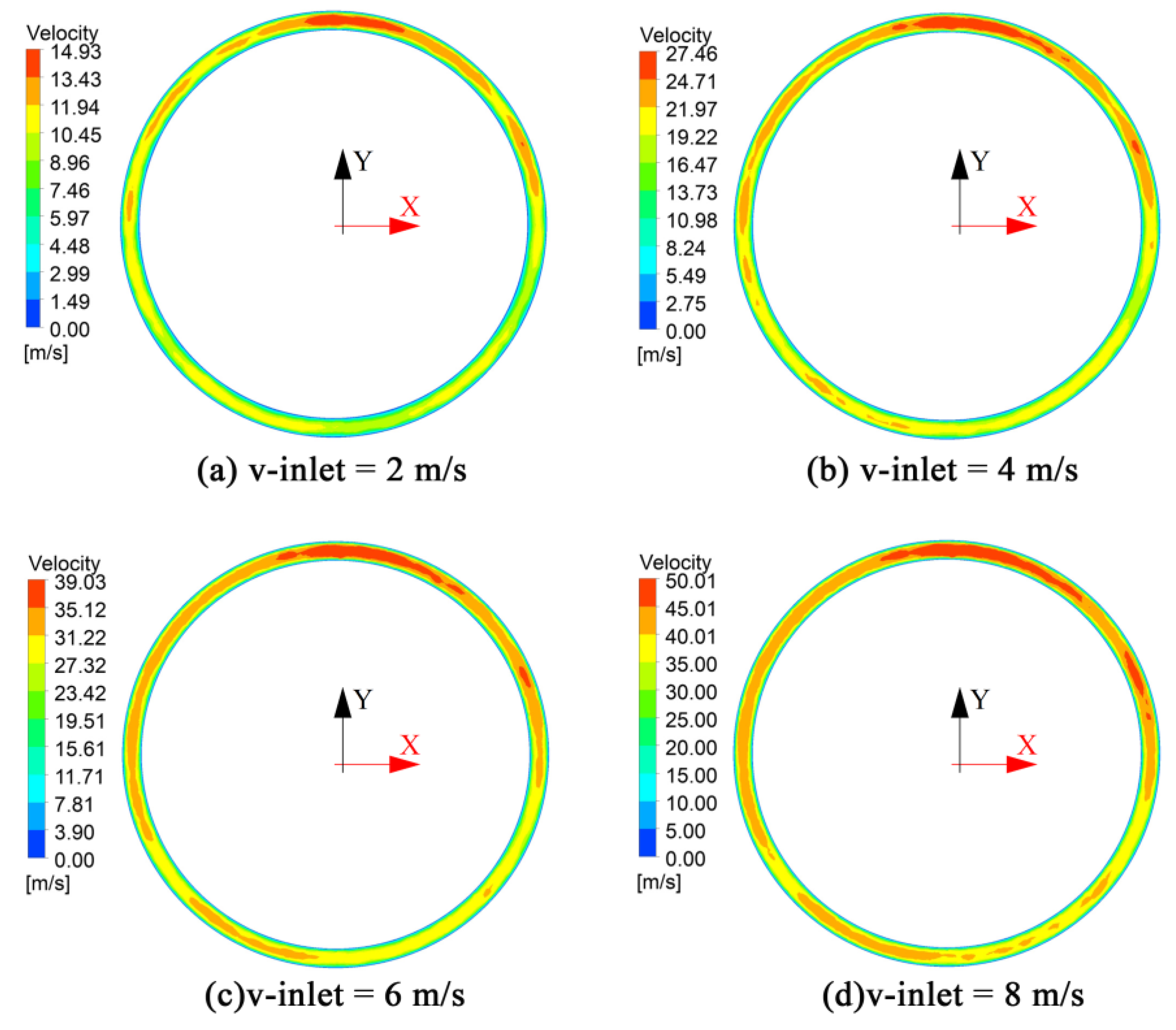
3.1. Results of Velocity Fields
3.2. Results of Velocity Unevenness Coefficient
4. Experimental Results and Discussion
5. Conclusions
- The numerical simulation of the gas flow field in the gas distribution chamber shows that the gas chamber structure has a great influence on the unevenness coefficient of the gas outlet velocity. The outlet gas flow field of the double gas chamber die is more uniform than that of the single gas chamber die. The outlet velocity unevenness coefficient can be reduced with the increase in the gas inlet flow rate. The outlet velocity unevenness coefficient is 3% higher for the single gas chamber die than for the double gas chamber die. When the gas inlet velocity increases from 2 to 8 m/s, the outlet velocity unevenness coefficient decreases by 4%.
- In the gas-assisted extrusion process of a plastic micro-tube, the flow field of the auxiliary gas has a great impact on the wall thickness uniformity of the plastic micro-tube. Using a double gas chamber die, the formation of a gas cushion layer is easier and more stable, which can improve the wall thickness uniformity of the plastic micro-tube.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cho, S.; Lee, E.; Jo, S.; Kim, G.M.; Kim, W. Extrusion Characteristics of Thin Walled Tubes for Catheters Using Thermoplastic Elastomer. Polymers 2020, 12, 1628. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.G.; Lamnawar, K.; Maazouz, A.; Maia, J.M. A nonlinear shear and elongation rheological study of interfacial failure in compatible bilayer systems. J. Rheol. 2016, 60, 1. [Google Scholar] [CrossRef]
- Liu, W.; Kim, W.; Park, J.M. Numerical Study on the Optimization of Polymer Extrusion Process for a Single-Lumen Micro Catheter. Trans. Korean Soc. Mech. Eng. A 2018, 42, 1059–1065. [Google Scholar] [CrossRef]
- Tseng, H.H. Software Design and Experimental Verification of Polymer Flow through a Pipe Extrusion Die. Ph.D. Thesis, University of Massachusetts Lowell, Lowell, MA, USA, 1991. [Google Scholar]
- Sahmel, O.; Siewert, S.; Arbeiter, D.; Kreiner, C.F.; Guthoff, R.; Schmitz, K.P.; Grabow, N. Extrusion as a manufacturing process for polymer micro-tubes for various bio-medical applications. Curr. Dir. Biomed. Eng. 2019, 5, 489–491. [Google Scholar] [CrossRef]
- Deng, X.Z.; Xiao, B.; Tang, G.; Yan, X.X.; Yu, S.F. Effect of shaping length on lolymer precision extrusion for Micro Tube. Plastics 2018, 47, 118–121. [Google Scholar]
- Luo, X.L.; Mitsoulis, E. Memory phenomena in extrudate swell simulations for annular dies. J. Rheol. 1989, 33, 1307–1327. [Google Scholar] [CrossRef]
- Kim, J.H.; Lyu, M.Y. Predictions of flow behaviors and entrance pressure drop characteristics of a rubber compound in a capillary die using various rheological models. Polym. Eng. Sci. 2014, 54, 2441–2448. [Google Scholar] [CrossRef]
- Chien, R.D.; Jong, W.R.; Chen, S.C. Study on rheological behavior of polymer melt flowing through micro-channels considering the wall-slip effect. J. Micromech. Microeng. 2005, 15, 1389. [Google Scholar] [CrossRef]
- Wang, M.J.; Tian, H.Q.; Zhao, D.Y. Micro-scale shear viscosity testing approach and viscosity model of polymer melts. Chin. J. Mech. Eng. 2012, 48, 21–29. [Google Scholar] [CrossRef]
- Fernandes, C.; Fakhari, A.; Tukovic, Z. Non-Isothermal Free-Surface Viscous Flow of Polymer Melts in Pipe Extrusion Using an Open-Source Interface Tracking Finite Volume Method. Polymers 2021, 13, 4454. [Google Scholar] [CrossRef]
- Sombatsompop, N.; O-Charoen, N. Extrudate swell behavior of PS and LLDPE melts in a dual die with mixed circular/slit flow channels in an extrusion rheometer. Polym. Adv. Technol. 2003, 14, 699–710. [Google Scholar] [CrossRef]
- Tang, D.; Fang, W.L.; Fan, X.H.; Li, D.Y.; Peng, Y.H. Effect of die design in microchannel tube extrusion. Procedia Eng. 2014, 81, 628–633. [Google Scholar] [CrossRef] [Green Version]
- Jin, G.B.; Zhao, D.Y.; Wang, M.J.; Jin, Y.F.; Tian, H.Q.; Zhang, J. Study on design and experiments of extrusion die for polypropylene single-lumen micro tubes. Microsyst. Technol. 2015, 21, 2495–2503. [Google Scholar] [CrossRef]
- Nithi-Uthai, N.; Manas-Zloczower, I. Numerical Simulation of Sharkskin Phenomena in Polymer Melts. Appl. Rheol. 2003, 13, 79–86. [Google Scholar] [CrossRef]
- Zhou, H.B.; Fan, H.H.; Zhai, Y.H.; Peng, Q. A new utility calculation model for axial flow of non-Newtonian fluid in concentric annuli. Can. J. Chem. Eng. 2014, 92, 945–952. [Google Scholar] [CrossRef]
- Mu, Y.; Zhao, G.Q.; Wu, X.G.; Zhai, J.Q. Finite-Element Simulation of Polymer Flow and Extrudate Swell Through Hollow Profile Extrusion Die with the Multimode Differential Viscoelastic Model. Adv. Polym. Technol. 2013, 32, E1–E19. [Google Scholar] [CrossRef]
- Baldi, F.; Briatico-Vangosa, F.; Franceschini, A. Experimental study of the melt fracture behavior of filled high-density polyethylene melts. Polym. Eng. Sci. 2014, 54, 364–377. [Google Scholar] [CrossRef]
- Xu, X.M.; Zhao, G.Q.; Qin, S.X.; Wang, W.W. Numerical Simulation of Viscoelastic Extrudate Swell Through Elliptical Ring Die. Chin. J. Chem. Eng. 2011, 19, 10–17. [Google Scholar] [CrossRef]
- Luo, C.; Huang, X.Y.; Liu, T.K.; Liu, H.S. Research on Inner Gas Inflation Improvements in Double-layer Gas-assisted Extrusion of Micro-tubes. Polymers 2020, 12, 899. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.Y.; Liu, H.S.; Huang, X.Y.; Wan, Q.F.; Ren, Z. Numerical Simulation of Gas-assisted Extrusion Process of Microtube. China Plast. Ind. 2015, 43, 44–48. [Google Scholar] [CrossRef]
- Deng, X.Z.; Xiao, B.; Ren, Z. Research progress of polymer gas—Assisted extrusion. Polym. Mater. Sci. Eng. 2022, 38, 151–158. [Google Scholar] [CrossRef]
- Yin, H.N.; Huang, X.Y.; Liu, T.K.; Song, M.J. Effects of gas-assisted extrusion on slip in the cable coating process. J. Polym. Eng. 2021, 41, 329–337. [Google Scholar] [CrossRef]
- Liang, R.F.; Mackley, M.R. The gas-assisted extrusion of molten polyethylene. J. Rheol. 2001, 45, 211–226. [Google Scholar] [CrossRef] [Green Version]
- Ren, Z.; Huang, X.Y.; Liu, H.S.; Deng, X.Z.; He, J.T. Numerical and experimental studies for gas assisted extrusion forming of molten polypropylene. J. Appl. Polym. Sci. 2015, 132, 1–13. [Google Scholar] [CrossRef]
- Ren, Z.; Huang, X.Y.; Liu, H.S.; Deng, X.Z.; He, J.T. Non-isothermal viscoelastic numerical analysis of compressible gas-assisted polymer extrusion molding. CIESC J. 2015, 66, 1615–1623. [Google Scholar] [CrossRef]
- Ren, Z.; Huang, X.Y.; Xiong, Z.H. Experimental and numerical studies for the gas-assisted extrusion forming of polypropylene micro-tube. Int. J. Mater. Form. 2020, 13, 235–256. [Google Scholar] [CrossRef]
- Liu, T.K.; Huang, X.Y.; Ren, Z.; Luo, C.; Tan, J.M. Analysis of Superimposed Influence of Double Layer Gas Flow on Gas-Assisted Extrusion of Plastic Micro-Tube. Int. Polym. Process. 2020, 35, 158–168. [Google Scholar] [CrossRef]
- Yin, H.N.; Huang, X.Y.; Liu, H.S.; Liu, T.K.; Luo, C.; Wang, D.Y. Viscoelastic numerical simulation of gas-assisted extrusion of cable cladding. Polym. Mater. Sci. Eng. 2021, 37, 114–122. [Google Scholar] [CrossRef]
- Liu, T.K.; Huang, X.Y.; Luo, C.; Wang, D.Y. The Formation Mechanism of the Double Gas Layer in Gas-Assisted Extrusion and Its Influence on Plastic Micro-Tube Formation. Polymers 2020, 12, 355. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.; Jiang, G.J.; Wu, X.Y.; Wang, Y.P.; Fang, H.S.; Shentu, B.Q. Air Recirculation and Its Effect on Microfiber Spinning in Blunt-Die Melt Blowing. Fiber. Polym. 2021, 22, 703–710. [Google Scholar] [CrossRef]
- Hassan, M.A.; Anantharamaiah, N.; Khan, S.A.; Pourdeyhimi, B. Computational Fluid Dynamics Simulations and Experiments of Meltblown Fibrous Media: New Die Designs to Enhance Fiber Attenuation and Filtration Quality. Ind. Eng. Chem. Res. 2016, 55, 2049–2058. [Google Scholar] [CrossRef]
- Shang, S.S.; Yu, C.W.; Li, M.L. Numerical simulation of swirling airflow dynamics in vortex spinning. Text. Res. J. 2017, 88, 833–843. [Google Scholar] [CrossRef]
- Xie, S.; Jiang, G.J.; Ye, B.L.; Shentu, B.Q. Particle Image Velocimetry (PIV) Investigation of the Turbulent Airflow in Slot-Die Melt Blowing. Polymers 2020, 12, 279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krutka, H.M.; Shambaugh, R.L.; Papavassiliou, D.V. Effects of Die Geometry on the Flow Field of the Melt-Blowing Process. Ind. Eng. Chem. Res. 2003, 42, 5541–5553. [Google Scholar] [CrossRef]
- Li, H.L.; Wang, C.; Hu, J.; Yu, H.M.; Li, Q.D.; Zhang, X.Y. Simulation and Optimum Design on Airflow Distribution Chamber of Pneumatic Forming Machine for Rice Seeding-growing Tray. Trans. Chin. Soc. Agric. Mach. 2018, 49, 94–101. [Google Scholar] [CrossRef]
- Liu, B.; Huang, X.Y.; Ren, S.Y.; Luo, C. Effect of Pressure Difference between Inner and Outer Gas Layer on Micro-Tube Deformation during Gas-Assisted Extrusion. Polymers 2022, 14, 3559. [Google Scholar] [CrossRef]
- Ren, Z.; Huang, X.Y. Effect of gas flow rate on the double gas-assisted extrusion forming of plastic pipes. IOP Conf. Ser. Earth Environ. Sci. 2019, 267, 042059. [Google Scholar] [CrossRef]
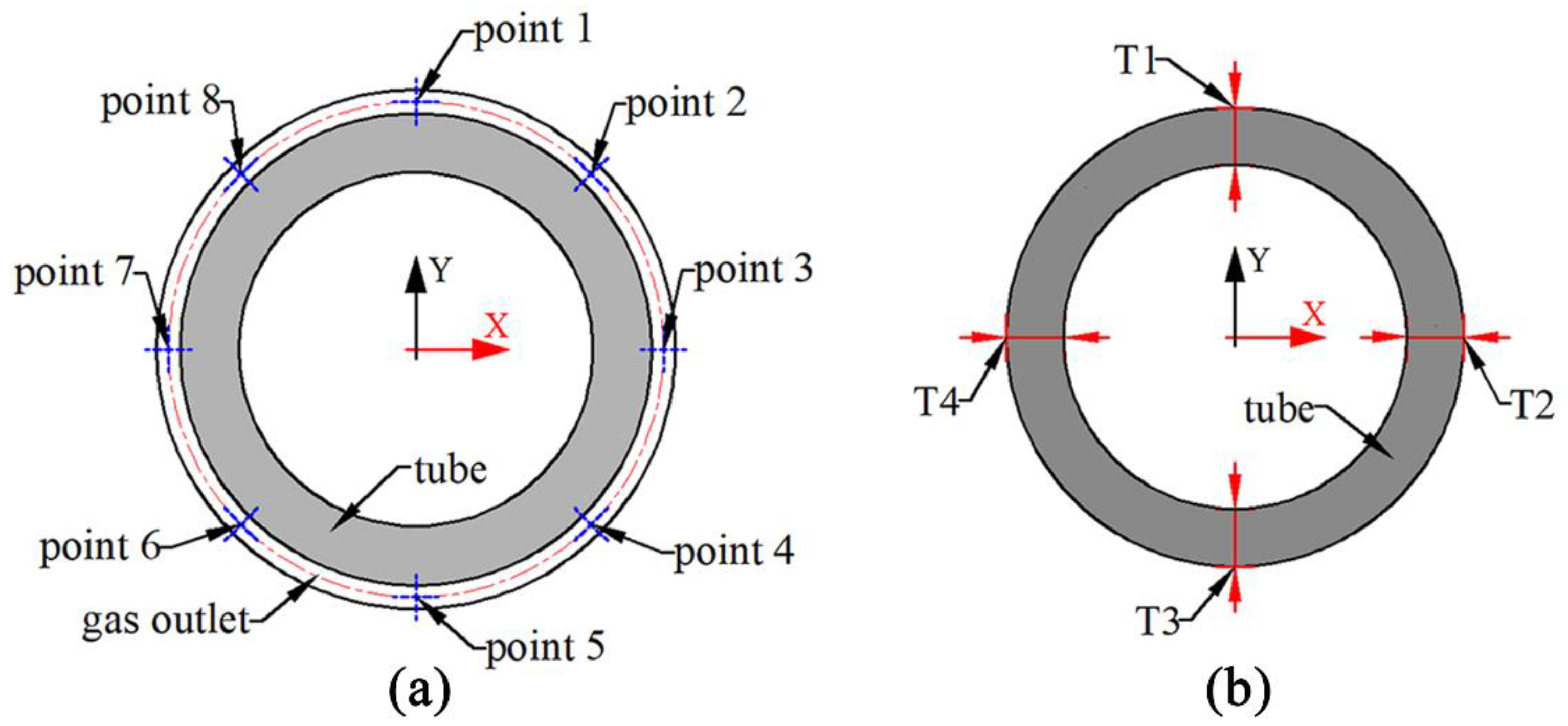

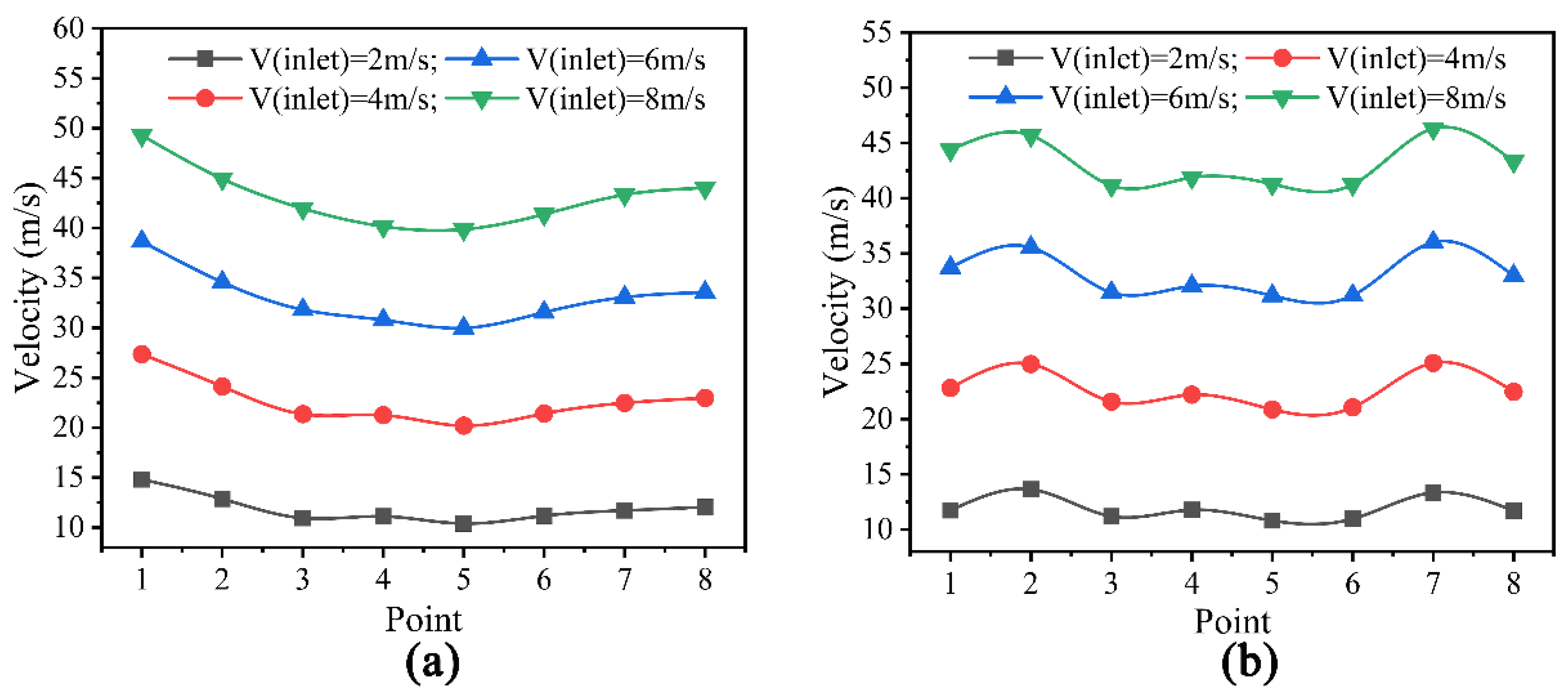




| Calibration Point | Point 1 | Point 2 | Point 3 | Point 4 | Point 5 | Point 6 | Point 7 | Point 8 |
|---|---|---|---|---|---|---|---|---|
| X (mm) | 0 | 1.4849 | 2.1 | 1.4849 | 0 | −1.4849 | −2.1 | −1.4849 |
| Y (mm) | 2.1 | 1.4849 | 0 | −1.4849 | −2.1 | −1.4849 | 0 | 1.4849 |
| Experiment Conditions | Gas-Assisted Extrusion | Non-Gas-Assisted Extrusion |
|---|---|---|
| Gas inlet volume flow rate (m3/s) | 3 × 10−5, 6 × 10−5 | / |
| Temperature of the die (°C) | 215 | 215 |
| Extruder speed (r/min) | 5 | 5 |
| Temperature of the gas (°C) | 210 | / |
| Pulling speed (r/min) | 4 | 4 |
| Temperature of the melt (°C) | 215 | 215 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Huang, X.; Zhang, X.; Ren, S.; Lan, Q.; Luo, C. Numerical and Experimental Studies on the Improvement of Gas Chamber Structure during Gas-Assisted Extrusion. Polymers 2022, 14, 5272. https://doi.org/10.3390/polym14235272
Liu B, Huang X, Zhang X, Ren S, Lan Q, Luo C. Numerical and Experimental Studies on the Improvement of Gas Chamber Structure during Gas-Assisted Extrusion. Polymers. 2022; 14(23):5272. https://doi.org/10.3390/polym14235272
Chicago/Turabian StyleLiu, Bin, Xingyuan Huang, Xiaohui Zhang, Shaoyi Ren, Qiang Lan, and Cheng Luo. 2022. "Numerical and Experimental Studies on the Improvement of Gas Chamber Structure during Gas-Assisted Extrusion" Polymers 14, no. 23: 5272. https://doi.org/10.3390/polym14235272
APA StyleLiu, B., Huang, X., Zhang, X., Ren, S., Lan, Q., & Luo, C. (2022). Numerical and Experimental Studies on the Improvement of Gas Chamber Structure during Gas-Assisted Extrusion. Polymers, 14(23), 5272. https://doi.org/10.3390/polym14235272






