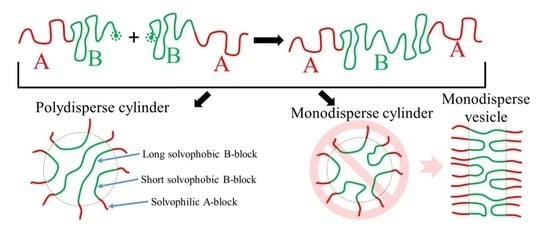
Phase Diagrams of Polymerization-Induced Self-Assembly Are Largely Determined by Polymer Recombination
Abstract
1. Introduction
2. Methods
3. Results and Discussion
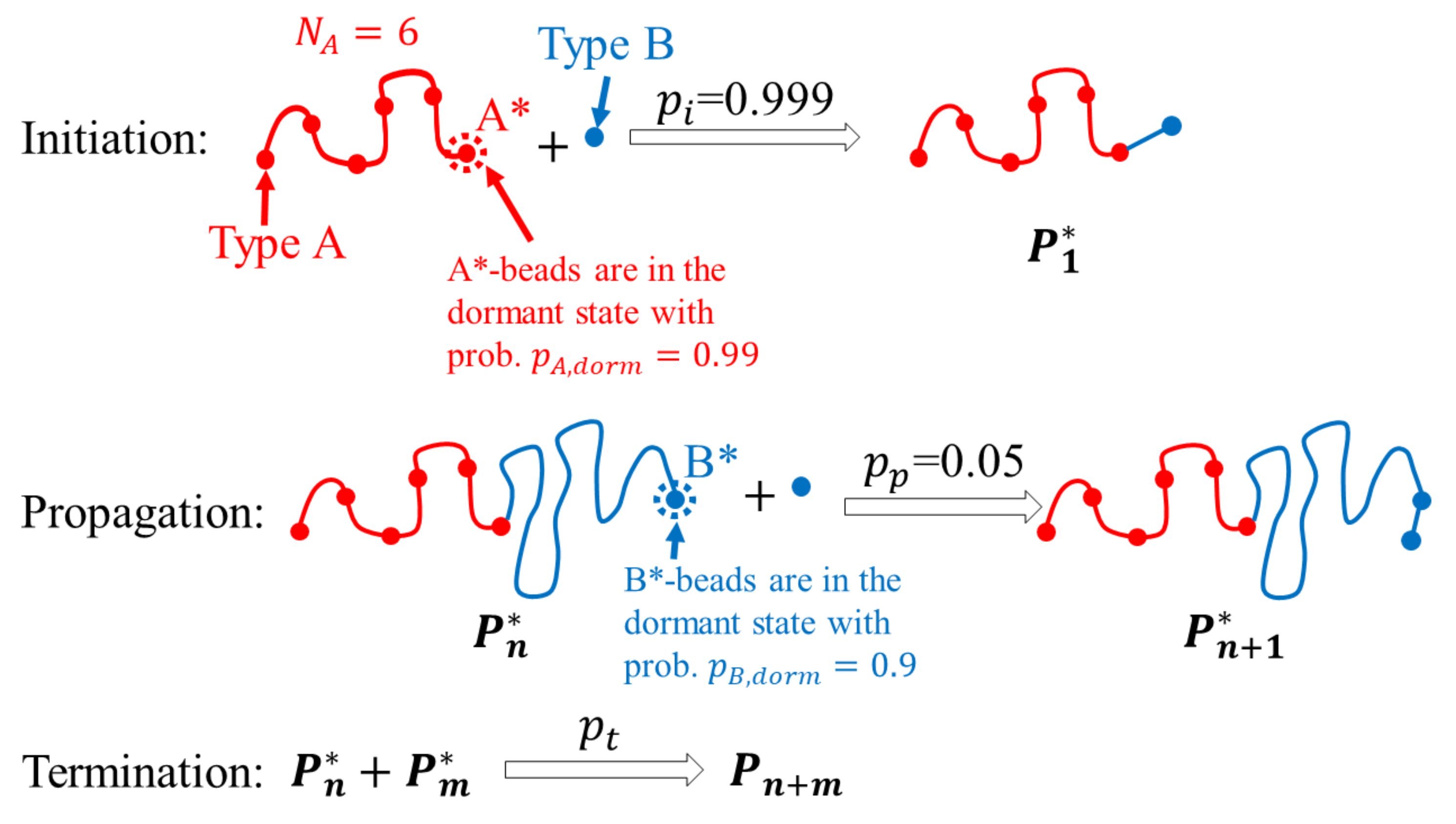
3.1. ATRP without Recombination
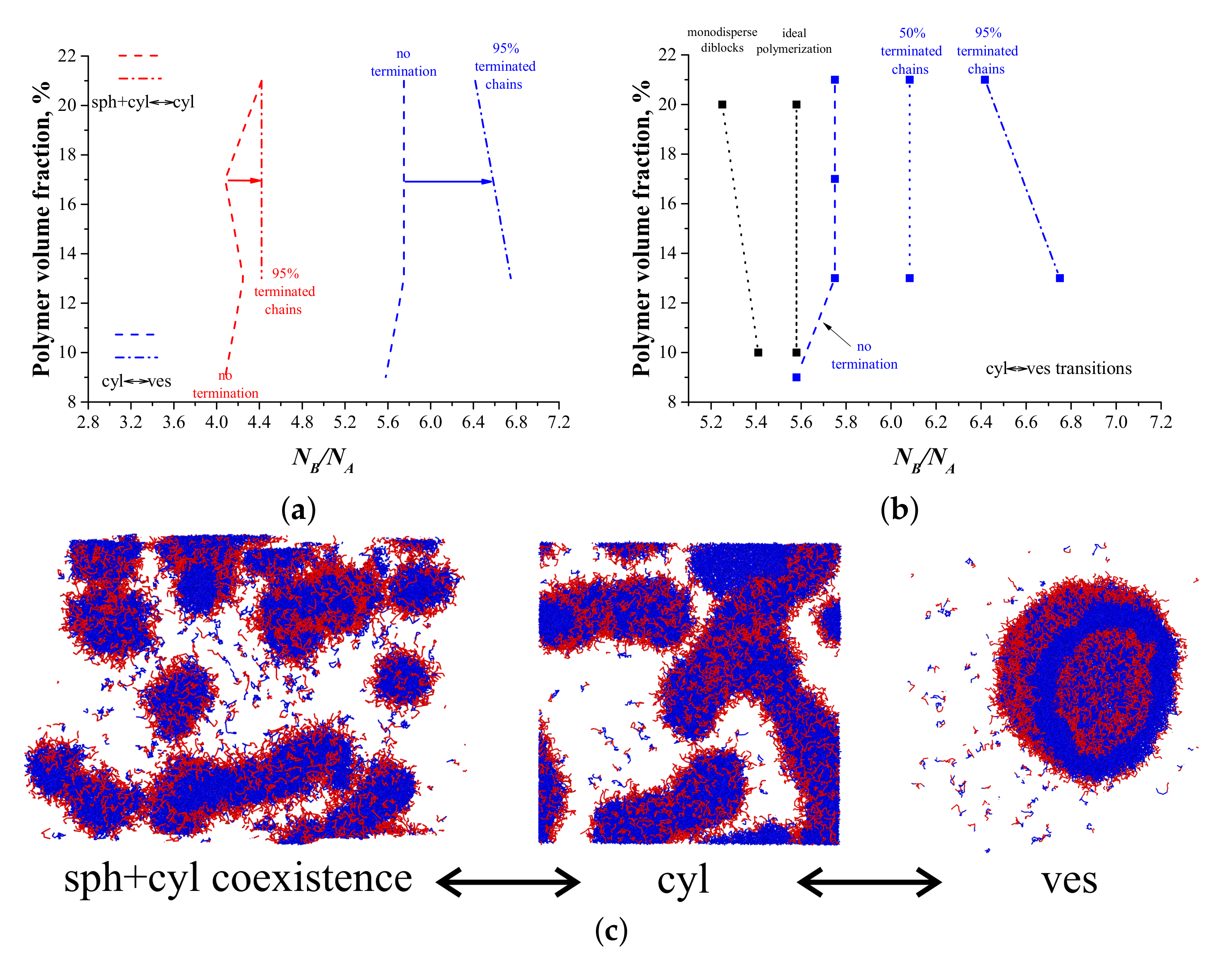
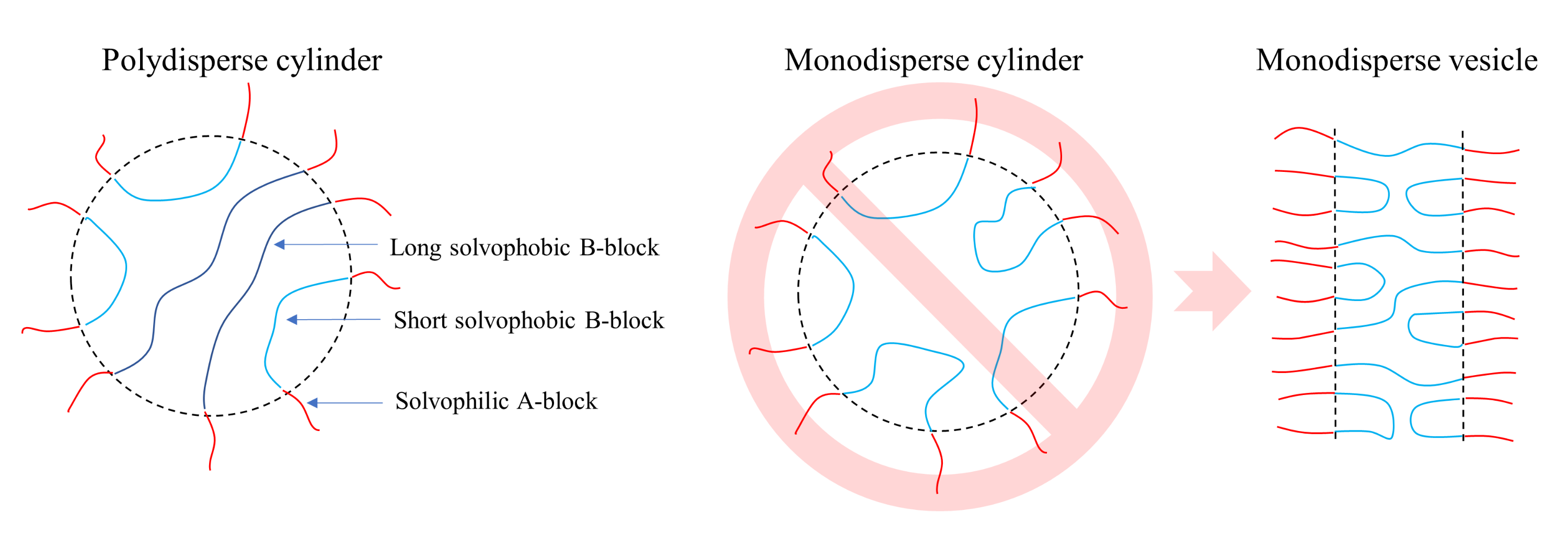
3.2. ATRP with Recombination
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mai, Y.; Eisenberg, A. Self-assembly of block copolymers. Chem. Soc. Rev. 2012, 41, 5969–5985. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Tan, Y.; Chen, Y.; Zhang, L.; Tan, J. Expanding the Scope of Polymerization-Induced Self-Assembly: Recent Advances and New Horizons. Macromol. Rapid Commun. 2021, 42, 2100498. [Google Scholar] [CrossRef] [PubMed]
- Blanazs, A.; Madsen, J.; Battaglia, G.; Ryan, A.J.; Armes, S.P. Mechanistic insights for block copolymer morphologies: How do worms form vesicles? J. Am. Chem. Soc. 2011, 133, 16581–16587. [Google Scholar] [CrossRef]
- Tritschler, U.; Pearce, S.; Gwyther, J.; Whittell, G.R.; Manners, I. 50th anniversary perspective: Functional nanoparticles from the solution self-assembly of block copolymers. Macromolecules 2017, 50, 3439–3463. [Google Scholar] [CrossRef]
- Sugihara, S.; Blanazs, A.; Armes, S.P.; Ryan, A.J.; Lewis, A.L. Aqueous dispersion polymerization: A new paradigm for in situ block copolymer self-assembly in concentrated solution. J. Am. Chem. Soc. 2011, 133, 15707–15713. [Google Scholar] [CrossRef]
- Warren, N.J.; Mykhaylyk, O.O.; Mahmood, D.; Ryan, A.J.; Armes, S.P. RAFT aqueous dispersion polymerization yields poly (ethylene glycol)-based diblock copolymer nano-objects with predictable single phase morphologies. J. Am. Chem. Soc. 2014, 136, 1023–1033. [Google Scholar] [CrossRef]
- Wan, W.M.; Pan, C.Y. Atom transfer radical dispersion polymerization in an ethanol/water mixture. Macromolecules 2007, 40, 8897–8905. [Google Scholar] [CrossRef]
- Wang, G.; Schmitt, M.; Wang, Z.; Lee, B.; Pan, X.; Fu, L.; Yan, J.; Li, S.; Xie, G.; Bockstaller, M.R.; et al. Polymerization-induced self-assembly (PISA) using ICAR ATRP at low catalyst concentration. Macromolecules 2016, 49, 8605–8615. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Zhang, W. Synthesis of diblock copolymer nano-assemblies by PISA under dispersion polymerization: Comparison between ATRP and RAFT. Polym. Chem. 2017, 8, 6407–6415. [Google Scholar] [CrossRef]
- Groison, E.; Brusseau, S.; D’Agosto, F.; Magnet, S.; Inoubli, R.; Couvreur, L.; Charleux, B. Well-defined amphiphilic block copolymer nanoobjects via nitroxide-mediated emulsion polymerization. ACS Macro Lett. 2012, 1, 47–51. [Google Scholar] [CrossRef] [PubMed]
- Qiao, X.; Lansalot, M.; Bourgeat-Lami, E.; Charleux, B. Nitroxide-Mediated Polymerization-Induced Self-Assembly of Poly (poly (ethylene oxide) methyl ether methacrylate-co-styrene)-b-poly (n-butyl methacrylate-co-styrene) Amphiphilic Block Copolymers. Macromolecules 2013, 46, 4285–4295. [Google Scholar] [CrossRef]
- Qiao, X.; Dugas, P.Y.; Charleux, B.; Lansalot, M.; Bourgeat-Lami, E. Nitroxide-mediated polymerization-induced self-assembly of amphiphilic block copolymers with a pH/temperature dual sensitive stabilizer block. Polym. Chem. 2017, 8, 4014–4029. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Chertovich, A.V. Simulation of the RAFT polymerization in 3D: Steric restrictions and incompatibility between species. Polym. Chem. 2022, 13, 2143–2154. [Google Scholar] [CrossRef]
- Cai, D.; Li, J.; Ma, Z.; Gan, Z.; Shao, Y.; Xing, Q.; Tan, R.; Dong, X.H. Effect of Molecular Architecture and Symmetry on Self-Assembly: A Quantitative Revisit Using Discrete ABA Triblock Copolymers. ACS Macro Lett. 2022, 11, 555–561. [Google Scholar] [CrossRef]
- Huo, M.; Xu, Z.; Zeng, M.; Chen, P.; Liu, L.; Yan, L.T.; Wei, Y.; Yuan, J. Controlling vesicular size via topological engineering of amphiphilic polymer in polymerization-induced self-assembly. Macromolecules 2017, 50, 9750–9759. [Google Scholar] [CrossRef]
- Terreau, O.; Luo, L.; Eisenberg, A. Effect of poly (acrylic acid) block length distribution on polystyrene-b-poly (acrylic acid) aggregates in solution. 1. Vesicles. Langmuir 2003, 19, 5601–5607. [Google Scholar] [CrossRef]
- Terreau, O.; Bartels, C.; Eisenberg, A. Effect of poly (acrylic acid) block length distribution on polystyrene-b-poly (acrylic acid) block copolymer aggregates in solution. 2. A partial phase diagram. Langmuir 2004, 20, 637–645. [Google Scholar] [CrossRef]
- Gao, Z.; Eisenberg, A. A model of micellization for block copolymers in solutions. Macromolecules 1993, 26, 7353–7360. [Google Scholar] [CrossRef]
- Linse, P. Micellization of poly (ethylene oxide)-poly (propylene oxide) block copolymers in aqueous solution: Effect of polymer polydispersity. Macromolecules 1994, 27, 6404–6417. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, T.; Ye, F.; Liang, H.; Shi, A.C. Effect of polydispersity on the formation of vesicles from amphiphilic diblock copolymers. Macromolecules 2005, 38, 6710–6717. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Shupanov, R.M.; Chertovich, A.V. Phase Diagram for Ideal Diblock-Copolymer Micelles Compared to Polymerization-Induced Self Assembly. Polymers 2020, 12, 2599. [Google Scholar] [CrossRef]
- Huang, F.; Lv, Y.; Wang, L.; Xu, P.; Lin, J.; Lin, S. An insight into polymerization-induced self-assembly by dissipative particle dynamics simulation. Soft Matter 2016, 12, 6422–6429. [Google Scholar] [CrossRef]
- Yan, Y.D.; Xue, Y.H.; Zhao, H.Y.; Liu, H.; Lu, Z.Y.; Gu, F.L. Insight into the Polymerization-Induced Self-Assembly via a Realistic Computer Simulation Strategy. Macromolecules 2019, 52, 6169–6180. [Google Scholar] [CrossRef]
- Wang, J.; Fang, T.; Li, J.; Yan, Y.; Li, Z.; Zhang, J. Precise Mesoscopic Model Providing Insights into Polymerization-Induced Self-Assembly. Langmuir 2020, 36, 8009–8016. [Google Scholar] [CrossRef] [PubMed]
- Lv, Y.; Wang, L.; Liu, F.; Feng, W.; Wei, J.; Lin, S. Rod–coil block copolymer aggregates via polymerization-induced self-assembly. Soft Matter 2020, 16, 3466–3475. [Google Scholar] [CrossRef] [PubMed]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. Europhys. Lett. (EPL) 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Koelman, J.M.V.A.; Hoogerbrugge, P.J. Dynamic Simulations of Hard-Sphere Suspensions Under Steady Shear. Europhys. Lett. (EPL) 1993, 21, 363–368. [Google Scholar] [CrossRef]
- Schlijper, A.G.; Hoogerbrugge, P.J.; Manke, C.W. Computer simulation of dilute polymer solutions with the dissipative particle dynamics method. J. Rheol. 1995, 39, 567–579. [Google Scholar] [CrossRef]
- Español, P.; Warren, P. Statistical Mechanics of Dissipative Particle Dynamics. Europhys. Lett. (EPL) 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Blanazs, A.; Ryan, A.; Armes, S. Predictive phase diagrams for RAFT aqueous dispersion polymerization: Effect of block copolymer composition, molecular weight, and copolymer concentration. Macromolecules 2012, 45, 5099–5107. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Chertovich, A.V. Copolymerization of partly incompatible monomers: An insight from computer simulations. Macromolecules 2017, 50, 4677–4685. [Google Scholar] [CrossRef]
- Tan, J.; Bai, Y.; Zhang, X.; Zhang, L. Room temperature synthesis of poly (poly (ethylene glycol) methyl ether methacrylate)-based diblock copolymer nano-objects via Photoinitiated Polymerization-Induced Self-Assembly (Photo-PISA). Polym. Chem. 2016, 7, 2372–2380. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Z.; Lee, B.; Yuan, R.; Lu, Z.; Yan, J.; Pan, X.; Song, Y.; Bockstaller, M.R.; Matyjaszewski, K. Polymerization-induced self-assembly of acrylonitrile via ICAR ATRP. Polymer 2017, 129, 57–67. [Google Scholar] [CrossRef]
- Zhao, D.; Ma, Y.; Wang, E.; Lodge, T.P. Micellization of Binary Diblock Co-polymer Mixtures in an Ionic Liquid. Macromolecules 2019, 52, 4729–4738. [Google Scholar] [CrossRef]
- Wang, Y.; Han, G.; Duan, W.; Zhang, W. ICAR ATRP in PEG with Low Concentration of Cu (II) Catalyst: A Versatile Method for Synthesis of Block Copolymer Nanoassemblies under Dispersion Polymerization. Macromol. Rapid Commun. 2019, 40, 1800140. [Google Scholar] [CrossRef]
- Genzer, J. In silico polymerization: Computer simulation of controlled radical polymerization in bulk and on flat surfaces. Macromolecules 2006, 39, 7157–7169. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrov, A.; Chertovich, A.V.; Gavrilov, A.A. Phase Diagrams of Polymerization-Induced Self-Assembly Are Largely Determined by Polymer Recombination. Polymers 2022, 14, 5331. https://doi.org/10.3390/polym14235331
Petrov A, Chertovich AV, Gavrilov AA. Phase Diagrams of Polymerization-Induced Self-Assembly Are Largely Determined by Polymer Recombination. Polymers. 2022; 14(23):5331. https://doi.org/10.3390/polym14235331
Chicago/Turabian StylePetrov, Artem, Alexander V. Chertovich, and Alexey A. Gavrilov. 2022. "Phase Diagrams of Polymerization-Induced Self-Assembly Are Largely Determined by Polymer Recombination" Polymers 14, no. 23: 5331. https://doi.org/10.3390/polym14235331
APA StylePetrov, A., Chertovich, A. V., & Gavrilov, A. A. (2022). Phase Diagrams of Polymerization-Induced Self-Assembly Are Largely Determined by Polymer Recombination. Polymers, 14(23), 5331. https://doi.org/10.3390/polym14235331